Abstract
This study examines the extent to which a Zernike-based optical correction can restore acuity in keratoconus as a function of disease severity and contrast level. Increasingly complete Zernike corrections in the presence of Zernike-fit error were simulated. Acuity for keratoconic eyes with <60 D maximum corneal power reached 20/13 with a fifth-order Zernike correction under high-contrast conditions and exhibited a loss of 0.1 logMAR (minimum angle of resolution) (from 20/32 to 20/40) for low-contrast conditions. Acuity for keratoconic eyes with >60 D maximum corneal power approached 20/13 with sixth-tenth-order corrections under high-contrast conditions but did not return to similar levels with a tenth-order correction for low-contrast conditions. The results suggest that fit error affects visual performance for more difficult tasks and that restoring high-contrast acuity (20/16 or better) using a fifth-order Zernike correction is not limited by Zernike-fit error for over 88% of keratoconus cases.
1. INTRODUCTION
Advances in wavefront-sensing techniques have provided the researcher and clinician with a quick, objective, non-invasive method of assessing the quality of the optics of the human eye.1 Wavefront-aberration data can be transformed to describe a variety of optical quality metrics related to visual performance.2-4 Currently, the Zernike expansion is the ANSI standard (ANSI Z80.28) fitting function for describing ocular wavefront error.5 This fitting procedure decomposes the measured three-dimensional wavefront error into a set of basis functions, each with a coefficient representing the component’s relative magnitude in the fitted function. The basis functions are ordered radially by increasing exponential powers and rotationally by sine and cosine functions of increasing angular frequency. The orientation of nonrotationally symmetric Zernike modes (such as coma and trefoil) is determined from the relative contribution of both the sine and cosine components.
Optical defects caused by the corneal disease keratoconus can lead to elevated wavefront error6 and reduced visual performance.7 The validity of the Zernike polynomial for fitting highly aberrated, diseased eyes such as keratoconic eyes has been called into question.8,9 Depending on the number of orders fitted, the Zernike expansion acts as a low-pass filter that can disregard higher-frequency wavefront errors contained in the measurement. Residual fit error describes the portion of the wavefront that cannot be described with a truncated (noninfinite) Zernike expansion. While small levels of fit error may be ignored, larger levels may be visually significant, in which case it would not be practical to use the truncated Zernike expansion to describe keratoconic wavefront error.
Incorporation of customized wavefront error correction into contact lenses has been previously suggested.10-13 The benefit of such contact lens corrections can be offset by translation and rotation.14-17 These previous studies, however, indicate that visual benefit is real even in the presence of translation and rotation as long as the translation and rotation are reasonably small.
State-of-the-art lathing platforms now make implementation of wavefront profiles including higher-order aberrations possible in phase plate and contact lens designs. Equipment for manufacturing customized contact lenses is currently available and not the subject of this paper. The research reported here examines the minimal number of Zernike modes that must be corrected to restore normal visual acuity (VA) in keratoconus in the presence of Zernike error and residual fit error.
If the Zernike expansion is to be used to design custom contact lenses for keratoconic subjects, it is important to understand the visual consequence of residual fit error in conjunction with the use of a truncated Zernike expansion. In this study, we assess the effect of residual fit error on visual performance in keratoconic eyes, assuming the correction is perfectly aligned to the wavefront error of the eye. Approaching the problem in this manner allows the examination of fit error associated with a truncated Zernike expansion independent of errors induced by translation and rotation of the correction.
Assessment of fit error is made in the presence of increasingly complex Zernike corrections (increasing radial orders used to correct the eye). This design permits both the evaluation of the impact of fit error and the identification of a minimum number of Zernike orders that must be corrected to restore visual performance (as a function of disease severity and task difficulty).
Although wavefront aberration stems from all components of the optical system, the bulk of the refractive power of the eye is found at the air/tear interface. When the cornea is highly aberrated, such as in keratoconic subjects, corneal aberration describes the bulk of the higher-order ocular aberration, and can be used as a model for whole-eye aberration.18 Consistent with this finding, corneal first surface wavefront error in the keratoconic eyes evaluated in this study is in agreement with whole-eye wavefront error values previously reported (see Table 1).6
Table 1.
Summary of 4 mm Aberration Data for the Eight Keratoconic Eyes Studieda
| Maximum Corneal Power (D) | 44 | 49 | 54 | 59 | 64 | 68 | 71 | 78 | Maeda et al.6 RMS (μm) Corneal (Whole Eye) |
|---|---|---|---|---|---|---|---|---|---|
| 2nd-order RMS (μm) | 0.633 | 1.520 | 2.178 | 2.254 | 2.696 | 5.264 | 5.129 | 5.004 | - |
| 3rd-order RMS (μm) | 0.322 | 0.781 | 0.994 | 0.837 | 0.912 | 2.667 | 2.786 | 4.720 | 0.59 (0.75) |
| 4th-order RMS (μm) | 0.031 | 0.278 | 0.095 | 0.538 | 0.676 | 0.826 | 1.113 | 1.307 | 0.23 (0.23) |
| 5th-order RMS (μm) | 0.021 | 0.068 | 0.063 | 0.058 | 0.100 | 0.097 | 0.382 | 0.330 | - |
| 6th-order RMS (μm) | 0.026 | 0.053 | 0.016 | 0.061 | 0.112 | 0.112 | 0.237 | 0.401 | - |
| 7th-order RMS (μm) | 0.012 | 0.030 | 0.009 | 0.026 | 0.038 | 0.085 | 0.065 | 0.067 | - |
| 8th-order RMS (μm) | 0.011 | 0.029 | 0.009 | 0.016 | 0.037 | 0.081 | 0.054 | 0.073 | - |
| 9th-order RMS (μm) | 0.012 | 0.021 | 0.009 | 0.026 | 0.030 | 0.061 | 0.057 | 0.077 | - |
| 10th-order RMS (μm) | 0.008 | 0.02 | 0.007 | 0.009 | 0.023 | 0.045 | 0.075 | 0.132 | - |
| Fit error RMS (μm) | 0.006 | 0.007 | 0.008 | 0.009 | 0.012 | 0.014 | 0.014 | 0.018 | - |
Here, root-mean-square RMS wavefront aberration is reported as a function of radial order. Fit error portion of the wavefront not described by the Zernike polynomial is also reported for the keratoconic eyes. Also listed are values of third- and fourth-order aberration over a 4 mm pupil in keratoconus-suspect to mild keratoconus previously reported by Maeda et al.6 Dash indicates the data were not reported.
We used low-contrast targets as well as high-contrast targets as measures of visual performance because low contrast tasks have been shown to be more sensitive to visual degradation in the presence of aberrations than high-contrast targets,19 especially in keratoconus eyes.20 Moreover, low-contrast tasks have been argued to illustrate better the effect of visual correction relevant to real-world activities.21
Here we wish to explore whether a truncated Zernike expansion correction can restore high- and low-contrast acuity to normal levels in mild to severe keratoconus in the presence of residual fit error.
2. METHODS
Appropriate university Institutional Review Board approvals and informed consents were obtained prior to conducting the study. Keratoconus topographies were captured in an ophthalmology outpatient setting where fullscope care of keratoconus patients is practiced, including contact lens fitting and corneal transplantation. The data were collected on an EyeSys Corneal Analysis System Model 2 (EyeSys Laboratories Inc., Houston, Texas) corneal topographer. Eight keratoconus corneal topographies were identified from an existing database of 117 corneal topographies of clinically diagnosed keratoconus subjects. Figure 1 shows the distribution of these 117 topographies by maximum corneal power. Eight topographies were chosen to represent a wide range of keratoconus severity from mild to severe. Maximum corneal powers of the eight chosen topographies were 44, 49, 54, 59, 64, 68, 71, and 78 D. Maximum corneal power was determined using Visual Optics Laboratory Professional 6.70 or VOLPro (Sarver and Associates, Carbondale, Illinois) by locating the steepest location on a given topography. All topographies reported complete data over the central 4 mm zone.
Fig. 1.
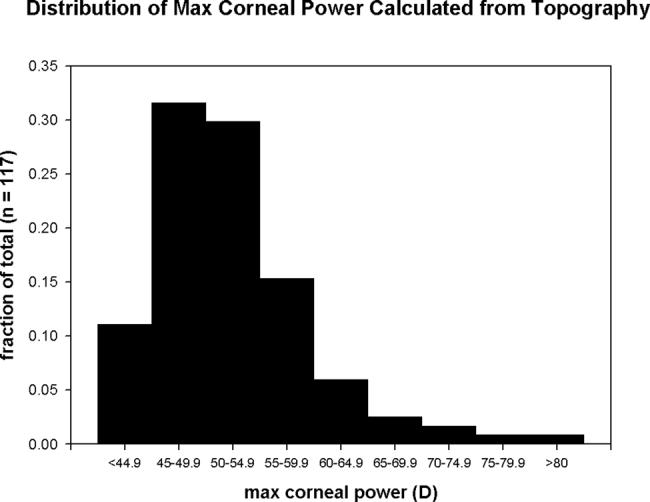
Distribution of maximum corneal dioptric power in a clinical sample of 117 keratoconic subjects.
VOLPro was used to construct unaberrated logMAR (minimum angle of resolution) letter charts by selecting letters randomly from an equally identifiable letter set. However, VOLPro will not allow any one letter to be duplicated on any given line of an acuity chart. This ensures all letters within one line of the chart are unique. Maximum logMAR letter size and chart test distance are input by the user to ensure proper chart size and scaling. Each tested aberration condition was associated with the same random letter chart for the three trials. Corneal first-surface wavefront aberration was calculated from the topographical data using VOLPro. The aberration structure for a given eye was determined by first extracting the central 4 mm circular area from the topography data (typically over two thousand data points decreasing in sampling density as distance from the corneal apex increases) and fitting the resulting surface points with a B-spline fitting function. For all practical purposes there was no error between the measured data points and the B-spline within the fit zone. To determine leading and lagging portions of the wavefront, comparison was made with a reference sphere obtained by fitting the average curvature of the B-spline. Using this reference sphere, the optical path difference for a dense grid of over 3000 points within the 4 mm circular zone was computed as the difference between the optical path length for a general ray at one of these grid locations and a reference optical path length for a ray through the center of the zone. The wavefront aberration represented by the optical path difference values was fitted to a second B-spline function to represent the wave-front aberration of the cornea. This grid of over 3000 points was also used to fit the tenth-order Zernike polynomial.
The difference between the wavefront B-spline surface and wavefront truncated Zernike expansion surface defines the residual fit error. This residual portion of the wavefront error would remain in the system for each truncated Zernike expansion correction. Table 1 lists the 4 mm RMS by order and the RMS fit error for the eight data files used in this experiment. The third- and fourth-order corneal and whole-eye wavefront error reported by Maeda et al.6 for 35 keratoconus-suspect to mildly keratoconic eyes, also at 4 mm, is included in the table for comparison purposes.
Wavefront error as measured by the tenth-radial-order fit was cumulatively corrected by setting to zero successive radial orders of the Zernike representation. We started by setting radial orders zero through two to zero. Removal of Zernike modes through a given radial order is equivalent to the complete optical correction of all modes through that particular order. For instance, when all modes through the second order are removed, the resulting Zernike wavefront description simulates the wave-front after optical correction of the zeroth-through second-order modes for a given keratoconic eye. Said differently, a second-order correction leaves all higher-order aberrations and fit error in place. More complicated Zernike wavefront corrections were systematically studied by cumulatively removing entire additional Zernike orders. For each test condition n (where n ranges from 1 to 9), Zernike orders zero to n+1 were removed from the Zernike portion of the wavefront representation. This gave a possibility of simulating second- to tenth-order Zernike aberration corrections for each of the eight keratoconic wavefront errors.
For each condition, the remaining Zernike wavefront aberration was combined with the residual fit error. This procedure is analogous to phase compensation, where modes of entire radial orders are multiplied by -1 and added to the B-spline wavefront. A point spread function (PSF) was calculated from the resulting wavefront aberrations. PSFs from each test condition were convolved with the logMAR high- and low-contrast letter charts and were printed at 600 dpi. Placing the aberration in the object as opposed to the image and having normally sighted individuals view the object is not a new idea. Burton and Haig employed this technique in their 1984 work examining the effects of aberration on object detection.22
The measured Michelson contrast of the unaberrated acuity charts was 89% (high-contrast) and 5% (low-contrast), respectively. Each chart encompassed a log-MAR acuity range of 0.7 to -0.3 or Snellen equivalent of 20/100 to 20/10. These charts simulate the affect of the residual fit error and uncorrected Zernike aberration terms on retinal image quality. As previously noted, high-contrast charts were used because they are a clinical standard for assessing visual performance. Low-contrast charts were used because low contrast tasks are more sensitive to the impact of aberration and have been shown to identify losses of vision in keratoconus not detected with high-contrast testing.18,19 Figure 2 demonstrates the effects of the convolution process for the wavefront error of the keratoconic eye with 54 D maximum corneal power. Figure 3 shows the wavefront aberration including and excluding Zernike fit error for the eye with 54 D maximum corneal power.
Fig. 2.
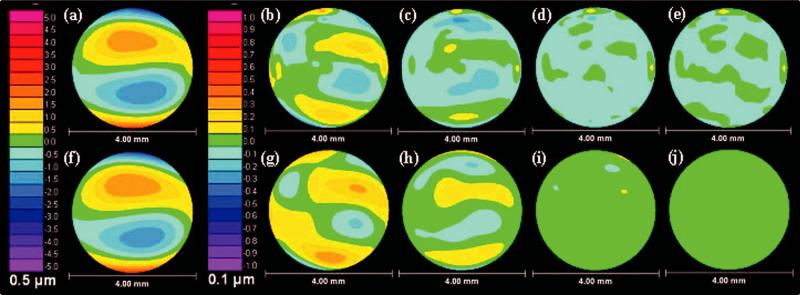
Visual performance charts demonstrating (b) second-through (f) sixth-order Zernike corrections for the keratoconic eye with maximum corneal power of 54 D pictured in (a). Zernicke fit error is included in the simulations shown in (b) through (f).
Fig. 3.
Wavefront aberration, including Zernike fit error (the portion of the wavefront not characterized by the Zernike polynomial), for the (a) second-through (e) sixth-order corrections of the 54 D eye are shown. Also shown are wavefront maps for the (f) second-through (j) sixth-order corrections with fit error excluded. (a) through (e) show the wavefront errors used in the simulations for this keratoconic patient. (f) through (j) are shown to provide the reader with a feel of the distribution of the fit error shown in (a) through (e).
A. Subjects
A total of five healthy, normal subjects were recruited to read charts for this study and were split among the high- and low-contrast VA tasks. The high-contrast letter charts were read by subjects S1, S2, and S3 aged 55, 33, and 25 yr, respectively. The low-contrast letters were read by subjects S1, S4, and S5 aged 55, 54, and 34 yr, respectively. All subjects were free of ocular pathology and had normal high-contrast, best corrected VA ranging from 20/13 to 20/16.23 The high- and low-contrast chart sets contained three nonconvolved “perfect” charts that were used to establish a baseline for both the high- and low-contrast VA. The high-contrast unaberrated charts and the high-contrast simulations for all eight keratoconus eyes were randomized together. Similarly, the low-contrast unaberrated charts and the low-contrast simulations for all eight keratoconus eyes were randomized together. Conditions were tested until the data reached a plateau, leaving some conditions untested (plateau point was determined from a trial run on one observer). In total, there were 54 high-contrast charts and 65 low-contrast charts tested.
After subject dilation, subjects in each contrast cohort read each chart througha3mm pupil and best subjective refraction. The number of correctly read letters on each chart up to the fifth miss was recorded. All tested charts were read three times and an average score on the chart calculated for each observer. On average, the time required for any given subject to complete the three trials was approximately 3 h. Subjects were given 30-min breaks between the three trials.
B. Analysis
The analysis employed here is not new. Similar published studies used the analysis method described below to demonstrate that the effects of individual Zernike aberrations on acuity are not equal,24,25 and when Zernike terms are combined, they interact either to increase or to decrease the adverse effects of aberration.26
In overview, each subject’s high- or low-contrast base-line VA was subtracted from the number of letters correctly read by that subject on each chart, generating a visual performance metric of “letters lost.” For instance, if a subject on average correctly read 40 letters on a given chart, and on average correctly read 50 letters on the “perfect” baseline charts, the subject had a score of -10 letters lost on that chart. This procedure normalized each subject’s score on each aberrated letter chart to their own baseline VA. After this normalization, the results for each chart were combined across the three observers by calculating the mean of means and standard deviation of means. Values of mean of means of the letters lost were plotted as a function of Zernike orders corrected for the chart under test. Error bars for the perfect (nonaberrated) charts are shown as dashed lines in Figs. 4 and 5, and were calculated as the standard deviation of the means of three subjects reading perfect charts.
Fig. 4.
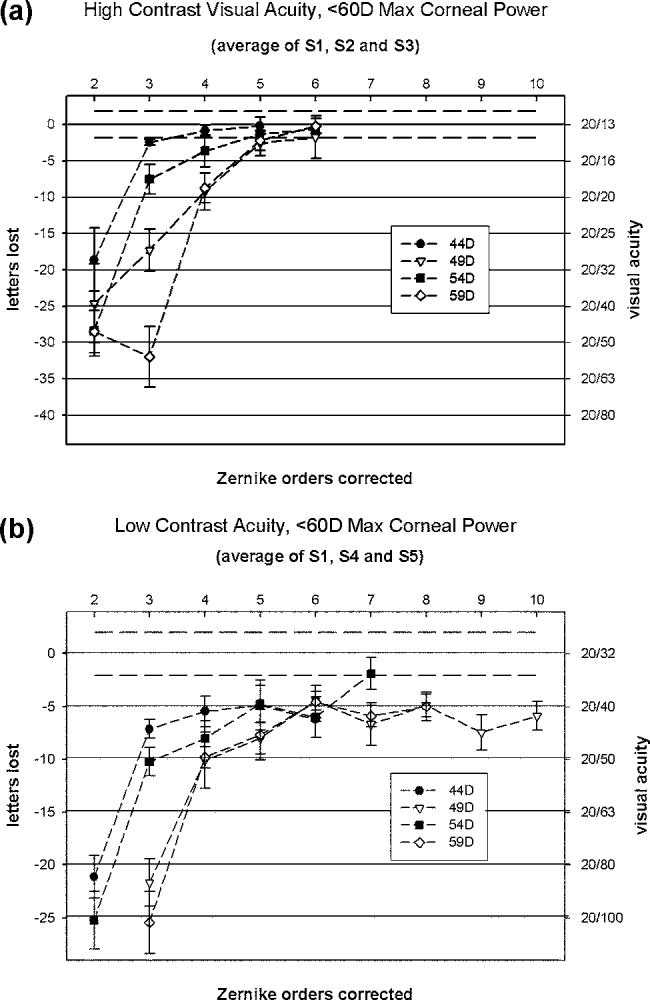
Letters-lost mean of means for (a) high-contrast and (b) low-contrast VA charts convolved with PSFs derived from keratoconic wavefront errors for eyes with corneas having <60 D maximum corneal power. Letters lost from baseline (left vertical axis) is plotted as a function of Zernike orders corrected. Letters lost is converted to VA (right vertical axis). Zero letters lost from baseline (charts having no wavefront error) corresponds to an average acuity of 20/13 for high contrast and 20/32 for low contrast. At fifth-radial-order Zernike correction, high-contrast visual performance in the presence of sixth-through tenth-order aberrations and residual fit error has returned to baseline levels. At fifth order, low-contrast visual performance in the presence of sixth-through tenth-order aberrations and residual fit error has reached a plateau at a loss of approximately five letters, or 0.1 log MAR. For these subjects a one line loss reduces low-contrast acuity from 20/32 to 20/40. Dashed lines represent one standard deviation of the average scores on “perfect” high contrast charts. All tested points are plotted.
Fig. 5.
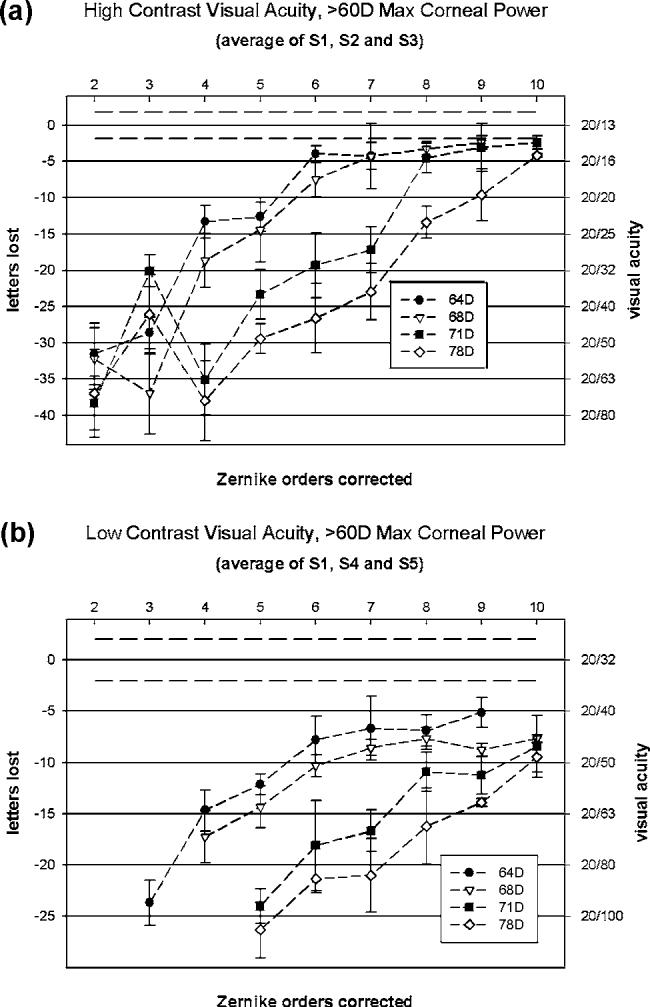
Letters-lost mean of means for both (a) high- and (b) low-contrast VA charts convolved with PSFs derived from keratoconic wavefront errors for corneas having >60 D maximum corneal power. Letters lost from baseline (left vertical axis) is plotted as a function of Zernike orders corrected. Letters lost is converted to VA (right vertical axis). Zero letters lost from base-line corresponds to an average acuity of 20/13 for high contrast and 20/32 for low contrast. As corneal power increases, the number of Zernike orders required for optimal correction increases. Dashed lines represent one standard deviation of the scores on “perfect” charts. All tested points are plotted.
3. RESULTS
The results naturally divided into two groups. The first group is composed of visual performance data collected for keratoconus wavefront errors representing eyes with corneas having a maximum power <60 D [Figs. 4(a) and 4(b)]. The second group is composed of data for keratoconic wavefront errors representing eyes with corneas having a maximum power >60 D [Figs. 5(a) and 5(b)]
A. High- and Low-Contrast Visual Acuity, <60 D Maximum Corneal Power
Under high-contrast conditions, VAs for charts convolved with keratoconic wavefront errors representing eyes with <60 D maximum corneal power reached baseline levels (acuities not statistically different from those measured on unaberrated charts) at or before the application of a fifth-order Zernike correction [Fig. 4(a)]. The mean of all traces at sixth order fall within one standard deviation of baseline. Table 2 shows P values obtained from ANOVAs that compare mean high-contrast baseline acuity to the mean acuity obtained for the 44 D, 49 D, 54 D, and 59 D charts with various Zernike orders corrected. Values of P<0.05 indicate that the two measures are significantly different. Low-contrast VA for charts convolved with wavefront errors derived from keratoconic eyes having <60 D maximum corneal power also rapidly improved with the addition of second-fifth orders and gained little with additional orders. For these data, the mean of only one test condition fell within one standard deviation of baseline. Across conditions tested, visual performance reached a plateau at a loss of five letters or one line on a logMAR chart as additional Zernike orders were added to the correction [Fig. 4(b)].
Table 2.
Values of P Obtained from ANOVAs That Compare Mean High-Contrast Baseline Acuity with the Mean Acuity Obtained for Charts Aberrated with the Corrected Wavefront Error Obtained from <60 D Keratoconic Eyes
| Max Corneal Power (D) | Zernike Orders Corrected |
|||
|---|---|---|---|---|
| Through 3rd | Through 4th | Through 5th | Through 6th | |
| 44 | 0.169 | 0.594 | 0.878 | —a |
| 49 | 0.000 | 0.003 | 0.274 | 0.297 |
| 54 | 0.009 | 0.048 | 0.561 | 0.697 |
| 59 | 0.000 | 0.004 | 0.270 | 0.919 |
Data were not reported.
B. High- and Low-Contrast Acuity, >60 D Maximum Corneal Power
At high contrast levels, visual acuities approached base-line for wavefront errors derived from keratoconic eyes having maximal corneal powers of 64 D, 68 D, 71 D, and 78 D [Fig. 5(a)]. For these more highly aberrated eyes, low-contrast visual acuities were improved with a Zernike correction but never returned to baseline [Fig. 5(b)].
4. DISCUSSION
For each keratoconic wavefront error representing eyes with corneas having <60 D maximum corneal power, high-contrast VA sharply improves as the number of Zernike orders corrected increases, returning to normal at the fifth radial order. Examination of Fig. 4(a) reveals that while a fifth-order correction is not significantly different from baseline, there appears to be a slight visual benefit in correcting the sixth-radial-order aberration terms as reflected by its data being closer and better centered on the baseline by about one letter. However, the benefit may be offset in practice because of alignment issues. For low-contrast testing in these same eyes, acuity improved with each additional radial order added up to the fifth radial order and reached a plateau at about -5 letters lost, lowering the patient’s normal low-contrast acuity from 20/32 to 20/40 [Fig. 4(b)].
For each keratoconus wavefront error representing eyes with corneas of >60 D, each added order to the Zernike correction improved acuity. The sharp rise in acuity with second-through-fourth-order correction seen in both Figs. 4(a) and 4(b) is not observed in Figs. 5(a) and 5(b). The improvements in VA gradually increase with Zernike order. This suggests a more complicated Zernike correction than a tenth-radial-order fit is required to correct these eyes and that the fit error affects low-contrast acuity even with a tenth-radial-order correction.
Figure 4(b) also demonstrates a ceiling effect for the wavefront error generated from the keratoconic eyes having 49 D and 59 D maximum corneal power. That is, the subjects were unable to read the letter charts when only a second-order correction was used. Thus, the corresponding traces begin at a third-radial-order Zernike correction. Similar results are seen in low-contrast data for all wavefront errors generated from keratoconic eyes having maximum corneal powers >60 D. This is consistent with the clinical finding that glasses (a close approximation to a Zernike second-order correction) are of little use in moderate and advanced keratoconus.
The Collaborative Longitudinal Evaluation of Keratoconus (CLEK) Study Group performed a large-scale prospective study of keratoconic subjects and systematically examined visual performance. This group has reported that 86% of 1204 keratoconic subjects had best corrected, high-contrast monocular VA of 20/21 or worse in at least one eye.27 This level of visual function suggests that it may be possible to improve visual performance in keratoconus subjects. The onset of keratoconus usually occurs at about the age of puberty,7 allowing for proper neural development of the visual system. Consequently, improved visual performance should result from a custom optical correction providing improved retinal image quality.
As with all applications of wavefront aberration measurement, pupil size is critically important. Here a 4mm pupil diameter was chosen because it is a good estimation of the photopic pupil size6 and is consistent with other reports on Zernike-fit error.8
The proposal that a fifth-order Zernike correction may be adequate for custom contact lenses could be premature considering the reduced visual performance that is predicted for eyes with >60 D of maximum corneal power. However, the frequency with which such eyes will appear in the population of keratoconic eyes is low. The eight sample wavefronts studied here were chosen from a sample of 117 keratoconus eyes of varying severity drawn from an ophthalmology outpatient setting, which is probably a more severe population than would be found in a wider community. In this sample, 88% of measurements had maximum corneal power < 60 D (Fig. 1). There are probably two reasons for this: Most keratoconic eyes do not progress beyond 60 D of maximum corneal power and those that do often undergo penetrating keratoplasty. Keratoconic subjects with an average or a maximum keratometry reading >55 D are significantly at risk for penetrating keratoplasty.28,29 Supporting this argument, in 83% of a series of 93 penetrating corneal grafts for keratoconus, mean keratometry was >52 D.30
A previous study has found a correlation between best spectacle-corrected VA and corneal elevation fit error in keratoconus.8 That study concluded that the existence of a correlation suggests that there is visually significant information in the fit error. In this paper, we have further explored this idea by examining the impact of residual wavefront aberration on visual performance for increasingly complex Zernike corrections. We further dissect visual performance as a function of disease severity and task difficulty.
The results presented in the current study are consistent with the previous report in that the most severe eyes do suffer from reduced performance in the presence of Zernike-fit error. However, unlike the previous report,8 the results presented here strongly support the claim that the Zernike polynomial can represent the visually significant aberrations of the keratoconic eye in the majority of cases and fails to categorize visually important aberration only in the most severe cases. One difference in the studies is that our design did not use the generalizing metric of RMS error correlated with visual performance. Different Zernike aberrations affect visual performance differently,25 and the affect is not necessarily represented by the magnitude of the mode coefficient. This makes RMS a less than ideal predictor of visual performance. Another difference is that the correlations drawn in the previous study were done cross sectionally, whereas our data set uses a normalization process so that effects other than those of wavefront error on VA are removed from consideration.
Here we provide data demonstrating that a well-aligned Zernike-designed correction has the very real potential to return high-contrast acuity in the keratoconus eye to normal levels in the majority of cases. It has also been demonstrated that Zernike corrections have the potential to significantly improve low-contrast acuity to near normal levels in most keratoconic eyes.
These results suggest that a well-aligned fifth-order Zernike correction will restore high-contrast acuity in the majority of keratoconic eyes to normal levels. The fact that 63.9% of keratoconic subjects in the CLEK study have best corrected, high-contrast VA of 20/21 to 20/40 in at least one eye,27 combined with the results reported here (Fig. 4), indicates that similar high-contrast acuity could be reached with a soft contact lens containing a third- or fourth-order Zernike correction (eyes with <60 D max corneal power). Contact lenses that use a minimal set of Zernike modes to correct optical aberrations may be optically more tolerant of rotation and translation than lenses that use more Zernike terms or that attempt to fully correct all aberrations of these diseased eyes. Further, and just as important, if not more so, soft contact lenses should provide for increased comfort and longer wearing time in keratoconus.
ACKNOWLEDGMENTS
The authors thank Daniel Kist for his support in data collection and Sanjeev Kasthurirangan for his helpful discussions. We acknowledge the following grants to the authors and institution indicated: NIH/NEI T32 EY07024 to J.D.M., NIH/NEI RO1 EY05280 to R.A.A., NIH/NEI P30 EY007551 to UHCO, and NHMRC NHF Fellowship 0061 to KP. Corresponding author Jason Marsack can be reached as follows: Visual Optics Institute, University of Houston, College of Optometry, 505 J. Davis Armistead Building, Houston, Texas 77204; phone, 713-743-0661; fax, 713-743-2053; e-mail, jmarsack@optometry.uh.edu.
REFERENCES
- 1.Liang J, Grimm B, Goelz S, Bille JF. “Objective measurement of wavefront aberrations of the human eye with the use of a Hartmann-Shack wave-front sensor,”. J. Opt. Soc. Am. A. 1994;11:1949–1957. doi: 10.1364/josaa.11.001949. [DOI] [PubMed] [Google Scholar]
- 2.Guirao A, Williams DR. “A method to predict refractive errors from wave aberration data,”. Optom. Vision Sci. 2003;80:36–42. doi: 10.1097/00006324-200301000-00006. [DOI] [PubMed] [Google Scholar]
- 3.Thibos LN. “The optics of wavefront sensing,”. Ophthalmol. Clin. N. Am. 2004;17:111–117. doi: 10.1016/j.ohc.2004.02.004. [DOI] [PubMed] [Google Scholar]
- 4.Thibos LN, Hong X, Bradley A, Applegate RA. “Accuracy and precision of objective refraction from wavefront aberrations,”. J. Vision. 2004;4:329–351. doi: 10.1167/4.4.9. [DOI] [PubMed] [Google Scholar]
- 5.American National Standards. American National Standards for Ophthalmics “Methods for reporting optical aberrations of eyes,”. ANSI Z80. :28–2004. [Google Scholar]
- 6.Maeda N, Fujikado T, Kuroda T, Mihashi T, Hirohara Y, Nishida K, Watanabe H, Tano Y. “Wavefront aberrations measured with Hartmann-Shack sensor in patients with keratoconus,”. Ophthalmology. 2002;109:1996–2003. doi: 10.1016/s0161-6420(02)01279-4. [DOI] [PubMed] [Google Scholar]
- 7.Krachmer JH, Feder RS, Belin MW. “Keratoconus and related noninflammatory corneal thinning disorders,”. Surv. Ophthalmol. 1984;28:293–322. doi: 10.1016/0039-6257(84)90094-8. [DOI] [PubMed] [Google Scholar]
- 8.Smolek MK, Klyce SD. “Zernike fitting fails to represent all visually significant aberrations in keratococnus,”. Invest. Ophthalmol. Visual Sci. 2003;44:4676–4681. doi: 10.1167/iovs.03-0190. [DOI] [PubMed] [Google Scholar]
- 9.Klyce SD, Karon MD, Smolek MK. “Advantages and disadvantages of the Zernike expansion for representing wavefront aberration of the normal and aberrated eye,”. J. Refract. Surg. 2004;20:S537–541. doi: 10.3928/1081-597X-20040901-25. [DOI] [PubMed] [Google Scholar]
- 10.Thibos LN. “Design principles and limitations of wavefront guided contact lenses,”. Eye Cont. Lens. 2003;29:S167–S170. doi: 10.1097/00140068-200301001-00046. [DOI] [PubMed] [Google Scholar]
- 11.Cox IG, Lagana M. “Feasibility of wavefront customized contact lenses,”. In: Krueger RR, Applegate RA, MacRae SM, editors. Wavefront Customized Visual Correction: the Quest for Super Vision II. Slack Inc.; 2004. pp. 279–284. [Google Scholar]
- 12.Kollbaum P. “Seeing into the future with contact lenses,”. Cont. Lens. Spect. 2003 February;:25–29. [Google Scholar]
- 13.Marsack JD, Milner TE, Rylander HG, III, Leach NL, Roorda A. “Applying wavefront sensors and corneal topography to keratoconus,”. Biomed. Sci. Instrum. 2002;38:471–476. [PubMed] [Google Scholar]
- 14.Guirao A, Cox IG, Williams DR. “Method for optimizing the correction of the eye's higher-order aberrations in the presence of decentrations,”. J. Opt. Soc. Am. A. 2002;19:126–128. doi: 10.1364/josaa.19.000126. [DOI] [PubMed] [Google Scholar]
- 15.Guirao A, Porter J, Williams DR, Cox IG. “Calculated impact of higher order monochromatic aberrations on retinal image quality in a population of human eyes,”. J. Opt. Soc. Am. A. 2002;19:620–628. doi: 10.1364/josaa.19.000620. [DOI] [PubMed] [Google Scholar]
- 16.Guirao A, Williams DR, Cox IG. “Effect of rotation and translation on the expected benefit of an ideal method to correct the eye’s higher-order aberrations,”. J. Opt. Soc. Am. A. 2001;18:1003–1015. doi: 10.1364/josaa.18.001003. [DOI] [PubMed] [Google Scholar]
- 17.de Brabander J, Chateau N, Marin G, Lopez-Gil N, Van Der Worp E, Benito A. “Simulated optical performance of custom wavefront soft contact lenses for keratoconus,”. Optom. Vision Sci. 2003;80:637–43. doi: 10.1097/00006324-200309000-00008. [DOI] [PubMed] [Google Scholar]
- 18.Barbero S, Marcos S, Merayo-Lloves J, Moreno-Barriuso E. “Validation of the estimation of corneal aberrations from videokeratography in keratoconus,”. J. Refract. Surg. 2002;18:263–70. doi: 10.3928/1081-597X-20020501-09. [DOI] [PubMed] [Google Scholar]
- 19.Pesudovs K, Marsack JD, Donnelly WD, Thibos LN, Applegate RA. “Measuring visual acuity-mesopic or photopic conditions and high or low contrast letters,”. J. Refract. Surg. 2004;20:S508–514. [PubMed] [Google Scholar]
- 20.Pesudovs K, Schoneveld P, Seto RJ, Coster DJ. “Contrast and glare testing in keratoconus and after penetrating keratoplasty,”. Br. J. Ophthamol. 2004;88:653–657. doi: 10.1136/bjo.2003.027029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mannis MJ, Zadnik K, Johnson CA, Adams C. “Contrast sensitivity after penetrating keratoplasty,”. Arch. Ophthalmol. (Chicago) 1987;105:1220–1223. doi: 10.1001/archopht.1987.01060090078032. [DOI] [PubMed] [Google Scholar]
- 22.Burton JG, Haig ND. “Effects of the Seidel aberrations on visual target discrimination,”. J. Opt. Soc. Am. A. 1984;1:373–385. doi: 10.1364/josaa.1.000373. [DOI] [PubMed] [Google Scholar]
- 23.Elliott DB, Yang KCH, Whitaker D. “Visual acuity changes throughout adulthood in normal, healthy eyes: seeing beyond 6/6,”. Optom. Vision Sci. 1995;72:186–191. doi: 10.1097/00006324-199503000-00006. [DOI] [PubMed] [Google Scholar]
- 24.Applegate RA, Sarver EJ, Khemsara V. “Are all aberrations equal?”. J. Refract. Surg. 2002;18:S556–562. doi: 10.3928/1081-597X-20020901-12. [DOI] [PubMed] [Google Scholar]
- 25.Applegate RA, Ballentine C, Gross H, Sarver EJ, Sarver CA. “Visual acuity as a function of Zernike mode and level of root mean square error,”. Optom. Vision Sci. 2003;80:97–105. doi: 10.1097/00006324-200302000-00005. [DOI] [PubMed] [Google Scholar]
- 26.Applegate RA, Marsack JD, Ramos R, Sarver EJ. “Interaction between aberrations to improve or reduce visual performance,”. J. Cataract Refract. Surg. 2003;29:1487–1495. doi: 10.1016/s0886-3350(03)00334-1. [DOI] [PubMed] [Google Scholar]
- 27.Zadnik K, Barr JT, Edrington TB, Everett DF, Jameson M, McMahon TT, Shin JA, Sterling JL, Wagner H, Gordon MO. “Baseline findings in the Collaborative Longitudinal Evaluation of Keratoconus (CLEK) Study,”. Invest. Ophthalmol. Visual Sci. 1998;39:2537–2546. [PubMed] [Google Scholar]
- 28.Lass JH, Lembach RG, Park SB, Hom DL, Fritz ME, Svilar GM, Nuamah IF, Reinhart WJ, Stocker EG, Keates RH, Moran CT, Cobo LM, Foulks GN. “Clinical management of keratoconus. A multicenter analysis,”. Ophthalmology. 1990;97:433–45. doi: 10.1016/s0161-6420(90)32569-1. [DOI] [PubMed] [Google Scholar]
- 29.Dana MR, Putz JL, Viana MA, Sugar J, McMahon TT. “Contact lens failure in keratoconus management,”. Ophthalmology. 1992;99:1187–1192. doi: 10.1016/s0161-6420(92)31825-1. [DOI] [PubMed] [Google Scholar]
- 30.Lim L, Pesudovs K, Coster DJ. “Penetrating keratoplasty for keratoconus: visual outcome and success,”. Ophthalmology. 2000;107:1125–1131. doi: 10.1016/s0161-6420(00)00112-3. [DOI] [PubMed] [Google Scholar]