Abstract
Background
An index of age-associated health/well-being disorders (deficits), called the “frailty index” (FI), appears to be a promising characteristic to capture dynamic variability in aging manifestations among age-peers. In this study we provide further support toward this view focusing on the analysis of the FI age patterns in the participants of the National Long Term Care Survey (NLTCS).
Methods
The NLTCS assessed health and functioning of the U.S. elderly in 1982, 1984, 1989, 1994, and 1999. Detailed information for our sample was assessed from about 26,700 interviews. The individual FI is defined as a proportion of health deficits for a given person.
Results
The FI in the NLTCS exhibits accelerated age patterns. The acceleration is larger for elderly who, at younger ages, had a lower FI (low FI group) than for those who showed a higher FI at younger ages (high FI group). Age-patterns for low and high FI groups tend to converge at advanced ages. The rate of deficit accumulation is sex-sensitive.
Conclusions
The accelerated FI age patterns suggest that FI can be considered as a systemic measure of aging process. Convergence of the (sex-specific) FI age patterns for low and high FI groups by extreme ages might reflect the limit of the FI-specific (or systemic) age as well as the limit of adaptation capacity in aging individuals.
Keywords: Frailty, aging, stress-resistance, population heterogeneity, sex differences
1. Introduction
Despite increasing attention to the concept of frailty as a characteristic of the aging process, there is still not a universally-recognized definition that is valid across various settings (Rockwood et al., 2005; Bortz, 2002). There is, however, growing consensus for viewing frailty as a physiological state of non-specific vulnerability to stressors, which typically arises and progresses at advanced ages (Fried et al., 2004). This concept suggests that a frail person may experience health decline due to an age-related lack of stress-resistance or stress-recovery rather than a particular predisposition to specific stresses. Degradation of the organism’s defense function occurs due to decreasing physiological reserves and, possibly, deregulation of multiple physiologic systems (Fried et al., 2004), which results in difficulty maintaining homeostasis in response to even “normal” stresses that might not create such problems at younger ages. On the cellular level, frailty can be associated with a process of gradual accumulation of damage in cellular tissues (Kirkwood, 2002). Consequently, frailty is not necessarily associated with a specific disease or disability but is rather a systemic disorder that may be manifested through health/well-being disorders.
The physiological concept of frailty suggests a simple method for its assessment through tracking health/well-being deficits (i.e., signs, symptoms, impairments, etc.) accumulated by individuals during their life course (Rockwood et al., 2000; 2004; Mitnitski et al., 2004). These arguments are based on a systemic approach to health; i.e., on the hypothesis that declining neuroendocrine and immune functions of an organism can result in a wide spectrum of adverse health outcomes (Vanitallie, 2003). This view is also supported by the idea that frailty and aging are accompanied by stochastic processes that result in variable deficit accumulation at the subcellular, tissue and organ system levels (Kirkwood et al., 2005). The frailty state thus can be described by a composite measure of the health/well-being deficits. Rockwood and Mitnitski and colleagues propose to characterize the frailty state by a frailty index (FI) calculated as the proportion of deficits in an individual. According to this systemic approach, frailty appears to be characterized not by the substance of the individual deficits used to define the FI but by their aggregate (or systemic) ability to describe the decline in physiological performance (Vanitallie, 2003) in an organism – and, thus to characterize its overall function.
The validity and robustness of the frailty concept on the basis of self-reported deficits has been justified by the ability of the FI to predict death and health risk in Canadian (see Mitnitski et al., 2004 and references therein) and Chinese (Goggins et al., 2005) studies. Nevertheless, such a systemic concept requires further testing in other settings. In this paper, we apply the Rockwood-Mitnitski approach to extend prior analyses to U.S. elderly using data from the National Long Term Care Survey (NLTCS). We test hypotheses about the (accelerated) increase of the FI with age in males and females using cross-sectional data collected in the NLTCS. Different population structures represented in different NLTCS waves allow us to compare the FI age patterns across waves and for “disabled” (high proportion of disabled individuals) and “non-disabled” (normal or an unbiased mixture of disabled and non-disabled subjects) samples of the population. Recent studies (Fried et al., 2004) suggest that, while intersecting, disability and frailty are rather distinct concepts. Distinguishing disabled from non-disabled individuals provides a test for similarities/dissimilarities between the concepts of disability and frailty. We compared findings for distinct groups in the NLTCS and subsequently compared those with published results from Canadian and Chinese studies as well. Our analysis show possible connections between the FI, stress-resistance, and stress-strength providing support for the view that the FI can be considered as a systemic measure of aging process. We show that the FI age patterns for disabled and non-disabled groups tend to converge at advanced ages, which indicates the presence of a limit of the FI-specific (or systemic) age. We also show that this limit coincides with the mean limit of behavioral and physiological adaptation capacity of aging organisms.
2. Methods
The NLTCS assesses the health and functioning of U.S. elderly (65+) individuals over 18 years (1982, 1984, 1989, 1994, and 1999). It uses a sample of individuals drawn from Medicare enrollees and contains longitudinal and cross-sectional nationally-representative components. A two-stage-selection interviewing process is used. A screening interview assessing chronic (90+ days) disability was given to all members of the sample. A detailed interview was given to i) those who reported at least one chronic (Instrumental) Activities of Daily Living (I)ADL impairment, ii) institutionalized individuals, and iii) those who received a detailed interview in a prior survey. For each new survey, a cohort sample of about 5,000 persons was added to the surviving sample to replace the deaths occurring since the prior survey and to ensure that the new sample was representative of the entire U.S. elderly population (65+). Such a procedure ensures a valid longitudinal and cross-sectional design for the survey (for details see Manton and Gu (2001)). In our study, detailed information on the health of the community-survey participants is assessed from about 26,700 interviews in all five NLTCS waves.
In the 1994 NLTCS, an additional sub-sample of 1,762 “non-disabled” persons (the “healthy” supplement [HS]) was selected. These persons were designated to receive a detailed interview even if screened initially as non-institutional and unimpaired. The HS was selected from the entire sample, excluding only the 95+ supplement and persons who screened in automatically because they had detailed interviews in 1989. The 1999 HS includes 1,262 survivors from the 1994 HS, persons newly selected from the replacement (aged-in) component of the 1999 sample (219), and persons newly selected from the longitudinal component of the 1999 sample who were screened out in 1989 and not selected for the 1994 wave (64) – producing a total of 1,545 persons.
To operationalize the FI concept for the NLTCS data, we use the same, or similar, health deficits as assessed in the Canadian Study of Health and Aging (CSHA) (Mitnitski et al., 2001; 2004). The essential issue in constructing the FI is not the specific substance of deficits, but their systemic nature; i.e., their ability to capture the widest possible spectrum of health/quality-of-life disorders. Specifically, we selected the following 32 questions presented in all waves: difficulty with eating, dressing, walk around, getting in/out bed, getting bath, toileting, using telephone, going out, shopping, cooking, light house work, taking medicine, managing money, arthritis, Parkinson’s disease, glaucoma, diabetes, stomach problem, history of heart attack, hypertension, history of stroke, flu, broken hip, broken bones, self-rated health, trouble with bladder or bowels, dementia, as well as problems with vision, hearing, ear, teeth, and feet. Following Mitnitski-Rockwood’s approach, we define the FI as an unweighted count of such deficits divided by the total number of all deficits considered for an individual (Mitnitski et al., 2002a); thus, the FI can, in theory, vary from 0 to 1.
To ensure the reliability of our inferences, we adopted a three-stage strategy. First, for most of our analyses we consider two variants of the FI: one constructed using the full set of 32 deficits and the other a reduced set of the 26 most comprehensively assessed deficits (fewer than 1% missing values). Second, we verify the consistency of our findings across NLTCS waves. Finally, we compare our findings with those from Canadian and Chinese populations.
3. Results
We first evaluate the FI age-patterns for each NLTCS wave. Despite the relatively large samples, estimates for single years of age are not sufficiently precise at advanced ages (90+), where there are less than 100 cases per year. To improve statistical precision, and to smooth estimates, we used two-year age groupings in our analyses. Figure 1 shows the two-year age-patterns of the full (32 deficits) FI for five waves. The 26-deficit FI shows a similar age-pattern and thus is not depicted.
Figure 1.
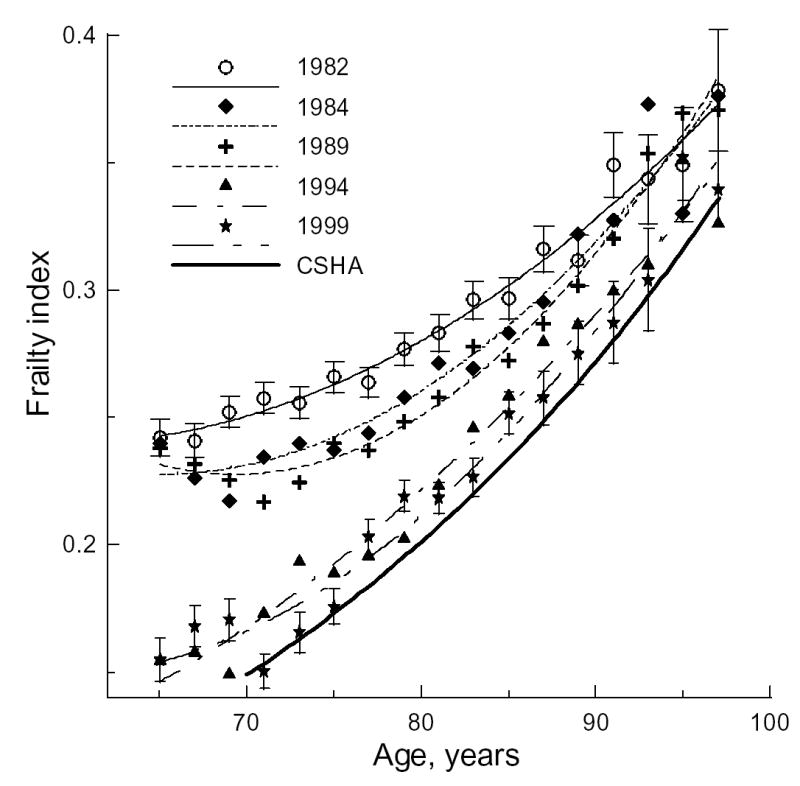
The two-year frailty index age-patterns for each National Long Term Care Survey (NLTCS) along with model estimates of the frailty index age distribution for the Canadian Study of Health and Aging (CSHA; thick line FI=exp(0.029Age−4.05), (8)). The standard errors (±SE) of means are shown by bars for the 1982 and 1999 NLTCS.
Visual inspection of the age-patterns in Figure 1 reveals a nonlinear (accelerated) increase of the FI with age. Sex-differences in the two-year FI age-patterns were not statistically significant. Averaging the FI over five-years of age (Table 1) shows that statistically significant differences between FIs for males and females are seen only for the 90–94 age group of the 1982 NLTCS and for three age groups (70–74, 80–84, 90–94) of the 1994 NLTCS. For the entire sample (65+), mean FIs for males and females are statistically different for each NLTCS wave – lower for males than for females.
Table 1.
Sex-specific FIs and the number of males (M) and females (F) for each NLTCS.
| Age groups | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NLTCS | Sex | N | 65+ | 65–69 | 70–74 | 75–79 | 80–84 | 85–89 | 90–94 | 95+ |
| 1982 | M | 2166 | .266 (.003)+ | .244 (.007) | .262 (.006) | .259 (.007) | .289 (.009) | .289 (.010) | .311 (.018)* | .337 (.027) |
| F | 3921 | .277 (.002)+ | .243 (.005) | .252 (.005) | .274 (.005) | .282 (.005) | .311 (.006) | .352 (.010)* | .374 (.021) | |
| 1984 | M | 2038 | .250 (.003)* | .229 (.007) | .238 (.007) | .244 (.007) | .264 (.008) | .283 (.011) | .321 (.018) | .355 (.034) |
| F | 3891 | .259 (.002)* | .226 (.005) | .231 (.005) | .244 (.005) | .269 (.005) | .297 (.006) | .349 (.010) | .344 (.018) | |
| 1989 | M | 1470 | .241 (.004)+ | .235 (.010) | .214 (.007) | .234 (.008) | .259 (.010) | .274 (.013) | .294 (.021) | .341 (.055) |
| F | 2992 | .258 (.003)+ | .230 (.007) | .226 (.006) | .247 (.005) | .261 (.006) | .283 (.007) | .337 (.010) | .376 (.020) | |
| 1994 | M | 1736 | .191 (.004)+ | .150 (.008) | .163 (.008)* | .187 (.006) | .206 (.009)+ | .255 (.013) | .255 (.023)* | .335 (.031) |
| F | 3336 | .221 (.003)+ | .159 (.007) | .184 (.006)* | .195 (.004) | .238 (.006)+ | .272 (.007) | .317 (.012)* | .339 (.012) | |
| 1999 | M | 1805 | .196 (.004)+ | .162 (.008) | .148 (.008) | .190 (.008) | .212 (.007) | .247 (.011) | .256 (.020) | .353 (.023) |
| F | 3341 | .220 (.003)+ | .167 (.007) | .165 (.006) | .202 (.005) | .224 (.005) | .266 (.008) | .290 (.012) | .344 (.013) | |
An asterisk (plus) denotes .01<p<.05 (p<.01). Other sex differences are insignificant.
To find the best description of the age-patterns in Figure 1, we estimated several functions: linear, log-linear (or exponential), power, and quadratic. In all five NLTCS waves, and for FIs with both 32 and 26 deficits, the best fit is obtained by the quadratic function, FI = U + B1 × Age + B2 × Age2, as determined by comparisons of coefficients of determination (R2). A t-test shows statistical significance for all coefficients except for B1 and U for the 1994 wave. Because the quadratic function has three parameters, the standard errors of its coefficients are larger than for the log-linear (ln(FI) = U + B1 × Age) function (Table 2). For comparison, Table 2 also shows the R2 statistics for the linear functions in parenthesis. Two-year averaging significantly improved these estimates, increasing the percentage of total variation explained by the nonlinear relations between age and FI by up to 50%. The use of five-year age categories did not noticeably improve fits. Thus, a quadratic function accurately describes the FI age-patterns in NLTCS data (Figure 1). The best fit was obtained for 1989 (R2 = 98%).
Table 2.
Coefficients for the log-linear (Ln) and quadratic (Q) functions along with coefficients of determination (R2) for each NLTCS wave.
| NLTCS | Fit | B1 (SE) × 102 | B2 (SE) × 104 | U (SE) | R2, % |
|---|---|---|---|---|---|
| 1982 | Ln | 1.37 (.071) | −2.346 (.058) | 96.1 (93.6) | |
| Q | −1.10 (.313) | 0.93 (.193) | 0.563 (.125) | 97.7 | |
| 1984 | Ln | 1.63 (.139) | −2.615 (.113) | 90.2 (87.7) | |
| Q | −1.90 (.597) | 1.46 (.368) | 0.846 (.239) | 94.2 | |
| 1989 | Ln | 1.66 (.157) | −2.655 (.128) | 88.2 (86.0) | |
| Q | −2.81 (.360) | 2.03 (.222) | 1.202 (.144) | 98.0 | |
| 1994 | Ln | 2.72 (.116) | −3.689 (.095) | 97.3 (96.3) | |
| Q | −0.58 (.517)# | 0.75 (.318) | 0.210 (.207)# | 97.4 | |
| 1999 | Ln | 2.67 (.150) | −3.667 (.122) | 95.5 (93.8) | |
| Q | −1.63 (.514) | 1.39 (.317) | 0.627 (.206) | 97.4 |
R2 in parentheses is given for linear functions for the sake of comparison. Estimated coefficients are significant at or below the 0.05 level. A superscript “#” denotes insignificant estimates.
Despite the qualitative (shape) similarity of the age-patterns, there are quantitative differences among the waves. The largest mean age-specific FIs are for the 1982 NLTCS (Figure 1). Their difference from those of the other NLTCS waves is likely due to over-sampling of disabled individuals in the 1982 community questionnaire (91.2% in 1982 vs. 83.5% in 1984). Deviations of the 1982 NLTCS FI estimates from the exponential pattern of the age-specific FI in the CSHA is also the largest – which is also reflected in the regression coefficients (Table 2).
In 1994, the NLTCS design was changed by adding the “healthy” supplement (HS). Since individuals in the HS were designated before the survey to receive a detailed interview, the proportion of non-disabled individuals in these groups is significantly lower than in the remaining (“disabled”) group (DG) of individuals (selected for a community interview by the screener) and is closer to the proportion in the general U.S. elderly population. Specifically, according to the age-adjusted estimates in Manton and Gu (2001), the prevalence of non-disabled elderly individuals in the U.S. national population in 1999 was 80.3% and in 1994 was 77.5%. The prevalence of non-disabled respondents to the community questionnaire in the HS of the NLTCS without age standardization is 65.5% in 1999 and 80.5% in 1994. The addition of the HS reduces the mean FI for the 1994 and 1999 waves, especially at younger ages, and, as can be seen in Figure 1, brings the age-specific prevalence estimates for the FI into relatively close agreement with estimates from the CSHA.
The presence of the HS in the 1994 and 1999 waves provides an opportunity to evaluate an hypothesis on similarities/dissimilarities between the concepts of disability and frailty by estimating the difference between groups with over-sampling of disabled individuals (the Disabled Group, DG) and group with a normal (unbiased) mixture of disabled and non-disabled individuals (HS). Figure 2 shows that the age-pattern for the DG shifts up, becoming closer to the 1982–1989 patterns. By comparison, age-patterns for the HS shift down, exhibiting smaller mean FIs than those assessed from the CSHA for all age groups. Again, better fits are obtained for the quadratic function with the exception of the 1999 HS, for which the log-linear (exponential) fit is better (Table 3).
Figure 2.
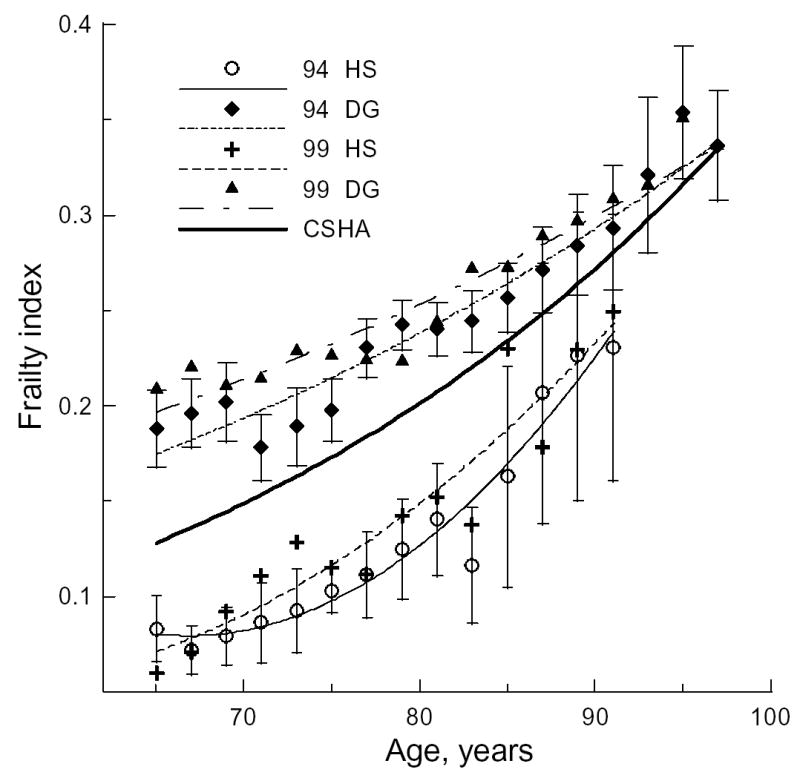
The two-year frailty index (FI) age-patterns for the “healthy” sample (HS) and the group with over-sampling of the disabled individuals (DG) for the 1994 and 1999 NLTCS. The 95% confidence intervals (CI) of means are shown by bars for 1994 HS and 1994 DG.
Table 3.
Coefficients for the quadratic and log-linear (denoted by “#”) functions fitting the data in Figure 2 for the HS and DG in 1994 and 1999 NLTCS waves.
| R2, % | |||||||
|---|---|---|---|---|---|---|---|
| NLTCS | Group | B1 (SE) × 102 | B2 (SE) × 104 | U (SE) | Q | Ln | Lin |
| 1994 | HS | −3.66 (.95) | 2.73 (.61) | 1.30 (.37) | 95.1 | 92.3 | 86.2 |
| DG | −1.54 (.55) | 1.27 (.34) | 0.65 (.22) | 95.8 | 92.9 | 91.6 | |
| 1999 | HS# | 4.83 (.46) | −5.79 (.36) | 89.0 | 90.2 | 87.3 | |
| DG | −1.54 (.45) | 1.23 (.28) | 0.69 (.18) | 96.2 | 92.5 | 91.0 | |
R2 is also given for linear (Lin) function. For all estimates p<.05.
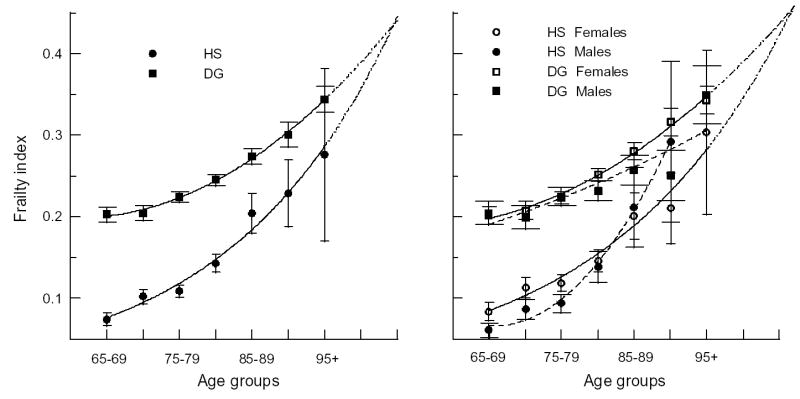
Figure 2 suggests that individuals from the HS group (small FI at young ages) accumulate deficits faster than those from the DG group (large FI at young ages). To increase statistical power, we pooled data for the 1994 and 1999 waves and averaged the FI over five-years of age. Figure 3 exhibits the 1994 and 1999 FI age-patterns for the entire pooled sample (left panel) and for both sexes (right panel), along with their nonlinear fits (Table 4). Figure 3 clearly shows that individuals from the HS accumulate deficits faster than those from the DG. The rate of deficit accumulation varies by sex. Males in the HS have smaller FIs at younger ages than females. However, HS males accumulate deficits faster than females, resulting in convergence of their FI age-patterns and a crossover at advanced ages (~85).
Figure 3.
The five-year frailty index age-patterns for the unstratified (left panel) and sex-specific (right panel) HS and DG samples for pooled 1994&1999 data. Dashed-dotted line denotes extrapolation of the respective fitted curves. Bars show 95% CI. Dashed (continuous) line on the right panel denotes fits for males (females).
Table 4.
Coefficients of the best statistically significant (p<.05) fits corresponding to the curves in Figure 3.
| Group | Sex | Fit | B1 (SE) × 102 | B2 (SE) × 104 | U (SE) | R2, % |
|---|---|---|---|---|---|---|
| HS | M&F | Ln | 4.42 (.27) | −5.45 (.22) | 98.1 | |
| M | Q | −5.05 (.96) | 3.84 (.62) | 1.73 (.37) | 99.3 | |
| F | Ln | 4.02 (.31) | −5.08 (.25) | 97.1 | ||
| DG | M&F | Q | −1.51 (.23) | 1.24 (.15) | 0.66 (.09) | 99.7 |
| M | Ln | 1.57 (.34) | −2.68 (.27) | 81.0 | ||
| F | Q | −1.07 (.37) | 0.98 (.23) | 0.48 (.14) | 99.4 |
4. Discussion and Conclusions
Our results reveal large differences between FI age-patterns for the 1982, 1984, and 1989 NLTCS waves as compared to the 1994 and 1999 waves, which appear to be due to the presence of a “healthy” sample in the two later waves. The age-patterns for the last two waves resemble those from the CSHA. Our analyses show that in all cases (i.e., for each NLTCS wave and for 32- and 26-deficit FIs) the mean FI increases with age and that this increase is nonlinear: i.e., older people accumulate more deficits per year than younger individuals. Thus, we confirm the accelerated increase of the FI with age revealed in several national studies (Mitnitski et al., 2005; Mitnitski and Rockwood, 2006).
In most cases, the age-pattern is best described as a quadratic function. This means that the rate of increase also increases with age (in a linear fashion), stressing the nonlinear nature of deficit accumulation. The best fits, when quadratic fits are insignificant, were exponential. Comparison of our results across NLTCS waves as well as with those from Canadian (Mitnitski et al., 2004) and Chinese (Goggins et al., 2005) studies allows us to conclude that the particular form of the FI age-patterns might be different across settings – largely depending on the survey design. However, what seems to be essential and holds across settings is the accelerated increase of the FI with age (although it can decelerate at advanced ages; see Goggins et al., 2005).
An aging marker monotonically changing with chronological age can be considered as a candidate for a measure of biological (or functional) age. Although aging indicators are usually expected to have a linear relation with chronological age (Karasik et al., 2005), it can be argued that the relation should be, generally, nonlinear. One basis for this expectation is the high plasticity and age-dependence of mortality rate variation in experiments with anti-aging interventions aimed to increase longevity (Vaupel et al., 2003). Valid markers of aging must capture these properties; i.e., they must have a nonlinear relation with chronological age. Another argument is that the overall rate of somatic aging might be a superposition of different biological processes, each with distinct age dynamics, which then might result in nonlinear change of biological age indices with chronological age (Nakamura et al., 1998; Ukraintseva and Yashin, 2001; Arbeev et al., 2005).
An essential difference between FI and conventional biomarkers of aging is that the FI characterizes integrative (i.e., systemic) changes in aging individuals. These changes can be attributed to physiological aging per se and its interaction with environment, as follows from the nonlinear (accelerated) FI age-patterns. The evidence for that can be obtained from the general conception of frailty as a physiological state of non-specific vulnerability to stressors (Fried et al., 2004). Indeed, individuals will likely accumulate deficits when stresses exceed the limits of an organism’s stress-resistance. It is reasonable to assume that deficits accumulate proportionally to the difference between the stress-strength and stress-resistance, which can be called as the stress-load. Then, if the stress-load is constant with age, the FI would change linearly due to its cumulative nature. But an accelerated increase of the FI with age indicates that the stress-load increases with age. This can occur when: i) stress-strength increases while stress-resistance is constant, ii) stress-resistance decreases while stress-strength is constant, and iii) both these levels decline with distinct rates. The loss of stress-resistance is a fundamental feature of biological aging (Jazwinski et al., 1998). Recent population studies of aging in laboratory animals confirm a connection between the decline in stress-resistance and aging for many types of stress factors (Semenchenko et al. 2004). This suggests that the first scenario (i) is unrealistic. Unlike laboratory experiments with animals, humans live embedded in environments. Therefore, in addition to aging changes similar to those in experimental animals, they also experience the effects of various environmental factors. In fact, individuals do not respond to stresses in the same way across their life span, but rather experience age-associated behavioral adaptation (Boerner, 2004). This adaptation will result in a decline of the stress-strength level with aging. Therefore, the second scenario (ii) is also unrealistic. Consequently, we have to assume that both levels (i.e., stress-strength and stress-resistance) decline with aging. Then, the nonlinear change of the FI with age seems to be an inherent feature of valid systemic cumulative indicators of aging.
Furthermore, the decline of stress-resistance with aging is also a multi-component process with major contributions of somatic aging and the environment. The environmental contribution results in changes in allostasis (i.e., capacity for physiological adaptation). Inefficiency in allostasis leads to cumulative effects over the long run (allostatic load) which results in over-declining stress resistance for non-experimental subjects (which can be termed an allostatically loaded stress-resistance decline). Therefore, the FI likely reflects the complex interplay of distinct aging-associated processes in a whole organism and, thus, can be considered as a systemic measure of aging. Further evidences toward this view follows from similarity between the FI and mortality-rate age patterns (Mitnitski et al., 2004; Kulminski et al., 2006), as well as from the association of the mortality rates and relative risks of death with FI (Kulminski et al., 2006; Goggins et al., 2006). Consequently, the FI might be a useful systemic indicator of aging, specifically for large-scale population-based studies for which biomarkers of aging are rarely available. It can be also a useful characteristic for describing population heterogeneity in various models of aging and mortality, which can be implemented using, for instance, microsimulation procedures designed to assess the impact of individual states (Akushevich et al., 2005).
Our data allow us to show that the nonlinear relationship between FI and chronological age also holds for the general population of community-dwelling elderly, although the FI age-patterns for them tend to shift to lower FI values. Indeed, individuals for the DG were selected following standard NLTCS procedures (i.e., screening in disabled individuals), while for the HS they were selected irrespective of disability. Since the screener NLTCS participants were primarily selected from among U.S. Medicare-eligible persons to provide a nationally-representative sample according to demographic factors, the likelihood of systematic bias resulting in selection of individuals for HS with specific health problems is low. This fact has been also verified by comparing the FI age-patterns for the HS and for the U.S. community-dwelling elderly. The latter sample was obtained from the respective NLTCS wave (1994 or 1999) using weights developed by the U.S. Bureau of the Census and the Center for Demographic Studies (Duke University) to produce national estimates. Both (weighted and HS) estimates show excellent agreement, especially at younger ages – suggesting that despite a lower mean age-specific FI in the general population of community-dwelling elderly, the nonlinear shape of the FI age-patterns remains.
The NLTCS data also provide evidence on complex (nonlinear) relationships between the FI, sex, and chronological age. To understand this complexity, we make four observations. First, the mean FI for males is smaller than for females for each NLTCS wave. This agrees with other findings (Mitnitski et al., 2004; Goggins et al., 2005). However, this difference is not large. Second, there generally are not statistically significant sex differences between age-specific FIs. Third, there is no overall trend in the data for the FI for males to be less than for females. Fourth, analysis of the sex-specific FIs for different age groups shows two opposite tendencies in the sex-sensitivity of FI behaviors with age (Table 1). Specifically, at younger ages in the early waves, FIs are nearly identical but have a tendency to diverge with age. For the two latest waves, there is a tendency towards convergence of these indices at extreme ages. Since the two later waves have a smaller proportion of disabled individuals due to the presence of the HS, it is reasonable to assume that the latter fact is responsible for such a change. Indeed, when considering the DG and HS separately (Figure 3), the qualitative change of the FI with age becomes more pronounced. Males and females in the DG have essentially similar FIs at younger ages — but the opposite is seen for the HS. This is a clear nonlinear effect – the relation between FIs for males and females is both FI- and age-dependent. A consequence is that in different settings (e.g., institutional vs. hospital vs. community) the relation between FI for males and females can be qualitatively different.
An intriguing finding of our study is that FIs for HS and DG converge at the oldest-old ages; i.e., the rate of deficit accumulation for individuals in the HS is larger than in the DG. Such behavior becomes even more pronounced in male and female sub-groups. The rate of deficit accumulation for females is larger than for males for the DG. For the HS, we see the opposite situation. As a consequence, the difference in the rates results in a divergence of FI age-patterns for males and females in the DG and in their convergence in the oldest-old ages for the HS. Convergence of the FI age-patterns for males and females was also observed in Mitnitski et al. (2002b), supporting the general nature of this phenomenon. This behavior was discussed in terms of the “compensation law of mortality” (Gavrilov and Gavrilova, 2006) suggesting the presence of the “frailty compensation relationship” (Mitnitski et al., 2002b). Figure 3 (right panel) also suggests that sensitivity to the quantity of the accumulated deficits is higher for males than for females. This follows from the fact that males and females accumulate deficits with age at different rates and differently in the DG and the HS. Changes in rates between the DG and HS are larger for males than for females.
Our findings suggest that concepts of frailty and disability can be either entangled or untangled depending on age; i.e., they can be age-sensitive. At early ages, our data supports the hypothesis that disability and frailty are untangled concepts (Fried et al., 2004). However, at advanced ages, it seems that the difference between them tends to vanish. More interestingly, such behavior is sex-insensitive – suggesting that disability and frailty reflect more fundamental aging processes than those related to sex differences. Our findings can be also interpreted as a cross-sectional manifestation of a compression of morbidity in that “healthy” individuals accumulate deficits faster than “unhealthy” – supporting the argument that morbidity can be postponed to advanced ages.
Convergence of the FI age-patterns for the DG and HS provides further support for considering the FI as a systemic measure of the aging process. Indeed, it is likely that individuals in the DG accumulated deficits earlier in life (before age 65) because they experienced larger stresses at certain age period (e.g., due to stresses associated with retirement) and/or their levels of stress resistance were lower than those of more healthy individuals (i.e., because of genetic or other factors affecting this trait). In such circumstances, DG individuals acquiring deficits will experience a larger decrease in stress-resistance than individuals from the HS. However, this is not the only process affecting aging since individuals will also experience complex processes of adaptation of their function to declining health/well-being status, as discussed above.
In fact, we can distinguish at least two adaptation processes. The first process is one of behavioral adaptation, which is associated with the fact that less healthy individuals experience larger assimilative and accommodative adaptation (by changing their behavior) to their declined health/well-being status (Boerner, 2004; Menzel et al., 2002). Such behavioral responses will result in over-declining the stress-strength level for individuals from the DG with respect to that for individuals from the HS (Figure 4).
Figure 4.
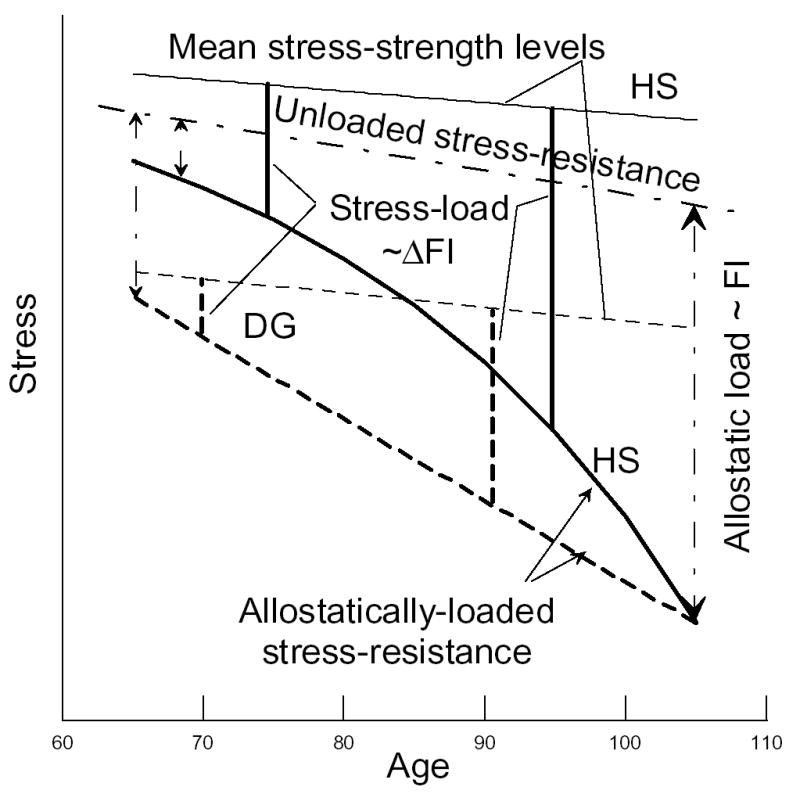
Schematic representation of aging-associated processes and connections between the FI and declining stress-resistance. The continuous (dashed) line depicts the more healthy, HS, (less healthy, DG) individuals at younger ages. Dashed-dotted line denotes the impact of the allostatic load (proportional to the FI) on stress-resistance. Increments in the FI (ΔFI) are proportional to the stress-load. See text for discussion.
Recent studies show that individuals with health disorders can also experience adaptation of their physiological functions at physiological, tissue, cellular and molecular levels. For instance, the human brain can experience functionally relevant adaptive changes even after serious neurological damages (e.g., stroke) (Ward, 2005). The heart and artery walls can remodel their geometry, structure and composition adaptively responding to altered stress-loading conditions (e.g., hypertension) (Satcher et al., 1997; Patten et al., 1998). Elder coronary patients can improve peak aerobic capacity due to adaptation of their peripheral skeletal muscle (Ades et al., 1996). Thus, the second process is due to physiological adaptation, which results in relative increasing (with respect to the HS individuals) stress-resistance levels. Superposition of the physiological processes (i.e., decrease of stress-resistance due to accumulated deficits and physiological adaptation to this declined health/well-being status) result in allostatically loaded stress-resistance. Since we characterize health/well-being disorders by the FI, and since allostatic load reflects gradual damage to an organism by allostasis, it is reasonable to propose that allostatic load is proportional to the FI. Then the FI will provide a measure of the difference between unloaded (i.e., when FI=0) and allostatically loaded stress-resistance. This is schematically shown in Figure 4, assuming, for simplicity, that the unloaded stress-resistance is the same for HS and DG.
An individual’s capacity for adaptation does not remain constant during the life course. The role of the accommodative behavioral adaptation, for instance, can increase with age (Boerner, 2004). Individuals acquiring deficits at younger ages have larger chances for physiological adaptation than at older ages due to larger allostatic capacity at younger ages (Testa et al., 2005). These processes can result in age-dependence of the rates of stress-resistance and/or stress-strength decline. Age-sensitivity of the physiological adaptation suggests that individuals from the HS will experience a more rapid decline since they acquire deficits later in life and, thus, have lower reserves for an adaptive physiological response. The FI can capture this process since the FI increment (ΔFI, e.g., FI at 70 years minus FI at 69 years) is proportional to the difference between declining stress-strength and stress-resistance levels (i.e., stress-load), i.e., ΔFI is a measure of the stress-load at a given age. Our analysis shows that the stress-load for HS individuals is nonlinear function of age. However, it remains uncertain what the nature of this nonlinearity and the contributions of the physiological and behavioral adaptation processes are. Further analysis is needed to clarify the roles of the physiological and behavioral processes as well as to distinguish between nonlinearity in the mean stress-strength level decline (e.g., due to aging-associated changes in the behavioral adaptation) and in allostatically-loaded stress-resistance decline (e.g., due to aging-associated changes in the physiological adaptation). Assuming that the stress-strength level declines linearly with age, individuals from the DG will experience a linear increase of the stress-load and, respectively, a linear decline of the allostatically-loaded stress-resistance, ALSR, (ALSR = −3.6·10−4 + 0.052Age, R2 = 1.0) since they accumulate deficits according to quadratic function (Table 4, Figures 3 and 4). Individuals from the HS accumulate deficits (FI) exponentially (Table 4 and Figure 3). Consequently, their stress-resistance will decline according to quadratic law, i.e., ALSR = −2.2·10−3 + 9.76·10−4 Age −8.27·10−6 Age2 (R2 = 0.999) (Figure 4). Note that an alternative justification of the nonlinear nature of the process of deficit accumulation is suggested by the reliability theory as discussed by Gavrilov and Gavrilova (2006).
The allostatic load at the highest ages, when all individuals die, can be considered as a measure of a mean limit of adaptive capacity (both behavioral and physiological) of organisms. Consequently, the FI will provide an observable outcome for this limit. Surprisingly, in our study these limits are the same for individuals with essentially distinct health/well-being histories and are given by the crossover of the respective FI age patterns (Figure 3), at which only a few individuals remain alive. An important message from this finding is that less healthy individuals at younger ages have an opportunity to live as long as more healthy individuals provided that sufficient care is devoted to training of their physiological and/or behavioral adaptation capacities.
Since the FI can characterize the aging process, it is possible to introduce respective systemic measure of aging (i.e., FI-specific or systemic age), which can be quantified similarly to as biological age, i.e., as the mean age of individuals with the same FI. It can be estimated from an inverse regression of the age on FI (Mitnitski et al., 2002a). Then the crossover point of the FI age patterns for the DG and the HS will indicate the limit of the FI-specific age which coincides with the limit of the organism’s adaptive capacity. Specifically, the extrapolated FI-pattern fits for the HS and DG samples have a crossover at FI = 0.437 and the estimated inverse regression of age on FI for HS as A = 122.5 + 22.2 ln FI. Substituting FI = 0.437 into this expression, we obtain an estimate of a mean systemic age limit of 104.1 years. Our data show that males and females follow different aging trajectories. Interpolation of the female-specific fits for the HS and DG to extreme ages provides a reasonable estimate for the female FI-specific age limit of approximately 106.1 years (FI = 0.455). For males, we obtain a limit of 87.1 years (FI = 0.277). This estimate, however, was imprecise due to the small sample of males at those ages. The difference in these limits for males and females may be the reason why there are opposite tendencies in the sex-specific FI age-patterns in the DG and HS. Indeed, since males have a lower limit, those who are in the HS accumulate deficits with age faster than females. For the same reason, males in the DG accumulate deficits with age slower than females.
Convergence of the FI age-patterns at the oldest ages does not mean that longevity cannot be extended beyond those ages. It rather exhibits a systemic feature of the aging process and indicates the need for development of adequate systemic methods of coping with this phenomenon. Methods focusing on slowing down the rates of deficit accumulation, decline in stress-resistance, adaptive capacity, and/or stress-strength will result in extension of both life span and active life span. Consequently, the FI-specific age limit might be changed with improvements in economic standard of living, social conditions, education, dietary and life style practices, and medical progress (Riley, 2001). Clearly, the cross-sectional design of this study produces only initial insights into the FI as an indicator of aging. Further insights require longitudinal analyses of the rates of deficit accumulation. This work is now in progress and will be published elsewhere.
Acknowledgments
The research reported here was supported in part by P01-AG-017937-05, 5R01AG027019-02, and 5R01AG028259-02 grants from the National Institute on Aging (NIA). A.K. also acknowledges support from K12-AG-000982-05 NIA grant.
References
- Ades PA, Waldmann ML, Meyer WL, Brown KA, Poehlman ET, Pendlebury WW, Leslie KO, Gray PR, Lew RR, LeWinter MM. Skeletal muscle and cardiovascular adaptations to exercise conditioning in older coronary patients. Circulation. 1996;94:323–330. doi: 10.1161/01.cir.94.3.323. [DOI] [PubMed] [Google Scholar]
- Akushevich I, Kulminski A, Manton K. Life Tables with Covariates: Dynamic Model for Nonlinear Analysis of Longitudinal Data. Mathematical Population Studies. 2005;12:51–80. [Google Scholar]
- Arbeev K, Ukraintseva S, Arbeeva L, Yashin A. Mathematical Models for Human Cancer Incidence Rates. Demographic Research 12-10. 2005:237–271. [Google Scholar]
- Boerner K. Adaptation to disability among middle-aged and older adults: the role of assimilative and accommodative coping. J Gerontol B Psychol Sci Soc Sci. 2004;59:35–42. doi: 10.1093/geronb/59.1.p35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bortz W., 2nd A conceptual framework of frailty: a review. J Gerontol Med Sci. 2002;57:M283–288. doi: 10.1093/gerona/57.5.m283. [DOI] [PubMed] [Google Scholar]
- Fried L, Ferrucci L, Darer J, Williamson J, Anderson G. Untangling the Concepts of Disability, Frailty, and Comorbidity: Implications for Improved Targeting and Care. J Gerontol Med Sci. 2004;59:255–263. doi: 10.1093/gerona/59.3.m255. [DOI] [PubMed] [Google Scholar]
- Gavrilov L, Gavrilova N. Reliability Theory of Aging and Longevity. In: Masoro EJ, Austad SN, editors. Handbook of the Biology of Aging. Academic Press; San Diego, CA, USA: 2006. pp. 3–42. Sixth Edition. [Google Scholar]
- Goggins W, Woo J, Sham A, Ho S. Frailty index as a measure of biological age in a Chinese population. J Gerontol Med Sci. 2005;60:1046–1051. doi: 10.1093/gerona/60.8.1046. [DOI] [PubMed] [Google Scholar]
- Jazwinski S, Kim S, Lai CY, Benguria A. Epigenetic stratification: The role of individual change in the biological aging process. Exp Gerontol. 1998;33:571–80. doi: 10.1016/s0531-5565(98)00029-1. [DOI] [PubMed] [Google Scholar]
- Karasik D, Demissie S, Cupples L, Kiel D. Disentangling the genetic determinants of human aging: biological age as an alternative to the use of survival measures. J Gerontol Med Sci. 2005;60:574–587. doi: 10.1093/gerona/60.5.574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkwood TB, Feder M, Finch CE, Franceschi C, Globerson A, Klingenberg CP, LaMarco K, Omholt S, Westendorp RG. What accounts for the wide variation in life span of genetically identical organisms reared in a constant environment? Mech. Ageing Dev. 2005;126:439–443. doi: 10.1016/j.mad.2004.09.008. [DOI] [PubMed] [Google Scholar]
- Kirkwood TB. Molecular gerontology. J Inherit Metab Dis. 2002;25(3):189–196. doi: 10.1023/a:1015625811569. [DOI] [PubMed] [Google Scholar]
- Kulminski A, Yashin A, Akushevich I, Ukraintseva S, Land K, Arbeev K, Manton K. Cumulative Index of Age-Associated Health Disorders as a Major Indicator of Aging Processes and Mortality Risks in Elderly Populations: Results From Analyses of the National Long Term Care Survey; Final program and abstracts, 2006 Population Association of America annual meeting; 30 March – 1 April, 2006; Los Angeles, USA. 2006. p. 203. [Google Scholar]
- Manton K, Gu X. Changes in the prevalence of chronic disability in the U.S. black and non-black population above age 65 from 1982 to 1999. PNAS. 2001;98:6354–6359. doi: 10.1073/pnas.111152298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menzel P, Dolan P, Richardson J, Olsen JA. The role of adaptation to disability and disease in health state valuation: a preliminary normative analysis. Soc Sci Med. 2002;55:2149–2158. doi: 10.1016/s0277-9536(01)00358-6. [DOI] [PubMed] [Google Scholar]
- Mitnitski A, Mogilner A, Rockwood K. Accumulation of deficits as a proxy measure of aging. Sci World. 2001;1:323–336. doi: 10.1100/tsw.2001.58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitnitski A, Graham J, Mogilner A, Rockwood K. Frailty, fitness and late-life mortality in relation to chronological and biological age. BMC Geriatr. 2002a;2:1–8. doi: 10.1186/1471-2318-2-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitnitski A, Mogilner A, MacKnight C, Rockwood K. The accumulation of deficits with age and possible invariants of aging. Sci World. 2002b;2:1816–1822. doi: 10.1100/tsw.2002.861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitnitski A, Song X, Rockwood K. The Estimation of Relative Fitness and Frailty in Community-Dwelling Older Adults Using Self-Report Data. J Gerontol Med Sci. 2004;59:M627–632. doi: 10.1093/gerona/59.6.m627. [DOI] [PubMed] [Google Scholar]
- Mitnitski A, Song X, Skoog I, Broe GA, Cox JL, Grunfeld E, Rockwood K. Relative fitness and frailty of elderly men and women in developed countries and their relationship with mortality. J Am Geriatr Soc. 2005;53:2184–2189. doi: 10.1111/j.1532-5415.2005.00506.x. [DOI] [PubMed] [Google Scholar]
- Mitnitski A, Rockwood K. Decrease in the relative heterogeneity of health with age: a cross-national comparison. Mech Ageing Dev. 2006;127:70–72. doi: 10.1016/j.mad.2005.09.007. [DOI] [PubMed] [Google Scholar]
- Nakamura E, Lane M, Roth G, Ingram D. A strategy for identifying biomarkers of aging: further evaluation of hematology and blood chemistry data from a calorie restriction study in rhesus monkeys. Exp Gerontol. 1998;33:421–443. doi: 10.1016/s0531-5565(97)00134-4. [DOI] [PubMed] [Google Scholar]
- Patten RD, Udelson JE, Konstam MA. Ventricular remodeling and its prevention in the treatment of heart failure. Curr Opin Cardiol. 1998;13:162–167. [PubMed] [Google Scholar]
- Riley J. Rising Life Expectancy: A Global History. Cambridge: Cambridge Univ. Press; 2001. [Google Scholar]
- Rockwood K, Hogan D, MacKnight C. Conceptualization and Measurement of Frailty in Elderly People. Drugs Aging. 2000;17:295–302. doi: 10.2165/00002512-200017040-00005. [DOI] [PubMed] [Google Scholar]
- Rockwood K, Mogilner A, Mitnitski A. Changes With Age in the Distribution of a Frailty Index. Mech Ageing Dev. 2004;125:517–519. doi: 10.1016/j.mad.2004.05.003. [DOI] [PubMed] [Google Scholar]
- Rockwood K, Song X, MacKnight C, Bergman H, Hogan DB, McDowell I, Mitnitski A. A global clinical measure of fitness and frailty in elderly people. CMAJ. 2005;173:489–95. doi: 10.1503/cmaj.050051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satcher R, Dewey CF, Hartwig JH. Mechanical remodeling of the endothelial surface and actin cytoskeleton induced by fluid flow. Microcirculation. 1997;4:439–453. doi: 10.3109/10739689709146808. [DOI] [PubMed] [Google Scholar]
- Semenchenko GV, Khazaeli AA, Curtsinger JW, Yashin AI. Stress resistance declines with age: analysis of data from a survival experiment with Drosophila melanogaster. Biogerontology. 2004;5(1):17–30. doi: 10.1023/b:bgen.0000017681.46326.9e. [DOI] [PubMed] [Google Scholar]
- Testa JA, Malec JF, Moessner AM, Brown AW. Outcome after traumatic brain injury: effects of aging on recovery. Arch Phys Med Rehabil. 2005;86:1815–1823. doi: 10.1016/j.apmr.2005.03.010. [DOI] [PubMed] [Google Scholar]
- Ukraintseva SV, Yashin AI. How individual aging may influence human morbidity and mortality patterns. Mech Ageing Dev. 2001;122:1447–1460. doi: 10.1016/s0047-6374(01)00277-9. [DOI] [PubMed] [Google Scholar]
- Vanitallie T. Frailty in the elderly: contributions of sarcopenia and visceral protein depletion. Metabolism. 2003;52:22–26. doi: 10.1016/s0026-0495(03)00297-x. [DOI] [PubMed] [Google Scholar]
- Vaupel J, Carey J, Christensen K. It's Never Too Late. Science. 2003;301:1679–1681. doi: 10.1126/science.1090529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward NS. Mechanisms underlying recovery of motor function after stroke. Postgrad Med J. 2005;81:510–514. doi: 10.1136/pgmj.2004.030809. [DOI] [PMC free article] [PubMed] [Google Scholar]