A PDZ domain recapitulates a unifying mechanism for protein folding

Abstract

A unifying view has been recently proposed according to which the classical diffusion–collision and nucleation–condensation models may represent two extreme manifestations of an underlying common mechanism for the folding of small globular proteins. We report here the characterization of the folding process of the PDZ domain, a protein that recapitulates the three canonical steps involved in this unifying mechanism, namely: (i) the early formation of a weak nucleus that determines the native-like topology of a large portion of the structure, (ii) a global collapse of the entire polypeptide chain, and (iii) the consolidation of the remaining partially structured regions to achieve the native state conformation. These steps, which are clearly detectable in the PDZ domain investigated here, may be difficult to distinguish experimentally in other proteins, which would thus appear to follow one of the two limiting mechanisms. The analysis of the (un)folding kinetics for other three-state proteins (when available) appears consistent with the predictions ensuing from this unifying mechanism, thus providing a powerful validation of its general nature.

Providing a complete characterization of the mechanism of protein folding is one of the great challenges in molecular biology (1–5). Classically, two distinct mechanisms have been used to describe the folding of many small globular proteins (1). Some proteins, such as barnase (6), En-HD (7), and the λ_6–85 repressor fragment (8, 9), appear to fold in a stepwise manner, with rapid formation of individual nuclei, typically comprising secondary structure elements, followed by their rate limiting docking and consolidation (diffusion–collision model) (2, 10). The folding of several other proteins, with chymotrypsin inhibitor 2 as a paradigm (11), takes place via the formation of a weakly structured local nucleus with simultaneous formation of extended structure (nucleation–condensation model) (12). The recent discovery that proteins within the homeodomain-like family may fold either by diffusion–collision or by nucleation–condensation led to the view that these two types of behavior may represent opposite manifestations of a common unifying mechanism (13, 14). Until now, however, no protein has been identified that exhibits clearly all of the steps predicted by such a unifying mechanism.

An effective strategy to characterize the folding mechanism of a protein is to identify the intermediates in the reaction and the transition states between them, and to characterize their structures. However, because transition states never accumulate, information about their structures can only be obtained indirectly. By mutating systematically well chosen side chains while measuring their effect on kinetics and stability, it is possible to map out interaction patterns in the transition state (15). Following this approach, the extent of the contacts formed by a residue in the transition state is measured by the Φ value, which reflects the change in activation free energy divided by the change in stability of the native state upon mutation. Furthermore, because mutations that destabilize the transition state target contacts formed while crossing the barrier, the experimentally determined Φ values can be used as restrains in molecular dynamics simulations to determine ensembles of structures representing folding transition states (16), following a procedure similar to that used when interproton distances are measured through nuclear Overhauser effects in NMR spectroscopy (17).

In a previous study, we extensively characterized the kinetic folding mechanism of the second PDZ repeat from Protein Tyrosine Phosphatase-Bas Like (PDZ2), a small αβ protein (Protein Data Bank ID code 1GM1). Experimental results suggested the presence of a high-energy intermediate as revealed by a pronounced nonlinear dependence of the logarithm of unfolding rate constants on denaturant concentration (18). Such an intermediate may become experimentally undetectable depending on the conditions, giving rise to an apparent two-state folding kinetics in the presence of a stabilizing salt (sodium sulfate). By employing classical kinetic analysis, we identified two activation barriers along the reaction coordinate, corresponding to a more unfolded transition state TS1 and a more native-like transition state TS2. Here we present the results of an approach that enables us to describe the folding mechanism of PDZ2 at atomic resolution. In particular, we characterize the structure of both TS1 and TS2 employing the Φ value analysis to impose structural restraints in molecular dynamics simulations. By analyzing the structures and energetics of different states along the PDZ2 folding process, we provide evidence that its folding mechanism is distinct from the pure diffusion–collision as well as from the nucleation–condensation mechanism, but displays characteristic features of both models. On the basis of these observations, we suggest that PDZ2 provides a clear example of a unifying folding mechanism, and use this protein to characterize the canonical steps involved in such a mechanism.

Results and Discussion

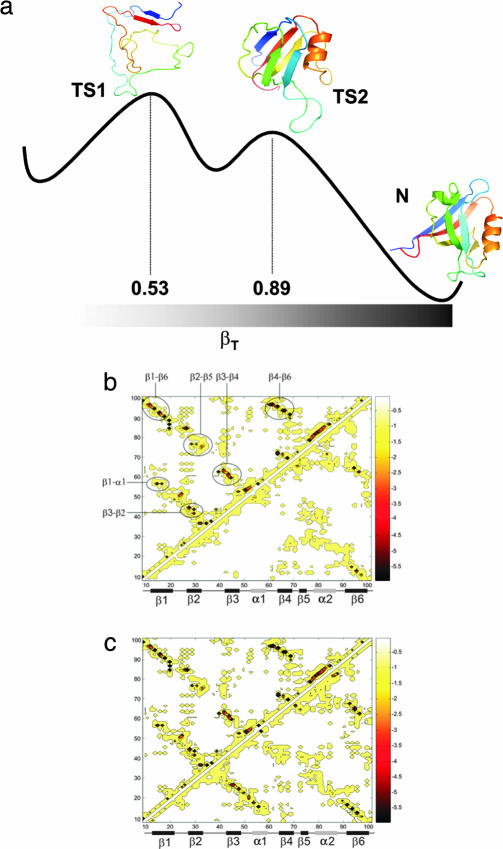
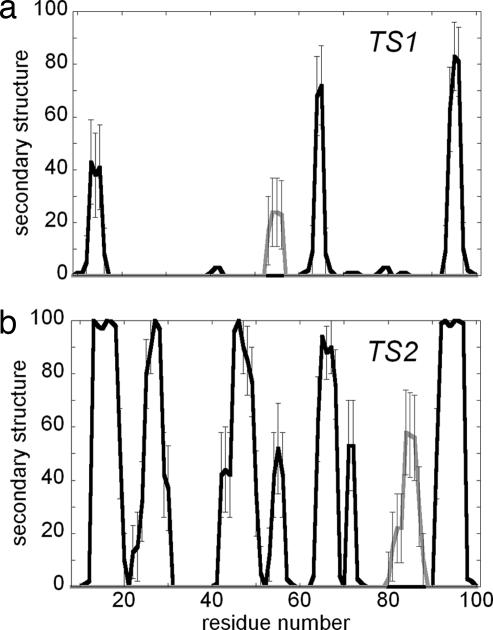
We studied the folding pathway of PDZ2 by Φ-value analysis. Thirty-one mutants were produced, expressed, purified and characterized (Table 1). Urea-induced equilibrium and kinetic denaturation experiments were carried out both in the presence and in the absence of a stabilizing salt (0.4 M sodium sulfate). Twenty-two Φ values could be calculated from the pool of well chosen (19) mutants. For each of these mutants, in the absence of stabilizing salt, it was possible to obtain two sets of Φ values (Φ_TS1 and Φ_TS2), whereas only one (Φ_TS1) was obtained in the presence of 0.4 M sodium sulfate, where folding is dominated by only one rate-limiting barrier (18). Calculated Φ values were found to be essentially insensitive to denaturant concentration (data not shown). Despite the apparent dependence of the folding kinetics of PDZ2 on the presence of sodium sulfate, there was an excellent agreement between Φ_TS1 values calculated under the two experimental conditions (with a correlation coefficient of 0.95), indicating that sodium sulfate stabilizes the protein (and the native-like TS2 energy barrier) without significantly altering the folding mechanism. We then determined two ensembles of structures representing the transition states for folding of PDZ2 using molecular dynamics simulations restrained by the experimentally measured Φ values (16). In these simulations, Φ values are interpreted as the fraction of native interactions formed by a given residue in the transition state (see Materials and Methods). Representative structures for the two transition states ensembles are shown in Fig. 1a, together with a schematic energy diagram for the observed folding reaction. The overall topology of the early transition state (TS1) appears to be very heterogeneous and quite expanded [β Tanford value of 0.53 ± 0.03 and solvent-exposed surface area (SASA) of 8,800 ± 500 Ų; for comparison the native state value is 5,450 ± 100 Ų]. A specific cluster of strong interresidue interactions in β strands 1, 4, and 6 could be identified in all of the structures of the ensemble; these interactions (see Fig. 1b) include Leu-66–Leu-95 and Arg-64–Glu-97 (between β4 and β6) and Asp-12–Lys-98, Phe-14–Leu-96 and Val-16–Leu-94 (between β1 and β6). The presence of this cluster restricts significantly the number of possible conformations of the polypeptide chain committing the structure to a native-like topology. The energy map shown in Fig. 1b provides a complementary illustration of how some specific native-like interactions (indicated by circles labeled with the corresponding interactions between secondary structure elements) are already present in TS1, and are crucial to establish a native-like topology by creating a weakly formed folding nucleus. The second transition state (TS2) is more compact (β Tanford value of 0.89 ± 0.03, SASA of 6,240 ± 350 Ų) and displays a more pronounced native-like topology (Fig. 1c) together with a high degree of secondary structure formation (the β sheet content increases from ≈40% in TS1 to ≈75% in TS2, Fig. 2). The overall architecture of TS2 is defined by the presence of stabilizing interactions between residues in β1, β3, β4, and β6 with further supporting interactions involving residues in β1 and α1; these interactions (see Fig. 1c), in addition to those already present in TS1, include Gly-26–Ile-48 and Ser-28–Ala-46 (between β2 and β3), and Glu-17–Asp-56 and Ala-19–Glu-54 (between β1 and α1). All these contacts display high Φ values and, according to a diffusion–collision description, represent individual nuclei for the folding of PDZ2.

Table 1.

Φ value for the folding of PDZ2

Mutant	ΔΔGD—N	ΦTS1*	ΦTS1†	ΦTS2†
V16A	2.14 ± 0.12	0.27 ± 0.04	0.23 ± 0.02	0.62 ± 0.05
L18A	3.52 ± 0.14	0.22 ± 0.03	0.09 ± 0.01	0.37 ± 0.01
T21S	0.05 ± 0.09	—‡	—‡	—‡
L25A	2.41 ± 0.12	0.13 ± 0.04	0.18 ± 0.15	0.33 ± 0.11
I27V	1.58 ± 0.13	0.24 ± 0.06	0.15 ± 0.03	0.43 ± 0.04
V29A	3.23 ± 0.15	0.09 ± 0.02	0.10 ± 0.09	0.44 ± 0.12
T30S	0.23 ± 0.08	—‡	—‡	—‡
V33A	−0.21 ± 0.06	—‡	—‡	—‡
V33G	0.1 ± 0.07	—‡	—‡	—‡
T35S	0.1 ± 0.09	—‡	—‡	—‡
T35G	−0.31 ± 0.04	—‡	—‡	—‡
I42V	0.72 ± 0.08	0.20 ± 0.11	0.17 ± 0.09	0.61 ± 0.06
V44A	3.66 ± 0.16	0.04 ± 0.03	−0.04 ± 0.01	0.39 ± 0.03
A46G	0.88 ± 0.04	0.28 ± 0.17	0.18 ± 0.05	0.67 ± 0.05
I47V	0.11 ± 0.04	—‡	—‡	—‡
A52G	2.22 ± 0.16	0.00 ± 0.05	0.02 ± 0.03	0.20 ± 0.03
A53G	2.39 ± 0.16	−0.01 ± 0.04	0.04 ± 0.03	0.12 ± 0.03
I59V	1.08 ± 0.09	0.06 ± 0.06	0.08 ± 0.06	0.41 ± 0.06
V65A	4.01 ± 0.15	0.49 ± 0.02	0.41 ± 0.09	0.60 ± 0.09
L66A	2.34 ± 0.14	0.57 ± 0.03	0.45 ± 0.06	0.81 ± 0.07
V68A	2.17 ± 0.16	0.62 ± 0.05	0.45 ± 0.03	0.80 ± 0.09
L73A	3.07 ± 0.14	0.34 ± 0.02	0.25 ± 0.04	0.42 ± 0.05
K79A	−0.67 ± 0.05	—§	—§	—§
K79G	1.21 ± 0.10	0.41 ± 0.06§	0.45 ± 0.09§	0.96 ± 0.04§
A81G	1.86 ± 0.13	0.54 ± 0.04	0.45 ± 0.08	0.91 ± 0.04
E83A	0.82 ± 0.04	—§	—§	—§
E83G	1.28 ± 0.04	0.43 ± 0.06§	0.39 ± 0.02§	0.77 ± 0.05§
L85A	4.20 ± 0.16	0.33 ± 0.02	0.18 ± 0.07	0.49 ± 0.09
V92A	1.56 ± 0.11	0.72 ± 0.1	0.70 ± 0.06	0.72 ± 0.09
L94A	4.50 ± 0.13	0.48 ± 0.01	0.38 ± 0.05	0.57 ± 0.12
L96A	3.36 ± 0.14	0.57 ± 0.02	0.57 ± 0.09	0.76 ± 0.11

Calculated in the presence (∗) and

in the absence (†) of 0.4 M sodium sulfate using standard equations. In the case of PDZ2, Φ values were found to be essentially insensitive to denaturant concentrations.

^‡These mutants display thermodynamic stabilities similar to wild-type PDZ2 (ΔΔG < 0.5 kcal·mol⁻¹), which prevents accurate calculation of Φ values.

^§Ala—Gly scanning mutants. In order to detect structure formation in helix2, the two solvent exposed residues in such a helix (K79 and E83) were mutated into Ala and Gly. A Φ value can be then calculated by comparing the folding kinetics of the Gly variant with its Ala counterpart. Characterization of the shorter helix1 was obtained directly from A52G and A53G mutants.

Fig. 1.

Schematic illustration of the free energy landscape for folding of PDZ2. (a) Schematic free energy landscape for the folding reaction of PDZ2. Representative structures of TS1 and TS2, chosen by the clustering procedure described in Materials and Methods, are reported together with the native state (Protein Data Bank ID code 1GM1). Structures are represented in rainbow colors from N-terminal (blue) to C-terminal (red) ends. (b and c) The energy map of the native state (above the diagonal) is compared with those (below the diagonal) of TS1 (b) and TS2 (c). The most favorable interactions between different regions of the native protein are indicated in b. This figure illustrates that the interactions β1–β6 and β4–β6 are already formed in TS1, and that additional interactions, in particular those between β1–α1 and between β2–β4 are formed in TS2. The secondary structure elements are: β1 (residues 11–20), β2 (residues 26–32), β3 (residues 41–48), α1 (residues 52–55), β4 (residues 63–69), β5 (residues 71–73), α2 (residues 79–86), and β6 (residues 90–99).

Fig. 2.

Secondary structure propensities in TS1 (a) and TS2 (b). Black lines represent β strands and gray lines α helices.

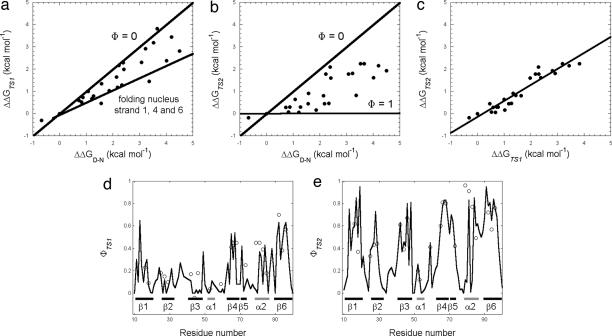
It is extremely difficult to distinguish between nucleation–condensation and diffusion–collision. Two different tests may be applied to distinguish between these two mechanisms: the magnitude of measured Φ values and their structural distribution. The nucleation–condensation model postulates the formation of a weak nucleus (nucleation) coupled with a global compaction (condensation) of the whole polypeptide chain, so that tertiary and secondary structure are formed simultaneously (12). Formation of a small folding nucleus is not the only rate determining event, as a significant fraction of the overall structure must also be in the correct conformation for the network of residues in the nucleus to be able to come together; the protein thus appears to collapse around an extended forming substructure. A crucial consequence of such a mechanism is represented by the linearity in the double logarithmic plot of the (un)folding rate vs. equilibrium constant (i.e., Brønsted, or Leffler, plot) (11). This type of behavior implies that, although folding is driven by the formation of a weak nucleus, most of the polypeptide chain is involved to some extent in stabilizing the transition state. The transition state resembles a distorted version of the native state, its free energy being proportional to the stability of the native state. This prediction is supported by the energy landscape theory of protein folding (5, 20, 21). Following this view, the stability of transition state ensembles is largely acquired through interactions similar to those present in the native structure (4), implying a general correlation between folding stability changes and folding rates (5, 20). The presence of native-like topological features in folding transition states has also been demonstrated by the observation that folding rates are related directly to the topological complexity of native states (22). Linear Brønsted plots, the hallmark of nucleation–condensation, have been observed for a number of two-state proteins (11, 23). An additional fingerprint of the nucleation–condensation model is provided by the distribution of Φ values along the sequence. In particular, nearly all positions should cluster around a low average Φ value (typically of ≈0.3). By contrast, the diffusion–collision model postulates the rapid formation of individual nuclei, represented by secondary structure elements, followed by their rate limiting docking and consolidation (2, 3). Under such conditions, there is heterogeneous structure localization in the transition state, with some regions having high Φ values and others displaying low Φ values, distributed in contiguous blocks and indicative of preformed secondary structure elements. The fingerprint of this situation is a scatter in the Brønsted plot, as observed for barnase (24), En-HD (13), and FF domain (25). The Brønsted plots for the folding of PDZ2 and the sequence distribution of observed Φ values are reported in Fig. 3. In the case of TS1 (Fig. 3a), many mutants lie on the Φ = 0 line with some points (corresponding to the folding nucleus) having fractional Φ values. When the late transition state TS2 is plotted vs. native stability, there is a considerable scatter in the Brønsted plot (Fig. 3b), with several residues clustering around the Φ = 1 line and the rest of the structure in the process of being formed, a pattern that would be expected if there were a diffusion–collision mechanism. Interestingly, at variance with the scatter detected when the two transition states are considered with respect to native stability, a Brønsted plot of TS1 vs. TS2 stabilities follows a simple linear behavior (Fig. 3c), as expected from the nucleation–condensation mechanism. Furthermore, whereas, for TS2, discrete blocks of high Φ values correspond to the secondary structure elements of native PDZ2 (Fig. 3e), in the case of TS1, observed Φ values cluster around a low average value throughout the sequence (Fig. 3d), as expected from a nucleation–condensation scenario. This trend was further confirmed by considering the conditional probability for a residue to be in a secondary structure element and to display a high Φ value. This analysis indicated a significantly increased conditional probability for TS2 (0.7) as compared with TS1 (0.4); the probability for uncorrelated events being 0.36, given the secondary structure content and sequence length of PDZ2.

Fig. 3.

Relationships between the free energy differences of the different states along the folding pathway of the PDZ2 domain. Brønsted plots referring to the energy of TS1 (a) and TS2 (b) as a function of native state stability are shown. Lines reflecting denatured-like structure (Φ = 0), the weak folding nucleus (strands 1, 4, and 6) and native-like structure are reported. (c) Relationship between the stabilities of TS1 and TS2 in PDZ2 folding (ΔΔG_TS1 vs. ΔΔG_TS2); the line is the best fit to a linear function (R = 0.95). Φ-value profiles for TS1 (d) and TS2 (e): open circles represent experimentally determined Φ values, the black line indicates the calculated Φ values.

These results indicate that the folding of PDZ2 appears to embody the main aspects of both the nucleation–condensation and the diffusion–collision mechanisms. We therefore suggest that folding of small globular proteins will in general involve three major events: (i) the formation of a weak nucleus formed by a cluster of residues having fractional Φ values, whereas the remainder of the protein adopts an ensemble of structures rather heterogeneous but consistent with a native-like topology; (ii) a global compaction of the entire polypeptide chain, yielding a linear Brønsted plot of TS1 and TS2; and (iii) a consolidation of the remaining partially structured regions with a late energy barrier displaying high Φ values in contiguous blocks. Whereas the first events resemble in part those expected from a nucleation–condensation description, the latter tend to take place through the establishment of different sets of interactions between partially preformed structural elements, more consistent with a diffusion–collision scenario. The case of PDZ2 is especially remarkable because all these events are finely balanced and can be observed in the same protein, whereas for other proteins analyzed so far, and indeed also for PDZ2 in the presence of a stabilizing salt, folding is dominated by one of the limiting events, which becomes the only experimentally detectable one.

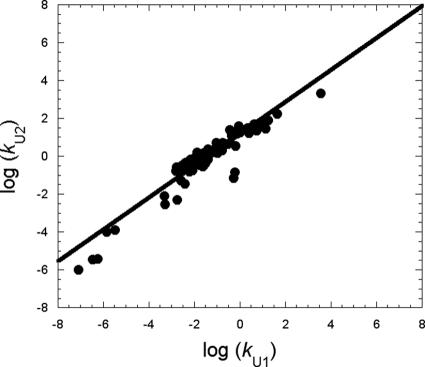
The folding pathway of PDZ2 is distinct from the pure diffusion–collision as well as from the nucleation–condensation mechanism, but displays characteristic features of both models. Indeed, although the native-like transition state TS2 has the structural features and the Φ value distribution expected from diffusion–collision, a Brønsted plot of TS1 vs. TS2 follows a linear behavior, as expected from a global compaction of the whole polypeptide chain. In an effort to test whether the folding mechanism emerging from PDZ2 can be extended to other unrelated proteins, we examined the unfolding kinetics of different proteins reported in literature. In fact, in analogy to what observed for PDZ2, it is tempting to speculate that when and if two consecutive barriers can be identified, their free energies should be correlated, as indicated by the linear Brønsted plot of TS1 and TS2 in the case of PDZ2 (Fig. 3c). We tested this hypothesis by comparing the unfolding kinetics of a set of different three-state proteins all displaying an intermediate in their folding pathways, as revealed either by a curvature in the unfolding limbs or by biphasic kinetics. In the latter case, calculation of the two unfolding rate constants k_U1 and k_U2 was only possible when all four microscopic rate constants had previously been determined by using classical kinetics analysis (26). Inclusion of proteins displaying biphasic kinetics is particularly important as only in these cases complex folding kinetics cannot be assigned to broad barrier effects (27). Fig. 4 shows the double logarithm plot of the two unfolding rate constants k_U1 and k_U2 (which refer to the apparent unfolding rate constants from the native to TS1 and TS2, respectively) for different three-state proteins; over-and-above mutants of PDZ2, these include several mutants of R16 (28), the only other system where two unfolding rate constants are reported along with a Φ analysis, which displays a folding behavior similar to PDZ2. In excellent agreement with our expectations, a strong correlation (R = 0.94) between the early and late events in protein folding is observed (Fig. 4). The proteins considered exhibit a wide spectrum of architectures (from all α to all β), unfolding rates (from ≈10⁻⁶ to 10³ s⁻¹), and stabilities. Such a correlation seems independent of experimental conditions (i.e., temperature, salt concentration, and pH). The generality of a unifying mechanism is further supported by a recent study on a similar pool of three-state proteins that reported a correlation between the microscopic rate constants for intermediate and native state formation (29). In the light of the present results, this observation indicates that the stabilities of the two consecutive transition states and the intervening intermediate in the folding pathway are correlated.

Fig. 4.

Double logarithm plot of the two unfolding rate constants for different three-state proteins, including mutational variants of PDZ2 (this work) and of R16 (28), and different proteins available in literature, including the Engrailed homeodomain (7), tendamistat (23), the FF domain in the presence/absence of sulfate (39), cytochromes c₅₅₂ from Thermus termophilus and Hydrogenobacter termphilus at three different pH values (refs. 40 and 41 and unpublished data), Im7 (42), acil-CoA binding protein (43), lysozyme (44), B1 domain of protein G (45), horse cytochrome c (46), and a stabilized three-state mutant of cytochrome c from Pseudomonas aeruginosa (47). The line is the best fit to a linear function (R = 0.94).

In conclusion, the characterization of the folding pathway of the PDZ domain presented here shows that the two transition states of this protein have structural features consistent with both the nucleation–condensation and the diffusion–collision mechanisms. Therefore, we believe that this PDZ domain represents a paradigmatic example of a protein that folds via a unifying mechanism and suggests that other proteins may appear to fold by either the nucleation–condensation or the diffusion–collision models, depending on the stability of their relative transition states.

Materials and Methods

Mutagenesis.

Site-directed mutants were produced by using a QuikChange site-directed mutagenesis kit (Stratagene, La Jolla, CA). Site-directed variants were purified as described (18). All experiments were carried out in the presence of 50 mM phosphate buffer pH 7.0 at 25°C. All reagents were analytical grade.

Stopped-Flow Measurements.

Kinetic folding experiments were carried out on Applied Photophysics (Leatherhead, U.K.) Pi-star and SX18-MV stopped-flow instruments; the excitation wavelength was 280 nm and the fluorescence emission was measured by using a 320-nm cut-off glass filter. In all experiments, refolding and unfolding were initiated by an 11-fold dilution of the denatured or the native protein with the appropriate buffer. Final protein concentrations were typically 1 μM. The observed kinetics was always protein concentration independent (from 0.5 to 5 μM), as expected from unimolecular reactions without effects due to transient aggregation (30).

Experimental Data Analysis.

Equilibrium experiments.

Assuming a standard equilibrium two-state model, the urea-induced denaturation transitions were fitted to the equation

where ΔG_d is the free energy of folding at a concentration D of denaturant, m_D–N is the slope of the transition (proportional to the increase in solvent-accessible surface area in going from the native to the denatured state) and D₅₀ is the midpoint of the denaturation transition. An equation that takes into account the pre- and post-transition baselines has been used to fit the observed unfolding transition (31).

Kinetic experiments.

Analysis was performed by nonlinear least-squares fitting of single exponential phases using the fitting procedures provided in the Applied Photophysics software. The chevron plots were fitted by standard numerical analysis based on a three-state model (26) using the Kaleidagraph software package. The logarithm of each microscopic rate constant was assumed to vary linearly with denaturant concentration.

Structure Determination.

To model the protein sequence studied experimentally, we created the mutant Y43W by starting from the native structure of the wild-type protein (the first model in the NMR ensemble of 1gm1.pdb). This structure was energy minimized with 200 steps steepest descent in the CHARMM19 force field (32) with the EEF1 implicit solvent (33). The program MOLDEN (34) was used to model the side chain, and the resulting structure was minimized again with 800 steps steepest descent. The conformation obtained at the end of this procedure was used as the initial structure in the restrained simulations.

Native State.

Unrestrained molecular dynamics simulations in the CHARMM19 force field and the EEF1 implicit solvent were carried out for 2 ns at 300 K to study the structural properties of the native state. From these simulations, we calculated a SASA of 5,450 ± 100 Ų, a radius of gyration (Rg) of 12.6 ± 0.1 Å, and a Cα rmsd to the starting structure of 1.8 ± 0.1 Å.

Transition State 1 Ensemble.

Molecular dynamics simulations with structural restraints derived from Φ-value measurements were used to determine the structure of the two transition states for folding of PDZ2 (16, 35). From the β Tanford value of 0.53 ± 0.03 (18) we estimated the SASA of transition state 1 to be 8,800 ± 500 Ų (16). This criterion was used as a filter to select the structures obtained from the restrained molecular dynamics simulations (36). We also used the condition that the average calculated Φ-value, computed over all residues, measured or not experimentally, should be between 70% and 100% of the average value (〈Φ^exp〉) of the experimental Φ-values (36). The resulting structures were refined by molecular dynamics simulations in explicit solvent with the same type of Φ-value restraints. The secondary structure computed with DSSPcont (37). Representative structures were selected according to a cluster analysis of the transition state ensembles (38), using a threshold of 2.0 Å on the C_α rmsd. The representative structures shown in Fig. 1a are chosen as the centers of the most populated clusters in each transition state ensemble.

Transition State 2 Ensemble.

From the β Tanford of 0.89 ± 0.03 (18), we estimated the SASA of the transition state 2 to be 6,240 ± 350 Ų. By applying the same protocol used in the case of TS1, we generated a set of 61 structures, which were analyzed to obtain the properties of the transition state ensemble 2. We clustered similar ones together using a 3-Å cutoff to determine the homogeneity of the ensemble and found three cluster centers. We found a SASA of 6,400 ± 100 Ų, a Rg of 13.4 ± 0.3 Å, and a rmsd to the starting structure of 4.8 ± 0.3 Å The average Φ value, calculated over all residues, measured experimentally or not, was of 0.41 (experimental 0.53).

Abbreviation

SASA

solvent exposed surface area.