Sequential structure of neocortical spontaneous activity in vivo

Abstract

Even in the absence of sensory stimulation, the neocortex shows complex spontaneous activity patterns, often consisting of alternating “DOWN” states of generalized neural silence and “UP” states of massive, persistent network activity. To investigate how this spontaneous activity propagates through neuronal assemblies in vivo, we simultaneously recorded populations of 50–200 cortical neurons in layer V of anesthetized and awake rats. Each neuron displayed a virtually unique spike pattern during UP states, with diversity seen amongst both putative pyramidal cells and interneurons, reflecting a complex but stereotypically organized sequential spread of activation through local cortical networks. Spike timing was most precise during the first ≈100 ms after UP state onset, and decayed as UP states progressed. A subset of UP states propagated as traveling waves, but waves passing a given point in either direction initiated similar local sequences, suggesting local networks as the substrate of sequential firing patterns. A search for repeating motifs indicated that their occurrence and structure was predictable from neurons' individual latencies to UP state onset. We suggest that these stereotyped patterns arise from the interplay of intrinsic cellular conductances and local circuit properties.

The neocortex contains a rich variety of neural classes that are connected together in a complex, but stereotyped manner (1–3). Only a fraction of cortical synapses carry ascending information from the thalamus; the majority arises from other cortical cells. It has been suggested that this recurrent connectivity allows the cortex to process information through the sequential activation of neuronal assemblies (4). Consistent with this picture, cortical activity exhibits coordinated dynamics beyond that predicted from common modulation by sensory input (5–7). Even in the absence of sensory stimulation (e.g., during sleep) the cortex shows complex spontaneous activity patterns, which have been suggested to reflect an “off-line” mode of information processing (7–12).

During sleep and quiet wakefulness, cortical spontaneous activity is dominated by the “slow oscillation,” consisting of alternating “DOWN” states of generalized neural silence and “UP” states of massive, persistent network activity (13). The dynamics of spontaneous UP states show striking similarities to those of sensory-evoked activity (14), suggesting that spontaneous patterns may be a useful experimental model for the flow of activity through cortical circuits. The way spontaneous activity propagates through cortical populations is unclear: whereas in vivo optical imaging results suggest a random and unstructured process (15), in vitro models suggest a more complex picture involving local sequential organization and/or traveling waves (16–21).

Here, we study the spatiotemporal structure of spontaneous activity in vivo by recording populations of 50–200 cells in rat neocortex by using multisite silicon microelectrodes. We find that transitions from DOWN to UP states are accompanied by a stable, sequential firing pattern with majority of neurons (≈90%) exhibiting individually unique temporal profiles. Spike times occur with up to millisecond precision at the start of a sequence; as the sequence progresses, timing accuracy decays in a scalar manner similar to that seen in behavioral timing tasks (22). A subset of UP states propagate as traveling waves, but the activity sequence in a local population is consistent regardless of direction of wave propagation, suggesting a stereotyped mode of information flow in a local cortical population.

Results

Sequential Activation of Neurons at UP State Onset.

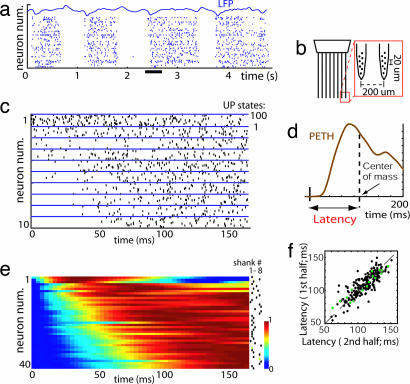
To investigate the structure of cortical spontaneous activity in vivo, we recorded from the somatosensory cortex of anesthetized and unanesthetized rats by using 64-site silicon electrodes. The electrodes, consisting of eight eight-site recording shanks spaced 200 μm apart, allowed for the isolation and localization of ≈50–200 single units. Fig. 1a shows a representative example of population activity under urethane anesthesia, recorded with the electrode configuration illustrated in Fig. 1b. An ≈1 Hz alternation between UP and DOWN states is visible. Fig. 1c presents a rastergram of a subset of the recorded neurons, triggered by UP state onset. Neurons exhibited diverse temporal profiles. To quantify this diversity, we computed each neuron's latency, defined as mean spike time within 200 ms of UP state onset [Fig. 1d; see supporting information (SI) Materials and Methods]. Neurons displayed a continuous distribution of latencies, revealing that UP state onsets initiate a sequential spread of activity across the population (Fig. 1e); this diversity also was observed amongst neurons recorded from a single location (maximum latency differences at a single shank were 87 ± 14% of total latency spread over all shanks; data pooled from all 15 rats). To verify that these diverse latencies did not result from averaging of random fluctuations, each data set was divided in two, and the latency computed for each half of the data. The latencies measured in each half were tightly correlated (Fig. 1f; R = 0.84, P < 0.001 for 180 cells pooled from six rats; P < 0.01 for each rat individually).

Fig. 1.

Sequential activity at UP state onset. (a) Spontaneous activity of neurons in S1 of a urethane anesthetized rat. DOWN states of complete silence alternate with UP states of generalized activity (underlined area is expanded in Fig. 3a). Neurons are arranged vertically by physical location of recording shank. (b) Schematic of silicon microelectrode used in these studies. (c) Raster plots for 10 example neurons triggered by UP state onset for 100 UP states, showing a diversity of temporal profiles. (d) Neural latency is defined as the center of mass of the PETH. (e) Pseudocolor plot showing normalized activity of a simultaneously recorded population triggered by UP state onset, vertically arranged by latency. The dots indicate at which shank neurons were recorded. (f) Neural latencies were stable, as illustrated by comparison of latencies calculated separately for the first and the second halves of data set (>30 min). Black and green dots represent putative pyramidal cells and interneurons, respectively.

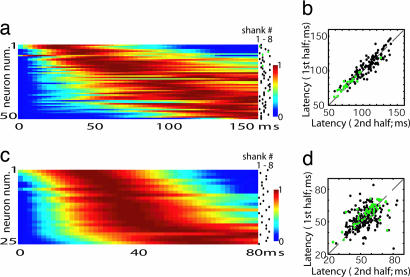
To investigate whether sequential activity was a general phenomenon, and not specific to urethane anesthesia, we recorded both ketamine-xylazine anesthetized (n = 3), and unanesthetized head-fixed rats (n = 5). Under ketamine-xylazine, clear UP and DOWN states were observed, and UP state-triggered activity showed similar sequential structure as under urethane anesthesia (Fig. 2a and b; correlation of latencies for the first and second half of data: R = 0.85; P < 0.001 for pooled 150 cells >2 Hz; P < 0.01 for each rat individually). In unanesthetized animals, UP and DOWN states usually are observed during slow wave sleep and periods of drowsiness, but not awake alertness (9, 23). We therefore restricted our analysis to periods where clear DOWN states could be observed. Consistent sequential activation of neurons again was seen (Fig. 2 c and d; R = 0.56; P < 0.001 for 263 pooled cells >2 Hz; P < 0.01 for four of five rats). Latencies were on average 53 ms shorter (P < 0.001; Kolmogorov–Smirnov test) in unanesthetized rats, indicating an accelerated sequence of activity as compared with the anesthetized case.

Fig. 2.

Sequential activity is not anesthetic-dependent. (a and c) UP state triggered PETH sorted by latency for ketamine-xylazine and unanesthetized animals, respectively (cf. Fig. 1e). (b and d) Consistency of neural latencies across the two halves of the experiment for ketamine-anesthetized and -unanesthetized rats, respectively. Green dots represent putative interneurons. Note that unanesthetized latencies are approximately half those observed under urethane or ketamine.

To what extent does the observed temporal diversity reflect the properties of different cell classes? In extracellular recordings, spike width can be used to distinguish putative fast-spike interneurons and pyramidal cells (ref. 24; see SI Fig. 6). The temporal relationship of putative pyramidal and interneuronal populations varied with anesthetic condition. Under urethane anesthesia, no significant difference was observed (mean ± SD: latency_pyram = 110 ± 17 ms, latency_intern = 109 ± 22 ms; Fig. 1f). In unanesthetized animals, the distribution of both classes again largely overlapped with a weak but significant difference (latency_pyram = 53 ± 8 ms, latency_intern = 57 ± 9 ms; Fig. 2d). Under ketamine-xylazine, however, interneuron latencies markedly were shorter (latency_pyram = 102 ± 19 ms, latency_intern = 81 ± 13 ms; Fig. 2b). We therefore conclude that (i) sequential activity does not simply reflect the preferred latencies of individual cell classes, and (ii) whereas UP-state activity has a sequential structure in all conditions investigated, the speed of activity flow and the role of different cell classes varies by condition.

Traveling Waves Initiate Consistent Local Activity Sequences Independent of Wave Direction.

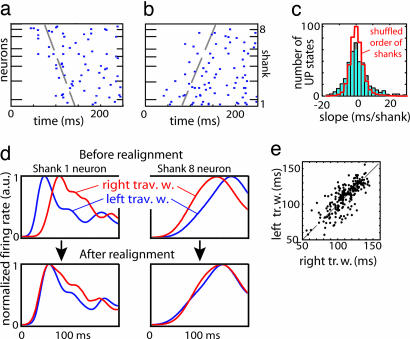
In cortical slices (19) and surface recordings (23, 25–27), spontaneous activity has been reported to take the form of traveling waves. In our data, traveling waves were observed and could spread in either direction across the recording sites (Fig. 3a and b). We therefore wondered whether the sequences we observed reflected consistent wave propagation. Because neural latencies were not correlated with either shank position (R² < 0.1, P > 0.1, for 13 of 15 rats) or vertical location on the multisite electrodes (R² < 0.1, P > 0.1 for all rats), we concluded that the sequences do not merely reflect wave propagation.

Fig. 3.

Interaction of traveling waves and local sequences. (a) Example of a traveling wave spreading from shank 8 to shank 1 under urethane anesthesia (expansion of underlined area in Fig. 1a). Neurons arranged vertically by recording shank location. Dashed line indicates propagation front fit by linear regression (see Materials and Methods). (b) Another traveling wave, propagating in the opposite direction, recorded during the same experiment. (c) Distribution of propagation front slopes. Red curve denotes distribution of slopes after shuffling shank order. (d Upper) PETHs computed separately for traveling waves moving to left (blue) and right (red), for two example neurons, aligned to global UP state onset defined by first spike time on any recording shank. (d Lower) PETHs realigned to shank-specific UP state onset times computed from propagation front slope, demonstrating increased stereotypy after realignment. (e) Scatter plot showing each neuron's latency for traveling waves moving to the left and right, computed from realigned PETHs. The strong correlation indicates that regardless of wave direction, neurons at a local site follow the same activation sequence.

Wave velocity was estimated for each UP state by linear regression of mean latency for each shank against shank location. The distribution of estimated velocities had a maximum at zero, indicating that activity most often began on all recording sites simultaneously (Fig. 3c). Nevertheless, the wide-tailed velocity distribution, compared with that obtained after shuffling electrode locations, confirmed that traveling waves occur in a significant number of cases (Kolmogorov–Smirnov test; P < 0.01 for 9 of 10 anesthetized and 3 of 5 unanesthetized rats; note this analysis underestimates traveling wave occurrence, because it cannot detect waves propagating perpendicular to the recording shanks).

The time at which any given neuron fires on a given UP state therefore reflects an interaction of global wave propagation and local factors. We hypothesized that a similar activity sequence is initiated in a local populations of neurons by the arrival of a traveling wave, regardless of wave direction. To test this hypothesis, we realigned each cell's spike train to the time of UP state onset at the cell's recording location (Fig. 3d, see Materials and Methods). The hypothesis predicts that this correction should increase the stereotypy of observed sequences, which was found to be the case [Euclidian distance between single UP state peri-event time histograms (PETHs) and mean PETH was significantly reduced; P < 0.01 for all rats]. To further investigate whether local sequences depended on the direction of wave propagation, we extracted from the data the 30% of UP states with the largest propagation slope for each direction. Neural latencies after realignment to local UP state onset were highly correlated regardless of traveling wave direction (Fig. 3e; urethane: R = 0.78; P < 0.001; n = 180 cells; ketamine: R = 0.88; P < 0.001; n = 150 cells; unanesthetized: R = 0.51; P < 0.001; n = 263 cells). We conclude that at each location, the same stereotyped activity sequence is initiated by UP state onset, with little dependence on wave direction.

Fine-Scale Structure of Firing Patterns.

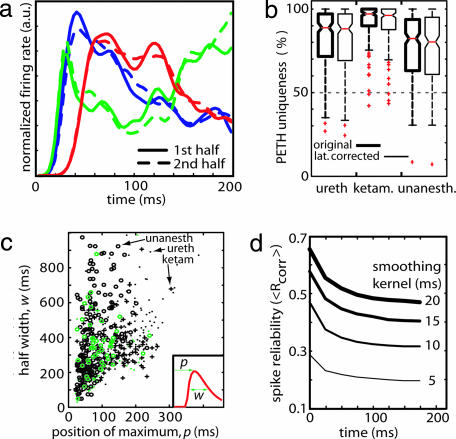
We next asked whether latency alone could account for the diversity of temporal patterns after UP state onsets. Fig. 4a shows UP state triggered PETHs for three representative neurons, computed from the first and second halves of the data set. The close similarity between PETH shapes computed from the first and second half of the data indicates that neuronal activity profiles during UP states are more complex and unique than latency-shifted versions of the same pattern. This observation was confirmed by using a “PETH uniqueness” measure (see Materials and Methods), which revealed that on average a neuron's PETH has consistent features which differentiate it from ≈90% of other neurons (Fig. 4b; urethane, 89%; ketamine, 96%; unanesthetized, 83%; chance level = 50%). This uniqueness persisted after shifting PETHs to compensate for mean latencies (Fig. 4b; boxes with thin lines). Applying principal component analysis to the set of PETH shapes did not reveal clusters, suggesting a continuous distribution of PETHs across the population (see SI Fig. 7). We conclude that each neuron exhibits a basically unique temporal firing pattern after UP state onset.

Fig. 4.

Uniqueness and precision of temporal profiles. (a) Normalized UP state triggered PETHs for three representative neurons estimated during the first (solid lines) and second halves (dashed lines) of a urethane experiment. Each neuron has a unique PETH shape that is consistent across the two halves of the experiment. (b) The difference between each neuron's PETH and the overall population was quantified with a “PETH uniqueness measure” (see Materials and Methods). PETHs are ≈90% unique for anesthetic and drug-free conditions. The distributions of this measure for the original data (thick lines) and after time-shifting by each neuron's mean latency (thin lines) were similar, indicating that uniqueness reflects PETH shapes, not just latency shifts. (c) Precision of neuronal firing decays as UP state progresses. PETH half-width w and peak position p were estimated from a gamma function fit (Inset); the graph shows the half-width and peak position for all neurons. Black or green symbols identify putative pyramidal cells or interneurons, respectively; symbol shape identifies anesthetic condition. Note that neurons with late onset latencies do not exhibit narrow half-width. (d) Spike timing reliability measure (R_corr; see Results and SI Fig. 8) decays as a function of time after UP state onset. Line width indicates the size of smoothing kernel.

Scalar Timing of Firing Patterns.

Many biological timing systems exhibit a “scalar” property in which accuracy decreases proportionally to the interval being timed (22). To investigate whether this property held for the spike sequences accompanying UP states, we estimated the onset time and half-width of each PETH by fitting a gamma function (Fig. 4c; see Materials and Methods). PETH width was correlated with peak latency for all cell classes, in anesthetic (R_ureth = 0.76; R_ket = 0.67) and drug-free conditions (R_aw = 0.61). Importantly, no cells were observed to exhibit short half-width and late onset, indicating that cells responding to the UP state with a precisely timed burst or spike, did so only immediately after UP state onset. This analysis, however, does not rule out precisely timed spikes late in the UP state, if they are part of a temporally extended spike pattern (as seen when neurons are stimulated with extended temporally structured stimuli; refs. 28 and 29). To investigate this possibility, we adapted the method of Schreiber et al. (30) to measure the reliability of spike times across UP states. For each neuron, spike trains were smoothed with a variable width Gaussian, and the mean correlation between spike trains from all pairs of UP states (<R_corr>) was computed in a 50-ms sliding window (Fig. 4d; see Materials and Methods). This analysis confirmed that the reliability of the UP state-evoked response decayed with time after UP state onset. Further analyses indicate that the asymptotic value of this measure is that expected from a homogeneous Poisson process (see SI Fig. 8).

Precisely Repeating Spike Triplets.

We thus have seen that neurons display diverse but consistent temporal relationships to UP state onsets, indicating that a stereotyped activity sequence accompanies the arrival of an UP state in a local population. Precisely repeated spike templates have been reported in a number of cortical systems (16–18, 21, 31, 32), although the interpretation of these results has been controversial (33, 34). We hypothesized that the individual relationships of neurons to the onset of UP states could account for precisely repeating spike patterns seen at the population level. Confirmation of this hypothesis would provide both convincing evidence for the precise repetition of spike patterns and a simple explanation for it.

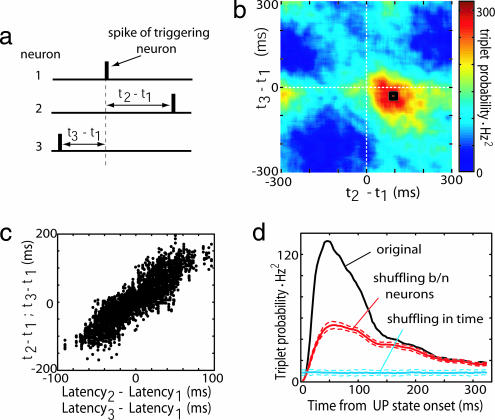
For computational tractability we restricted our search to spike triplets occurring across three distinct cells (35) (Fig. 5a). For each cell trio, one cell was designated the trigger for calculation of the joint distribution of spike times of the other two (35). Often, a clear mode was seen in these plots, suggesting that a particular sequence occurred preferentially (e.g., Fig. 5b). The location of the mode could be predicted from the neurons' individual latencies to UP state onset (Fig. 5c; P < 0.001 for each rat individually). Repeating triplets [defined as those whose interspike intervals were within ±10 ms of the mode, indicated by the black square in Fig. 5b] occurred preferentially shortly after UP state onset (Fig. 5d). To gauge the statistical significance of these triplets, we used shuffling methods to compare the number of triplets observed to those predicted from two separate null hypotheses. A time-shuffling method was used to investigate the prediction of an independent Poisson hypothesis, corresponding to completely unstructured activity (blue line in Fig. 5d; see SI Materials and Methods). With reference to this null, significant numbers of repeating triplets occurred throughout the UP state; however, this significance simply could reflect the elevated firing rate during the UP state periods. We therefore investigated a second “common excitability” model, in which the rate functions of all cells were assumed variable but proportional in fixed ratio (red line in Fig. 5d, see SI Materials and Methods). Using this second null hypothesis, significantly repeating triplets were seen only in the first ≈100 ms after UP state onset, the period during which neurons exhibit precise and unique temporal relationships to UP state onset. We therefore conclude that the timing and structure of repeating triplets in our data set is predicted by individual neurons' relationships to UP state onsets.

Fig. 5.

The structure of precisely repeating triplets is predicted by individual neural latencies. (a) For every trio of neurons, a spike triplet is described by two interspike intervals (t₂ − t₁ and t₃ − t₁). (b) Count matrix for a representative triplet of neurons, indicating the probability of different interspike interval combinations. Black square denotes triplets occurring within ± 10 ms of mode. (c) Triplet structure reflects individual neural latencies. Each triplet is represented by two points: (x₁ = t₂ − t₁, y₁ = latency₂ − latency₁) and (x₂ = t₃ − t₁, y₂ = latency₃ − latency₁). The strong correlation indicates that the structure of the triplets is predicted by the neurons' mean latencies to UP state onset. (d) Occurrence of precisely repeating triplets peaks shortly after the start of UP states. Blue and red curves denote shuffled data for independent Poisson and common excitability models, respectively (dashed lines indicate SD).

Discussion

We have found that (i) in both unanesthetized and anesthetized conditions, UP states are associated with a progressive, stereotypically organized spread of activation through local cortical networks; (ii) The time scale of this spread is ≈100 ms, with spike timing precision decaying as the UP state progresses; (iii) cortical spontaneous activity may take the form of a traveling wave, but waves passing in either direction initiate similar local sequences; and (iv) the sequential patterns reflect diverse individual neuronal relationships to UP state onset, with diversity seen within both putative pyramidal cells and putative interneurons.

Our findings are in broad agreement with results in cortical slices (16, 19, 36) but contrast with a recent in vivo calcium imaging study of urethane anesthetized rats (15), which found activity within UP states to be unstructured. This discrepancy may reflect a difference between the cortical areas (motor vs. somatosensory) or layers (II/III vs. V) recorded; however, another possible explanation involves differences between recording methodologies. We found that sequential structure was expressed only in the first ≈100 ms after UP state onset and was most readily detected among neurons with the highest firing rates (>2 Hz). The lower temporal resolution of two-photon imaging methods and the lower firing rates of layer II/III neurons under urethane anesthesia (≈0.1 Hz) therefore might account for a lack of detected structure after UP state onset.

Spikes occurring immediately after UP state onset could be timed with millisecond precision; the accuracy of spike timing decayed thereafter. Such “scalar timing” is a robust property of many biological timing systems (22, 37). In contrast, previous research in cortical systems in vivo and in vitro has detected activity sequences that may continue to exhibit millisecond timing up to seconds after the sequence has begun (18, 32). This apparent discrepancy may reflect the statistical methods used to detect these sequences. If a search is conducted for repeating patterns of millisecond precision, these are the only sequences that can be found. If more sequences are found than predicted by a given null hypothesis, this is a valid reason to reject the null hypothesis but does not indicate that the particular type of sequences searched for are biologically meaningful. Here, we have taken an alternative approach: by recording from a large population of cells, we show that local populations of neurons fire at diverse latencies after UP state onsets. By performing a search of the entire data set for repeating triplets, we find that the structure and timing of these triplets can be predicted from individual neurons' latencies to UP state onset. This suggests that UP state onsets are the principal sources of repeating spike patterns in this data. In keeping with this view, analyses in behaving animals have shown that repeating spike sequences often may be attributed to stereotyped neuronal latencies to punctuate events such as motion onsets (33, 34).

Traveling waves and local sequential activity were observed in unanesthetized animals and under two different anesthetic conditions. Nevertheless, some differences were observed between states. Sequences observed under anesthesia lasted almost twice as long as those in unanesthetized animals. Ketamine-xylazine anesthesia also led to a reduced mean latency of putative interneurons compared with pyramidal cells. These observations may result from both local effects of anesthetics on cortical circuits and systemic phenomena. For example, ascending neuromodulatory inputs, which are likely to be affected by anesthesia, have been shown to affect the strength of thalamocortical and corticocortical connections as well as the intrinsic properties of thalamic and cortical neurons (38–40).

We observed a wide diversity between simultaneously recorded neurons, with each neuron having a virtually unique temporal pattern of activity that it consistently exhibited at UP state onsets. We suggest that the diversity of cellular responses at UP state onset arises from the interplay of intrinsic cellular properties and network dynamics. Cortical neurons vary in their responses to in vitro current injection, which may result from differences in morphology as well as ion channel expression (41). When injected with step currents, layer 5 pyramidal cells show stereotypical temporal patterns at step onset, which differ between cells; after a few hundred milliseconds, however, most cells fire repetitive spike trains (42). Thus, even if each neuron experienced an identical step of input current during the UP state, diverse spike patterns and sequential activity still would follow UP state onset. It is likely, however, that the input current profiles experienced by cortical cells are also diverse. Cortical pyramidal cells are heterogeneous in their excitatory and inhibitory inputs (1, 43–46), and neighboring neurons can receive input from quite different presynaptic populations (47). Intracellular recordings in vivo have shown that although the broad structure of membrane potential oscillations can be remarkably correlated between neurons (48), individual neurons depolarize with consistent latency after UP state onset (49). In cortical slices, complex intracellular waveforms evoked by focal stimulation suggest that neurons experience diverse but reliable patterns of polysynaptic input up to 300 ms after the initial stimulus (36). We thus propose that the transition to UP state in a cortical column initiates a complex dynamical pattern that is sculpted by patterns of recurrent connections and cellular dynamics. Computational models have suggested that spike timing-dependent synaptic plasticity may lead to connection patterns that reinforce intrinsic dynamics and conduction delays, leading to stable sequential activity of the type we observe (50).

What role might sequential activity play in information processing? The first possibility we must consider is that it has no function, that is, if it were possible to scramble the temporal dynamics, this would have no effect on the operation of the brain. We consider this to be unlikely: Given that neuronal integration times are on the order of tens of milliseconds (51), sequentially structured activity spread over hundreds of milliseconds will have a different impact on downstream neurons than uncoordinated activity. A second interpretation, the “synfire chain” hypothesis, posits that precisely timed activity stabilizes propagation of spike patterns in the face of variable conduction delays (18, 52, 53). Our data are not fully consistent with this interpretation: Millisecond-level precision is only observed immediately after UP state onset, after which timing precision progressively deteriorates. We suggest another possibility in which sequential activation of a cortical network allows for serial execution of multiple steps in an information processing task (7). Neurons firing earliest in the sequence would reflect an initial processing of incoming information; neurons firing at later times would have access to the results of computations made by earlier firing ones and, thus, be capable of more sophisticated analyses. In several sensory systems, short-latency responses correlate with simple stimulus features, whereas later responses evolve to represent more complex features (54–56). We hypothesize the same dynamical processes that give rise to sequential patterns under anesthesia may underlie the generation of these patterns in awake animals.

Materials and Methods

Surgery and Recording.

Detailed descriptions of surgery and recording procedures have been published in ref. 24. Briefly, six rats (Sprague–Dawley; 400–900 g) were anesthetized with urethane (1.5 g/kg), and another three with a mixture (4 ml/kg) of ketamine (25 mg/ml) and xylazine (1.3 mg/ml), injected i.p. Rats were placed in a stereotaxic frame, and a window in the scalp was prepared over the somatosensory cortex. Five rats were recorded unanesthetized with their head restrained: one week before the experiment, a headpost was implanted on the head of the animal under ketamine-xylazine. The animal was trained to remain motionless in the restraining apparatus for increasing periods. On the day of the surgery, the animal was anesthetized with isoflurane, the skull opened and the dura resected; after a 1-h recovery period, recording began.

Extracellular signals were recorded with silicon probes (NeuroNexus Technologies, Ann Arbor, MI) consisting of eight shanks (Fig. 1b; see SI Materials and Methods). The location of the recording sites was determined to be layer V by histological reconstruction of the electrode tracks, electrode depth, and firing patterns (24).

Units were isolated by a semiautomatic algorithm (available at http://klustakwik.sourceforge.net) followed by manual clustering (57) (http://klusters.sourceforge.net). Multiunit activity, clusters with low separation quality (57, 58) (isolation distance <20), or firing rates <2 Hz were excluded from analysis. The mean number of recorded cells per experiment was N_ureth = 59 (range 27–93), N_ket = 126 (range 98–169), and N_awake = 137 (range 41–179); the mean number of cells used for analysis: N_ureth = 30 (range 14–41), N_ket = 50 (range 25–70), and N_awake = 52 (range 25–83).

UP states were identified from the spiking activity of all recorded cells. UP state onset was defined as the time of the first spike marking a transition from a period of global silence (30 ms with at most one spike from any cell) to a period of activity (60 ms with at least 15 spikes from any cells; see SI Materials and Methods). The mean number of analyzed UP states per experiment (±SD) was N_ureth = 611 ± 133, N_ket = 531 ± 41, and N_awake = 244 ± 102.

Correction for Traveling Wave Slope.

To determine the speed of propagation of UP state onset across recording shanks, we calculated for each shank the mean time of the first five spikes of any cell after UP state onset and fitted a least squares line to these times as a function of shank location (varying the number of spikes used did not alter our findings). To correct for traveling waves, spikes times at each shank were shifted by an amount calculated from the fitted line for each UP state separately, and PETHs and latencies were recomputed.

PETH Uniqueness.

To investigate the uniqueness of PETH shapes, we divided each data set in two and computed normalized PETHs for all cells in each half. For each pair of neurons i and j, we computed the Euclidean distance d_ij between the PETHs of neuron i in the first half and neuron j in the second half. The PETH uniqueness measure of neuron i was defined to be the percentage of all other neurons j for which d_ii < d_ij. The uniqueness measure was computed from the original PETHs and from transformed data in which PETHs were shifted in time to equalize their onset latencies (Fig. 4b, boxes with thick and thin lines, respectively).

Gamma Fit and Spike Timing Reliability.

To estimate the temporal precision of neural firing, PETHs were fitted with a function based on the gamma probability density function:

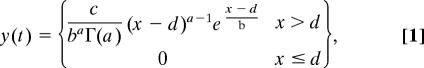where Γ(a) is the standard gamma (factorial) function. The parameters a, b, c, and d were optimized to minimize the Euclidian distance between y(t) and the observed PETH by using the simplex method; optimization was repeated with multiple initial parameter values, and the best fit chosen if different solutions were obtained. After fitting, both the peak position p and half-width w of gamma function fit were computed numerically (Fig. 4c Inset).

Spike timing reliability (R_corr) was assessed for each neuron separately by using the measure of Schreiber et al. (30):

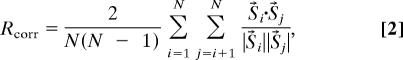where N is the number of UP states, and S⃗_i denotes the binned (3.2 ms) and smoothed (Gaussian kernel of width 5, 10, 15, and 20 ms) spike train during ith UP state. Reliability was computed for 50-ms time windows starting at 0, 25, 50, …, 200 ms after UP state onset.

Abbreviation

PETH

peri-event time histogram.