Multiple-motor based transport and its regulation by Tau

Abstract

Motor-based intracellular transport and its regulation are crucial to the functioning of a cell. Disruption of transport is linked to Alzheimer's and other neurodegenerative diseases. However, many fundamental aspects of transport are poorly understood. An important issue is how cells achieve and regulate efficient long-distance transport. Mounting evidence suggests that many in vivo cargoes are transported along microtubules by more than one motor, but we do not know how multiple motors work together or can be regulated. Here we first show that multiple kinesin motors, working in conjunction, can achieve very long distance transport and apply significantly larger forces without the need of additional factors. We then demonstrate in vitro that the important microtubule-associated protein, tau, regulates the number of engaged kinesin motors per cargo via its local concentration on microtubules. This function of tau provides a previously unappreciated mechanism to regulate transport. By reducing motor reattachment rates, tau affects cargo travel distance, motive force, and cargo dispersal. We also show that different isoforms of tau, at concentrations similar to those in cells, have dramatically different potency. These results provide a well defined mechanism for how altered tau isoform levels could impair transport and thereby lead to neurodegeneration without the need of any other pathway.

Directed movement of cargos along microtubules (MTs) is a key component of transport within a cell. Abnormalities of MT-based transport are observed in many neurodegenerative diseases (1, 2). Numerous studies suggest that cargos in vivo are moved by more than one MT-based motor (1–3), but so far little is known about the combined function of multiple motors. It has been established qualitatively via in vitro experiments that cargos moved by multiple motors tend to travel with similar velocities (4) but farther than those driven by single motors (5), yet it is not known how cargo travel distance and motor force production scale with the number of motors. We would therefore like to experimentally establish the underlying dynamics of multiple motor transport, to quantify the extent to which transport is improved by more than one motor, and to probe how the kinesin motor performance scales with the number of motors in absence of any additional cofactors. In addition, if cargos moved by more than one motor have different transport properties than single-motor driven cargos, this represents a potential target of regulation, and we would like to know how such regulation might occur. These are difficult questions to definitively address in vivo, because of the many interacting cellular components and complicated cellular architecture contributing to cargo dynamics and transport. To clarify how fundamental aspects of biological function emerge from specific molecular components, we employ an in vitro model system that allows precise quantitative characterization of motor function and regulation. Our experiments are conducted in a well defined architecture with selected proteins whose concentrations are under our control.

Results and Discussion

We first consider how cargo transport depends on the number of participating motors. In a statistical sense, we can control the average number of motors moving the cargo by incubating beads with different amounts of kinesin [supporting information (SI) Fig. 6) using a well established bead assay (6). At low kinesin concentrations, beads are moved by a single motor, and stall forces (SI Fig. 7A) are ≈5 pN and distributed in a Gaussian manner as expected (5, 7) (Fig. 1a). As the incubation concentration is increased, the rate of bead–MT binding events increases (Fig. 2 and SI Fig. 8A) consistent with an increase in the average number of motors per bead. Moreover, one starts to observe higher force events (Fig. 2b) in addition to the low force events (Fig. 2). These events are not only significantly higher in force than what a single motor can exert in our assay (Fig. 1a) but they also often have a characteristic shape indicating that additional force is exerted on top of what appears to be one motor close to stalling (Fig. 2b). The frequency of such events increases with increasing incubation concentration. Note that on a given bead there are likely many individual active kinesins that could move the bead, but only a few of those are close enough to a second motor that the two motors could engage simultaneously. Thus, the same bead can be a “1 motor” or a “2 motor” bead depending on its geometric orientation relative to the MT. The increased frequency of multimotor events is therefore expected and mirrors the increased density of kinesin motors on a typical bead.

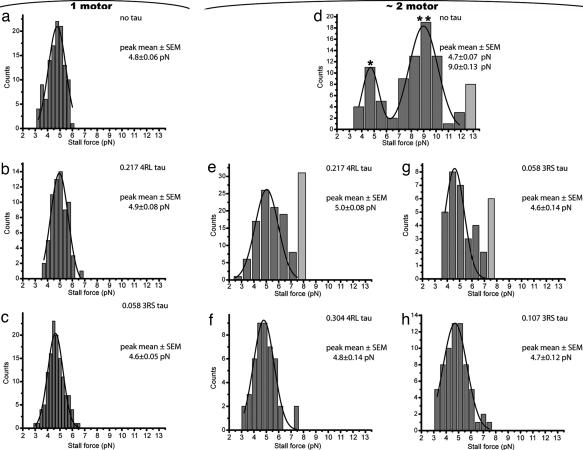
Fig. 1.

Changes in the number of engaged motors are revealed by the analysis of stall forces. Comparison of single motor no tau baseline case (a) with single motor assays with moderate amounts of 4RL (b) or 3RS (c) tau shows that tau does not affect the amount of force a single motor can produce against external load. Note that as tau is added to the assay, increased numbers of binding attempts are required to observe one stall event (serving as an effective experimental limitation for further increases in tau concentration). In contrast to the single-motor case (a–c), stall forces in the ≈2 motor assay are strongly affected by tau. The bare MT assay (d) shows contributions from both single motor (*) and 2 motor events (**), with rare contributions from 3 or more motor events (gray bar). Comparing the bare MT assay (d) with assays featuring progressively higher 4RL (e and f) and 3RS (g and h) tau concentrations reveals that the frequency of two-motor stall events is gradually suppressed. The high-force (>7.0 pN) events account for 72.7% of the total in the no tau case (d), but the percentage is significantly reduced in e and g (28.7% and 20.0% respectively). The solid lines are fits to Gaussian form (the peak locations are reported in each subplot). The molar ratio of tau to tubulin dimer as well as the isoform of tau used are shown, as appropriate.

Fig. 2.

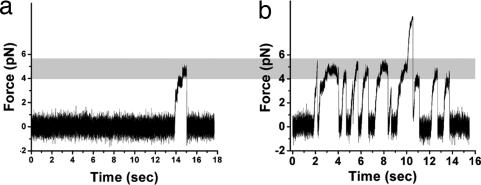
Binding events provide information on the motor density and motor force contributions for typical assay cargos. (a) Some beads incubated with low concentration of kinesin are able to bind MT. One can detect such binding events by monitoring the bead in an optical trap for systematic displacements from the center of the trap. The binding events are rare (0.15 ± 0.06 events per second; mean ± STD; seven beads) and do not reveal force production in excess of the range of forces observed for single kinesin motors (Fig. 1a). (b) On the other hand, beads incubated with higher concentrations of kinesin show increasing rate of binding events and an increasing number of those events shows very high corresponding forces (up to ≈10 pN). For example for the specific assay shown in b the binding events rate was 0.38 ± 0.25 events per second (mean ± STD; 20 beads). The overlap between the broad range of rates in b and a more narrow range in a is qualitatively consistent with the expectation that some beads incubated with higher concentrations of kinesin still only have one active kinesin on their surface.

If we restrict our consideration to only clean stalling events at high incubation concentration, we observe two prominent peaks: one at 4.7 pN and one at ≈9 pN (Fig. 1d). We attribute these peaks to one and two motor activity respectively. Such attribution is consistent with the gradual increase in the frequency of high-force events described above. Note that, in the same assay, we also observe rare stall events of large magnitude (Fig. 1d), which we interpret as contributions from three or more motors.

The beads incubated with very low kinesin concentration most often do not bind to the MT at all (binding fraction 0.3). Those beads that do bind are almost certain to be moved by only one motor (5). However, at higher incubation concentrations, any given bead will in general be moved by different numbers of motors at different times. Therefore, rather than focusing on the instantaneous number of motors propelling a given bead, we chose to classify our assays in a statistical sense. For given kinesin incubation conditions, we determine the “dominant” bead propulsion contribution using the force distributions (Fig. 1). Thus, if most of the stall events are at ≈9 pN (Fig. 1d), we call it the ≈2-motor assay. However, note that there are beads in this population that are instantaneously moved by 1, 3, or more motors (see Materials and Methods for further discussion of 1, ≈2, and 3+ motor assay designations).

In addition to stalling forces, we also characterized cargo run lengths. We confirmed (5) that single kinesin molecules move cargos ≈1 μm (Fig. 3a and SI Movie 1). For the ≈2 and 3+ motor assays (Figs. 1d, 3b, and 4a), we observe very long travel distances (>8 μm), indicating a dramatic change in transport as we transition from one-motor-driven motion to one where beads are typically propelled by more than one motor. Because these experiments are done in vitro with purified kinesin, we conclude that these effects are caused by multiple kinesin motors and that motor force production roughly scales with the number of motors without the need of additional cofactors to coordinate their activity (Fig. 4).

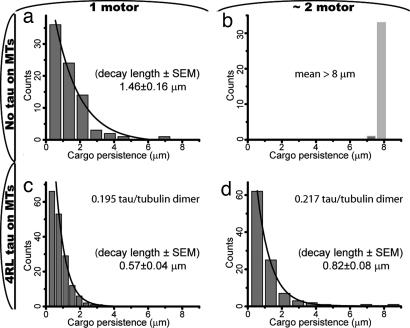
Fig. 3.

How far cargos typically travel critically depends on the number of participating motors. The single-motor assay, as expected, shows exponentially distributed cargo travel distances (a), but the beads in a ≈2 motor assay consistently traveled beyond the edge of our field of view (>8 μm) (b). The fact that the ≈2 motor assay shows more robust transport (compared with single motor case) is not in itself surprising (5). However, the amount of transport improvement is remarkable: adding (on average) just one extra motor increases cargo run lengths by at least one order of magnitude. A similar effect is seen for smaller beads incubated with the same kinesin/bead molar ratio as in b, suggesting that the transport enhancement is relevant to cargos of a wide range of sizes, including many cellular cargos (see SI Movie 3). Thus, two motors appear to be the minimum configuration sufficient for robust MT-based transport on biologically relevant length scales. When MTs are covered with a high concentration of tau (c and d), cargo travel is consistently reduced compared with the no tau baseline. A small but significant reduction is observed for a single motor assay (c); however, the most drastic change is seen for the ≈2 motor assay: here tau is seen to reduce robust long-distance transport (b) to submicron length scale (d), a >10-fold decrease in travel distance. Solid lines show exponential fits (the decay length is reported in each subplot, where appropriate).

Fig. 4.

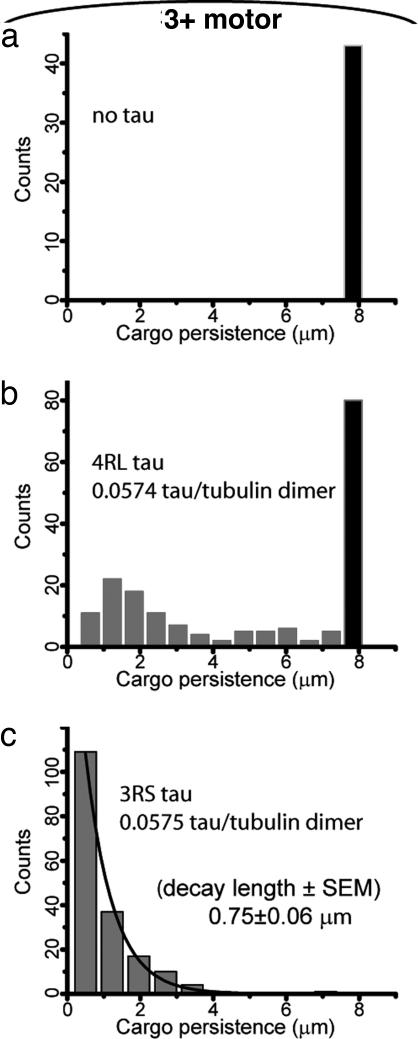
Different tau isoforms have drastically different effect on transport at tau levels similar to those in cells. Transport of beads in a 3+ motor assay is very robust on bare MTs (a), so beads in this assay never detached before escaping the field of view of our microscope (represented by the black bar on the right). Adding 4RL tau somewhat reduced cargo travel distances (b); however close to half of the beads (46%) still exceeded 8 μm of travel. A parallel assay with the same concentration of 3RS tau reveals just how much more potent this isoform is at regulating transport: the distribution of cargo travel lengths here (c) can be fit with a single exponential decay with a sub-micrometer decay constant (solid line shows a fit to a single exponential decay). Mean travel here is decreased at least 10-fold in comparison to travel on bare MTs (a).

The dramatic increase in mean travel distance described above could be explained via a model (Fig. 5) where motors do not simply work in succession, but rather individual motors moving a cargo detach and reattach from the MT multiple times before the cargo ultimately detaches from the MT. In fact, our results are in qualitative agreement with previous theoretical expectations (8) that cargo travel distances go up as the number of participating motors increases. Although the transport we observe may be more robust than previously appreciated (see SI Movies 2 and 3), it is difficult to directly compare our experiments with theory (see SI Text).

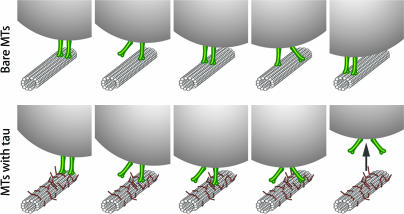
Fig. 5.

A model of multiple-motor driven cargo transport. Here we model a two-motor arrangement, the simplest case of multiple motor transport. Higher numbers of motors will not alter the qualitative picture presented below. Note that the actual number of participating motors is not resolved in our experiments for each binding event and for each bead. Rather, we determine the frequency of one, two, and more motor events in a statistical sense for a given bead assay. Without tau (top row sequence), motors frequently detach and reattach; however, at least one motor always tethers the cargo to the MT. In the presence of tau (lower row sequence), rebinding is suppressed. Therefore, once the first motor disengages from the MT, it is unlikely to reattach before the second motor also detaches. The bead then ceases its processive motion and diffuses away (arrow). One important net result of this tau effect is reduced cargo travel distances. Notice also that, by blocking rebinding, tau reduces the number of motors that on average drive the cargo. Therefore, tau is also expected (and indeed observed) to reduce the total force that the motors can apply to move the cargo. Likewise, tau is expected to reduce the force needed to detach the cargoes from MTs, an effect that is indeed observed in our pull-off experiments.

This model (Fig. 5) suggests that it might be possible to regulate the number of engaged motors by controlling motor on rate, i.e., how long it takes motors to bind to the MT. The more quickly the motors can reattach to a MT, the more time they will spend actively participating in transport. Conversely, if the motors' on rates were lowered, on average fewer of the geometrically available active motors would be bound at any given time. As discussed above, changing the number of engaged motors can lead to drastic changes in cargo transport. Thus, in vivo, changing the motor on rate is a potentially important mechanism of local regulation of transport when a cell needs to terminate or alter efficient reliable long-range transport.

It was possible to directly test this on-rate hypothesis in vitro using the MT-associated protein (MAP) tau, which had been shown to decrease kinesin's on rate (9, 10). Human tau isoforms have either three (3R isoforms) or four (4R isoforms) MT-binding repeat motifs at the C-terminal end, and both types of isoforms also vary in the length of their N-terminal projection domain (which does not bind the MT surface) (11). The longest and the shortest human tau isoforms were used in this work (4RL and 3RS, respectively). Moreover, misregulation of the ratio of 3R and 4R tau isoforms is known to cause frontotemporal dementia with Parkinsonism-17 (11). Do these isoforms have different effects on transport? If so, then to what extent?

Our control experiments (SI Fig. 8) found that when cargo-bound, the motor's on rate was decreased by tau in a concentration-specific and also isoform-specific manner. In the single motor assay stalling forces were not significantly altered (Fig. 1 b and c), and the mean cargo transport distance was modestly reduced to a mean value of 0.57 μm.^§. In contrast, our measurements in the multiple-motor regime demonstrate a strong alteration of the motion of cargos expected to be driven by more than one kinesin. We find that both travel distances and stalling forces decrease as a function of increasing tau concentration on the MTs (Figs. 1 e–h and 3d). Both 4RL and 3RS tau can reduce two motor activity (Fig. 1d) to the single-motor case (Fig. 1 f and h); however, higher levels of 4RL tau are needed to achieve a comparable reduction in motor activity. In fact, at levels similar to those in living cells only 3RS tau could convert multiple-motor based transport to approximate single-motor based transport in the ≈2 motor assay (data not shown). Similarly, 4RL tau had limited effect (Fig. 4b) on 3+ motor assay transport at levels similar to those in living cells (12), yet 3RS tau had a dramatic effect (Fig. 4c), converting multiple-motor transport (Fig. 4a) close to single-motor limit. These effects were consistent with our model (Fig. 5) because at a given concentration, 3RS tau is observed to have a much larger effect on kinesin's on rate than 4RL tau (ref. 10 and SI Fig. 8). The above observations suggest a potential new role for tau, where some isoforms, at physiological levels in healthy neurons, could regulate transport by locally altering the number of motors moving a cargo. Previous overexpression studies in vivo suggested that at high levels, tau can aberrantly impair transport. Our results in vitro suggest that this picture may be incomplete: some isoforms of tau likely control/alter transport even when not overexpressed.

What relevance do these in vitro studies have for our understanding of how transport actually occurs and is regulated in the animal? First, the findings provide a way to resolve a long-standing inconsistency in the transport field: overexpression of tau in vivo is known to decrease cargo run lengths quite significantly, but past in vitro studies suggested that tau did not affect the motive properties of individual kinesin motors. Coupling reports (9) of significant decreases of run lengths due to tau overexpression with our results, implies that in vivo cargos are moved by more than one motor, and that increased tau on average decreases the number of engaged motors, resulting in the observed changes in transport. Therefore, the tau level itself could be an important transport regulator. In this case, not only abnormally high but also abnormally low tau levels could be harmful to in vivo transport, independent of other effects where extreme loss of tau leads to MT impairment (see below).

Consistent with the hypothesis that distinct tau isoforms can differently regulate transport at physiological levels, we note that the higher in vitro potency of 3RS tau to regulate MT-based transport stands in stark contrast with the higher in vitro potency of 4RL tau to stabilize MTs (13). This observation suggests that one reason for cells to have various isoforms of tau could be to (at least partially) decouple tau's regulation of transport from tau's regulation of MT dynamics. The results also have implications for diseases that alter the relative amounts of tau isoforms (e.g., frontotemporal dementia with Parkinsonism-17), because isoform imbalance can potentially affect MT dynamics, transport, or both.

There are several instances where a local reduction in the number of engaged motors could in principle be beneficial to a living cell. For instance, tau-induced decrease of the number of engaged kinesins could facilitate switching from MTs to actin filaments by making it easier for the myosin motors to pull the cargo off the MT (for example, at synapses). To test this mechanism in vitro, we quantified the success rate of pulling a cargo off a MT with a laser trap using the ≈2 motor assay. We applied ≈15–16 pN forces to the beads using a 105 mW trap perpendicular to the MT axis (for further details, see Materials and Methods). The rate of successful release of cargo from bare MTs was 21 ± 4% (n = 102). On the other hand when MTs were decorated with 4RL tau (bound tau/tubulin ratio of 0.15) we observed a pull-off success rate of 69 ± 12% (n = 16). Thus, in principle, having a high local concentration of tau (or localizing 3R vs. 4R tau to a specific region) could be used to help the myosin motors locally capture cargos from the MTs.

Similarly, we speculate that MT–MT switching (e.g., at axonal branch points) likely involves a tug-of-war between motors attempting to move along each of the intersecting filaments. The dynamics of this tug-of-war would then depend on the number of engaged motors moving the cargo. More motors would likely reduce switching efficiency, because a struggle between many motors attached to intersecting filaments would likely take longer to get resolved. Moreover, because motors working together exert additive forces, as shown above, the stress induced by such a tug-of-war would grow linearly with the number of motors involved. We used a model in vitro system to test whether a cell could alleviate this stress and improve switching efficiency by using tau. A 3+ motor assay with no tau on MTs showed most beads trapped at MT intersections (18 of 31 observed). Motion at intersections could only occur when MTs were distorted by the moving cargos to the point where the MT–MT intersections were physically moved by the bead (12 of 31 switched after severely deforming the MTs, often ripping them off the surface of the slide, one bead switched without any visible deformation of MTs). On the other hand, if either of the crossed MTs were decorated with as little as 0.087 bound 4RL tau/tubulin, then most beads under observation would switch at MT intersections with no bending of MTs (of the 33 beads observed, 30 switched with no MT deformation, and only three visibly deformed the MTs before switching). Past work does, indeed, indicate that 3R tau is localized to axonal branch points, whereas 4R tau is localized along the neurite processes (14). Similarly, tau is reported to be enriched at the distal ends of axons, a distribution pattern consistent with the proposed tau role as an aid in switching cargoes from MT- to actin-based transport (15, 16). These could be in vivo glimpses of a tau's switch-enhancing role. Future work will be needed to fully understand the ramifications of having a cargo moved by a specific number of motors.

In conclusion, we have shown in vitro that multiple kinesin proteins can move cargos very long distances without any additional accessory factors, and while doing so can exert high (additive) forces on the cargos. We establish a model for how multiple motors work together, which in turn indicates that altering the motors' on rate can regulate the average number of engaged motors. We show that the presence of tau is one way to control this on rate, and that at physiological concentrations different tau isoforms can have widely different effects both on the on rate and also consequently on the number of motors driving the cargo and thus its transport properties. In principle, other proteins affecting the on rate could also regulate the number of engaged motors, although we have only demonstrated it for tau. Our conclusions are derived from controlled in vitro experiments; in addition to investigating the consequences and control of motor number by tau, we explored two simple in vitro models that suggest that control of motor number could play an important role in regulating switching between filaments. The work here provides a model for a new regulatory function of tau in the animal. This model suggests why altering tau's concentration of isoform ratio could contribute to a variety of neurodegenerative diseases.

Materials and Methods

In Vitro Motility Assay.

Twice-cycled tubulin was purified over a phosphocellulose column as described (17) and then frozen drop-wise until used. Both tau isoforms (4RL and 3RS) were bacterially expressed and purified as described (18) (also see SI Fig. 9). Tau was flash frozen in a 1× PM buffer, and stored at −80°C until used. Kinesin I was purified from cow brain essentially as described (19) except that the 9S kinesin was eluted from the Mono-Q resin using a series of customized salt gradients to separate the kinesin from other polypeptides present in the 9S sucrose fractions. Western blotting and antibody probing determined that the purified kinesin-I sample contained only a single kinesin isoform and no trace of dynein or dynactin. Kinesin (tetramers consisting of two light chains and two heavy chains; concentration of 72 nM) was flash frozen in PMEE buffer with 45% glycerol, and stored at −80°C until used.

The overall experimental details are similar to the ones previously reported (20, 21). Briefly, upon initial incubation, taxol-stabilized MTs were further incubated with equal amounts of 10 mM GTP (diluted in 100 mM Pipes buffer, pH 6.9) and various amounts of tau isoforms for 25 min at 37°C. The amount of tau that bound to MTs was estimated according to the previously reported model (22)

We used the binding parameters n, K_d, and p, which were previously reported for the longest form of human tau (4RL tau) and for the shortest natural splice variant of human tau (3RS tau) (22). The binding curves we used to estimate MT binding for 4RL and 3RS tau are shown in SI Fig. 8c.

To test tau binding, 19.8 μM polymerized MT were incubated with 1.4 μM of either 3RS or 4RL tau. The mixture was spun in an ultracentrifuge, and supernatant and pellet fractions were collected. Pellets were resuspended in 1× PMEE, solubilized with SDS sample buffer, and loaded on a 7.5% polyacrylamide gel. Proteins were transferred to a poly(vinylidene fluoride) membrane and probed with a 5A6 anti-tau monoclonal antibody (Developmental Studies Hybridoma Bank, University of Iowa, Iowa City, IA). The blots were probed with goat anti-mouse IgG-HRP (Jackson ImmunoResearch Laboratories, West Grove, PA) and detected with the Western Lightning Chemiluminescence Reagent Plus (PerkinElmer Life Sciences, Boston, MA). SI Fig. 10 summarizes our results and demonstrates that tau is competent to bind to MTs and also that, under identical incubation conditions, similar amounts of 3RS and 4RL tau become attached to MTs. Therefore, the stronger effect of 3RS tau on kinesin-MT binding and kinesin-based transport reported above is not due to higher accumulation of this isoform on MTs.

Tau-coated MTs prepared using this procedure were then injected into a flow cell and allowed to incubate at room temperature for 20 min in a high humidity environment. This allowed MTs to get attached to the flow cell glass surface preincubated with poly-l-lysine). The loose MTs were then washed out and a casein buffer (13.5 mg/ml casein) was injected to block the surface of the slide. Each flow cell was further incubated for at least 30 min before a separately prepared bead/motor assay was injected into the flow cell immediately before the start of the experiments.

Our kinesin assay was similar to the one described in ref. 6. Before experiments, kinesin solution was thawed and mixed with assay buffer (66.4 mM Pipes, pH 6.9/50 mM potassium acetate/3.4 mM MgSO₄/0.8 mM DTT/0.84 mM EGTA/10.1 μM Taxol). The carboxylated polystyrene beads (489-nm diameter; Polysciences, Warrington, PA) were incubated with the motors in the presence of 10 μM MgATP. Note that the stock 0.6 nM bead solution was further diluted to 0.6 pM in the assays reported here. An oxygen scavenging solution (250 μg/ml glucose oxidase, 30 μg/ml catalase, 4.6 mg/ml glucose) was added to the solution upon incubation immediately before injection into the flow cell.

MT Binding.

To test binding, we captured the beads with an optical trap and positioned them close to MTs. We used very low laser power (10 mW) for such testing. The testing time was fixed for all assays. Consistent timing constraint is important because tau on MTs may present steric hindrance for binding so that it may take longer for motors to diffuse to the MT in the presence of tau. Thus, longer waiting times may result in increased overall binding fraction. We chose to wait 15–20 s for each binding test, because longer waiting times proved to make little difference in any assay on bare MTs.

Travel Length Measurements.

The beads were captured with an optical trap and positioned close to MTs. When the bead bound to an MT, we manually shuttered the laser beam. Again, low laser power (10 mW) was used to minimize disturbance to bead travel as the laser beam was being turned off. The manual response of the operator may have introduced a time delay, and thus may have resulted in lower counts in the first bin of the histograms shown in Fig. 3. Total travel of the beads was recorded to S-VHS tapes at NTSC frame rate (29.97 fps). The video was subsequently digitized (without compression) and analyzed by using a described template matching algorithm (23).

Force Measurements.

In general, force measurements were performed as described (20, 21). In this study, we used a 980-nm single-mode diode laser (Axcel Photonics, Marlborough, MA). We estimate that the peak force that a 55 mW trap can apply to our polystyrene beads (0.489 μm diameter) is ≈8 pN. Therefore, a bead driven by only one kinesin motor (assuming the mean of 4.8 pN and standard deviation of 0.6 pN reported in the main text in Fig. 1a) would have a <0.00025% chance of escaping from the trap. However, measurements of multiple kinesin-I motor stalls required the use of high laser powers to assure that motor motion does not exceed the linear response range of the trap. We have found that 130 mW laser power produced no detectable laser damage for at least 1 min of operation. Therefore, force measurements at high laser powers were designed as follows: beads were captured at low laser power (10 mW) and manually positioned slightly to the side of MTs. Custom LabView program was then used to slowly move the bead across a MT (typical settings: 50 nm steps with 500 ms between steps), detect directed processive motion, and then quickly (typical timing of 150 ms) ramp the power to 130 mW. In this way the beads were exposed to high laser powers only when actually moving along MTs.

Determination of the Typical Number of Motors Per Bead.

For single motor beads, an assay was chosen with binding fraction of beads of 0.3 (18 pM kinesin). Force measurements were used to confirm that only a single motor is driving a given bead. Furthermore, in all such assays, none of the beads we tested could escape from a 55 mW trap. The cargo travel distances in these assays were in good agreement with existing estimates of the processivity for single kinesin motors (Fig. 3a).

The assays we designate as being ≈2 motors (0.36 nM kinesin) were prepared so that when used on tau-free MTs, all beads we tested bound to MTs and could eventually (sometimes after a few attempts) escape from a 55 mW trap but not from a 105 mW trap (≈ 15–16 pN peak force). The force measurements for such beads are shown in Fig. 1d. Both single- and two-motor events are observed (the fraction of three or more motor events does not exceed 9%). Notably, all beads could eventually produce stalls corresponding to forces of 7 pN and above (more than two standard deviations away from the mean of the single motor peak). Importantly, these assays showed effectively infinite cargo travel: all cargoes could reach the edge of our field of view (≈8 μm). We have followed some beads by manually repositioning the field of view as necessary and observed that beads in a ≈2 motor assay could reach the end of very long MTs (as much as 50–60 μm of travel).

When beads were incubated with even higher amounts of kinesin (0.72 nM kinesin), most of the resulting beads could escape the 105 mW trap after repeated attempts. Even beads that could not escape the trap within the limited testing time still showed displacements beyond 250–300 nm from the center of the trap (just below the escaping threshold). This finding suggests that for all beads at least three motors were engaged some of the time during their motion. Therefore, we designated this assay as 3+ motor.

MT–MT Switching Assay.

The cross-MT assay was prepared similar to the unidirectional case; however, the size of the flow cell was reduced (total volume ≈5 μl) and the cell was shaped as a cross to allow flow in orthogonal directions. The geometry of the flow cell is shown in SI Fig. 11. The flow cell was initially filled with the same buffer in which MTs were incubated. In this way, whenever liquid was injected into the cell from either direction, the sides of the cross were essentially stagnant pockets of liquid (surface tension of water was sufficient to prevent the injected solution from spilling out unless it was wicked away) assuring a nearly laminar unidirectional flow through the cell. All buffers and solutions injected into the cell were injected from one and then the other direction to assure complete replacement of the previous buffer with the new one. MTs were first injected into the flow cell in one direction, followed 5 min later by an injection of MTs in the orthogonal direction. Afterward, the regular protocol was followed. An example of the resulting MT arrangement is shown in SI Fig. 12.

To test the influence of tau on MT–MT switching, we first injected tau-decorated MTs followed by bare MTs injected orthogonally to the first layer. Beads were brought near the lower MTs and allowed to attach and proceed to the intersection with the bare MTs.

Pull-Off Experiments.

We have used custom software written in LabView to determine the location of a bead moving on a MT (23), position the center of the optical trap over this location, turn the trap on by opening the laser beam shutter, and then move the trap center perpendicular to the MT direction (at a rate of 1 μm/s). We observed two types of outcomes: the bead was either still attached to the MT or was fixed in a trap several microns away from the MT. Each outcome was logged, and the fraction of each outcome is reported here.

Abbreviations

MT

microtubule

MAP

MT-associated protein.