Skip to main content
NCBI home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2006 Nov 28;274(1609):527–533. doi: 10.1098/rspb.2006.3743

Unexpected heterozygosity in an island mouflon population founded by a single pair of individuals

Renaud Kaeuffer 1,2,*, David W Coltman 3, Jean-Louis Chapuis 4, Dominique Pontier 2, Denis Réale 1
PMCID: PMC1766376  PMID: 17476773

Abstract

In population and conservation genetics, there is an overwhelming body of evidence that genetic diversity is lost over time in small populations. This idea has been supported by comparative studies showing that small populations have lower diversity than large populations. However, longitudinal studies reporting a decline in genetic diversity throughout the whole history of a given wild population are much less common. Here, we analysed changes in heterozygosity over time in an insular mouflon (Ovis aries) population founded by two individuals in 1957 and located on one of the most isolated locations in the world: the Kerguelen Sub-Antarctic archipelago. Heterozygosity measured using 25 microsatellite markers has actually increased over 46 years since the introduction, and exceeds the range predicted by neutral genetic models and stochastic simulations. Given the complete isolation of the population and the short period of time since the introduction, changes in genetic variation cannot be attributed to mutation or migration. Several lines of evidence suggest that the increase in heterozygosity with time may be attributable to selection. This study shows the importance of longitudinal genetic surveys for understanding the mechanisms that regulate genetic diversity in wild populations.

Keywords: heterozygosity, island population, selection, longitudinal study

1. Introduction

In population and conservation genetics it is widely accepted that small, isolated populations rapidly lose genetic diversity as a result of genetic drift (Falconer & Mackay 1996; Frankham 1996; Keller & Waller 2002) that could drive the population to extinction (Spielman et al. 2004). The theoretical reduction in heterozygosity (H) in a closed random mating population is predicted by the classical formula (Hedrick 2000):

HtH0=(1−12Ne)t, (1.1)

where Ne is the effective population size, H0 is the heterozygosity at generation 0, Ht is the heterozygosity expected at generation t, and t is the number of generations. Since the loss of genetic diversity is faster in small compared with large populations, a population experiencing a bottleneck or fluctuating dynamics is assumed to be subject to stronger drift than a stable population with a similar average population size (Nei et al. 1975; Motro & Thomson 1982; Vucetich & Waite 1999; Groombridge et al. 2000; England et al. 2003). The loss of H can be predicted in a cyclic fluctuating population using a more complex model (Motro & Thomson 1982).

In support of these population genetic models, numerous empirical studies have reported the loss of genetic diversity following a bottleneck (England et al. 2003), a positive relationship between diversity and population size (Frankham 1996) and the lower diversity in insular compared with mainland populations (Frankham 1997). This support generally comes from transversal comparative studies of populations that may be characterized by different demographic characteristics and are often interpreted in the absence of detailed historical demographic data. Such ‘snapshot’ studies may illustrate the global effect of drift on genetic diversity, but they do not capture the temporal dynamics of genetic diversity. A more appropriate way of testing for the loss of genetic diversity by genetic drift would be to use changes in H observed over time within the same population. However, longitudinal genetic data of natural populations are very scarce. Furthermore, migration or population demography may interfere with drift making genetic changes in natural populations difficult to predict. An insular population with a well-known history therefore provides an appropriate model for testing the predictions of population genetic theory with empirical data on gene dynamics.

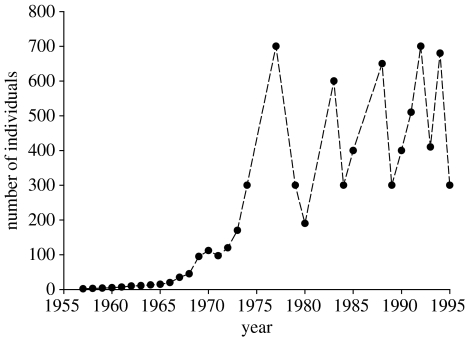
In 1957, one yearling male and one yearling female mouflon (Ovis aries) were introduced onto Haute Island (6.5 km2; Chapuis et al. 1994), one of the islands of the very remote Kerguelen archipelago located in the Sub-Antarctic Indian Ocean. The demographic history of the Kerguelen mouflon population is well documented from the introduction to the mid-1990s (Chapuis et al. 1994). The two founders originated from a captive population at Vincennes Zoo (Paris, France). The Kerguelen population reached 100 individuals at the beginning of the 1970s (figure 1), and then grew exponentially to culminate with 700 individuals in 1977. Since then the population has been characterized by cyclical dynamics, fluctuating between 250 and 700 individuals (Chapuis et al. 1994), with winter crashes occurring at a periodicity of 3–5 years after the number of individuals exceeds about 600. Crash survival is female-biased due to the costs of inter-male competition during the pre-winter rut (Boussès et al. 1994). Given the strong founder effect, the cyclical population dynamics and the total isolation of the population, we expected very low heterozygosity in this population.

Figure 1.

Figure 1

Open in a new tab

Number of individuals estimated on the Kerguelen mouflon population.

Here, we combine longitudinal genetic data and detailed information on demographic history from an island population and its ancestral source to study changes in genetic diversity over the time. Using simulations we also explore in more detail what would be the expected change of heterozygosity in the Kerguelen mouflon population under neutrality and the observed demographic history.

2. Materials and Methods

(a) Population and study site

The Kerguelen archipelago (48°25′–50° S, 68°27′–70°35′ E) is very remote and accessible only by boat, usually from La Réunion Island 3000 km away. The very limited access to the archipelago is under the supervision of the administration of the French Austral and Antarctic Territories (T.A.A.F.). The probability of an uncontrolled introduction or undetected migration of mouflons to the Haute Island is therefore negligible. The Sub-Antarctic climate of the archipelago is characterized by an average temperature of 1.9°C in winter and 7.4°C in summer. Haute Island is rocky with a weak grass cover (only 30% of the island) and, in 1972, fodder grass was introduced to increase the foraging resources of the island. The population was founded by two lambs from the Vincennes Zoo (Paris, France). The population was monitored with the help of scientists, hunters, the administration of the T.A.A.F. and an intensive scientific research program between 1988 and 1996 (Boussès et al. 1994; Chapuis et al. 1994; Boussès & Réale 1996). Mouflon (Ovis aries) exhibit a promiscuous mating system and strong sexual dimorphism (Bon et al. 1992), males being heavier than females (male carcass weight=28.7±0.9 kg; female carcass weight=19.5±0.5 kg; Boussès & Réale 1996). In the Kerguelen population, female annual fecundity averages 1.1 and the variance in fecundity equals 0.7 (data obtained from 100 females culled in 1994). In male ovids, age can be estimated precisely using the number of horn segments (Geist 1971). Age in females in this population could be approximated by counting the number and wear of definite incisors (Boussès & Réale 1994). We estimated the average adult lifespan to be 3.5 years using the average age of adult carcasses found between 1993 and 1995 (n=412). Given the low adult life span and the early age at first reproduction in that population (Boussès & Réale 1998), we estimated the generation time to be close to 2 years.

(b) Genotyping

Most of the tissue samples (hair, skin and horns) from the Kerguelen population come from hunted individuals. Between 1960 and 2003, 144 samples were collected from the Haute Island population. A few horns were collected from carcasses found on the ground. The year of birth (cohort) was determined by subtracting the individual's age from the year of death. Tissue samples (teeth and dry tissues) from seven individuals born between 1959 and 1970 at the Vincennes Zoo, and kept at the Muséum National d'Histoire Naturelle (Paris, France), allowed us to genotype the population of origin. At the time of the introduction on Haute Island, the Vincennes population was composed of about 40 individuals (Boussès & Réale 1998).

Tissue samples were kept in 95% ethanol. Horns were drilled, teeth smashed, and the dust was used for DNA extraction with the QIAamp tissue extraction mini kit (Qiagen, Inc., Mississauga Ontario). Polymerase chain reaction (PCR) amplification was performed at the following 25 ungulate-derived microsatellite loci: ARO28; HEL10; MCM64; MCM152; BM3413; BM848; HUJ177; MAF64; MCM527; TGLA13; Ilsts059; TGLA176; RT1; AGLA226; Il2ra; MCM218; NRAMP; OarCP49; TEXAN4; DRBps; INRA26; oMHC1; TGLA387; CSSM022; and MAF33 (see Maddox et al. 2001 for details).

Reaction conditions (see http://www.thearkdb.org/) were optimized using temperature and MgCl2 gradient PCR. PCR products were analysed with an automatic sequencer (ABI 3730, Applied Biosystems).

We tested primers for 100 different microsatellite loci on six historical samples (i.e. collected prior to 1970, both at Kerguelen and at Vincennes) and six contemporary samples (i.e. collected in 2003). Sixty-six of the 100 microsatellite loci amplified products of the expected size range. We selected 25 loci primers among the 66 tested, based on their readability and a minimum allelic diversity of 2 (i.e. 16 loci with 2 alleles, 7 with 3 alleles and 2 with 4 alleles, the average for both new and old samples equals 2.44). The oldest samples used may have been of low quality or may have contained a small amount of DNA (Lindahl 1993), which could have decreased H estimated as a result of allelic dropout (i.e. the random amplification of only one of the two alleles at a heterozygous locus; Taberlet et al. 1996). This effect can inflate the difference between H at the introduction and 2003. To limit this potential bias, DNA extractions were repeated three times and PCR three to seven times for the oldest samples to ensure reliable genotyping. The deviation from Hardy–Weinberg for each locus was tested using Genepop 3.4 (Raymond & Rousset 2003).

(c) Heterozygosity

Average individual heterozygosity is estimated by the number of heterozygote loci observed divided by the total number of loci used for an individual. We denote HO as the average individual heterozygosity observed in the population and HE as the expected heterozygosity under Hardy–Weinberg assumptions.

We calculated HO for each cohort. We analysed the change in HO with time from introduction to 2003 using an analysis of co-variance, where the mean value of HO (log transformed for normality) per cohort was regressed as a function of cohort, sex and the interaction between cohort and sex. Since cohorts differed in the number of individuals used to calculate HO, we used a weighted least square method, where the weight equals the sample size of each cohort.

(d) The population genetic model

The model of Motro & Thomson (1982) describes the change in heterozygosity over time in a population subject to fluctuations in size. Expected value of H (HE) at generation t is

Ht=2u(1+∑j=1t−1∏i=jt−1yi)+H0∏i=0t−1yi, (2.1)

where

yi=(1−2u)(1−12Net), (2.2)

where u is the mutation rate (fixed at 0.001; Weber & Wong 1993) and Net is the effective population size at generation t. From equation (2.1), we estimated the initial heterozygosity in the Haute Island population given H observed in the ancestral population. As mentioned above, we chose an average generation time of 2 and therefore approximated the effective population size at generation t, using the harmonic mean population size (Motro & Thomson 1982; Hartl & Clark 1997) over two consecutive years.

(e) Simulation

We simulated the demography and the genealogy of a population using individual based models. The genetic composition of the founder individuals was created by randomly combining alleles at 25 loci (i.e. 2 loci with 4 alleles, 7 with 3 alleles and 16 with 2 alleles; similar to the composition of loci observed in the population). The genotype of a newborn individual was produced by the random combination of two alleles at each locus, one coming from a male and the other from a female randomly chosen from the previous generations. The individual heterozygosity was estimated as the number of heterozygous loci divided by the total number of loci. We fixed several demographic parameters based on empirical observations of the population (Chapuis et al. 1994). The demographic model was density-dependent and the carrying capacity was fixed at 600 individuals and survival rate above the carrying capacity was set to 0.7. We used a model with two age classes because ungulates generally have a stable adult survival rate (Gaillard et al. 2000). We also integrated juvenile mortality rate (0.2 and 0.35) and adult maximum lifespan (3 and 4 years). These values were chosen to produce a demography similar to the one observed on the island (figure 1).

We investigated the effect of initial heterozygosity at the foundation of the population on subsequent gene dynamics using two founder individuals characterized by either the highest heterozygosity level (H=1) or the lowest possible heterozygosity (H=0.22) given the number of alleles per gene observed in the Kerguelen population. Under each set of conditions, we created 1000 population replicates and calculated the mean heterozygosity from 60 individuals randomly sampled from the population at year 47 (i.e. the equivalent of year 2003). The simulated heterozygosity denoted as ‘HS’ can differ from HE (H expected under Hardy–Weinberg assumptions).

In our simulation model, selection was mimicked by removing from the population all the newborns with an H lower than a threshold value (i.e. H=0.2, 0.3 and 0.4). For simulations with selection, juvenile mortality rate was fixed to 0.3 and maximum lifespan to 4. Selection had a negligible effect on the demography of the population, although it slightly increased juvenile mortality rate.

3. Results and discussion

(a) Theoretical expectations

Historical samples from Vincennes Zoo allowed us to estimate the observed heterozygosity of the ancestral population (HOa=0.45±0.12 s.d.) which we used as the initial heterozygosity of the Kerguelen population. Using the model of Motro & Thomson (1982) for a fluctuating population allowing mutation, we predicted a remaining HE of 0.12 in 1995, the last year for which we have accurate demographic data. Heterozygosity predicted for the first generation after introduction (HE1=0.34) matched that observed for the first individual sampled (HO1=0.31), a male collected in 1966 and estimated to be born in 1960. Since the initial H could be underestimated, we also predicted the expected HE in 1995 assuming the highest possible initial heterozygosity (i.e. H=1). Given this initial value, heterozygosity predicted for 1995 was 0.26. Motro and Thomson's model therefore predicts a decrease of 73% of H. The average individual heterozygosity observed (HO) in the population in 2003 was 0.48±0.11 s.d., which is 1.8–4 times that expected by Motro and Thomson's model. Furthermore, in 2003, the absence of any excess or lack of heterozygosity (table 1) shows that the population has probably reached the Hardy–Weinberg equilibrium. Our observations therefore differ dramatically from the model predictions, even though the mouflon population is in many ways ideally suited for that model (i.e. isolation, no mutation).

Table 1.

Heterozygosity observed and (H obs) expected (H exp) for each loci under Hardy–Weinberg assumption in the 1970s, 1988 and 2003. (Only two loci (in bold) in the 1970s deviated from the HW equilibrium and showed a deficit of heterozygosity.)

Microsatellites ID 1970s 1988 2003
H obs H exp H obs H exp H obs H exp
ARO28 0.428 0.337 0.277 0.323 0.381 0.444
HEL10 0.625 0.594 0.638 0.548 0.571 0.578
MCM64 0.571 0.571 0.533 0.615 0.619 0.661
MCM152 0.75 0.469 0.457 0.460 0.452 0.500
BM3413 0.428 0.5 0.478 0.466 0.524 0.499
BM848 0.375 0.43 0.311 0.369 0.476 0.472
HUJ177 0 0.5 0.383 0.472 0.429 0.482
MAF64 0.143 0.133 0.149 0.173 0.238 0.210
MCM 527 0.142 0.337 0.404 0.370 0.429 0.408
TGLA13 0.25 0.656 0.745 0.691 0.643 0.672
Ilsts059 0.167 0.375 0.390 0.450 0.405 0.436
TGLA176 0.5 0.656 0.587 0.619 0.595 0.632
RT1 0.143 0.336 0.152 0.211 0.238 0.210
AGLA226 0.5 0.65 0.630 0.665 0.595 0.610
Il2ra 0.375 0.492 0.532 0.456 0.429 0.496
MCM218 0.625 0.586 0.596 0.490 0.548 0.511
NRAMP 0.5 0.5 0.361 0.361 0.357 0.452
OarCP49 0.571 0.49 0.556 0.533 0.548 0.589
TEXAN4 0.571 0.49 0.340 0.400 0.381 0.444
DRBps 0.286 0.49 0.333 0.459 0.595 0.486
INRA26 0.125 0.117 0.255 0.254 0.238 0.210
oMHC1 0.5 0.531 0.488 0.603 0.595 0.513
TGLA387 0.571 0.408 0.565 0.496 0.524 0.482
CSSM022 0.428 0.459 0.489 0.456 0.429 0.408
MAF33 0.714 0.724 0.732 0.701 0.714 0.721
Average 0.411 0.473 0.455 0.466 0.478 0.485
(SE) 0.204 0.147 0.162 0.141 0.135 0.133
Open in a new tab

Several factors may explain the difference between expected and observed H. On one hand, using the harmonic mean as an estimate of Ne has been shown to overestimate the temporal decrease of H when the population experiences a strong founder effect (Motro & Thomson 1982; Caballero 1994). On the other hand, we have not included in our estimate of Ne effects such as a skewed sex ratio or a high variation in family size, which could further increase the reduction of H. Furthermore, the model of Motro & Thomson (1982), as most of the population genetic models widely used in studies of wild populations, does not consider overlapping generations (Waples 2005). The rate of decrease of H per generation equal to 1/(2Ne) predicted by these models is not valid when generations overlap (Johnson 1977; Nunney 1993). Our results show a simple example where the reduction in H can be overestimated and illustrate how classical population genetic models may produce biased predictions when their underlying assumptions are violated.

(b) Simulation results

Given the potential limitations of the applicability of the model of Motro & Thomson (1982) to the Kerguelen mouflon population, we performed stochastic simulations to predict the impact of initial heterozygosity, lifespan and juvenile mortality rate on gene diversity dynamics. Heterozygosity predicted by simulations (HS) ranged from 0.33 to 0.4 (initial H=1). The initial value of H had a weak effect on contemporary HS; with two different homozygous individuals at the first generation, individuals were completely heterozygous at the second generation (H=1). Heterozygosity (HO=0.48) observed in the Kerguelen population was still higher than the values predicted by simulations (table 2; in all the cases: p<0.001, N=42, t-test). Simulations mimicked the demography of the mouflon population (year and duration of the exponential growth, number of demographic peaks and crashes). Although they are probably more appropriate than Motro and Thomson's model for predicting the dynamics of H for populations with overlapping generations, simulations may still be conservative. In our simulations, in the absence of information on the variance of reproductive success among males, we used a random mating system. Mouflons, however, are characterized by a promiscuous mating system which could increase the loss of H (Nunney 1991; Nunney 1993). Furthermore, HS increases with maximum lifespan and our highest value of heterozygosity (HS=0.39) corresponds to a maximum lifespan of 4 years, which overestimates the lifespan in the Haute Island population.

Table 2.

Comparison of heterozygosity observed in 2003 in the Kerguelen mouflon population and heterozygosity estimated in 2003 from different simulations based on the population demography. (Initial heterozygosity was set up using two founders characterised by either the highest heterozygosity level (H=1) or the lowest possible heterozygosity (H=0.22) given the number of alleles per gene observed in the Kerguelen population. Juvenile mortality rate occurs randomly according to juvenile characteristics. Selection level represents the minimum H under which the individual dies. Comparison between simulated and observed H2003 are made with Student's t-tests.)

Hinitial maximum lifespan juvenile mortality rate selection level H2003 t p
observed values 0.45±0.12 s.d. — — — 0.48±0.11 s.d. — —
simulations 1 4 0.35 — 0.37 6.275 0.001
1 4 0.3 — 0.38 5.699 0.001
1 3 0.25 — 0.33 8.439 0.001
1 3 0.2 — 0.35 7.306 0.001
0.22 4 0.35 — 0.38 5.384 0.001
0.22 4 0.3 — 0.39 4.801 0.001
0.22 3 0.25 — 0.36 6.650 0.001
0.22 3 0.2 — 0.34 7.662 0.001
1 4 0.3 0.2 0.39 5.001 0.001
1 4 0.3 0.3 0.43 2.730 >0.01
1 4 0.3 0.4 0.50 1.244 >0.2
Open in a new tab

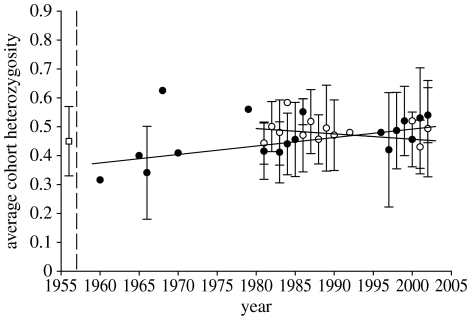
(c) Interaction with sex and cohort

In order to better understand the gene diversity dynamics, we analysed the change in HO per cohort by sex between the introduction and 2003 (figure 2). We found a significant interaction between sex and cohort (F1,27=6.784, p=0.015). HO significantly increased with time only for males, but not for females (figure 2), probably because we did not have data for females during the early years. These results suggest that some other mechanisms may promote heterozygosity in the Kerguelen population. Despite a strong founder effect and a strong potential for genetic drift, heterozygosity has increased over time. This increase could be explained by selection in favour of heterozygous individuals. Two hypotheses can explain the evolutionary advantage of heterozygosity: (i) the overdominance hypothesis, according to which the fitness of the heterozygote is superior to that of both the homozygotes, and (ii) the dominance hypothesis, which implies that heterozygosity prevents the expression of deleterious recessives alleles (Charlesworth & Charlesworth 1987).

Figure 2.

Figure 2

Open in a new tab

Average cohort heterozygosity observed (and standard deviation) on Kerguelen mouflon population. (Filled circles represent males and open circles represent females. The open square represents the average heterozygosity observed in the ancestral population.)

With the exception of HUJ177 and TGLA13 in the 1970s, the loci did not show any departure from the Hardy–Weinberg expectation (table 1; all p>0.05). The average heterozygosity estimated at each locus increased from 0.41 to 0.48 over the three periods 1970s, 1988 and 2003 (table 1). However, given the large SEs associated with the heterozygosity estimates we could not show significant differences between these three periods (table 1; Friedman χ2=2.686, p=0.26).

(d) Selection as a possible mechanism

We therefore used the simulation approach to identify the range of demographic parameters that could explain the high H observed in the population under neutral conditions. We extended the simulations using a larger panel of demographic parameters (i.e. range: life span=3–8 years; juveniles mortality=0.2–0.6). It should be noted that these new parameters exceeded the plausible range of demographic parameters observed in the population, but that they permitted the dynamics observed to be kept (figure 1). None of the heterozygosity values obtained with these simulations exceeded 0.43, and all of them were significantly lower than the observed H in the population in 2003 (all p<0.05; data not shown, but see table 3).

Table 3.

Heterozygosity estimated after 47 years (HS) in a simulated population using a subsample of loci that have lost or not lost alleles during the history of the population. (Wilcoxon matched paired rank test was used to test for the difference between HS in the two conditions. t-Test was used to test the significance of the difference between HO in the mouflon population (i.e. HO=0.48 after 47 years, in 2003) and HS.)

maximum lifespan juveniles mortality rates HS HS W Pw t Pt
loss no loss
3 0.25 0.33 0.38 1247 <0.0001 5.569 <0.001
4 0.35 0.36 0.40 1154.5 <0.0001 4.434 <0.001
5 0.45 0.39 0.41 1080 <0.0001 3.866 <0.001
6 0.5 0.40 0.42 891 <0.001 3.298 <0.01
7 0.5 0.41 0.42 1026 <0.0001 3.298 <0.01
Open in a new tab

The use of loci that had not lost alleles during the history of the population (average number of alleles=2.44) could generate ascertainment bias and potentially explain the high HO observed. We therefore simulated 50 populations and estimated HS after 47 years (i.e. equivalent of 2003 on Haute Island; see §2) from a dataset that includes all the loci or sub sample of loci that have not lost alleles. Using loci that have not lost any alleles can lead to some ascertainment bias in HO (Wilcoxon matched paired rank test, all p<0.001; table 3). Comparisons between HS after 47 years and HO in 2003 in the mouflon population (t-test, all p<0.01; table 3), however, reveal that ascertainment bias alone cannot explain the increase in heterozygosity over time in the Haute Island population. It is interesting to note that the ascertainment bias is reduced when generation time increases because longer generations limit the loss of genetic diversity.

Simulations including selection in favour of heterozygotes (see §2; table 2) showed that under the conditions tested (HO initial of 1, maximum lifespan of 4 years and juvenile mortality rate of 0.3), selection against individuals with a heterozygosity under or equal to 0.4 led to an increase of the HS up to 0.5 in 2003. These results are therefore consistent with selection as a possible mechanism for the maintenance or increase of heterozygosity over time. In these simulations, however, we used a simple model with a constant rate of selection on newborns, when selection in the Kerguelen population could have been more complex. For example, mortality rate varies between year, sex and age classes (Boussès et al. 1994), suggesting that selection could fluctuate over time. Fluctuating selection may be less efficient at increasing H than consistent selection. It is worth noting that these simulation models did not allow us to answer the question of whether selection acts as a genome-wide process or by local effects at some specific loci.

Three of our loci (DRBPs, TGLA387 and oMHC1) are know to be closely linked to the MHC gene complex (Maddox et al. 2001), which is involved in resistance to disease, and are known to be under strong overdominance selection (Aguilar et al. 2004). Two of these loci (DRBPs and oMHC1) show an increase of H between 1988 and 2003 (table 1). It is therefore possible that selection at some loci in linkage disequilibrium with our microsatellites could explain the increase in H over time in the Kerguelen mouflon population (Charlesworth 1991). The maintenance of heterozygosity at neutral microsatellite markers reported here should be attributed to a combination of linkage disequilibrium and selection at linked loci (i.e. ‘local effects’; Hansson et al. 2004). Alternatively, the maintenance of heterozygosity could be attributed to the effects of selection against inbreeding across the whole genome (‘general effects’; Hansson et al. 2004). Balloux et al. (2004) have suggested that a strong H–H correlation is required in order for average H to reflect whole genome heterozygosity under inbreeding. We followed Balloux et al. (2004) by calculating the average correlation between the mean H calculated from two random subsets of markers over 1000 replicates. The low H–H correlation (Balloux et al. 2004; r=0.149±0.002 SE) observed among our loci suggests that our observed changes in H are less likely to be explained by genome-wide processes than by local effects.

4. Conclusion

The quasi-experimental situation and the longitudinal data of the Kerguelen mouflon population allowed us to detect an increase in individual heterozygosity over time. Our results suggest that selection is the likely mechanism responsible for the increase in H in an insular population founded by two individuals. These results raise the question of the generality of this process in other populations under different conditions. In some populations, selection may affect H, but may be hidden by the effect of genetic drift. Selection, on the other hand, may lower the impact of drift on the loss of genetic diversity. Information from longitudinal studies such as the Kerguelen mouflon population are therefore needed to help us understand the respective roles of selection and drift on the change in genetic diversity in small isolated populations.

Acknowledgments

We thank P. Boussès, T. Micol (T.A.A.F.), B. Tollu, the Amical des Missions Australes et Polaires Françaises and all fieldworkers who collected mouflon samples and data, A. Krupa and A. Llewellyn for their help with molecular analyses, O. Gingras for programming, F. Balloux, T. Coulson, S. Devillard, J. M. Gaillard, B. Hansson and D. Waller for discussions. This work was supported by the Institut Polaire Français Paul-Emile Victor and the Centre National de la Recherche Scientifique to J.L.C. and D.P., the Natural Sciences and Engineering Research Council and the Canadian Foundation for Innovation to D.R., and the Royal Society to D.W.C.

References

  1. Aguilar A, Roemer G, Debenham S, Binns M, Garcelon D, Wayne R.K. High MHC diversity maintained by balancing selection in an otherwise genetically monomorphic mammal. Proc. Natl Acad. Sci. USA. 2004;101:3490–3494. doi: 10.1073/pnas.0306582101. doi:10.1073/pnas.0306582101 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Balloux F, Amos W, Coulson T. Does heterozygosity estimate inbreeding in real populations? Mol. Ecol. 2004;13:3021–3031. doi: 10.1111/j.1365-294X.2004.02318.x. doi:10.1111/j.1365-294X.2004.02318.x [DOI] [PubMed] [Google Scholar]
  3. Bon R, Gonzalez G, Bosch M.A, Cugnasse J.-M. Ram rut-involvement in a hunted population of mouflons. Acta Theriol. 1992;37:63–71. [Google Scholar]
  4. Boussès P, Réale D. Valeur du masque facial comme critère d'âge des femelles de mouflons Corse (Ovis musimon) dans la population de Kerguelen. Mammalia. 1994;58:301–304. [Google Scholar]
  5. Boussès P, Réale D. Syndrome d'insularité dans une population récente de mouflon (Ovis musimon) des îles Kerguelen. Vie Milieu. 1996;46:285–290. [Google Scholar]
  6. Boussès P, Réale D. Biology of twinning and origin of an unusually high twinning rate in an insular mouflon population. Z. Säuget. 1998;63:147–153. [Google Scholar]
  7. Boussès P, Réale D, Chapuis J.L. Mortalité hivernale massive dans la population de mouflons Corse (Ovis musimon) de l'archipel subantarctique de Kerguelen. Mammalia. 1994;58:211–223. [Google Scholar]
  8. Caballero A. Developments in the prediction of effective population size. Heredity. 1994;73:657–679. doi: 10.1038/hdy.1994.174. [DOI] [PubMed] [Google Scholar]
  9. Chapuis J.L, Boussès P, Barnaud G. Alien mammals, impact and management in the French Subantarctic islands. Biol. Conserv. 1994;67:97–104. doi:10.1016/0006-3207(94)90353-0 [Google Scholar]
  10. Charlesworth D. The apparent selection on neutral marker loci in partially inbreeding populations. Genet. Res. 1991;57:159–175. [Google Scholar]
  11. Charlesworth D, Charlesworth B. Inbreeding depression and its evolutionary consequences. Annu. Rev. Ecol. Syst. 1987;18:237–228. doi:10.1146/annurev.es.18.110187.001321 [Google Scholar]
  12. England P.R, Osler G.H.R, Woodworth L.M, Montgomery M.E, Briscoe D.A, Frankham R. Effects of intense versus diffuse population bottlenecks on microsatellite genetic diversity and evolutionary potential. Conserv. Genet. 2003;4:595–604. doi:10.1023/A:1025639811865 [Google Scholar]
  13. Falconer D.S, Mackay T.F.C. Longman; Harlow, UK: 1996. Introduction to quantitative genetics. [Google Scholar]
  14. Frankham R. Relationship of genetic variation to population size in wildlife. Conserv. Biol. 1996;10:1500–1508. doi:10.1046/j.1523-1739.1996.10061500.x [Google Scholar]
  15. Frankham R. Do island populations have less genetic variation than mainland populations? Heredity. 1997;78:311–327. doi: 10.1038/hdy.1997.46. doi:10.1038/sj.hdy.6880980 [DOI] [PubMed] [Google Scholar]
  16. Gaillard J.M, Festa-Bianchet M, Yoccoz N.G, Loison A, Toigo C. Temporal variation in fitness components and population dynamics of large herbivores. Annu. Rev. Ecol. Syst. 2000;31:367–393. doi:10.1146/annurev.ecolsys.31.1.367 [Google Scholar]
  17. Geist V. Chicago University Press; Chicago, IL: 1971. Mountain sheep: a study behavior and evolution. [Google Scholar]
  18. Groombridge J.J, Jones C.G, Bruford M.W, Nichols R.A. Conservation biology—‘Ghost’ alleles of the Mauritius kestrel. Nature. 2000;403:616–616. doi: 10.1038/35001148. doi:10.1038/35001148 [DOI] [PubMed] [Google Scholar]
  19. Hansson B, Westerdahl H, Hasselquist D, Akesson M, Bensch S. Does linkage disequilibrium generate heterozygosity-fitness correlations in great reed warblers? Evolution. 2004;58:870–879. doi: 10.1111/j.0014-3820.2004.tb00418.x. doi:10.1554/03-368 [DOI] [PubMed] [Google Scholar]
  20. Hartl D.L, Clark A.G. Sinauer Associates, Inc.; Sunderland, MA: 1997. Principles of population genetics. [Google Scholar]
  21. Hedrick P.W. Jones and Bartlett; Boston, MA: 2000. Genetics of populations. [Google Scholar]
  22. Johnson D.L. Inbreeding in populations with overlapping generations. Genetics. 1977;87:581–591. doi: 10.1093/genetics/87.3.581. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Keller L.F, Waller D.M. Inbreeding effects in wild populations. Trends Ecol. Evol. 2002;17:230–241. doi:10.1016/S0169-5347(02)02489-8 [Google Scholar]
  24. Lindahl T. Instability and decay of the primary structure of DNA. Nature. 1993;362:709–715. doi: 10.1038/362709a0. doi:10.1038/362709a0 [DOI] [PubMed] [Google Scholar]
  25. Maddox J.F, et al. An enhanced linkage map of the sheep genome comprising more than 1000 loci. Genome Res. 2001;11:1275–1289. doi: 10.1101/gr.135001. doi:10.1101/gr.GR-1350R [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Motro U, Thomson G. On heterozygosity and the effective size of populations subject to size changes. Evolution. 1982;36:1059–1066. doi: 10.1111/j.1558-5646.1982.tb05474.x. doi:10.2307/2408083 [DOI] [PubMed] [Google Scholar]
  27. Nei M, Maruyama T, Chakraborty R. The bottleneck effect and genetic variability in populations. Evolution. 1975;29:1–10. doi: 10.1111/j.1558-5646.1975.tb00807.x. doi:10.2307/2407137 [DOI] [PubMed] [Google Scholar]
  28. Nunney L. The influence of age structure and fecundity on effective population size. Proc. R. Soc. B. 1991;246:71–76. doi: 10.1098/rspb.1991.0126. [DOI] [PubMed] [Google Scholar]
  29. Nunney L. The influence of mating system and overlapping generations on effective population size. Evolution. 1993;47:1329–1341. doi: 10.1111/j.1558-5646.1993.tb02158.x. doi:10.2307/2410151 [DOI] [PubMed] [Google Scholar]
  30. Raymond, M. & Rousset, F. 2003 GENEPOP, version 3.4: population genetics software for exact tests and ecumenicism. Montpellier, France.
  31. Spielman D, Brook B.W, Frankham R. Most species are not driven to extinction before genetic factors impact them. Proc. Natl Acad. Sci. USA. 2004;101:15 261–15 264. doi: 10.1073/pnas.0403809101. doi:10.1073/pnas.0403809101 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Taberlet P, Griffin S, Goossens B, Questiau S, Manceau V, Escaravage N, Waits L.P, Bouvet J. Reliable genotyping of samples with very low DNA quantities using PCR. Nucleic Acids Res. 1996;24:3189–3194. doi: 10.1093/nar/24.16.3189. doi:10.1093/nar/24.16.3189 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Vucetich J.A, Waite T.A. Erosion of heterozygosity in fluctuating populations. Conserv. Biol. 1999;13:860–868. doi:10.1046/j.1523-1739.1999.98268.x [Google Scholar]
  34. Waples R.S. Genetic estimates of contemporary effective population size: to what time periods do the estimates apply? Mol. Ecol. 2005;14:3335–3352. doi: 10.1111/j.1365-294X.2005.02673.x. doi:10.1111/j.1365-294X.2005.02673.x [DOI] [PubMed] [Google Scholar]
  35. Weber J.L, Wong C. Mutation of human short tandem repeats. Hum. Mol. Gen. 1993;2:1123–1128. doi: 10.1093/hmg/2.8.1123. [DOI] [PubMed] [Google Scholar]

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES