Promoting motions in enzyme catalysis probed by pressure studies of kinetic isotope effects

Abstract

Use of the pressure dependence of kinetic isotope effects, coupled with a study of their temperature dependence, as a probe for promoting motions in enzymatic hydrogen-tunneling reactions is reported. Employing morphinone reductase as our model system and by using stopped-flow methods, we measured the hydride transfer rate (a tunneling reaction) as a function of hydrostatic pressure and temperature. Increasing the pressure from 1 bar (1 bar = 100 kPa) to 2 kbar accelerates the hydride transfer reaction when both protium (from 50 to 161 s⁻¹ at 25°C) and deuterium (12 to 31 s⁻¹ at 25°C) are transferred. We found that the observed primary kinetic isotope effect increases with pressure (from 4.0 to 5.2 at 25°C), an observation incompatible with the Bell correction model for hydrogen tunneling but consistent with a full tunneling model. By numerical modeling, we show that both the pressure and temperature dependencies of the reaction rates are consistent with the framework of the environmentally coupled tunneling model of Kuznetsov and Ulstrup [Kuznetsov AM, Ulstrup J (1999) Can J Chem 77:1085–1096], providing additional support for the role of a promoting motion in the hydride tunneling reaction in morphinone reductase. Our study demonstrates the utility of “barrier engineering” by using hydrostatic pressure as a probe for tunneling regimes in enzyme systems and provides added and independent support for the requirement of promoting motions in such tunneling reactions.

Enzymes are efficient catalysts that can achieve rate enhancements of up to 10²¹ over the uncatalyzed reaction rate (1). Our quest to understand the physical basis of this catalytic power, which is pivotal to our understanding of biological reactions and our exploitation of enzymes in chemical, biomedical, and biotechnological processes, is challenging and has involved sustained and intensive research efforts for >100 years (for reviews see, e.g., refs. 2–6). Recent experimental studies employing the temperature dependence of kinetic isotope effects (KIEs) have emphasized the role of quantum mechanical tunneling in enzymatic hydrogen-transfer (H-transfer) reactions (7–18). These data, which can be explained neither by conventional transition state theory (TST) nor by the Bell tunneling correction to TST (19), are in agreement with environmentally coupled models of hydrogen tunneling (H-tunneling) (12, 20, 21) and can be simulated computationally (22–30) within the framework of modern TST (31). In the Kuznetsov and Ulstrup environmentally coupled model of H-tunneling (20), as used quantitatively by Klinman and coworkers (32), temperature-independent KIEs arise from Marcus-like (33) vibrations (collective thermally equilibrated motions) that lead to degenerate reactant and product states, whereas temperature-dependent KIEs arise from “gating motions” (motion along the reaction coordinate) that enhance the probability of tunneling at this configuration by bringing the reactant and product wells closer together.

Apart from temperature, the only other experimental parameter that has been exploited to study enzymatic H-tunneling reactions is that of hydrostatic pressure, an approach pioneered by Northrop in recent years (34–38). Semiclassical TST dictates that pressure effects are associated with differences in vibrational frequencies of isotopic and nonisotopic atoms (39, 40). These stretching vibrations are insensitive to pressures of a few kilobars (1 bar = 100 kPa), and this has been confirmed with chemical reactions in the low kilobar range (39). For chemical systems with inflated isotope effects that cannot be explained by semiclassical TST, Isaacs has shown a pressure dependence over 10⁻³ to 2 kbar, consistent with a tunneling mechanism (38). For nontunneling reactions, substrate isotope effects usually arise from a single transition state, and the primary KIEs for these reactions are independent of pressure (37, 40). This differing pressure dependence provides a convenient baseline for distinguishing between over-the-barrier and through-the-barrier (quantum tunneling) processes.

The reductive half-reaction of morphinone reductase (MR) involves hydride transfer from the C4 R-hydrogen of NADH to the N5 atom of flavin mononucleotide (FMN). This reaction is directly observed in a rapid-mixing stopped-flow instrument and is kinetically resolved from steps involving coenzyme binding and formation of an enzyme–NADH charge-transfer (CT) complex, and the observed KIE is essentially the intrinsic KIE (13, 41, 42). The reductive half-reaction of this enzyme has been extensively characterized (13, 41, 42). One of the crucial findings from these studies is that the 1° KIE of MR is highly temperature-dependent (13). These data, coupled with a recent study showing that the 2° KIE is also exalted and consistent with preorganization in MR (42), have led us to describe the reaction within the context of modern environmentally coupled models of H-tunneling (12, 20, 43, 44) such that the enzyme requires a promoting motion to move the nicotinamide C4-H sufficiently close to the FMN N5 atom to facilitate tunneling. Herein, we further this study by measuring the simultaneous temperature and pressure dependencies of the 1° KIE in this reaction.

Results

Initial Characterization.

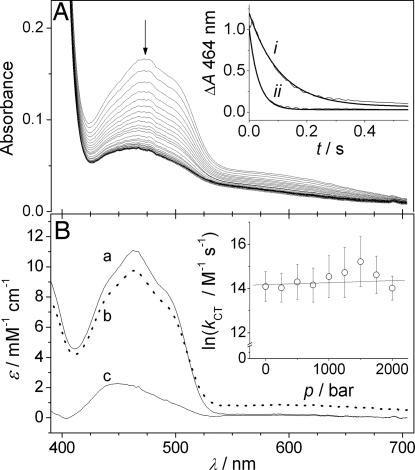
The reductive half-reaction of MR (from Pseudomonas putida M10) involves a hydride transfer from the coenzyme NADH to enzyme-bound FMN (13, 41). This step can be directly measured by using stopped-flow methods and was monitored as a bleaching of the oxidized MR FMN absorbance at 464 nm (Fig. 1A). The rate of hydride transfer was determined by fitting a single-exponential function (42) to traces extracted at 464 nm (Fig. 1A Inset). When NADH binds to MR, a CT complex is formed with a broad absorbance centered at ≈552 nm (41). Furthermore, the absorbance spectrum of the CT complex can be deconvoluted with single-value decomposition from spectra acquired during the reaction with a diode array by using an irreversible a→b→c reaction (13). The effect of pressure on the CT complex was examined with this method (Fig. 1B Inset), and the deconvoluted spectra of oxidized MR (a), the CT complex (b), and reduced MR (c) obtained (Fig. 1B). There is no measurable spectral shift or change in magnitude in the absorbance of either the oxidized enzyme or the CT complex [supporting information (SI) Fig. 5). These data are highly suggestive that, over the 2-kbar pressure range accessible to the high-pressure stopped-flow spectrophotometer, there is no significant alteration to the local environment around the active site of MR. Thus, MR shows no signs of pressure-induced unfolding/conformational changes at 2 kbar.

Fig. 1.

The reductive half-reaction of MR at high pressure. (A) MR (20 μM) mixed with NADH (5 mM) at 2 kbar and 10°C. (Inset) Traces at 464 nm (marked with an arrow) extracted at 1 bar (i) and 2 kbar (ii). (B) Spectral deconvolution of the reaction of 20 μM MR mixed with 50 μM NADH at 2 kbar and 10°C by using an irreversible two-step reaction (a→b→c), where a is the fully oxidized enzyme, b is the enzyme–NADH CT complex, and c is the reduced enzyme. (Inset) The pressure dependence of the rate of CT formation (b) measured at 552 nm. This rate constant is second-order, and these values were determined at 50, 100, and 250 μM NADH concentrations.

The pressure dependence of an observed rate constant arises in absolute rate theory (34, 45) when assuming a quasiequilibrium between the reactant and transition state:

where R_p = 83.13 cm³·mol⁻¹·bar·K⁻¹ when the pressure, p, is measured in bar, k₀ is the rate constant extrapolated to 0 bar, and ΔV ^‡ is the apparent difference between the volume of the reactant state and the transition state, and has units of cm³−mol⁻¹. Although a tunneling reaction does not pass through a transition state, this analysis proved useful here. Additionally, Eq. 1 is used for pressure effects on electron transfer (ET) (tunneling) reactions (46).

The second-order rate of CT formation was determined by using 50, 100, and 250 μM NADH at 10°C as a function of pressure. By fitting the data to Eq. 1 (Fig. 1B Inset), k₀ was found to be 1.4 ± 0.2 μM⁻¹·s⁻¹, and ΔV^‡ = −2.5 ± 3.4 cm³·mol⁻¹. Thus, because ΔV^‡ is not significantly different from zero, there is no observed effect of pressure on the rate of CT formation. Because this reaction is second-order, the effect of pressure on NADH binding to MR was also examined.

The Effect of Pressure on NADH Binding to MR.

The dependence of the observed rate of MR reduction on NADH concentration was measured at 10°C and 40°C (283 and 313 K) as a function of pressure. The data were fit to a binding isotherm: k_obs = k_max[NADH]/(K_d + [NADH]) to determine the apparent dissociation constant, K_d (SI Fig. 6). At 10°C, the K_d increased from 93 ± 14 μM at 1 bar to 219 ± 37 μM at 2 kbar. At 40°C, there is no significant difference in the K_d measured at 1 bar (302 ± 44 μM) to that at 2 kbar (297 ± 49 μM). The different behavior at these two temperatures may reflect a partial enthalpy/entropy compensation. Because substrate binding was not the focus of this work, we did not examine it further.

The observed activation volume (ΔV^‡) for a multistep enzyme reaction includes volume changes in the rate-limiting step plus all steps preceding this step, most notably substrate binding (47). Because flavin reduction in MR becomes pseudo-first-order at saturating concentrations of NADH, the pressure dependence of coenzyme binding can essentially be neglected because this step is not rate-limiting. Thus, a saturating NADH concentration of 5 mM [taken to be >10 × K_d (13)] was used throughout this study. This approach highlights an advantage of using rapid-mixing (stopped-flow) methods over steady-state methods to study the pressure effects in specific steps of the enzyme-catalyzed reaction.

Primary Kinetic Isotope Effects.

The primary kinetic isotope effect (1° KIE) of the hydride transfer during the flavin reduction step in MR was investigated by using NADH and (R)-[4-²H]NADH (NAD²H). The reaction with each substrate was measured every 250 bar between 1 bar and 2 kbar and every 5°C between 5°C and 40°C (278–313 K). The pressure-dependent data were fit to Eq. 1, and the temperature-dependent data were fit to the Eyring equation:

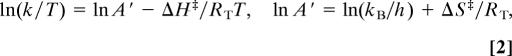where ΔH^‡ and ΔS^‡ are the enthalpy and entropy of the reaction and R_T is the gas constant (8.314 J·mol⁻¹·K⁻¹), whereas the other terms have their usual meanings. We will refer to A′ here as the Eyring prefactor (akin to the Arrhenius prefactor, A). The effect of pressure on the observed rates and on the corresponding Eyring plots, and the pressure/temperature dependence of the KIE are shown in Fig. 2A, B, and C, respectively. The parameters obtained from fitting the data to Eqs. 1 and 2 are described in turn below and summarized in Table 1.

Fig. 2.

The combined pressure and temperature dependencies of the reductive half-reaction of MR with NADH and NAD²H. (A) Plot of k_red versus p for the reaction with both cofactors at the limits of the temperature range, 5°C and 40°C. The solid lines are fits to Eq. 1; note the log scale for k. (B) Eyring plots of the reaction at atmospheric pressure and at 2 kbar. (C) The combined effect of pressure and temperature on the resulting KIE.

Table 1.

Parameters obtained from the temperature and pressure dependence of the hydride transfer step in MR

Parameters	NADH	NAD2H	KIE
k0, s−1 (25°C)	50.2 ± 1.9	12.4 ± 0.3	4.0 ± 0.3
ΔV‡, cm3·mol−1 (25°C)	−15.6 ± 0.8	−11.6 ± 0.5	−4.0 ± 1.3
dΔΔV‡/dT, cm3·mol−1·K−1	−0.09 ± 0.03	−0.04 ± 0.03	−0.05 ± 0.06
ΔH‡, kJ·mol−1
1 bar	32.0 ± 1.3	41.3 ± 2.5	9.3 ± 3.8
2 kbar	30.1 ± 2.2	43.7 ± 1.5	13.6 ± 3.7
dΔΔH‡/dp, kJ·mol−1·kbar−1	0.4 ± 0.7	1.0 ± 0.4	0.6 ± 1.1
ΔS‡, J·mol−1·K−1
1 bar	−103 ± 5	−83 ± 9	20 ± 13
2 kbar	−99 ± 8	−66 ± 5	32 ± 13
dΔΔS‡/dT, J·mol−1·K−1·kbar−1	6.8 ± 2.6	7.3 ± 1.6	0.5 ± 4.1
lnA′,	11.4 ± 0.6
1 bar		13.8 ± 1.0	0.09 ± 0.15
2 kbar	11.8 ± 0.9	15.7 ± 0.6	0.02 ± 0.03
dlnA′/dp, kbar−1	0.8 ± 0.3	0.9 ± 0.2	0.1 ± 0.5

KIE values are the differences in magnitude except for lnA′, where the prefactor ratio, A′_H:A′_D is given.

Activation Volume, ΔV^‡.

The rate of flavin reduction increases exponentially with pressure (Fig. 2A), resulting in negative apparent ΔV^‡ values (from Eq. 1). The reactions with NADH and NAD²H show significantly different pressure dependencies with ΔV^‡ = −15.6 ± 0.8 and −11.6 ± 0.5 cm³·mol⁻¹ at 25°C, respectively. The resulting pressure dependence of the KIE, ΔΔV^‡ = −4.0 ± 1.3 cm³·mol⁻¹ at 25°C [where ΔΔV^‡ = ΔV^‡H − ΔV^‡D using Northrop's convention (34)]. Consequently, the KIE increases with pressure (Figs. 2C and 4). There is a small but significant increase in the magnitude of both ΔV^‡H (ΔV^‡ for the reaction with hydrogen) and ΔV^‡D [ΔV^‡ for the reaction with deuterium (D)] with increasing temperature but dΔΔV^‡/dp is not significantly less than zero (SI Fig 7). Thus, whereas the KIE increases with pressure, the magnitude of this increase does not change measurably with temperature (SI Fig 7).

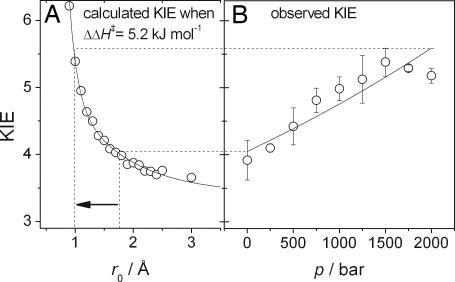
Fig. 4.

Correlation of observed KIEs with calculated r₀ values as a function of pressure. (A) The calculated KIE dependence on r₀ from Eqs. 4 and 5 (shown in Fig. 3) when ΔΔH^‡ is fixed to 5.2 kJ·mol⁻¹. (B) The measured KIE versus p at 25°C. The solid line is a fit to KIE = k_0,H/k_0,D exp(−ΔΔV^‡p/R_pT). The increase in observed KIE is consistent with a decrease in the equilibrium separation, r₀, from ≈1.7 Å to ≈1.0 Å (depicted by the arrow).

Activation enthalpy, ΔH^‡.

We have previously shown that MR has a temperature-dependent 1° KIE (13, 42), which is defined as ΔΔH^‡ = (ΔH^‡D − ΔH^‡H) > 0. There is no significant effect of pressure on ΔH^‡H, but there is a small but significant increase in ΔH^‡D of 2.0 ± 0.8 kJ·mol⁻¹ over 2 kbar (SI Fig. 8A). However, dΔΔH^‡/dp is not significantly greater than zero; therefore, the temperature dependence of the KIE does not change measurably with pressure.

Activation Entropy, ΔS^‡ and lnA′.

The reactions with both NADH and NAD²H showed negative activation entropies, ΔS^‡, which decrease in magnitude at elevated pressure (SI Fig. 8). As this is a pseudo-first-order reaction, the observed ΔS^‡ values will not have a contribution from substrate binding and, as ΔS^‡ is negative, suggest that the “transition state” is more organized than the reactant state. The decrease in ∣ΔS^‡∣ with pressure is consistent with the enzyme adopting a more ordered state at elevated pressure. The Eyring prefactor ratio, A′_H, does not show a pressure dependence (Fig. 8C) as dΔS^‡H/dp ∼ dΔS^‡D/dp.

Discussion

Ruling Out the Bell Correction Model.

The large temperature dependence of the 1° KIE for hydride transfer in MR (13, 42) can be explained by either a Bell-type correction model (19) or by a full environmentally coupled tunneling model (20, 43). Northrop's initial treatment (34) of pressure effects on the hydride (tunneling) transfer from chloranil to leucocrystal violet measured by Isaacs et al. (39) made use of a Bell-type model:

where k_TST and k_tun are the classical (over the barrier) and tunneling contributions to the overall rate of reaction for each isotope. Although this model nicely fits the data of Isaacs, it only reproduced the data for MR when k_TST^D ≫ k_TST^H or k_tun^D ≫ k_tun^H, which is physically unrealistic. Northrop and Cho (35) treatment of pressure effects on tunneling in yeast alcohol dehydrogenase (35) and formate dehydrogenase (36) are based on Eq. 3 [reviewed in refs. 37 and 38)], and, although these more elaborate models can account for their data, they model steady-state V/K data that we have not measured. Additionally, Northrop explained the only increase in KIE with pressure observed [in formate dehydrogenase (36)] as arising solely from within the transition state and ruled out a tunneling contribution to the reaction. Because we have strong evidence for a tunneling contribution to the reductive half-reaction of MR (13, 42), we will attempt to use a full tunneling model to account for the observed pressure dependence of the KIE in MR.

A Full Tunneling Model.

The rate of a (nonadiabatic) tunneling reaction can be determined by using Fermi's golden rule (33)

where T_DA is the tunneling matrix element (electronic factor), F.C. is the Franck–Condon (nuclear) factor, and ℏ is the reduced Planck's constant. Recently, a theoretical treatment of the effect of pressure on ET reactions in proteins has emerged (48). Interestingly, a survey of the literature by these authors showed that typical ΔV ^‡ values for a protein ET (tunneling) reaction are −10 to −20 cm³·mol⁻¹, a range bracketing the values measured here for H and D transfer in MR. The authors concluded that, whereas volume changes associated with both the T_DA and F.C. terms contribute to the observed ΔV^‡, unless ΔV^‡ is very small (i.e., <1–2 cm³·mol⁻¹) then the contribution from T_DA can be ignored. To our knowledge, T_DA has not been measured for any enzymatic H-tunneling reaction. Additionally, as ΔV ^‡H and ΔV ^‡D are both quite large, we will assume here that the observed ΔV ^‡ in MR arises solely from the F.C. term. This assumption may not prove to be strictly valid in the case of hydrogen transfer reactions and the effect of pressure on T_DA in MR will be the focus of future work.

The pressure-dependence of the F.C. factor for an ET reaction is caused by pressure-induced changes to the Marcus (33) reorganization energy (λ) and driving force (ΔG⁰) (48). By examining the pressure dependence of the KIE rather than the individual rate constants for the H-transfer in MR, we can ignore dλ/dp and dΔG⁰/dp. Specifically, because λ and ΔG⁰ are largely isotope-insensitive, their contributions to ΔV ^‡ will largely cancel when solving for the KIE. The pressure dependence of the KIE must then arise from other elements of the F.C. term.

Numerical Modeling of the Temperature and Pressure Dependence of the 1° KIE in MR.

The temperature/pressure dependence of the observed KIE was examined by using the environmentally coupled tunneling model of Kuznetsov and Ulstrup (20). We have implemented the model in a similar manner to that used by Knapp and Klinman (12, 32) and have recently used this approach to describe the H-tunneling reaction in aromatic amine dehydrogenase (L. O. Johannissen, S.H., N.S.S., and M.J.S., unpublished data). The rate of a tunneling reaction is described by

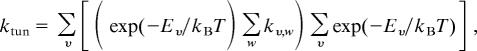and

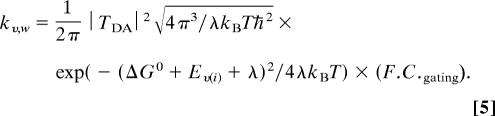To incorporate gating and, thus, a strongly temperature-dependent KIE, a Franck–Condon term incorporating a gating mode is used:

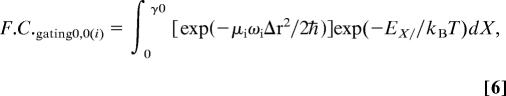where μ_i is the average reduced mass and ω_i the angular frequency of the transferred isotope (μ_average, H = 0.95 g·mol⁻¹; μ_average, D = 1.74 g·mol⁻¹; average C/O–H/D stretching frequencies: f_H = 3,000 cm⁻¹; f_d = 2,200 cm⁻¹). Δr = (r₀ − r_X) is the tunneling distance reduced from an equilibrium separation, r₀, by the distance of gating, r_X. The gating motion is treated classically as a harmonic oscillator with an isotope-independent gating energy, E_X = (1/2)ℏω_XX², where X is the reduced tunneling coordinate, $X=r_X\sqrt{m_X{\omega }_X/\hslash }$, and m_X and ω_X are the mass and frequency of the gating motion along X, respectively. Eq. 6 gives the F.C. term for ground-state tunneling. Transfer to and from vibrationally excited states was also incorporated into this model by using modified F.C. terms (the section in square brackets) (49), which are also listed in ref. 32. Other terms in Eqs. 5 and 6 have their usual meaning and are defined in ref. 32.

Preliminary x-ray diffraction data of MR with bound tetrahydro-NADH indicates that the coenzyme nicotinamide and MR flavin moieties are coplanar with the coenzyme C4 and FMN N5 atoms in close proximity (D. Leys and N.S.S., unpublished work). These data are consistent with the structure of a homologous Old Yellow Enzyme, which was solved with an NADPH analogue that was bound coplanar to the enzyme-bound flavin (50). Molecular modeling of the crystal structure coordinates of the MR tetrahydro-NADH complex allowed the position of the transferred hydride in the reactant (NADH C4-RH) and product states (FMN N5-H) to be determined. From this model, the equilibrium tunneling distance, r₀, was then estimated to be ≈1.7 Å (Fig. 3B). This distance would appear much too large for tunneling to occur, because the de Broglie wavelength of hydrogen is only ≈0.6 Å (reviewed in ref. 12). This ≈1-Å difference provides a further justification for the use of an environmentally coupled tunneling model over a tunneling correction model.

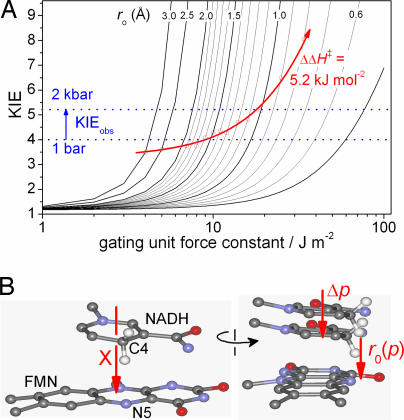
Fig. 3.

The effect of pressure on an environmentally coupled H-tunneling reaction. (A) The Kuznetov and Ulstrup model (20) (Eq. 5) showing the effects of the force constant of the gating mode (k_HO) and the donor–acceptor separation (r₀) on the KIE. If pressure reduces r₀ but not ΔΔH^‡, then the observed KIE will increase (red arrow, see text). (B) Orthogonal views of a model of the active site of MR based on the structure of Old Yellow Enzyme (Protein Data Bank ID code OYEA; see ref. 50) We propose that pressure will reduce the separation of the nicotinamide and flavin heavy atoms, [r₀(p)] along the gating coordinate X. Note that neither the compression of the nicotinamide/flavin separation nor the gating motion of the nicotinamide and flavin need to be exclusively along the gating coordinate X, but Δp (a vectoral component of any compression) and X (in the figure) need to be parallel.

By systematically varying E_X, T, and r₀, while solving for the experimentally determined KIE, temperature dependence (ΔΔH^‡) and A′_H:A′_D values at each pressure measured, we can estimate the effect of pressure on gating during this reaction. In practice, it is easier to vary the force constant, k_HO = m_Xω_X², rather than the energy of the gating mode. We will in turn look at the temperature dependence of the KIE, then the effect of pressure on this temperature dependence.

Temperature Dependence of the KIE.

ΔΔH^‡ and the temperature dependence of the KIE arise primarily from the gating energy term, E_X, in Eq. 6, with a smaller contribution arising from thermal population of vibrationally excited reactant and product states. The gating energy is the energy required to change the distance between the donor and acceptor wave functions before tunneling. This distance, r_X, is modulated by the static component of the F.C. term (Eq. 6, square brackets) such that the distance of D-transfer is less than the distance of H-transfer. If the gating motion, r_X, is of sufficient amplitude such that Δr approaches the de Broglie wavelength, then there will be a high tunneling probability, assuming that “passive,” or thermally equilibrated, motion in the enzyme is able to achieve degenerate donor–acceptor wave functions (12, 20, 33). We think this is likely to be the case in MR, because hydride transfer in a closely related homologue of MR, pentaerythritol tetranitrite reductase, exhibits behavior typical of an environmentally coupled tunneling reaction without a promoting vibration (13, 42).

At 298 K and 1 bar, we have measured here that the KIE = 4.0, ΔΔH^‡ = 9.3 ± 3.8 kJ·mol⁻¹ and A′_H:A′_D = 0.09 ± 0.15 (Table 1). These values are comparable to our previous reports (13, 42). In Fig. 3A, Eqs. 5 and 6 are plotted as KIE versus the force constant of the gating mode, k_HO, for a range of reasonable r₀ values. Decreasing the force constant allows greater motion of the gating mode and thus allows larger r₀ values to achieve the same KIE (SI Fig. 9A). Increasing r₀ causes the corresponding ΔΔH^‡ for a given KIE to increase roughly hyperbolically from 0, when r₀ = Δr (Eqs. 5 and 6 when E = 0), to a maximum value (SI Fig. 9B). For a KIE of 4.0 at 298 K, the maximum ΔΔH^‡ value is ≈5.7 kJ·mol⁻¹ (SI Fig. 9B), falling within the MR value of ΔΔH^‡ determined at 1 bar (Table 1). The frequency of the gating mode, the “promoting vibration,” ω_X, can be determined from k_HO if the mass, m_X, of the gating mode is known. Unfortunately, as is typical of almost all enzymes, an atomic description of the gating mode of MR is not available. The values of ω_X (KIE = 4.0 and T = 298 K) for reasonable values of m_X are shown in SI Fig. 9C. At an r₀ value of 1.7 Å (see above), ω_X is <120 cm⁻¹ for all m_X values greater than ≈10 Da. This frequency range is sensible, because ω_X ≪ k_BT (≈200 cm⁻¹ at room temperature) in order for the vibration to be reasonably thermally excited. Because k_HO decreases at large r₀ values, the Eyring prefactor ratio decreases to a minimum value, and, in this case, the minimum value of A′_H:A′_D is ≈0.4 (SI Fig. 9D). This value is in quite good agreement with the measured value of ≈0.1 (Table 1) (13, 42). In summary, the experimentally determined magnitude and temperature dependence of the KIE can be accounted for by using Eqs. 5 and 6 when r₀ = 1.7 Å (the experimentally determined separation) and when ω_X < 100 cm⁻¹ (k_HO = 5.3 J·m⁻²).

Pressure Dependence of the KIE.

The measured KIE of MR increases from 4.0 to 5.2 at 25°C when the pressure is increased from 1 bar to 2 kbar (Fig. 2C), yet there is no significant change in ΔΔH^‡ (Table 1 and SI Fig. 8). Increased pressure will likely lead to a compression of the tunneling barrier; i.e., it will decrease r₀ in Eq. 6 (Fig. 3B), which will result in an increase in the absolute rate of the reaction, as we have observed (Fig. 2A and Table 1). Because pressure did not significantly perturb the observed ΔΔH^‡, this value was fixed as 5.2 kJ·mol⁻¹ (the value calculated when r₀ = 1.7 Å and KIE = 4.0), and Eqs. 5 and 6 were solved as a function of r₀. Under these conditions, decreasing r₀ from 1.7 to ≈1.0 Å, has only a modest effect on the Eyring prefactor ratio (SI Fig. 9D), which we also found to be invariant with pressure (SI Fig. 8 and Table 1). When dΔΔH^‡/dr₀ = 0, the KIE is found to increase with decreasing r₀ values. To maintain a fixed ΔΔH^‡ value as r₀ was decreased, k_HO was allowed to increase (Fig. 3A). Because the mass of the gating mode is not likely to change with pressure, the gating frequency (the frequency of the promoting vibration) will increase with pressure, as ${\omega }_X=\sqrt{k_{\text{HO}}/m_X}$. Importantly, this prediction allows this model to be tested in later work. Of particular interest are the H-tunneling reactions of the thermophilic alcohol dehydrogenase (8) and dihydrofolate reductase (14) enzymes, which show break-points in their Arrhenius and KIE vs. 1/T plots. The model presented here predicts that the slopes of the Arrhenius plots will not change with pressure (unless ΔV ^‡ is very large), but, if the break-point is truly related to promoting vibrations within the enzymes, then the break-point will shift with pressure, moving to higher temperatures (larger ω_X) at increased pressure if ΔΔV ^‡ < 0 and conversely to lower temperatures if ΔΔV ^‡ > 0.

The calculated KIE values in Figs. 3 and 4A were calculated with a fixed ΔΔH^‡ value (5.2 kJ·mol⁻¹), yet it may not be obvious why this should be the case. An advantage of using pressure rather than temperature to perturb the tunneling reaction is that the internal energy, ΔE, of the system does not change with pressure: ΔG = [ΔE + pΔV] − TΔS, where the term in brackets is collectively the enthalpy (for a review, see ref. 47). The enthalpy will significantly change with pressure only if ∣ΔE∣ ∼ ∣pΔV∣. Although the ΔV^‡ values measured in this work do not reflect the entire volume change of the reaction, they are probably of the correct order of magnitude. For a ΔV^‡ value of 15.6 cm³·mol⁻¹ (the value measured at 25°C for the reaction with NADH), pΔV^‡ increases from ≈10⁻³ to 3 kJ·mol⁻¹ upon increasing the pressure from 1 bar to 2 kbar. The expected change in ΔΔH^‡ is obviously even smaller (<0.8 kJ·mol⁻¹) and is well within the experimental error of the measurements. Incorporating this small correction into the model described above (Figs. 3 and 4) will not significantly change the results.

The pressure dependence of the experimentally measured KIE values (25°C) are compared with the r₀ dependence of the calculated KIE values in Fig. 4. By directly comparing the measured and calculated values, we can estimate the extent of the barrier compression caused by 2 kbar of hydrostatic pressure. The arrow in Fig. 4 shows the apparent decrease in r₀, which appears to be ≈0.7 Å, decreasing from 1.7 Å to ≈1.0 Å. The magnitude of the apparent decrease in r₀ is not unprecedented. The effect of 1 kbar of hydrostatic pressure on the x-ray crystal structure of lysozyme has been determined by Kundrot and Richards (51). They found that, although the average rms shift of atoms was 0.2 Å, a few atoms moved >1 Å. The gating “unit” will consist of many atoms. Additionally, the rms displacement of the gating motion ($r_{X,\text{rms}}=\sqrt{k_{\text{B}}T/k_{\text{HO}}}$) when r₀ = 1.7 and KIE = 4.0 is quite large (≈0.22 Å), suggesting that the gating unit will be quite susceptible to compression.

We mentioned earlier that there appears to be no significant alteration to the local environment around the active site of MR judging by the pressure independence of the CT complex formation (SI Fig. 5), which is not inconsistent with the above idea that the gating “unit” is pressure dependent. The cofactor arrangement in the CT complex need not be at the equilibrium separation, r₀, if further thermally equilibrated motion moves the system to r₀. We have recently described a similar rearrangement in another tunneling enzyme: aromatic amine dehydrogenase (ref. 17 and L. O. Johannissen, S.H., N.S.S., and M.J.S., unpublished data).

Conclusions.

We have demonstrated the utility of pressure-dependent studies of KIEs to probe full tunneling models for enzymatic H-transfer. Our work is consistent with the need for a promoting motion, the frequency of which we predict increases with pressure in MR, within the environmentally coupled tunneling framework. Studies of the pressure dependence of KIEs provide important information on tunneling mechanisms complementing observations derived from other experimental methods.

Materials and Methods

All materials were obtained from Sigma–Aldrich (St. Louis, MO), except NADH (which was obtained from Melford Laboratories, Chelsworth, U.K.) and [²H₆]ethanol (Cambridge Isotope Laboratories, Andover, MA). MR was purified as described previously (13, 41), and the enzyme concentration was determined by ε = 11.3 mM⁻¹·cm⁻¹ at 462 nm. NAD²H was prepared through stereospecific reduction of NAD⁺ with [²H₆]ethanol by using equine liver alcohol dehydrogenase coupled with aldehyde dehydrogenase as described in ref. 52, then purified by anion exchange chromatography and freeze-dried as described previously (13, 42). The isotopic purity of NAD²H was determined by using NMR (NAD²H had ≈6% pyridyl R-C4 H⁺ detected at 2.8 ppm) and by mass spectrometry (m/z NADH = 666.1, m/z NAD²H = 667.1) (42). NADH prepared by this method with [¹H₆]ethanol behaved identically to a commercial source of the coenzyme purchased from Melford Laboratories (13, 42). Isotopic purity was not corrected for in this study (42). Coenzyme solutions were made fresh, and their concentrations were determined by ε = 6.22 mM⁻¹·cm⁻¹ at 340 nm.

All reactions were performed in 50 mM Tris·HCl/2 mM 2-mercaptoethanol, pH 8.0. Tris buffer at pH 8.0 was chosen to minimize pressure-dependent changes in pH because it has a small volume of ionization [4.3 ± 0.5 cm³·mol⁻¹ (53)]. To prevent the oxidase activity of MR, all samples were made anaerobic by the addition of 5–10 units·ml⁻¹ glucose oxidase and 10 mM glucose. The samples were then immediately loaded into the stopped-flow syringes and placed within the stopped-flow instrument, where they were incubated for at least 30 min before any measurement. This treatment was sufficient to remove enough oxygen such that when the enzyme was mixed with an equimolar concentration of NADH, no reoxidation of the enzyme was observed within 1,000 s.

Rapid reaction kinetic experiments at pressures between 1 and 2,000 bar were performed with a Hi-Tech Scientific HPSF-56 high-pressure stopped-flow spectrophotometer (TgK Scientific, Bradford on Avon, U.K.). A saturating coenzyme concentration of 5 mM was used, because this confers pseudo-first-order reaction kinetics (13, 42). The apparent K_d of NADH binding was not particularly sensitive to pressure (see Results). Spectral changes accompanying flavin reduction were monitored at 464 nm, and rate constants were determined by fitting a single exponential function to each trace (42). Alternatively, rate constants and deconvoluted spectra were determined from data collected between ≈300 and 700 nm using a diode array. In this case, the rate constant was determined by global analysis using SpecFit/32 (Bio-Logic Science Instruments, Grenoble, France). Rate constants and errors were estimated by taking the standard deviation of typically three measurements at each pressure and temperature value. The values determined by single-wavelength measurements at 464 nm and by global analysis were equivalent.

Abbreviations

CT

charge transfer

ET

electron transfer

FMN

flavin mononucleotide

KIE

kinetic isotope effect

MR

morphinone reductase

TST

transition state theory.