The loss of adaptive plasticity during long periods of environmental stasis

Abstract

Adaptive plasticity allows populations to adjust rapidly to environmental change. If this is useful only rarely, plasticity may undergo mutational degradation and be lost from a population. We consider a population of constant size N undergoing loss of plasticity at functional mutation rate m and with selective advantage s associated with loss. Environmental change events occur at rate θ per generation, killing all individuals that lack plasticity. The expected time until loss of plasticity in a fluctuating environment is always at least $\overline{\tau }$, the expected time until loss of plasticity in a static environment. When mN > 1 and Nθ >> 1, we find that plasticity will be maintained for an average of at least 10⁸ generations in a single population provided $\overline{\tau }$ > 18/θ. In a metapopulation, plasticity is retained under the more lenient condition $\overline{\tau }$ > 1.3/θ, irrespective of mN, for a modest number of demes. We calculate both exact and approximate solutions for $\overline{\tau }$ and find that it is linearly dependent on only the logarithm of N, and so surprisingly, both the population size and the number of demes in the metapopulation make little difference to the retention of plasticity. Instead, $\overline{\tau }$ is dominated by the term 1/(m + s/2).

Some traits may be strongly adaptive, but only on very rare occasions. This is typically true for plastic traits that are expressed only when the need arises. Such traits are particularly common in microbes, and there has been much interest recently in phenotypic switching behaviors as a response to novel and hostile environments (Hallet 2001; Henderson et al. 1999). Examples of potentially adaptive phenotypic switching include pili expression in bacteria (Abraham et al. 1985), phage growth limitation machinery (Sumby and Smith 2003), bacterial persistence (Balaban et al. 2004; Kussell and Leibler 2005), the yeast prion [PSI⁺] (Masel 2005; Masel and Bergman 2003; True and Lindquist 2000), sporulation, and biofilm formation. Adaptive phenotypic plasticity is also common in multicellular organisms (West-Eberhard 2003).

The ability to undergo phenotypic switching is a complex trait in the sense that it is easy to lose by mutation but hard to gain back. Although the trait may be strongly adaptive under certain circumstances, these circumstances arise only rarely. The trait may be eroded and lost through mutational degradation during the potentially long gaps between times when the trait is needed. This is not an issue in an infinite population, in which traits are never lost, but instead only become vanishingly rare. In a finite population, however, with restoration through compensatory mutation too rare to be significant, all complex but rarely needed traits will eventually be lost, given infinite time. What then accounts for their observed persistence? Here we develop an approach based on Markov models of finite populations to find the parameter range required for the expected time until trait loss to be sufficiently large (taken arbitrarily as > 10⁸ generations) so that trait loss is effectively negligible on evolutionary time scales.

Mathematical Model and Results

Trait Loss from a Single Population

Overall approach

Consider, for mathematical simplicity, a haploid population of size N under the Moran model: i.e., at each time step, one individual is chosen at random to reproduce, and one to die. One generation consists of N time steps of the Moran model, and so as N gets larger, the length of a time step decreases. The plasticity trait is subject to mutational loss at rate m per replication. Note that a complex trait may be lost through mutations at a range of loci, and so the functional mutation rate m may be considerably higher than a point mutation rate or even than a per-gene mutation rate. A constant rate of mutational loss assumes that epistatic effects are not important in this context. This is consistent with data showing that an additional mutation has either the same (Elena 1999; Elena and Lenski 1997; Peters and Keightley 2000; West et al. 1998; Wloch et al. 2001) or a very similar (Azevedo et al. 2006; Bloom et al. 2005) effect in a mutationally loaded genetic background as it does in a wild-type background. Mutational loss may be accelerated by a selective advantage of loss s, when there is a metabolic or other cost to maintaining the trait, although we can also set the cost s = 0. Using this Moran model with mutation, selection and drift, we calculate in Online Appendix A the mean time $\overline{\tau }$ for all individuals in the population to lose the trait in a static environment, given that they all have the trait initially. To avoid confusion with the time until trait loss in a fluctuating environment, we refer to the time τ as the sojourn time, although it should be noted that this time includes the waiting time for the appearance of a mutant lacking the trait, and also accounts for possible acceleration of trait loss due to the independent appearance of multiple mutants lacking the traits as part of a “soft sweep” (Hermisson and Pennings 2005).

Assume that environmental change events making the trait useful occur at rate θ, and occur according to a Poisson process. Assume that these events purge the population of all individuals not carrying the trait. The extreme nature of this assumption will be addressed later in this paper. Trait loss occurs if the waiting time until the next event is longer than the sojourn time τ. Both of these are stochastic. As a Poisson process, the waiting time until the next event has an exponential distribution. No analytical expression exists for the probability distribution of the sojourn time (Ewens 2004), and so we calculate two tractable extreme cases, corresponding to very large and very small populations. Results for populations of intermediate size should fall in between these two extreme scenarios. We verify this by computing expected times until trait loss numerically, which can be done without explicitly computing the distribution of sojourn times (see Online Appendix B).

Large population approximation

In the first scenario, we assume that populations are large so that mN >> 1. In this case, sojourn times are highly deterministic, and we approximate variance in the sojourn time τ as zero (see Online Appendix A). The constant sojourn time τ = $\overline{\tau }$ can be calculated as described in Online Appendix A as a function of N, m and s. Since the waiting time until the next environmental change event has an exponential distribution, the probability that environmental change occurs before trait loss is then given by ${\int }_0^{\overline{\tau }}\theta e^{-t\theta }dt=1-e^{-\theta \overline{\tau }}$, purging the population of all genotypes that have lost the trait. The mean number of times this happens in succession is then $(1-e^{-\theta \overline{\tau }})/e^{-\theta \overline{\tau }}$. The mean interval between environmental change events, given that trait loss does not occur, is

$$\frac{{\int }_0^{\overline{\tau }}t\theta e^{-t\theta }dt}{1-e^{-\theta \overline{\tau }}}=\frac{e^{-\theta \overline{\tau }}\left(e^{\theta \overline{\tau }}-1-\theta \overline{\tau }\right)}{\theta \left(1-e^{-\theta \overline{\tau }}\right)}.$$

The expected waiting time until trait loss occurs is given by the number of times that environmental change occurs before trait loss multiplied by the mean interval time until environmental change on each of these occasions, plus the sojourn time following the last of these events, in which trait loss is not interrupted by environmental change. This can be expressed as

$$\frac{e^{\theta \overline{\tau }}-1-\theta \overline{\tau }}{\theta }+\overline{\tau }=\frac{e^{\theta \overline{\tau }}-1}{\theta }\text{generations}\text{.}$$ (1)

For a rarely used trait to be maintained, this number needs to be very large. For very small values of θ, Eq. (1) gives approximately $\overline{\tau }$, which is unlikely to be sufficient for trait retention. For larger values of θ, Eq. (1) increases approximately exponentially with $\overline{\tau }$. We now ask for what parameter range is the waiting time until trait loss, as given by Eq. (1), greater than some large number of generations, taken here arbitrarily as 10⁸. The exponentially steep character of Eq. (1) means that the precise arbitrary choice of 10⁸ matters very little. For trait loss to take longer than 10⁸ generations, we need

$$\overline{\tau }>ln({10}^8\theta +1)/\theta .$$ (2)

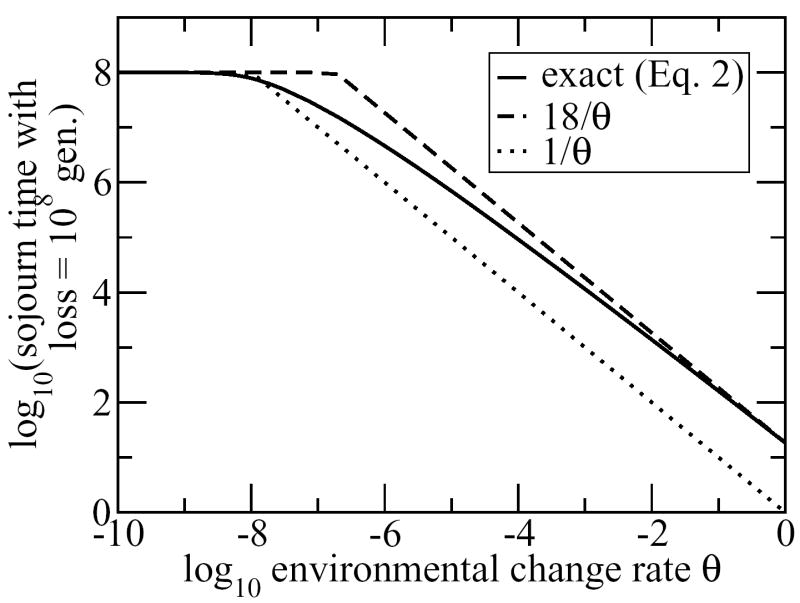
The behavior of the cutoff value of $\overline{\tau }$ is shown in Figure 1. For sufficiently large values of θ, this means that we need $\overline{\tau }$> ln(10⁸)/θ ≈ 18/θ. This captures the fact that environmental change must frequently interrupt trait loss. As environmental change gets rarer and θ approaches the seemingly unrealistic value of 10⁻⁸, this requirement is relaxed in the direction of the looser requirement $\overline{\tau }$ > Minimum(10⁸, 1/θ).

Figure 1.

Minimum sojourn time required in order for trait loss in a single population to take an average of at least 10⁸ generations in the large N (fixed τ) case, shown as a function of the frequency θ with which environmental change purges the population of all individuals that have lost the trait. For large values of θ, the trait is retained so long as $\overline{\tau }$ > ln(10⁸)/θ ≈ 18/θ. For small values of θ, this requirement is gradually weakened towards $\overline{\tau }$ > Minimum(10⁸, 1/θ).

Small population approximation

In the second limiting scenario, we assume that populations are small so that mN << 1. In this case the expected sojourn time has two components: the expected waiting time until the first mutation destined for fixation, equal to 1/m for the neutral case, and the expected subsequent time required for fixation, equal to N − 1 in the neutral case. For mN << 1, the former component dominates.

Mutations destined for fixation appear according to a Poisson process. When N is sufficiently small, we can make the approximation that environmental change never interferes with the subsequent fixation process. Since the mean sojourn time of a neutral mutant destined for fixation is N − 1, a sufficient condition for this approximation to be accurate is θN << 1. When selection is also present, this condition is relaxed further.

With the small population size approximation, trait loss events now occur at random points in time according to the same Poisson process that governs the appearance of mutations destined for fixation. In this case, the expected time until trait loss is independent of the environmental change rate and is given by $\overline{\tau }$, and so we need $\overline{\tau }$ > 10⁸. The waiting time until the next trait loss event has an exponential distribution with mean $\overline{\tau }$.

Mean sojourn time for populations of any size

To interpret the approximate results for mN >> 1 and mN << 1, we need to know the value of $\overline{\tau }$. Exact formulae to calculate $\overline{\tau }$ are derived in Online Appendix A. In addition, the following approximate formula is derived as Eq. A5

$${\overline{\tau }}_{approx}\approx \frac{1}{mN{p}_{fix}}+\left\{\begin{array}{cc}\frac{ln((m+s)N)+\gamma }{m+s/2}& \text{if}ln\hspace{0.17em}((m+s)N)>0\\ N-1& \text{otherwise}\end{array}\right\}$$ (3)

where p_fix is the probability that a mutation present in a single individual will go on to become fixed and γ is Euler’s constant, with numerical value 0.577216. In Figures 2A and 2B, we show how $\overline{\tau }$ depends on N, m and s, and in Figure 2C we see that the approximation is good over a wide range of parameter values. We see different behavior of $\overline{\tau }$ in two distinct ranges for N. For small N with mN < 1, the sojourn time is dominated by the waiting time 1/(mNp_fix) until the appearance of the first mutant destined for fixation. For small enough N with sN << 1, this simplifies to 1/m. As N increases within the mN < 1 parameter range, then if s > m, p_fix increases with N as selection becomes more effective, and so sojourn times decrease with N. If s < m, then the second parameter range begins before this effect becomes appreciable.

Figure 2.

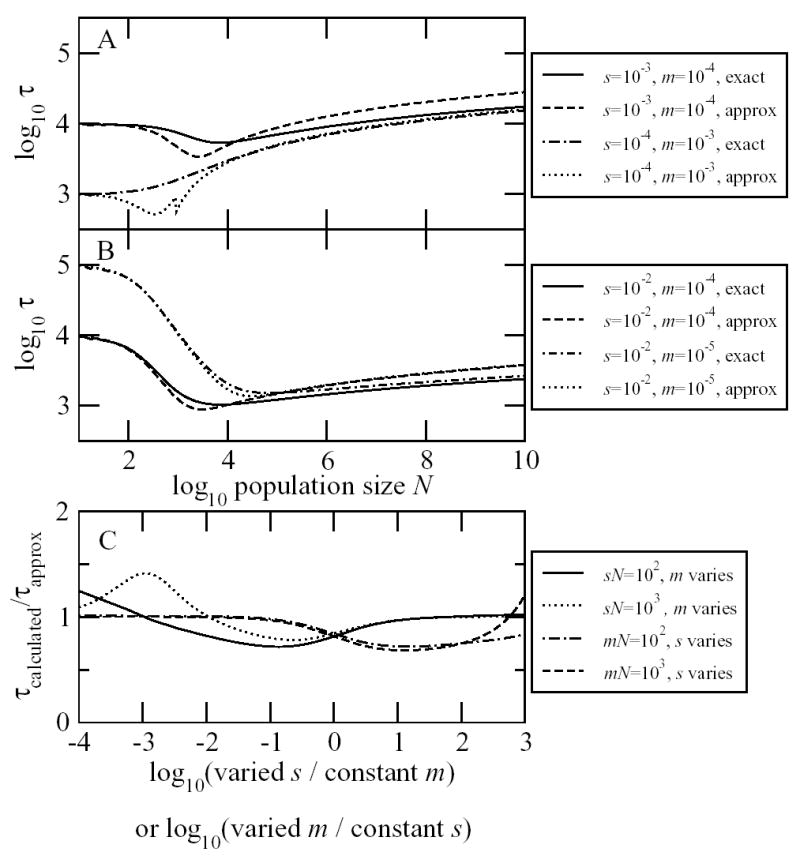
The mean sojourn time $\overline{\tau }$ as a function of the population size N, the mutation rate m and the selection coefficient s, as calculated exactly by Eqs. A1 and A2 and approximately by Eq. 3. A and B. We see different behavior of $\overline{\tau }$ depending on whether mN < 1 or mN > 1. C. The approximate formula is reasonably accurate for a wide range of parameter values. Calculations shown were performed with N = 10⁶.

In the second parameter range of larger N with mN > 1, the sojourn time is dominated by the spread of mutations through the population, rather than by the time until the arrival of the first mutation. This arrests any decline in $\overline{\tau }$ in the first parameter range, and subsequently leads to a gentle increase in the sojourn time with N.

What sets the sojourn time in this second parameter range? Under neutral drift, conditional on fixation, the total sojourn time is equal to N − 1 generations. Both selection and recurrent mutation as part of a “soft sweep” (Hermisson and Pennings 2005) can substantially accelerate this sojourn time, however. We see in Eq. 3 that for mN > 1 and/or sN > 1, this acceleration can be captured by the term $\frac{ln((m+s)N)+\gamma }{m+s/2}.$ Note that this term depends only weakly on N, and is largely set by the value of 1/(m + s/2). If instead we have both mN << 1 and sN << 1, then we have $\overline{\tau }$ ≈ 1/m.

Comparison to exact solution

In Online Appendix B, we describe a method for calculating the mean time until trait loss that avoids the need for the approximations mN >> 1 or mN << 1. This method is shown schematically in Figure 3. In Figure 4 we test the conditions under which our previous approximations break down. We see that our large population size approximation (given by Eq. 2 and approximated still further in Figure 1 as $\overline{\tau }$ > 18/θ) is sufficient whenever mN > 1 and N >> 1/θ. Our small population size approximation (the requirement that $\overline{\tau }$ > 10⁸) is always sufficient and is necessary whenever N < 1/θ. A smooth transition between the two approximate requirements is seen for intermediate values of N.

Figure 3.

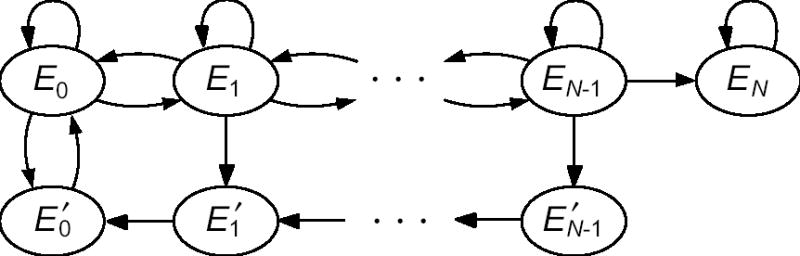
State space of the Markov chain used for exactly computing the expected time until trait loss in a single population. States E_i and E′_i represent populations in which i of the N individuals lack the trait, in the original and new environments, respectively. Edges between states indicate transitions that can happen in one step of the Markov chain, with probabilities given in Online Appendix B. The chain begins in state E₀, and the trait is lost when the chain first reaches state E_N .

Figure 4.

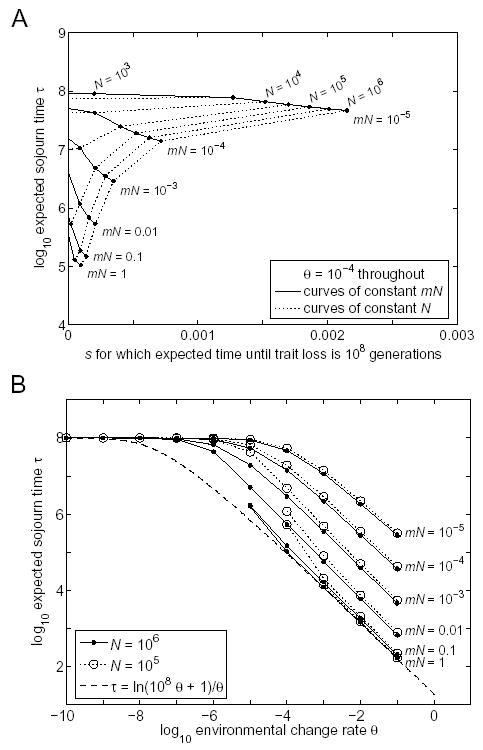
Exact computations of the time until trait loss in a single population. For a given θ, the expected time until trait loss depends not just on $\overline{\tau }$--- the expectation of the sojourn time τ --- but on the distribution of τ. For each combination of θ, N, and m plotted above, s was chosen so that the expected time until trait loss was exactly 10⁸ generations (see Online Appendix B). The corresponding value of $\overline{\tau }$ in shown on the vertical axes, computed as a function of N, m, and s. A: θ is fixed at 10⁻⁴, and the values of s are explicitly shown. B: θ varies, but the values of s are not explicitly shown; points for which the corresponding value of s is negative are not shown, so some curves are truncated asθ decreases. Depending on θ, N, and m, $\overline{\tau }$ can range from the lower bound of ln(10⁸θ + 1)/θ to the upper bound of 10⁸. Note that for fixed θ, the mean sojourn time for which the expected time until trait loss is 10⁸ generations tends to increase as mN decreases, as N decreases, and as s decreases --- these are changes that tend to increase the variance of the sojourn time relative to its mean.

Requirement to avoid trait loss

To integrate the calculations for $\overline{\tau }$ with the requirements on $\overline{\tau }$ for trait loss to be avoided, note from Figure 4 that we need $\overline{\tau }$ > 18/θ for large N, $\overline{\tau }$ > 10⁸ for small N, and an intermediate requirement strongly dependent on the relationship between $\overline{\tau }$ and 1/θ for intermediate values of N. $\overline{\tau }$ is dominated by the term $\frac{ln((m+s)N)+\gamma }{m+s/2}$ in Eq. 3, particularly the denominator term 1/(m + s/2). In other words, to avoid trait loss, the sum of the mutation and selection coefficients must be small relative to the rate of environmental change, with the population size modifying the precise interpretation of “small”. When both mN << 1 and sN << 1, the relevant approximation for $\overline{\tau }$ becomes simply 1/m.

Trait Loss from a Metapopulation

Consider a metapopulation in which environmental change occurs independently in each deme. In this scenario, one deme may not encounter environmental change for a long period, and therefore undergo trait loss. When the environment finally does change, this deme goes extinct. The extinct deme may, however, be recolonized by a different deme, which might, by chance, have experienced the event more regularly and hence maintained the trait. This rescue phenomenon may lead to persistence of the rarely used trait under a wider range of circumstances. In other cases, the extinct deme may be recolonized by a deme that lacks the trait: we assume that environmental change events represent an episode of selection, rather than permanent change.

We treat the metapopulation as a Markov process with j out of n demes lacking the trait. Environmental change events occur independently at rate θ in each of the n demes, for a total rate of nθ. When an environmental change event occurs in a deme that lacks the trait, then it is destroyed and recolonized from another deme chosen at random. This can sometimes lead to a decrease in the number of demes lacking the trait j; j can also increase due to trait loss events within demes.

We consider two limiting cases. In the first, populations are small, trait loss occurs according to a Poisson process and τ therefore has an exponential distribution. In the second, populations are large, and hence τ is constant. These two limiting cases are treated mathematically in Online Appendices C and D, respectively. Both approximate analytic and exact simulated results are calculated when τ is fixed as a constant.

In Figure 5A we plot the minimum number of demes needed to maintain the trait for an average of 10⁸ generations, given $\overline{\tau }$ and θ. We see from the steep shape of the curves that beyond a very modest number of demes, the precise number of demes is not important. In Figure 5B we see that a trait can be maintained in a metapopulation of modest size so long as $\overline{\tau }$ > 1.3/θ. This expands the criterion $\overline{\tau }$ > 18/θ for trait retention in a single population around 15-fold in a metapopulation, and perhaps slightly more for large population sizes with exponentially-distributed τ.

Figure 5.

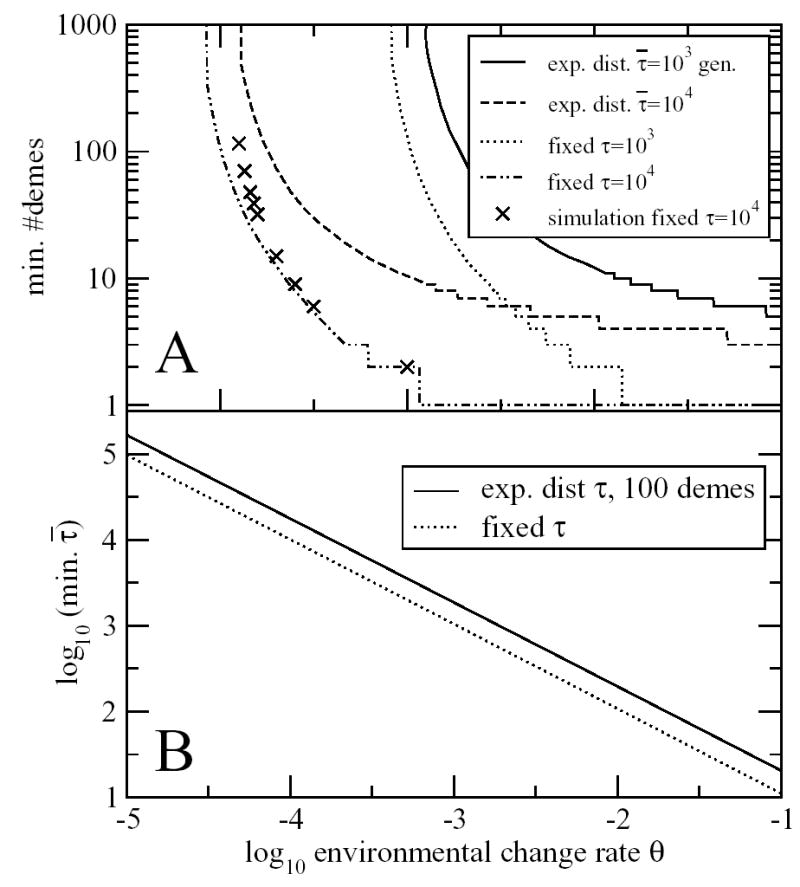
Conditions for trait loss to take longer than 10⁸ generations in a metapopulation. A. The minimum number of demes needed as a function of $\overline{\tau }$ and θ. Eqs. C1 and C2 are used for exponentially-distributed sojourn times, Eqs. D1, D2 and D3 for fixed sojourn times, and simulations are performed as described in Online Appendix D. We see that there is little difference between the large N (fixed τ) and small N (exponentially-distributed τ) curves, unless the minimum number of demes is very small. B. By fitting a straight line of gradient −1 to the curves shown, we calculate that the trait can be maintained with 100 demes so long as $\overline{\tau }$ > 1.3/θ for exponentially distributed τ or $\overline{\tau }$ > 1/θ for fixed τ. The simulation results in part A suggest that the true cutoff for exponentially distributed τ may also be closer to $\overline{\tau }$ > 1.3/θ, so this conservative criterion is used throughout. This criterion is fairly insensitive to the precise number of demes: for example, for 50 demes, the criterion for exponentially-distributed τ is $\overline{\tau }$ > 1.5/θ.

Complete vs. Partial Purging by Environmental Change

To generate these results, we have assumed that when environmental change occurs, every last individual that lacks the trait is purged from the population. In a single population, the extreme nature of this assumption is primarily a mathematical convenience. Recurrent mutation means that individuals lacking the trait will in any case swiftly reappear, and so it isn’t likely to matter whether all individuals without the trait are purged, or whether it is simply most that are purged.

In the metapopulation model, complete purging causes demes that lack the trait to go extinct, and hence creates opportunities for new trait-bearing demes to be created through colonization. The results of the model should be robust so long as environmental change causes a highly elevated probability of deme replacement. For example, pathogens encounter a fluctuating environment with frequent “adapt or die” dynamics. Under these circumstances, all demes turn over as the environment keeps shifting, and the model is a good description.

Quantitative Roles of Mutation and Selection in Trait Loss

Note the partial symmetry between parameters m and s in Eq. (3). This symmetry is weakest for small populations: when both mN << 1 and sN << 1, then m and N alone set the value of $\overline{\tau }$, irrespective of whether m > s. For large populations with both mN >> 1 and sN >> 1, the symmetry is not obvious a priori: in particular, m will have a larger effect than s when individuals lacking the trait are rare. Nevertheless, the close fit shown in Figure 2 between the exact and approximate solutions shows the effects of m and s are close to symmetric in practice in large populations.

This symmetry means that in larger populations with mN > 1 and/or sN > 1, trait loss is primarily driven by the larger of s and m. Mutation rates are normally thought of as small, but note that the parameter m refers to the functional mutation rate, which may be the sum of many possible mutations over multiple genes. Data on functional mutation rates is sparse, but one study on loss of sporulation ability in Bacillus subtilis gives m = 0.0003 in non-mutator strains (J. Masel and H. Maughan, manuscript submitted). Data on gene deletions in yeast suggests that in most cases s < 0.005 (Sliwa and Korona 2005).

Mutational degradation of the ability to switch between adaptively plastic phenotypes may occur through damage to the switching mechanism itself, or it may cause the switch to reveal lethal variation that was hidden in the “off” state (Masel 2006). Either way, the ability to switch is effectively eroded. In the former case, there is likely to be a selective advantage to trait loss, as inappropriate switching events are minimized. In the latter case, however, there is unlikely to be a selective advantage to trait loss, and there may even be a slightly selective penalty.

Note that if estimates or bounds on m and s are available, we can infer the minimum rate θ of environmental change required to explain the fact that an observed adaptively plastic trait persists. For example, the yeast prion [PSI⁺] appears spontaneously at a rate of about 10⁻⁷ to 10⁻⁵ per replication (Liu and Lindquist 1999; Lund and Cox 1981; Nakayashiki et al. 2001), and is likely deleterious on these occasions (Nakayashiki et al. 2005). Yeast have effective population size N_e ≈ 10⁸ (Lynch and Conery 2003; Wagner 2005). If we assume a mutational degradation rate m < 0.0003 and selection s < 10⁻⁶ against inappropriate appearance of the prion, then for the ability to form prions to persist, we need $\overline{\tau }$ > 1.3/θ. Using our bounds, we calculate $\overline{\tau }$ > $\overline{\tau }$ (N = 10⁸ ;m = 0.0003;s = 10⁻⁶) = 36200 generations according to the exact methods given in Equations A1 and A2, yielding the condition θ > 3.6 × 10⁻⁵ as sufficient for persistence. This value of θ corresponds to environmental changes that favor the trait occurring every 1/θ = 28000 generations, on average. With such a low value of θ needed, the inability to catch [PSI⁺] “in the act” (Nakayashiki et al. 2005) is insufficient evidence that rare selection events are not responsible for the maintenance of the ability to form [PSI⁺].

Different Forms of Weak Selection

How does strong but rarely applied selection compare to constant but weak selection in the context of trait loss? Weakly advantageous selection for trait retention can be represented in our model by setting s to a negative value. To obtain a comparable scenario with constant weak selection, we take the strong, rare selection studied here so far and “spread it out” over time by setting s equal to −θ, and then calculating the sojourn time for a single population with no environmental change.

This case of positive selection and mutational degradation as opposing forces has been described in detail elsewhere, in work showing that trait loss can sometimes be so rapid that it occurs even before a novel sequence has fixed in the population (Berg and Kurland 2002). For trait retention rather than fixation (i.e. expected time until trait loss > 10⁸), we find, unsurprisingly, that we need −s > m, i.e., selection must be stronger than mutation. This criterion is similar to the corresponding criterion for rarely used traits. A second, additional criterion for constant weak selection, however, is that we need −s > 1/N. Considering a metapopulation rather than a single population does not significantly weaken this second criterion, which is based on the population size within a deme.

This criterion has no correspondent in the case of a rarely used trait. In other words, rarely applied but strong selection to a modest number of small demes can be effective even when the same selective force, made constant by being averaged out, is not effective. This is because the total frequency of selective events in a metapopulation is given by nθ and hence scales linearly with the total population size of the metapopulation, while with constant selection the sojourn time scales only very weakly with the logarithm of N. For this reason, the population size makes surprisingly little difference to the retention of a rarely used trait.

Population Extinction

If the trait is lost, will this cause population extinction? As the model is formulated so far, recolonization of lost demes is instant. Even once all demes have lost the trait, demes go extinct one at a time, since environmental change is not synchronized. Rapid recolonization follows each deme loss event, and so population extinction will never occur in a metapopulation.

Relaxing this, let β be the rate at which a deme sends out emigrants, and so the number of migrants able to settle is βk, where k is the number of demes occupied out of a maximum of n. The probability that a migrant settles in an empty deme and is therefore able to colonize it is (1 − k/n), and so the total rate of recolonization is βk(1 − k/n). Now the criterion for population persistence is β > θ according to the standard criterion for persistence in a deterministic Levins’ model (Levins 1969). In a stochastic setting, this criterion remains sound for modest minimum values of n (Gurney and Nisbet (1978); reviewed by Hanski et al. (1996); see Alonso and McKane (2002) for extension to mainland-island metapopulations).

Previous work studied trait loss within demes as well as deme extinction, and calculated the proportion of remaining demes that retain the trait (Wagner 2003). The conclusions were in agreement with results for infinite populations (Wagner 2003). Although this work allowed for the extinction of individual demes, it did not allow for the extinction either of the trait within the metapopulation or for the extinction of the metapopulation itself (Wagner 2003).

Here we have taken treatment of extinction further by explicitly including extinction processes at the metapopulation level. We have calculated the parameter regime required for negligibly slow processes both of trait loss within an entire metapopulation and of extinction of the metapopulation itself.

Discussion

Data on mutational degradation

Here we have considered whether mutational degradation can be a powerful enough force to override the selective benefits of a rarely needed trait. Mutational degradation of a complex switching trait is likely to occur at a much higher rate than its restoration by compensatory mutations. In practice, mutational degradation of sporulation has been observed in the laboratory in as few as 4200 to 6000 generations (H. Maughan, J. Masel, C.W. Birky and W.L. Nicholson, manuscript in preparation). This is consistent with observations from natural populations of bacteria where studies of whole bacterial genomes support the notion that traits are frequently lost throughout evolutionary time, especially in species that have colonized relatively constant environments (reviewed in Bentley and Parkhill (2004)).

The relationship between environmental change and functional degradation is also supported by genome size data. In bacteria, genome size is a good indicator of the frequency of environmental change because more genes are needed to deal with the various environments that are encountered. Genomes of soil bacteria, which encounter frequent environmental change, are notoriously large, while genomes of obligate endosymbiotic bacteria, which live in a comparatively static host environment, are invariably small (reviewed in Bentley and Parkhill (2004)). Genome degradation under such static environments is likely due to deletional biases in bacterial genomes (Mira et al. 2001), where genes that are not under selection are degraded and ultimately lost from the genome.

Persistence across time vs. space

Here we have considered the question of whether the ability to switch between alternative strategies can be maintained in the face of mutational degradation. Our results can be interpreted as a statement of the parameter range for which retained alternative strategies persist in a spatial and/or a temporal context (Venable and Lawlor 1980). When a rarely used trait is retained in a single population, this constitutes persistence across time. This occurs when $\overline{\tau }$ > 18/θ for mN > 1 and Nθ >> 1 or else $\overline{\tau }$ > 10⁸. When a rarely used trait is retained only in the context of a metapopulation, this constitutes persistence over time that relies on interaction with persistence across space. This occurs when the above condition is not met, but $\overline{\tau }$ > 1.3/θ. When the trait is lost, but the population nevertheless persists within a metapopulation context, this corresponds to persistence across space alone. This occurs when $\overline{\tau }$ < 1.3/θ and β >θ. Finally, when none of these apply, the population goes extinct.

Tradeoffs

Evolutionary biology is often about identifying the appropriate tradeoff(s). Switching phenomena have been seen as a tradeoff between inappropriate switching, failing to switch when necessary, and the metabolic costs of sensing when to switch (Kussell and Leibler 2005). This falls in the most common evolutionary biology tradition of identifying tradeoffs between selection for the benefits of a trait vs. selection against the costs, with a solution found using geometric mean fitness calculations. Another well understood form of tradeoff is between selection for benefits vs. stochasticity associated with genetic drift in a finite population. The well-known solution to this tradeoff is that selection is stronger than chance so long as s > 1/N.

Here we have solved for another distinct tradeoff: that associated with stochasticity in the timing of events rather than stochasticity associated with the finiteness of a population. This is relevant for recent models of switching phenomena that have emphasized precisely these very rare environmental shifts, such that the dynamics of allele frequencies following an environmental change are rapid relative to the intervals between environmental changes (Kussell and Leibler 2005; Masel 2005; Masel and Bergman 2003).

We have analyzed the tradeoff between selection for benefits vs. irreversible drift in the long intervals between rare selection events. We have found that the results depend surprisingly little on the population size, but instead depend on the relative magnitude of mutation and selection coefficients eroding the adaptively plastic trait vs. the frequency of environmental change events that cause the benefits of the trait to be selected. Note that although the population size does not appear explicitly in this condition, it nevertheless applies only to a finite population. This is because extinction of alleles never occurs in a truly infinite population. In practice, however, the sojourn time until extinction depends only mildly on the population size, and so no population is ever large enough to be accurately approximated as infinite.

MATHEMATICAL APPENDICES: ONLINE APPENDIX A Sojourn Time τ within a Deme

Mean Sojourn Time

Consider a population of size N that has the trait. Mutants that lack the trait appear at rate m per replication, with a negligible back mutation rate. At a given a point in time there are N − i individuals with and i individuals without the trait, and we denote these types plastic⁺ and plastic⁻ respectively. At each time step, one individual is chosen at random to reproduce, and one to die, where plastic⁻ individuals have a selective advantage s in reproduction. The probability that the new individual is plastic⁻ is therefore given by

$$\frac{i(1+s)+(N-i)m}{N+is}.$$

The probability that the next individual chosen to die is plastic⁻ is given by i / N. The probability that the number of plastic⁻ variants increases from i by one is then given by the probability that a plastic⁻ individual is produced by reproduction while a plastic⁺ individual is chosen to die:

$${\lambda }_i=\frac{(i(1+s)+(N-i)m)(N-i)}{(N+is)N}.$$

The probability that the number of plastic⁻ variants decreases from i by one is given by the probability that a plastic⁺ individual is produced by reproduction while a plastic⁻ individual is chosen to die:

$${\mu }_i=\frac{(N-i)(1-m)i}{(N+is)N}.$$

The ratio is given as

$${\rho }_j=\frac{{\mu }_j}{{\lambda }_j}=\frac{(1-m)j}{j(1+s)+(N-j)m}.$$

Then the mean sojourn time ${\overline{\tau }}_{0i}$ during which there are i plastic⁻ individuals, given that there are none initially, is given by Ewens (2004) Eq. 2.161

$$\begin{array}{l}{\overline{\tau }}_{0i}=\frac{1+\sum _{k=0}^{N-i-2}\prod _{j=i+1}^{N-1-k}{\rho }_j}{{\lambda }_i},\hspace{0.17em}i=0,\dots ,N-1\\ =\frac{1+\sum _{k=0}^{N-i-2}{\left(\frac{1-m}{1-m+s}\right)}^{N-1-k-i}\frac{(N-1-k)!\mathrm{\Gamma }\left(i+1+\frac{mN}{1-m+s}\right)}{i!\mathrm{\Gamma }\left(N-k+\frac{mN}{1-m+s}\right)}}{N{\lambda }_i}\end{array}$$ (A1)

where Γ is the gamma function and the unit of time is 1 generation, corresponding to N rounds in the Moran model, each of which involve a single death and a single reproduction. The mean total sojourn time before all individuals are plastic⁻, given an initial population of pure plastic⁺, is

$${\overline{\tau }}_0=\sum _{i=0}^{N-1}{\overline{\tau }}_{0i}.$$ (A2)

When N is large, the summations in Eqs. A1 and A2 are performed by interpolation using an adaptive algorithm.

Equation (A2) can be used to calculate the mean sojourn time exactly for arbitrary values of m, s and N. In certain circumstances, much simpler, more intuitive approximations are available. When s = 0, we have from Ewens (2004) Eq. 9.11

$${\overline{\tau }}_0=N\left(N+\frac{mN}{1-m}\right)\sum _{j=1}^N\frac{1}{j\left(j+\frac{mN}{1-m}-1\right)}.$$

When mN >> 0 and m << 1, this is well approximated by

$${\overline{\tau }}_0\approx \frac{ln(mN)+\gamma }{m}$$ (A3)

where γ is Euler’s constant, with numerical value 0.577216. When selection dominates the sojourn time, i.e. s >> m and mN >> 1, we have a second limiting case from Hermisson and Pennings (2005) Eq. (A17)

$${\overline{\tau }}_0\approx 2\frac{ln(sN)+\gamma }{s}.$$ (A4)

Based on Equations A3 and A4, we therefore attempted to fit the approximate solution

$${\overline{\tau }}_{approx}\approx \frac{1}{mN{p}_{fix}}+\left\{\begin{array}{cc}\frac{ln((m+s)N)+\gamma }{m+s/2}& \text{if\hspace{0.17em}}ln((m+s)N)>0\\ N-1& \text{otherwise}\end{array}\right\}$$ (A5)

where p _fix is the probability of fixation, beginning with a single plastic⁻ mutant and not returning to having zero mutants. The first term captures the expected waiting time until the appearance of the first mutant destined for fixation and hence the behavior of the system when mN << 1. The second term captures the expected sojourn time once such a mutant has appeared both in the limiting case of mN >> 1 and/or sN >> 1 and in the neutral limiting case of mN << 1 and sN << 1. From Ewens (2004) Eq. 2.158, we have

$$p_{fix}=\frac{1}{1+\sum _{k=1}^{N-1}\prod _{j=1}^k{\rho }_j}.$$

We see in Figure 2 that the approximation given in Eq. (A5) performs reasonably well in practice. For s < m, the exact and approximate solutions converge very quickly for large N. For s > m the approximation was good, but retained systematic biases. For some parameter combinations, a denominator of (m + s) performed better than that of (m + s/2) given in Eq. (A5), but overall the latter seemed to give a closer approximation for a greater range of the parameter space.

Variance in Sojourn Time

From Ewens (2004) Eq. 2.145, the variance of the sojourn time, given an initial state of zero, is equal to

$${\sigma }_0^2=2\sum _{j=1}^{N-1}{\overline{\tau }}_{0j}{\overline{\tau }}_j-{\overline{\tau }}_0-{({\overline{\tau }}_0)}^2.$$ (A6)

As a generalization of Eq. (A1), the mean sojourn time ${\overline{\tau }}_{ji}$ during which there are i plastic⁻ individuals, given that there are j initially, can also be derived from Ewens (2004) Eq. 2.161, and used to calculate ${\overline{\tau }}_j$ and hence Eq. (A6). These calculations were performed (data not shown) and numerically confirmed that the variance in the sojourn time is negligible for mN >> 1, hence justifying our assumption of fixed τ = $\overline{\tau }$ in this case. Since increasingly large values of N yield many more time steps in the Moran model, but only slight increases in $\overline{\tau }$ measured in generations, the variance scales approximately with the average of an increasing number of random waiting times. The law of large numbers therefore applies, making the total sojourn time highly deterministic.

ONLINE APPENDIX B Exact solution for a single population

Consider states E_i and E′_i for i = 0, …, N, where i represents the number of individuals lacking the trait, and E and E′ represent the original and the new environment, respectively. We define a Markov chain on this state space as follows: For 0 ≤ i < N, from state E_i the chain moves to state E′_i with probability 1 − e^−θ/N (corresponding to an environmental change), moves to state E_i−1 with probability e^−θ/N λ_i, moves to state E_i+1 with probability e^−θ/N μ_i, and remains in state E_i otherwise. State E_N is an absorbing state, corresponding to trait loss. From state E′_i, the chain moves to state E′_i−1 with probability 1, unless i = 0, in which case it moves to state E₀ with probability 1. Figure 3 shows the states and the allowable transitions between them.

Let p(X, Y) denote the probability of moving from state X to state Y in one step of the Markov chain, which corresponds to 1/N generation. Then the expected number of generations until trait loss starting from state X, which we denote f(X), is the solution to the following systems of 2N + 1 linear equations (see e.g. Ewens (2004), section 2.1.2):

$$\begin{array}{l}f(x)=\sum _{Y}p(X,Y)f(Y)+1/N\hspace{0.17em}\text{for\hspace{0.17em}}X\ne E_N\\ f(E_N)=0\end{array}$$

If we order the states E_0, E′_0, E_1, E′₁, ..., E_{N − 1,} E′_{N − 1,} E_N, then this system of equations is pentadiagonal, so can be solved directly with requirements in memory and computational time of order N (see e.g. Golub and Van Loan (1996), section 4.3). The expected time until trait loss is given by f(E₀). This reduces to the expected sojourn time ${\overline{\tau }}_0$ of Eq. A2 when θ = 0.

Note that this formulation differs slightly from the formulation introduced earlier, in which the system jumps immediately to state E₀ following an environmental change. This formulation captures the time required for the population to regrow after ill-adapted individuals lacking the trait die following environmental change. The resulting difference in the time until trait loss is less than a single generation per environmental change event. But note that the solution to the modified system of equations

$$\begin{array}{l}f(x)=\sum _{Y}p(X,Y)f(Y)+1/N\hspace{0.17em}\text{for\hspace{0.17em}}X\in \{E_0,\dots ,E_{N-1}\}\\ f(x)=\sum _{Y}p(X,Y)f(Y)\hspace{0.17em}\text{for\hspace{0.17em}}X\in \{E_0^{\prime },\dots ,E_{N-1}^{\prime }\}\\ f(E_N)=0\end{array}$$

gives the expected time until trait loss in the case where the state immediately jumps to E₀ following an environmental change, while retaining the pentadiagonal structure. For consistency with the approximate solution, the calculations shown in Figure 4 use this modified system, although in practice it makes very little difference.

ONLINE APPENDIX C Metapopulations with Exponentially-Distributed Sojourn Times within Demes

Consider a metapopulation of n demes that initially bear the trait. At a given a point in time there are n − j demes with and j demes without the trait. Each time step is an environmental change event or a trait loss, whichever occurs first. The probability that the number of demes without the trait increases by one is given by the probability that in the next time step a deme with the trait undergoes a trait loss event

$${\mathrm{\Lambda }}_j=\frac{1/\overline{\tau }}{1/\overline{\tau }+\theta }\frac{n-j}{n}.$$

Note that in this Section we have mN << 1, and can therefore make the approximation that the sojourn time is dominated by time waiting for a mutation destined for fixation. This means that at a given moment in time, we can make the approximation that all individuals in trait-bearing demes bear the trait. We therefore take the probability that the number of demes without the trait decreases by one as the probability that in the next time step a deme without the trait undergoes an event and is recolonized by a deme that bears the trait

$${\text{M}}_j=\frac{\theta }{1/\overline{\tau }+\theta }\frac{j(n-j)}{n^2}.$$

We now have the ratio

$${\text{P}}_j=\frac{{\text{M}}_j}{{\mathrm{\Lambda }}_j}=\frac{\theta j\overline{\tau }}{n}.$$

Then the mean sojourn time ${\overline{\text{T}}}_{0j}$ during which there are j demes without the trait, given that all demes initially have the trait, is given by Ewens (2004) Eq. 2.161

$$\begin{array}{l}{\overline{\text{T}}}_{0j}=\frac{1+\sum _{k=0}^{n-j-2}\prod _{x=j+1}^{n-1-k}{\text{P}}_x}{{\mathrm{\Lambda }}_i}\\ =\frac{n(1+\theta \overline{\tau })}{n-j}\left(1+\sum _{k=0}^{n-j-2}\frac{(n-k-1)!}{j!}{\text{P}}_1^{n-j-k-1}\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}j=0,\dots ,n-1\end{array}$$ (C1)

where the unit of time is 1 time step in the Markov process, which corresponds to an environmental change event or a potential trait loss, whichever occurs first, with combined rate $n(1/\overline{\tau }+\theta )$ events per generation. The total sojourn time before all demes lose the trait, given that all initially bear it, is

$${\overline{\text{T}}}_0=\sum _{j=0}^{n-1}{\overline{\text{T}}}_{0j}.$$ (C2)

When n is large, the summations in Eqs. C1 and C2 are performed by interpolation using an adaptive algorithm.

ONLINE APPENDIX D Metapopulations with Fixed Sojourn Times within Demes

Approximate Solution

Fixed sojourn times are more difficult to capture within a Markov model, since although the environmental change events follow a Markov process, trait loss events do not. As an approximation, each time environmental change occurs, we check whether trait loss will occur before the next environmental change event in that deme. If so, we then approximate trait loss as rapid for all but the last deme to undergo trait loss. We make adjustments at the beginning and the end of the Markov process used for the analytical model. At the beginning, we check all n demes bearing the trait, to see if they lose it before they have their first environmental change event. At the end, we consider the additional time for the last deme to lose the trait. Now our quantity of interest, instead of being ${\overline{\text{T}}}_0$, is

$$\overline{\text{T}}=\frac{\sum _{i=0}^{n-1}\left(\begin{array}{c}n\\ i\end{array}\right)e^{-\theta \overline{\tau }i}{(1-e^{-\theta \overline{\tau }})}^{n-i}{\overline{\text{T}}}_i}{n\theta }+\overline{\tau }$$ (D1)

where the unit of time is generations, and the denominator corrects for the fact that in this Markov process, each time step is an environmental change event. We now go on to calculate the sojourn time ${\overline{\text{T}}}_i$ before all demes lose the trait, given that i demes initially lack it. The probability that the number of demes without the trait increases by one is given by the probability that a deme with the trait undergoes an environmental change event, and is destined to lose the trait before the next event in that deme:

$${\mathrm{\Lambda }}_j=e^{-\theta \overline{\tau }}\frac{n-j}{n}.$$

The probability that the number of demes without the trait decreases by one is given by the probability that a deme without the trait undergoes an event and is recolonized by a deme that bears the trait, multiplied by the probability that the newly colonized deme is not destined to lose the trait before the next event in that deme:

$${\text{M}}_j=\frac{j(n-j)}{n^2}(1-e^{-\theta \overline{\tau }})$$

Note that this is an approximation. On the one hand, not all colonizing individuals from a trait-bearing deme are trait-bearing individuals, making M an overestimate. On the other hand, some recolonization may come from demes that are destined to lose the trait before their deme encounters an event, but they have not yet lost the trait when another deme encounters an event. This makes M an underestimate. The model was verified by numerical simulations to test the effects of these two factors, as described in the section below. Figure 5 shows fairly good agreement between the analytical model and the simulations, suggesting that the two effects largely cancel each other out.

Now the mean sojourn time ${\overline{\text{T}}}_{ij}$ during which there are j demes without the trait, given that i demes initially lack it, is given by Ewens (2004) Eq. 2.161

$${\overline{\text{T}}}_{ij}=\left\{\begin{array}{c}\prod _{x=j}^{i-1}\frac{{\text{M}}_{x+1}}{{\mathrm{\Lambda }}_x}=\prod _{x=j}^{i-1}\frac{x(n-x-1)}{n(n-x)}(e^{\theta \overline{\tau }}-1){\overline{T}}_{ii}=\frac{(n-i)i!}{(n-j)j!}{\left(\frac{e^{\theta \overline{\tau }}-1}{n}\right)}^{i-j}{\overline{T}}_{ii}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}j=0,1,\dots ,i-1\\ \frac{\text{1}+\sum _{k=0}^{n-j-2}\prod _{x=j+1}^{n-1-k}\frac{{\text{M}}_x}{{\mathrm{\Lambda }}_x}}{{\mathrm{\Lambda }}_j}=\frac{n{e}^{\theta \overline{\tau }}}{n-j}\left(1+\sum _{k=0}^{n-j-2}\frac{(n-k-1)!}{j!}{\left(\frac{e^{\theta \overline{\tau }}-1}{n}\right)}^{n-j-k-1}\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}j=i,i+1,\dots ,n-1\end{array}\right\}$$ (D2)

where the unit of time is 1 step in the Markov process, which corresponds to one environmental change event, with rate n θ events per generation. The total sojourn time before all demes lose the trait, given that i demes initially lack it, is

$${\overline{\text{T}}}_i=\sum _{j=0}^{n-1}{\overline{\text{T}}}_{ij}.$$ (D3)

When n is large, the summations in Eqs. D1, D2 and D3 are performed by interpolation using an adaptive algorithm.

Simulated Exact Solution

We performed simulations according to the following algorithm. Initialize time t = 0 and set up n demes with both trait-bearing status and the value x₁ = x₂ = … = x_n = $\overline{\tau }$ to specify the time at which they are due to undergo trait loss. Sample the time of the next environmental change event from the exponential distribution with mean 1/n θ. Increment t and switch any deme j for which x_j < t to trait-loss status. Choose a new deme j at random to undergo the environmental change event. If deme j bears the trait, reset x_j to t + $\overline{\tau }$. If deme j lacks the trait, we assume that it is destroyed, and choose a second deme i at random to recolonize it. If deme i bears the trait, reset x_j to x_i: this assumes that recolonization involves a representative sample of the colonizing population, rather than a single individual. Then repeat this procedure for the next environmental change event, stopping when all demes lack the trait.

Calculating the minimum number of demes needed for the mean sojourn time to be less than 10⁸ generations is computationally expensive, since it is difficult to find an algorithm that avoids calculating very long sojourn times greatly in excess of 10⁸ generations. We truncated our simulations at 10⁸, and found a minimum deme number according to how often simulations were truncated. When the trait was lost, we incremented the deme number by 1, and when the simulation was truncated since the trait was not lost, we decremented the deme number by 1. We then calculated the average deme number sampled by this procedure over a large number of iterations.