What is heterogeneity and is it important?

Abstract

This is the first in a series of occasional articles explaining statistical and epidemiological tests used in research papers in the BMJ

Three systematic reviews published in the BMJ, including one in this issue, have referred to heterogeneity and dealt with it in three different ways.^{1 2 3} So what is heterogeneity, and how do we assess its importance in a systematic review?

Clinical heterogeneity

Sometimes trials are just looking at different concepts. Reviewers might set out to summarise interventions for improving patients' ability to make treatment choices; the trials, however, might have covered diverse interventions, such as information leaflets, CD Roms, counselling sessions with a nurse, and training in consultation techniques for doctors. Although the interventions try to achieve the same end result (to improve patients' ability to make choices), they are different in nature.

In theory, we could add all the trials in this review together and come up with a number, but would this be useful? Would the averaged number apply to all these diverse interventions? The interventions are so different that combining them does not make clinical sense. This is an example of clinical heterogeneity. Other circumstances that may give rise to clinical heterogeneity include differences in selection of patients, severity of disease, and management. Judgments about clinical heterogeneity are qualitative, do not involve any calculations, and can be made by putting forward a convincing argument about similarities (or differences) between the trials.

Statistical heterogeneity

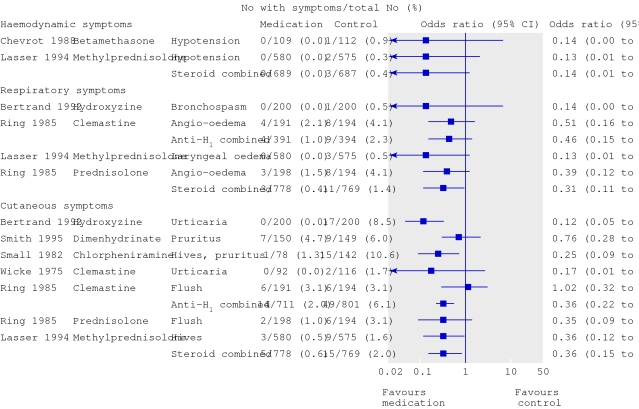
Individual trials in a systematic review may seem to measure the same outcome but may have results that are not consistent with each other. Some trials show a benefit while others show harm, or the trials are inconsistent in the size of benefit or harm. This is the case in the systematic review of medications to prevent allergic reactions caused by contrast media.¹ The trials that measured effects on cutaneous symptoms of allergy showed a range of odds ratios from 0.12 favouring the medication to 1.02 favouring the control (fig 1). This is an example of statistical heterogeneity.

Forest plot adapted from Tramèr et al¹ showing statistical heterogeneity in the odds ratios for medications to prevent cutaneous allergic reactions (P for χ² test for heterogeneity for anti-H₁ combined was 0.03)

How can you detect it and does it matter?

Statistical heterogeneity is apparent only after the analysis of the results. Heterogeneity may be judged graphically (by looking at the forest plot) and be measured statistically. In a forest plot from the systematic review of calcium supplementation,² the error bars for each trial include the summary result, which suggests that statistical heterogeneity is not a problem and that the message is a consistent one (fig 2).

Forest plot adapted from Winzenberg et al² showing absence of statistical heterogeneity in the odds ratios for the effect of calcium supplementation on bone mineral density. SMD=standardised mean difference

To determine whether significant heterogeneity exists, look for the P value for the χ² test of heterogeneity. A high P value is good news because it suggests that the heterogeneity is insignificant and that one can go ahead and summarise the results. Because statistical tests for heterogeneity are not very powerful it is sensible to use a higher P value than usual (say, P>0.1) as the cut-off for a decision and to think about clinical heterogeneity anyway.

The systematic review of calcium supplementation passes the test, and the authors have rightly summarised the effects on bone density using a simple fixed effects model. This model assumes that all trials are trying to measure the same thing and that more influence should be given to larger trials when computing an average effect.⁴

But what if the P value for the χ² test of heterogeneity is low, suggesting significant heterogeneity? What can be done? Two approaches are possible. We can either avoid summarising the result and look for reasons for the heterogeneity, or we can summarise the effects using another method—the random effects model. Reasons for heterogeneity, other than clinical differences, could include methodological issues such as problems with randomisation, early termination of trials, use of absolute rather than relative measures of risk, and publication bias.

The authors of the systematic review of medications used to prevent allergic reactions caused by contrast media took the first approach.¹ The forest plots suggest that the two classes of drugs have different effects, particularly for skin reactions, and the P value for the statistical test for heterogeneity was significant at 0.03. They decided not to summarise an average effect and felt that the difference between treatments was part of the message of the review.

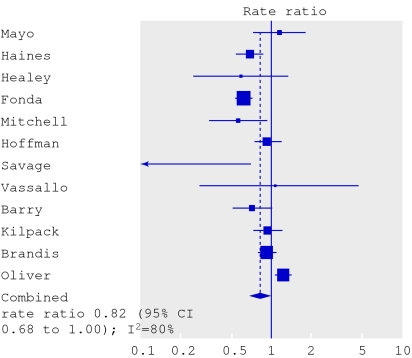
The authors of the review of interventions to prevent falls and fractures took the second approach.³ The forest plot for falls in hospital shows a wide spread of results (fig 3). Some trials suggest benefit and others suggest harm from the multifaceted interventions. The authors present the I ² statistic, which measures the percentage of variation that is not due to chance. A high percentage, such as the 80% seen here, suggests important heterogeneity. (An I ² value of <25% is considered low.⁵)

Forest plot from Oliver et al³ showing rate ratios (random effects model) for the effects of strategies to prevent falls

Nevertheless, the authors felt that all the trials were trying to measure essentially the same thing and that it was worth summarising the results. They used the random effects model, which uses a different formula to calculate more conservative 95% confidence intervals. The effects of treatment are assumed to vary around some overall average treatment effect, as opposed to a fixed effects model, in which it is assumed that each study has the same fixed common treatment effect.⁴

Systematic reviews with a meta-analysis try to provide better numerical answers to the questions, “what is the effect of this intervention and how sure are we about that?” But before believing the results of this method, it might be useful to consider four questions (see box).

Useful questions to consider

• Was it really a good idea to combine the trials?

• Is there too much clinical heterogeneity for the review to make sense?

• Do the forest plots look consistent?

• Do the statistical tests suggest that heterogeneity is a problem?

Further reading

• Chalmers I, Altman DG. Systematic reviews. London: BMJ Publishing, 1995.

• Thompson SG. Why sources of heterogeneity in meta-analyses should be investigated. BMJ 1994;309:1351-5.