Abstract
Objectives: To examine the generalisability of multivariate risk functions from diverse populations in three contexts: ordering risk, magnitude of relative risks, and estimation of absolute risk.
Design: Meta-analysis of prospective cohort studies.
Patients: Participants from various epidemiological studies.
Main outcome measure: Death from coronary heart disease (CHD).
Results: The analysis included 105 420 men and 56 535 women 35–74 years of age and free of CHD at baseline from 16 observational studies with a total of 27 analytical groups. The area under the receiver operating characteristic curve (AUC) was used to judge the ability of the multivariate risk function to order risk correctly. AUCs ranged from 0.60 to 0.80. The AUCs differed significantly between the studies (p < 0.01) but were very similar for different risk functions applied to the same population, indicating similar ability to rank risk for different models. The magnitudes of the relative risks associated with major risk factors (age, systolic blood pressure, serum total cholesterol, smoking, and diabetes) varied significantly across studies (p < 0.05 for homogeneity). The prediction of absolute risk was not very accurate in most of the cases when a model derived from one study was applied to a different study.
Conclusions: When considered qualitatively, the major risk factors are associated with CHD mortality in a diverse set of populations. However, when considered quantitatively, there was significant heterogeneity in all three aspects: ordering risk, magnitude of relative risks, and estimation of absolute risk.
Keywords: coronary heart disease, risk factors, risk ordering
Coronary heart disease (CHD) is a leading cause of death in many countries. Prospective studies around the world have identified major risk factors for developing CHD and, based on these risk factors, functions have been developed to predict the occurrence of CHD in individual patients. Although many researchers have examined whether a risk function based on a single population is valid when applied to other populations,1–12 most have involved a small number of studies and the various aspects of predictive accuracy have not been systematically examined. In this report we examine the predictive accuracy of risk functions using three successively stronger sets of criterion: ordering risk, estimating relative risk, and estimating absolute risk.
The lowest level of validity for a predictive function is its ability to rank individual patients within a population according to their risk, differentiating patients with higher risk from those at lower risk levels. The absolute level of risk is not a concern; only the ordering is important. Several reports have examined the ability of a single risk function to order risk across studies and judged the validity of the risk function by this criterion.1,2
Estimating relative risk is more difficult than ordering. A more stringent criterion would require that the model parameters relating risk factors to disease be the same in different populations. Comparisons in the literature based on this criterion have yielded conflicting results.3–12
In recent years, some treatment guidelines have endorsed a multifactorial strategy that attempts to quantify the contributions of various coronary risk factors along a continuum of risk.13–17 Aggressive preventive treatment and intervention are justified if a patient's absolute risk exceeds a certain cut off point. In this context, it is important that the prediction of individual absolute risk be valid. Studies that have compared the estimation of absolute risk across populations have reported conflicting results.3,10,18–24
We used person-level data from 16 observational studies to test the heterogeneity of the relations between CHD mortality and age and the four major risk factors (that is, blood pressure, serum cholesterol, cigarette smoking, and diabetes status). We applied the three criteria described above and examined whether a common risk function exists that is valid for predicting CHD death in these diverse samples.
METHODS
Studies
The Diverse Populations Collaboration examines epidemiological results in samples from populations from many countries and cultures. The 16 studies reported here comprise national representative samples from the USA, participants from cohort studies in the USA, the Middle East, Europe, Asia, and the Caribbean, and participants from clinical trials.
In this analysis we report results using data from the NHANES I (first national health and nutrition examination survey) epidemiologic follow up study,25 NHANES II (second national health and nutrition examination survey) mortality follow up study,26 the Framingham study,27,28 the Tecumseh community health study,29 the Honolulu heart program,30 the LRC (lipid research clinics) prevalence study,31 the Tuzla cohort of the Yugoslavia cardiovascular disease study,32 the Scottish collaborative study,33 the Renfrew and Paisley study,34 the Glostrup population studies,35 the Norwegian counties study,36 the Reykjavik Iceland study,37 the Israeli ischemic heart disease study,38 the Puerto Rico heart health program,39 the control group from the HDFP (hypertension detection and follow up program),40 and the control group from MRFIT (multiple risk factor intervention trial).41 To be consistent with recent Framingham reports, we pooled data for participants who attended the 11th examination (1971–1974) of the original Framingham heart study27 and from the initial examination (1971–1975) of the Framingham offspring study28 to form a single Framingham cohort.
The underlying cause of death was determined according to the International classification of diseases, ninth revision in most of the studies (codes 410–414 and 429.2 as CHD), except for the Glostrup population studies, HDFP, and the LRC mortality follow up study, in which the International classification of diseases, eighth revision was used (codes 410–414 as CHD). Cause of death was assigned by a panel of physicians in the Framingham cohort and in the Yugoslavia cardiovascular disease study.
Data analysis
Requirements for inclusion in this analysis were as follows: (1) age 35–74 years at the time of the baseline examination; (2) complete data on systolic blood pressure, serum total cholesterol, cigarette smoking, and diabetes status; (3) known vital status and underlying cause of death for decedents; and (4) absence of CHD at baseline. Data for men and women were analysed separately. The studies often contained subgroups based on factors such as area of residence (urban or rural) and other characteristics of the study samples (for example, random sample or hyperlipidaemic patients). Each distinct subgroup was analysed as a separate cohort. For clinical trials, only participants in the control groups were included. Any analytical group with fewer than 60 CHD deaths was excluded to assure at least 10 end point cases for each independent variable. This criterion resulted in the exclusion of CORDIS (cardiovascular occupational risk factor determination in Israel study), the Guangzhou Chinese cohorts from the People's Republic of China, and female samples from the lipid research clinics study, the Scottish collaborative study, and the Glostrup population studies. The final analysis considered 27 analytical groups (19 for men and eight for women).
The multivariate proportional hazards model was used to examine the relation between CHD death and five risk factors: age, systolic blood pressure, serum total cholesterol, current cigarette smoking, and diabetes status. There were only six people with diabetes in the rural samples from the Yugoslavia cardiovascular study; so that diabetes status was not included in the model for this cohort. Smoking status was dichotomised as current smoker or non-smoker. The follow up period was limited to 20 years; if a person had been followed up for more than 20 years, he or she was censored at 20 years. For presentation purposes, the usual transformation of the model coefficients to relative risk was used (that is, exp(xb), where x is an increment in a characteristic). The units of increment to calculate the relative risks were 10 years for age, 20 mm Hg for systolic blood pressure, and 1.04 mmol/l (∼40 mg/dl) for serum cholesterol. These units were approximately equal to 1 SD of the measures.
Three approaches were used to examine the risk factor–CHD relations across studies. Firstly, a receiver operating characteristic (ROC) curve analysis was used to measure how well an equation ordered the risk of CHD death.42,43 The area under the ROC curve (AUC) was compared across studies.42,44 The AUC was calculated first using a model derived from the specific (internal) cohort and then calculated using a model estimated from an external cohort (for example, the Framingham cohort or the Renfrew and Paisley study). To calculate these different AUCs, the predicted survival probability of CHD death in eight years was used. Two examinations of these results were conducted: we first examined whether the results from the studies differed significantly using the χ2 statistic suggested by DerSimonian and Laird44; we also compared the AUCs within studies using different models to calculate them.
We next examined the relative size of the coefficients from the proportional hazards model for each risk factor. The coefficients were compared across studies using the χ2 test suggested by DerSimonian and Laird44 to determine whether variation between studies was significant.
Finally, the observed eight year CHD death rate of each cohort was compared with the predictive rate when a risk function based on another cohort (such as the Framingham study) was applied to the cohort.
RESULTS
Descriptive analysis
Tables 1 and 2 present the numbers of participants, baseline characteristics, and numbers of all cause and CHD deaths during follow up for men and women, respectively, in each cohort. Altogether, this analysis included 161 955 participants (105 420 men and 56 535 women) with 29 662 deaths (21 841 men and 7821 women), among which 8316 were deaths from CHD (6442 men and 1874 women). In men, the mean age was between 48–54 years in most of the cohorts. The Norwegian counties study recruited only people aged 35–49 years (table 1). Excluding the HDFP, in which all participants were hypertensive, men from the Renfrew and Paisley study had the highest average systolic blood pressure. Omitting clinical trials, samples from northern Europe in general had a higher mean serum total cholesterol concentration. Cigarette smoking was most prevalent in the Yugoslavia cardiovascular disease study (around 70%). Among women (table 2), mean ages were 52–54 years in most of the cohorts and the Norwegian women had a lower mean age (42 years). Women from the Renfrew and Paisley study also had a higher average systolic blood pressure than did women in the other cohorts. Three cohorts from northern Europe had the highest average concentrations of serum cholesterol. The highest prevalence of smoking was found in the Renfrew and Paisley study (47%) and the lowest in the NHANES I and II cohorts (26–27%). The mean age of all cohorts combined was 49 years. Standardising to this age, men and women from the Renfrew and Paisley study and from the Tecumseh community health study had the highest CHD mortality.
Table 1.
Numbers of participants, baseline characteristics, and numbers of deaths during follow up in men
| Number of deaths | ||||||||||
| Study | Baseline numbers | Age range (years) | SBP, mean (SD) (mm Hg) | Serum TC, mean (SD) (mmol/l) | Smoking rate (%) | DM rate (%) | Median follow up (years) | All | CHD | CHD rate* |
| NHANES I | 3856 | 35–74 | 139 (22) | 5.82 (1.19) | 36 | 3.9 | 17 | 1843 | 551 | 4.1 |
| NHANES II | 3354 | 35–74 | 135 (20) | 5.75 (1.14) | 37 | 5.2 | 14 | 965 | 258 | 2.4 |
| Framingham cohort | 2274 | 35–74 | 133 (20) | 5.57 (1.02) | 47 | 4.5 | 19 | 713 | 188 | 3.2 |
| Tecumseh community health study | 1257 | 35–74 | 139 (20) | 5.82 (1.07) | 61 | 3.2 | 19 | 416 | 153 | 6.5 |
| Honolulu heart program | 7625 | 45–68 | 134 (21) | 5.63 (0.99) | 44 | 9.1 | 20 | 2045 | 293 | 1.2 |
| Puerto Rico heart health program | ||||||||||
| Urban | 6612 | 35–74 | 134 (23) | 5.30 (1.09) | 41 | 6.4 | 16 | 1152 | 236 | 1.4 |
| Rural | 2879 | 35–74 | 128 (22) | 5.05 (1.00) | 50 | 2.2 | 16 | 468 | 78 | 1.0 |
| Yugoslavia cardiovascular disease study | ||||||||||
| Urban | 3472 | 35–64 | 136 (19) | 5.27 (1.16) | 69 | 1.1 | 17 | 660 | 131 | 2.9 |
| Rural | 2868 | 35–62 | 131 (18) | 4.26 (0.91) | 72 | 0.2 | 17 | 642 | 82 | 2.0 |
| Scottish collaborative study | 5734 | 35–72 | 134 (18) | 5.88 (1.04) | 55 | 0.5 | 20 | 1578 | 609 | 5.7 |
| Renfrew and Paisley study | 6999 | 45–64 | 148 (23) | 5.86 (0.96) | 57 | 1.3 | 16 | 2529 | 994 | 6.0 |
| Glostrup cohort | 3844 | 39–71 | 130 (18) | 6.27 (1.18) | 57 | 2.9 | 10 | 489 | 109 | 2.0 |
| Norwegian counties study | 24204 | 35–49 | 136 (16) | 6.41 (1.29) | 48 | 0.7 | 17 | 2292 | 753 | 3.2 |
| Iceland Reykjavik study | 8151 | 36–74 | 140 (19) | 6.35 (1.06) | 28 | 1.8 | 19 | 2026 | 683 | 3.4 |
| Israeli ischemic heart disease study | 9712 | 40–73 | 135 (20) | 5.40 (1.03) | 51 | 4.6 | 20 | 2678 | 816 | 4.1 |
| Lipid research clinics follow-up study | ||||||||||
| Random sample | 1992 | 35–74 | 126 (18) | 5.43 (0.96) | 36 | 1.4 | 13 | 226 | 74 | 2.3 |
| Hyperlipidaemic | 1628 | 35–74 | 129 (17) | 6.29 (1.25) | 37 | 2.0 | 13 | 195 | 71 | 3.0 |
| HDFP (regular care) | 2531 | 35–69 | 156 (21) | 6.01 (1.20) | 42 | 6.1 | 8 | 387 | 137 | 4.6 |
| MRFIT (usual care) | 6428 | 35–58 | 138 (15) | 6.65 (0.96) | 59 | 2.7 | 11 | 536 | 226 | 3.8 |
| Total | 105420 | 21841 | 6442 | |||||||
*Age standardised coronary heart disease (CHD) mortality per 1000 person years. DM, diabetes mellitus; HDFP, hypertension detection and follow-up program; MRFIT, multiple risk factor intervention trial; NHANES, national health and nutrition examination survey; SBP, systolic blood pressure; TC, total cholesterol.
Table 2.
Numbers of participants, baseline characteristics, and numbers of death during follow up in women
| Number of deaths | ||||||||||
| Study | Baseline numbers | Age range (years) | SBP, mean (SD) (mm Hg) | Serum TC, mean (SD) (mmol/l) | Smoking rate (%) | DM rate (%) | Median follow up (years) | All | CHD | CHD rate* |
| NHANES I | 5378 | 35–74 | 138 (25) | 5.98 (1.26) | 26 | 4.5 | 19 | 1660 | 480 | 1.8 |
| NHANES II | 3994 | 35–74 | 134 (24) | 6.09 (1.30) | 27 | 6.3 | 14 | 751 | 199 | 1.0 |
| Framingham cohort | 2625 | 35–74 | 131 (21) | 5.76 (1.15) | 39 | 2.9 | 19 | 603 | 90 | 0.8 |
| Tecumseh community health study | 1286 | 35–74 | 141 (25) | 5.91 (1.21) | 32 | 4.0 | 19 | 250 | 77 | 2.1 |
| Renfrew and Paisley study | 8265 | 45–64 | 150 (25) | 6.42 (1.10) | 47 | 1.2 | 17 | 1878 | 562 | 2.2 |
| Norwegian counties study | 23863 | 35–49 | 131 (18) | 6.26 (1.23) | 37 | 0.5 | 17 | 1144 | 134 | 0.6 |
| Iceland Reykjavik study | 8899 | 36–74 | 137 (20) | 6.59 (1.22) | 38 | 1.4 | 17 | 1314 | 266 | 0.9 |
| HDFP (regular care) | 2227 | 35–69 | 163 (24) | 6.22 (1.28) | 32 | 8.2 | 8 | 251 | 66 | 2.0 |
| Total | 56535 | 7821 | 1874 | |||||||
*Age standardised CHD mortality per 1000 person years.
ROC curve analysis
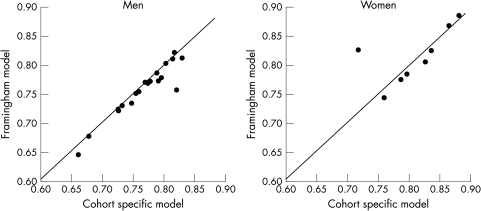
AUC derived internally at eight years in men ranged from 0.66 to 0.83 (table 3 and x axis in fig 1). In women, the ranges were 0.72 to 0.88 (table 4 and fig 1). The heterogeneity of the AUCs was significant across studies for both men and women (p < 0.001). The AUC of each cohort calculated from its own model is plotted against that when the Framingham risk function is applied to the cohort (y axis in fig 1). Except for two outliers (rural men from the Yugoslavia cardiovascular disease study and women from the Norwegian counties study), the plots are by and large distributed along the 45° line (the line of identity), indicating a similar ability of ordering risk by either function. When risk equations from other cohorts (such as the Renfrew and Paisley study) were applied to each cohort, instead of the Framingham study, the results were very similar (data not shown). The differences in AUCs between applying the Framingham model and the Renfrew and Paisley model were very small and ranged from −0.014 to 0.003 in men and from −0.018 to 0.029 in women. The Pearson correlation coefficients between AUCs derived from the cohorts' internally derived function, the Framingham model, and the Renfrew and Paisley model were 0.95–0.99, suggesting that the ability of these three different risk functions to order risk within a given cohort was nearly identical. Thus, the ability to rank risk in a population was determined by the intrinsic discriminatory power of the major risk factors measured in that population and not the multivariate predictive function chosen.
Table 3.
Multivariate adjusted relative risk (95% confidence interval (CI)) and area under the receiver operating characteristic curve in men
| Multivariate adjusted relative risk (95% CI) | ||||||
| Study | AUC | Age | SBP | Serum TC | Smoking | DM |
| NHANES I | 73 | 2.19 (1.98 to 2.42) | 1.28 (1.20 to 1.38) | 1.11 (1.04 to 1.18) | 1.33 (1.11 to 1.59) | 2.17 (1.60 to 2.94) |
| NHANES II | 78 | 2.84 (2.39 to 3.37) | 1.28 (1.16 to 1.43) | 1.12 (1.01 to 1.25) | 2.03 (1.57 to 2.64) | 1.73 (1.15 to 2.60) |
| Framingham cohort | 80 | 2.12 (1.81 to 2.48) | 1.34 (1.17 to 1.53) | 1.22 (1.07 to 1.40) | 1.37 (1.03 to 1.82) | 1.99 (1.23 to 3.21) |
| Tecumseh community health study | 81 | 2.48 (2.10 to 2.94) | 1.46 (1.28 to 1.67) | 1.32 (1.14 to 1.53) | 1.86 (1.32 to 2.63) | 1.85 (0.94 to 3.66) |
| Honolulu heart program | 80 | 2.12 (1.73 to 2.60) | 1.59 (1.45 to 1.75) | 1.39 (1.25 to 1.55) | 2.02 (1.61 to 2.55) | 2.85 (2.17 to 3.75) |
| Puerto Rico heart health program | ||||||
| Urban | 76 | 2.01 (1.63 to 2.49) | 1.56 (1.43 to 1.70) | 1.27 (1.16 to 1.40) | 1.43 (1.10 to 1.87) | 2.88 (2.07 to 4.03) |
| Rural | 77 | 2.23 (1.56 to 3.19) | 1.66 (1.43 to 1.94) | 1.15 (0.95 to 1.41) | 1.44 (0.92 to 2.25) | 2.86 (1.23 to 6.60) |
| Yugoslavia cardiovascular disease study | ||||||
| Urban | 82 | 2.11 (1.64 to 2.71) | 1.56 (1.35 to 1.80) | 1.33 (1.16 to 1.52) | 1.54 (1.03 to 2.30) | 4.63 (2.15 to 9.96) |
| Rural | 82 | 2.20 (1.58 to 3.06) | 1.81 (1.49 to 2.20) | 0.86 (0.67 to 1.10) | 2.05 (1.13 to 3.71) | |
| Scottish collaborative study | 75 | 2.03 (1.77 to 2.32) | 1.45 (1.34 to 1.56) | 1.28 (1.19 to 1.38) | 1.90 (1.61 to 2.25) | 1.65 (0.78 to 3.51) |
| Renfrew and Paisley study | 68 | 2.13 (1.90 to 2.40) | 1.31 (1.24 to 1.37) | 1.18 (1.11 to 1.26) | 1.58 (1.39 to 1.79) | 2.73 (1.93 to 3.87) |
| Glostrup cohort | 77 | 2.09 (1.67 to 2.61) | 1.53 (1.28 to 1.83) | 1.20 (1.05 to 1.38) | 2.09 (1.38 to 3.16) | 2.52 (1.26 to 5.02) |
| Norwegian counties study | 73 | 2.25 (1.88 to 2.69) | 1.54 (1.43 to 1.65) | 1.29 (1.24 to 1.34) | 2.55 (2.18 to 2.98) | 3.98 (2.62 to 6.03) |
| Iceland Reykjavik study | 75 | 2.36 (2.13 to 2.61) | 1.40 (1.31 to 1.50) | 1.34 (1.25 to 1.44) | 1.75 (1.49 to 2.05) | 1.78 (1.17 to 2.71) |
| Israeli ischemic heart disease study | 79 | 2.08 (1.88 to 2.31) | 1.51 (1.43 to 1.60) | 1.33 (1.24 to 1.42) | 1.56 (1.35 to 1.79) | 2.31 (1.86 to 2.87) |
| Lipid research clinics follow-up study | ||||||
| Random sample | 83 | 2.50 (1.92 to 3.26) | 1.40 (1.13 to 1.72) | 1.40 (1.10 to 1.77) | 1.91 (1.18 to 3.09) | 8.05 (3.80 to 17.03) |
| Hyperlipidaemic | 79 | 2.39 (1.85 to 3.09) | 1.17 (0.92 to 1.50) | 1.27 (1.16 to 1.39) | 1.82 (1.11 to 2.99) | 3.79 (1.60 to 8.98) |
| HDFP (regular care) | 73 | 1.95 (1.56 to 2.44) | 1.31 (1.13 to 1.52) | 1.12 (0.99 to 1.25) | 1.60 (1.14 to 2.25) | 1.79 (1.06 to 3.05) |
| MRFIT (usual care) | 66 | 1.74 (1.37 to 2.20) | 1.41 (1.19 to 1.66) | 1.22 (1.06 to 1.41) | 2.02 (1.51 to 2.71) | 1.24 (0.61 to 2.51) |
The multivariate adjusted relative risks and the 95% CIs were estimated using a proportional hazards models with age, SBP, serum TC, current smoking, and DM status included as independent variables in the models. Relative risks associated with specified increments of the characteristics were calculated based on this multivariate model. The increments used were 10 years of age, 20 mm Hg SBP, 1.04 mmol/l TC, current smoking versus current non-smoker, and DM versus non-DM.
Figure 1.
Areas under the receiver operating characteristic curve (AUC) for death from coronary heart disease at eight years by sex in diverse populations. For each cohort, AUC calculated from the cohort specific model (x axis) is plotted against AUC when the Framingham model was applied to that specific cohort (y axis). Data points distributed along the 45° line indicate similar AUCs calculated from the two models.
Table 4.
Multivariate adjusted relative risk (95% CI) and AUC in women
| Multivariate adjusted relative risk (95% CI) | ||||||
| Study | AUC | Age | SBP | Serum TC | Smoking | DM |
| NHANES I | 84 | 2.95 (2.62 to 3.33) | 1.29 (1.21 to 1.39) | 1.05 (0.97 to 1.13) | 2.08 (1.67 to 2.58) | 2.50 (1.89 to 3.30) |
| NHANES II | 80 | 2.84 (2.28 to 3.55) | 1.35 (1.21 to 1.50) | 1.17 (1.05 to 1.30) | 1.92 (1.38 to 2.69) | 2.76 (1.92 to 3.97) |
| Framingham cohort | 86 | 2.26 (1.72 to 2.97) | 1.60 (1.32 to 1.93) | 1.41 (1.17 to 1.69) | 1.80 (1.14 to 2.82) | 4.67 (2.70 to 8.07) |
| Tecumseh community health study | 88 | 2.71 (2.08 to 3.53) | 1.48 (1.27 to 1.73) | 1.14 (0.94 to 1.37) | 1.93 (1.09 to 3.38) | 1.32 (0.62 to 2.82) |
| Renfrew and Paisley study | 76 | 2.68 (2.26 to 3.17) | 1.34 (1.27 to 1.43) | 1.20 (1.12 to 1.29) | 2.07 (1.75 to 2.45) | 3.65 (2.36 to 5.65) |
| Norwegian counties study | 72 | 1.71 (1.10 to 2.65) | 1.72 (1.51 to 1.96) | 1.37 (1.26 to 1.49) | 3.01 (2.11 to 4.28) | 8.67 (3.81 to 19.77) |
| Iceland Reykjavik study | 83 | 2.84 (2.39 to 3.38) | 1.45 (1.32 to 1.60) | 1.31 (1.20 to 1.43) | 3.34 (2.60 to 4.28) | 3.81 (2.25 to 6.44) |
| HDFP (regular care) | 79 | 2.74 (1.92 to 3.92) | 1.19 (0.99 to 1.44) | 1.30 (1.17 to 1.44) | 1.87 (1.10 to 3.18) | 2.57 (1.37 to 4.81) |
The multivariate adjusted relative risks and the 95% CIs were estimated using a proportional hazards models with age, SBP, serum TC, current smoking, and DM status included as independent variables in the models. Relative risks associated with specified increments of the characteristics were calculated based on this multivariate model. The increments used were 10 years of age, 20 mm Hg SBP, 1.04 mmol/l TC, current smoking versus current non-smoker, and DM versus non-DM.
Relative risk
The risk of CHD death associated with each risk factor was examined with the use of the multivariate Cox proportional hazards model (table 3 for men and table 4 for women). With only a few exceptions, as expected, the major risk factors were significantly and independently related to CHD death for both sexes. However, the magnitude of the relative risks varied between the cohorts. For example, among men, with clinical trials omitted the relative risk associated with systolic blood pressure ranged from 1.28 in the NHANES I and II cohorts to 1.81 in the rural samples from the Yugoslavia cohort (table 3). For serum total cholesterol, the relative risk ranged from 0.86 (the rural samples from the Yugoslavia cohort) to 1.40 in the random sample of the lipid research clinic follow up study. The relative risk associated with smoking ranged from 1.33 in the NHANES I to 2.55 in the Norwegian counties study. Large relative risks and 95% confidence intervals were found in several studies in which the number of participants with diabetes was small. The DerSimonian and Laird χ2 tests suggest the existence of significant heterogeneity of the relative risks (p < 0.05) between studies for systolic blood pressure, serum cholesterol, smoking, and diabetes but not for age in both men and women. To examine a possible quadratic relation between age and risk of CHD death, both age and squared term of age were included in the Cox proportional hazards model. Among 27 analytical groups, a significantly quadratic relation was found in only three groups (men from the Scottish collaborative study, the Renfrew and Paisley study, and the Israeli ischemic heart disease study). Hence, age quadratic term was not included in the model in the analyses.
Absolute risk
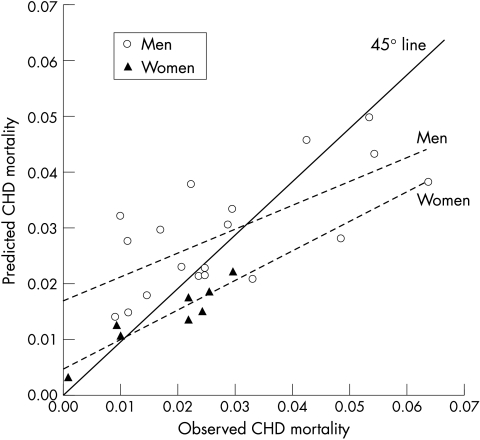
Figure 2 plots the observed eight year CHD mortality of each cohort against mortality predicted from the Framingham model. Among men, the Framingham model tended to overpredict absolute risk in populations with a low observed CHD mortality (< 0.03/8 years) and to underpredict risk in populations with a high CHD mortality (≥ 0.03/8 years). This effect can be summarised by noting that the best fit regression (dotted) line through the data in fig 2 deviated from the line of identity with a slope of ∼0.4. The three most severe instances of overpredictions were for the Honolulu cohort (by 225%) and the rural and urban samples from the Puerto Rico cohort (148% and 76%, respectively). The three most severe cases of underpredictions were for the Tecumseh cohort (by 42%), the Renfrew and Paisley study (40%), and the Scottish collaborative study (37%). Among women, the Framingham model underpredicted eight year CHD mortality for five of eight cohorts: the Tecumseh community health study (by 38%), the Renfrew and Paisley study (38%), the NHANES II mortality follow up study (28%), the HDFP (25%), and the NHANES I epidemiologic follow up program (20%).
Figure 2.
Observed and predicted eight year mortality from coronary heart disease (CHD) by sex in diverse populations. For each cohort, observed mortality rate (x axis) is plotted against the predicted rate when the Framingham model was applied to that specific cohort (y axis). Data points above the 45° solid line represent overprediction and those below the 45° line represent underprediction. The two dotted lines are the fitted regression line through the data points for men (circles) and women (triangles), respectively.
The eight year CHD mortality in the Renfrew and Paisley study was twice as high as in the Framingham study. On the basis of this observation, we repeated our analyses using the Renfrew and Paisley model to predict CHD mortality in the other cohorts. The model from the Renfrew and Paisley study overpredicted CHD mortality for most of the cohorts (data not shown).
DISCUSSION
Using person-level data from diverse populations we examined variations of risk functions in three aspects: ordering risk, magnitude of relative risk, and estimation of absolute risk. Altman and Royston45 suggest that the validity of a model must be judged in the context in which it will be used. Historically the investigation of coronary risk was undertaken with the goal of identifying causal factors, which could then be avoided to prevent the disease. That task has been accomplished to a large degree and can be credited with a large proportion of the decline in CHD death rates over the past half century. To serve as the basis for a prevention policy the relative magnitude of harm associated with a lifestyle factor, such as smoking, need not be known with precision in all populations since uniform advice to abstain is effective. A need is now recognised, however, to characterise the risk of individual patients as a guide to treatment decisions. In this setting, the models are not being asked to identify risk factors but rather people at risk. In effect, the models are applied as diagnostic tests and are used to assign patients to treatment above a threshold. The requirements for a successful diagnostic procedure are different and quantitatively more stringent than those required to inform public health policy. In this analysis we have made an initial assessment of the robustness of these models for classifying patients based on risk. The quantitative results suggest mixed results, with acceptable precision for some purposes but not others.
Ordering risk
A commonly used method to compare the ability of different predictive functions to order CHD risk is to rank the participants by quantile (for example, quintile or decile) of estimated risk based on an internal or an external multivariate function. The distributions of the observed CHD cases and expected value are displayed by quantile categories. Similar distributions of CHD death cases by risk quintile derived from the internal predictive functions were reported for the four regions (north, west, east, and south) of Europe.5 External evaluations showed that different risk functions had similar ranking power for middle aged men from several US based epidemiological studies in the same era.1 The Framingham model was able to separate lower risk from higher risk participants in several US4,46 and European populations.2,9 In the seven countries study, the expected and observed CHD cases by deciles of risk were highly correlated (r = 0.93–0.98) using either internal predictive models or external predictive models.18 In this report we used ROC curve analysis, which takes into account sensitivity and specificity and avoids the need to separate the whole sample concurrently into many small groups (for example, quintile or decile). In the current analysis the AUCs of the studies varied from 0.60s to 0.80s. However, for a specific population, the AUCs derived internally and those derived from an external risk function were very similar. The performance of different external functions was also very similar when they were applied to the same population. These results imply that the ability to order depends primarily on the accuracy with which risk factors are characterised at the beginning of a study, not the relative size of the multivariate coefficient that is generated from that study.
Estimation of relative risk
Similar relative risks across studies require ordering not only a person's risk of disease similarly but also a similar estimate of the ratio of the probabilities that two different people will develop disease. Even though the percentage of the observed cases in the quintiles of estimated risk were comparable among the four regions in Europe,5 there were substantial variations in the multiple logistic coefficients of the major risk factors. Similar coefficients for the major CHD risk factors were reported between the Framingham Study and several US1,4,46 and non-US cohorts9; between northern Europe and southern Europe10; between Italian men from the RIFLE (risk factors and life expectancy) pooling project and American men among MRFIT primary screenees6; and between eight nations of the seven countries study.8 However, Chambless and colleagues,11 reviewing the results of 15 studies in the literature, found considerable variation in the magnitude of the odds ratios for fatal and non-fatal CHD events. It appears that significant differences were usually not found in the previous reports because the analysis consisted of pairwise comparisons involving two or a small number of populations. Using person-level data from 16 studies (27 analytical groups) and a global test for heterogeneity, we found significant variation in the coefficients across populations.
Estimation of absolute risk
The absolute risk or absolute rate defines the probability that a person will develop an event over a defined period of time. For different predictive functions derived from different populations to estimate absolute risk correctly, not only is it necessary for patients to be correctly ordered and for the magnitude of relative risk to be the same, but also the “background” or average risk across groups with a comparable set of risk characteristics must be the same. With few exceptions,3 studies that showed a good comparability of predictive functions did not examine comparability of absolute risk.2,4–9,46 Those studies that did examine this question usually found non-comparability across populations.10,12,18,20–24 The multiple logistic solutions for the American railroad men in the seven countries study overestimated CHD risk of the European men but underpredicted it for several large cohorts in the USA combined.18 Among cohorts from Finland, the Netherlands, and Italy, the prediction of events within each country using the risk function of the others produced errors ranging from –19% to 51%.20 The absolute risk was overestimated when applying the northern European model to southern European populations and vice versa.10 The Framingham predictive function for white middle aged men overestimated absolute CHD risks in Japanese American and Hispanic men and Native American women,19 in France,22 in Sweden,47 and in Italy.24 In the UK, it reliably predicted the absolute risk of heart disease in white men and women when the annual risk is above 1.5% but underestimated the risk when the absolute risk is lower.23
Several explanations may be offered for the systematic bias observed in absolute risk prediction across populations. The tendency for external models to overpredict in low risk populations and underpredict in high risk populations is in part a consequence of the mathematical procedure being used. The models are constrained to predict the number of cases that are observed and therefore pull the external population towards the level of absolute risk of the population from which they were generated. Hence, D'Agostino and colleagues19 suggested that the model be recalibrated so that the mean values for risk factors, as well as CHD incidence rates of non-Framingham cohorts, were substituted to the Framingham model to improve prediction. In addition, the model can adjust for only the five major risk factors. Factors not accounted for in the model can alter the background risk in a population. Since CHD risk tends to cluster in populations, groups that are at high risk based on hypertension, hypercholesterolaemia, smoking, and diabetes tend to be higher on those factors outside the model (for example, sedentarism), increasing risk beyond what a five factor model would predict. It is also obvious that the lifetime “dose” from risk exposure—particularly smoking—may vary systematically across groups. Prediction based on one initial baseline measurement instead of characteristics of the lifetime exposure limits the precision because of “regression dilution bias”. Other factors influencing the heterogeneity found in our results are differences in the age distributions between studies and the possibility that some subgroups (such as occupational samples) are not representative of the general population in specific countries.
Implications and conclusions
Predicting risk for CHD may be a valuable tool for clinicians, healthcare planners, and researchers, and a source of critical information for individual patients. Health professionals have been using equations, charts, or tables to estimate individual risk for many years.13–17,48–57 Most of these algorithms13–17,48–52,54,55 are based on equations derived from the Framingham heart study, most likely because of its familiarity and availability. The data presented here show that comparability and generalisation of the risk functions should be evaluated comprehensively based not just on one but on several criteria. The heterogeneity of the risk factor–CHD relation across population groups should not be overlooked. Expert panels must exercise caution in generalising from one population to another when making clinical guidelines. Using estimated risk that is too low or too high results in the proportion of treated patients being incorrect. For example, when a risk of CHD death of 10% over 10 years was used as the cut off for treatment decision, the proportion of men from the Honolulu study needing to be treated was 0.9% based on the cohort specific (internal) model, whereas it was 5.3% based on the Framingham model. Similarly, using a model specific to the Renfrew and Paisley study, we estimate that 29.4% of the male cohort would be treated while only 8.2% of the men would be treated if treatment were based on the Framingham model.
We showed that there was significant variation between the studies in all aspects of multivariate risk. These findings have implications for inferences that can be drawn based on meta-analysis. While it is valid to report an “average” effect, the average may not be interpreted as appropriate to all studies. We emphasise, however, that these results show “quantitative” rather than “qualitative” variation among the studies. We find that the characteristics examined here are significantly related to CHD mortality universally. A future direction of our research is to examine study characteristics that may explain the significant variability in the results from the different studies.
While we found clear evidence of random and systematic error in the comparisons of prediction models between populations, a judgement about the importance of these findings must include a consideration of the purposes to which they are to be used. It must also be acknowledged that, given the limited information that is used to characterise individual participants, the lack of standardisation, and the wide range of unmeasured cultural influences in these populations, the models are remarkably robust compared with similar epidemiological tools. What remains to be evaluated, therefore, is whether they are accurate enough for specific applications—for example, as aids to clinical and policy decision making. That judgement would require further analysis of the magnitude of misclassification at the individual level.
Acknowledgments
The views expressed in this paper are those of the authors and do not necessarily reflect the views of their agencies. Data from the following studies were obtained from the National Heart, Lung, and Blood Institute (USA): the Framingham heart study, the Framingham offspring study, the Honolulu heart program, the lipid research clinics mortality follow-up study, the hypertension detection and follow-up program, and the multiple risk factor intervention trial. The public use data of the first national health and nutrition examination survey epidemiologic follow-up study and the second national health and nutrition examination survey mortality follow-up study were obtained from the National Center for Health Statistics (USA). Data from all other studies were obtained from the investigators of the studies. This work was supported by a grant HL 61769 from the National Institutes of Health, National Heart, Lung, and Blood Institute, USA.
Abbreviations
AUC, area under the curve
CHD, coronary heart disease
CORDIS, cardiovascular occupational risk factor determination in Israel study
HDFP, hypertension detection and follow-up program
LRC, lipid research clinics
MRFIT, multiple risk factor intervention trial
NHANES, national health and nutrition examination survey
RIFLE, risk factors and life expectancy
ROC, receiver operating characteristic
Appendix
The Diverse Populations Collaborative Group Investigators
The Tecumseh community health study: Dr Victor Hawthorne; The Yugoslavia cardiovascular disease study: Drs Djordje Kozarevic and Nikola Vojvodic; The Scottish collaborative study and The Renfrew and Paisley survey: Drs Charles Gillis, Victor Hawthorne, and David Hole and Ms Carole Hart; The Glostrup population studies: Drs Torben Jorgensen and Troels Thomsen; The Norwegian counties study: Dr Randi Selmer and Aage Tverdal; The Iceland Reykjavik study: Dr Emil Sigurdsson; The Israeli ischemic heart disease study: Dr Uri Goldbourt and Ms Shlomit Yaari; The Israeli CORDIS study: Dr Paul Froom; The Guangzhou Chinese cohorts: Drs Shuguang Lin, Yihe Li, and Xiaoqing Liu; Evans County: Drs Dan Lackland and Curtis Hames; Charleston heart study: Drs Peter Gazes, Julian Keil, Dan Lackland, and Susan Sutherland. Consultants: Dr Zhaohai Li, George Washington University; Dr Richard Cooper, Loyola University Stritch School of Medicine; Dr Ronan Conroy, Royal College of Surgeons, Dublin, Ireland; Dr Christopher Sempos, School of Medicine and Biomedical Sciences, SUNY, Buffalo, New York. Coordinating Center: Medical University of South Carolina: Janet Bean, Guichan Cao, Christopher Khedouri, Drs Ramon Durazo-Arvizu, Daniel Lackland, Youlian Liao, Stuart Lipsitz, Daniel McGee, Sundar Natarajan, Debjyoti Sinha, and Barbara Tilley.
REFERENCES
- 1.Pooling Project Research Group. Relationship of blood pressure, serum cholesterol, smoking habit, relative weight and ECG abnormalities to incidence of major coronary events: Final report of the Pooling Project. J Chronic Dis 1978;31:201–306. [DOI] [PubMed] [Google Scholar]
- 2.Schulte H, Assmann G. CHD risk equations, obtained from the Framingham heart study, applied to the PROCAM study. Cardiovasc Risk Factors 1991;1:126–33. [Google Scholar]
- 3.Brand RJ, Rosenman RH, Sholtz RI, et al. Multivariate prediction of coronary heart disease in the Western Collaborative Group study compared to the findings of the Framingham Study. Circulation 1976;53:348–55. [DOI] [PubMed] [Google Scholar]
- 4.Leaverton PE, Sorlie PD, Kleinman JC, et al. Representativeness of the Framingham risk model for coronary heart disease mortality: a comparison with a national cohort study. J Chronic Dis 1987;40:775–84. [DOI] [PubMed] [Google Scholar]
- 5.ERICA Research Group. Prediction of coronary heart disease in Europe. The 2nd report of the WHO-ERICA project. Eur Heart J 1991;12:291–7. [PubMed] [Google Scholar]
- 6.Menotti A, Farchi G, Seccareccia F, RIFLE Research Group. The prediction of coronary heart disease mortality as a function of major risk factors in over 30,000 men in the Italian RIFLE pooling project. A comparison with the MRFIT primary screenees. J Cardiovasc Risk 1994;1:263–70. [DOI] [PubMed] [Google Scholar]
- 7.Menotti A, Seccareccia F, Blackburn H, et al. Coronary mortality and its prediction in samples of US and Italian railroad employees in 25 years within the seven countries study of cardiovascular diseases. Int J Epidemiol 1995;24:515–21. [DOI] [PubMed] [Google Scholar]
- 8.Menotti A, Keys A, Blackburn H, et al. Comparison of multivariate predictive power of major risk factors for coronary heart diseases in different countries: results from eight nations of the seven countries study, 25-year follow-up. J Cardiovasc Risk 1996;3:69–75. [PubMed] [Google Scholar]
- 9.Knuiman MW, Vu HTV. Prediction of coronary heart disease mortality in Busselton, Western Australia: an evaluation of the Framingham, national health epidemiologic follow up study, and WHO Erica risk scores. J Epidemiol Community Health 1997;51:515–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Menotti A, Lanti M, Puddu PE, et al. Coronary heart disease incidence in northern and southern European populations: a reanalysis of the seven countries study for a European coronary risk chart. Heart 2000;84:238–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chambless LE, Dobson AJ, Patterson CC, et al. On the use of a logistic risk score in predicting risk of coronary heart disease. Stat Med 1990;9:385–96. [DOI] [PubMed] [Google Scholar]
- 12.Liao Y, McGee DL, Cooper RS, et al. How generalizable are coronary risk prediction models? Comparison of Framingham and two national cohorts. Am Heart J 1999;137:837–45. [DOI] [PubMed] [Google Scholar]
- 13.Ramsay LE, Haq IU, Jakson PR, et al. Targeting lipid-lowering drug therapy for primary prevention of coronary disease: an updated Sheffield table. Lancet 1996;348:387–8. [DOI] [PubMed] [Google Scholar]
- 14.British Cardiac Society, British Hyperlipidaemia Association, British Hypertension Society, British Diabetic Association. Joint British recommendations on prevention of coronary heart disease in clinical practice. Heart 1998;80(suppl 2):S1–29. [PMC free article] [PubMed] [Google Scholar]
- 15.Wood D, De Backer G, Faergeman O, et al. Prevention of coronary heart disease in clinical practice: recommendations of the Second Joint Task Force of European and other Societies on Coronary Prevention. Eur Heart J 1998;19:1434–503. [DOI] [PubMed] [Google Scholar]
- 16.Ramsay LE, Williams B, Johnston GD, et al. British Hypertension Society guidelines for hypertension management: summary. BMJ 1999;319:630–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Jackson R. Updated New Zealand cardiovascular risk-benefit prediction guide. BMJ 2000;320:709–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Keys A, Aravanis C, Blackburn H, et al. Probability of middle-aged men developing coronary heart disease in five years. Circulation 1972;45:815–28. [DOI] [PubMed] [Google Scholar]
- 19.D'Agostino RB, Grundy S, Sullivan LM, et al. Validation of the Framingham coronary heart disease prediction scores. Results of a multiple ethnic groups investigation. JAMA 2001;286:180–7. [DOI] [PubMed] [Google Scholar]
- 20.Menotti A, Keys A, Kromhout D, et al. Twenty-five-year mortality from coronary heart disease and its prediction in five cohorts of middle-aged men in Finland, the Netherlands, and Italy. Preve Med 1990;19:270–8. [DOI] [PubMed] [Google Scholar]
- 21.Haq IU, Ramsay LE, Yeo WW, et al. Is the Framingham risk function valid for northern European populations? A comparison of methods for estimating absolute coronary risk in high risk men. Heart 1999;81:40–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Laurier D, Chau NP, Cazelles B, et al and the PCV-METRA Group. Estimation of CHD risk in a French working population using a modified Framingham model. J Clin Epidemiol 1994;47:1353–64. [DOI] [PubMed] [Google Scholar]
- 23.Ramachandran S, French JM, Vanderpump MPJ, et al. Using the Framingham model to predict heart disease in the United Kingdom: retrospective study. BMJ 2000;320:676–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Menotti A, Puddu PE, Lanti M. Comparison of the Framingham risk function-based coronary chart with risk function from an Italian population study. Eur Heart J 2000;21:365–70. [DOI] [PubMed] [Google Scholar]
- 25.National Center for Health Statistics. Plan and operation of the NHANES I epidemiologic follow-up study, 1987. Vital and health statistics, series 1, no 27, DHEW publication no (PHS) 92–1303. Washington: US Government Printing Office, 1992.
- 26.National Center for Health Statistics. Plan and operation of the second national health and nutrition examination survey. Vital and health statistics, series 1, no 15, DHEW publication no (PHS) 81–1317. Washington: US Government Printing Office, 1981.
- 27.Dawber TR, Meadors GF, Moore FE Jr. Epidemiological approaches to heart disease: the Framingham study. Am J Public Health 1951;41:279–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kannel WB, Feinleib M, McNamara PM, et al. An investigation of coronary heart disease in families: the Framingham offspring study. Am J Epidemiol 1979;110:281–90. [DOI] [PubMed] [Google Scholar]
- 29.Epstein FH, Ostrander LD Jr, Johnson BC, et al. Epidemiological studies of cardiovascular disease in a total community: Tecumseh, MI. Ann Intern Med 1965;62:1170–87. [DOI] [PubMed] [Google Scholar]
- 30.Kagan A, Harris BR, Winkelstein W Jr, et al. Epidemiologic studies of coronary heart disease and stroke in Japanese men living in Japan, Hawaii and California: demographic, physical, dietary and biochemical characteristics. J Chronic Dis 1974;27:345–64. [DOI] [PubMed] [Google Scholar]
- 31.Gordon DJ, Ekelund LG, Karon JM, et al. Predictive value of the exercise tolerance test for mortality in North American men: the lipid research clinics mortality follow-up study. Circulation 1986;74:252–61. [DOI] [PubMed] [Google Scholar]
- 32.Kozarevic D, Pirc B, Dawber TR, et al. Prevalence and incidence of coronary disease in a population study: the Yugoslavia cardiovascular disease study. J Chronic Dis 1971;24:495–505. [DOI] [PubMed] [Google Scholar]
- 33.Blane D, Hart CL, Davey Smith G, et al. Association of cardiovascular disease risk factors with socioeconomic position during childhood and during adulthood. BMJ 1996;313:1434–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Isles CG, Hole DJ, Gillis CR, et al. Plasma cholesterol, coronary heart disease, and cancer in the Renfrew and Paisley survey. BMJ 1989;298:920–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Schroll M, Jorgensen T, Ingerslev J. The Glostrup population studies, 1964–1992. Dan Med Bull 1992;39:204–7. [PubMed] [Google Scholar]
- 36.Bjartveit K, Foss OP, Gjervig T, et al. The cardiovascular disease study in Norwegian counties: background and organization. Acta Med Scand Suppl 1979;634:1–70. [PubMed] [Google Scholar]
- 37.Vilbergsson S, Sigurdsson G, Sigvaldason H, et al. Prevalence and incidence of NIDDM in Iceland: evidence for stable incidence among males and females 1967–1991: the Reykjavik study. Diabet Med 1997;14:491–8. [DOI] [PubMed] [Google Scholar]
- 38.Goldbourt U, Yaari S, Medalie JH. Factors predictive of long-term coronary heart disease mortality among 10,059 male Israeli civil servants and municipal employees. Cardiology 1993;82:100–21. [DOI] [PubMed] [Google Scholar]
- 39.Garcia-Palmieri MR, Costas R Jr, Cruz-Vidal M, et al. Risk factors and prevalence of coronary heart disease in Puerto Rico. Circulation 1970;42:541–9. [DOI] [PubMed] [Google Scholar]
- 40.Daugherty SA. Mortality findings beyond five years in the hypertension detection and follow-up program (HDFP). J Hypertens 1988;6(suppl):S597–601. [DOI] [PubMed] [Google Scholar]
- 41.The Multiple Risk Factor Intervention Trial Research Group. Mortality rates after 10.5 years for participants in the multiple risk factor intervention trial. JAMA 1990;263:1795–801. [DOI] [PubMed] [Google Scholar]
- 42.Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982;143:29–36. [DOI] [PubMed] [Google Scholar]
- 43.Katz D, Foxman B. How well do prediction equations predict? Using receiver operating characteristic curves and accuracy curves to compare validity and generalizability. Epidemiology 1993;4:319–26. [DOI] [PubMed] [Google Scholar]
- 44.DerSimonian R, Laird N. Meta-analysis in clinical trials. Control Clin Trials 1986;7:177–88. [DOI] [PubMed] [Google Scholar]
- 45.Altman DG, Royston P. What do we mean by validating a prognostic model. Stat Med 2000;19:453–73. [DOI] [PubMed] [Google Scholar]
- 46.McGee D, Gordon T. The results of the Framingham study applied to four other U.S.- based epidemiologic studies of cardiovascular disease. In: Kannel WB, Gordon T (eds). The Framingham study: an epidemiologic investigation of cardiovascular disease. DHEW publication no (NIH) 76–1083, section 31. Washington: US Government Printing Office, 1976.
- 47.The Swedish Council on Technology Assessment in Health Care. Moderately elevated blood pressure. J Intern Med 1995;737(suppl):1–225. [PubMed] [Google Scholar]
- 48.Anon. Coronary risk handbook. Estimating risk of coronary heart disease in daily practice. New York: American Heart Association, 1973.
- 49.Anderson KM, Wilson PWF, Odell PM, et al. An updated coronary risk profile: a statement for health professionals. Circulation 1991;83:356–62. [DOI] [PubMed] [Google Scholar]
- 50.Wilson PWF, D'Agostino RB, Levy D, et al. Prediction of coronary heart disease using risk factor categories. Circulation 1998;97:1837–47. [DOI] [PubMed] [Google Scholar]
- 51.D'Agostino RB, Russell MW, Huse DM, et al. Primary and subsequent coronary risk appraisal: new results from the Framingham study. Am Heart J 2000;139:272–81. [DOI] [PubMed] [Google Scholar]
- 52.Shaper AG, Pocock SJ, Phillips AN, et al. A scoring system to identify men at high risk of a heart attack. Health Trends 1987;19:37–9. [PubMed] [Google Scholar]
- 53.Tunstall-Pedoe H. The Dundee coronary risk disk for management of change in risk factors. BMJ 1991;303:744–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Haq IU, Jackson PR, Yeo WW, et al. Sheffield risk and treatment table for cholesterol lowering for primary prevention of coronary heart disease. Lancet 1995;346:1467–71. [DOI] [PubMed] [Google Scholar]
- 55.National Heart Foundation. Clinical guidelines for the assessment and management of dyslipidaemia. NZ Med J 1996;109:224–32. [PubMed] [Google Scholar]
- 56.Knuiman MW, Vu HTV, Bartholomew HC. Multivariate risk estimation for coronary heart disease: the Busselton health study. Aust NZ J Public Health 1998;22:747–53. [DOI] [PubMed] [Google Scholar]
- 57.Hingorani AD, Vallance P. A simple computer program for guiding management of cardiovascular risk factors and prescribing. BMJ 1999;318:101–5. [DOI] [PMC free article] [PubMed] [Google Scholar]