ECGSIM: an interactive tool for studying the genesis of QRST waveforms

Abstract

Background: Discussion about the selection of diagnostic features of the ECG and their possible interpretation would benefit from a model of the genesis of these signals that has a sound basis in electrophysiology as well as in physics. Recent advances in computer technology have made it possible to build a simulation package whereby the genesis of ECG signals can be studied interactively.

Design: A numerical method was developed for computing ECG signals on the thorax, as well as electrograms on both endocardium and epicardium. The source representation of the myocardial electric activity is the equivalent double layer. The transfer factors between the electric sources and the resulting potentials on the heart surface as well as on the body surface were computed using a realistic thorax model.

Results and conclusion: The resulting transfer factors were implemented in a simulation program. The program allows the user to make interactive changes in the timing of depolarisation and repolarisation on the ventricular surface, as well as changing the local source strength, and to inspect or document the effect of such changes instantaneously on electrograms and body surface potentials, visualised by waveforms as well as by potential maps and movies. The entire simulation package can be installed free of charge from www.ecgsim.org.

Most diagnostic methods used in clinical electrocardiography are statistically based forms of pattern recognition. Over the years, the selection of the features used in this approach has been guided by the knowledge that has been gleaned from invasive electrophysiology.

The development of diagnostic ECG criteria has been accompanied by the development of biophysical models aimed at linking the electrophysiology of cardiac function to the waveforms of the ECG signals observed on the body surface. The need for the use of models stems from the fundamental impossibility of deriving a unique specification of internal bioelectric sources on the basis of observations of the potentials on the body surface: a multitude of different sources gives rise to identical data outside the actual source region. In fact two models need to be involved: a model of the bioelectric generator—that is, a source model—and a model for describing the effects on the observed signals of the body tissues that surround the active electric sources—a volume conductor model. The computation of the resulting potentials based on these two models is referred to as the forward problem.

The interactive simulation program announced in this communication, ECGSIM, is based on a particular variant of the forward problem. It allows the user to make interactive changes to the timing of depolarisation and repolarisation on the ventricular surface, as well as changing the local source strength, and to study the effect of such changes on electrograms on the heart surface and on body surface potentials.

The theory behind this forward computation is outlined here briefly, focusing on the aspects of the source parameters that can be changed interactively. The theory has been described in full¹ along with some of its implications.² A discussion on various alternative approaches to the forward problem can be found in van Oosterom, 2002.³

THEORY

The EDL source model

The source model used in the simulation is the equivalent double layer (EDL). This is a particular variant of the so called equivalent surface source models. In such models all myocardial electric activity is represented by equivalent sources on a surface encompassing the myocardium, the epicardial potential source model⁴,⁵ being another one of these.

The EDL model expresses the entire electrical activity within the ventricles by means of a double layer source situated on the closed surface S_V bounding the ventricular myocardium—that is, epicardium, endocardium, and their connection at the base. For any position on S_V the time course of the local source strength is taken to be proportional to the transmembrane potential, φ_m(t), of the cells near S_V.⁶,⁷ The value of the EDL for simulating body surface potentials during both the depolarisation and the repolarisation phase of the ventricular myocardium was shown in previous papers.¹,² For the depolarisation phase the EDL has a direct link with the classic uniform double layer (UDL), located at the depolarisation wave front. This follows from the application of the solid angle theory.⁸,⁹ The application of the EDL to the genesis of the T wave is a more recent development.¹,²,⁶,⁷

The forward transfer

The transfer between the elements of the EDL and the potentials on the thorax is dominated by the position and orientation of the heart inside the thorax, the position of the electrodes on the thorax, and the overall geometry of the thorax. Other major factors are those regions having an electric conductivity of the tissue that is substantially different from that of the neighbouring tissues. Included in this work is the effect of the relatively low conductivity of the lungs and the relatively high conductivity of blood in the ventricular cavities.^10–12

Matrix formulation of the forward problem

The solution of the forward problem by using a computer requires the representation in a numerical form of the variables involved. In this work, the discretisation of the EDL is carried out by specifying the time course of the electric source strengths of N elements of the EDL at T subsequent time instants. This leads to a matrix representation of the source, the S matrix (dimension N*T), having as its elements: sn,t, n = 1...N; t = 1...T.

In the same manner, the volume conduction effects are represented by a transfer matrix A (dimension L*N), having elements a_l,n representing the potential in lead l (l = 1...L) generated by a source of unit strength at node n. By using both matrix formulations the forward computation can be expressed simply by the matrix multiplication Φ = A S, with Φ a matrix (dimension L*T) representing the potentials at L thorax locations (lead positions) at the T discrete time instants.¹ The same formalism, involving a dedicated transfer matrix, can be used to compute the waveforms of the electrograms at the nodes of S_V based on the identical source matrix S.

METHODS

The source model

The source model is the EDL as discussed above. The surface S_V bounding ventricular mass was derived from magnetic resonance imaging (MRI) data. The surface was discretised by small triangles, the N nodes, of which (N = 257) served as the locations of the equivalent double layer elements. For any position on S_V the time course of the local double layer strength is taken to be proportional to the transmembrane potential, φ_m(t), of the cells near the boundary.

The time course of the source strength of any node n is assigned a stylised version of the shape of the transmembrane potential of ventricular muscle cells, specified at 1 ms intervals. The general shape of this curve was taken to be identical for all nodes. This shape was derived from a weighted mean of the measured ECG during the T wave.¹,² The timing of local depolarisation (taken to be the moment of maximum slope of the upstroke) at node n of S_V is denoted as δ_n. Similarly, the time instant of the maximum negative slope is taken as a marker for the timing of local repolarisation. For node n it is denoted as ρ_n. The interval α_n = ρ_n−δ_n is taken as a measure of the local action potential duration.

The magnitudes of the upstroke of the local transmembrane potential for node n, denoted by m_n, are used to specify local source strength. These magnitudes scale the corresponding rows of the source matrix S. The default settings of these values are at a uniform maximum. By reducing the magnitude of the source strength at node n the effect of, for example, local ischaemia on body surface potentials may be studied.

The transfer matrix

The transfer between the elements of the EDL and the potentials on the thorax was computed by using the geometry of the torso and that of the relevant conductivity interfaces, measured by means of MRI. The model takes into account the relatively low conductivity of the lungs and the relatively high conductivity of blood in the ventricular cavities.

The elements of the computed transfer matrix A express the source strengths of all N (N = 257) nodes on the heart as potentials at L (L = 198) lead positions on the thorax surface S_T. A subset of these elements is involved in the simulation of the standard 12 lead ECG. Single rows and single columns of this matrix can be viewed by means of ECGSIM. Row l represents the contributions by the individual nodes on S_V to the potential of lead l. Accordingly, these values may be shown as a map on S_V. Such a row is a generalisation of the concept of a lead vector in vectorcardiography. Similarly, any column n of matrix A represents the potential distribution on the thorax as generated by node n when active in isolation, and may be viewed as a map on S_T.

A separate dedicated transfer matrix was computed for linking the source strength to the potential distribution on S_V.

Using ECGSIM

Defaults

ECGSIM has default settings for the parameters δ_n, and ρ_n. These were found by means of an inverse procedure applied to measured body surface potentials.¹,¹² The default setting for the source magnitude m_n is 100%, corresponding to a normal upstroke of the action potential. The distribution of each of the source parameters may be viewed on S_V.

The simulated potentials on both the heart surface and the body surface may be viewed as waveforms (electrograms or ECGs), potential maps, or movies. A set of measured body surface potentials serves as a reference.

Operation

Starting from their default setting any of the source parameters may be varied at any of the nodes; the effect of this on heart and body surface potentials is visible instantaneously.

While changing the value of a node parameter value, the values at the surrounding nodes may be set to change by a factor that decreases with distance. The distance involved (corresponding to, for example, the extent of an ischaemic region) may be set interactively, and may be chosen to be effective either over the surface that carries the node operated on, or throughout the myocardium. In this way epicardial, endocardial, or transmural changes may be induced.

Another option for manipulating the parameters is to modify their overall statistics: mean and standard deviation. Examples of the usefulness of this option are the study of the expression of the dispersion of the source parameter values—for example, action potential duration—on body surface potentials (QT dispersion) or the expected changes in T wave morphology associated with the long QT syndrome.

Parameter settings adapted during a session, as well as the resulting potentials, may be stored for subsequent processing outside ECGSIM. These stored sets may also be reloaded for subsequent use in ECGSIM.

The operation of the package is mainly mouse controlled and fully supported by the type of features that are commonly used in PC software, such as drop-down menus, dialogue boxes, tool bars, and so on. Elaborate on-line help functions are included. Downloads of the relevant cited publications that may not be easily available are indicated in the reference list shown in ECGSIM.

RESULTS

The entire package is available from: www.ecgsim.org

Using the links indicated at the site will download the package on your PC. An icon will appear on your desktop, which you can use to start the simulation. The entire package takes up about 3.5 Mb of disk space. Separate versions are provided for the use on either a Windows (98 or XP) or a Unix operating system. A version to be used on a Mac operating system is nearing completion. Its release will be indicated on the site. The package will be upgraded in response to requests from its users. Major developments will be announced to users that indicate their interest to be informed. The most recent version that is under “construction” can be downloaded as a so called β version.

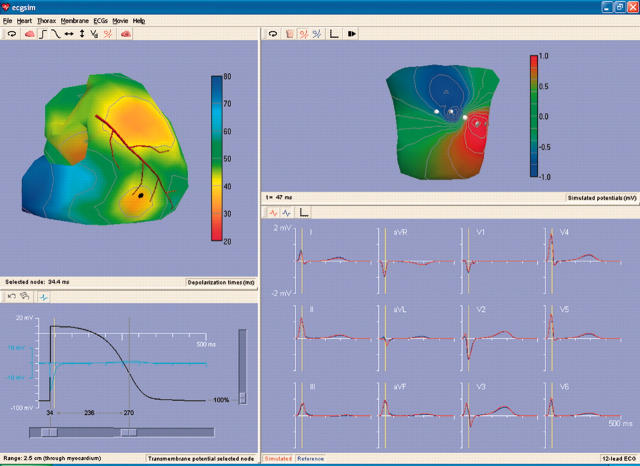
An example of the type of display that may be realised in ECGSIM is shown in fig 1. Here the default parameter settings are used. The upper left pane of the window displays the timing of depolarisation on S_V. The heart is rotated slightly with respect to normal in order to emphasise that both epicardial and endocardial source elements are involved in the simulation. When using ECGSIM the orientation of S_V may be varied at will so that all individual nodes may be selected. On this (upper left) pane an interactively selected node on the epicardium of the right ventricle is marked by a heavy dot. The time course of the local source strength at this node is shown in the lower left pane. The light blue curve is the electrogram at the selected (epicardial) node. The pane on the lower right depicts (in blue) the QRST complexes of the standard 12 leads as measured on the (healthy) subject serving as a reference in this work. Superimposed in red are the corresponding simulated potentials. By comparing the simulations to the measured data it can be seen that the quality of the simulation is high. The vertical yellow bar identifies a time instant within the QRS complex (nadir in lead V2) for which the corresponding body surface map is depicted in the upper left pane.

Figure 1.

Display of the ECGSIM window for a particular set of options, using the default settings of the parameters δ_n, ρ_n, and m_n. The upper left pane of the window displays the ventricular surface S_V. The colour coded function shown on S_V is the timing of depolarisation (δ_n). A stylised version of the LAD serves as a landmark. An interactively selected node on the epicardium of the right ventricle is marked by a heavy dot. The heart is rotated slightly with respect to normal. The signals shown in the lower left pane are: (in black) the source strength at the selected node and (in light blue) the local (epicardial) electrogram. This pane also carries the sliders that can be used to modify the setting of the local values of the parameters δ_n, ρ_n, and m_n. The lower right pane depicts (in blue) the QRST complexes of the standard 12 leads and (in red) the corresponding simulated signals. The vertical yellow bar marks the timing of the nadir in lead V2. In the upper right pane the body surface map is shown pertaining to the time instant indicated by the vertical yellow line in the lower panes. Note the two different colour codes used in the two upper panes.

A second example is shown in fig 2. The function shown on S_V (left upper pane) is now the magnitude of the local source strength. Starting from its default uniform distribution, a small region of S_V beneath the position of electrode V3 has been assigned a reduced source strength, modelling the situation during an acute ischaemic episode. The resulting effects waveforms of the standard leads are shown (in red) in the lower right pane. Note that the effect of the reduced local source strength appears as an ST elevation in lead V3, as expected. For more distant leads the effects are less prominent, with clear indications of a corresponding reciprocal ST depression in leads aVF, II, and III. Although the effect of the assigned change is most clearly visible during the early part of the ST segment, differences in the QRS waveforms in fact appear right from the time when the sources in the affected region start contributing to the QRS complex. In a clinical situation such reference signals are generally not available and such effects on the QRS complexes may remain undetected. The upper right pane displays the body surface potential map early in the ST segment, the moment indicated by the vertical yellow line.

Figure 2.

The ECGSIM window in an application to simulate the effect of acute local ischaemia. The function shown on S_V (left upper pane) is now the magnitude of the local source strength. An option allowing the display of the precordial electrode is activated. Shown are electrodes V1 to V4, the remaining two falling outside the pane. A node beneath the position of electrode V3 was assigned a source strength of 75% of its normal value, simulating the local source strength during en episode of acute local ischaemia. The effects of this on the waveforms of the standard leads are shown (in red) in the lower right pane. Note the prominent effect of an ST elevation in lead V3, the smaller effects on the more distant leads, and the reciprocal ST depression in leads aVF, II, and III. Also note the differences within the QRS interval (see text for explanation).The upper right pane displays the body surface potential map early in the ST segment, the moment indicated by the vertical yellow line in the lower two panes. Note that the program allows the partitioning of the windows (the size of its panes) to be varied at will.

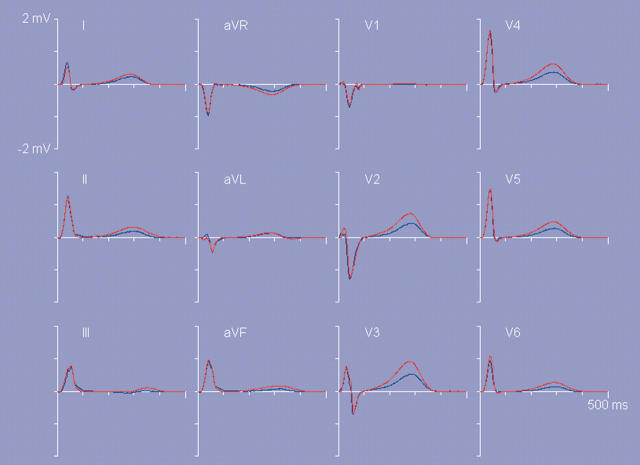
In a final example (fig 3) the effect of the magnitude of the dispersion of the timing of repolarisation ρ_n on the T wave amplitudes is demonstrated. In this figure the results on the T wave signals are shown when all ρ_n values that produced the T waves shown in fig 1 were replaced by values 1.5(ρ_n−ρ̄)+ρ̄, with ρ̄ denoting the mean of the original ρ_n values. In this manner the dispersion of repolarisation times is increased by a factor of 1.5, while keeping their pattern, as well as their mean value, unaltered. The most prominent aspect of the increased dispersion in the timing of repolarisation is an associated increase in the T wave amplitudes.¹

Figure 3.

Lower right pane of ECGSIM: the standard 12 lead ECG waveforms. Blue curves: measured reference data. In red: simulated signals resulting from scaling the dispersion of repolarisation times used in figure 1 by a factor of 1.5, while keeping the mean repolarisation time as well as the pattern of repolarisation constant.

DISCUSSION

The provided default parameter settings show that a realistic simulation of QRST waveforms can be reached by using the EDL source model. For the QRS complex this conclusion was reached earlier.¹² The extension to the T wave is a recent development.¹ That same paper also discusses the assumptions implied in the model and the ensuing limitations.

We have used the model to simulate several ECG abnormalities. The observed effects of changing the dispersion of repolarisation times on general T wave properties (fig 3) are in agreement with those found in the independent study by di Bernardo and Murray.¹³ Such effects can easily be studied by using ECGSIM.

We feel confident that this package will be of great practical use to others studying or teaching the basic properties of the genesis of the QRST waveforms.