Frequency of testing for detecting visual field progression

Abstract

Aims: To investigate the effect of frequency of testing on the determination of visual field progression using pointwise linear regression (PLR).

Methods: A “virtual eye” was developed to simulate series of sensitivities over time at a given point in the eye. The user can input the actual behaviour of the point (for example, stable or deteriorating steadily), and then a configurable amount of noise is added to produce a realistic series over time. The advantage of this over using patient data is that the actual status of the eye is known. Series were generated using different frequencies of testing, and the diagnosis that would have been made from each series was compared with the true status of the eye. A point was diagnosed as progressing if the regression line for the series showed a deterioration of at least 1 dB per year, significant at the 1% level. From these results, graphs were produced showing the number of points correctly or incorrectly diagnosed as progressing.

Results: With the virtual eye deteriorating at a rate of 2 dB/year, it was found that the point was determined to be progressing quicker when more tests were carried out each year. With a stable virtual eye, it was found that increasing the frequency of testing increased the number of series that were falsely labelled as progressing during the first 3 years of testing.

Conclusions: As the frequency of testing increases, the sensitivity of PLR increases. However, the specificity decreases; possibly meaning more unnecessary changes in treatment. Three tests per year provide a good compromise between sensitivity and specificity.

Visual field results from computerised perimetry are the standard measurement of a patient's visual function and are likely to remain so in future years, especially with the promise of better measurement strategies.^1,2 Perimetry shows the actual effect on the patient's vision, which will vary even among patients with, for example, the same degree of inflated intraocular pressure or damage to the optic nerve. Evaluation of change in a series of visual fields remains an important aspect of monitoring patients for disease progression. New methods, using linear regression analysis of individual sensitivity values against time of follow up have been developed.^3–6 These techniques, known as pointwise linear regression (PLR), have been shown by several studies to compare favourably with other methods for detecting visual field progression in patients with glaucoma.^7–12

The main purpose of this study was to investigate the effect of frequency of testing on the performance of PLR in detecting gradual sensitivity deterioration. This is particularly important to the clinical management of patients with glaucoma. This type of investigation, like others examining methods for quantifying visual field changes, is hampered by the lack of an external “gold standard” for progression. Computer simulations have been extensively used as an alternative to analysing actual patient data to develop improved perimetric testing strategies^13–16: they offer a more reproducible and controllable means of examining the behaviour of visual field data. This suggests that they may also be useful in examining the problems of detecting progression in series of visual field data. Hence, this study utilises a computer generated “virtual eye” to produce series of sensitivity values typical of longitudinal visual field data.

METHODS

Virtual eye

The “Virtual eye” simulation program was purpose written using object oriented statistical software (S-PLUS 2000 for Windows, StatSci Europe, MathSoft Inc, Oxford). It generates series of sensitivity values typical of those found at individual test locations within the visual field. The virtual eye allows control over components (parameters) that affect the behaviour of a series of sensitivity values against time:

1. Length of series (years)

2. Frequency of observations (fields per year)

3. Initial level of sensitivity (dB)

4. Number of simulations (series)

5. Size of loss (dB per year)

6. Type of loss (gradually or suddenly deteriorating)

7. Criteria for progression used by PLR

8. Noise (variability between and within sensitivity values).

The benefit of having a virtual eye is that the user can specify the actual, noise free behaviour of the eye, and then add noise in later. Thus, knowing that the eye is in fact (for example) stable, it can be seen how many times a correct decision is made when the noisy series are tested. The virtual eye is simplified by considering the behaviour of the sensitivity at one location in the visual field.

Because we know the exact actual sensitivity at each point in the eye (as these are specified), the virtual eye only needs to consider the sensitivity at one point. This assumes that given the actual sensitivity at each point, the noise is independent between points. Note that we are not assuming that actual (noise free) progression is independent between points; but because we have specified this exactly, the noise free behaviour of neighbouring points is irrelevant.

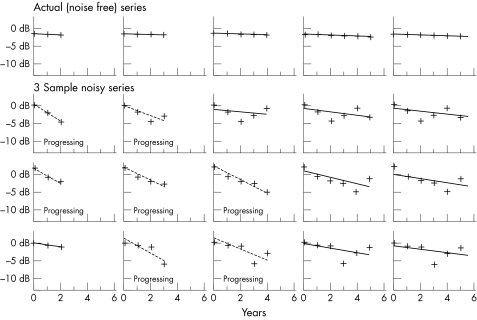
The idea is best explained by example. The results from a simulation can be displayed as individual plots of sensitivity values against time of follow up. In Figure 1, the top row shows the actual sensitivity values as specified for a stable eye. This is defined to be one which shows only the expected age related deterioration of 0.1 dB/year.¹⁷ The lines are those produced by linear regression based on the first three points of the series, then the first four points, and so on; so the graphs show how the results would change as more tests were carried out in subsequent years and added on to the end of the series.

Figure 1.

Illustrative series for a stable virtual eye. In the top row, the sensitivity at a point is specified as deteriorating at 0.1 dB/year over 6 years; as the series gets longer (moving from left to right along the series) with the addition of more points, PLR is used to determine whether the point would be flagged as progressing based on the readings so far. The second, third, and fourth rows represent three possible series of artificial sensitivities, after noise has been added in.

Each point on the graph can be thought of as a threshold deviation (dB) from baseline labelled as 0 dB on the vertical axes. No assumption is made about the actual starting sensitivity. For this illustration it is assumed that the visual field tests are taken at yearly intervals. The criteria for progression are specified as regression slope worse than −1 dB/year and also statistically significant at the 1% level.

Subsequent rows illustrate three different examples of possible artificial series; noise has been added to the actual noise free values in the top row. It is now seen that owing to the effect of the noise, it is possible for the series to be labelled as progressing according to the specified criteria even though we know that the point is actually stable. As time goes on, the diagnosis will get more accurate, with fewer stable series being falsely labelled as progressing.

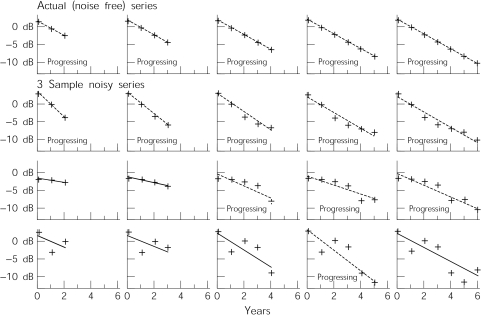
In Figure 2, the actual sensitivity of the point (as seen in the top row) is deteriorating at a rate of 2 dB/year. This represents approximately 20 times the normal rate of decay,¹⁷ and double the criteria for progression of 1 dB/year we are using for PLR (see above). When noise is added, the point is regularly labelled as being stable, even though we know this not to be the case. This is either because the slope is not sufficiently steep, or because the series is too noisy for the slope to be statistically significant.

Figure 2.

Illustrative series for a progressing virtual eye. In the top row, the sensitivity at a point is specified as deteriorating at 2 dB/year over 6 years; as the series gets longer with the addition of more points, PLR is used to determine whether the point would be flagged as progressing based on the readings so far. This is then done for three sample series of artificial sensitivities, after noise has been added in.

In both stable and progressing cases, as the series gets longer, a higher proportion of series will be correctly flagged. This study seeks to discover whether increasing the frequency of testing will also improve the success rate.

Simulation experiment

Series of actual sensitivity values over a period of 6 years were generated. These series were either designated as “stable,” having an age related deterioration of 0.1 dB/year; or “progressing,” deteriorating at 2 dB/year. Next, at each test date (determined by the number of tests being carried out each year, which were assumed to be equally spaced through the year), a noisy sensitivity reading was generated by randomly sampling from a normal distribution, with a mean value equal to the calculated actual sensitivity at that time, and a standard deviation of 2 dB. This noise is assumed to be the combination of both short term (within test variability) and long term (between test variability) fluctuation. Moreover, we utilise the simplifying assumption that the amount of noise present in each reading is constant throughout the series. In fact, some patients, and some points within each patient's visual field, will be noisier than others. Also the amount of noise actually increases as the eye deteriorates.^18,19 For example, a point measured at 20 dB will have a higher level of noise than one measured at 30 dB. However, to obtain a fair comparison between different methods, it is essential that precisely the same conditions occur in each case. After all, this possibility is the basic advantage of using a virtual eye in the first place. Therefore in this experiment the same level of noise is used throughout. Henson et al¹⁸ demonstrate that noise of approximately 2 dB would be expected if the point was initially at its age related normal level (that is, about 30 dB sensitivity). Heijl et al²⁰ show that for central points whose initial sensitivity equals the age corrected normal sensitivity, 95% of the points will have an intertest variation (the difference between consecutive tests) of between roughly −5 dB and +3 dB, including any actual deterioration over that time. For normally distributed noise, 95% of the distribution falls within 1.96 standard deviations of the mean; and so the standard deviation is approximately 2 dB. However, for lower sensitivities, and (as a result) for points in the periphery, which generally have a lower sensitivity, the amount of noise would be much higher.

The criteria for progression were defined as a slope of at least −1 dB/year, statistically significant at the 1% level. These criteria have been used in several published studies using PLR.^8,9,21–23 The minimum slope guards against significant age related decline, and has also been shown to be related to other methods of pointwise change detection.^3,4 PLR was then carried out on the first three readings to see if they would be flagged as progressing or not. This was then repeated for the first four readings, then five readings and so on. This way it can be seen how the diagnosis (progressing or stable) would change over time as more readings were added to the series. Then, the percentage of correctly diagnosed series (out of 1000) at each point in time was calculated. This experiment was repeated for different numbers r of readings per year.

RESULTS

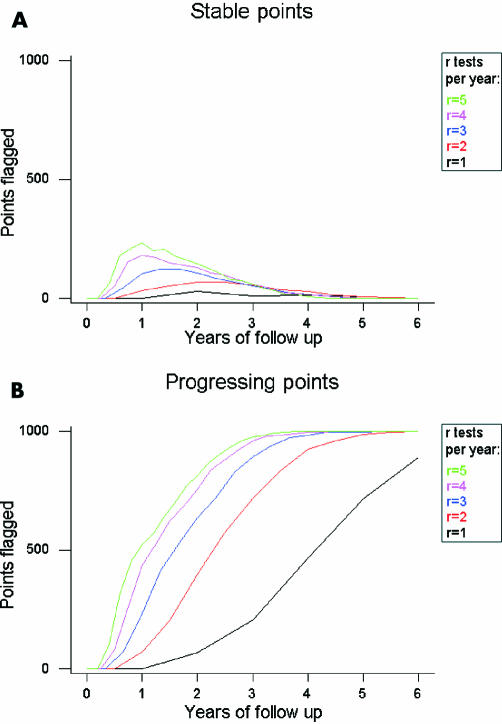
We compare the number of series of points which would be flagged as progressing when simulated as before, for different numbers r of readings per year. Figure 3A gives stable points, and Figure 3B is points with an actual deterioration of 2 dB/year. They show that, for example, if there is a small local defect of say five points that are actually progressing, then after 3 years at two tests per year the method will flag on average around four of these truly progressing points, and also two or three points elsewhere in the eye that are actually stable.

Figure 3.

Performance of PLR, for different numbers of tests per year. (A) Each line shows how many actually stable points were flagged as progressing out of 1000 simulated series, when r sensitivity readings were simulated per year. (B) Shows the same for points that were actually deteriorating at 2 dB/year.

Clearly, as the number r of tests per year increases, so does the proportion of points labelled as progressing. This confirms the intuitive notion that a progressing eye will be detected quicker with more frequent testing. However, there are also an increased number of early false positives—that is, stable points being labelled as progressing. More frequent testing will result in a higher number of incorrect decisions being made for non-deteriorating patients when the follow up is relatively short. Over the first 2 years of testing, doubling the frequency of testing also doubles the proportion of false positive results—that is, stable points being incorrectly flagged as progressing by PLR. More than 3 years have passed before the lines converge, and this higher error rate disappears, but by this time the sensitivities are also converging, and so the benefits of carrying out more tests per year have vanished. Under the conditions of this experiment, it is never worthwhile carrying out more than three tests per year; the extra expense and inconvenience to the patient of doing so brings no reward.

DISCUSSION

Computer simulations have been widely used to investigate perimetric testing strategies by modelling the patient response during a perimetric examination.^13–16 The virtual eye simulation described in this study may be useful for exploring the behaviour of visual field progression. Previously we have used a computer simulation similar to the one described here to show that PLR is equally sensitive to detecting both gradual (linear) and sudden (episodic) sensitivity loss.²⁴ The detection rates, however, were moderate in most cases because of the variability between observations. More recently Spry et al²⁵ have used a computer simulation approach to investigate longitudinal visual field data. This simulation differed from the virtual eye presented here, in that sequences of complete visual fields were generated by interpolating between two “real” measured fields. Simulations allow different test parameters to be analysed using large materials in a short time, and the effect of single variables or parameters can be isolated. The latter is not possible using patient data alone and our plan is to develop this methodology further.

The experiment described in this study has shown that although increasing the number of tests per year speeds up the detection of progression (Fig 3B), it does so at the expense of, initially at least, falsely labelling far more stable points as progressing (Fig 3A); the extra tests are actually making the performance worse. This is because the noise becomes far more significant than the amount of change that may or may not have occurred over the shorter period of time. If the PLR slope based on one test per year for 5 years is k, then the same sensitivities compressed into just 1 year (that is, five tests per year) would give a PLR slope of 5k, even though the eye may not actually be deteriorating any faster.

The first priority is, in many cases, specificity; because this reduces the chances of incorrect changes in clinical management. If, for example, there is a 3% probability that any given stable point will be incorrectly flagged as progressing (which is the level of false positives seen after as much as 3 or 4 years of follow up in Fig 3), then the chance of at least one point out of the 52 test locations in a 24-2 Humphrey visual field being incorrectly flagged is:

Prob(≥1 incorrect point) = 1 − prob (a given point is incorrect)⁵²

= 1 – 0.97⁵²

= 79.5%

This alarmingly poor performance is improved dramatically by a seemingly small improvement in the specificity at one point (see Table 1).

Table 1.

The dramatic effect of a relatively small increase in specificity

Prob (given point is FP)	Prob (≥1point is FP)
3%	79.5%
2%	65.0%
1%	40.7%

Hence we have shown that having an increased number of tests per year reduces specificity when the follow up is relatively short. Although the lines in Figure 3 do converge as the series lengthens, a clinical management decision based on a significant slope would be unwise with frequent testing in say the first 2 or 3 years. One strategy is to use one or more confirmation fields which may or may not be part of the actual follow up. This has been done in recent studies using PLR^20,23 and applied to other methods for detecting progression.²⁶ Of course, this means even more visual field testing to detect progression; and even though this is a sensible approach, ad hoc confirmation fields do not have any exact specificity associated with them. We believe the virtual eye described in this paper could provide more accurate estimates of this specificity, or indeed the diagnostic precision of any visual field progression criteria being used as an outcome measure in investigations and clinical trials.

The second clinical priority is to improve the sensitivity of the test; in other words detecting true visual field progression. From Figure 3B it is clear that the detection of progressing points with just one test carried out per year is extremely poor. Even with two tests per year, points deteriorating at 2 dB/year would only be picked up on in 75% of cases after 3 years; by this time a loss of 6 dB has occurred, which is severe enough that any decent method should have identified it. Clinically, this means that a substantial fraction of visual field locations have to be truly deteriorating before progression can be reliably detected. Therefore, approximately three tests per year, resources permitting, seem to achieve a better success rate at determining which points are progressing and which are not. This supports and extends findings on patient data in glaucoma.²¹

This model provides a much simplified version of reality. The assumption of noise being normally distributed, though commonly used, is unproved and the amount of noise present in readings would typically be larger than the estimates used here^{19,20,27–29} and increase as the measured sensitivity at a location decreases.^18,19 As the amount of noise increases, the performance of PLR becomes even worse than in Figure 3. Several years' worth of follow up is needed before satisfactory results can be obtained. Clinically, it is common practice to use confirmation fields to look for points that are persistently progressing.^22,23 The uses of confirmation fields, and different levels of noise have also been tried using our simulation model and although the values for specificity and sensitivity naturally altered, the qualitative results (most importantly the recommendations on ideal frequency of testing) were unchanged. For clarity, the simplest case, without confirmation fields, has been described.

It is also common practice to look for clusters of points that are all progressing, rather than individual points. While this is beyond the scope of this simulation model (because the spatial pattern of deterioration is not clearly known, and varies according to the location in the eye), it is still desirable to have an accurate determination of progression for each of the points in the cluster. The findings, in the present form, may have limited clinical generalisability; but it is our opinion that the conclusions drawn from them are more widely applicable. Non-glaucomatous change (that is, effect of concomitant cataract) is currently indistinguishable for glaucomatous change using PLR and so cannot be included in the virtual eye simulation. Nevertheless, use of simulation enables results to be found which would be extremely hard to achieve using patient data, because for a real world patient, the underlying noise free state of the eye is, as yet, unknown.

Our findings suggest that the current PLR, a popular method for measuring visual field progression^3–12,22,23 still needs improvement. Methods are needed which are more sensitive without compromising specificity; this way, accurate results and faster diagnosis could be obtained with just one or two tests per year over shorter periods of time than at present. This relies primarily on reducing the amount of noise present in the readings.

In conclusion, we believe that three tests per year is a good compromise between sensitivity and specificity. There are certainly large benefits to be had in sensitivity when compared with carrying out just one test per year.