Measurement error of visual field tests in glaucoma

Abstract

Aim: Psychophysical strategies designed for clinical visual field testing produce rapid estimates of threshold with relatively few stimulus presentations and so represent a trade-off between test quality and efficiency. The aim of this study was to determine the measurement error of a staircase algorithm similar to full threshold with standard automated perimetry (SAP) and frequency doubling perimetry (FDP) in glaucoma patients.

Methods: Seven patients with early open angle glaucoma (OAG) were prospectively recruited. All were experienced in laboratory based psychophysics. Three matched test locations were examined with SAP (externally driven Humphrey field analyser) and FDP (CRT) in a single arbitrarily selected eye of each subject. Each location was tested twice with a 4-2-2 dB staircase strategy, similar to full threshold, and then with the method of constant stimuli (MOCS). Accuracy (threshold estimation error) was quantified by determination of differences between “true” threshold measurements made by MOCS and single staircase threshold estimates. Precision (repeatability) was quantified by the differences between repeated staircase threshold estimates.

Results: Precision was relatively high for both tests, although higher for FDP than SAP at depressed sensitivity levels. The staircase strategy significantly underestimated threshold sensitivity for both test types, with the mean difference (95% CI) between staircase and MOCS thresholds being 4.48 dB (2.35 to 7.32) and 1.35 dB (0.56 to 1.73) for SAP and FDP respectively. Agreement levels (weighted kappa) between MOCS and staircase thresholds were found to be 0.48 for SAP and 0.85 for FDP. Although this “bias” appeared constant for FDP across all sensitivity levels, this was not the case for SAP where accuracy decreased at lower sensitivity levels.

Conclusion: Estimations of threshold sensitivity made using staircase strategies common to clinical visual field test instrumentation are associated with varying degrees of measurement error according to visual field test type and sensitivity. In particular, SAP significantly overestimates the “true” level of sensitivity, particularly in damaged areas of the visual field, suggesting that clinical data of this type should be interpreted with caution.

Clinical visual field tests are designed to provide information about both the spatial extent and the depth of visual deficits in a time interval that is sufficiently short to avoid tiring the patient and negatively impacting reliability. Although many well described psychophysical approaches can provide rigorous, high quality measurements of threshold sensitivity, these typically employ a considerable number of stimulus presentations at a single test location and therefore are unsuitable for clinical use.¹ Rapid thresholding strategies used in clinical visual field instrumentation therefore represent a trade-off between test measurement quality and temporal efficiency. Inevitably, use of rapid threshold estimation strategies may induce a degree of measurement error.

In order to understand and evaluate the performance of different visual field test types and thresholding strategies, it is necessary to quantify (1) the ability to produce precise, or repeatable, measurements and (2) the accuracy, or degree of error between the threshold estimation and the “true” threshold sensitivity. Conceptually, these attributes are equivalent to reliability and validity respectively.² While there are numerous reports describing the precision of clinical thresholding strategies for a variety of visual field test types, empirical data on accuracy are scarce. Accuracy data have been derived from simulation exercises^3–6 or from theoretical calculations.^7,8

The aim of this experiment was to evaluate visual field measurement error in patients with early glaucoma for two commercially available visual field test types, standard automated perimetry (SAP) and frequency doubling technology perimetry (FDP) using a staircase strategy similar to full threshold.

METHODS

The institutional review board of Legacy Health System approved this study and all subjects gave informed consent before participating in the investigation.

Subjects

Seven patients (two male, five female) with early and moderate open angle glaucoma were recruited for this study from individuals under the care of the glaucoma service at Devers Eye Institute, Portland, OR, USA. The mean (SD) age of these individuals was 75.7 (8.2) years. For the purpose of this investigation, open angle glaucoma was defined at a previous clinical consultation on the basis of both typical glaucomatous optic nerve head changes as determined by a US glaucoma fellowship trained ophthalmologist, characteristic glaucomatous visual field loss, and gonioscopically open anterior chamber angles. Characteristic glaucomatous visual field loss was defined on previous testing with program 24-2 full threshold SAP as an “abnormal” corrected pattern standard deviation (CPSD) and/or glaucoma hemifield test (GHT) (p<5% for CPSD, “outside normal limits” for GHT), in conjunction with a pattern of visual field loss consistent with glaucoma. In particular, early and moderate glaucoma was defined as no test locations with total deviations worse than –10 dB at the most recent clinical examination. Table 1 presents the visual field characteristics and other clinical information for the seven glaucoma patients.

Table 1.

Visual field characteristics and other clinical information for subjects at the most recent clinical visit

Subject	Age	Eye	MD	CPSD	CDR	BCVA
1	70	LE	−6.01	5.45	0.7	20/20
2	86	RE	−3.86	4.22	0.8	20/25
3	55	LE	−4.98	13.22	0.8	20/20
4	75	RE	−5.45	6.25	0.9	20/25
5	58	LE	−7.50	13.17	0.8	20/25
6	46	LE	−8.56	9.75	0.7	20/20
7	65	RE	−4.03	8.68	0.6	20/25

MD = mean deviation, CPSD = corrected pattern standard deviation, CDR = cup to disc ratio, BCVA = best corrected visual acuity.

All subjects had previously demonstrated reliable clinical visual field test results (false positives and negative <33% and fixation losses <25% on catch trials with full threshold SAP) and were experienced in laboratory based psychophysical tests with both achromatic and frequency doubling stimuli, having attended on at least five separate previous occasions for similar experiments.

Visual field testing

Three test locations were examined in one arbitrarily selected eye of each subject. Test locations were chosen individually for each subject based on the results of the most recent routine clinical examination in order obtain measurements from a variety of sensitivity levels from normal to moderate degrees of sensitivity loss. Locations were therefore not standardised among the sample. These same locations were tested with both SAP and FDP. Test order was randomised to minimise learning or fatigue effects. SAP testing was performed on an HFA model 610 (Humphrey Systems Inc, Dublin, CA, USA), which was externally driven by computer using custom software. Test conditions identical to routine testing were employed: size III test target, 200 ms stimulus duration and 31.5 asb (10 cd/m²) background illumination. Frequency doubling stimuli were presented on a 21” Sony Multiscan G500 video monitor driven by a Cambridge Research Systems VSG2/3 video board (Cambridge Research Systems Ltd, Kent, UK), using the same spatiotemporal properties employed by the commercially available FDT perimeter (0.25 c/deg spatial frequency sinusoidal waveforms and 25 Hz counterphase flicker). Mean luminance was 50 cd/m². Other properties of frequency doubling stimuli were also controlled to emulate the commercially available FDP instrumentation, including test target configuration (square 10° × 10°) and stimulus duration (720 ms total stimulus duration, with 160 ms linear on-ramp from 0% to tested contrast, 400 ms at test contrast, and 160 ms off-ramp returning to 0% contrast).

It is important to recognise that although both SAP and FDT perimetry make measurements of sensitivity in dB, their measurement scales are not the same as they have different ranges and intervals. In this study, SAP sensitivity measurements use the proprietary logarithmic HFA scale of retinal sensitivity. The scale used for FDT perimetry in this study is also logarithmic, but is a dB scale of FDT stimulus contrast sensitivity ((1 dB = log (1/contrast threshold)) × 10). Although 1 dB on the HFA measurement scale is therefore fundamentally different from 1 dB on the FDT measurement scale, this does not preclude comparison of the instruments. In this study it is critical that comparison between the measurement errors of the instruments is based upon the number of scale intervals that characterise measurement error, although regrettably both instruments use the same dB nomenclature.

Psychophysical test procedures

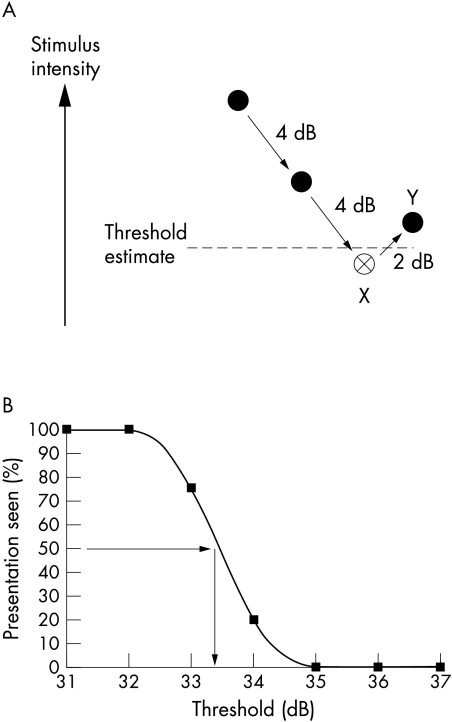
Thresholds were quantified using two techniques, as shown in Figure 1, for each visual field test type. Firstly, an adaptive staircase, or bracketing strategy, was performed to produce a threshold estimate typical of clinical visual field testing scenarios whereby testing is performed rapidly using relatively few stimulus presentations. This strategy was performed twice in succession, with a rest period between the first and second sets of estimations. The dynamics of the staircase strategy used in this study were selected to reproduce the “full threshold” strategy of the HFA (“4-2-2”) whereby 4 dB step sizes were used before the first reversal of response, followed by 2 dB steps until the second reversal was reached which represented the end point of testing⁹ (see Fig 1A). Stimulus presentations were randomised and interleaved among test locations. For the purposes of this study, threshold was defined as the mean of the two reversals and it is important to note that this differs from “last seen” threshold definition employed by the HFA. This alternative definition was adopted because of the need for a fair comparison between the staircase and MOCS which makes it essential to obtain a similar threshold end point from each method. A staircase where the reversals are averaged results in an estimate of the 50% correct point.¹⁰ Similarly, it has been shown that use of the “last seen” end point has been shown to induces a systematic measurement bias and results in underestimation of sensitivity⁴ and increased test-retest variability.¹¹

Figure 1.

(A) The staircase strategy. Solid circles represent “not seen” stimuli and open circles “seen” stimuli. This threshold estimation strategy uses 4 dB increments until the first reversal of response (X) and then 2 dB steps until the second reversal (Y). This staircase is similar to the full threshold strategy used by commercial instrumentation excepting that it uses the mean value to the two reversals to define the threshold estimate (broken line), rather than the “last seen” end point used with full threshold. (B) A frequency of seeing curve derived from fitting data obtained with the method of constant stimuli with a cumulative Gaussian function. The 50% detection level (horizontal arrow) is used to extrapolate the “real” or gold standard threshold measurement (vertical arrow).

On completion of testing with the staircase strategy, the MOCS was undertaken. This established psychophysical approach represents a relatively lengthy and intensive strategy that is designed to produce a rigorous, high “quality” threshold measurement rather than a rapid estimation and is therefore unsuitable for clinical use. For MOCS, seven stimulus levels (luminance increments for SAP and contrast increments for FDP) were examined with 20 presentations at each stimulus level. Step sizes between stimuli were adjusted in order to approach both 0% and 100% seen, and ranged from 1–3 dB. Stimuli presentations were randomised and interleaved among test locations. Frequency of seeing (FOS) curves were constructed from MOCS data by fitting with a cumulative Gaussian function (Tablecurve 2D, SPSS Inc, San Rafael, CA, USA). These FOS curves were used to quantify the reference, or “gold standard” threshold using the 50% detection level in dB (see Fig 1B). FOS curves also provided information on within test variability (interquartile range, dB).

Data analysis

Precision of the staircase strategy was assessed for both SAP and FDP by comparison of the first set of threshold estimations with those obtained from the second, repeated set. Accuracy, or threshold estimation error, was assessed for each visual field test type by comparison of the first set of staircase strategy threshold estimations with the “true,” or gold standard threshold measurement obtained from MOCS.

Both precision and accuracy were quantified using two distinct approaches. Firstly, the technique described by Bland and Altman was used whereby attention was focused on differences in threshold at the level of individual paired measures, by plotting mean threshold against measurement difference.¹² Using this approach, paired threshold measurements were examined for evidence of systematic bias (mean difference and corresponding 95% confidence interval) and also to identify whether this varies with position along the measurement scale. The second technique involved calculation of the intraclass correlation coefficient (ICC). This coefficient is equivalent to a quadratic weighted kappa statistic, an agreement measure that weights discrepancies between paired measurements by the square of their difference.¹³ There is no universally applicable standard ICC value that represent adequate reliability, but to aid presentation the following convention is followed here: ICC <0.20 “slight agreement”; 0.21–0.40 “fair agreement”; 0.41–0.60 “moderate agreement”; 0.61–0.80 “substantial agreement”; and above 0.80 “almost perfect agreement.”¹⁴ The ICC was used in preference to the usual (Pearson) correlation coefficient because the latter measures association rather than agreement. Unlike the Pearson correlation, the ICC only indicates perfect agreement if the two assessments are numerically equal—that is, if a plot of the two measurements has zero intercept and a slope of unity.

Quantification of fatigue effect

It was anticipated that owing to the number of presentations used with MOCS testing (420 presentations per eye) change in threshold with test length (fatigue effect) may interfere with quantification of accuracy. This was considered to be of particular importance to threshold estimates and measures made with SAP, as a number of previous reports have suggested that lower threshold estimates found with lengthier strategies may be due to fatigue.^15–17 An attempt was made to quantify change in threshold between the first and second halves of MOCS stimulus presentations by equal division of MOCS data for each patient test location. Frequency of seeing curves were constructed for each half and the difference in the resulting thresholds, which may be considered as change in threshold due to fatigue, was calculated.

RESULTS

The average SAP mean deviation (MD) among the subjects was –5.77 dB. The average response (within test) variability (interquartile range of frequency of seeing curve) was 1.5 dB (plus or minus 0.42 dB) for FDP and 6.2 dB (plus or minus 5.03 dB) for SAP.

Precision

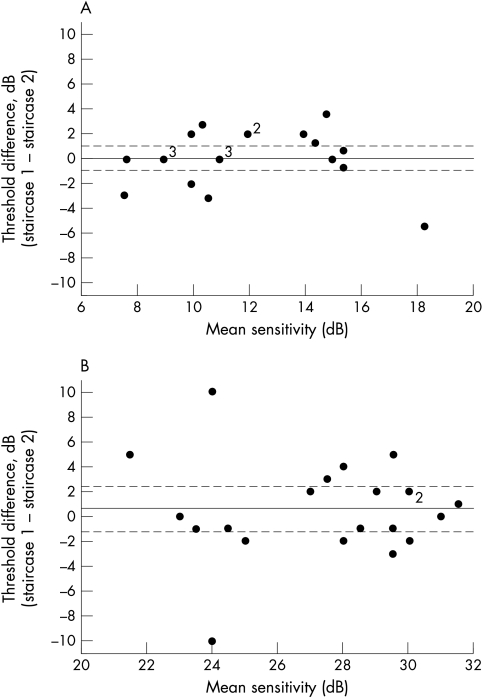
For FDP, “substantial” agreement (ICC = 0.79) was found between first and second threshold estimations made using the staircase strategy, with a group mean difference of 0.1 dB, which is less than one measurement scale interval. The 95% confidence interval (CI) for this mean difference included zero and extended from 1.01 to −0.80 dB, demonstrating that no systematic bias existed between first and second set threshold estimations for the sample examined in this study. Precision data for FDP are shown graphically in Figure 2A. This plot shows that spread of differences was not dependent upon the level of mean threshold sensitivity estimation and indicated that the variability of repeated threshold estimates is similar across the range of thresholds studied.

Figure 2.

Precision data for FDP (A) and SAP (B). For both graphs, the solid horizontal lines represent the group mean difference of the first and second threshold estimations. Broken lines represent the upper and lower 95% confidence limits for the group mean difference.

In a similar manner to FDP, the group mean difference between repeated threshold estimations for SAP was small and less than one measurement scale interval at 0.62 dB, with no evidence of systematic bias between sequential threshold estimations (95% CI 2.30 to −1.06). However, unlike FDP, although precision from repeated SAP threshold estimations were found to be relatively high at “normal” levels of threshold sensitivity this appeared to decrease at lower levels of threshold sensitivity (see Fig 2B), although the possibility of outlying data producing this effect should be entertained. This impacted upon the degree of agreement between the successive sets of threshold estimations, which was quantified as “moderate” (ICC = 0.50) and thus lower than that obtained for FDP.

Accuracy

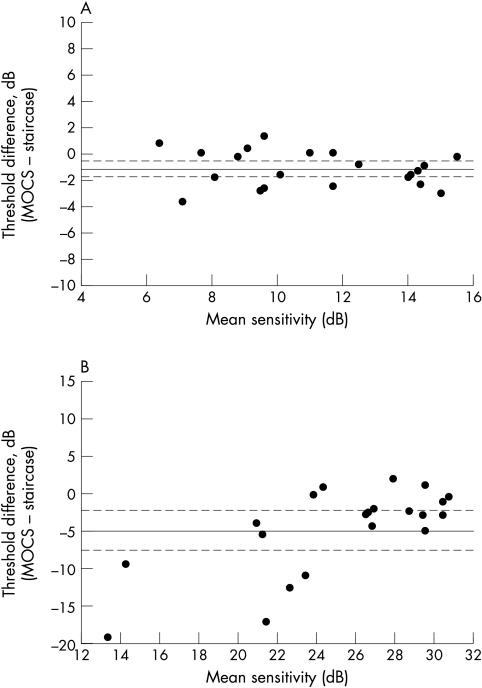
Accuracy data for FDP and SAP are shown in Figure 3. For FDP, threshold sensitivity estimations made using the staircase strategy were significantly higher than the “true,” or gold standard, threshold measurement by 1.35 dB (95% CI 0.56 to 1.73). Figure 3A shows that this degree of threshold estimation error appeared constant across the range of thresholds studied. This small systematic bias was also confirmed by the high (“almost perfect”) level of agreement between the staircase threshold estimations and gold standard threshold measurement (ICC = 0.85). For SAP, estimations of threshold sensitivity made by the staircase strategy threshold were on average 4.48 dB higher that the “true” threshold (95% CI 2.35 to 7.32). Furthermore, this average threshold estimation error was not constant: greater errors, specifically overestimates of threshold sensitivity, were observed at lower sensitivity levels (see Fig 3B). The greatest threshold error in this dataset was 19 dB at a mean sensitivity of 13 dB. Agreement between staircase strategy threshold estimation and true threshold for SAP was “moderate” (ICC = 0.48).

Figure 3.

Accuracy data for FDP (A) and SAP (B). For both graphs, the solid horizontal lines represent the group mean difference of the gold standard threshold measurement, (50% detection level of the frequency of seeing curve) and the first threshold estimation. Broken lines represent the upper and lower 95% confidence limits for the group mean difference.

Fatigue effect

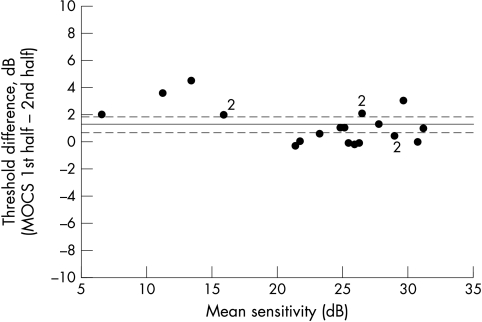
The difference between threshold measurements obtained from the first and second halves of the SAP data collected during the longer MOCS strategy are shown in Figure 4. The mean (95% confidence interval) difference between these threshold measurements was 1.25 dB (1.86 to 0.65) denoting a significant drop in threshold between the first and second halves of testing with this strategy.

Figure 4.

Mean versus difference plot for SAP threshold measurements made during first and second halves of data acquisition during MOCS testing, designed to extract information about any fatigue occurring during the course of testing with this threshold measurement strategy. The solid line represents the mean group difference and the broken lines denote upper and lower 95% confidence limits for the group mean difference.

DISCUSSION

This investigation has demonstrated that varying degrees of measurement error are associated with threshold estimations made using a staircase algorithm similar to that used in clinical test situations. Levels of precision and accuracy for the full threshold staircase strategy appeared dependent upon both test type and threshold sensitivity. Overall, the precision (repeatability) of threshold estimates was relatively high for both SAP and FDP in normal or near normal areas of the visual field, although FDP demonstrated greater agreement between repeated estimations. FDP also maintained a similar degree of precision at all thresholds, although SAP precision was reduced at test locations with depressed threshold sensitivity. Data on precision for SAP in this experiment are in agreement with previous reports that have described higher degrees of scatter, or variability, among repeated threshold estimations at damaged locations in the visual field,^18,19 and also that variability increased as sensitivity reduced.²⁰ Also, our data are consistent with other investigations that have shown FDP variability to be lower in terms of number of scale intervals than that of SAP in damaged areas of the visual field and thereby supports suggestions that FDP may have potential for monitoring for progressive glaucomatous visual field loss.^21,22 Also of importance is that, unlike SAP, FDP precision is consistent in areas of field loss and is therefore predictable.

Quantification of accuracy in this study demonstrated that the staircase strategy significantly overestimated the “true” threshold sensitivity for both visual field test types. The magnitude of this error was relatively small and systematic for FDP at between 1 and 2 dB throughout the range of sensitivities examined, although for SAP the average error was between 4 and 5 dB and was not constant: sensitivity overestimations could be considerable in areas of the visual field with moderate or advanced sensitivity loss.

Previous investigations of visual field test accuracy were performed using a variety of computer simulation techniques based on frequency of seeing curves obtained from normal individuals and patients with optic nerve diseases.^3–6,^23–25 Simulation offers advantages over empirical data collection as it permits iterative investigation of alternative thresholding estimation strategies, in addition to allowing assessment of different parameters and end points for the same strategy. Also, it provides a useful complement to empirical data collection as it can be performed in a controlled manner to assess the effects of variables that influence strategy performance, such as different levels of response errors and variability. Also, simulation exercises are not constrained by patient time, degree of experience and fatigue. However, it is important to recognise that the results of simulations should be validated clinically by testing in appropriate patient populations. To date, simulation has been used primarily to optimise threshold estimation strategies and for staircase strategies this process illustrated the inverse relation between accuracy and efficiency.^3,5 Additionally, simulation suggested that SAP accuracy may be reduced in areas of glaucomatous visual field loss⁴ and this previous report suggested that for glaucomatous visual fields typical of those investigated in this experiment (average MD ≈ −6 dB), the mean error of threshold estimated with the full threshold strategy should be around 2.2 dB. Our empirical data suggest that this is a conservative estimate.

When interpreting visual field test results in clinical environments, it is convenient to assume that the measurements reliably represent visual function. It is therefore essential for visual field test “readers” to be aware that a considerable disparity may exist between “real” visual field sensitivity and that estimated in the course of a visual field test. In this experiment, the finding that the threshold estimation error results in sensitivity overestimation also means that those interpreting visual field test results may mistakenly underestimate the true degree of visual field loss. Awareness of test accuracy is therefore clinically important, and should also be recognised in the design and interpretation of research projects and clinical trials that employ visual field test instrumentation. Our data demonstrated that both SAP and FDP tests have a degree of inaccuracy, or threshold estimation error, and it is possible that this may be caused, at least in part, by fatigue of the patient or their visual system during the more lengthy MOCS strategy used to obtain the gold standard threshold measurement. Reduction in threshold due to fatigue was quantified at 1.25 dB for SAP, and so may account for some of the threshold estimation error. However, the finding that accuracy differed according to test type, with FDP exhibiting higher overall accuracy than SAP, cannot be explained by fatigue as the number of presentations was equal for each test and also because test order was randomised. Furthermore, the two different visual field test types studied exhibited different accuracy characteristics, with FDP threshold estimation error being systematic, while SAP error increased at lower threshold sensitivities. The reason for this finding is unclear; however, it is likely that it may be attributable to differences in response variability known to exist between the FDP and SAP. As described in previous reports, testing with frequency doubling stimuli yielded steeper frequency of seeing curves than those obtained for SAP stimuli.²² Furthermore, while FDP frequency of seeing curve slopes have been shown to remain relatively consistent across the dynamic measurement range of clinical instrumentation,^22,26 frequency of seeing curves for SAP become shallower in areas of visual loss.^27,28 This difference in variability characteristics between the two test types means that the zone of uncertainty between “always seen” and “always missed” stimuli remain similar across the measurement range for FDP, in terms of number of measurement scale intervals, but for SAP will increase with greater defect depths, thereby exerting increasing impact upon accuracy as sensitivity becomes depressed. It is therefore important to note that the systematic threshold estimation error of FDP lends itself to simple mathematical correction, while the more complex nature of the inaccuracy in SAP threshold estimations is not straightforward.

Although the comparison of measurement error between the two types of visual field tests performed in this investigation demonstrate lower levels of measurement error with FDP, interpretation of the data presented should be made with full knowledge of the differences between the test types. Firstly, it should be emphasised that SAP uses a 40 increment differential light sensitivity scale while FDP uses a 20 increment contrast sensitivity scale and therefore it is obvious that such measurement scales are fundamentally different and cannot be directly compared. In spite of this difference, the comparisons made in the course of the study may be considered highly appropriate in the context of scale intervals as used in current clinical instrumentation. Secondly, the reader should also be reminded that FDP stimuli are considerably larger (10°) than SAP stimuli (Goldmann size III, 0.42°), which may influence measurement error. Indeed, previous reports have shown that the variability of SAP is reduced when larger stimuli are used.²⁹ However, a recent investigation demonstrated that reduction in FDP stimulus size to achieve 24-2 test pattern resolution did not significantly effect variability.²⁶ Finally, it is important to be aware that while the FDP stimulus parameters used in this experiment were designed to emulate those found in the commercially available FDT perimeter, the equipment was not identical to the clinical device. It should also be noted that the modified binary search thresholding strategy employed in the commercially available FDT perimeter was not evaluated.

In this study, care has been taken to investigate both the precision and accuracy attributes of visual field tests. Although both of these parameters are important, it is necessary to ask which is preferable. It may be argued that tests with higher precision may be of greater clinical value, especially in the context of monitoring glaucoma, as repeatability is desirable for detection of progressive loss.³⁰ Of course it is important to consider the sensitivity of any given test to progressive glaucomatous visual field loss. While SAP is well established as a clinical tool for monitoring progressive loss, the results of longitudinal studies evaluating the ability of FDP to perform the role are awaited with interest. Higher accuracy demonstrates that clinical visual field test results provide valid representations of patients' visual function and so is also desirable. However, provided accuracy remains constant (a “systematic” threshold estimation error) across the threshold measurement range, it is unlikely to impact upon interpretation of results unless it becomes necessary to alternate between different threshold estimation strategies with different levels of accuracy. If accuracy is not constant across the measurement range, this may also negatively affect sensitivity to true threshold changes, because a change in true threshold is not linearly related to a change in estimated threshold. Overall, it is reasonable to suggest that accuracy and precision are equally valuable.

In summary, accuracy and precision are important prerequisites of clinical test strategies. It has been demonstrated that measurements made using staircase strategies typical of clinical environments lack high degrees of accuracy, and have differing levels of precision. Both accuracy and precision appeared dependent on test type. Limited accuracy of SAP staircase threshold estimations at test locations with low sensitivity suggests that clinical data of this type should be interpreted with caution. Investigation of the accuracy and precision of other clinically used threshold estimation strategies are currently under way in our laboratories.