Intrinsic β-sheet propensities result from van der Waals interactions between side chains and the local backbone

Abstract

The intrinsic secondary structure-forming propensities of the naturally occurring amino acids have been measured both experimentally in host–guest studies and statistically by examination of the protein structure databank. There has been significant progress in understanding the origins of intrinsic α-helical propensities, but a unifying theme for understanding intrinsic β-sheet propensities has remained elusive. To this end, we modeled dipeptides by using a van der Waals energy function and derived Ramachandran plots for each of the amino acids. These data were used to determine the entropy and Helmholtz free energy of placing each amino acid in the β-sheet region of φ—ψ space. We quantitatively establish that the dominant cause of intrinsic β-sheet propensity is the avoidance of steric clashes between an amino acid side chain and its local backbone. Standard implementations of coulombic and solvation effects are seen to be less important.

Understanding the relationship between a sequence of amino acids and its folded three-dimensional structure is of paramount importance for protein design and protein-folding studies. Conceptually, the relationship can be simplified by considering the formation of secondary and tertiary structure separately. One may then independently consider what forces drive the formation of secondary structure and how these structures then pack together to form the tertiary structure. Our concern here is with the first of these considerations.

Examination of the frequencies of occurrence of the naturally occurring amino acids in α-helices or β-sheets of proteins of known structure led to the early recognition that amino acids have differing propensities to form secondary structure (1). The existence of stable helical peptides then enabled relatively unambiguous experimental determination of α-helical propensities (2–5), which agree with the results of statistical studies of the protein structure database (6). Together, these studies quantify the concept of α-helical propensity but do not elucidate the physical–chemical basis of the propensities. Clarification of the physical–chemical basis of α-helix propensities awaited theoretical studies that compared distributions of side-chain dihedral angles for each amino acid in a 9- or 11-residue α-helix and in a dipeptide standard state (7, 8). These studies supported the view that the α-helical propensities of hydrophobic amino acids result from the loss of side-chain entropy on folding. Thus, alanine has the best α-helical propensity, because it loses no side-chain entropy when its backbone is constrained to a helical conformation. Other studies have used molecular-dynamics simulations with an elaborate energy expression (9).

Because β-sheets do not seem to fold in isolation, experimental determination of β-sheet propensities has been more difficult than it was for α-helices. A model protein with a suitable host site is required, and different choices yield different propensity scales (refs. 10–13 and J.-Y. Luo, R. Langen, B. D. Olafson, J. H. Richards, and S.L.M., unpublished work). The preference for a certain amino acid to be in a β-sheet is therefore a more complicated issue than it is for α-helices, depending also on the structural context of the amino acid in the β-sheet. A statistical survey of the protein structure database nevertheless correlates well with an average of the experimental scales, supporting the idea that intrinsic β-sheet propensities do play an important role in determining the stability of a protein (6).

Correlation has been observed between one experimental β-sheet propensity scale and the ability of a side chain to interfere sterically with the formation of hydrogen bonds between its neighboring peptide group and solvent molecules (14). Electrostatic screening has also been proposed as an important factor (15). Other work has modeled equilibrium constants for secondary-structure formation by using a complex energy function (16), which was extended to model β-sheet propensities (17). There has also been related work modeling NMR coupling constants (18, 19). However, no concise theoretical description that fully explains the β-sheet propensities of the naturally occurring amino acids has emerged yet.

METHODS

We modeled each Xaa in a dipeptide environment, Ala-Xaa-Ala, with fixed bond angles and lengths (20). Each model peptide chain was created de novo by using backbone and side-chain dihedral angles chosen randomly from a uniform distribution. Chains were discarded as self-colliding if the DREIDING (21) van der Waals energy of any atom exceeded a threshold of 2.5 kcal/mol; this threshold was chosen to make the best reproduction of the standard Ramachandran plot for Ala (the results were not overly sensitive to changes in this value). The 1–4 van der Waals interaction energy was included except for intra-side-chain contacts. Using chains that terminated at the Cα position on each flanking residue instead of full dipeptide chains did not affect the results significantly. All runs consisted of 10⁵ successful chains, with relative standard errors of < 0.5%.

Our definition of β-space is based on the definition of Muñoz and Serrano (6), bounded by the closed polygon with the following vertices (φ, ψ): (−180, 180), (−54, 180), (−54, 90), (−144, 90), (−144, 108), (−162, 108), (−162, 126), and (−180, 126).

It is noted that the absolute propensities obtained depend quite sensitively on the N–Cα–Cβ bond angle, although the relative propensities do not. However, when this bond angle was allowed to vary according to a Gaussian distribution with a mean of 110° and a standard deviation of 2°, the reported correlations were not significantly affected.

Surface areas were calculated by using the Connolly algorithm (22), with a dot density of 10 Å⁻², a probe radius of 0 Å, and an add-on radius of 1.4 Å (23). Atoms that contribute to the hydrophobic surface area are carbon, sulfur, and hydrogen atoms attached to carbon and sulfur. Trials were conducted by using the side-chain area only as well as the side-chain and backbone areas together.

Electrostatic energies were calculated by using Gasteiger (24) or charge equilibration (25) point charges; neutral and charged versions of the side chains, where appropriate, were both tried, as were both 1/r and 1/r² forms of the Coulomb potential (where r is the interatomic distance). Trials were conducted by using energies of the side chain only and, alternatively, of the full residue.

RESULTS

We constructed an ensemble of self-avoiding states of a dipeptide chain by fixing the bond angles and lengths and allowing the dihedral angles (φ, ψ, and χ) to vary randomly over a uniform distribution. The resulting ensemble of structures represents the denatured state of the peptide. Assuming a microcanonical ensemble, the entropy change (ΔS) on occupying β-space is

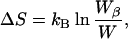1

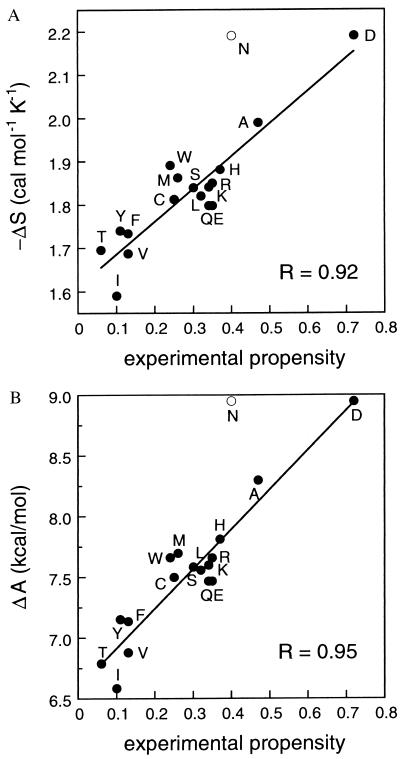
where k_B is the Boltzmann constant, W is the number of members in the entire ensemble, and W_β is the number of members in β-space (i.e., those members with appropriate φ and ψ angles). A comparison of ΔS calculated in this way (Table 1) with the experimentally observed β-sheet propensities is shown in Fig. 1A. To average out, as much as possible, the context effects in individual experimental studies, we compare our results here with the average of the normalized available experimental data (J.-Y. Luo, R. Langen, B. D. Olafson, J. H. Richards, and S.L.M., unpublished work). Excluding the amino acids Pro, Gly, and Asn (discussed below), the correlation coefficient R is 0.92.

Table 1.

Calculated change in entropy (ΔS) and Helmholtz free energy (ΔA) on folding into a β-sheet and the average normalized experimental propensity of the naturally occurring amino acids

Amino acid	ΔS, cal⋅mol−1⋅K−1	ΔA, kcal⋅mol−1	Average normalized experimental propensity
I	−1.59	6.58	0.10
V	−1.69	6.88	0.13
T	−1.70	6.79	0.06
F	−1.73	7.14	0.13
Y	−1.74	7.15	0.11
E	−1.80	7.47	0.35
Q	−1.80	7.47	0.34
C	−1.81	7.50	0.25
L	−1.82	7.56	0.32
K	−1.84	7.60	0.34
S	−1.84	7.58	0.30
R	−1.85	7.66	0.35
M	−1.86	7.70	0.26
H	−1.88	7.81	0.37
W	−1.89	7.66	0.24
A	−1.99	8.30	0.47
D	−2.19	8.95	0.72
N	−2.19	8.95	0.40

The average normalized experimental propensities are calculated from four published studies (10–13) and a similar study on apo-azurin (J.-Y. Luo, R. Langen, B. D. Olafson, J. H. Richards, and S.L.M., unpublished work). Each scale was normalized to range from zero to one, with Pro excluded, and averaged. 

Figure 1.

Correlation between calculated and average normalized experimental β-sheet propensities (J.-Y. Luo, R. Langen, B. D. Olafson, J. H. Richards, and S.L.M., unpublished work). All amino acids except Gly and Pro are shown. Asn, represented by the open circle, is discussed in the text. (A) The negative of the entropy calculated by using Eq. 1. (B) Helmholtz free energy calculated by using Eq. 2, Eq. 3, and 1/β = 9 kcal⋅mol⁻¹. R, correlation coefficient.

With the inclusion of an additional parameter to calibrate the calculated energies, this analysis can be taken further by assigning an energy ɛ_i to each self-avoiding chain i. The partition function over a canonical ensemble (Q) is

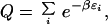2

where β = 1/k_BT, T is the temperature, and the summation is over all chains i in the ensemble. The change in Helmholtz free energy on folding into a β-sheet is then

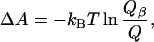3

where Q is the partition function for the entire ensemble and Q_β is the partition function for the β-space ensemble. However, the assigned energies ɛ_i may need to be scaled to correspond to experimental energies. This scaling can be achieved by appropriately selecting a value of β. In order for the range of ΔAs to reproduce the experimental range of the ΔGs (for central strands, the experimental scales each range over ≈2.5 kcal/mol, excluding Gly and Pro), we select 1/β to be 9 kcal/mol. Comparison of ΔA calculated in this way with the experimentally observed β-sheet propensities is shown in Fig. 1B, with R = 0.95.

It is conceivable that forces other than the van der Waals force may play important roles in determining β-sheet propensity. The canonical ensemble formalism provides a convenient framework to explore this possibility, because the energies ɛ_i of each chain may include terms other than just the van der Waals energy. We therefore considered additional energy terms proportional to the amount of exposed (or, mathematically equivalently, buried) hydrophobic surface area and electrostatic energies. No combination of these terms improved the correlation beyond that shown in Fig. 1B. Coulombic and solvation effects, in their standard implementations, are thus less important in determining β-sheet propensity.

DISCUSSION

Our results reproduce the markedly high preference in β-sheets for the β-branched amino acids Ile, Val, and Thr, as well as the aromatic amino acids Phe and Tyr, and the markedly low preference for Ala and Asp. Gly and Pro are excluded because of the imprecise determination of their experimental propensities. The only amino acid that lies significantly off the line of best fit in the figures is Asn. We note that, sterically, Asn and Asp have very similar side chains, so the calculated energies for the two are expected to be similar despite the wide experimentally determined difference between their propensities. However, including surface area or charge terms in our energy expression does not improve the position of Asn. One possible explanation for Asn’s better-than-expected experimental propensity is that hydrogen bonding may play a greater role in determining the β-sheet propensity of Asn than for the other amino acids (26, 27).

One important implication of this work is that inherent β-sheet propensities can indeed be dissociated from context, as they are for α-helical propensities. In fact, the results of this study indicate that β-sheet propensity arises from even more local phenomena than α-helical propensity—namely, the steric interaction of an amino acid side chain with its local backbone. Thus, even in the absence of neighboring β-strands (28), the notion of β-sheet propensity remains valid. The context independence of β-sheet propensities agrees with studies in which a high correlation is seen between the statistically derived preferences of amino acids in β-sheets and β-coils, where β-coils are defined to be residues in β-space but not in true β-sheets (29). However, the existence of neighboring β-strands imposes additional contextual constraints; in particular, edge strands and central strands may present consistently different environments (13). In contrast to the local nature of our description of β-sheet propensities, α-helical propensity is believed to arise from interactions between a side chain and the backbone of the neighboring turns (7) (i.e., from nonlocal interactions).

We have established that the dominant cause of intrinsic β-sheet propensity is the avoidance of steric clashes between an amino acid side chain and its local backbone. Standard implementations of coulombic and solvation effects are less important. Our work shows, surprisingly, that the origins of β-sheet propensities may be more straightforward than those of α-helices.