The signature of balancing selection: Fungal mating compatibility gene evolution

Abstract

A key problem in evolutionary biology has been distinguishing the contributions of current and historical processes to the maintenance of genetic variation. Because alleles at self-recognition genes are under balancing selection, they exhibit extended residence times in populations and thus may provide unique insight into population demographic history. However, evidence for balancing selection and extended residence times has almost exclusively depended on identification of transspecific polymorphisms; polymorphisms retained in populations through speciation events. We present a broadly applicable approach for detecting balancing selection and apply it to the b1 mating type gene in the mushroom fungus Coprinus cinereus. The comparison of neutral molecular variation within and between allelic classes was used to directly estimate the strength of balancing selection. Different allelic classes are defined as encoding different mating compatibility types and are thus potentially subject to balancing selection. Variation within an allelic class, where all alleles have the same mating compatibility type, provided an internal standard of neutral evolution. Mating compatibility in this organism is determined by the complex A mating type locus, and b1 is one of several redundantly functioning genes. Consequently, we conducted numerical simulations of a model with two subloci and varying levels of recombination to show that balancing selection should operate at each sublocus. Empirical data show that strong balancing selection has indeed occurred at the b1 locus. The widespread geographic distribution of identical b1 alleles suggests that their association with differing A mating types is the result of recent recombination events.

Recent phylogenetic analyses of self-recognition loci have shown promise in untangling historical and ongoing demographic events because these systems share the common property of extreme levels of allelic divergence and often also demonstrate an excess of nonsynonymous over synonymous substitutions (1, 2) and transspecific polymorphism (1–4). Theoretical investigations suggest that balancing selection maintaining numerous alleles must be responsible for the greatly extended residence time of alleles in populations and for high sequence diversity (5–8). However, although extended genealogies provide a window into historical population demography (e.g., refs. 9 and 10), these efforts have been critically dependent on the observation of transspecific polymorphism. Transspecific polymorphism has limited value as a test of balancing selection in systems such as gamete-recognition proteins of sea urchins (11) or sexual compatibility loci in fungi (this report), where they have not been observed. Moreover, alternative hypotheses for the observation of transspecific polymorphism have been suggested, such as very large population sizes at the time of speciation (12). Furthermore, although many self-recognition systems are determined by multigenic loci, explicit treatment of complex loci has trailed analysis of single-gene loci. To evaluate the generality of predictions about patterns of molecular evolution in self recognition systems, and to develop a broadly applicable approach for estimating the effect of balancing selection on allelic genealogies, this study focused on the evolution of the b1 mating-compatibility gene of the mushroom fungus Coprinus cinereus. The b1 gene is one of several redundantly functioning genes embedded within the multigenic A mating type locus (13).

The requirement of heterozygosity at A for sexual compatibility enforces strong frequency-dependent selection (5), reflected in the estimation that over 100 different A mating compatibility types exist in the worldwide population of this fungus (14). The A locus of C. cinereus is made up of three subloci (ref. 15; see Fig. 1), and because sexual compatibility requires only a difference at one such sublocus, they are redundant in function (13). The subloci are made up of gene pairs characterized by having oppositely transcribed genes encoding different and distinctive homeodomain-like proteins. Surprisingly, sexual compatibility requires that these different homeodomain proteins interact, e.g., the b1 protein from one allele interacts with the b2 protein from another allele (16). Thus, the gene pair is the unit of transmission and evolution with recombination between but not within subloci generating the observed variation in A mating types (15, 17).

Figure 1.

The organization of the A43 mating type locus of C. cinereus. Arrows designate direction of transcription; the a2 gene is transcribed but nonfunctional (gray arrow). Boxes denote the location of predicted homeodomain-like (HD) motifs. The members of a gene pair, e.g., the b1 and the b2 genes, are characterized by the presence of two types of HD motifs, HD1 and HD2. The hypervariable 5′ regions are shown as shaded boxes. The open boxes indicate two regions of recombination. (Adapted from refs. 13 and 20.)

We estimated the effect of balancing selection on the b1 gene by contrasting the levels of molecular variation maintained by neutral evolution with that maintained under balancing selection. The approach is based on the recognition that two genealogical processes with markedly different time scales are occurring at loci under balancing selection (6, 7). First, Takahata (6) recognized that functionally distinct allelic classes, evolving under balancing selection over extended periods of time, produce genealogies with a topology like that of neutral alleles but rescaled in time. Takahata’s scaling factor, fs, is then proportional to the force of selection, with fs = 1 in a strictly neutral model. Second, allele copies within an allelic class are evolving neutrally because they encode the same compatibility type but with a low effective population size determined by the frequency of the corresponding allelic class. Hence, allele copies, defined here as replicate alleles, show genealogical relationships similar to neutral gene genealogies but on a much shorter time scale (7). Taking advantage of our ability to identify replicate alleles at b1, we gathered molecular data pertaining to these two distinct processes to provide an empirical estimate of fs based on sequence data.

The strength of this approach is that it can be applied to any locus, however complex. In particular, we explore two features of this fungal system; that the mating individuals are haploids and that the A mating type locus is intrinsically multigenic with different genes acting redundantly. Using numerical simulations, we tested whether the main properties of single-locus balancing selection models, increased polymorphism and extended residence time of alleles (6), are still valid under a haploid model with two loci and varying levels of recombination. The simulations thus broaden the application of this theory to multigenic systems. Our results suggest a 278-fold difference in time scale between genealogies of b1 allelic classes and those of replicate alleles. The results provide strong evidence of balancing selection acting at the b1 locus even though embedded within the complex A locus. Replicate alleles not only provide an internal control for neutral variation, but the geographic distribution of these alleles suggests that they will also help to distinguish historical and current demographic events.

MATERIALS AND METHODS

Sequence of b1 Alleles.

Our approach was to compare molecular variation within and between allelic classes, as defined above. We sampled representative alleles for 7 of the 10 different allelic classes estimated for b1 (15). Two allelic classes are represented by sequences previously reported [b1-1 (16); b1-2 (18)], and five are represented by additional alleles for which we could obtain genomic clones of the entire b1 gene (19). The following alleles (strain, location, A type) were obtained: b1-3 (strain 218; Britain, A3), b1−4 [Java(a); Java, A41], b1-5 (3v-1, North Carolina, USA, A71), b1-6 (5b-6, North Carolina, A73), b1-9 (5b-3, North Carolina, A72). We assumed that the alleles representing different allelic classes encode different mating compatibility types, an assumption supported by transformation assays of mating-type differences (19, 20). For replicate alleles, we sampled seven replicate alleles from the b1-2 allelic class and four replicate alleles from the b1-4 allelic class. Strains harboring the replicate alleles had previously been identified in a survey of natural populations by hybridization intensities and common restriction fragment sizes (15). Thus, sampling of b1 alleles does not represent a random sample of all b1 alleles in a population but rather sampling designed to compare variation within and between allelic classes.

Complete double-strand nucleotide sequence of the coding region (1,965 bp) was obtained for all alleles. For different allelic classes, DNA sequence data was obtained from genomic clones, and for replicate alleles, DNA fragments and DNA sequences were obtained by using PCR. For all alleles, DNA sequence data were obtained by using either manual (Sequenase, version 2.0, United States Biochemical) or automated (Applied Biosystems) sequencing methods (19).

Analysis of Sequence Data.

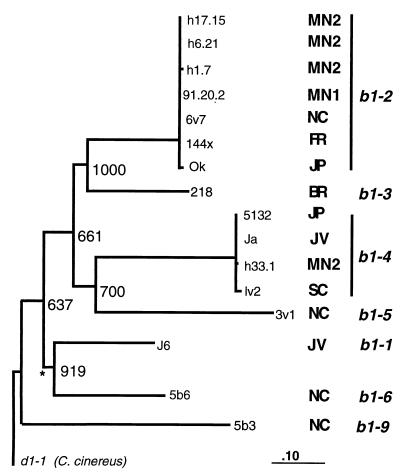
DNA and amino acid sequences were aligned in clustalw (21) with minor manual corrections under gde version 2.2 (22) such that amino acid coding frames were conserved. The topology of Fig. 2 was obtained by using the Neighbor-Joining algorithm in clustalw with 1,000 bootstrap replications (21) from uncorrected distances based on the amino acid alignment between codons 126 and 531. Preliminary analyses demonstrated that inclusion of codons 531–646, which are subject to recombination, or of codons 1–126, the hypervariable N-terminal region (19), decreased the resolution of relationships among allelic classes.

Figure 2.

Genealogy for alleles at the b1 mating compatibility gene. The topology was obtained by a Neighbor-Joining algorithm with bootstrap values shown for 1,000 replicates, and branch lengths are proportion of synonymous substitutions per codon (see Methods and Materials). Locations are Britain (BR), France (FR), Japan (JP), Java (JV), Minnesota population 1 (MN1), Minnesota population 2 (MN2), North Carolina (NC), and Scotland (SC). The d1-1 allele (see Fig. 1) was used as an outgroup. ∗, Branch lengths not significantly greater than 0.0 in Generalized Least Squares.

We used the Generalized Least Squares approach (23, 24) to estimate and compare branch lengths for different allelic classes in the genealogy. In this implementation, we first calculated pairwise synonymous and nonsynonymous distances and their covariance matrices separately. Sequences were compared at each codon, and each nucleotide substitution was assigned to a synonymous or nonsynonymous class. The proportion of synonymous (or nonsynonymous) sites differing between two sequences is the ratio of the number of homologous codons that have synonymous (or nonsynonymous) differences between them to the total number of potential synonymous (or nonsynonymous) codon pairs. The Jukes–Cantor correction for multiple hits (25) was applied. We then used Generalized Least Squares to fit the corrected pairwise synonymous distances to the topology and obtain estimates of branch lengths. The null hypothesis that the rate of sequence divergence was the same between a pair of sequences emanating from a branch point was tested by using likelihood ratios (24). For an unrooted tree with six branch points, 21 comparisons and tests are possible. No adjustment for multiple testing was made.

The very high similarity among replicate alleles leads to a negative covariance matrix in Generalized Least Squares (24), and branch lengths could not be obtained as above. However, noting that each group of replicate alleles forms a “bush” topology (Fig. 2), branch lengths for replicate alleles were represented simply as the corrected synonymous distances. The divergence among replicate alleles was compared with that among allelic classes by using a permutation method (see Results).

Estimation of fs.

We estimated fs for the b1 alleles by combining information on genealogies within and between allelic classes. We assume a neutral mutation rate v, independent of the mutation process that generates new allelic classes at a rate μ. The expected number of nucleotide differences per site for replicate alleles (π_within) and the expected number of nucleotide differences per site between allelic classes (π_between) can be defined (26). If we also assume that population size (N) and v are constant and apply to both genealogies, we obtain an estimate of fs as [π_between/(n × π_within)] − 0.5, where n is an estimate of the number of allelic classes (see Appendix).

Numerical Simulations.

In Basidiomycete fungi such as C. cinereus, haploid colonies persist until a compatible mate is found. After mating, a binucleate dikaryon is formed and grows as a colony until it produces mushrooms. Consequently, we conducted a simulation study of reproduction in a haploid fungal population of size 2N with nonoverlapping generations. In each generation, the following mating process is repeated until N new dikaryons are produced. Two of the 2N individuals are chosen for sexual reproduction, and compatibility of gametes is checked according to the mating system model used. In the single-locus haploid model (HSI1), the mates are compatible only if the allelic classes of the two haploids do not match. In the two-locus haploid model (HSI2), compatible interactions occur whenever alleles in at least one of the mating loci belong to different allelic classes. If the mates are compatible, a new dikaryon is formed. If they are incompatible, then a new potential mate is drawn at random from the population. A number of mutations, drawn from a Poisson distribution with mean 2Nμ, where μ is the mutation rate to new allelic classes, are then applied at random to genes in the dikaryons. Under HSI2, recombination between the two loci is enforced in each dikaryon with a probability equal to r, where r is the recombination rate. Each dikaryon is then assumed to produce two haploid individuals. Each run started with 2N different allelic classes in the population at each locus, and evolved until a mutation–selection–drift equilibrium was reached.

The genealogy was tracked in a forward manner by the method of Vekemans and Slatkin (7). Simulations were continued for a number of generations equal to five times the expected coalescence time, T_c, of all allelic classes. Simulations with 100 replications were performed for each of the following four parameter sets and the two mating models: 2n = 100, μ = 2 × 10⁻⁴; 2n = 400, μ = 5 × 10⁻⁵; 2n = 100, μ = 2 × 10⁻³; 2n = 400, μ = 5 × 10⁻⁴. We computed the mean number of extant allelic classes (n), the average pairwise divergence times between allelic classes (T_d), and the average substitution rate (α), in units of 1/μ generations. For both the HSI1 and HSI2 models, information on the structure of the genealogy was generated by drawing a random sample of five allelic classes from the population for the case of n = 750 and μ = 10⁻⁵. For each of 500 replicate runs, the time intervals between successive coalescent events in the genealogy [T(i)] was computed and averaged over replications.

Genealogies of replicate alleles within allelic classes were investigated in the two-locus model with different recombination rates in the case of n = 750 and μ = 10⁻⁵ with 500 replicate runs. For each allelic class present at the end of each run, we computed the average pairwise divergence time between replicate alleles, T_dwithin, the current frequency of the allelic class, the harmonic mean over time of the frequency of the allelic class.

RESULTS

Two striking results are illustrated in the genealogy of b1 alleles. First, the terminal branches representing allelic classes are very long compared with the length of the basal branches. Second, in contrast to divergence among allelic classes, very few differences were observed among replicate alleles within an allelic class (Fig. 2). Our assumption that all replicate alleles encode the same b1 compatibility type is supported by the finding that among the b1-4 replicate alleles, there were no amino acid substitutions. Among all of the b1-2 replicate alleles, there were only three conservative amino acid substitutions, and all of these were located outside the N-terminal region known to encode mating type (27).

To determine whether the rate of nonsynonymous substitution was accelerated relative to the rate of synonymous substitution in any portion of the genealogy, synonymous (d_s) and nonsynonymous (d_n) branch lengths were calculated separately and compared. No individual branch exhibited d_n > d_s (results not shown). The result did not change when only the N-terminal region was used in the analysis, confirming our previous result that d_n was not greater than d_s for any region of the gene (19).

Generalized Least Squares analysis provided evidence for unequal rates in the genealogy, with a significantly longer branch length associated with the b1-5 allelic class and significantly shorter branch lengths associated with the b1-1 and b1-6 allelic classes. We used transformation experiments (by the method of ref. 28) to test whether b1-5 represented a nonfunctional pseudogene and thus resulted in accelerated substitution rates. The b1-5 allele was introduced into a recipient strain carrying a different b gene pair (strain 218, A3), and we verified that this allele could direct A-regulated development, a result obtained for all allelic classes (19).

Estimation of fs.

A permutation test was used to assess the statistical significance of the observation that variation among replicate alleles was much lower than variation among allelic classes. The null hypothesis that variation is the same among all sequences can be tested by calculating fs for every possible assignment of individual sequences to replicate and allelic class categories. For seven allelic classes compared with either seven replicate b1-2 alleles or to four b1-4 replicate alleles, there are 1,718 and 310 possible groupings, respectively. For each permutation, fs was calculated as [π_between/(n × π_within)] − 0.5, using corrected synonymous substitutions per codon as above but over the entire coding sequence (1,965 bp) and an estimate of n = 10 b1 allelic classes (15). For the b1-2 replicate alleles, only the hypothesized grouping resulted in the highest fs value (35.1), giving a p value of 1/1,718 or 0.0005. Similarly, for the b1-4 replicate alleles, fs = 15.0 and the p value = 1/310 or 0.003. Obtaining a weighted average of the fs estimates, fs ≈ 27.8, and assuming a constant mutation rate through time, these values suggest a 278-fold difference in time scale between the two genealogical processes.

Numerical Simulations.

The results of simulations of two haploid models, HSI1 and HSI2, with unlinked loci are given in Table 1. Mean values of the number of allelic classes maintained per locus, n, are increasing with N and μ for both models and are 30–43% lower for the HSI2 model than the HSI1 model. The average pairwise divergence time between allelic classes, T_d, is increasing with N but decreasing with μ for both models, as reported for plant gametophytic self-incompatibility (7). Values of T_d for the HSI2 are on the order of 40% lower than for HSI1. Observed values of n and T_d for the single-locus model are close to expected values for an overdominant model with lethal homozygotes. Values of the substitution rate, α, are much higher than 1, the value expected under a neutral model. Altogether, these results indicate that balancing selection is operating at each sublocus of a haploid model with two unlinked mating-type loci but that the strength of selection is lower than for a single-locus model. Higher numbers of allelic classes and substitution rates are observed under HSI2 when the two loci are partially or fully linked (data not shown).

Table 1.

Numerical results for single-locus (HSI1) and two-locus (HSI2) haploid models

	4Nμ	2N	μ	n	Td	α
HSI1
	0.04	100	2  × 10−4	4.63  ±  0.78 (4.56)	44.0 ± 28.0 (32.1)	5.11  ±  1.05
		400	5  × 10−5	7.85  ±  1.06 (8.49)	54.5 ± 30.2 (52.8)	6.79  ±  1.14
	0.4	100	2  × 10−3	7.21  ±  1.40 (6.83)	9.8 ± 5.6 (8.2)	2.95  ±  0.53
		400	5  × 10−4	11.57  ±  1.51 (11.63)	13.0 ± 6.1 (11.6)	3.95  ±  0.59
HSI2
	0.04	100	2  × 10−4	2.93  ±  0.79	26.8 ± 17.2	4.33  ±  0.94
		400	5  × 10−5	4.45  ±  0.88	33.5 ± 22.6	5.58  ±  1.04
	0.4	100	2  × 10−3	5.06  ±  1.54	5.8 ± 3.5	2.43  ±  0.48
		400	5  × 10−4	7.02  ±  1.79	7.9 ± 4.7	3.02  ±  0.48
Ratio HSI2/HSI1
	0.04	100	2  × 10−4	0.64	0.61	0.85
		400	5  × 10−5	0.57	0.61	0.82
	0.4	100	2  × 10−3	0.70	0.59	0.82
		400	5  × 10−4	0.60	0.61	0.76

Mean values are given ±SD across 100 replicates. Analytical expectations for a single overdominant locus with lethal homozygotes in parentheses. N, number of zygotes produced at each generation μ, mutation rate to new allelic classes; 1, number allelic classes; T_d, average pairwase divergence time between allelic classes in units of N generation; α, substitution rate in units of 1/μ generations. 

The effect of linkage between loci in HSI2 on the time scale of genealogies of replicate alleles within allelic classes was also investigated. Summarizing the results for two unlinked loci, we observe that values of T_dwithin are increasing with the frequency of the allelic class at the time of sampling and are very well approximated by the harmonic mean over time of the frequency of the allelic class. This has been reported for gametophytic self-incompatibility (7) and indicates that replicate alleles are evolving in a neutral fashion. In contrast, for two fully linked loci, T_dwithin is substantially higher than estimators based on the harmonic mean of allelic frequency, but only for allelic classes with frequencies higher than average. In the case of an intermediate recombination rate between the two loci, on the order of 10 times the mutation rate, a similar pattern is observed for allelic classes with high frequency, but the increase in divergence time is lower.

The simulation results thus demonstrate that linkage of replicate alleles to a new allelic class at the second locus will cause a hitchhiking effect, and the divergence times among replicate alleles will be increased over that for neutral alleles (26). Because we have previously demonstrated that the subloci making up the A locus of C. cinereus are in linkage equilibrium in natural populations (15), the magnitude of this hitchhiking effect among subloci should be negligible, and the genealogies of replicate alleles within a given compatibility class are neutral.

Analyses of Genealogical Structure.

To compare our results with expected neutral topologies, the observed b1 genealogy for seven allelic classes and the simulation results were analyzed by using two approaches, a graphical method using standardized time intervals between coalescent events (8) and an analytical approach using ratios of branch lengths (29).

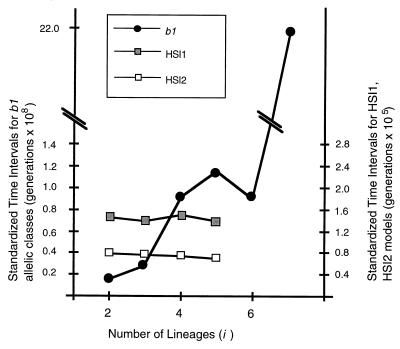
In the graphical analysis, we plotted the time intervals between successive coalescent events [T(i)] against i, the number of lineages present during each time interval (2 ≤ i ≤ 7). Time intervals were standardized by multiplying by i × (i − 1) so that the expected pattern under an expanded-neutral topology is a horizontal line crossing the y axis at value 4N × fs (8). To allow comparison with simulation results, we converted empirical values of the time intervals, expressed in number of substitutions, to generations by assuming that 4N × fs = 161,854, the expected value under overdominant selection with n = 750, μ = 10⁻⁵, and lethal homozygotes. For both the HSI1 and HSI2 simulation models, the observed pattern is close to the expected horizontal line, with time intervals on average 47% lower for the two-locus than for the single-locus model (Fig. 3). In strong contrast, the resulting graph for the b1 genealogy shows the standardized time intervals generally increasing with the number of lineages. The sharpest distinction between expectations and empirical results is shown in the extreme value of the most recent time interval, which emphasizes the lack of recently evolved allelic classes.

Figure 3.

Graphical analysis of standardized time intervals [T(i) × i × (i − 1)] expressed in generations and the number of lineages (i) present in the genealogy at each T(i). □ and ■, values for the numerical simulations with two haploid models, HSI1 and HSI2, respectively. ●, values for the b1 genealogy of Fig. 2.

The second approach used four ratios of divergence times (29) that describe the relationship of external and internal branch lengths to total time in the tree (T) or to maximum divergence time (D). R_PT and R_ST analyze the relationship of the average pairwise divergence time (P) and the sum of external branch lengths (S) to T, respectively. The ratios R_SD and R_BD analyze the relationship of S and the average length of the base branches emanating from the root (B) to D, respectively. When scaled by functions of allele number, each of these ratios has an expected value of 1 in the case of a random sample of neutral genes. In the empirical study, averages and variances of these ratios were computed by using the corrected synonymous branch lengths for seven b1 allelic classes (Fig. 2). We used the distributions of the above ratios under simulations with 500 replications to test the empirical values computed for the b1 alleles (Table 2).

Table 2.

Ratios of divergence time, scaled by functions of allele numbers for allelic genealogies

Source	RPT	RST	RSD	RBD
Simulation results
HSI1	0.98  ±  0.19	1.05  ±  0.44	1.19  ±  0.66	0.91  ±  0.27
HSI2, unlinked	1.00  ±  0.13	1.04  ±  0.42	1.14  ±  0.59	0.93  ±  0.22
Empirical results
b1 allele sequences	1.06  ±  0.12	2.26  ±  0.06*	5.15  ±  0.06*	0.11  ±  0.09*

HSI1 (single-locus) and HSI2 (two-locus, unlinked) haploid models with N = 750, μ = 10⁻⁵, 500 replicates. Mean values ± SD for ratios (34). Values shown are mean values ± SD for b1 gene tested against distributions obtained by simulations. 

^*, P < 0.01. 

Under both the HSI1 and HSI2 models, mean values of the ratios are close to 1. Significant departure from the simulation results were found in three of the four computed ratios, with a value close to 1 observed only for ratio R_PT (Table 2). The values of R_ST and R_SD were significantly greater than the simulation values, demonstrating long external branches relative to time in the tree. The value of R_BD was significantly lower than the simulation values, indicating short internal branches relative to time in the tree. However, R_BD is sensitive to topology; in alternate topologies where a basal branch is also terminal, R_BD values increased.

Geographic and Historical Processes.

Perhaps the most remarkable feature of the genealogy is that closely related or, in some cases, identical b1 replicate alleles are found in widely separated geographic regions and in association with different A mating compatibility types. For example, of the b1-4 replicate alleles, strains from Japan and Java carried identical alleles, and the allele from MN2 USA differed from these two alleles by only one synonymous substitution. Similarly, of the b1-2 replicate alleles, one strain each from MN1, NC, and France and two strains from MN2 locations produced identical b1-2 sequences (Fig. 2). Because each of these haploid strains harbors the same allelic specificity at the b sublocus, the differing A mating compatibility types that these strains carry must be the result of differences at one of the other subloci and thus, to the association of different subloci by recombination.

DISCUSSION

In this paper, we take an original approach recognizing that replicate alleles—allele copies within a given allelic class—provide a strong internal control for variation maintained by balancing selection at the b1 locus. Comparing the variation in replicate alleles to the extreme diversity of alleles representing different allelic classes, we provided evidence for the effect of balancing selection on b1 allelic classes.

Our simulation studies were aimed at testing that Takahata’s expanded-neutral theory applies also to haploid models of mating compatibility and to multigenic models. Allelic genealogies under our two-locus haploid model with unlinked loci show a neutral topology rescaled in time, although the scaling factor is substantially reduced as compared with the single-locus model. Under the two-locus model with partially or completely linked loci, the strength of selection was higher than for two unlinked loci because alleles at one sublocus are hitchhiking on selection at the second locus. For models of plant single-locus sporophytic self-incompatibility with dominance interactions, Schierup et al. (8) demonstrated that allelic genealogies also fit the expanded-neutral model of Takahata. The extension of Takahata’s theory to haploid, multigenic systems is important because many self-recognition systems are multigenic complexes, e.g., plant resistance genes (30) or major histocompatibility complex genes (26), and many diverse organisms have haploid life cycles. Taken together, results of simulation studies demonstrate that Takahata’s model for balancing selection is robust to differences in the ploidy level of individuals and to the genetic complexity of the system.

However, the empirical data for b1 show marked departures from the topologies expected under Takahata’s expanded-neutral model. Assuming that the branch lengths in the b1 genealogy based on synonymous substitutions are proportional to time, new allelic classes have not continuously evolved but instead diverged over a relatively short period of time and then were maintained for extended periods of time. Two different analyses of relative branch lengths clearly demonstrate a genealogical process with shortened internal branches and extended terminal branches. The result is not likely due to undersampling because the remaining b1 allelic classes are more divergent, based on Southern blot hybridization. Hence, the observation of long terminal branch lengths of alleles under balancing selection is now extended over the broadest of range of eukaryotes; the fungal b1 gene, one plant species with gametophytic SI (29) and two with sporophytic SI (8), and an major histocompatibility complex class II locus of the mouse (4).

The pattern of extended terminal branches in both plant and animal systems has been attributed to various causal evolutionary processes; linked deleterious alleles or functional constraints leading to a slowdown of the incorporation of new lineages (29) or to preferential retention of more divergent lineages through population bottlenecks (4). Linkage to deleterious alleles seems an unlikely explanation in C. cinereus because recombination is not suppressed in noncoding regions within or flanking the A locus (17). Constraint on the total number of alleles could occur, although available evidence suggests that only a few amino acid substitutions may suffice to determine a new mating specificity (31, 32). The suggestion that older lineages allow broader recognition capabilities and thus are preferentially retained through speciation events (4) is intriguing and could best be explored in a fungal system where site-directed mutations in compatibility genes can be made.

We propose an alternative mechanism for multilocus systems under balancing selection that would generate a slowdown of the incorporation of new lineages. Our model predicts that as the number of allelic classes at each sublocus increases as a result of mutation and selection, recombination between subloci becomes more efficient in producing new compatibility types than does mutation. For example, for a complex locus having two subloci, each initially with two alleles, recombination between those subloci would generate only four mating compatibility types. However, as the number of alleles at each sublocus increases, the number of compatibility types determined by this complex locus will increase exponentially, resulting in a rapid decrease in the strength of frequency-dependent selection and thus the rate of incorporation of new allelic classes at each sublocus.

The incorporation of replicate allele data into the analyses of self-recognition loci allows two important observations of evolutionary process. First, comparing branch lengths in the genealogy of neutral alleles with those in the genealogy of alleles hypothesized to be under selection, we obtain a direct estimate of fs = 27.8, somewhat higher than that of major histocompatibility complex loci (mean over five loci = 10.3; ref. 33), in spite of the fact that both systems share a multigenic nature. Lacking observation of transspecific lineages between C. cinereus and related species, our data do not establish when diversification occurred relative to the species’ history. Nonetheless, obtaining an internal measure of neutral variation gives a clear demonstration of the extended residence time of b1 allelic classes, the signature of balancing selection.

Second, the evolutionary process generating variation at the A mating type locus is occurring on a different time scale than that generating variation among allelic classes at b1. We found identical replicate alleles in association with different A mating types and in distant geographic locations. Because we must suppose that these replicate alleles were moved across wide geographic regions very recently, within the last 10⁴ to 10⁵ years (assuming a mutation rate of 10⁻⁸), the recombinational association of different allelic classes at three subloci to generate the observed diversity of A mating types must also be very recent. C. cinereus is a saprophyte of horse dung, and the distribution of identical b1 alleles could be due to the movement of domesticated animals by humans. Consequently, although balancing selection has strongly impacted variation at the individual b1 gene over long periods of time, in extant C. cinereus populations, recombination rather than allelic diversification is apparently an ongoing and remarkably efficient mechanism generating new A mating types.

ABBREVIATIONS

fs

scaling factor

HSI1

single-locus haploid model

HSI2

two-locus haploid model

μ

mutation rate to new allelic class

π

expected pairwise substitutions

T_c

total coalescence time of all alleles

T_d

average pairwise divergence time between allels

T(i)

time interval between successive coalescent events

Appendix

Derivation of Estimate for fs.

Under balancing selection, the expected pairwise divergence time between allelic classes is given by Takahata (7) as:

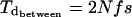1

where N is the population size. For sequence data, assuming an infinite site model of mutation at a rate v, the expected number of neutral nucleotide differences between allelic classes, π_between, is then given by

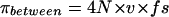2

For genealogies of replicate alleles within a given compatibility class, the expected pairwise divergence time between replicates, T_dwithin, is (29)

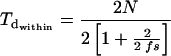3

where n is the number of allelic classes in the population. For sequence data, the expected number of neutral nucleotide differences between replicates, π_within, is

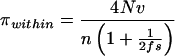4

If we assume that N and v are constant through time, the same values of N and v apply to both genealogies. Putting Eqs. 2 and 4 together, we obtain

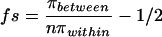5