Abstract
Picosecond time-resolved Stokes and anti-Stokes resonance Raman spectra of all-trans-β-carotene are obtained and analyzed to reveal the dynamics of excited-state (S1) population and decay, as well as ground-state vibrational relaxation. Time-resolved Stokes spectra show that the ground state recovers with a 12.6 ps time constant, in agreement with the observed decay of the unique S1 Stokes bands. The anti-Stokes spectra exhibit no peaks attributable to the S1 (2Ag−) state, indicating that vibrational relaxation in S1 must be nearly complete within 2 ps. After photoexcitation there is a large increase in anti-Stokes scattering from ground-state modes that are vibrationally excited through internal conversion. The anti-Stokes data are fit to a kinetic scheme in which the C=C mode relaxes in 0.7 ps, the C–C mode relaxes in 5.4 ps and the C–CH3 mode relaxes in 12.1 ps. These results are consistent with a model for S1–S0 internal conversion in which the C=C mode is the primary acceptor, the C–C mode is a minor acceptor, and the C–CH3 mode is excited via intramolecular vibrational energy redistribution.
Introduction
The electronic structure and photodynamics of carotenoids are of interest because carotenoids play important roles as light-harvesting and photoprotective agents in photosynthetic systems.1 The visible absorption band in carotenoids is due to the 1Ag− (S0) → 1Bu+ (S2) transition. In general, the S2 state relaxes to the S1 (2Ag−) state on the subpicosecond time-scale in all carotenoids, but the S1–S0 relaxation rate is slower and depends on the conjugation length.2 The time-scale for S1 → S0 relaxation ranges from ∼0.5 ps for long carotenoids with 19 conjugated C=C bonds, to ∼300 ps for short carotenoids with 7 conjugated C=C bonds.3,4 In β-carotene, S2 to S1 internal conversion (IC) occurs in ∼200 fs5-9 and internal conversion from S1 to S0 occurs in ∼8–10 ps.5,10,11 Both IC rates follow the energy gap law formulated using an adiabatic weak-coupling model.12 Recently, however, conical intersections have been discovered in shorter polyenes and implicated in both IC processes.13,14 The conical-intersection model of IC reproduces the same energy gap dependence but invokes dynamic relaxation and strong coupling between the electronic states at the conical intersection.
In photosynthetic systems, the ability of a carotenoid to transfer excitation to nearby chlorophylls is determined by the relative energies of the carotenoid S1 state and the chlorophyll Qy state. To explore these energetics, the rate of intramolecular vibrational energy redistribution (IVR) and vibrational cooling in the S1 state of carotenoids has been extensively investigated.4,15-18 Two of these studies suggested that vibrational relaxation in S1 occurs more slowly than IC. Zhang et al.15 assigned several features in the S1 absorption band of lycopene to vibrational hot-bands and found that these bands did not decay faster than the other bands in the spectrum. However, their time-resolution was limited to ∼3 ps, which is longer than the usual time-scale for excited-state IVR.19 Yoshizawa et al.16 suggested that β-carotene relaxed in 600 fs to the v = 1 (C=C) state but that relaxation to v = 0 proceeded more slowly than IC. However, their conclusions depended on a complicated interpretation involving competing stimulated and inverse Raman effects and a 40 cm−1 anharmonic shift in the S1 C=C frequency. These conclusions are inconsistent with femtosecond transient absorption studies of β-carotene,17 spheroidene,18 and long-chain carotenoids,4 which found that IVR and vibrational cooling in S1 occur in <1 ps. It is evident that a more complete understanding of IVR and vibrational cooling in the S1 states of carotenoids is needed.
Previous time-resolved anti-Stokes Raman experiments on carotenoids have observed the expected increase in S0 anti-Stokes signals after photoexcitation to S2 and subsequent IC. The anti-Stokes signal from spirilloxanthin grew in by ∼3 ps, closely matching the S1–S0 IC time constant, and decayed with a ∼10–15 ps cooling time.20,21 In a related study of canthaxanthin, the anti-Stokes rise-time fit the known S1–S0 IC time constant and the signal decayed with a 15–20 ps time constant.22 Additionally, it was shown that at 6 ps, the signal arose from molecules in low (v = 1 or 2) vibrational states, indicating that IVR must have occurred in <6 ps. However, these studies did not observe any S1 features or kinetics that would report on excited-state IVR processes.
Here, we have performed simultaneous Stokes and anti-Stokes time-resolved Raman experiments on β-carotene in order to elucidate the time-scales of vibrational relaxation in both the S1 and S0 states. Our results show that S1 vibrationally relaxes in <2 ps, much faster than the S1–S0 internal conversion time, and that IVR and vibrational cooling in the ground state occur over a range of times (1–12 ps) suggesting mode-specific cooling rates in S0.
Materials and Methods
all-trans-β-Carotene (Aldrich) was recrystallized from benzene and methanol. An ∼18 μM solution of β-carotene (λmax = 463 nm, OD463 = 0.247 mm−1, εmax = 139 000 M−1 cm−1) in toluene was prepared from dried crystals under dim light and stored under nitrogen. The sample was kept on ice and circulated through a 2 mm square cell in a closed loop under nitrogen. The flow rate of the solution (200 μm/ms) was chosen so that the illuminated sample volume was completely replaced between shots. The OD at the pump wavelength was 0.075 mm−1 and the OD at the probe wavelength was 0.010 mm−1. The absorption spectrum did not exhibit any observable changes over the course of the experiment.
Instrumentation
The picosecond resonance Raman laser system has been described in detail elsewhere.23,24 Briefly, a picosecond Ti:Sapphire oscillator (Spectra-Physics Tsunami model 3950) seeds a Ti:Sapphire regenerative amplifier (Spectra-Physics Spitfire) that produces a 1 kHz, 3 ps pulse train. After frequency doubling in BBO, the resultant 403 nm beam is Raman-shifted in a 0.5 m pipe filled with 1000 psi D2 to produce the 531.5 nm second Stokes probe beam, while the residual SHG beam is used as the pump. The pulse width of the probe was 1.5 ps (16 cm−1 fwhm) and the pump/probe cross-correlation was 4.1 ps with an approximately Gaussian shape. Deconvolution of the cross-correlation, assuming Gaussian pulse shapes, indicates that the pump pulse fwhm was 2.9 ps. The pump−probe time delay was calibrated with sum-frequency generation in BBO to within ±0.5 ps.
The pump and probe beams were focused onto the flowing sample with a 50 mm f.l. spherical lens, producing a 50 μm diameter focal point. The average pump power at the sample point was 420 μW (4.3 × 1016 photons/cm2/pulse) and the probe power at the sample point was 190 μW (2.6 × 1016 photons/cm2/pulse). With a 5 ps pump−probe delay, the growth in intensity of the S1 Stokes peaks and S0 anti-Stokes peaks and the decrease in intensity of the S0 Stokes peaks were linear in pump power from 350 to 550 μW. The changes in intensity of all Stokes and anti-Stokes peaks were linear in probe power from 150 to 260 μW.
Raman scattering was collected with an f/1.2, 50 mm f.l. camera lens and imaged onto the 200 μm (26 cm−1) entrance slit of the spectrograph (Spex 500 M, 500 g/mm, 560 nm blaze) with an f/4, 200 mm f.l. singlet lens. The pump scattering was removed with a long-pass filter (Schott GG435), whereas the probe scattering was removed with a 1064.0 nm notch filter (Kaiser Optical) using its second-order blocking capability at 532 nm. The width of the optical notch was 10 nm, which allowed simultaneous collection of Stokes and anti-Stokes scattering to within 300 cm−1 of the probe wavelength. The dispersed light was detected with a liquid nitrogen cooled CCD (Princeton Instruments, LN/CCD-1100-PB/UVAR). The instrument response was determined with a tungsten standard lamp. Wavelength calibration was performed using a neon lamp. All absolute Raman shifts are accurate to ±4cm−1, whereas relative shifts are accurate to ±0.5 cm−1.
Pump + probe spectra were collected for 10 min at each pump + probe time delay, with probe-only and pump-only spectra measured for 5 min between each pump + probe time point. Spectra with twenty different time delays between −6 and 100 ps were acquired. The fluorescence background in the pump-only spectra exhibited no change over the approximately 12 h of data collection. Pump-only, probe-only, and pump + probe spectra of neat toluene were measured for 5 min each to provide solvent spectra.
Spectral Subtraction
Examples of corrected pump + probe, pump-only, and probe-only data are presented in Figure 1. In the pump + probe spectrum with Δt = 1 ps (solid line), the Raman lines of toluene and β-carotene are superimposed on the broad fluorescent background which is also evident in the pump-only spectrum (dashed). Comparing the Stokes Raman peaks of the pump + probe spectrum with the probe-only spectrum (dotted), the decreased relative intensity of the β-carotene peaks is visible, indicative of ground-state depletion by the pump pulse.
Figure 1.
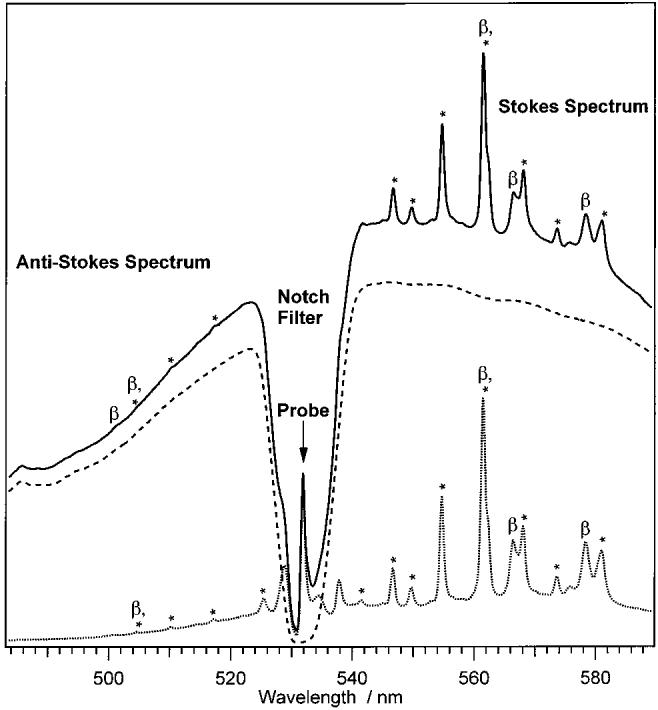
Representative pump + probe (solid-line), pump-only (dashed line), and probe-only (dotted line) spectra of β-carotene. The pump + probe time delay is 1 ps. The dip in the middle of the spectrum is due to the notch filter, which removes scattered light within 5 nm of the probe wavelength (visible as the peak in the middle of the notch). Pump-induced fluorescence from S2 spans the entire spectral window. Peaks labeled with an asterisk (*) are due to toluene. Peaks due to β-carotene are labeled “β”.
To visualize the pump-induced changes quantitatively, background-free time-resolved Raman spectra were generated from the pump + probe spectra using the subtraction procedure shown in Figure 2. The pump-induced fluorescence was removed by subtracting the pump-only spectrum (B) from the pump + probe spectra (A). The spectra were then corrected for self-absorption, using the toluene peaks as an internal standard, by dividing by the transmission spectrum (T(λ)) of a 1.4 mm effective path length β-carotene solution to produce spectrum C. This large effective path length indicates that the dynamic self-absorption occurring in the 50 μm illuminated spot has a negligible contribution relative to the static ground-state absorption. The toluene Raman peaks were then removed by subtracting the pure toluene probe-only spectrum (D), resulting in spectum E. Because of slight changes in the spectral profile of the probe beam over the course of the experiment, it was sometimes necessary to shift the toluene spectra slightly to obtain a proper solvent subtraction. The broad fluorescence background under the Stokes and anti-Stokes spectra was fit to a 19th order polynomial (F) and subtracted, leaving the background-free, time-resolved Raman spectrum of the ground and excited states of β-carotene (G). It was necessary to use a high-order polynomial to effectively fit the structure of the fluorescence over the broad spectral range of both the Stokes and anti-Stokes windows and to describe the decreased instrument response approaching the notch filter wavelength. A background-free Raman spectrum of S0 β-carotene was obtained from the averaged probe-only spectra using the same spectral subtraction procedures as described above.
Figure 2.
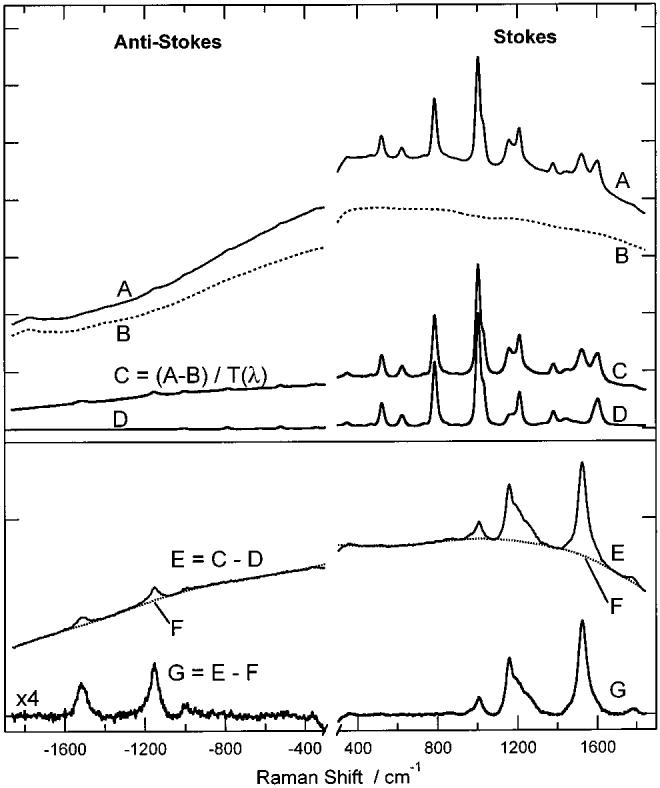
Subtraction procedure used to produce time-resolved Raman spectra of β-carotene. The pump + probe spectrum (A) with Δt = 6 ps, pump-only spectrum (B, dashed), and toluene probe-only spectrum (D) were collected under the conditions described in the text. The pump induced fluorescence (B) is subtracted from the pump + probe spectrum (A) and corrected for β-carotene self-absorption by dividing by T(λ), the β-carotene transmission spectrum. The toluene peaks in this spectrum (C) are removed by subtracting the toluene probe-only spectrum (D). The resultant spectrum (E) contains both β-carotene Raman scattering and residual fluorescence. The fluorescence background is fit (F, dotted) and subtracted to give the background free pump + probe Raman spectrum of β-carotene (G). The anti-Stokes region of spectrum G has been magnified ×4 for display.
Kinetic Analysis
The kinetics of the Raman intensities were first analyzed by empirically fitting to the convolution of our Gaussian instrumental response with a single or double exponential molecular response
| (1) |
The functional form of eq 1 varied depending on the dynamics being considered. For the S0 recovery, the parameters in eq 1 were chosen to produce an instantaneous bleach followed by a single-exponential recovery. For the S1 peaks, the molecular response was set to a biexponential representing the fast formation and the slower decay of the S1 population. The anti-Stokes signals were fit to a biexponential molecular response with different amplitudes for the two exponential terms allowing an instantaneous decrease in intensity followed by exponential rise above baseline and subsequent decay back to the baseline.
To more effectively analyze the anti-Stokes dynamics, it was necessary to develop a first-order kinetic model of the relaxation encompassing excitation from S0 to S2, fast relaxation from S2 to S1, internal conversion from S1 to vibrationally hot S0, and then cooling from hot S0 to the final relaxed S0 state. (Here, we use “hot” to refer to any molecular state that has excess vibrational energy relative to what would be expected for a Boltzmann population at 10 °C, the bulk sample temperature. We use “cooling” to refer to any process that reduces the excitation present in a particular vibrational mode. This cooling may occur by IVR or vibrational energy dissipation to the solvent.) Excitation creates an initial population in S2 and relaxation of this population and subsequent time-dependent population changes in the other states can be solved exactly using first-order kinetics, assuming the relaxation scheme
| (2) |
where k21 and k10 are the S2 → S1 and S1 → S0 internal conversion rates, and k00 is the mode-specific cooling rate in S0. With the conditions , and , the solutions to the time-dependent populations are as follows
| (3) |
| (4) |
| (5) |
| (6) |
Where The net observed intensity of the S0 Stokes and anti-Stokes peaks, relative to that observed in the probe-only spectrum, is
| (7) |
where the coefficient, d, represents the relative increase or decrease in scattering from relative to the room-temperature S0 population. The enhancement factor, d, parametrizes all contributions to the scattering intensity of the hot species including population and resonance enhancement changes. Because of the decrease in Stokes scattering cross-section with increasing temperature,25 we might expect d ≤ 1 for the Stokes peaks. However, this effect may be significantly attenuated by our use of a probe wavelength on the red edge of the absorption spectrum, where increased relative enhancement of vibrationally hot molecules is expected.25 In the anti-Stokes spectrum, however, the increase in population in excited vibrational states in hot S0 would increase anti-Stokes signal and therefore we would expect d > 1. Substituting eqs 5 and 6 into eq 7, we get
| (8) |
The S0 Stokes and anti-Stokes kinetics were fit to the convolution of eq 8 with the Gaussian instrumental response. In all of the fits, the zero of time was adjusted as discussed below. It should be noted that the only variable parameters in eq 8 are [S2(0)], d, k21, k10, and k00; the α's and β's are functions of k21, k10, and k00 and are therefore not independent variables.
Results
Representative pump + probe spectra are presented in Figure 3 along with the probe-only spectrum. On both the Stokes and anti-Stokes sides of the probe-only spectrum, the three largest S0 vibrational peaks are visible at 1004, 1157, and 1523 cm−1 corresponding to the methyl rock (C–CH3), carbon single-bond stretch (C=C) and carbon double-bond stretch (C=C) normal modes.26 Comparing the +2 and −2 ps pump + probe Stokes spectra, the decrease in intensity of the S0 C–C and C–CH3 peaks at 1157 and 1004 cm−1 is clearly visible. In addition, growth of the Stokes S1 signal is evidenced by the broad shoulder that develops on the high-frequency side of the C=C band (∼1230 cm−1) and by the high-frequency C=C band (1781 cm−1). The large increase in S0 anti-Stokes scattering at positive time delays is due to the formation of hot S0 molecules after internal conversion from S2 through S1 to S0. Note also that no S1 peaks are visible in the anti-Stokes spectra.
Figure 3.
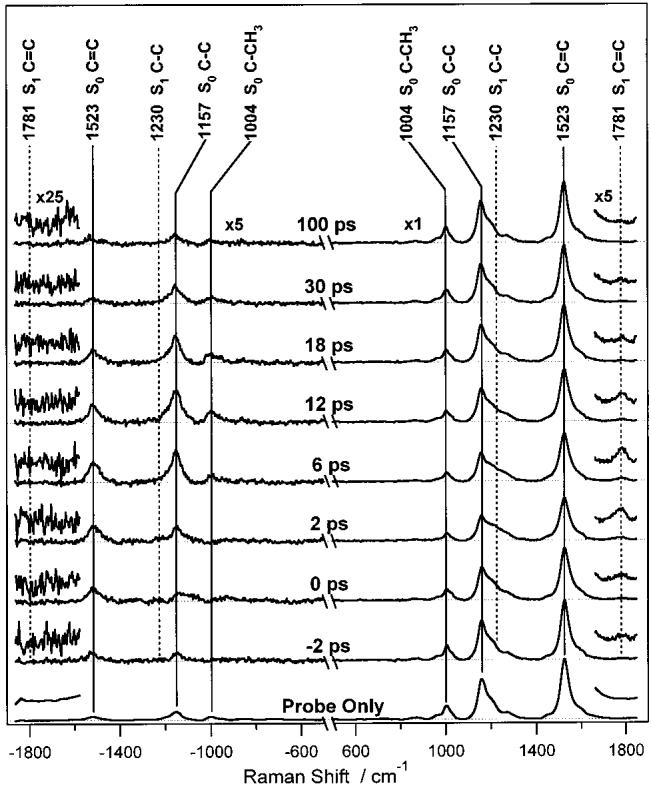
Time-resolved pump + probe Raman spectra of β-carotene. Peaks from S1 (marked by dashed vertical lines) are superimposed on peaks from S0 (solid vertical lines). The anti-Stokes spectra (left side) are blown up ×5 for display. Note the decrease in intensity and subsequent recovery of the S0 Stokes peaks and the large increase in S0 anti-Stokes scattering caused by internal conversion from S1 to S0. The magnifications around ±1800 cm−1 reveal the appearance and decay of the S1 C=C Stokes peak at 1781 cm−1 and the fact that no corresponding anti-Stokes peak is observed.
To clarify the positions and shapes of the S1 and hot S0 bands, the S0 probe-only Stokes spectrum was subtracted from the pump + probe Stokes spectra until the S0 peaks at 1004 and 1157 cm−1 were completely removed. The subtraction coefficient, c(t), varied between 60 ± 2% at 6 ps and 101 ± 2% at 100 ps. A representative set of these Stokes difference spectra is presented in Figure 4. In the early difference spectra, the S1 C–C band at 1230 cm−1, the S1 C=C peak at 1543 cm−1, and the high-frequency S1 C=C peak at 1781 cm−1 are observed. Although most of the S0 peaks are removed by the subtraction, at longer time delays peaks from the hot ground state are visible on the low-frequency side of the S0 C–C and C=C peaks at 1145 and 1509 cm−1. These hot S0 bands are not completely removed by the subtraction because they are anharmonically downshifted. Attempts to decompose the ∼1200 and ∼1530 cm−1 bands into separate S1 and hot S0 peaks were unsuccessful because of the complex shape and intensity evolution of the hot S0 peaks.
Figure 4.
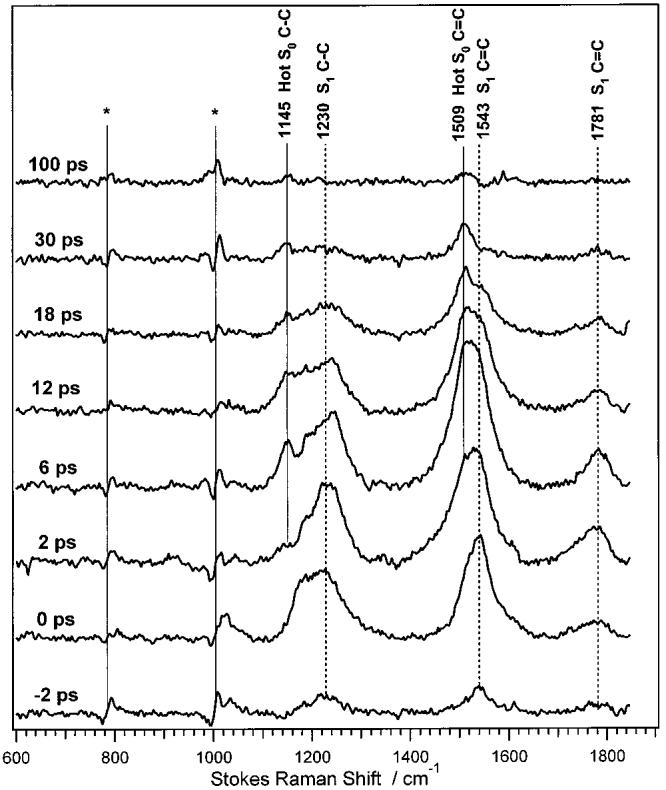
Time-resolved Stokes difference spectra of β-carotene, produced by subtracting the probe-only S0 spectrum from the time-resolved pump + probe spectra. Peaks attributed to S1 are indicated with the dashed vertical lines. Residual scattering from the hot S0 state is also observed, anharmonically red-shifted from the S0 C–C and C–C bands. Features marked with an asterisk (*) are due to imperfect subtraction of toluene.
Analysis of the kinetics of the Stokes spectra using eq 1 (see below) revealed that the decay-time, τ0, was very sensitive to variations in the rise-time, τ1, and the zero of time, Δt0. It was thus necessary to adjust Δt0 and to choose and fix the rise-time, τ1, of the S1 peaks. To determine τ1, the S1 peak kinetics (Figure 5c-e) were first fit using eq 1 and all parameters except a0, a1, and B were allowed to vary. The weighted mean of the best-fit values of τ1 (0.2 ± 0.2 ps) was chosen and fixed in subsequent analyses that determined Δt0 and τ0. This value of τ1 is consistent with the 144 ± 10 fs S2 → S1 IC time constant determined in previous fluorescence upconversion experiments in toluene.9 To determine Δt0, both the S1 kinetics, with τ1 fixed at 0.2 ps, and the S0 recovery kinetics (Figure 5a,b) were fit. The weighted mean of all five fits gave Δt0 = 0.3 ± 0.1 ps, and this zero of time was used in all subsequent analyses.
Figure 5.
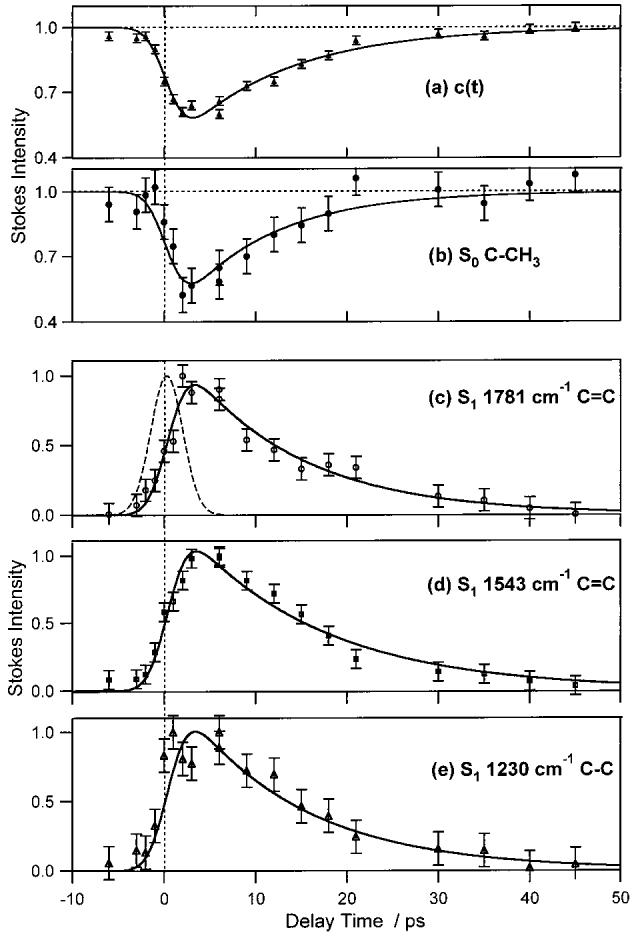
Kinetics of the time-resolved Stokes spectra of β-carotene. The top two panels present the dynamics of S0 population depletion and recovery. The subtraction coefficient, c(t), was used to scale the probe-only spectrum in the generation of the Stokes difference spectra. The S0 C–CH3 intensity (b) is the integrated area of the methyl-rock peak at 1004 cm−1 in the pump + probe spectra. The bottom three panels present the dynamics of the S1 state monitored by the Stokes difference spectra. The data points are the integrated areas of the S1 C=C peak at 1781 cm−1 (c), the C=C band at 1543 cm−1 (d), and the C–C band at 1230 cm−1 (e). The 4.1 ps fwhm Gaussian instrumental response is shown as the dashed curve in (c). The solid curves are the fits of a convolution of the instrument response with the exponential molecular response described in eq 1. The fitting parameters are summarized in Table 1.
The dynamics of ground state bleaching and recovery are revealed by the kinetics of the probe-only subtraction coefficients, c(t) in Figure 5a, as well as the Stokes S0 C–CH3 intensity in Figure 5b. Although the bleaching of the ground state is also visible in the S0 C–C and C=C Stokes peaks, the overlap of these features with S1 bands dictates that their integrated areas are not strictly proportional to S0 population. The c(t) and the C–CH3 kinetics were fit by a single-exponential molecular response using eq 1 with the best-fit parameters of A = 56%, τ0 = 12.0 ± 0.7 ps, and A = 59%, τ0 = 10.2 ± 2.3 ps, respectively. The weighted mean of these two amplitudes indicates that each pump pulse excited 56 ± 2% of the β-carotene in the illuminated sample. The kinetic model fits of the S0 Stokes data using eq 8 gave poorer fits than the single-exponential molecular response. This is most likely because the Stokes scattering cross-section of hot S0 is nearly the same as cool S0 at our probe wavelength, making d ≈ 1 in eqs 7 and 8 and the observed dynamics essentially independent of the cooling rate.
The analysis of the kinetics of the 1781 cm−1 C=C, 1543 cm−1 C=C, and ∼1230 cm−1 C–C peaks of the S1 excited state is presented in Figure 5c-e. As described previously, the rise time of the S1 peaks was fixed at 0.2 ps. With this constraint, the decay times were determined to be 12.6 ± 1.3, 15.1 ± 1.2, and 13.2 ± 1.8 ps for the 1781, 1543, and 1230 cm−1 peaks respectively (see Table 1). Because the C=C peak at 1781 cm−1 is unencumbered by any overlap with S0 peaks, it provides the best measure of the S1 → S0 kinetics and indicates that this IC time constant is 12.6 ps. However, the fact that the decay time constants of the other Stokes kinetics in Figure 5 agree with this value within the error limits indicates that the contribution of hot S0 scattering to the 1543 and 1230 cm−1 S1 kinetics does not significantly perturb the results (see discussion below).
TABLE 1.
Exponential Analysis of β-Carotene Stokes and Anti-Stokes Intensitiesa
| figure | component | Ab,c | a0 | τ0 (ps) | a1 | τ1 (ps) |
|---|---|---|---|---|---|---|
| 5a | c(t) Stokes subtraction coef. | −0.56 (0.02) | 1 | 12.0 (0.7) | 0 | n.a. |
| 5b | S0 Stokes C–CH3 (1004 cm−1) | −0.59 (0.08) | 1 | 10.2 (2.3) | 0 | n.a. |
| 5c | S1 Stokes C–C (1781 cm−1) | 1.27 (0.07) | 1 | 12.6 (1.3) | −1 | 0.2d |
| 5d | S1 Stokes C–C (1543 cm−1) | 1.35 (0.06) | 1 | 15.1 (1.2) | −1 | 0.2d |
| 5e | S1 Stokes C–C (1230 cm−1) | 1.42 (0.11) | 1 | 13.2 (1.8) | −1 | 0.2d |
| 6a | S0 anti-Stokes C–C (1523 cm−1) | 5.9 (1.6) | 1 | 11.7 (2.6) | −1 | 1.4 (0.7) |
| 6b | S0 anti-Stokes C–C (1157 cm−1) | 1 | 6.1 (2.2) | 15.3 (3.7) | −8.3 (1.8) | 3.1 (1.4) |
| 6c | S0 anti-Stokes C–CH3 (1004 cm−1) | 1 | 8.8 (16) | 16 (11) | −10.9 (15) | 6.8 (5.5) |
Parameters were determined using eq 1 to model the data in Figures 5 and 6. The offset, B, was set to 1 in Figure 5a,b, 0 for 5c-e, and 1 for 6a–c.
The Δt = 0 offset, Δt0, was determined by initially allowing it to vary as a fitted parameter. The weighted average of these, 0.3 ± 0.1 ps, was chosen as the best overall value and fixed for these calculations.
The amplitude, A, in 5a,b corresponds to the proportion of sample excited by the pump pulse. In 5c–e and 6a, A is a scaling factor without any molecular significance. In 6b,c, A is fixed at 1 to prevent redundancy when a0 and a1 are allowed to vary.
The rise time, τ1, of the S1 peaks was much faster than the time resolution of this experiment and could not be accurately determined. The value of 0.2 ps was chosen as described in the text.
The normalized intensities of the S0 anti-Stokes bands are presented in Figure 6. The S0 anti-Stokes signal is expected to decrease instantaneously due to ground state depletion, to then increase above the probe-only level due to the formation of vibrationally excited molecules after internal conversion from S1, and finally to decay back to the probe-only level via vibrational cooling. This is the observed behavior, although the initial decrease is only suggested in the C–CH3 anti-Stokes data. Attempts to fit the anti-Stokes kinetics to a biexponential molecular response function (eq 1) were hampered by large uncertainty in the parameters. For completeness, however, these results are reported in Table 1 and Figure 6 (dotted). These fits indicated that the decay times of the C=C, C–C, and C–CH3 peaks were 11.7 ± 2.6, 15.3 ± 3.7, and 16 ± 11 ps, respectively. The respective rise times of the peaks were 1.4 ± 0.7, 3.1 ± 1.4, and 6.8 ± 5.5 ps.
Figure 6.
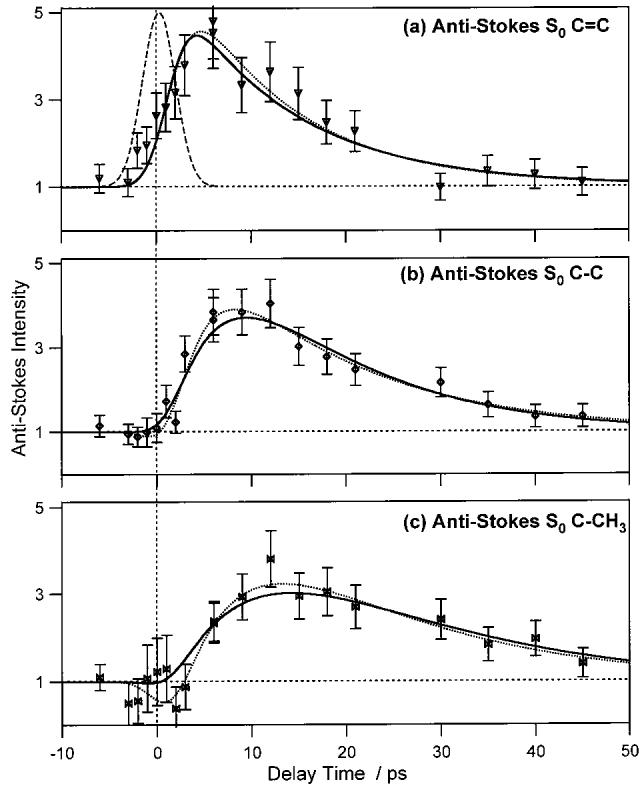
Kinetics of the time-resolved anti-Stokes β-carotene spectra. Data points are the integrated areas of the anti-Stokes S0 C=C peak at 1523 cm−1 (a), the S0 C–C peak at 1157 cm−1 (b) and the S0 C–CH3 peak at 1004 cm−1 (c). The 4.1 ps fwhm Gaussian instrumental response is shown as the dashed curve in (a). The other curves are the best-fit convolutions of the instrument response with either a biexponential (eq 1, dotted) or kinetic (eq 8, solid) model of the molecular response. Values of the best fit parameters are summarized in Tables 1 and 2. Each peak area has been normalized to its area in the probe-only spectrum.
A more precise analysis of the anti-Stokes kinetics was obtained by fitting the anti-Stokes data to the convolution of our instrument response with the kinetic model described by eq 8. The results of these fits are shown in Figure 6 (solid) and Table 2. These analyses were constrained by setting k21 and k10 to the values determined by the biexponential fits of the S1 peaks, and [S2(0)] to the value determined by the S0 Stokes data. This allowed for the determination of the following: (1) the cooling rate, k00, for each vibrational mode, and (2) the enhancement factor, d, which measures the increase of anti-Stokes signal from relative to the room temperature S0. Unconstrained fits, in which k10 was allowed to vary, converged to essentially the same value of k10 as the exponential fits, but with much larger errors in the parameters because of their interdependence. In Figure 6, it is apparent that the kinetic model and the exponential fits agree well with each other, although the initial incipient decrease in the C–CH3 kinetics is not reproduced with the kinetic model. The expected decrease is too small compared with the measurement error to be statistically significant. The benefit of the kinetic model is that we can definitively assign the mode-specific cooling rate associated with the observed anti-Stokes kinetics. The cooling time of the S0 C=C peak is extremely fast, 0.7 ± 0.4 ps, and this band exhibits a very large enhancement factor of 171 ± 85. The S0 C–C peak has a slower cooling time of 5.4 ± 0.9 ps and a smaller enhancement factor of 25 ± 3. The S0 C–CH3 peaks shows the slowest cooling time, 12.1 ± 2.5 ps, and the lowest enhancement factor, 12 ± 2.
TABLE 2.
Kinetic Model Analysis of β-Carotene Anti-Stokes Intensitiesa
| figure | component | τ21 (fixed) (ps)b | τ10 (fixed) (ps)c | τ00 (fit) (ps) | d (fit)d |
|---|---|---|---|---|---|
| 6a | S0 C–C (1523 cm−1) | 0.2 | 12.6 | 0.7 (0.4) | 171 (85) |
| 6b | S0 C–C (1157 cm−1) | 0.2 | 12.6 | 5.4 (0.9) | 25 (3) |
| 6c | S0 C–CH3 (1004 cm−1) | 0.2 | 12.6 | 12.1 (2.5) | 12 (2) |
The time constant for S2 ← S1 internal conversion, τ21, was much faster than the time resolution of this experiment and could not, therefore, be experimentally determined. The value of 0.2 ps was chosen as described in the text.
The S1 ← S0 time constant was calculated as the weighted mean of the decay times, τ0, determined from the exponential fits to the Stokes kinetics (see Table 1).
The enhancement factor, d, is an empirical measure of the increase in population in v = 1 of the hot S0 state relative to the room-temperature S0 state (see text).
The cooling rates in S1 and S0 can also be monitored by the time-dependent frequencies of the S1 Stokes and the S0 Stokes and anti-Stokes peaks. Figure 7 shows that the S1 C=C peak blue shifts 10 cm−1 in <2 ps and that both the Stokes and anti-Stokes S0 C–C peaks blue shift 3–4 cm−1 in <10 ps. The S1 C=C frequency shift is fit with a 1.4 ps exponential rise time, consistent with the <2 ps S1 cooling time determined using anti-Stokes intensity analysis (see below). The S0 C–C frequency shifts with a ∼5 ps time constant, consistent with the 5.4 ps C–C cooling time determined by the anti-Stokes intensity kinetics.
Figure 7.
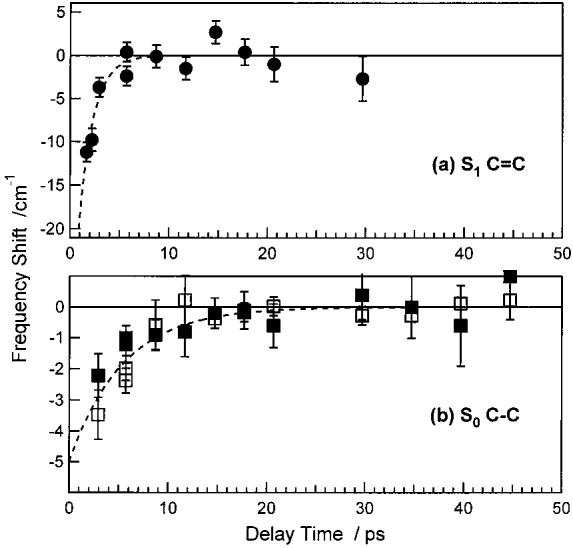
Time-dependent frequency shifts of the S1 C=C and S0 C–C Raman peaks of β-carotene. (a) The frequency of the Stokes S1 C=C mode relative to 1781 cm−1. The dashed line is a 1.4 ps exponential decay. (b) The frequency shifts of the Stokes (open squares) and anti-Stokes (filled squares) S0 C–C peaks relative to 1157 cm−1. The dashed line is a 5.4 ps exponential decay, determined by the anti-Stokes C–C kinetics.
Discussion
Excited-State Spectra
Our S1 Raman spectra of β-carotene are consistent with previous time-resolved Raman studies showing that vibrational bands of S1 are highly shifted from the ground-state frequencies.10,27-29 The 1157 cm−1 S0 C=C peak splits into approximately 3 overlapping peaks at 1204, 1243, and 1282 cm−1 in S1 and the 1523 cm−1 S0 C–C peak splits into two peaks at ∼1530 and ∼1780 cm−1. These frequency changes have been reproduced by the nonadiabatic vibronic coupling model of Zgierski et al.30 Investigations of the high-frequency S1 C–C peak in different solvents,29 carotenoids,31 and isotopomers10 revealed that the S1–S0 frequency shift can be directly correlated with the extent of S1–S0 vibronic coupling. The 1781 cm−1 frequency of our S1 C=C peak is consistent with previous observations in polarizable solvents.29 However, our low-frequency 1543 cm−1 C=C peak can only be compared with previous experiments in a relatively nonpolarizable solvent (THF) in which the two S1 C=C peaks were observed at 1530 and 1796 cm−1.10,32 The solvent dependence of the high-frequency C=C peak frequency has been attributed to a breakdown of C2h symmetry in S1 and the accompanied increase in S1-S2 vibronic coupling.29 The upshift in our low-frequency C=C peak and the downshift of our high-frequency C=C peak relative to previous work by Koyama et al.10,32 may be due to solvent dependent changes in the S1–S2 vibronic coupling. It is also possible that the lower C=C frequency observed in the previous work was affected by the spectral subtraction technique used, which is difficult because of the inherent spectral broadening of the ground-state spectrum at high powers and the close proximity of the S0 and S1 peaks around 1530 cm−1.
Excited-State Vibrational Relaxation
One of our primary results is that there are no observable S1 peaks in our high signal-to-noise anti-Stokes spectra. As summarized in Figure 8, this indicates that following fast internal conversion from S2, molecules in S1 equilibrate most of the excess photon energy (4600 cm−1) as well as the energy of the S2 → S1 internal conversion (5800 cm−1) within 2 ps. As a result, there is no observable S1 population in the high-frequency v ≥ 1 vibrational levels. We estimate a maximum vibrationally excited population of <10% at 2 ps: On the basis of our limit-of-detection, we can place an upper limit on the anti-Stokes:Stokes intensity ratio of 15% for the C=C peak and 3% for the C–C peak at a time delay of 2 ps. Factoring in the vs3 dependence of the Raman scattering, the population in v ≥ 1 must be less than 10% and 2% of the total excited population within 2 ps after excitation for the C=C and C–C modes, respectively. Because it is unlikely that by 2 ps there would be more excitation in the higher frequency mode, we can place an upper bound of <2% on the S1 vibrational excitation. However, because under these resonance conditions the anti-Stokes scattering strength could be 5 times less than the Stokes scattering strength, a more conservative upper bound of <10% excitation is suggested. These results contrast with the conclusions of Yoshizawa et al.15 on β-carotene and Zhang et al.16 on lycopene who both hypothesized that relaxation in S1 proceeds normally until the molecule is trapped in the v = 1 C–C vibrational state. If this were the case, then we would expect the percentage of vibrationally excited molecules in S1 to be nearly 100% at and beyond 2 ps. A vibrationally excited population of this magnitude would almost certainly produce a large anti-Stokes signal, which we clearly do not observe. It is likely that the 0.6 ps relaxation rate observed by Yoshizawa et al. is reporting on the completion of the IVR process in S1, rather than an incomplete relaxation to v = 1.16 This fast IVR process, which has been observed in several other studies,4,17 is much faster than could be detected with the 2–3 ps time resolution of Zhang et al.15
Figure 8.
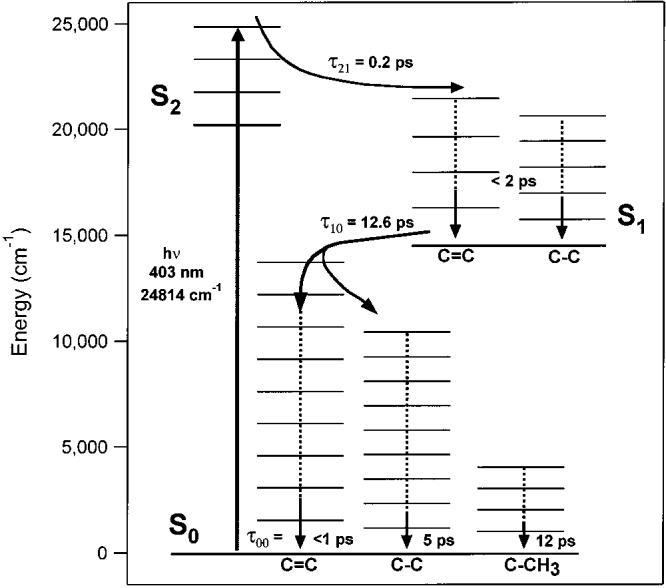
Vibronic relaxation scheme of β-carotene. After excitation to S2 (1Bu+), the molecule relaxes in 0.2 ps to S1 (2Ag−). In S1 IVR occurs very rapidly, such that the population of vibrational states with v = 1 is less than 10% within 2 ps. Internal conversion from S1 to S0 (1Ag−) occurs with a 12.6 ps time constant. The C=C mode is the primary accepting mode of the IC process and relaxes in <1 ps through IVR. The C–C mode is excited directly by IC, as a minor accepting mode, and relaxes with a ∼5 ps time constant. The C–CH3 mode is excited by the IVR process and then relaxes with a 12 ps time constant, which is likely the molecular cooling rate.
Excited-State Lifetime
The 12.6 ps S1 lifetime determined here is slightly longer than those determined previously for β-carotene in aromatic solvents by transient absorption (8.4 ± 0.6, 10 ± 2, and 8.8 ± 0.2 ps).16,33,34 This difference is most likely due to the fact that our experiment was performed at ∼0–10 °C, whereas previous experiments were all performed at room temperature. Decreasing the sample temperature can as much as double the internal conversion time constant for carotenoids.11 We can eliminate the possibility that our measured lifetimes are systematically increased as a result of interference with ground-state cooling features by noting the agreement of the S1 lifetime measured by the 1781 cm−1 C=C peak with the average of the other four Stokes decay times. If there was a contribution from slow ground-state cooling process, we would expect the kinetics of the S1 peaks at 1230 and 1543 cm−1 to be significantly longer than the kinetics of the 1781 cm−1 peak. However, since all of these decay times are within one standard deviation of each other, we conclude that ground-state cooling has a negligible affect on the measured lifetimes.
Ground-State Vibrational Relaxation
Analysis of the anti-Stokes kinetics is complicated by the slow rate of internal conversion between S1 and S0. Because IC necessarily occurs before the formation of hot S0, any faster dynamics occurring within the ground-state manifold will be hidden. By examining the preexponential factors (αι and β ι) in eq 5, it is apparent that with , the kinetics of will be dominated by a rising term determined by k00, the mode specific cooling rate, and a decaying term determined by k10, the S1 → S0 internal conversion rate. This is counterintuitive considering that schematically is formed via k10 and is removed via k00. As a result, the exponential decays of the anti-Stokes kinetics (τ0, Table 1) can be assigned to the S1 → S0 internal conversion time and, as expected, they are all within one standard deviation of the 12.6 ps time constant determined in the Stokes kinetics. We assign the rising terms of the anti-Stokes kinetics (τ1, Table 1) to the cooling times of these vibrational modes, however, these cooling times are better determined using the kinetic model (τ00, Table 2). In general, it is apparent that the cooling times increase as the vibrational frequency decreases. As summarized in Figure 8, the 1523 cm−1 C=C relaxes in ∼ 1 ps, the 1157 cm−1 C–C relaxes in ∼5 ps, and the 1004 cm−1 C–CH3 relaxes in ∼12 ps. Our revised relaxation scheme becomes
| (9) |
The enhancement factor, d, determined by the anti-Stokes kinetic model is a measure of the increase in anti-Stokes scattering in relative to (cool) S0. The enhancement arises from either an increase in the resonance enhancement or from an increase in the vibrationally excited population. A large change in resonance enhancement can occur through two mechanisms, both of which are unlikely in this system. First, an increase in resonance enhancement of could occur if the scattering arose from a different vibrational transition than the S0 scattering, which comes entirely from the v = 0 ← 1 transition. Our probe wavelength is approximately one vibrational quantum (∼1400 cm−1) below the S2–S0 electronic origin and is therefore very near the maximum in the v = 0 ← 1 anti-Stokes Raman excitation profile. Hence, at this wavelength we would expect to see only a decrease in relative scattering strength from molecules excited to vibrational states above v = 1.35 Also, given that the rate of vibrational relaxation scales approximately linearly with vibrational quantum number,36 it is unlikely that any high vibrational quantum number states would be present on the picosecond time-scale of our experiment. Second, changes in the resonance enhancement may occur with increasing temperature, even if the anti-Stokes scattering is generated from the v = 0 ← 1 transition. This would occur if there existed low-frequency modes that were strongly coupled to the resonant electronic transition; however, β-carotene has no strongly displaced low-frequency modes and, hence, should be relatively insensitive to this thermal multi-mode quenching.25 We therefore conclude that most of the anti-Stokes scattering generated after IC is due to the v = 0 ← 1 transition in each mode and that the enhancement factors can be attributed to an increase in population of the v = 1 state.
Based on this conclusion, we can use our measured enhancements to estimate the degree of vibrational excitation in . Table 3 compares the observed occupation numbers after IC with the thermal occupation numbers that we would expect for different energy partitioning models. The thermal occupation numbers of each vibration in S0 at 10 °C are 0.00043, 0.0028, and 0.0061 for the C=C, C–C, and C–CH3 modes, respectively. Multiplying these values by d determines the observed occupation numbers in , which are 0.074, 0.070, and 0.073, respectively. If the S1–S0 internal conversion energy (14 500 cm−1)37 is thermally distributed among all 282 normal modes of the molecule, the temperature will increase to 468 K. At this temperature the thermal occupation numbers for the C=C, C–C, and C–CH3 modes will be 0.0093, 0.029, and 0.046, respectively, which are 22, 10, and 8 times larger than at 283 K but much less than necessary to generate the observed enhancements of 171, 25, and 12. Alternatively, if we distribute the full photon energy (24 814 cm−1) in a Boltzmann population in S0, then the temperature increases to 568 K. This would give occupation numbers of 0.021, 0.053, and 0.079 and enhancement factors of 49, 19, and 13 for the C=C, C–C, and C–CH3 modes, respectively. The observed enhancements of the C=C and C–C modes are much larger than we would expect for a fully thermalized molecule, but the enhancement of the C–CH3 mode is very nearly what we would expect based on thermalization of the photon energy throughout the molecule. This indicates that the C=C and C–C modes are preferentially excited by the IC process, whereas the C–CH3 mode has no more excitation than that dictated by thermalization.
Table 3.
Observed and Calculated Thermal Occupation Numbers of β-Carotene
| source | energy (cm−1) | T (K) | occupation number, ñ (ratio to 283 K value)a |
||
|---|---|---|---|---|---|
| C–C | C–C | C–CH3 | |||
| observedb | n.a. | 850–550 | 0.074 (171) | 0.070 (25) | 0.073 (12) |
| sample temp.c | 9388 | 283 | 0.00043 (1) | 0.0028 (1) | 0.0061 (1) |
| int. conv.d | 14 500 | 468 | 0.0093 (22) | 0.029 (10) | 0.046 (8) |
| photond | 24 814 | 568 | 0.021 (49) | 0.053 (19) | 0.079 (13) |
Occupation numbers defined for a Boltzmann population at a given temperature as ñ = exp(-hv/kT). The energy stored at a given temperature is given by: , where the vibrational frequencies of β-carotene were calculated by Gaussian 9839 at the HF/3-21G level and scaled by 0.834. The scaling factor was chosen to place the calculated frequencies of the C–C, C–C, and C–CH3 modes at the observed frequencies.
Calculated by multiplying the sample temperature occupation numbers by the enhancement factor, d, determined spectroscopically. Note that the enhancement factors in parentheses are those determined in Figure 6 and shown in Table 2. The temperatures noted are the range of temperatures necessary to produce the calculated occupation numbers.
Calculated assuming a Boltzmann distribution of vibrational excitation at 10 °C.
The temperature was determined by adding either the S1−S0 internal-conversion energy (14 500 cm−1) or the pump-photon energy (24 814 cm−1) to the 9388 cm−1 of energy stored at 10 °C and distributing the net energy into a thermalized Boltzmann population of vibrations.
Vibrational Cooling
Following IVR, the energy of internal conversion is dissipated to the surrounding solvent environment through vibrational cooling. Our spectra reveal no long-term increase in anti-Stokes signal from β-carotene, indicating that vibrational cooling must occur in less than 13 ps. If the cooling rate were slower than the rate of internal conversion then there would be a build-up of anti-Stokes signal at long times and the decay of the anti-Stokes signal would exhibit biexponential kinetics. The relaxation time of the C–CH3 mode (12 ps) is consistent with the 5–15 ps cooling time observed in longer carotenoids4 and with our condition that the cooling must occur in <13 ps, so it is quite likely that the cooling time of the C–CH3 mode is equivalent to the overall rate of energy dissipation to the solvent.
Implications for the Mechanism of IC and Ground-State IVR
Our cooling times and enhancement factors are consistent with a model of β-carotene relaxation in which the C=C and C–C stretching modes are the dominant acceptor modes in the internal conversion process. Because the observed enhancements are much larger than those calculated for a fully thermalized molecule, we conclude that the anti-Stokes signal from the C=C and C–C modes arises from hot ground-state molecules that have not fully thermalized on the ground state surface and that these modes must have received preferential excitation during IC. The extremely large enhancement factor of the C–C mode and the modest enhancement of the C–C mode indicate that the C–C mode is the primary acceptor, with the C=C mode being a minor acceptor. In contrast, the similarity of the C–CH3 mode enhancement to that expected in a thermalized molecule indicates that its anti-Stokes signal is generated after IVR has been completed but before a significant amount of the photon energy has been dissipated to the environment. The rapid appearance of increased anti-Stokes signal from the C–CH3 indicates that this mode must be excited by relaxation of the C=C mode.
It has been well established that the C=C is the primary promoting mode for S1–S0 internal conversion.10,11,38 However, the accepting modes are not as well defined. Previous investigations of IC in β-carotene have been formulated in terms of the energy-gap law, which assumes that there is only one accepting mode that is weakly coupled to the electronic transition.12 With this assumption, the insensitivity of the IC rate to deuteration,11 and the sensitivity to 13C substitution10 has led to the conclusion that the C=C mode is the only acceptor. However, the assumption of a single accepting mode is not valid in β-carotene, which falls in Englman's strong-coupling limit12 and has several modes of similar frequency and with very large displacements between S1 and S0 that may act as acceptor modes during IC.37 By partitioning the IC energy into both the C=C and C–C modes, the Franck-Condon overlap between the relaxed S1 state and the isoenergetic S0 state can be dramatically increased. Also, because each of these modes would be similarly affected by 13C-substitution, the isotope affect on the internal conversion rate would be the same as previously observed and predicted by the energy gap law.10 The excitation of both the C=C and C–C modes by IC is also consistent with a twin-state model of the IC process, in which the S1–S0 conical intersection lies highly displaced from the S0 equilibrium geometry along the bond-inversion coordinate.13 Relaxation from the conical intersection to equilibrium would require simultaneous lengthening of C–C bonds and contraction of C=C bonds and so excitation of both of these normal modes would be expected.
Summary
Picosecond Stokes and anti-Stokes Raman spectra of photo-excited β-carotene have allowed us to directly observe relaxation processes in both the excited (S1, 2Ag−) and ground (S0, 1Ag−) states. The kinetics of the observed Stokes S1 bands at 1781, 1543, and 1230 cm−1 as well as the kinetics of the S0 Stokes spectral recovery, establish the S1 → S0 IC time as 12.6 ps. The lack of any observable S1 anti-Stokes signal indicates that β-carotene vibrationally relaxes via IVR within 2 ps in S1, and that there is <10% residual vibrationally excited population by this time. Internal conversion between S1 and S0 partitions the IC energy between the C=C and C–C modes of the ground state. Although both of these modes act as acceptors, the magnitude of the anti-Stokes scattering indicates that the C=C mode is dominant. In the ground state, the mode-specific cooling rates are established by observing the growth and decay of the S0 anti-Stokes signal. The 1523 cm−1 C–C mode relaxes in <1 ps, the 1157 cm−1 C=C mode in 5 ps, and the 1004 cm−1 C–CH3 mode in 12 ps. The magnitude of the 1004 cm−1 mode anti-Stokes enhancement is consistent with a model of ground-state IVR in which the C–CH3 mode is excited by IVR from the C=C mode. Finally, vibrational energy dissipation to the solvent must occur faster than the 12.6 ps S1 → S0 IC because there is no long-lived enhancement of anti-Stokes scattering in S0.
Acknowledgment
We thank Michael Tauber for many helpful discussions, Duohai Pan for performing the ab initio frequency calculations, and Kaiser Optical Systems, Inc. for the use of the notch filter. This work was supported by grants from the National Institutes of Health (EY02051) and the National Science Foundation (CHE-9801651).
References and Notes
- 1.Ritz T, Damjanovic A, Schulten K, Zhang JP, Koyama Y. Photosynth. Res. 2000;66:125. doi: 10.1023/A:1010750332320. [DOI] [PubMed] [Google Scholar]
- 2.Sashima T, Koyama Y, Yamada T, Hashimoto H.Recently, the presence of a third short-lived excited state, the 1Bu−state, lying between the 2Ag- and the 1Bu+ states has been proposed J. Phys. Chem. B 20001045011 Cerullo, G.; Lanzani, G.; Zavelani-Rossi, M.; De Silvestri, S. Phys. Rev. B2001, 63, 241 104) [Google Scholar]
- 3.Andersson PO, Bachilo SM, Chen RL, Gillbro T. J. Phys. Chem. 1995;99:16 199. [Google Scholar]
- 4.Andersson PO, Gillbro T. J. Chem. Phys. 1995;103:2509. [Google Scholar]
- 5.Shreve AP, Trautman JK, Owens TG, Albrecht AC. Chem. Phys. Lett. 1991;178:89. [Google Scholar]
- 6.Zhang JP, Inaba T, Watanabe Y, Koyama Y. Chem. Phys. Lett. 2000;332:351. [Google Scholar]
- 7.Kandori H, Sasabe H, Mimuro M. J. Am. Chem. Soc. 1994;116:2671. [Google Scholar]
- 8.Akimoto S, Yamazaki I, Takaichi S, Mimuro M. Chem. Phys. Lett. 1999;313:63. [Google Scholar]
- 9.Macpherson AN, Gillbro T. J. Phys. Chem. A. 1998;102:5049. [Google Scholar]
- 10.Nagae H, Kuki M, Zhang JP, Sashima T, Mukai Y, Koyama Y. J. Phys. Chem. A. 2000;104:4155. [Google Scholar]
- 11.Wasielewski MR, Johnson DG, Bradford EG, Kispert LD. J. Chem. Phys. 1989;91:6691. [Google Scholar]
- 12.Englman R, Jortner J. Mol. Phys. 1970;18:145. [Google Scholar]
- 13.Fuss W, Haas Y, Zilberg S. Chem. Phys. 2000;259:273. [Google Scholar]
- 14.Garavelli M, Bernardi F, Olivucci M, Vreven T, Klein S, Celani P, Robb MA. Faraday Discuss. 1998;110:51. [Google Scholar]
- 15.Zhang JP, Chen CH, Koyama Y, Nagae H. J. Phys. Chem. B. 1998;102:1632. [Google Scholar]
- 16.Yoshizawa M, Aoki H, Hashimoto H. Phys. Rev. B. 2001;63:180 301. [Google Scholar]
- 17.Cerullo G, Lanzani G, Zavelani-Rossi M, De Silvestri S. Phys. Rev. B. 2001;63:241 104. [Google Scholar]
- 18.Polivka T, Zigmantas D, Frank HA, Bautista JA, Herek JL, Koyama Y, Fujii R, Sundstrom V. J. Phys. Chem. B. 2001;105:1072. [Google Scholar]
- 19.Seilmeier A, Kaiser W. In: Topics in Applied Physics. Ultrashort Laser Pulses: Generation and Applications. 2nd Kaiser W, editor. Vol. 60. Springer-Verlag; New York: 1993. p. 279. [Google Scholar]
- 20.Hayashi H, Brack TL, Noguchi T, Tasumi M, Atkinson GH. J. Phys. Chem. 1991;95:6797. [Google Scholar]
- 21.Okamoto H, Ogura M, Nakabayashi T, Tasumi M. Chem. Phys. 1998;236:309. [Google Scholar]
- 22.Nakabayashi T, Okamoto H, Tasumi M. J. Phys. Chem. A. 1997;101:3494. [Google Scholar]
- 23.Kim JE, McCamant DW, Zhu L, Mathies RA. J. Phys. Chem. B. 2001;105:1240. doi: 10.1021/jp001236s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhu L, Kim J, Mathies RA. J. Raman Spectrosc. 1999;30:777. [Google Scholar]
- 25.Shreve AP, Mathies RA. J. Phys. Chem. 1995;99:7285. [Google Scholar]
- 26.Saito S, Tasumi M. J. Raman Spectrosc. 1983;14:310. [Google Scholar]
- 27.Hashimoto H, Koyama Y. Chem. Phys. Lett. 1989;154:321. [Google Scholar]
- 28.Noguchi T, Kolaczkowski S, Arbour C, Aramaki S, Atkinson GH, Hayashi H, Tasumi M. Photochem. Photobiol. 1989;50:603. [Google Scholar]
- 29.Noguchi T, Hayashi H, Tasumi M, Atkinson GH. J. Phys. Chem. 1991;95:3167. doi: 10.1016/S0006-3495(91)82047-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Orlandi G, Zerbetto F, Zgierski MZ. Chem. Rev. 1991;91:867. [Google Scholar]
- 31.Noguchi T, Hayashi H, Tasumi M, Atkinson GH. Chem. Phys. Lett. 1990;175:163. [Google Scholar]
- 32.Hashimoto H, Koyama Y. Chem. Phys. Lett. 1989;163:251. [Google Scholar]
- 33.Wasielewski MR, Kispert LD. Chem. Phys. Lett. 1986;128:238. [Google Scholar]
- 34.Bondarev SL, Bachilo SM, Dvornikov SS, Tikhomirov SA. J. Photochem. Photobiol. A. 1989;46:315. [Google Scholar]
- 35.Okamoto H, Nakabayashi T, Tasumi M. J. Phys. Chem. A. 1997;101:3488. [Google Scholar]
- 36.Kenkre VM, Tokmakoff A, Fayer MD. J. Chem. Phys. 1994;101:10618. [Google Scholar]
- 37.Onaka K, Fujii R, Nagae H, Kuki M, Koyama Y, Watanabe Y. Chem. Phys. Lett. 1999;315:75. [Google Scholar]
- 38.Negri F, Orlandi G, Zerbetto F, Zgierski MZ. J. Chem. Phys. 1989;91:6215. [Google Scholar]
- 39.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Zakrzewski VG, Montgomery JA, Jr., Stratmann RE, Burant JC, Dapprich S, Millam JM, Daniels AD, Kudin KN, Strain MC, Farkas O, Tomasi J, Barone V, Cossi M, Cammi R, Mennucci B, Pomelli C, Adamo C, Clifford S, Ochterski J, Petersson GA, Ayala PY, Cui Q, Morokuma K, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Cioslowski J, Ortiz JV, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Gomperts R, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Gonzalez C, Challacombe M, Gill PMW, Johnson BG, Chen W, Wong MW, Andres JL, Head-Gordon M, Replogle ES, Pople JA. Gaussian 98, revision A.11.2. Gaussian, Inc.; Pittsburgh, PA: 2001. [Google Scholar]


