Binding Energies of the Proton-Bound Amino Acid Dimers Gly·Gly, Ala·Ala, Gly·Ala, and Lys·Lys Measured by Blackbody Infrared Radiative Dissociation

Abstract

Arrhenius activation energies in the zero-pressure limit for dissociation of gas-phase proton-bound homodimers of N,N-dimethylacetamide (N,N-DMA), glycine, alanine, and lysine and the heterodimer alanine·glycine were measured using blackbody infrared radiative dissociation (BIRD). In combination with master equation modeling of the kinetic data, binding energies of these dimers were determined. A value of 1.25 ± 0.05 eV is obtained for N,N-DMA and is in excellent agreement with that reported in the literature. The value obtained from the truncated Boltzmann model is significantly higher, indicating that the assumptions of this model do not apply to these ions. This is due to the competitive rates of photon emission and dissociation for these relatively large ions. The binding energies of the amino acid dimers are ~1.15 ± 0.05 eV and are indistinguishable despite the difference in their gas-phase basicity and structure. The threshold dissociation energies can be accurately modeled using a range of dissociation parameters and absorption/emission rates. However, the absolute values of the dissociation rates depend more strongly on the absorption/emission rates. For N,N-DMA and glycine, an accurate fit was obtained using frequencies and transition dipole moments calculated at the ab initio RHF/2-31G* and MP2/2-31G* level, respectively. In order to obtain a similar accuracy using values obtained from AM1 semiempirical calculations, it was necessary to multiply the transition dipole moments by a factor of 3. These results demonstrate that in combination with master equation modeling, BIRD can be used to obtain accurate threshold dissociation energies of relatively small ions of biological interest.

Introduction

The ionic hydrogen bond is important in many fundamental biological processes including protein folding and conformation, enzyme–substrate binding, and acid–base chemistry. Measurement of dissociation energies of biological ion–neutral complexes in the gas phase can provide information about the intrinsic properties of the ionic hydrogen bond in the absence of solvent. Such measurements of cation–benzene binding¹ have greatly improved our understanding of cation–π electron interactions in biological processes.² Internal ionic hydrogen bonding also plays a critical role in the gas-phase chemistry of biological ions, including ion conformation,^3–7 proton transfer,^8,9 and dissociation reactivity.^10–13 In combination with tandem mass spectrometry, dissociation of large biomolecular ions can provide rapid sequence verification of recombinant proteins and locate post translational modifications¹⁴ and active sites in complexes.¹⁵

The thermochemical properties of the ionic hydrogen bond have been studied by both experimental^16–31 and theoretical^32–36 techniques. From temperature-dependent equilibrium measurements using high-pressure mass spectrometry (HPMS), the dissociation enthalpy (ΔH_d) and entropy (ΔS_d) of a variety of proton-bound dimers have been obtained.^16–23 These results have revealed some empirical trends in binding energies which can be explained by structural effects such as partial charge transfer,^16–18 steric hindrance,^17,19 and multiple hydrogen bonding.^16.20 Symmetric proton-bound dimers of molecules containing single functional groups such as amines^18,20 (N--H⁺--N) and carbonyls²⁰ (O--H⁺--O) have typical binding energies of 23 ± 2 and 31 ± 2 kcal/mol, respectively. Meot-Ner has shown that the ΔH_d for asymmetric dimers decreases linearly with the difference in the proton affinities (PA) of the two monomers.¹⁷ Multiple ionic hydrogen bonds can form in dimers of molecules with more than one functional group which can result in complexes of even greater stability. For example, the second and third N--H⁺--X bond in a dimer, where X is either a carbonyl oxygen or an amine nitrogen, can stabilize the complex by an additional 8 ± 1 and 4 ± 1 kcal/mol, respectively.²² A recent ab initio study reported a bond energy of 22.9 kcal/mol for the proton bound ammonia dimer.³³ This value is in excellent agreement with measured values for proton-bound symmetric amine dimers.¹⁸ From these calculations, it was concluded that the electron distribution of an ionic hydrogen bond is qualitatively similar to that of the neutral hydrogen bond.

The dissociation energy of small noncovalently bound ions has been measured by kinetic methods such as energy-resolved collisionally activated dissociation (CAD).^24–26 For example, the dissociation threshold energy (E_o) of the water proton-bound dimer has been reported by several groups; values of 1.4, 1.58, and 1.36 eV were measured in quadrupole,²⁴ Fourier-transform ion cyclotron resonance (FTICR)²⁵ and guided ion-beam²⁶ mass spectrometers, respectively. For comparison, the HPMS measured²³ and high level ab initio calculated³⁶ ΔH_d is 1.52 and 1.54 eV, respectively.

“Soft” ionization techniques, such as electrospray ionization (ESI)^37,38 and matrix-assisted laser desorption/ionization (MALDI)³⁹ are capable of forming gas-phase proton-bound dimers of larger biomolecules. However, measuring the binding energies of these noncovalent biomolecule complexes using conventional methods is more difficult with increasing molecular size. Larger biomolecules have limited volatility which limits applications of equilibrium methods that require a steady-state background of neutral species. While a vapor pressure is not required for threshold dissociation methods, such as energy-resolved CAD, kinetic shifts must be taken into account. The kinetic shift arises from the increased energy deposition required to produce dissociations within the time frame of the experiment.

Both Meot-Ner et al.²⁷ and Busman et al.⁴⁰ have implemented an interesting thermal dissociation technique from which the Arrhenius activation energy (E_a) for the dissociation of larger biomolecule ions have been obtained. In this method, ions formed by ESI are dissociated in the heated metal capillary of the electrospray ion source⁴⁰ or in a variable temperature controlled reaction chamber maintained at pressures of 0.9 atm.²⁷ From the temperature dependence of the extent of dissociation, activation energies were determined. For dissociation of the proton-bound dimer of leucine enkaphalen, a value of 2.0 ± 0.2 eV and an Arrhenius preexponential factor of 10^21.7±1.9 s⁻¹ was reported.²⁷

Recently, McMahon and co-workers²⁸ demonstrated that the dissociation kinetics of small weakly bound clusters ions of the type (H₃O⁺)L_n and Cl⁻(H₂O)_n (n = 2–4) stored in an FTICR are independent of pressure below 10⁻⁸ Torr. The relative dissociation rates for deuterated cluster ions were consistent with the shifts in spectral overlap and intensity of the vibrational transition frequencies with a Planck blackbody distribution.^29,31 These results provide convincing evidence that ions can be activated by absorption of blackbody photons. From the temperature dependence of the dissociation rates, activation energies in the zero-pressure limit are obtained. Dunbar^30,41,42 has shown that E_o can be accurately extracted from the measured E_a for small weakly bound complexes using either master equation modeling or a simplified truncated Boltzmann model. For example, the measured zero-pressure limit E_a for the loss of water from (H₂O)₃Cl⁻ is 5.0 kcal/mol; from this value, the dissociation enthalpy calculated by master equation and truncated Boltzmann models are 9.5 and 9.1 kcal/mol, respectively.³⁰

Activation energies in the zero-pressure limit for dissociation of large biomolecule ions have been reported.^10,11,43 For these large ions, the radiative absorption and emission rates can greatly exceed the dissociation rate so that ions equilibrate with the blackbody radiation field.^10,11 Under these rapid energy-exchange conditions, the measured Arrhenius activation parameters should be the same as those measured in the high-pressure limit.¹¹ Here, the zero-pressure activation energies of several proton-bound amino acid dimers are reported. These ions are too large for the truncated Boltzmann method to apply but are not large enough to be in the rapid energy-exchange limit (REX). Using master equation modeling, we demonstrate that accurate binding energies for these small biological molecules can be obtained from the experimentally measured activation energies. This method provides a route to measuring accurate thermochemical properties of biomolecules that are difficult to obtain by other methods.

Experimental Section

Mass Spectrometry.

All measurements were performed on the Berkeley external ion source 2.7-T ESI-FTMS instrument described elsewhere.^10,43,44 Ions are guided by a series of electrostatic lenses through five stages of differential pumping into the ion cell. A mechanical shutter in the ion beam path is opened for 3–10 s to allow ions to accumulate in the cell. This shutter is subsequently closed during the reaction delay to prevent both ions and neutrals originating from the electrospray source from reaching the cell. Dry nitrogen gas is pulsed into the cell at a pressure of ~2 × 10⁻⁶ Torr while the shutter is open to improve ion trapping and to thermalize the ions. A 1.0 s delay prior to precursor ion selection was added to allow the N₂ to be pumped away. Under the experimental conditions used, only (M + H)⁺ and (2M + H)⁺ ions are formed directly by electrospray ionization. The proton-bound dimers were isolated by ejecting the protonated monomer with a single-frequency excitation and were allowed to dissociate for times up to 600 s. Ions were subsequently detected using a broadband chirp excitation with a sweep rate of 3200 Hz/μs and data acquired with a Finnigan Odyssey data system.

Details of the temperature control and calibration of the heated FTMS vacuum chamber for BIRD experiments have been described previously.^10,43 Briefly, a dc heating blanket controlled by an Omega proportionating temperature controller (Stamford, Ct., Model 4002A) heats the main chamber within the superconducting solenoid. The chamber ends are wrapped with resistive heating tape and the temperature is kept within 5 °C of the main chamber. Copper–constantan thermocouples placed on either side of the ion cell measure the temperature inside the chamber. In a previous experiment, these thermocouples were calibrated to one placed in the center of the cell. All temperatures reported are corrected to correspond to the temperature at the center of the cell. At the highest temperatures of these experiments, the chamber pressure was ≤6 × 10⁻⁹ Torr as measured by a calibrated ion gauge.¹⁰

All amino acids were obtained from Sigma Chemical Co. (St. Louis, MO) and used without further purification. Amino acids were electrosprayed from a 10⁻⁴ M 80:20 methanol/water solution with ~1% acetic acid added. N,N-Dimethylacetamide (N,N-DMA) was purchased from Aldrich Chemical Co. (Milwaukee, WI). Proton-bound dimers of N,N-DMA were formed by electrospray from a solution containing a 2:1 volume ratio of N,N-DMA and acetonitrile with ~3% formic acid added.

Errors in the Arrhenius activation parameters reported here are the standard deviations of the linear least-squares fit to the Arrhenius data. These value reflect only random error. Systematic error may be present and could manifest itself as nonuniform chamber temperature and/or detection efficiency differences between monomer and dimer ions. Both of these systematic errors affect the absolute rate constants but have little effect on the temperature dependence of these values; i.e., the Arrhenius activation energy and preexponential are not significantly changed. For example, if the detection efficiency of the N,N-DMA dimer is ½ that of the monomer, then the activation energy changes from 0.99 to 1.00 eV and the preexponential remains essentially unchanged. If the measured temperatures were 5 °C higher than the actual values, then the E_a and A factor would be only 0.02 eV and 10^0.2 s⁻¹ larger, respectively.

Modeling.

An ensemble of low-energy structures for each dimer was found by molecular modeling calculations using the CFF91 force field provided in the InsightII/Discover suite of programs (Biosym Technologies, San Diego, CA) on an IBM RS/6000 computer. The proton was placed on the N-terminus of one of the amino acids for each of the amino acid homodimers except for Lys which was protonated on the side-chain amine group. For the Gly·Ala heterodimer, the proton was placed on the N-terminus of the alanine due to its higher basicity. For N,N-DMA, the proton was added to the amide nitrogen which should be a more basic site than the carbonyl oxygen. Starting geometries for the dimers were randomly selected. Dynamics were run at 600 K for 10 ps using 1 fs intervals followed by simulated annealing over the course of 2 ps to 200 K. The structure was then energy minimized to 0 K and used as the starting geometry in the next dynamics cycle. This process was repeated 120 times for each of the dimers. All structures within 10 kcal/mol of the lowest energy one for each of the dimers were remarkably similar.

The lowest energy structure of each dimer found by molecular modeling was used as the starting geometry for AM1 calculations using MOPAC 6.0, also on an IBM RS/6000 computer. Minimum energy structures were found using the eigenvector following routine from which vibrational frequencies and transition dipole moments are calculated. AM1 structures of N,N-DMA and glycine homodimers were then used as starting geometries for ab initio calculations. Full optimization and force calculations were done at the RHF/2-31G* level for N,N-DMA and at the MP2/3-21G* level for glycine dimer. Further calculations at the MP2/3-21+G**//MP2/3-21G* and at the MP2/3-21+G**//RHF/3-21G* level were performed on the dimers, monomers, and protonated monomers of glycine and N,N-DMA dimer, respectively, for evaluation of the dissociation energy. All ab initio calculations utilized the Gaussian 92 suite (Gaussian, Inc., Pittsburgh, PA) on an IBM RS/6000.

Master equation modeling was performed with software developed in this laboratory using double precision Fortran 77 code on a DEC 5900. Integration of stiffly coupled equations was facilitated by library calls to a backward differentiation formula (BDF) routine (DO2NCF) provided within the NAG Mark 17 library. The NAG DO2KAF routine for solving large eigenvalue problems was also utilized.

Results

Blackbody Infrared Dissociation Kinetics.

BIRD of the proton-bound homodimers of Gly, Lys, and N,N-DMA results in protonated monomer ions exclusively over the temperature range investigated. Dissociation constants for these ions are obtained from the slope of a plot of ln([D⁺]/∑{[D⁺] + [M⁺]}vs. reaction time where D⁺ and M⁺ refer to the dimer and monomer ions, respectively. Kinetic plots for all dimer ions are shown in Figure 1a–e. These data at each temperature have excellent linear fits (R > 0.980) and have zero y-intercepts. This indicates that the ion population has reached a steady state distribution of energies prior to the start of the reaction delay and that this distribution is maintained throughout the time window of the experiment.

Figure 1.

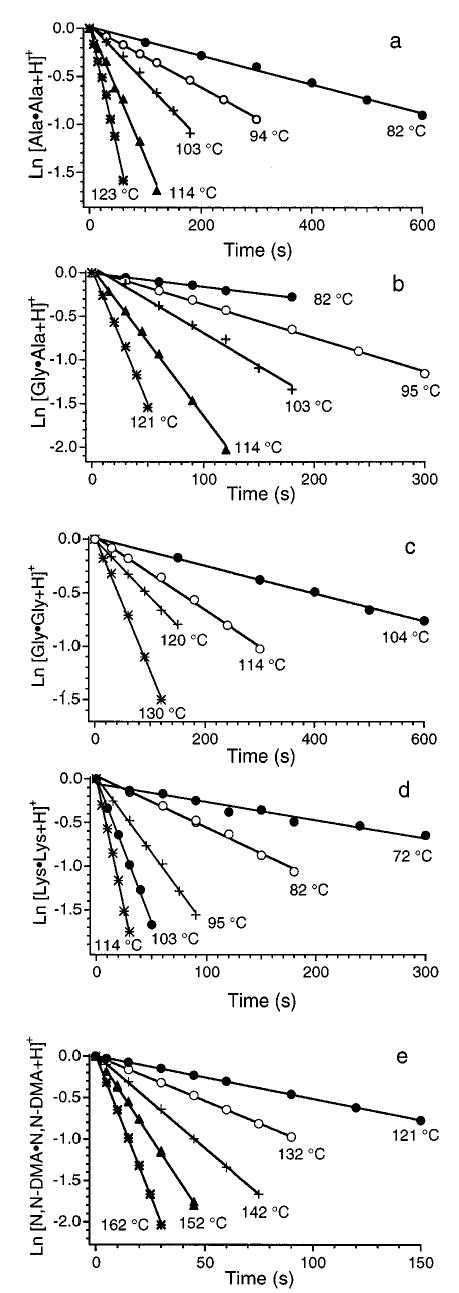
Blackbody infrared radiative dissociation kinetics of the proton-bound dimers of (a) alanine, (b) glycine·alanine, (c) glycine, (d) lysine, and (e) N,N-dimethylacetamide fit to unimolecular kinetics at the temperatures indicated.

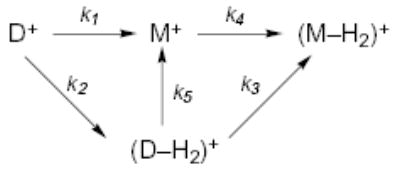
For the proton-bound dimers containing alanine, loss of H₂ is a competitive but minor process (Figure 2a). Isolation of protonated alanine indicates that this ion also undergoes H₂ loss. The primary dissociation product in the BIRD spectrum of the proton bound dimer of Gly·Ala is (Ala + H)⁺, although loss of H₂ occurs to a limited extent. No protonated Gly is observed consistent with the higher gas-phase basicity of alanine.⁴⁵ The loss of H₂ from the Ala-containing dimers as well as Ala itself results in a relatively complex reaction scheme involving both competitive and sequential dissociations (reaction scheme 1)

Figure 2.

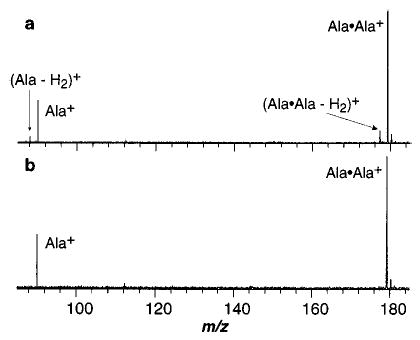
Blackbody infrared radiative dissociation spectra of the proton-bound dimer of alanine at (a) 82 °C with a reaction delay of 300 s and at (b) 123 °C with a reaction delay of 22.5 s.

(1).

The relative abundance of H₂ loss from the dimer of Ala is larger at lower temperatures than it is at higher temperatures (Figure 2). The different temperature dependence for loss of H₂ than for formation of M⁺ indicates that these dissociation processes have different Arrhenius parameters. In principle, the rate constants for the two primary dissociation pathways (k₁ and k₂) as a function of temperature could be determined by continuously ejecting the (D−H₂)⁺ product ion (a double resonance experiment). Due to the long delay times used, it is possible that the dimer ions can also be excited which would perturb the resulting kinetic measurements. The effect of this competitive dissociation process on the resulting Arrhenius parameters can be estimated by the following approximation. If the rate constants of all dimer to monomer processes are equivalent (k₁ = k₃ + k₅), then the E_a for the Ala dimer going to monomer is reduced by only 0.03 eV when compared to the value obtained by ignoring the competing loss of H₂ process. This is a small systematic error which produces a <0.05 eV difference in reported E_o for this ion (vide infra). This effect for Ala·Gly heterodimer is even less. Because of the minor influence of the competing channel, the reported rate constants and dissociation energies for these Ala containing ions are determined by ignoring the loss of H₂.

Pressure Dependence.

To confirm that the dissociation rate constants measured in this experiment are in the zero-pressure limit, the pressure dependence of these rates for N,N-DMA was investigated at 156 °C. At a pressure of 6 × 10⁻⁹ Torr, k_uni = 0.0391 ± 0.0005 s⁻¹. Increasing the cell pressure to 2 × 10⁻⁸ Torr by adding butane through a leak valve resulted in a k_uni = 0.0393 ± 0.0003 s⁻¹ (Figure 3), an indistinguishable change within our experimental error. Thus, collisions do not influence the dissociation kinetics under the experimental conditions used and the rate constants reported are in the zero-pressure limit. At higher cell pressures, the rate constants increase with pressure. At 1 × 10⁻⁶ Torr, k_uni = 0.0434 ± 0.0005 s⁻¹. This is only an 11% increase despite the >100-fold increase in pressure. These results are consistent with those of Dunbar and co-workers⁴² who found that the zero-pressure limit for Si-(C₂H₅)₄⁺ was reached at pressures ≤1 × 10⁻⁸ Torr. However, a much stronger pressure dependence was reported at higher pressures. The rate constant for this ion increased by a factor of ~8 when the cell pressure was changed from 10⁻⁸ to 10⁻⁷ Torr. In contrast, no pressure dependence was observed for small protonated peptides in this same pressure region.^10,43 The intermediate pressure dependences of the rates for the proton-bound dimer ions investigated here are consistent with the competitive up-pumping by blackbody photons and collisions at pressures >10⁻⁸ Torr. At background pressures of 2 × 10⁻⁹ to 6 × 10⁻⁹ Torr at which these experiments were performed, the Langevin collision rate with a typical hydrocarbon, butane, is ~0.04–0.12 s⁻¹. Thus, the collision and dissociation rates are of similar magnitude. The relatively minor influence of collisions at pressures above 2 × 10⁻⁸ Torr indicates that the efficiency and/or degree of energy transferred by collisions is significantly less than that transferred by photon exchange with the blackbody radiation field.

Figure 3.

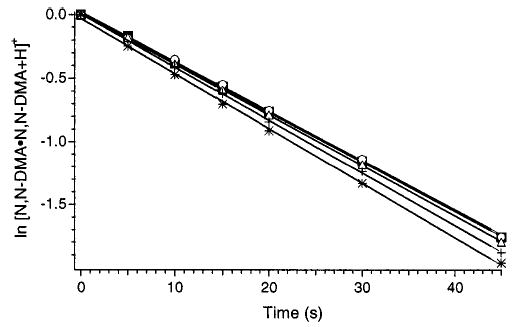
Dissociation kinetics of N,N-dimethylacetamide proton-bound dimer at cell pressures of (○) 6 × 10⁻⁹ Torr, (▪) 2 × 10⁻⁸ Torr, (▵) 1 × 10⁻⁷ Torr, (+) 5 × 10⁻⁷ Torr, and (*) 1 × 10⁻⁶ Torr at 152 °C. Butane was introduced into the chamber through a leak valve to attain elevated pressures. The rate constants in order of increasing pressure are 0.0391, 0.0393, 0.0400, 0.0418, and 0.0434 s⁻¹.

Zero-Pressure Arrhenius Activation Parameters.

From the temperature dependence of the dissociation rate constants, Arrhenius activation parameters in the zero-pressure limit are obtained. These data for each of the proton-bound dimers are shown in Figure 4. The values of E_a and A from these plots are given in Table 1. The zero-pressure activation energies (E_a) for the 5 dimers are nearly identical, ranging from 0.92 to 0.99 eV for the alanine and N,N-DMA dimer ions.

Figure 4.

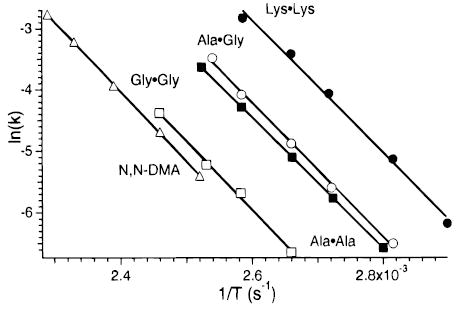
Arrhenius plot for the dissociation of the proton-bound dimer of (▵) N,N-dimethylacetamide, (□) glycine, (▪) alanine, (○) glycine·alanine, and (●) lysine.

TABLE 1.

Measured and Calculated Activation and Binding Energies of Proton-Bound Dimers

dimer	measd Ea (eV)	measd log A	trunc Boltzmann Eo (eV)	master eqn Eo (eV)
N,N-DMA	0.99 ± 0.02	10.1 ± 0.1	1.61	1.25 ± 0.05
GLY·GLY	0.96 ± 0.04	10.0 ± 0.5	1.34	1.15 ± 0.05
ALA·ALA	0.92 ± 0.01	10.1 ± 0.1	1.39	1.12 ± 0.03
GLY·ALA	0.94 ± 0.03	10.5 ± 0.4	1.34	1.15 ± 0.05
LYS·LYS	0.93 ± 0.04	11.0 ± 0.5	1.74	1.15 ± 0.05

Discussion

Unimolecular Kinetics in the Zero-Pressure Limit.

For small ions, the E_a and A factors measured in the zero-pressure limit can be significantly lower than their true high-pressure limit values, E_a^∞ A^∞. The precise meaning of the zero-pressure limit values is best described within the framework of the established Lindemann–Hinshelwood mechanism for thermal unimolecular dissociations. In this mechanism, a reactant ion (AB)⁺ is energized above its dissociation threshold (E_o) by collision(s) with an unreactive species (M) creating an “activated complex” (AB⁺*).

$${\text{AB}}^{+}+\text{M}\underset{k_{-1,\text{coll}}}{\overset{k_{1,\text{coll}}}{\iff }}{\text{AB}}^{+}*\stackrel{k_{\text{d}}}{\iff }{\text{A}}^{+}+\text{B}$$ (2)

This activated complex may subsequently dissociate to products or become deactivated by further collisions back to reactants. The overall unimolecular rate constant (k_uni) is given by eq 3,

$$k_{\text{uni}}=k_{\text{d}}\left(\frac{k_{1,\text{coll}}[\text{M}]}{k_{-1,\text{coll}}[\text{M}]+k_{\text{d}}}\right)$$ (3)

where k_1,coll and k_−1,coll are the energy-dependent rate constants for activation and deactivated by collision which are a function of cross section and efficiency of energy transfer and k_d is the energy-dependent dissociation constant.

This mechanism has been tremendously successful in accounting for the pressure dependence of unimolecular reactions. In the high-pressure limit where [M] is large, k_−1,coll[M] ≫ k_d (eq 3) and the reaction rate is first order in the reactant concentration and does not depend on the bath gas pressure ([M]). Physically, the exchange of energy between the reactant and bath gas is significantly faster than the dissociation rate. Under these conditions, the internal energy of a population of ions is characterized by a time-independent Boltzmann distribution. In this regime, k_uni is a reflection of the Boltzmann-weighted microcanonical dissociation rates only and contains no information on the dynamics of the energy exchange process. Canonical averaging reduces statistical unimolecular dissociation theories such as RRKM and phase-space theory to the wellknown transition-state theory of Eyring. Arrhenius plots yield activation energies which are within a few kT of the critical energy (E_o) and preexponential (or A^∞) factors that are a function of the entropy difference between the reactant and transition state ions. These values reflect the difference in chemical structure between the reactant and the transition state from which information about the mechanism and dynamics of dissociation can be inferred.

At lower concentrations of M, a decrease in k_uni is observed. This “falloff region” occurs when k_−1,coll[M] is of similar magnitude to k_d. At even lower pressures, where k_−1,coll[M] is much smaller than k_d (the low-pressure limit), k_uni is first order in both reactant and bath gas pressure. In both of these lower pressure regimes, the internal energy of a population of reacting species is non-Boltzmann and there is no longer a simple relationship between the measured activation energy and critical dissociation energy. To extract meaningful energetics from unimolecular dissociation rate constants at these pressures, the collisional energy transfer must be accurately modeled. In the Lindemann–Hinshelwood mechanism, k_uni approaches zero as [M] approaches zero.

Recently, McMahon²⁸ elegantly demonstrated that the Lindemann–Hinshelwood mechanism fails at extremely low pressures. Activation of ions stored in an FTMS cell can occur by the absorption of blackbody photons from the vacuum chamber walls. Below 10⁻⁸ Torr, the thermal dissociation rates can be nonzero and independent of pressure. Under these conditions, rate constants in the zero-pressure limit are measured.

A simple modification to the activating mechanism of eq 2 to account for the rates of absorption and emission of IR photons, k_1,rad, k_−1,rad, respectively, yields the form of the unimolecular rate constant in the zero-pressure limit:

$$k_{\text{uni},\text{zpl}}=k_{\text{d}}\left(\frac{k_{1,\text{rad}}}{k_{-1,\text{rad}}+k_{\text{d}}}\right)$$ (4)

Analogous to the collisionally activated scheme, there are also three regimes defined by the relative values of k_−1,rad and k_d for zero-pressure limit blackbody photon activated unimolecular dissociations. When k_−1,rad ≪ k_d,, ions that are activated above E_o by absorption of a single blackbody photon dissociate promptly. This can occur for small ions that have low values of E_o and rapid dissociation kinetics, e.g., weakly bound clusters. Dunbar⁴¹ has demonstrated that both master equation modeling and a simpler truncated Boltzmann model can be used to relate the measured zero-pressure limit E_a to E_o. The latter model has the advantage that the energy transfer processes do not need to be modeled explicitly. When k_−1,rad ≈ k_d,⁴⁶ the truncated Boltzmann model is not applicable. This can occur for intermediate size ions,⁴⁷ such as the proton-bound dimers investigated here. Master equation modeling which provides a detailed accounting of all activating, deactivating, and dissociating events can be used to extract E_o from the measured zero-pressure limit E_a. Finally, when k_−1,rad ≫ k_d, the rate of energy exchange with the blackbody radiation field is much greater than the dissociation rate. This can occur for larger ions, such as peptides¹⁰ and proteins,¹¹ that have more oscillators which increases the number of photons an ion exchanges with the vacuum chamber walls. In this REX limit, the internal energy of the reacting ion population is characterized by a Boltzmann distribution and the measured Arrhenius parameters should be the same as those measured in the traditional high-pressure limit!¹¹

Truncated Boltzmann Model.

For ions in which the microcanonical dissociation rates are greater than those of radiative emission when activated above their threshold dissociation energy (k_−1,rad ≪ k_d), dissociation will occur promptly. Dunbar⁴¹ has introduced a relatively simple truncated Boltzmann model which relates the measured zero-pressure activation energy to the true dissociation energy given by eq 5, where E_a

$$E_{\text{o}}=E_{\text{a}}+\langle E^{\prime }\rangle -\mathrm{\Delta }{E}_{\text{rad}}-\mathrm{\Delta }{E}_{\text{depl}}$$ (5)

is the measured zero-pressure activation energy, 〈E′〉 is the average energy of the entire reaction depleted ion population approximated by a steady-state Boltzmann distribution truncated at the critical threshold energy, i.e., truncated Boltzmann, and ΔE_rad and ΔE_depl are small and partially canceling terms that include the temperature dependence of the radiation field and the reactive depletion of the high-lying energy levels, respectively. For example, the values of ΔE_rad and ΔE_depl for the N,N-DMA homodimer at 134 °C are 0.06 and −0.03 eV, respectively.

A value of E_o for the proton-bound dimers investigated here was obtained using the truncated Boltzmann method. The value of 〈E′〉 depends on E_o; values of E_a, ΔE_rad, and ΔE_depl do not. Thus, the solution to the truncated Boltzmann model can be found iteratively. The internal energy distribution for the system is calculated using Boltzmann statistics and the harmonic oscillator approximation. An initial value of E_o is selected and 〈E′〉 is calculated. A new value for E_o is calculated from eq 5 and compared to the initial value. This process is repeated until the new value of E_o from eq 4 is within 5 cm⁻¹ of the previous value used to calculate 〈E′〉. The truncated Boltzmann model E_o is evaluated at one temperature. Typically, experimental activation energies are extracted from rate constants measured over a range of ~50 °C. For N,N-DMA, the truncated Boltzmann E_o at the lowest experimental temperature is 1.55 eV while at the highest temperature it is 1.67 eV. Values reported here are calculated at a temperature in the middle of the experimental range.

Values of E_o determined by the truncated Boltzmann method for each of the dimers are given in Table 1. Two pieces of evidence indicate that the truncated Boltzmann model overestimates E_o for these ions. For N,N-DMA, a value of 1.61 eV is obtained from the truncated Boltzmann model. A dissociation enthalpy of 1.35 eV at 500 K for this proton-bound dimer has been measured by Meot-Ner using HPMS.²⁰ For simple ion–molecule reactions, the reverse activation barrier is usually negligible and the enthalpy difference between reactants and products at 0 K is equal to E_o. Using standard thermodynamic relations,⁴⁸ we calculate a 0 K ΔH_d value of 1.25 eV from the measured HPMS value. This value is closer to the measured activation energy of 0.99 eV than to the truncated Boltzmann corrected E_o (1.61 eV). This indicates that the concentration of the excited state population is nonzero but less than that of a Boltzmann distribution.

The second indication that the truncated Boltzmann model overestimates E_o for these ions is that in the truncated Boltzmann model, the dissociation rate depends only on the radiative absorption rate (k_1,rad) and E_o. The rate contains no information about the dissociation process or k_d. For the homodimers, the dissociation rate at a given temperature increases with ion size for all the dimers in general agreement with the expected size dependence of k_1,rad. However, if k_1,rad was the only determining factor, then the mixed dimer Gly·Ala should have a dissociation rate intermediate to the Ala and Gly homodimers (the similar temperature dependence indicates a similar E_o). However, the mixed dimer has a higher rate than either of its constituent homodimers, indicating that these dissociation reactions are influenced by the transition state; i.e., the measured A factor contains information about the dynamics of the reaction. Both this result and the poor agreement with the HPMS binding energy indicate that the assumption that k_−1,rad ≪ k_d is not valid for these proton-bound dimers and the truncated Boltzmann model overestimates the true E_o.

Master Equation Model Description.

When the radiative absorption and emission rates are comparable to the microcanonical dissociation rates, detailed accounting of these processes is required to extract useful energetic information. To do this, master equation modeling in which the solutions to a complete set of coupled partial integro-differential kinetic equations that describe the time-dependent evolution of an ensemble of ions can be used.⁴⁹ This method is valid when the rates of all energy transfer processes can be described statistically, as should be the case for BIRD experiments. For small ions, Dunbar has demonstrated that master equation modeling can provide excellent agreement with the experimentally measured rates⁴¹ and the values of E_o determined by master equation modeling are nearly the same as those obtained by the truncated Boltzmann model.

To model the dissociation of these proton-bound dimers, a finite-difference approximation to the master equation is used. The coupled equations of motion given by eq 6, where N_j(0)

$$\text{d}{N}_i(t)=\sum _j{k}_{i,j}{N}_j(0)$$ (6)

and dN_i(t) are the initial population fraction in energy level j and the time-dependent change in population fraction in energy level i, respectively. These coupled equations can be expressed as a transport matrix, commonly referred to as the J matrix (see Figure 5). The J matrix contains all the detailed rate constants (k_i,j) describing the motion of the ion population into and out of each energy level. An energy grain size of 100 cm⁻¹ was used in these calculations. As an example, the matrix element k_2,2 (Figure 5) contains the sum of rate constants for absorption, spontaneous and stimulated emission, and dissociation which deplete the ion population fraction with internal energies between 100 and 199 cm⁻¹. In general, the diagonal matrix elements are given by

Figure 5.

Matrix form of the master equation describing the time evolution of a population of ions [dN_i(t)] relative to an initial population distribution [N_i(0)]. The transport (or J) matrix contains the detailed rate constants for all energy transfer and dissociation processes.

$$\begin{array}{l}{k}_{i,i}=-k_{\text{d}}(E_i)-\sum _{h\nu }{k}_{1,\text{rad}}(\mathrm{\Delta }{E}_{i\to j}=h\nu )-\\ \sum _{h\nu }{k}_{-1,\text{rad}}(\mathrm{\Delta }{E}_{j\to i}=h\nu )\end{array}$$ (7)

where k_d(E_i) is the microcanonical dissociation rate constant for the population of ions at the center of the ith energy grid, e.g., k_d(E_i) for the k_2,2 matrix element corresponds to the dissociation rate constant for an ion with 150 cm⁻¹ of internal energy. The values of k_d(E_i) are determined from RRKM theory. Internal rotations are treated as low-frequency vibrations and the effect of angular momentum is neglected. The sum and density of states were calculated using the direct count Beyer–Swinehart algorithm. The reactant frequency set was obtained from the lowest energy structure calculated at the AM1 semiempirical level. The transition state frequency set was formed from the reactant set with the stretching mode between monomer units as the reaction coordinate (typically 2200–2500 cm⁻¹). Ion–molecule dissociations are generally considered to be characterized by a “loose” transition state. As such, two sets of transition state frequencies, bracketing the “loose” range of high-pressure limit Arrhenius preexponential factors of 10^14.5 and 10^16.5 s⁻¹, were constructed for each system by systematically varying up to five intermediate frequencies to smaller values, thereby simulating the transition from vibrations to rotations.⁵⁰

The summation terms in eq 6 correspond to rates of absorption and emission processes summed over all transition frequencies available to the dimer ion. Overtone and combination frequencies are not considered. As an illustration, the absorption term for the k_2,2 matrix element is summed over all 3N – 6 transition frequencies greater than 50 cm⁻¹; frequencies less than 50 cm⁻¹ will not move the ion from the 150 cm⁻¹ energy bin to the 250 cm⁻¹ bin. The emission term is only summed over transition frequencies between 50 and 150 cm⁻¹ since emission of a photon of lower energy would not move the ion to the 50 cm⁻¹ bin and a photon of greater energy would produce an ion with less than its zero-point energy. A weakly-coupled harmonic oscillator model was used to calculate the detailed rate constants for blackbody absorption, k_1,rad, and for spontaneous and stimulated emission, k_−1,rad.

$$k_{1,\text{rad}}(\mathrm{\Delta }{E}_{i\to j}=h\nu )=\sum _m\rho (h\nu )B(h\nu )P_i^{mh\nu }$$ (8)

$$k_{-1,\text{rad}}(\mathrm{\Delta }{E}_{j\to i}=h\nu )=\sum _m\{A(h\nu )+\rho (h\nu )B(h\nu )\}{P}_j^{mh\nu }$$ (9)

where ρ(hν) is the radiation density at ν given by the Planck distribution A(hν) and B(hν) are the Einstein coefficients for stimulated and spontaneous radiative transition processes, respectively, given by

$$B(h\nu )={\mu }^2/6{є}_{\text{o}}{\hslash }^2$$ (10)

$$A(h\nu )=8\pi h{(\nu /c)}^3/B(h\nu )$$ (11)

Transition frequencies (ν) and transition dipole moments (μ) were calculated at the AM1 semiempirical level for all the dimers. For comparison, ν and μ for the proton-bound N,N-DMA and glycine dimers were also evaluated at the ab initio RHF/3-21g* and MP2/3-21g* levels, respectively. Although the transition frequencies calculated by the two methods are comparable, the integrated up-pumping rates for the glycine dimer using the ab initio values are approximately 8 times those using the AM1 values. The importance of this difference will be discussed below.

The coefficient $P_j^{mh\nu }$ is the product of two probability factors. First is the microcanonical occupation probability of an ion in the ith internal energy bin having m quanta of energy in the νth oscillator. Dunbar has calculated this value by estimating an internal temperature for the ion and using Boltzmann statistics to approximate its internal energy.⁴¹ Here, the occupation probability is calculated by exact state counting. The harmonic oscillator model is the only approximation made; no constraints on the internal energy distribution are imposed. The method for exact state counting used is described in the Appendix. For computational convenience, the enhanced transition probability of excited harmonic oscillators is also included in this term. That is, an absorption from level m to (m + 1) is (m + 1) times as intense as that from level m = 0 to m = 1. Conversely, an emission from m to (m − 1) is m times as intense as that from m = 1 to m = 0 transition.

The off-diagonal elements in the J matrix are coupling terms that satisfy the detailed balancing condition. That is, an ion undergoing a nondissociative transition from one diagonal matrix element must end up in some other diagonal element. To prevent nondissociating ions from “leaking” out of the high-energy end of the population, the J matrix was made to accommodate ions with internal energy 4 times the average energy and transitions were constrained to remain within the energy bounds of the matrix.

The unimolecular rate constant, k_uni, is equal to the largest, i.e., least negative, eigenvalue of the J matrix. To evaluate the time-dependent ion population distribution, the coupled set of stiff differential equations given by eq 6 is numerically integrated using a backward differentiation formula (BDF) algorithm. This provides the actual population distribution at selected simulation reaction times. A Boltzmann distribution at the temperature for which k_uni is calculated was used for the initial energy-state population. The system population was then allowed to “react” until a steady-state reactant population distribution was reached prior to extracting k_uni. The selection of the initial population distribution effects the number of BDF iterations required to reach the steady state but makes no difference on the final distribution. This process was repeated to find k_uni for one or two other temperatures spanning the experimental temperature range. The Arrhenius parameters obtained from the temperature dependence of these calculated rate constants are compared to the measured values.

Master Equation Modeling of the Experiment.

Three parameters can be varied to fit the temperature dependence of the experimental rate constants; E_o, μ, and the transition state frequency set. The effects of each of these parameters on k_uni, E_a, and A are illustrated in Figure 6, a and b, for N,N-DMA. Using the values of μ from the AM1 calculation, values of k_uni were calculated with E_o equal to 1.40, 1.25, and 1.10 eV, and high-pressure limit A factors (A^∞) of 10^14.5 and 10^16.5 s⁻¹ (Figure 6a). The value of E_o clearly has a large effect on both the slope (the zero-pressure limit E_a) and the and y-intercept (A factor). Increasing E_o from 1.10 to 1.40 eV (a 27% increase), changes E_a from 0.69 to 1.17 eV for A^∞ = 10^16.5 s⁻¹ (a 70% increase). An even larger effect on the zero-pressure limit A factor is observed; this value increases from 10^6.8 to 10^10.5 s⁻¹. The effect of the transition frequency set (A^∞) is much smaller. Changing A^∞ by 2 orders of magnitude only changes E_a by ≤ 0.05 eV and zero-pressure A factor by less than a factor of 2.

Figure 6.

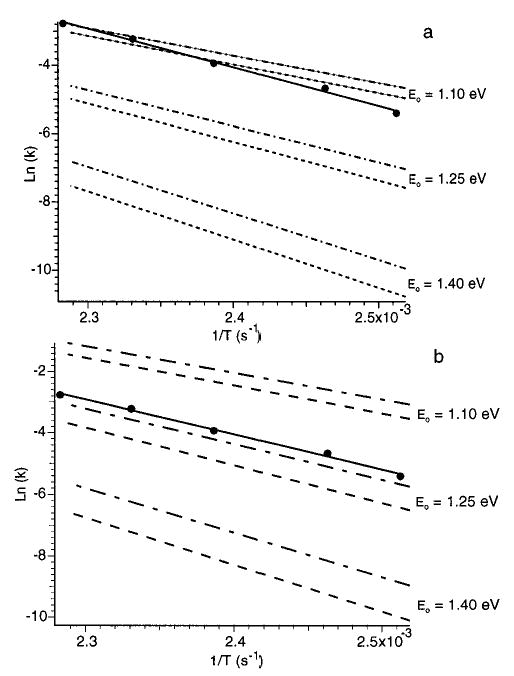
Zero-pressure limit Arrhenius plot for the N,N-dimethyl-acetamide proton-bound dimer measured (∘) and master equation modeled fits with (a) transition dipole moments calculated at the AM1 level and (b) transition dipole moments 3 times larger than the AM1 values. Fits with dissociation energies (E_o) of 1.10, 1.25 and 1.40 eV and Arrhenius preexponential factors (A^∞) of 10^14.5 (dash lines) and 10^16.5 s⁻¹ (dash-dot lines) are shown.

From the calculations shown in Figure 6a, it is clear that the slope of the experimental data (E_a) can be readily modeled. A best fit value was obtained by changing E_o in 0.05 eV increments between 1.10 and 1.40 eV. For A^∞ between 10^14.5 and 10^16.5 s⁻¹, E_o must be between 1.25 and 1.30 eV to fit the experimental E_a within the measured standard deviation. This is in excellent agreement with the HPMS value corrected to 0 K (1.25 eV). However, the absolute values of the calculated rate constants for E_o = 1.25 eV are approximately 5 times lower than the measured values. Increasing A^∞ increases the absolute rate, but a value significantly higher than 10^16.5 s⁻¹ is not expected for proton-bound dimers.^50,51 The absolute values of the rate constants calculated using E_o = 1.10 eV are comparable to the measured rate constants but have a temperature dependence that is significantly different and well outside the experimental error. Similarly, the absolute unimolecular dissociation rate constants for the proton-bound dimers of all the amino acids calculated using AM1 dipole moments and best fit values of E_o are significantly lower than the measured values. This indicates that the values of μ calculated at the AM1 level are too small which results in a significant underestimation of photon absorption and emission rates. Integrated up-pumping rates for N,N-DMA and glycine dimers using ab initio values are about 6 and 8 times higher, respectively, than those calculated using the AM1 values. Presumably, transition intensities calculated at the ab initio levels here should more closely resemble experimental values than those computed semiempirically.

Since ab initio calculations were not done for all the dimers, the AM1 transition dipole moments for each dimer were multiplied by 3 to obtain approximately the same increase in integrated up-pumping rate as was obtained using the ab initio values for N,N-DMA and glycine dimers. The results of master equation modeling of N,N-DMA using these higher values are shown in Figure 6b with the same values of E_o and A^∞ used in Figure 6a. Again, the value of E_o is the most critical parameter to fit E_a. In addition, the calculated rate constants using the best fit E_o are now nearly the same as those measured experimentally. The values of E_o that fit the experimental E_a within the standard deviation is between 1.20 and 1.25 eV. Increasing the transition dipole moments by a factor of 3 which increases the up-pumping rates by a factor of 9, decreases E_o by only 7%. Thus, the uncertainty in these values is not a significant impediment to extracting energetic information. However, accurate values of μ are critical to fit the absolute dissociation rates.

For small neutral molecules, RHF/3-21G* ab initio transition intensities are larger than measured values by a factor of ~2.^52,53 We are not aware of any comparison for ions. However, Dunbar³⁰ found that rates obtained by master equation modeling of (H₂O)₂Cl⁻ and (H₂O)₃Cl⁻ cluster ions using ab initio transition intensities calculated using density functional theory fit the experimental rates to a reasonably high degree of accuracy. Our results also indicate that the overall rates of radiative processes calculated using these values closely agree with experiment. It should be noted that our calculations do not include overtone and combination transitions which may have significant intensity for the anharmonic low-frequency vibrations.

The experimental data for each of the proton-bound dimers were modeled in a similar manner and the resulting values of E_o are given in Table 1. The errors reported for E_o values are determined from the highest and lowest calculated values that will fit E_a within the experimental standard deviation using the limits of the transition state frequency set and the transition dipole moments given above. For example, the threshold dissociation energy for N,N-DMA is given as 1.25 ± 0.05 eV. This error does not include any systematic error which may be present. However, the excellent agreement with the HPMS measured value for N,N-DMA suggests that any systematic error is small. The values of k_uni for all the proton-bound dimers calculated with the AM1 transition dipole moments multiplied by 3 are nearly the same as the measured k_uni. This indicates that the AM1 transition dipole moments are consistently about a factor of 3 too small.

Energy Distribution.

The steady state distribution of ion internal energies for N,N-DMA at 429 K calculated with the AM1 values of μ multiplied by 3 is shown in Figure 7a. The corresponding rate constants for absorption, emission, and dissociation are shown in Figure 7b. The energy distribution, although nearly Boltzmann in appearance, is depleted somewhat at the higher energies. This depletion is the origin of the measured value of E_a being lower than E_o. For the truncated Boltzmann model to apply, the population of ions with energies greater than E_o must be negligible. The Figure 7a data shows that this is not the case for N,N-DMA and that the truncated Boltzmann model is not applicable for this ion. The energy dependences of k_−1,rad and k_d differ dramatically (Figure 7b). These values are equal at an energy of ~1.7 eV. At this energy, the population is small but nonnegligible. For the rapid energy exchange limit to apply, k_−1,rad ≫ k_d over the entire energy range where there is a nonnegligible ion population under a Boltzmann distribution. The rate constants for absorption and emission are for the number of photons absorbed and emitted independent of their energy. At 〈E〉, the average energy of the photon absorbed and emitted is 1446 and 1319 cm⁻¹, respectively.

Figure 7.

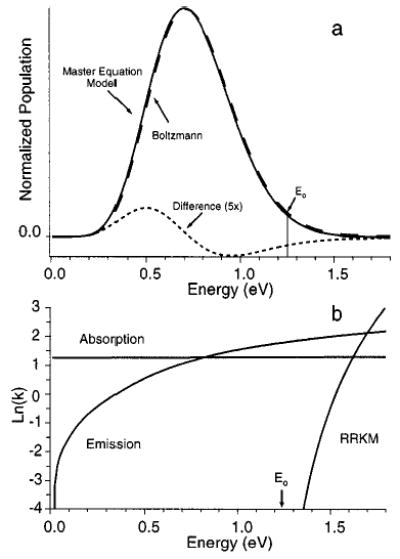
(a) Internal energy distributions for a population of proton-bound N,N-dimethylacetamide ions at 156 °C at thermal equilibrium (Boltzmann distribution, dashed line) and calculated from the master equation model (solid line). (b) Microcanonical absorption, emission, and dissociation rates for this same ion as calculated from the master equation model. The dissociation rate constants were calculated using a value of A^∞ = 10^16.5 s⁻¹ and E_o = 1.25 eV.

Binding Energies.

All of the proton-bound amino acid dimers have approximately the same dissociation energy of 1.15 eV. The lowest energy structures of the glycine (Figure 8a), alanine and glycine·alanine proton-bound dimers indicate that the charge on the N-terminus of one amino acid is “solvated” by both the carboxyl oxygen and the amine nitrogen of the other acid. The similar solvation for each of these ions is consistent with their similar dissociation energy. For lysine, the protonated side-chain nitrogen of one of the monomers is solvated by the carboxyl oxygen of both residues as well as the basic side chain amine group of the neutral (Figure 8b). Thus, more charge solvation occurs in this dimer than in the others. Effects of multiple bonding on the stability of the dimer ion are small when internal solvation of a charge in the dissociated monomer also occurs^16,20 as is the case for protonated lysine.⁴⁵ The interaction between the two residues is essentially the same as it is for the other amino acid dimers which is reflected by the similar binding energies. It is possible that the gas-phase lysine proton-bound dimer may exist in a salt-bridge structure. This is currently under investigation.

Figure 8.

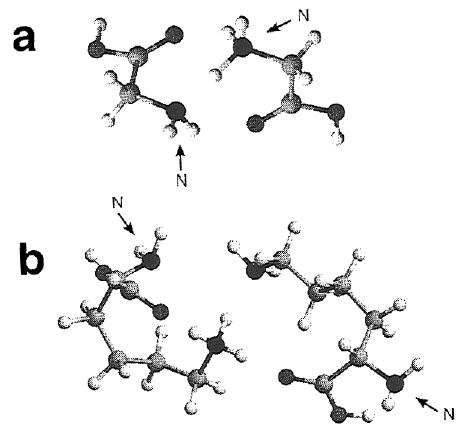
Minimum energy structures for the proton-bound dimers of (a) glycine at the MP2/3-21G* ab initio level and (b) lysine at the AM1 semiempirical level. The N-terminus of each residue is labeled.

For comparison, the binding energies of the proton-bound dimers of N,N-DMA and glycine were calculated from the lowest energy AM1 and ab initio structures. These values from the AM1 calculations are 0.81 and 0.85 eV, respectively. Thus, the AM1 calculations significantly underestimate the binding energies and also their relative order. From ab initio calculations at the MP2/3-21+g**//MP2/3-21G* level, a value of 1.41 eV for dissociation of the glycine dimer is obtained. The N,N-DMA dimer modeled at the MP2/3-21+g**//RHF/3-21G* level resulted in an E_o of 1.51 eV. These values are both 0.26 eV higher than the experimental values, indicating that the ab initio calculations at this level overestimate the true binding energies but provide relative energetics that are in excellent agreement with the experiment.

Conclusion

Arrhenius activation energies for the dissociation of proton-bound dimers of N,N-DMA and several amino acids were measured using BIRD. Dissociation threshold energies are obtained from these measurements by master equation modeling of the kinetic data. The reverse activation barrier for these reactions should be small so that the dissociation threshold energies should be approximately equal to the binding energies of these proton-bound dimer ions. The binding energy of N,N-DMA was found to be 1.25 ± 0.05 eV and is in excellent agreement with the literature value. The value obtained from the truncated Boltzmann model is significantly higher, indicating that the assumptions of the truncated Boltzmann are not valid due to the relatively large size of these ions. The binding energies of the amino acid dimers in the study were all ~1.15 ± 0.05 eV, despite the significant difference in gas-phase basicity and structure.

The modeled Arrhenius activation energy depends primarily on the threshold dissociation energy and is relatively insensitive to rates of absorption/emission and the microcanonical dissociation rates within the “loose” transition state assumption. However, the absolute value of the dissociation rate constant is sensitive to the absorption/emission rate. An accurate fit to the measured dissociation rate constant for N,N-DMA and glycine was obtained using absorption/emission rates calculated from vibrational frequencies and transition dipoles obtained from lowest energy structures obtained from ab initio calculations at the RHF/3-21G* and MP2/3-21G* level, repectively. To obtain a similar accuracy from the AM1 semiempirical values, it was necessary to multiply the transition dipoles by a factor of 3.

For relatively small molecules of biological interest, such as these proton-bound amino acid dimers, master equation modeling will typically be required to extract the threshold dissociation energy from BIRD measurements with high accuracy. For these ions, minimal information about the dynamics of the dissociation process is obtained, particularly if the absolute values of the radiative rates are not precisely known. For larger ions, the rates of radiative energy transfer with the vacuum chamber walls can vastly exceed the dissociation rate.^10,11 Under these conditions of rapid energy exchange, BIRD has the advantage that information about both the threshold dissociation energy as well as the dynamics of the dissociation process can be obtained directly from the measured Arrhenius values.

Appendix

Determining the microcanonical occupation probability is a combinatorial problem where we are interested in finding the number of possible combinations of assigning a quantity E′ of energy to a given vibrational mode ν in an ion with total internal energy E (E′ ≤ E). This is done by systematically eliminating each vibrational frequency from the density of states calculation and determining the vibrational density of states for the system 3N − 5 times, where N is the number of atoms in the dimer. The overall density of states is computed once and then each of the vibrational frequencies is individually eliminated in subsequent calculations. The microcanonical occupation probability is then given by the density of states calculated by omitting ν at the energy level (E − E′) normalized to the overall density of states at energy level E.

As an example, consider some nonlinear triatomic ion with three vibrational frequencies: 50, 100, and 150 cm⁻¹. The density of states for this system is calculated four times; first with all frequencies included and then for the three permutations of two frequencies. The results of these calculations for E < 700 cm⁻¹ are shown in Table 2 where the column label denotes the frequency excluded from the density of states calculation. For an ion with E = 600 cm⁻¹, the occupation probability of having 6 quanta of energy in the 50 cm⁻¹ oscillator is given by dividing the DOS at (E − E′) = 300 cm⁻¹ in the 50 cm⁻¹ column by the DOS at E in the total DOS column. This results in 2 out of 19 ways of distributing the energy such that 6 quanta are in the 50 cm⁻¹ oscillator. Similarly, 3 quanta in the 100 cm⁻¹ oscillator and 2 quanta in the 150 cm⁻¹ oscillator can be allocated in 3 and 4 out of 19 ways, respectively.

TABLE 2.

Calculated Density of States for a Hypothetical Trimer Ion

		DOS without
energy (cm−1)	total DOS	50 cm−1	100 cm−1	150 cm−1
0	1	1	1	1
50	1	0	1	1
100	2	1	1	2
150	3	1	2	2
200	4	1	2	3
250	5	1	2	3
300	7	2	3	4
350	8	1	3	4
400	10	2	3	5
450	12	2	4	5
500	14	2	4	6
550	16	2	4	6
600	19	3	5	7
650	21	2	5	7
700	24	3	5	8