Cochlear Pharmacokinetics with Local Inner Ear Drug Delivery Using a Three-Dimensional Finite-Element Computer Model

Abstract

Hypothesis:

Cochlear fluid pharmacokinetics can be better represented by three-dimensional (3D) finite-element simulations of drug dispersal.

Background:

Local drug deliveries to the round window membrane are increasingly being used to treat inner ear disorders. Crucial to the development of safe therapies is knowledge of drug distribution in the inner ear with different delivery methods. Computer simulations allow application protocols and drug delivery systems to be evaluated, and may permit animal studies to be extrapolated to the larger cochlea of the human.

Methods:

A finite-element 3D model of the cochlea was constructed based on geometric dimensions of the guinea pig cochlea. Drug propagation along and between compartments was described by passive diffusion. To demonstrate the potential value of the model, methylprednisolone distribution in the cochlea was calculated for two clinically relevant application protocols using pharmacokinetic parameters derived from a prior one-dimensional (1D) model. In addition, a simplified geometry was used to compare results from 3D with 1D simulations.

Results:

For the simplified geometry, calculated concentration profiles with distance were in excellent agreement between the 1D and the 3D models. Different drug delivery strategies produce very different concentration time courses, peak concentrations and basal-apical concentration gradients of drug. In addition, 3D computations demonstrate the existence of substantial gradients across the scalae in the basal turn.

Conclusion:

The 3D model clearly shows the presence of drug gradients across the basal scalae of guinea pigs, demonstrating the necessity of a 3D approach to predict drug movements across and between scalae with larger cross-sectional areas, such as the human, with accuracy. This is the first model to incorporate the volume of the spiral ligament and to calculate diffusion through this structure. Further development of the 3D model will have to incorporate a more accurate geometry of the entire inner ear and incorporate more of the specific processes that contribute to drug removal from the inner ear fluids. Appropriate computer models may assist in both drug and drug delivery system design and can thus accelerate the development of a rationale-based local drug delivery to the inner ear and its successful establishment in clinical practice.

Introduction

Clinical methods using drugs that are applied to the round window membrane are increasingly being used to treat inner ear disorders. The most widely used local inner ear therapy to date is the transtympanic injection of gentamicin into the middle ear for the treatment of Méniére’s disease. There are also an increasing number of clinical reports related to the local application of glucocorticoids for sudden idiopathic sensorineural hearing loss, immune-associated hearing loss, tinnitus and for Ménière’s disease. Other substances that have been tested in humans include local anesthetics, neurotransmitters and neurotransmitter antagonists. There is also interest in the use of growth factors, antioxidants or apoptosis inhibitors, some of which have been successfully tested in preclinical studies [for references see Salt and Plontke, 2005].

The idea of topical drug application to the inner ear is not new. Local anesthetics and aminoglycosides were applied by this method decades ago [Ersner et al., 1951; Schuknecht, 1956; Völger, 1952]. There is still, however, considerable uncertainty among clinicians with respect to the optimal dose, application interval or drug delivery system to be used. Clinical outcomes vary between different clinical reports with one factor being differences in the application protocols. As an example, while some authors report no hearing loss or deafness following single or repeated transtympanic injections of gentamicin for Ménière’s disease [Lange, 1995], others have reported complete deafness on the treated ear in more than 20% [Thomsen et al., 2000] or even 80% [Schoendorf et al., 2001].

A contributing factor to such variations appears to be the absence of reliable information on the pharmacokinetics of drugs in the inner ear. It is therefore necessary to develop an understanding of the quantitative substance distribution in the inner ear fluids after local application of medications. This is experimentally made difficult by technical problems in obtaining pure samples of the inner ear fluids [Salt and Plontke, 2005]. In humans, direct measurements of drug concentration time courses in the inner ear, as required for phase I clinical studies, are not presently possible. As an alternative, computer simulations provide a valuable tool for estimating drug concentrations in the inner ear [Salt, 2002]. Recently, simulations have been used to interpret published data on gentamicin and corticosteroid perilymph concentrations in the chinchilla and guinea pig cochlea [Plontke et al., 2002; Plontke and Salt, 2003]. Although an established one-dimensional (1D) simulation model (Washington University Cochlear Fluids Simulator, FluidSim 1.6, http://oto.wustl.edu/cochlea/model.htm [Salt, 2002]) provides a good representation of the longitudinal distribution of drugs [Mynatt et al., 2006; Salt and Thalmann, 1988; Salt and Ma, 2001], its ability to accurately predict the radial distribution of drugs (across and between scalae) is limited. Reduction of dimensionality from three-dimensional (3D) to two-dimensional (2D) or 1D is usually possible if the compartment is long relative to the cross-sectional area. This is true for most of the cochlear length in guinea pigs, but in the basal part of the cochlea, which is near the usual application location (i.e. the round window membrane), larger cross-sectional areas are found. Human scalae are also of substantially larger cross-sectional area than those of guinea pigs. Quantification of the ‘radial’ movement of drugs by local processes within each turn of the cochlea is also critical to understanding how drugs move from the base of the scala tympani into the vestibule, following their entry through the round window membrane. Kinetic analysis has shown that the time course of drug entry into the vestibule is dominated by local interscala movements in the basal turn and cannot be accounted for by passage through the helicotrema [Plontke et al., 2002]. A 3D model has therefore been suggested to better represent the complex geometry of the inner ear [Plontke et al., 2004]. The aim of such a 3D model would be to reduce those modeling errors that are caused by an inappropriate representation of the geometry.

Materials and Methods

Construction of the 3D Model of the Guinea Pig Cochlea

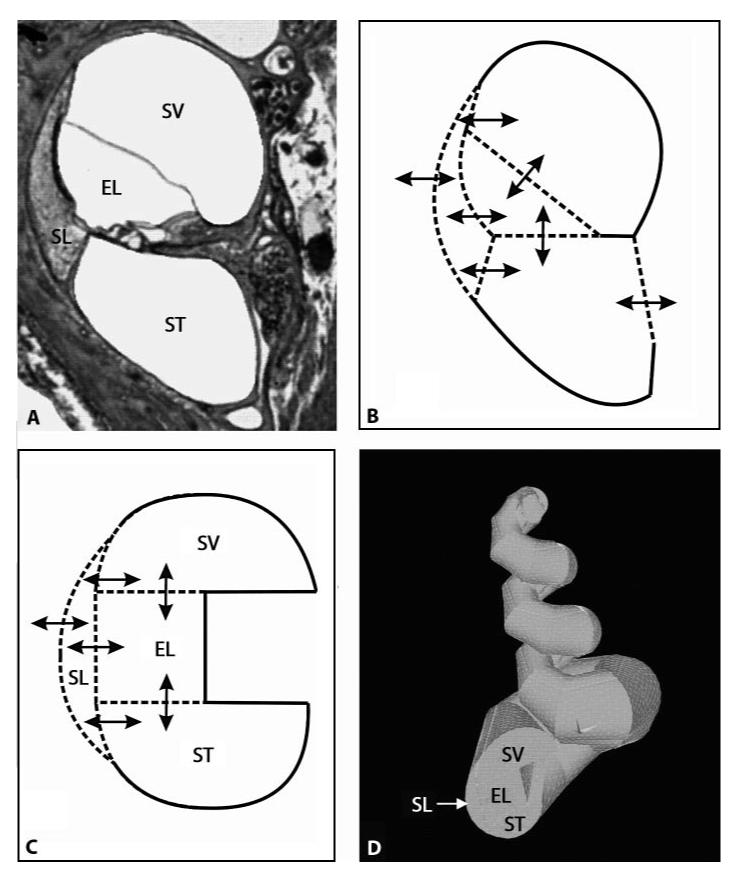
A 3D model of a coiled structure similar to the guinea pig cochlea was developed. The geometry was based on the simplified cross-sectional view of a guinea pig cochlea as shown in figure 1. It incorporates the volumes of the three cochlear scalae and the spiral ligament. The round window was placed in a plane perpendicular to the length axis of the scala tympani.

Fig. 1.

Construction of the 3D model of the guinea pig model. ST = Scala tympani; SV = scala vestibuli; ELS = endolymphatic space; SL = spiral ligament. A Cross-sectional view of one turn of the guinea pig cochlea. B Schematic showing the relevant ‘radial’ pharmacokinetic processes. Drugs are allowed to diffuse between the various compartments according to the respective concentration gradients and to the permeability at the specific border between two compartments as indicated by the arrows. C Simplified structure from B with pharmacokinetic processes incorporated into the 3D model. In addition, there is diffusion within the compartments along their longitudinal axis and through the helicotrema. D 3D model of the guinea pig cochlea in ANSYS based on the simplified cross-sectional view shown in C and on the functions describing the change of crosssectional area along distance shown in figure 2.

Drug propagation along and between compartments was described by passive diffusion within each compartment (i.e. scala tympani, ST; scala vestibuli, SV; cochlear endolymphatic space, EL, and spiral ligament, SL) and across the borders between the different compartments (ST-SL, ST-EL, SV-SL, SV-EL, EL-SL). In addition, substance transport across the round window membrane as well as substance movement between the spiral ligament and the systemic circulation, which can also be described as relative cochlear clearance, were incorporated. The relative cochlear clearance is defined as the clearance per surface area. The 3D model was implemented in a commercial software package for finite-element calculations (ANSYS, ANSYS Inc., Canonsburg, Pa., USA). The 3D structure was constructed from about 80,000 finite elements (tetrahedrons) with about 100,000 nodes (fig. 1D).

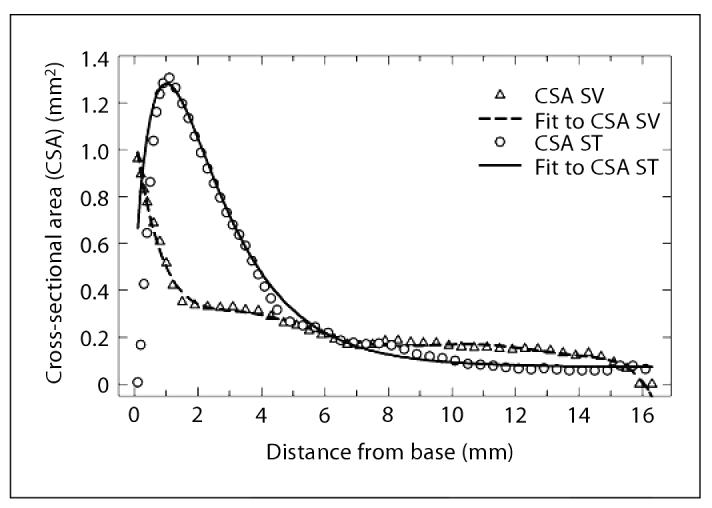
The change in cross-sectional area along the length of the scala tympani and vestibuli in the 3D model followed functions that closely approximated the change of cross-sectional area with distance for the guinea pig as published by Thorne et al. [1999] (fig. 2).

Fig. 2.

The 3D model of the guinea pig cochlea (fig. 1D) is based on the functions describing the change of cross-sectional area (CSA) for the fluid spaces of the ST and SV area along distance as published by Thorne et al. [1999] (open symbols) and their analytical approximation (lines). The following functions were fitted to the published cross-sectional area curves of SV and ST of the guinea pig cochlea:

$$f{\left(x\right)}_{\mathit{SV}}=a_1{x}^7+a_2{x}^6+\dots +a_{7}x+a_8,$$

$$f{\left(x\right)}_{\mathit{ST}}=a_1\frac{\ln (x+a_2)}{{(x+a_2)}^{a_3}}+a_4.$$

The constants a_i where chosen to fit the published data.

Simulation of Drug Distribution in the 3D Model

Substance distribution in the cochlea model was described as a system of partial differential equations. The equations are shown in detail in ‘Appendix A’ to this article, which is available online at: http://oto.wustl.edu/cochlea/model/threedee.htm. In brief: The concentration C_i in the scala tympani, scala vestibuli, the endolymphatic space, and in the spiral ligament is a function of time t and the 3D location $\overrightarrow{r}={(x,y,z)}^T$. Drug movement depends among other things on the diffusion coefficient k_i within the respective compartment Ω_i, (i = ST, SV, EL, SL).

The diffusion coefficient in perilymphatic and endolymphatic fluids can be calculated from the molecular weight of the substance applied and corrected for body temperature [Hobbie, 1997]. For simulation of the distribution of an example substance that has already been applied clinically for round window drug delivery (methylprednisolone succinate, molecular weight: 374.48 g/mol) a diffusion coefficient of 0.784·10^-3 mm²/s in the inner ear fluids spaces was used [Plontke and Salt, 2003]. Unlike the fluid-filled scalae, the spiral ligament consists of cells surrounded by extracellular fluid, which must be considered when calculating drug movements in this structure. As the volume is not all available for diffusion, the available volume has been expressed as a volume fraction. When investigating ion diffusion in the extracellular microenvironment of the rat cerebellum Nicholson and Phillips [1981] found a ‘volume fraction’ of approximately 0.2 (meaning about 20% of the total volume was extracellular space) [Nicholson and Phillips, 1981]. These authors also defined a ‘tortuosity factor’ (λ), which was an adjustment of the diffusion coefficient for the circuitous route molecules were forced to follow. The modified diffusion coefficient they defined, which we have adopted for our purposes, is

$$k_{\mathit{SL}}=\frac{k_{\mathit{ST},\mathit{EL},\mathit{SV}}}{{\lambda }^2}.$$

The tortuosity values (λ) they found were around 1.5 and for initial calculations we adapted this factor for the spiral ligament situation. Using this formula a diffusion coefficient for methylprednisolone succinate in spiral ligament tissue was calculated to be 0.3484·10^-3 mm²/s.

Substance transport between two neighboring compartments across a surface is proportional to the concentration difference (C_i-C_j) between the two compartments (i, j=ST, SV, EL, SL, i ≠ j) and depends on the transfer coefficient k_i-j,which is a measure of the barrier between two compartments.

The transfer coefficients k_i-j were derived from half-time values based on former simulations of methylprednisolone succinate distribution in the inner ear with an established 1D model [Plontke and Salt, 2003]. The half-time values were 45 min (SV-SL, ST-SL), 90 min (SV-EL, ST-EL, SL-EL) and 130 min (clearance from SL to systemic circulation, in millimeters per second): k_SV-SL: 0.11·10^-2, k_ST-SL: 0.5·10^-3, k_SV-EL: 0.6·10^-3, k_ST-EL: 0.4·10^-3 k_SL-EL: 0.5·10^-3).

At the round window membrane a constant concentration D was applied (D = 1, any unit, e.g. 1 g/ml). Relative clearance to the systemic circulation occurs through the spiral ligament (k_{SL, clear}: 0.18·10^-4 mm/s). All other compartments were considered as being completely isolated from the systemic circulation. A round window membrane permeability was used as calculated in former simulations of methylprednisolone succinate distribution using an established 1D model (β: 2.0·10^-8 mm/s) [Plontke and Salt, 2003].

After implementation of the geometry into the commercially available software package ANSYS, simulations were performed for the above set of parameters.

Comparison of 1D and 3D Simulations

It is of interest to compare the results from different modeling approaches, i.e. the predictions from the 3D model with those from the established 1D model (FluidSim 1.6). In addition, based on the 3D mathematical model a 1D model (1D-ITWM) was derived using a dimensionality reduction approach. For details of that dimensionality reduction approach see ‘Appendix B’, which is available online at http://oto.wustl.edu/cochlea/model/three-dee.htm.

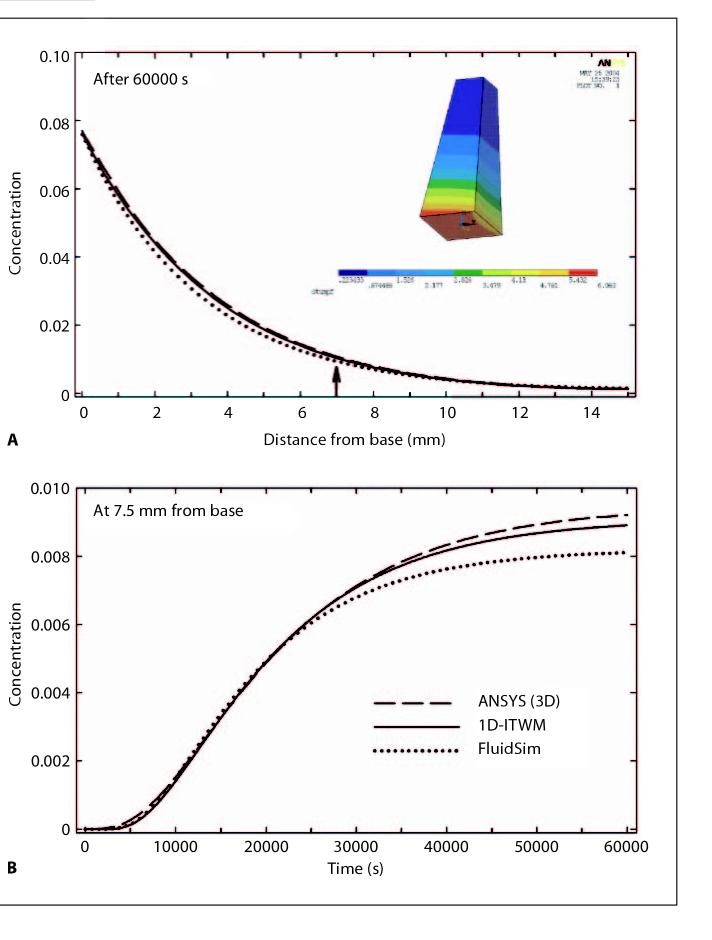
The calculated results for the three models (1D-FluidSim, 3D-ANSYS, 1D-ITWM) were first compared for a simple geometry. Specifically in each model a straight, tapered tube was defined with dimensions similar to that of the scala tympani of the guinea pig and with a basal ‘round window’ area: 1× 1 mm, apical area: 0.5× 0.5 mm, length: 15 mm. Distribution of methylprednisolone succinate was calculated for an application of 1000 min duration to a permeable membrane at the base (fig. 4, insert). The parameters used for the simulations were: diffusion coefficient: 0.784·10^-3 mm²/s; permeability at basal ‘round window’ area: 2.0·10^-8 mm/s; concentration at the basal ‘round window’ area: 1 (any unit, e.g. 1 g/ml); clearance half-time: 130 min.

Fig. 4.

A simplified geometry (insert in fig. 4 and ‘Appendix B’) was used to compare results from 3D with 1D simulations. A Concentration profiles with distance for the three models, the 3D model (ANSYS), the dimensionally reduced model (1D-ITWM) and the existing 1D model (Washington University Cochlear Fluids Simulator, FluidSim) calculated after an application time of 60000 s (1000 min) to the base. There is excellent agreement between the three models along the length of the structure. B Calculated concentration time courses for the middle of the structure (7.5 mm from the base, arrow). There is good correspondence between the three models for calculation times less than 25000 s (400 min).

Concentration Gradients for Two Different Drug Application Strategies

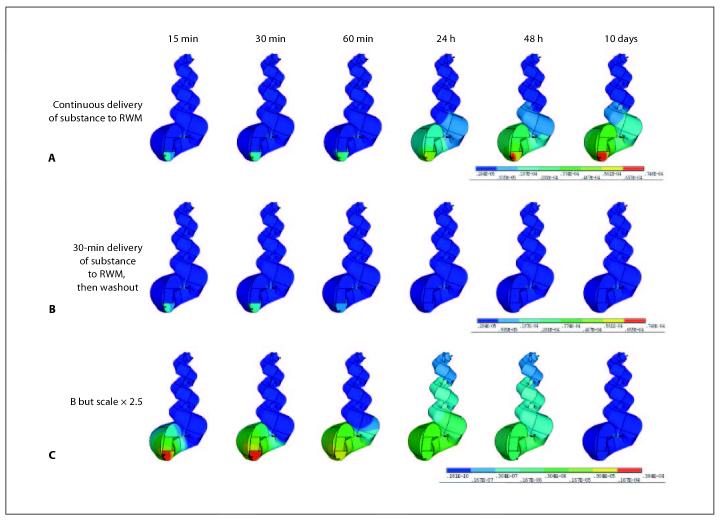
The constructed 3D model of the cochlea was then used to compare substance distribution in the cochlea model for two different drug application paradigms that are commonly used in clinical practice. One was a brief application of drug solution without stabilization of volume in the middle ear, comparable to a single transtympanic injection followed by washout from the middle ear cavity after 30 min, termed ‘intratympanic injection without volume stabilization’ [Parnes et al., 1999; Salt and Plontke, 2005; Ho et al., 2004]. The second paradigm was simulation of a continuous irrigation of the round window membrane such as via a catheter with an attached pump providing a constant drug concentration at the round window membrane for 10 days termed ‘continuous intratympanic drug delivery’ [Kopke et al., 2001; Plontke et al., 2005].

Results

An example of an ANSYS solution of the 3D model using parameters derived from fitting the 1D model to experimental data [Plontke and Salt, 2003] is shown in figure 3. It can be seen that during continuous application of methylprednisolone to the round window membrane a concentration gradient along the longitudinal axis of the scala tympani and scala vestibuli is built up, comparable to the findings with the 1D model. In addition, however, the 3D model demonstrates that significant gradients across the scalae are present in the basal turn. As the substance spreads longitudinally to regions of smaller cross section, radial gradients across the scalae become less apparent.

Fig. 3.

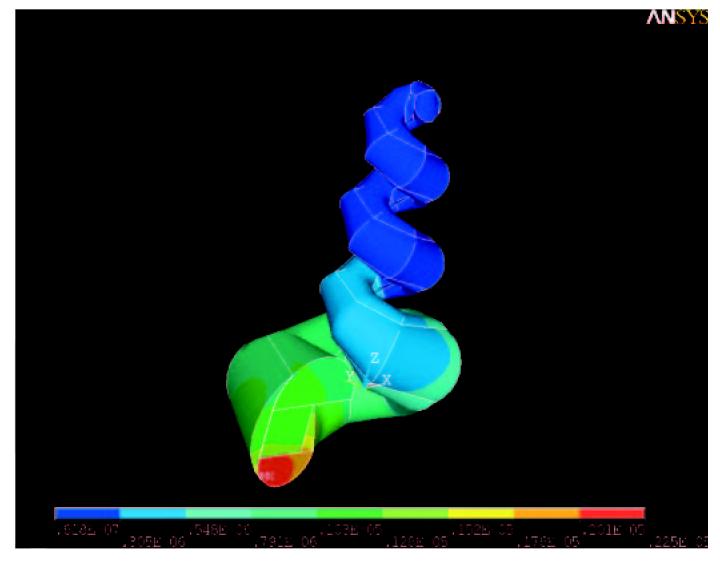
Sample calculation for the 3D-ANSYS model. The figure shows the saturation situation after continuous application of a substance to the round window membrane using the parameters from table 1.

A quantitative comparison of the 3D and 1D models is not possible due to the different geometries involved, which would not generate identical results. Instead, to permit a quantitative comparison between models, a dimensionality reduction approach was used in which substance distribution in straight, tapered tube geometry was calculated, as shown in figure 4. For the calculated concentration profiles with distance an excellent agreement between the three models along the length of the structure was observed (fig. 4A). The calculated concentration time courses for the middle of the structure (7.5 mm from the base) using the 3D model (ANSYS), the dimensionally reduced model (1D-ITWM) and the established 1D model (Washington University Cochlear Fluid Simulator, FluidSim) showed a good agreement for calculation times less than 25000 s (400 min) (fig. 4A). The deviations with longer calculation times are thought to arise from slight differences in the implementation of round window application and scala clearance algorithms.

The 3D-ANSYS model was then used to predict methylprednisolone distribution in the cochlea for two different clinically used drug delivery strategies, using parameters derived in a prior study [Plontke and Salt, 2003]. Results of two example scenarios are shown in figures 5 A-C. Simulation of chronic application of the drug for 10 days results in a high concentration at the basal, high frequency region and low concentrations in the apical, low-frequency region of the cochlea. Although drug may reach the apex in this scenario, the gradient along the length of the cochlea is maintained even after prolonged drug application. In addition, the concentration gradient between different scalae in the basal turn remains far greater than the gradients between scalae in higher turns (fig. 5A, last picture). After a brief application time (30 min), a much larger concentration gradient between the scalae in the basal turn and between the basal and apical parts of the cochlea is found (fig. 5 A-C: 30 min). The maximum concentration of methylprednisolone calculated for the two scenarios is higher for the continuous drug application strategy, demonstrating the importance of the application protocol to the drug level achieved. Soon after the end of the 30-min application, the concentration in the base of the scala tympani rapidly declines due to clearance from the cochlea and due to diffusion into other compartments and into apical regions. The basal-apical concentration gradient is then diminished (fig. 5B, C: 48 h, 10 days), although a very low drug level is present at this time. If compared to the same time point of the continuous application, a much lower drug concentration is present at the cochlear apex in the brief intratympanic application scenario (fig. 5A, B: 48 h).

Fig. 5.

Concentration gradients for two different application strategies. RWM = Round window membrane. A A basal-apical gradient persists even after continuous application of a substance to the base of the scala tympani for 10 days. High concentrations are found at the high frequency region of the cochlea compared to low concentrations at the low frequency region of the cochlea. Radial concentration gradients across the scalae and spiral ligament are also apparent. They are more pronounced in the basal compared to the apical part. B After a 30-min application time a much larger concentration gradient between the basal and apical regions of the cochlea is found. C Same application as in B but scaled up by a factor of 2.5. After stop of the brief application the gradients across the scalae in the base and between basal and apical regions are both diminished, even though the drug levels throughout the cochlea at this time are much lower compared to a continuous application strategy. Note that longitudinal concentration gradients and distribution in cross-sectional area are determined by pharmacokinetic parameters specific for the applied substance (i.e. diffusion coefficient, clearance and permeability of the boundaries between the various compartments).

Discussion

Finite-element models have been used in various fields of medicine, pharmacy or biomedical engineering. Examples are studies of drug distribution after local drug delivery to the vitreous humor of the eye [Friedrich et al., 1997], aerodynamic effects of inferior turbinate reduction in rhinosurgery [Wexler et al., 2005], modeling of components of the human middle ear [Beer et al., 1999] or modeling of cochlear dynamics [Parthasarathi et al., 2000]. The use of an initial 3D finite-element model in the present study of cochlear pharmacokinetics has shown that drug gradients both across and between the scalae in the basal turn are likely to be of substantial magnitude. This demonstrates the need to consider acrossscala gradients when calculating drug movements from the round window niche to the vestibule. In the higher turns, gradients across the scalae are less significant, but for the basal turn of the guinea pig a uniform distribution of drug across the scalae cannot be assumed. In calculating the movements of drug between ST and SV in the basal turn, 1D models may be limited in their accuracy. For cochlear scalae with larger cross-sectional area, such as those of the human, drug gradients across the scalae would be even larger than those shown here for the guinea pig, demonstrating the importance of 3D simulations for the human. Simple one-, two- or three-compartment models would not achieve similar results. Such simple models assume that each of the compartments is ‘stirred’ (such as when one of them is blood) and that there are no gradients across the compartments. Both 1D and 3D finite-element models and experimental data show that substantial gradients exist in the compartments and they are not ‘stirred’. Only a model which accurately represents the known drug gradients will generate meaningful results.

In addition, the results for 3D computations of two different delivery strategies showed very different concentration time courses, peak concentrations and basal-apical concentration gradients of the drug. The basal-apical concentration gradients that are predicted to exist in the cochlear fluids after round window drug delivery are of great importance for clinical applications. The magnitude of these gradients are possible indicators of which structure are likely to be reached by locally applied drugs. The existence of these gradients has also been suggested by former computer simulations using an established 1D model [Plontke et al., 2002; Plontke and Salt, 2003; Salt and Ma, 2001]. However, the intrascalae concentration gradients shown by the 3D model to likely exist in the basal turn cannot be represented in 1D models but are likely to have a substantial influence on the radial distribution of drug in the basal turn.

Although the present model is more accurate with respect to the 3D geometry, the simulations still need to be improved in several details. Firstly, the parameter set used for our simulations was based on parameters derived from former simulations with a 1D model. At present, the computation time for the 3D model does not allow multiple parameters to be fitted to experimental data in an appropriate time frame. In addition we need to define the 3D geometry of the inner ear in a more anatomically correct manner. For example, the basal part of the cochlea near the round window (‘hook region’) appears to play a significant role in substance transport from the scala tympani across the lateral wall to the scala vestibuli. Since we need to compare the 3D model with experimental measurements of the radial distribution of substances, an accurate comparison in this respect would need the fluid spaces near the basal turn to be better represented, including the vestibule itself. Without anatomically correct compartments, the accuracy of the 3D model in this region would be uncertain.

It has previously been shown that there is a fast communication between ST and SV across the lateral wall, resulting in early concentration peaks in the basal part of SV and in the vestibule [Plontke et al., 2002; Salt and Ma, 2001; Zou et al., 2005]. The vestibule itself acts as a ‘sink’, considerably influencing the pharmacokinetics in the cochlea. In addition, several inner ear disorders involve the vestibular part of the inner ear and the semicircular canals. Therefore, the 3D geometry of the entire inner ear needs to be incorporated into the finite-element software package to calculate substance concentrations in the peripheral vestibular system.

Also, in this version of the model some routes of communication and some processes that contribute to the distribution or removal of substance from the inner ear fluids have not yet been incorporated. At present it is assumed that clearance to blood occurs primarily at the major capillary beds of the lateral wall. Recent studies have suggested that communication routes also exist between perilymph in the scala tympani and the fluid spaces of the modiolus through the canaliculi perforantes [Shepherd and Colreavy, 2004]. Although the relative contributions of these pathways to drug clearance have not yet been established, all significant pathways must be incorporated into the model to ensure that radial gradients are accurately simulated. Similarly, although 1D modeling of experimental data has shown that the influence of convective flows, binding to receptors, proteins, entry into cells and metabolism do not represent major sources of clearance, it is possible that for some substances and under some conditions these processes may be significant and will need to be incorporated.

While the model is based on the physical principles of diffusion, which are universal and do not need specific validation, the magnitude and location of drug clearances need to be validated and supported by experimental data. In the past this has been problematic due to technical difficulties associated with obtaining pure perilymph samples [Plontke and Salt, 2003; Salt et al., 2003]. However, recently developed methods of sampling from the cochlear apex now permit longitudinal drug gradients in the scala tympani to be quantified, allowing model predictions to be compared and validated [Mynatt et al., 2006; Salt et al., 2006]. The confirmation of gradients across or between the scalae would not be easily demonstrated by fluid sampling. Instead, this would require spatially defined monitoring, such as by ion-selective microelectrodes. This is possible with ionic markers like TMPA, the concentration of which can be recorded in real time with a microelectrode [Salt and Ma, 2001].

Finally, for accurate simulations of substance distribution in the inner ear, numerous parameters are required, including diffusion coefficients, permeability values (across the round window membrane) and transfer coefficients between the scalae and to the systemic blood flow. Since these parameters cannot be directly measured, they need to be indirectly established by comparing simulations with measured drug concentration time courses. Defining such parameters requires multiple forward simulations. Despite modern computing techniques, the simulations take considerable effort in both time and computing power. Simulation approaches based on dimensionality reduction will continue to be justified for future investigations. It is probably best to have fast algorithms with 1D models resulting in parameter approximation in combination with detailed 3D models for fine-tuning of parameter estimation and extrapolation to the geometry of other species including the human. As a first step, the calculated results were compared between the two modeling approaches starting with a simple geometry. For this geometry, the concentration profiles calculated by the two models were closely comparable.

The next step is to use these validated 3D algorithms to compare diffusion characteristics in straight and spiral structures. In adding curvature into the 3D representation, cross-sectional areas, volumes and areas of intercompartment interaction (such as through the spiral ligament) become distorted. Comparisons of the differences between 3D structures and results from the original 1D model will establish how the more complex geometry influences calculated drug movements.

Conclusions

Computer simulations of drug distribution in the cochlea after round window application can be used as a valuable tool to evaluate application protocols and drug delivery systems, and to extrapolate from animal studies to the larger cochlea of the human. Compared to the established and validated 1D model the newly developed model demonstrates that 3D calculations are essential for accurate representation of the basal turn in guinea pigs and possibly all turns in the human. It was shown that radial (across-scalae and between scalae) gradients in the basal turn are highly significant in both the short-term and the long-term delivery states. The 3D model presented here is the first model that incorporates the volume of the spiral ligament and calculates diffusion through this structure. However, the current model needs to be further developed with respect to geometry and the complexity of pharmacokinetic processes and then validated by comparison with measured data. Since both 3D and lesser dimensional computer simulations appear to have different benefits in regard to accuracy or calculation speed for inverse determination of pharmacokinetic parameters, it is necessary to test and compare these approaches in more detail. An understanding of how drugs and other solutes move in the inner ear fluid spaces is critical to pharmacological manipulations of the inner ear. Appropriate computer models are invaluable in both drug and drug delivery system design, and they will be necessary for interpreting clinical treatment results and in designing future controlled clinical trials involving local drug delivery to the inner ear.

Appendix A: Calculation of Substance Distribution in the Cochlea

The aim was to calculate concentration values in the scala tympani, scala vestibuli, scala media and the spiral ligament depending on time t and location $\overrightarrow{r}{(x,y,z)}^T$. Substance distribution in the cochlea was described through diffusion equations.

If Ω_ST, Ω_SV, Ω_EL and Ω_SL are the domains occupied by ST, SV, EL and SL, substance diffusion can be described as follows:

$$\frac{\partial C_{\mathit{ST}}}{\partial t}(t,\overrightarrow{r})=k_{\mathit{ST}}\Delta C_{\mathit{ST}}(t,\overrightarrow{r}),\overrightarrow{r}\in {\Omega }_{\mathit{ST}},$$

$$\frac{\partial C_{\mathit{SV}}}{\partial t}(t,\overrightarrow{r})=k_{\mathit{SV}}\Delta C_{\mathit{SV}}(t,\overrightarrow{r}),\overrightarrow{r}\in {\Omega }_{\mathit{SV}},$$

$$\frac{\partial C_{\mathit{EL}}}{\partial t}(t,\overrightarrow{r})=k_{\mathit{EL}}\Delta C_{\mathit{EL}}(t,\overrightarrow{r}),\overrightarrow{r}\in {\Omega }_{\mathit{EL}},$$ (1)

$$\frac{\partial C_{\mathit{SL}}}{\partial t}(t,\overrightarrow{r})=k_{\mathit{SL}}\Delta C_{\mathit{SL}}(t,\overrightarrow{r}),\overrightarrow{r}\in {\Omega }_{\mathit{SL}}.$$

C is the concentration and k is the corresponding diffusion coefficient within the respective scala Ω.

For these equations, boundary conditions are necessary. The boundary conditions are described as follows: First, it is assumed that there is substance exchange across a common surface ∂ Ω between compartments as described in equations 2-1 to 2-5:

$$\overrightarrow{r}\in \partial {\Omega }_{\mathit{ST}-\mathit{EL}}$$ (2-1)

$$k_{\mathit{ST}}\frac{\partial C_{\mathit{ST}}}{\partial \overrightarrow{n}}=-k_{\mathit{ST}-\mathit{EL}}(C_{\mathit{ST}}-C_{\mathit{EL}}),$$

$$k_{\mathit{EL}}\frac{\partial C_{\mathit{EL}}}{\partial \overrightarrow{n}}=-k_{\mathit{ST}-\mathit{EL}}(C_{\mathit{EL}}-C_{\mathit{ST}}),$$

$$\overrightarrow{r}\in \partial {\Omega }_{\mathit{SV}-\mathit{EL}}$$

$$k_{\mathit{SV}}\frac{\partial C_{\mathit{SV}}}{\partial \overrightarrow{n}}=-k_{\mathit{SV}-\mathit{EL}}(C_{\mathit{SV}}-C_{\mathit{EL}}),$$

$$k_{\mathit{EL}}\frac{\partial C_{\mathit{EL}}}{\partial \overrightarrow{n}}=-k_{\mathit{SV}-\mathit{EL}}(C_{\mathit{EL}}-C_{\mathit{SV}}),$$ (2-2)

$$\overrightarrow{r}\in \partial {\Omega }_{\mathit{EL}-\mathit{SL}}$$

$$k_{\mathit{EL}}\frac{\partial C_{\mathit{EL}}}{\partial \overrightarrow{n}}=-k_{\mathit{EL}-\mathit{SL}}(C_{\mathit{EL}}-C_{\mathit{SL}}),$$

$$k_{\mathit{SL}}\frac{\partial C_{\mathit{SL}}}{\partial \overrightarrow{n}}=-k_{\mathit{EL}-\mathit{SL}}(C_{\mathit{SL}}-C_{\mathit{EL}}),$$ (2-3)

$$\overrightarrow{r}\in \partial {\Omega }_{\mathit{SV}-\mathit{SL}}$$

$$k_{\mathit{SV}}\frac{\partial C_{\mathit{SV}}}{\partial \overrightarrow{n}}=-k_{\mathit{SV}-\mathit{SL}}(C_{\mathit{SV}}-C_{\mathit{SL}}),$$

$$k_{\mathit{SL}}\frac{\partial C_{\mathit{SL}}}{\partial \overrightarrow{n}}=-k_{\mathit{SV}-\mathit{SL}}(C_{\mathit{SL}}-C_{\mathit{SV}}),$$ (2-4)

$$\overrightarrow{r}\in \partial {\Omega }_{\mathit{ST}-\mathit{SL}}$$

$$k_{\mathit{ST}}\frac{\partial C_{\mathit{ST}}}{\partial \overrightarrow{n}}=-k_{\mathit{ST}-\mathit{SL}}(C_{\mathit{ST}}-C_{\mathit{SL}}),$$ (2-5)

$$k_{\mathit{SL}}\frac{\partial C_{\mathit{SL}}}{\partial \overrightarrow{n}}=-k_{\mathit{ST}-\mathit{SL}}(C_{\mathit{SL}}-C_{\mathit{ST}}).$$

$\partial \mathrm{C}∕\partial \overrightarrow{\mathrm{n}}$denotes the directional derivate of C along the outer normal $\overrightarrow{\mathrm{n}}$.

From animal experiments and their interpretation with the established 1D model it is known that there must be a clearance from the cochlea most likely through the lateral wall to the systemic circulation [Plontke et al., 2002; Salt and Ma, 2001]:

$$\overrightarrow{r}\in \partial {\Omega }_{\mathit{SL},\text{clear}}$$

$$k_{\mathit{SL}}\frac{\partial C_{\mathit{SL}}}{\partial \overrightarrow{n}}=-k_{\mathit{SL},\text{clear}}{C}_{\mathit{SL}}$$ (3)

Here k_SL,clear denotes the relative clearance defined as clearance per surface area.

Apart from the outer part of the SL, the outer boundaries of all other compartments are considered as being completely isolated, i.e. on other outer surfaces

$$\frac{\partial C}{\partial \overrightarrow{n}}=0.$$

Substance will be delivered through the round window at the beginning of ST:

$$k_{\mathit{ST}}\frac{\partial C_{\mathit{ST}}}{\partial \overrightarrow{n}}=-\beta (C_{\mathit{ST}}-D),\overrightarrow{r}\in \partial {\Omega }_{\mathit{RW}-\mathit{ST}}$$ (4)

D is the concentration applied at the round window membrane, which in our example was set as a constant (table 1).

Table 1.

Parameters used for comparison of the three modeling approaches

Geometry
Length z	15 mm
Basal area	1 × 1 mm
Apical area	0.5 × 0.5 mm
Pharmacokinetic parameters
Diffusion coefficient	0.784 × 10-3 mm2/s
Permeability at base	2.0 × 10-8 mm/s
Concentration at base	1 (any unit)
Clearance half-time	130 min (7800 s)
Time calculated	1000 min (60000 s)
Parameters specific to the 3D model
Transfer coefficients at length zi
zi = 0 mm	8.89 × 10-5 mm/s
zi = 7.5 mm	6.66 × 10-5 mm/s
zi = 15.0 mm	4.44 × 10-5 mm/s

Drug entry was through the entire base. Clearance was only allowed from one side.

Appendix B: Reduction of Dimensionality

Instead of the 3D cochlea we consider a straight tapered tube Ωas presented in figure 4 (insert). Here, the figure below shows the projection of the tube into the (x, z) and (y, z) plane, where f(z) is an arbitrary continuously differentiable function.

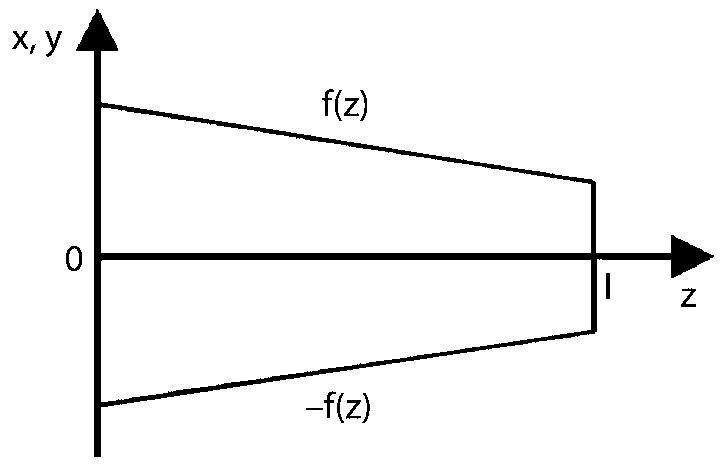
We formulate the diffusion equation for one compartment (for instance ST):

$$\frac{\partial C}{\partial t}(t,x,y,z)=k\Delta C(t,x,y,z),{(x,y,z)}^T\in \Omega ,0<t\le t^{\ast },$$ (5)

with boundary conditions at the base of the tube, z = 0, similar to equation 7

$$-k\frac{\partial C}{\partial z}(t,x,y,0)=-\beta [C(t,x,y,0)-D],$$ (6)

exchange conditions on one side x= f(z) (similar to equations 5)

$$k\frac{\partial C}{\partial \overrightarrow{n}}(t,f\left(z\right),y,z)=-\alpha [C(t,f\left(z\right),y,z)-B(t,y,z)],$$ (7)

where B(t, f(z), y, z) is some known concentration and αthe transfer coefficient.

All other boundaries we assume to be isolated

$$k\frac{\partial C}{\partial \overrightarrow{n}}=0.$$ (8)

At the beginning of the diffusion process the concentration inside the tube is given

$$C(0,x,y,z)=C_0(x,y,z).$$ (9)

Instead of the 3D concentration C(x, y, z) we consider a 1D concentration c(t, z) in z integrated over the cross section S(z) in the (x, y) plane

$$\stackrel{‒}{c}(t,z)=\frac{1}{S\left(z\right)}{\int }_{-f\left(z\right)}^{f\left(z\right)}{\int }_{-f\left(z\right)}^{f\left(z\right)}C(t,x,y,z)dxdy,$$

$$S\left(z\right)={\int }_{-f\left(z\right)}^{f\left(z\right)}{\int }_{-f\left(z\right)}^{f\left(z\right)}dxdy=4f^2\left(z\right).$$ (10)

If we assume that

$$\left(\mathrm{A}1\right)\frac{1}{2f\left(z\right)}{\int }_{-f\left(z\right)}^{f\left(z\right)}C(t,x^{\ast },y,z)dy=$$

$$=\frac{1}{2f\left(z\right)}{\int }_{-f\left(z\right)}^{f\left(z\right)}C(t,x,y^{\ast },z)dx=\stackrel{‒}{c}(t,z),$$ (11)

$$\left(\mathrm{A}2\right)C(t,-f\left(z\right),-f\left(z\right),z)=C(t,-f\left(z\right),f\left(z\right),z)=C(t,f\left(z\right),-f\left(z\right),z)=C(t,f\left(z\right),f\left(z\right),z)=c(t,z)$$ (12)

then the concentration c(t, z) averaged over the cross sections of the tube is the solution of the following 1D partial differential equation:

$$\frac{\partial \stackrel{‒}{c}}{\partial t}(t,z)=\frac{k}{S\left(z\right)}\frac{\partial }{\partial z}\left(S\left(z\right)\frac{\partial \stackrel{‒}{c}}{\partial z}(t,z)\right)-\frac{\sqrt{1+{\left(f^{\prime }\left(z\right)\right)}^2}}{2f\left(z\right)}\alpha [\stackrel{‒}{c}(t,z)-\stackrel{‒}{b}(t,z)],0<z<l,$$

$$k\frac{\partial \stackrel{‒}{c}}{\partial z}(t,0)=\beta (\stackrel{‒}{c}(t,0)-D),0<t\le t^{\ast },$$

$$k\frac{\partial \stackrel{‒}{c}}{\partial z}(t,l)=0,0<t\le t^{\ast },$$ (13)

$$\stackrel{‒}{c}(0,z)={\stackrel{‒}{c}}_0\left(z\right),0<z<l,$$

with

$${\stackrel{‒}{c}}_0\left(z\right)=\frac{1}{S\left(z\right)}{\int }_{-f\left(z\right)}^{f\left(z\right)}{\int }_{-f\left(z\right)}^{f\left(z\right)}{C}_0(x,y,z)dxdy,$$

$$\stackrel{‒}{b}(t,z)=\frac{1}{2f\left(z\right)}{\int }_{-f\left(z\right)}^{f\left(z\right)}B(t,y,z)dy.$$