Kinetic and functional analysis of transient, persistent and resurgent sodium currents in rat cerebellar granule cells in situ: an electrophysiological and modelling study

Abstract

Cerebellar neurones show complex and differentiated mechanisms of action potential generation that have been proposed to depend on peculiar properties of their voltage-dependent Na⁺ currents. In this study we analysed voltage-dependent Na⁺ currents of rat cerebellar granule cells (GCs) by performing whole-cell, patch-clamp experiments in acute rat cerebellar slices. A transient Na⁺ current (I_NaT) was always present and had the properties of a typical fast-activating/inactivating Na⁺ current. In addition to I_NaT, robust persistent (I_NaP) and resurgent (I_NaR) Na⁺ currents were observed. I_NaP peaked at ∼−40 mV, showed half-maximal activation at ∼−55 mV, and its maximal amplitude was about 1.5% of that of I_NaT. I_NaR was elicited by repolarizing pulses applied following step depolarizations able to activate/inactivate I_NaT, and showed voltage- and time-dependent activation and voltage-dependent decay kinetics. The conductance underlying I_NaR showed a bell-shaped voltage dependence, with peak at −35 mV. A significant correlation was found between GC I_NaR and I_NaT peak amplitudes; however, GCs expressing I_NaT of similar size showed marked variability in terms of I_NaR amplitude, and in a fraction of cells I_NaR was undetectable. I_NaT, I_NaP and I_NaR could be accounted for by a 13-state kinetic scheme comprising closed, open, inactivated and blocked states. Current-clamp experiments carried out to identify possible functional correlates of I_NaP and/or I_NaR revealed that in GCs single action potentials were followed by depolarizing afterpotentials (DAPs). In a majority of cells, DAPs showed properties consistent with I_NaR playing a role in their generation. Computer modelling showed that I_NaR promotes DAP generation and enhances high-frequency firing, whereas I_NaP boosts near-threshold firing activity. Our findings suggest that special properties of voltage-dependent Na⁺ currents provides GCs with mechanisms suitable for shaping activity patterns, with potentially important consequences for cerebellar information transfer and computation.

Granule cells (GCs) are small neurones that occupy a key position within the cerebellar-cortex circuitry forming the input layer of the major cerebellar afferent system. Mossy fibres activate GCs, which emit their output to other neurones in the cerebellar cortex through parallel fibres. In turn, GCs receive feed-forward and feed-back inhibition from Golgi cells (Eccles et al. 1967). Understanding the mechanisms that regulate GC action potential (AP) discharge upon excitation is particularly important, since GCs determine the AP code to be relayed into the cerebellar circuitry.

Voltage-dependent Na⁺ currents appear to play an important role in regulating the intrinsic activity patterns expressed by cerebellar neurones. Current-clamp recordings in acute cerebellar slices (D'Angelo et al. 1995, 1998; Brickley et al. 1996) and in vivo (Chadderton et al. 2004) have shown that GCs behave as regular spiking neurones in response to sustained, intense depolarizing stimuli. In the presence of just-threshold depolarization, however, GCs also show additional, peculiar patterns of activity and AP organization (D'Angelo et al. 1998, 2001). Single APs are preceded by slow, ramp-like depolarizing prepotentials, and are often followed by transient depolarizing afterpotentials (DAPs) that may also recur a few times before the subsequent AP is fired. APs are not regularly spaced, but tend to cluster into low-frequency bursts. It was suggested that prepotentials, DAPs and spike clustering reflect the intervention of a persistent Na⁺ current (I_NaP; D'Angelo et al. 1998), similar to I_NaP that in various neurones subtend sub- and near-threshold sustained depolarizing events (discussed in Magistretti & Alonso, 2002). Indeed, in the presence of K⁺- and Ca²⁺-channel block, the steady-state voltage-current (V–I) relationship of GCs shows an inward rectification region at about −55 to −30 mV that is abolished by tetrodotoxin (TTx) (D'Angelo et al. 1998). Modelling data also support the notion that the depolarizing envelope subtending AP bursts depends on I_NaP (D'Angelo et al. 2001). In addition, a resurgent Na⁺-current component (I_NaR; Raman & Bean, 1997) has recently been demonstrated in GCs (Magistretti et al. 2004; Afshari et al. 2004), and has also been suggested to participate in GC AP clustering (D'Angelo et al. 2001). I_NaR activates upon repolarization after depolarizations able to fully inactivate the transient Na⁺ current (I_NaT), and corresponds to Na⁺ channels transiently dwelling in the open state during return to closed states (Raman & Bean, 2001). In Purkinje cells, where it was first described, I_NaR has been proposed to promote the discharge of doublets or triplets of APs, instead of single spikes, in response to brief depolarizing pulses (Raman & Bean, 1997), thus contributing to AP conglomeration. In Purkinje cells, I_NaR also appears to have a role in enhancing firing frequency during tonic discharge (Khaliq et al. 2003). A similar role could also be played by I_NaR in GCs, which can produce relatively high maximal firing frequencies (120–150 Hz) (D'Angelo et al. 1998; Chadderton et al. 2004).

The above findings underscore the importance of determining the biophysical and functional properties of voltage-dependent Na⁺ currents (VDNCs) expressed by native GCs, and especially of those active in the sub- and near-threshold range of membrane potentials. Because a detailed analysis of VDNCs in native GCs is still lacking, in the present work we have carried out a thorough characterization of VDNCs in GCs in situ by performing whole-cell patch-clamp experiments in rat cerebellar slices. Besides I_NaT, persistent and resurgent Na⁺ currents were observed. We provide a biophysical characterization for each of these Na⁺-current components. We also present current-clamp and modelling data suggesting that I_NaR is involved in generating DAPs and enhances high-frequency firing, whereas I_NaP controls near-threshold firing activity, thus contributing to set the excitable properties of these neurones.

Methods

The animal experiments described in the manuscript conformed with the rules established by the University of Pavia for the use of animals in experimental studies, in compliance with the guidelines of the Italian Ministry of Health, the national laws on animal research (d.l. 116/92), and the EU guidelines on animal research (N. 86/609/CEE).

Slice preparation

Young Wistar rats (16–23 days old) were anaesthetized by inhalation of alothane (Sigma-Aldrich, Milan, Italy) and decapitated. The cerebellum was quickly extracted under hypothermic conditions and submerged in an ice-cold dissection Krebs solution composed of (mmol l⁻¹): 127 NaCl, 1.32 KCl, 26 NaHCO₃, 1.18 KH₂PO₄, 1.19 MgSO₄, 0.2 ethyleneglycol-bis-(β-aminoethyl ether)N,N,N′,N′-tetraacetic acid (EGTA), 16 d-glucose (pH 7.4 by saturation with 95% O₂, 5% CO₂). The cerebellar vermis was isolated from the hemispheres and blocked on the stage of a Microslicer DTK-1000 vibratome (Dosaka, Kyoto, Japan) using cyanoacrylate glue. During the sectioning procedure the tissue was submerged in an ice-cold (∼1–2°C) cutting solution containing (mmol l⁻¹): 130 potassium gluconate, 15 KCl, 20 N-2-hydroxyethylpiperazine-N′-2-ethanesulphonic acid (Hepes), 0.2 EGTA, 11 d-glucose (pH 7.4 with KOH). Using this high-K⁺ solution was found to improve neurone viability (Stéphane Dieudonné, unpublished results). Sagittal sections (250 μm thick) were cut, then rinsed in maintenance Krebs solution containing (mmol l⁻¹): 127 NaCl, 1.32 KCl, 26 NaHCO₃, 1.18 KH₂PO₄, 1.19 MgSO₄, 2 CaCl₂, 11 d-glucose (pH 7.4 by saturation with 95% O₂, 5% CO₂), and transferred to an incubation chamber filled with the same solution (continuously bubbled with 95% O₂, 5% CO₂). The slices were kept submerged in the incubation chamber at room temperature for at least 1 h before starting the recording.

Patch-clamp experiments: voltage-clamp recordings

The recording chamber was mounted on the stage of an inverted microscope (Axiovert 100; Zeiss, Oberkochen, Germany). Slices were transferred, one at a time, to the chamber and perfused with a solution suitable for isolating Na⁺ currents, containing (mmol l⁻¹): 100 NaCl, 26 NaHCO₃, 19.5 tetraethylammonium chloride (TEA-Cl), 3 KCl, 2 MgCl₂, 2 CaCl₂, 2 BaCl₂, 0.5 CdCl₂, 4 4-aminopyridine, 11 d-glucose (pH 7.4 by saturation with 95% O₂, 5% CO₂). The perfusion rate was about 1 ml min⁻¹. Patch pipettes were fabricated from thick-wall borosilicate glass capillaries (CEI GC 150–7.5; Harvard Apparatus, Edenbridge, UK) by means of a Sutter P-87 horizontal puller (Sutter Instruments, Novato, CA, USA). The pipette solution contained (mmol l⁻¹): 104 CsF, 50 TEA-Cl, 2 MgCl₂, 10 Hepes, 10 EGTA, Na₂ATP, and 0.2 NaGTP (pH adjusted to 7.2 with CsOH). The patch pipettes had a resistance of 5–8 MΩ when filled with the above solution. The recording electrode was inserted into the granular layer of the slice after application of positive pressure, and approached blindly to neurones in situ as described elsewhere (D'Angelo et al. 1993). Tight seals (>10 GΩ) and the whole-cell configuration were obtained by suction.

Voltage-clamp recordings of Na⁺ currents were performed at room temperature (21–24°C) by means of an EPC7 patch-clamp amplifier (List Electronics, Darmstadt, Germany). Series resistance (R_s) was continually monitored during the experiment using the amplifier built-in compensation section, and always compensated by 50–70% (average value, 55.5%; n = 128). Recordings in which R_s levels varied with time by more than 2 MΩ were discarded. Voltage protocols were commanded and current signals were acquired with a Pentium personal computer interfaced to a Tl–1 interface (Axon Instruments, Union City, CA, USA) using program Clampex of the pClamp 6.0.5 software package (Axon Instruments). In all recordings the holding potential was −80 mV. Current signals were low-pass filtered and digitized at different frequencies according to the experimental protocol applied: cut-off and sampling frequencies were 5 and 50 kHz, respectively, for I_NaT activation protocols and I_NaR protocols; 5 and 20 kHz, respectively, for I_NaT steady-state inactivation protocols and I_NaP 500 ms step protocols; 2 and 5–10 kHz, respectively, for ramp protocols. Currents were always on-line leak subtracted via a P/4 routine, except in the case of protocols applied for I_NaP study (see Fig. 3).

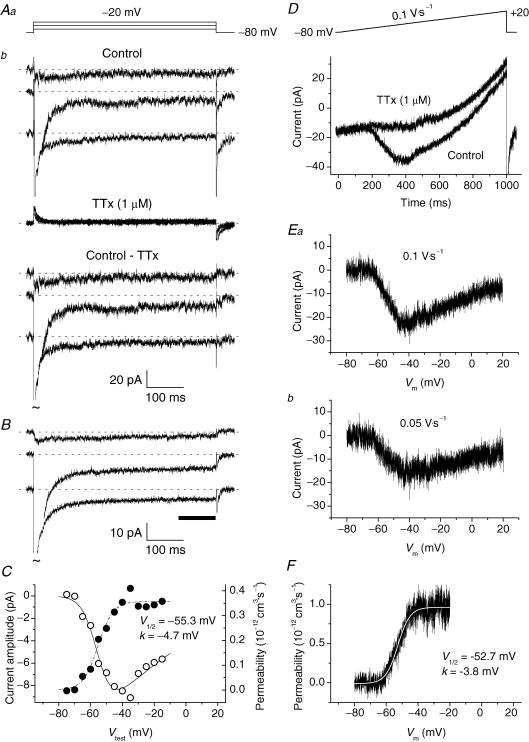
Figure 3. Persistent Na⁺ current (I_NaP) GCs.

I_NaP was activated by long-lasting step depolarizations (A–C) or ramp protocols (D–F). A, selected tracings from a representative GC (cell C3328). The current tracings shown in Ab have been recorded, in control conditions and in the presence of 1 μm TTx, in response to the voltage pulses illustrated in Aa. In this depolarizing-step protocol, the P/4 leakage subtraction routine was disabled to reduce background noise, and Na⁺ currents were isolated from capacitive and leakage currents and other contaminants via TTx subtraction. TTx-sensitive currents are shown in the lower part of Ab. Tildes indicate that I_NaT peaks have been truncated. B, average, TTx-subtracted current tracings obtained from 15 different neurones. The voltage protocol applied was the same as illustrated in Aa (test potentials are, from top to bottom, −60, −40 and −20 mV). The horizontal bar indicates the region of each tracing the data points of which were averaged to obtain a measure of current amplitude. C, I–V relationship (^) and plot of permeability as a function of V_test (•) for the average I_NaP (see B). Permeability values have been derived from current values as explained in the text. The dashed–dotted line is the best fitting obtained by applying a single Boltzmann function to permeability data points; fitting parameters are also specified. The continuous line has been derived from the same fitting function by converting permeability into current on the basis of the GHK equation. D, the current recorded in a representative GC (cell B3312), in control conditions and in the presence of 1 μm TTx, in response to the ramp depolarization illustrated in the upper part of the panel. E, TTx-sensitive, ramp-evoked currents in the same cell. The current shown in Ea has been obtained by subtraction from the two tracings of D. The current shown in Eb, also TTx-subtracted, was elicited by a voltage ramp twice less steep. Note that in the x-axis time values have been replaced by the corresponding potential values. F, plot of permeability as a function of voltage for the current illustrated in Ea. The ascending branch of the tracing has been best-fitted with a single Boltzmann function (smooth, white curve); fitting parameters are also specified.

Tetrodotoxin (TTx; Alomone Laboratories, Jerusalem, Israel) was applied in the bath with the superfusing solution.

Patch-clamp experiments: current-clamp recordings

Current-clamp recordings were obtained from GCs in cerebellar slices. Slices were perfused with a solution containing (mmol l⁻¹): 120 NaCl, 2 KCl, 1.2 MgSO₄, 26 NaHCO₃, 1.2 KH₂PO₄, 2 CaCl₂, 11 d-glucose, 1 kynurenic acid, 0.1 picrotoxin (pH 7.4 by saturation with 95% O₂, 5% CO₂). The pipette solution contained (mmol l⁻¹): 135 or 145 potassium gluconate, 5 KCl, 10 Hepes, 0.2 EGTA, 4.6 MgCl₂, 2 Na₂ATP, 0.4 NaGTP, pH 7.35. Recordings were performed at room temperature using a Multiclamp amplifier or an Axopatch 200B amplifier (both from Axon Instruments), the latter being used in the I_fast mode. Clampex 8.2 and a Digidata 1322A digitiser were used to inject current steps and acquire voltage signals. Sampling frequency was 50 kHz. No R_s compensation (bridge balance) was used. Voltage measurements were not corrected for errors introduced by R_s (≤1 mV).

Data analysis

Whole-cell current and voltage signals were analysed by means of program Clampfit of pClamp 6.0.5 and pClamp 8.2, respectively. Na⁺ currents were normally re-filtered off-line at 2–3.5 kHz. Current amplitude was measured at the peak of each tracing, unless otherwise specified. Na⁺ permeabilities (P_Na) were calculated from current amplitudes (I_Na) by applying the Goldman-Hodgkin-Katz equation in the form:

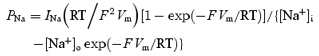(1)

in which the nominal intra- and extracellular Na⁺ concentration values (4.2 and 126 mm, respectively) were introduced.

To analyse I_NaT time course according to a Hodgkin-Huxley (HH) formalism, exponential fittings of I_NaT inactivation phase were first carried out. Second-order exponential functions were consistently required for proper fitting at test potentials of −35 to +15 mV. Because in the HH model the activation and inactivation processes are independent, current tracings were divided by their inactivation fitting functions, extrapolated to time zero of the depolarizing test pulse, to reconstruct the time course of the HH activation process. The curves thus obtained were then fitted with a HH activation function in the form:

(2)

where the power coefficient n was either left free to vary or kept at a fixed value (see Results).

Data fittings with exponential functions, I = ΣA_i exp(−t/τ_i) +C, were carried out using Clampfit. Fittings with Boltzmann functions, y = y_max/{1 + exp[(V−V_½)/k}, and HH activation functions (see above) were carried out using Origin 6.0 (OriginLab Corp., Northampton, MA, USA).

R_s was evaluated off-line by analysing the properties of capacitive current transients evoked by −10 mV voltage square pulses from the holding potential of −80 mV, as explained elsewhere (D'Angelo et al. 1993). Average R_s was 27.9 ± 1.2 MΩ (n = 84).

Average values are expressed as means ± s.e.m. Statistical significance was evaluated by means of a two-tail Student's t test for paired or unpaired data.

Computer simulations

Computer simulations of GC electrical activity were performed in the NEURON environment (Hines & Carnevale, 1997) by employing a GC single-compartment model described in detail elsewhere (D'Angelo et al. 2001). Modelling schemes and kinetic parameters were identical to those described in D'Angelo et al. (2001) for all membrane currents except Na⁺ currents. The HH-type formalism, previously employed to separately model I_NaT, I_NaP and I_NaR, was replaced with the 13-state, allosteric Na⁺-channel model by Raman & Bean (2001) in the modified form described by Khaliq et al. (2003), which simultaneously generates the three current components, and is shown in Scheme 1.

Scheme 1.

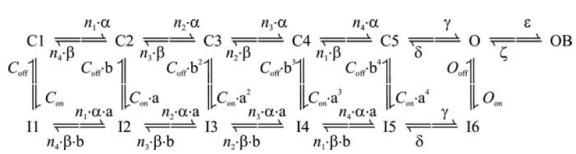
It is worth remarking that the model implicitly assumes the existence of a single Na⁺ channel accounting for all Na⁺-current components. The values of the kinetic parameters in Scheme 1 were adjusted to fit the observed properties of all Na⁺-current components, and were set as follows: α = 353.9 exp(V/k_α) ms⁻¹, β = 1.272 exp(−V/k_β) ms⁻¹, k_α = k_β = 13.9 mV, n₁ = 5.42, n₂ = 3.28, n₃ = 1.83, n₄ = 0.74; γ = 150 ms⁻¹, δ = 40 ms⁻¹, ɛ = 1.75 ms⁻¹, ζ = 0.0201 exp(−V/k_ζ) ms⁻¹, k_ζ = 25.0 mV; C_on = 0.005 ms⁻¹, C_off = 0.5 ms⁻¹, O_on = 0.75 ms⁻¹, O_off = 0.005 ms⁻¹, a = (O_on/C_on)^¼, b = (O_off/C_off)^¼. Na⁺ current was calculated as: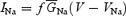, where f is the fraction of channels in the open (O) state as returned by numerical resolution of Scheme 1 for time and voltage; , the maximal Na⁺ conductance, was 8.0 mS cm⁻²; and V_Na, the Na⁺ equilibrium potential, was +87.4 mV.

To modify the persistent or the resurgent current components, kinetic constants were modified as follows: (1) I_NaR was switched off by setting the forward rate constant for the O → OB transition, ɛ, to zero. By itself, this modification (‘0-I_NaR⁻ condition’, for brevity) also resulted in considerable slowing of I_NaT decay (see Fig. 8C, violet tracing), due to the lack of the O → OB transition, which is a major exit path from the open state. (2) With ɛ set at zero, the rate constant of the O → I6 transition, O_on, was increased to 2.15 ms⁻¹ to restore the normal I_NaT decay speed. At the same time, the rate constant of the I6 → O transition, O_off, was increased to 0.01433 ms⁻¹ to prevent reduction of the persistent component. These changes (‘0-I_NaR⁺ condition’, for brevity) allowed us to obtain Na⁺ currents in which the I_NaR component was absent while the I_NaT and I_NaP components were largely unmodified (see Fig. 8C and D, red tracings). Note that the 0-I_NaR⁺ condition can be regarded as the equivalent of endowing the cell with a set of Na⁺ currents identical to control currents, with the only difference of I_NaR absence, whereas the 0-I_NaR⁻ condition can be viewed as the equivalent of removing the mechanism of I_NaR generation with no additional re-adjustments. (3) To reduce the steady-state I_NaP in the absence of other changes, the rate constant of the I6 → O transition, O_off, was decreased to 0.002 or 0.0015 ms⁻¹ (all other kinetic parameters were left unmodified). This resulted in an I_NaP reduction of 58 or 67%, respectively, at the steady state.

Figure 8. Simulated voltage-clamp activation of GC Na⁺ currents.

A, simulated I_NaT. Aa, the currents activated by a voltage-clamp protocol consisting of 15 ms depolarizing voltage steps at −70 to +20 mV in 5 mV increments, from a holding potential of −80 mV. Tracings corresponding to test potentials of −5, +5 and +15 mV have been omitted for clarity. The voltage-clamp protocol is schematized in the upper part of the panel. Ab, plot of normalized peak conductance () as a function of test voltage. The plot has been fitted with a single Boltzmann function (continuous line). Fitting parameters are also specified. B, simulated I_NaR. Ba, currents activated by repolarizing pulses at −15 to −70 mV in −5 mV increments, after a 19 ms depolarizing step at 0 mV (the voltage-clamp protocol is schematized in the upper part of the panel). Bb, the I–V relationship of the simulated I_NaR. In all simulations, the integration step size was 0.4 μs. C, effects on I_NaT of manipulations on the kinetic scheme aimed at modifying I_NaR. Simulated currents evoked by 15 ms depolarizing steps at 0 mV are shown. The current obtained under control conditions is shown in black. The violet tracing is the current obtained after setting the rate constant of the O → OB reaction, ɛ, to 0 (0-I_NaR⁻ condition: see kinetic Scheme 1 and the text for details). The red tracing is the current after setting ɛ to 0, the rate constant of the O → I6 reaction, O_on, to 2.15 ms⁻¹, and the rate constant of the I6 → O reaction, O_off, to 0.01433 ms⁻¹ (0-I_NaR⁺ condition). Note that the black and the red tracings are almost completely indistinguishable. D, modifications of I_NaP and I_NaR obtained by variously manipulating the kinetic scheme. The black tracing is the simulated control current evoked by the protocol shown in Ba (with a return potential of −35 mV). The red tracing is the current obtained in the 0-I_NaR⁺ condition (see above): note that I_NaR is abolished, whereas I_NaP is unmodified. The green tracing is the current obtained after setting O_off to 0.0015 ms⁻¹, and leaving all the other rate constants at their control settings: note that I_NaP is decreased at the steady state (arrow), whereas I_NaR is almost unaffected.

All other membrane parameters of the GC model, including specific membrane conductances, membrane surface area, and ion equilibrium potentials, as well as all parameters related to intracellular-Ca²⁺ dynamics, were the same as specified in D'Angelo et al. (2001). In both simulated voltage-clamp and current-clamp experiments, temperature was set at 22°C.

Results

Voltage-clamp experiments were performed under ionic conditions suitable to isolate Na⁺ currents (see Methods). Current tracings recorded in the presence of 1 μm TTx were routinely subtracted from control tracings to better isolate TTx-sensitive Na⁺ currents from contaminants. Recordings on GCs in situ were obtained from cells located in the external part of cerebellar lobules VI–IX. These experiments allowed us to identify three distinct Na⁺-current components in GCs.

Transient Na⁺ current

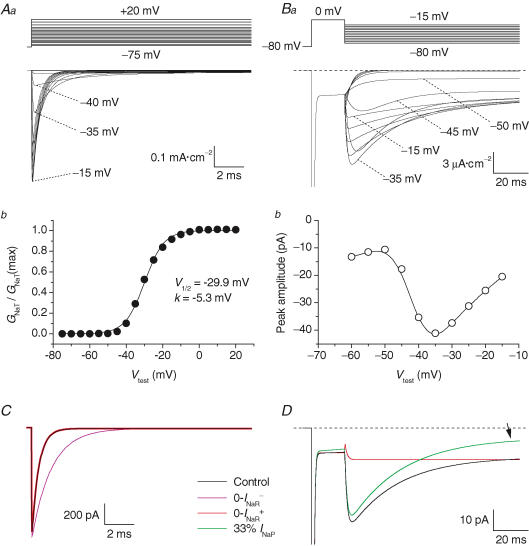
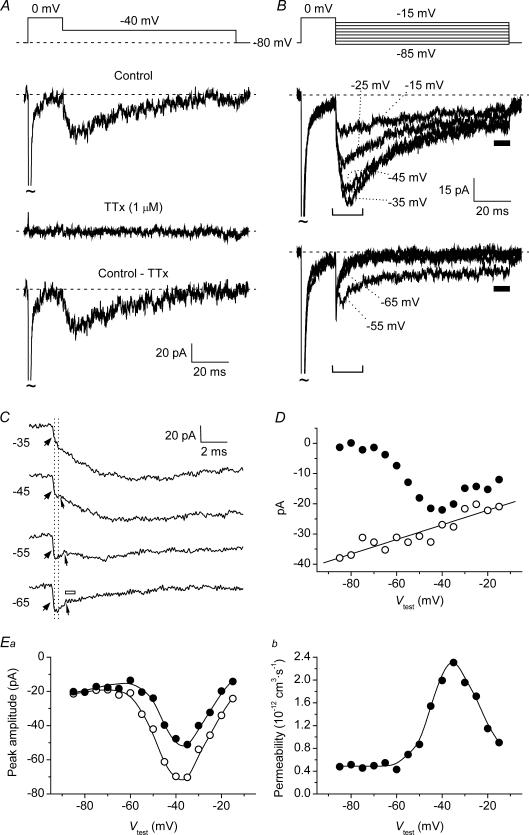
Transient Na⁺ currents (I_NaT) were studied by delivering 20 ms voltage square pulses at −75 to +20 mV in 5 mV increments. This depolarizing protocol elicited I_NaT that were always abolished by 1 μm TTx (Fig. 1A and B). In a large majority of GCs in situ (for brevity, named group 1 cells, n = 60 out of 84) I_NaTs showed signs of poor space clamp control (Fig. 1A). These currents included an unclamped component that was activated starting from −60 to −45 mV, typically after a more or less pronounced lag, and showed virtually no increase in amplitude in the subsequent one or two depolarizing steps. At more positive voltages a better-clamped component superimposed to the unclamped component, suggesting that in these cells the Na⁺ current was due to channels located partly in a membrane region electrotonically distant from the soma (presumably the axon), and partly in a more proximal region. In a few other cells (group 2, n = 12), the second, well-clamped Na⁺-current component was observed in isolation: an example of the currents recorded in these neurones is illustrated in Fig. 1Ba. In the remaining 12 cells, either currents with features intermediate between those of the two other groups (n = 6) or fully unclamped spikes (n = 6) were observed. Only the currents recorded in group 2 cells were used for the study of I_NaT biophysical properties. In group 2 cells, a measurable I_NaT was activated starting around −50 mV and the current-voltage (I–V) relationship peaked at −20/−15 mV (Figs 1Bb and 2A, open circles), with I_NaT amplitude at the I–V peak averaging −446.3 ± 74.9 pA (n = 12) (in group 1 cells, peak I_NaT amplitude was −640.3 ± 40.3 pA, n = 60). Peak current–amplitude values were used to calculate the permeability underlying I_NaT (P_NaT) as explained in the Methods, and P_NaT values were plotted as a function of test potential (Fig. 2A, filled circles). The P_NaT–V plots obtained were fitted with a Boltzmann function, which returned an average half-maximal activation potential (V_½) of −31.2 ± 1.9 mV and an average activation slope factor (k) of −4.7 ± 0.3 mV (n = 12). A steady-state inactivation protocol (Fig. 2Ba) was also routinely applied, and the results were analysed in group 2 cells (Fig. 2Bb): Boltzmann fitting of steady-state inactivation plots returned average V_½ and k values of −64.2 ± 3.6 mV and +5.5 ± 0.2 mV, respectively, (n = 5).

Figure 1. Transient Na⁺ currents (I_NaT) in granule cells (GCs) in situ.

A and B, the properties of the I_NaT recorded in two typical GCs (cell C4120 in A, and cell C4129 in B, representative of 60 and 12 cells, respectively). The voltage-clamp protocol applied to activate I_NaT is shown in the upper part of Aa and Ba. The middle part of the panels shows the experimental tracings thus obtained in control conditions (the tracings recorded at −75 to −30 mV, and at −25 to +20 mV, have been split in two different subpanels). The lower part of the panels shows the tracings recorded in the presence of 1 μm tetrodotoxin (TTx). Aa, example of the currents recorded in group 1 neurones (see the text), in which an unclamped and a well-clamped I_NaT component were apparent. The arrow points to the prominent lag preceding the activation of the unclamped component at its threshold. Ba, example of the currents recorded in group 2 neurones (see the text), in which the well-clamped I_NaT component was observed in isolation. Ab and Bb, current–voltage (I–V) relationships for I_NaT peak amplitude in the same two cells.

Figure 2. I_NaT in GCs: voltage dependence of activation, steady-state inactivation, and kinetics.

A, average, normalized (I–V) relationship of I_NaT in a representative group 2 GC (cell B3512) (^), and the corresponding permeability values (P_NaT, calculated as explained in Methods), plotted as a function of test potential, V_test (•). The P_NaT–V plot was best-fitted with a single Boltzmann function (dashed–dotted line): the fitting parameters thus obtained are also specified. The continuous line has been obtained from the same fitting function by converting permeability into current on the basis of the Goldman-Hodgkin-Katz (GHK) equation. Ba, voltage-clamp protocol applied to study I_NaT steady-state inactivation (top), and the currents thus obtained in the same cell illustrated in A (bottom). The duration of the conditioning prepulse was 125 ms. The inset shows a detail, over an expanded time scale, of the currents elicited by the activating pulse. Bb, plot of voltage dependence of I_NaT steady-state inactivation for the same cell. The peak amplitude values of the currents elicited by the activating pulse of the protocol illustrated in Ba were normalized for the maximal value observed and plotted as a function of conditioning-prepulse potential, V_cond (^). The continuous line is the best Boltzmann fitting to data points; fitting parameters are also specified. The activation P_NaT–V function obtained for this cell, normalized to its asymptotic value, is shown for comparison (dashed–dotted line: same as in A). The dotted line and the dashed line are average activation and steady-state inactivation functions, respectively, constructed as Boltzmann functions in which parameters V_½ and k equalled the respective average values (see the text). C, three exemplary I_NaT tracings recorded at the test potentials of −35, −20 and −5 mV in a representative group 2 GC (cell B4203). The inactivation phase of each current tracing has been best-fitted with a double exponential function (thick lines): the values of the fast and the slow inactivation time constants (τ_ina1 and τ_ina2, respectively) are also specified. D, plots of average I_NaT inactivation time constants (Da; ^ and •: τ_ina1 and τ_ina2, respectively) and relative amplitude of the fast exponential component (Db) as a function of V_test (n = 12). Note the logarithmic scale of the y-axis in Da.

I_NaT kinetics was also analysed in group 2 cells. I_NaT inactivation was first examined. The current inactivation phase was best described by a second-order exponential function at −35 to +15 mV (Fig. 2C). Both the fast and slow exponential components strongly accelerated with depolarization, as shown by the plot of the two inactivation time constants (τ_ina1 and τ_ina2) as a function of test potential (V_test) (Fig. 2Da). In addition, the relative weight of the fast exponential component tended to increase with depolarization (Fig. 2Db). I_NaT activation kinetics was then analysed by either considering rise time from 10 to 90% of peak amplitude (RT_10–90) or performing HH fittings of the current waveform (see Methods). RT_10–90 decreased from an average value of 1.3 ms at −45 mV to 155 μs at −10 to +10 mV (not shown). The application of the HH fitting procedure revealed that when n, the power coefficient of the HH fitting function (Methods, eqn (2)), was treated as a free fitting parameter, its value varied considerably at different V_test values, and markedly increased with depolarization (from ∼2 at −45/−40 mV to ∼9 at +5/+10 mV; see Supplemental Fig. A). Fixing the value of n at 4 or, even more, 3, returned a poorer correspondence of fittings with experimental tracings. The time constant of activation, τ_m, clearly tended to decrease with depolarization in HH fittings performed with free n (from 350 μs at −45/−40 mV to 65 μs at +5/+10 mV; Supplemental Fig. A, panel B1) and also, although to a lesser extent, with fixed n.

To evaluate the influence of series-resistance errors on the above measurements, we calculated the maximal estimated voltage error due to series resistance as V_err(max) = R_s(1 − f_comp)I_NaT(max), where R_s is series resistance, f_comp is the fraction of R_s compensation, and I_NaT(max) is the maximal Na⁺-current amplitude. In group 2 neurones, V_err(max) averaged 4.9 ± 0.9 mV (n = 12).

Persistent Na⁺ current

The application of long-lasting depolarizing steps and slow depolarizing ramps revealed that GCs in situ express, in addition to I_NaT, a small non-inactivating Na⁺-current component. Examples of such a persistent Na⁺ current (I_NaP) are illustrated in Fig. 3. Both group 1 and group 2 cells were considered for the study of I_NaP. The I_NaP evoked by 500 ms depolarizing pulses at −75 to −15 mV, in 5 mV increments, was first characterized (Fig. 3Ab). The application of this protocol revealed the presence of I_NaP as a sustained, TTx-sensitive inward-current component (Fig. 3Ab, lower tracings). Because of the very small size of this current, its properties were analysed after averaging experimental tracings obtained from a number of different cells, which substantially increased the signal-to-noise ratio and the reliability of measurements (Fig. 3B). The cells used to obtain the average current (10 group 1 cells plus 5 group 2 cells) were selected on the sole basis of optimal input-resistance and holding-current stability. I_NaP started to activate at about −65 mV, and its peak was at about −40 mV (Fig. 3C). The absolute amplitude of the average I_NaP (derived by considering the data points between 400 and 500 ms from the pulse onset) was −9.1 pA at the peak of the I–V relationship, which corresponds to 1.54% of the average maximal I_NaT amplitude observed in the same cells (−589.3 ± 82.9 pA, n = 15). The voltage dependence of the permeability underlying the average I_NaP (P_NaP) is also shown in Fig. 3C (filled circles). Boltzmann fitting to data points returned V_½ and k values of −55.3 mV and −4.7 mV, respectively.

In order to quickly explore the whole voltage range of I_NaP activation, slow ramp protocols able to inactivate I_NaT were also used. Ramp depolarizations from −80 to +20 mV at 100 mV s⁻¹ evoked currents that, after TTx subtraction, provided a continuous I–V relationship for I_NaP (Fig. 3D and E). The I–V relationships thus obtained showed a ‘threshold’ at −70/−60 mV and a peak at about −40 mV (Fig. 3E). P_NaP–V plots were also derived from ramp-activated currents and fitted with single Boltzmann functions, which returned V_½ and k values very similar to those obtained from the analysis of step protocols (Fig. 3F). We also found that if the ramp slope was decreased to 50 mV s⁻¹, the resulting I_NaP had a peak amplitude significantly lower than observed with 100 mV s⁻¹ ramps (−15.1 ± 2.4 versus−22.4 ± 3.4 pA, respectively; n = 29; P < 1 × 10⁻⁴, t test for paired data) (Fig. 3E), which suggests the existence of slow I_NaP inactivation during sustained depolarizations (see Discussion).

Resurgent Na⁺ current

The application of repolarizing pulses after I_NaT activation and decay led, in most GCs in situ, to activation of a resurgent Na⁺ current (I_NaR). Figure 4A shows the currents recorded in a representative cell in response to a voltage-clamp protocol consisting of a 20 ms step pulse at 0 mV that activated I_NaT, followed by a 100 ms pulse at −40 mV. The repolarizing pulse induced an extra inward current that activated and then decayed in a time-dependent manner, and was abolished by 1 μm TTx. This current was therefore identified as I_NaR. Both group 1 and group 2 cells were considered for the study of I_NaR. The presence of space-clamp problems, reported in group 1 cells by poor clamp control of part of I_NaT, is unlikely to significantly affect I_NaR, due to the relatively slow time course of this current component.

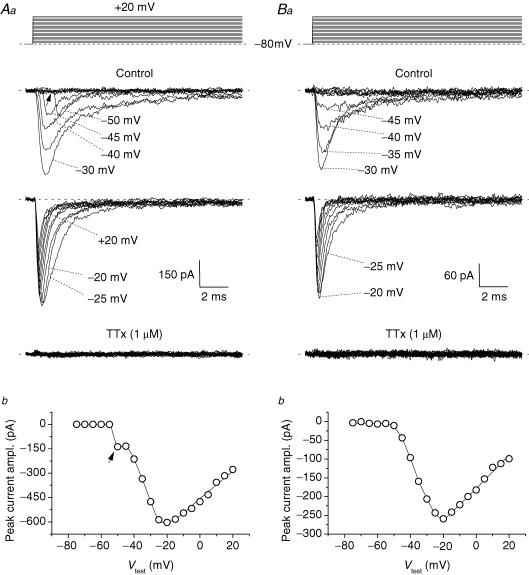
Figure 4. Resurgent Na⁺ current (I_NaR) in GCs.

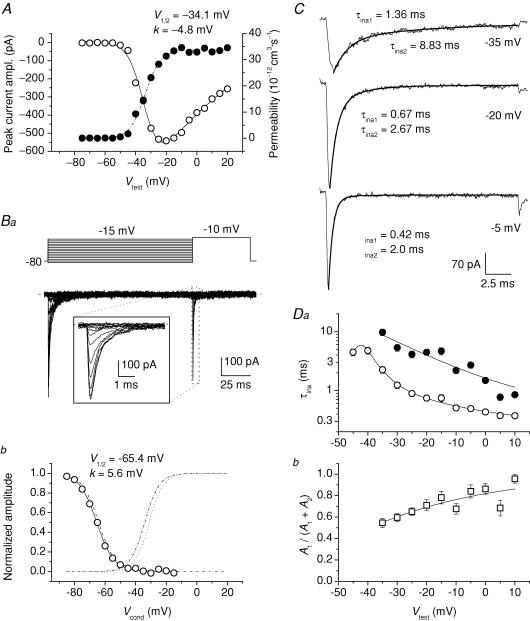
A, I_NaR in a representative GC (cell D4206). The experimental tracings are the currents recorded, in control conditions and in the presence of 1 μm TTx, in response to the depolarizing-repolarizing voltage command shown in the top panel. The bottom tracing is the TTx-sensitive current obtained by subtraction. B, I_NaR tracings obtained by averaging the currents recorded in six different neurones. Eight selected tracings are shown; the corresponding voltage commands are illustrated in the upper part of the panel. C, four tracings from B are shown in an expanded time scale to provide a detail of I_NaR onset. The tracing region highlighted corresponds to that embraced by the square brackets in B. The wide arrowheads point to the initial phase of current development, characterized by an abrupt and clearly faster rise (‘component (i)’). The narrow arrowheads point to the notch that may be observed between the initial phase and the late, slower phase of current development (‘component (ii)’). The two dotted, vertical lines delimit the tracing region the points of which were averaged to obtain a measure of component-(i) peak amplitude. The open bar next to the lowermost tracing marks the region in which I_NaR amplitude was measured in those tracings in which, due to the absence of an identifiable I_NaR peak, component (i) and component (ii) were not clearly separated: note that the region chosen immediately follows an evident reduction of the current's decline speed, indicative of I_NaP-tail subsiding (see the text). D, I–V relationship of component-(i) peak amplitude (^) and of the sustained inward current observed at the end of the 100 ms repolarizing pulses after I_NaR decay (I_end; •). Component-(i) peak amplitude was measured as illustrated in C. I_end amplitude was measured by averaging data points in the region marked by the horizontal bar in B. The straight line is the linear regression to component-(i) I–V plot, which returned an x-axis intercept at +71.7 mV, with R (regression coefficient) = 0.92, and P (the probability of R to be 0) < 1 × 10⁻⁴. E, voltage dependence of I_NaR peak amplitude and of the underlying permeability. Ea, the I–V relationship of raw I_NaR peak amplitude (^), and of ‘net’I_NaR peak amplitude (•), obtained by subtracting I_end amplitude from raw I_NaR peak amplitude. Eb, the voltage dependence of the permeability underlying the ‘net’I_NaR. Data points have been derived from those of Ea (•) by applying the GHK equation as described in Methods.

Although the majority of GCs expressed a measurable I_NaR, the current size was usually small, making its analysis problematic in individual cells. Therefore, average tracings from recordings made in different cells were constructed and used to perform an accurate analysis of I_NaR biophysical properties. A set of average tracings derived from six different GCs (4 group 1 cells, 2 group 2 cells) is shown in Fig. 4B. I_NaR was routinely elicited by commanding repolarizing pulses at −15 to −85 mV in 5 mV steps. Figure 4B (bottom) illustrates the currents evoked at 10 mV intervals. Several lines of evidence indicate that these currents were not merely tail currents due to current flow through non-inactivated Na⁺ channels (responsible for I_NaP): (1) peak current amplitude increased and then decreased as the level of repolarization was made more negative (Fig. 4Ea, open symbols), instead of increasing steadily; (2) at −15 to −55 mV, the current onset was not instantaneous but included a clearly gradual, time-dependent rising phase (Fig. 4C); and (3) the current decay was remarkably slow in a wide voltage window (see below, and Fig. 5). This notwithstanding, a close inspection of the current onset (Fig. 4C) clearly revealed the existence of two components: (i) an initial component that developed in an abrupt, nearly instantaneous fashion (Fig. 4C, wide arrowheads), followed by (ii) the gradually activating current. The distinction of the two components was particularly evident in a limited voltage window (−45 to −60 mV) in which component (ii) decreased in amplitude while maintaining relatively slow activation kinetics; in these cases, the two components were separated by a clear notch (Fig. 4C, narrow arrowheads), which indicates that component (i) is decaying as component (ii) is growing. Because the activating pulse at 0 mV also elicited a persistent Na⁺-current component (Fig. 4B), the above observations suggest that component (i) represents the I_NaP tail current. To verify this possibility, it was necessary to directly compare the amplitude of component (i) with that of I_NaP at various voltages. To this aim, the maximal amplitude of component (i) was estimated by measuring, at each voltage, the average current amplitude over the time interval delimited by the two dotted vertical lines in Fig. 4C: this time interval corresponds to a sharp change in the current rising-phase slope, which converts into a relative minimum when the notch appears at lower voltages. The resulting I–V plot showed a linear behaviour over the whole voltage range explored (Fig. 4D, open symbols), with an extrapolated x-axis intercept at +72.0 mV. This value is not far from the predicted Na⁺ equilibrium potential in our experiments (+86.7 mV). We also compared the voltage dependence of component (i) with that of I_NaP. As an estimate of I_NaP amplitude, we measured the sustained inward current at the end of the 100 ms repolarizing pulses following I_NaR decay (I_end) (Fig. 4B, horizontal bars). It can be seen in Fig. 4D that component (i) and I_end closely paralleled at −15 to −40 mV, a voltage window in which I_NaP activation reaches a plateau (see above, Fig. 3C and D). The slightly lower amplitude of I_end with respect to component (i) in this voltage range could be justified by I_NaP inactivation developing during the 100 ms depolarizing pulses (see the second section of Results, and Magistretti & Alonso, 1999). These data are consistent with component (i) of repolarization-elicited current onset corresponding to an I_NaP tail current.

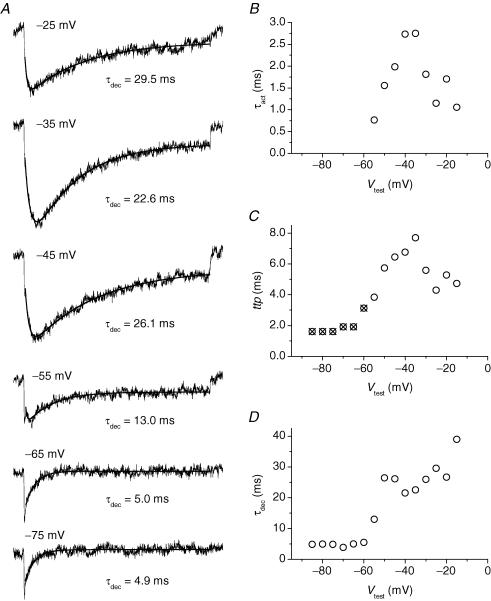
Figure 5. Kinetics of I_NaR activation and decay in GCs.

A, average I_NaR tracings at six selected potentials. These tracings are taken from those shown in Fig. 4B (note that here only the tracing region corresponding to the repolarizing pulses is shown; the preceding part of the protocol has been omitted). The repolarization level is specified next to each tracing. Smooth lines are second- (tracings 1–4) or first- (tracings 5 and 6) order exponential fittings to the currents' time course. The time constant of the exponential component describing the current's decay (τ_dec) is also specified next to each tracing. B, plot of I_NaR activation time constant (τ_act) as a function of V_test. τ_act values were returned by the fittings illustrated in A, in those cases in which I_NaR development was separated and distinguishable from I_NaP tails. C, plot of I_NaR time-to-peak (ttp) as a function of V_test. ttp was calculated taking the repolarizing pulse's starting point as time zero. Open circles and crossed circles correspond to ttp values obtained from measurements made in the presence and in the absence, respectively, of a true I_NaR peak region. In the latter case, the ‘peak’ region to be considered was chosen as illustrated in Fig. 4C (lowermost tracing). D, plot of I_NaR decay time constant (τ_dec) as a function of V_test.

Clearly, it would be desirable to determine the amplitude of the current specifically identifiable as I_NaR in isolation from the underlying I_NaP. At −15 to −40 mV, where I_NaP activation is saturating, this could be conveniently done by subtracting I_end (as an approximate estimate of the steady I_NaP level) from peak current amplitude; indeed, at these potentials the establishment of a new, steady I_NaP level upon repolarization will be nearly instantaneous. At more negative voltages, in which a step repolarization will result in a new I_NaP level after I_NaP-tail relaxation, this can also be done under the assumption that I_NaR activation is slow enough as compared to I_NaP-tail decay. The ‘net’I_NaR amplitude thus determined is plotted as a function of voltage in Fig. 4Ea (filled symbols). Current amplitude increased from −15 to −35 mV, where it showed a peak. At potentials negative to −35 mV, the current decreased back to reach, at about −60 mV, a non-zero level which then appeared to increase somewhat for further repolarizations. Note that at potentials negative to −55 mV, where I_NaP tail decay and I_NaR rising phase appeared to merge, I_NaR amplitude was obtained by considering the points that immediately followed a clear decrease in current–decay slope (see Fig. 4C, open bar), which presumably indicated I_NaP-tail subsiding. Permeability values were also calculated from ‘net’I_NaR amplitude values and plotted as a function of voltage (Fig. 4Eb): the plot was bell-shaped with a maximum at −35 mV and a pedestal level at −60 to −85 mV corresponding to about 20% of the peak.

I_NaR kinetics was then analysed (Fig. 5). At −15 to −55 mV, I_NaR activation and decay could be described by a double exponential fitting function (Fig. 5A). Component (i) of the current's rising phase (see above) was excluded from fitting. At potentials negative to −55 mV, a single exponential function was used to describe I_NaR decay. The activation time constant (τ_act) showed a bell-shaped dependence on voltage, with a peak of about 2.75 ms at −35/−40 mV (Fig. 5B). The plot of time to peak (ttp) versus voltage also showed a similar bell-shaped behaviour (Fig. 5C). The decay time constant (τ_dec; Fig. 5D) ranged from 35 to 20 ms at −15 to −40 mV, and appeared to decrease steadily with increasingly negative potentials in this voltage window. τ_dec also fell abruptly at −35 mV (34 ms) to −60 mV (5 ms), whereas at −60 to −85 mV it maintained a rather constant value of about 5 ms.

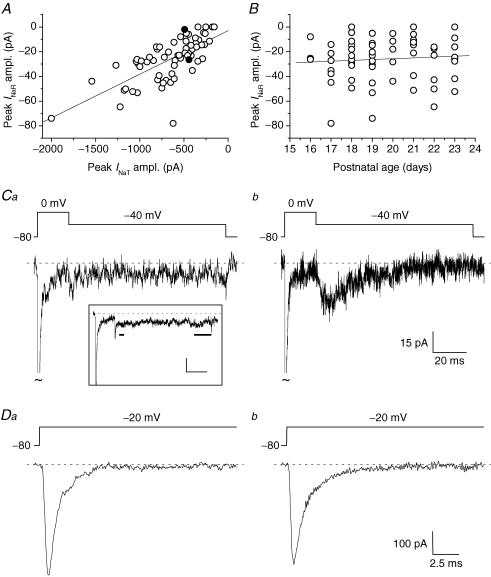
I_NaR amplitude varied considerably among cells. A strong correlation was found between I_NaR maximal amplitude and the size of I_NaT (measured at the peak of the I–V relationship) (Fig. 6A), whereas no significant correlation was observed with the animal's age in the time window considered (16–23 postnatal days) (Fig. 6B). A subset of cells displayed no measurable, or extremely little, I_NaR component (Fig. 6Ca). Because these cells also showed relatively small I_NaT (<500 pA), and because of the prominent correlation between I_NaR and I_NaT sizes, it could be suspected that in these instances I_NaR amplitude simply fell below the threshold of detection. This was not the case, however, since clear I_NaR components could be unequivocally detected in other cells that expressed I_NaT of similarly low amplitude (Fig. 6C and D). The above findings suggest the existence of heterogeneity in GC expression of I_NaR. Such diversity in I_NaR expression did not correlate with significant differences in I_NaT voltage dependence and kinetics. The half-activation potential (V_½) and slope factor (k) obtained from P_NaT–V plots averaged −30.9 ± 2.6 and −5.0 ± 0.6 mV, respectively, in I_NaR-lacking group 2 cells (n = 3), and −34.5 ± 3.1 and −4.5 0.6 mV, respectively, in group 2 cells in which I_NaR was present and greater than 15 pA in peak amplitude (n = 4; P > 0.4 in both cases). Moreover, in both groups, I_NaT kinetics was described by two exponential components with similar time constants. For instance, at −20 mV, decay time constants were 781.5 ± 115.2 μs and 6.46 ± 1.62 ms, and the relative A1 coefficient was 0.83 ± 0.05 in the former group (n = 3); and the same parameters averaged 691.4 ± 45.5 μs, 3.94 ± 1.13 ms, and 0.76 ± 0.02, respectively, in the latter group (n = 4; P > 0.16 in all cases). I_NaP peak amplitude relative to I_NaT peak amplitude was also not significantly different in I_NaR-lacking GCs (1.75 ± 0.71%, n = 5) and I_NaR-expressing GCs (1.87 ± 0.27%, n = 14; P = 0.86) (for this measure, only a subset of cells in which I_NaT peak amplitude was homogeneous and lower than 500 pA was considered for consistency).

Figure 6. I_NaR amplitude strongly correlates with I_NaT amplitude, but I_NaR expression and amplitude also show intrinsic variability in GCs.

A, scatter plot of I_NaR amplitude as a function of I_NaT amplitude. I_NaR and I_NaT amplitudes were measured at the peak of the respective I–V relationships (normally −40/−35 mV and −20 mV, respectively). The straight line is the linear regression to data points (slope factor = 35 pA nA⁻¹; R = 0.69, P < 1 × 10⁻⁴). B, scatter plot of I_NaR amplitude as a function of the postnatal age of the animal (in days after birth). The straight line is the linear regression to data points (slope factor = 0.51 pA day⁻¹; R = 0.062, P = 0.62). Data in A and B are from 67 cells. In both cases, I_NaR amplitude values are ‘net’ values, calculated as peak current minus I_end (see the text). C and D, I_NaR and I_NaT, respectively, recorded, at the peak of the I–V relationships, in two exemplary neurones (Ca and Da, cell B3428, representative of 7 cells; Cb and Db, cell B3327; both cells were classified as group 1 cells). Note the similar size of I_NaT, the presence of a clear I_NaR in Cb, and its almost complete absence in Ca. The two cells illustrated here are identified by the two filled symbols in A. Ca, inset, average tracing obtained from 7 cells (four group 1 cells, three group 2 cells) that were judged as devoid of a measurable I_NaR (same voltage protocol as in the main panel). Note that, at the time point at which an I_NaR peak would be expected (short horizontal bar), current amplitude was not different from that of the late I_NaP component (long horizontal bar). In the same 7 cells, the average I_NaT amplitude at the peak of the I–V relationship was −301.0 ± 47.0 pA. Calibration bars in the inset, 20 ms, 15 pA.

Current-clamp recordings: depolarizing afterpotentials

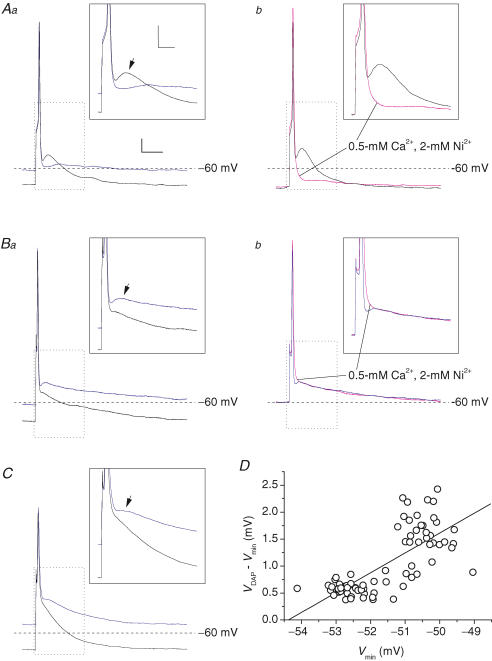
To investigate the presence of functional correlates of I_NaP and/or I_NaR in GC intrinsic excitability, we carried out current-clamp experiments in which single APs were evoked with short (0.5 ms) depolarizing square current pulses. Baseline membrane potential (V_bas) was held at stationary levels in the −55 to −75 mV range by steady current injection, and 0.5 ms current steps were repeatedly applied at 1 Hz frequency. Step amplitude was regulated to obtain just above-threshold stimulation. Firing responses consisted in single spikes, evoked with a 1–5 ms delay from stimulus. In 4 out of 16 GCs, the AP terminated with a profound fast afterhyperpolarization (AHP) (n = 2) or with a quick return directly to V_bas (n = 2). In the remaining 12 cells, the AP fast repolarization phase was followed by an evident depolarizing afterpotential (DAP), making a hump 5–10 ms after spike peak. The hump consisted, in different cells, in either a true peak following a postspike relative minimum (Fig. 7A and B; n = 10), or an inflection in the membrane potential (V_m) trajectory after fast spike repolarization (Fig. 7C; n = 2).

Figure 7. Depolarizing afterpotentials (DAPs) in GCs.

A–C, APs evoked in three typical GCs (A, cell D5518, representative of 2 cells; B, cell A5516, representative of 8 cells; C, cell G100305a, representative of 2 cells) by 500 μs depolarizing square current pulses. Aa, Ba and C show APs recorded in each cell starting from two different baseline voltage levels (V_bas) (−70 mV, black tracings; and −55/−60 mV, blue tracings). Ab and Bb, APs recorded, starting from the same V_bas, under control conditions (black or blue tracings) and during perfusion with a solution containing 0.5 mm Ca²⁺ and 2 mm Ni²⁺ (tracings in magenta). Calibration bars: 25 ms, 8 mV. The insets show a detail of the tracings, corresponding to the region delimited by the dotted-line box, of each main panel. The arrows point to the DAPs following single APs. Calibration bars in insets: 10 ms, 10 mV. The amplitude of depolarizing current pulses varied from 0.28 (Aa) to 1.3 nA (C). D, plot of the difference between the absolute voltage level at DAP peak (V_DAP) and the level of the relative minimum between the AP and the DAP (V_min; see the text for details) as a function of V_min for the same cell illustrated in B. Each point corresponds to the measure made in an individual AP. The straight line is the linear regression to data points (slope coefficient = 0.368 mV mV⁻¹; R = 0.74, P < 1 × 10⁻⁴).

We next examined whether the above-described DAPs could be underlain by I_NaR and/or I_NaP, or, alternatively, by other mechanisms, such as voltage-dependent Ca²⁺ currents. In two of the 12 cells, the DAP was prominent when resting potential was negative to −65 mV, but was markedly reduced by background depolarization (Fig. 7Aa). Moreover, in the same two cells the DAP was abolished by perfusion with a solution in which Ca²⁺ concentration was lowered to 0.5 mm and which contained 2 mm Ni²⁺ (Fig. 7Ab). These findings indicate that in a minority of GCs DAP generation depends on a Ca²⁺ current that requires hyperpolarization for repriming. In the remaining 10 GCs the DAP showed different properties. In all of these cells the DAP, either consisting in a true peak (n = 8) or in an inflection (n = 2), was reduced, rather that enhanced, by background hyperpolarization (Fig. 7Ba and C). In addition, in all cases tested, perfusion with the 0.5 mm Ca²⁺, 2 mm Ni²⁺ solution reduced AP repolarization speed and largely abolished the relative minimum between the AP and the DAP, consistent with a role for Ca²⁺-activated K⁺ channels in AP repolarization (D'Angelo et al. 1998), but did not decrease the depolarization level reached during the DAP (Fig. 7Bb; n = 5 out of 5). Hence, in a majority of GCs the DAP is not generated by Ca²⁺ current(s) reprimed upon hyperpolarization. Other possible candidates that could account for DAP generation in GCs are I_NaP and I_NaR. In particular, due to its property of activating upon repolarization in a time-dependent manner, I_NaR appears particularly suitable to sustain a depolarization following AP repolarization. Slow perfusion with 200 nM TTx resulted in gradual, parallel reduction, and eventually suppression, of both the AP and the DAP (n = 4). Therefore, this approach did not allow us to establish whether the DAP depended on TTx-sensitive Na⁺ channels or, rather, on the AP in itself. However, an indication about the nature of the DAP was provided by further analysis of its voltage dependence. In 6 out of 10 cells it was possible to regulate the level of the relative minimum between the AP and the DAP (V_min) by modifying the resting potential with steady current injection. In these cells, V_min varied in a voltage window comprised between −45 and −65 mV. If the DAP depends on I_NaR activation, its amplitude is expected to decrease as V_min is made increasingly negative, for two reasons: (i) with increasing hyperpolarization, I_NaR amplitude either decreases (at −45 to −60 mV) or remains relatively stable (negative to −60 mV), while its decay becomes progressively faster; and, simultaneously (ii) the negative current injected to hyperpolarize the cell counteracts positively going voltage deflections. Therefore, for the above six cells we plotted the difference between the absolute voltage level at DAP peak (V_DAP) and V_min as a function of V_min. In all cases, the difference V_DAP−V_min, which is an index of DAP amplitude, positively correlated with V_min (Fig. 7D). The slope coefficient returned by linear regression of these plots averaged 0.30 ± 0.06 mV mV⁻¹, and the correlation was statistically significant (P < 0.003 in all cases). Hence, in these cells the DAP was enhanced as the voltage relative minimum that preceded it was made more positive in the −65 to −45 mV voltage range. This behaviour is compatible with the properties of I_NaR.

Roles of I_NaR and I_NaP: computer modelling

To obtain further insight into the consequences of I_NaR and I_NaP expression on GC excitability, we resorted to computer modelling. Simulations were based on a previous single-compartment GC model (D'Angelo et al. 2001) implemented with the 13-state, allosteric Na⁺-channel model by Raman & Bean (2001). This model, which generates I_NaT, I_NaP and I_NaR simultaneously, was re-parameterized to adequately reproduce the specific properties of GC VDNCs (see the Methods). Figure 8 illustrates the main properties of I_NaT and I_NaR returned, in simulated voltage-clamp experiments, by the model. The main properties of Na⁺ currents were reproduced with good approximation. The voltage dependence of simulated I_NaT was very similar to that observed, on average, in experimental currents: the conductance-voltage plot showed V_½ and k values of −28.9 mV and −5.4 mV, respectively (Fig. 8Ab; cf. Fig. 2Bb). The decay kinetics of simulated I_NaT closely approximated the fast decay component of experimental I_NaT (for instance, at 0 mV simulated I_NaT decayed monoexponentially with a time constant of 476.6 μs, to be compared with an average value of 431.1 μs for τ_ina1 in experimental currents: cf. Fig. 2Da). Also, the properties of simulated I_NaR and I_NaP were reasonably close to those of experimental currents. Simulated I_NaR showed a peak in the I–V relationship at −35 mV, a monoexponential decay (with τ_dec = 29.3 ms at −35 mV), and an abrupt acceleration of decay at −55 mV (Fig. 8B; cf. Figs 4Ea and 5D). Simulated I_NaP peaked at −35 mV, with a half-maximal activation potential of the underlying conductance of −48 mV (not shown). It should be noted that the model did not generate the slow component of I_NaT decay, suggesting that further kinetic details would be needed to fully reproduce the behaviours of real Na⁺ channels.

The maximal specific Na⁺ conductance 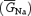chosen for current-clamp simulations was 8 mS cm⁻², which yielded a peak Na⁺-current density of −541.6 μA cm⁻². If one assumes Na⁺ channels to be uniformly distributed on the somatic membrane, the latter value would correspond to a peak I_NaT amplitude of −957.1 pA (with a soma diameter of 7.5 μm), a value somewhat greater than those typically observed in real GCs (cf. Fig. 6A). However, Na⁺-channel expression may be confined to more limited, highly excitable membrane subcompartments in GCs, including the axon initial segment (see Schaller & Caldwell, 2003). The ratios of I_NaP and I_NaR peak amplitudes to I_NaT peak amplitude were within the range of values observed in GCs (0.0078 and 0.026, respectively). With these settings, the model GC responded to injection of depolarizing current steps by firing regular trains of APs (Fig. 9A and B). AP frequency showed an approximately linear relationship with injected current amplitude, and the slope of the frequency–current plot (constructed for a stimulating-current range of 3.5–8.0 pA) was 11.2 Hz pA⁻¹ (Fig. 9Ca). The apparent threshold for AP firing was at about −50 mV. All these properties are consistent with those experimentally observed for real GCs (D'Angelo et al. 1998).

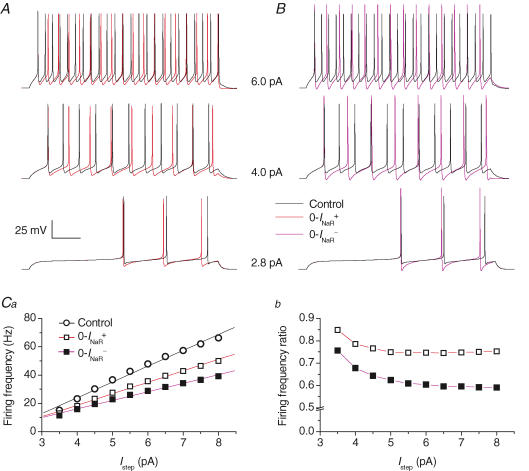
Figure 9. Effects of I_NaR on repetitive firing in a model of GC electrical activity.

A and B, repetitive AP firing elicited by injection of 1 s (lower tracings) and 500 ms (middle and upper tracings) depolarizing current steps. Step current amplitude was 2.8 pA (lower tracings), 4 pA (middle tracings) and 6 pA (upper tracings). Black tracings are simulated voltage signals obtained under basal conditions. Red tracings (A) and violet tracings (B) were obtained after abolishing I_NaR by adopting the 0-I_NaR⁺ condition settings, and the 0-I_NaR⁻ condition settings, respectively (see the text for details). The x-axis calibration bar is 150 ms for lower tracings, and 75 ms for middle and upper tracings. Ca, plot of firing frequency as a function of injected step current amplitude (I_step) (^, basal conditions; □, 0-I_NaR⁺ condition; ▪, 0-I_NaR⁻ condition). Straight lines are linear regression fittings to data points. Slope coefficients are 11.2 Hz pA⁻¹ (^), 8.1 Hz pA⁻¹ (□), and 6.0 Hz pA⁻¹ (▪). Cb, plot of the ratio of firing frequency in the 0-I_NaR⁺ condition (□) and in the 0-I_NaR⁻ condition (▪) to control firing frequency, as a function of stimulation intensity.

We next examined the specific effects of I_NaR and I_NaP on AP firing. To do this, the two current components were manipulated separately as explained in Methods. In the 0-I_NaR⁺ condition, in which I_NaR is switched off with no changes in I_NaT kinetics, the frequency of tonic firing was reduced (Fig. 9A, red tracings), and the slope of the frequency–current plot decreased to 8.1 Hz pA⁻¹ (Fig. 9Ca). The decrease in firing frequency was more marked at high stimulation levels (Fig. 9Cb), and maximal decrease was of about 25%. At just-threshold stimulation levels, AP firing was not impaired by the 0-I_NaR⁺ condition, and, instead, firing frequency was slightly increased (Fig. 9A, lower tracings), probably due to an enhancement of postspike AHP and, consequently, an acceleration of Na⁺-channel recovery from activation. In the 0-I_NaR⁻ condition, in which I_NaR is suppressed by abolishing the O → OB transition with no compensation for I_NaT inactivation slowdown (see Methods), the changes in AP repetitive firing were similar to those observed in the 0-I_NaR⁺ condition, but more pronounced. The slope of the frequency–current plot further decreased to 6.0 Hz pA⁻¹ (Fig. 9Ca). The maximal decrease in firing frequency, here again observed at high stimulation levels (Fig. 9Cb), was about 40%. The more prominent effects of the 0-I_NaR⁻ condition, as compared with the 0-I_NaR⁺ condition, on tonic firing, are probably the consequence of a markedly enhanced postspike AHP (Fig. 9B; see also below), which more effectively opposes the stimulating current in the interspike period.

I_NaP was modified by decreasing the rate constant of the I6 → O transition, O_off (see Methods). This change reduced the steady-state I_NaP component while negligibly affecting I_NaT and I_NaR (Fig. 8D). Decreasing the steady-state I_NaP by 58 to 67% impaired AP generation at just-threshold stimulation levels (Fig. 10A, lower tracings). The frequency of repetitive firing was moderately affected at slightly above-threshold stimulation levels, and very little at still higher stimulation levels (Fig. 10A, middle and upper tracings; Fig. 10Ba and Bb). It should be noted that in the 13-state Na⁺-channel model, the I_NaP reduction obtained by lowering O_off is less prominent at early times of sustained depolarizations than at the steady state (see Fig. 8D). This is a consequence of slow release of channels from the OB state to the O state during sustained depolarization. Therefore, lowering O_off could have little effect on the amplitude of the I_NaP fraction activated during short interspike periods, and this could limit the significance of the above observation that reducing I_NaP by lowering O_off has little influence on tonic high-frequency firing. However, we also verified the effect of lowering O_off after abolishing the transitions to the OB state (0-I_NaR⁺ condition above), a situation in which I_NaP amplitude is equally decreased at the steady state and at earlier times (Supplemental Fig. B, panel A). Again, we found that I_NaP reduction markedly affects AP firing at just-threshold stimulation levels, but has no major effects on high-frequency tonic firing (Supplemental Fig. B, panels B and C).

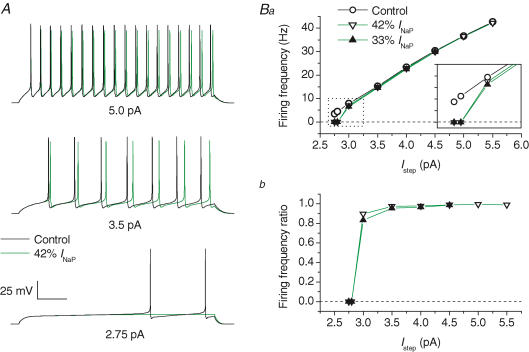
Figure 10. Effects of I_NaP on repetitive firing in model GCs.

A, AP firing elicited by 1 s (lower tracings) and 500 ms (middle and upper tracings) depolarizing current steps. Step current amplitude was 2.75 pA (lower tracings), 3.5 pA (middle tracings) and 5 pA (upper tracings). Black tracings correspond to basal conditions, green tracings to a 58% reduction of the steady-state I_NaP component obtained by lowering the rate constant, O_off (see Scheme 1 and the text for details) to 40% of its control value. The x-axis calibration bar is 150 ms for lower tracings and 75 ms for middle and upper tracings. Ba, plot of firing frequency as a function of I_step for basal conditions (^), for 58% reduction of I_NaP (▿), and for 67% reduction of I_NaP (▾). A detail of the plot at low stimulation intensities (dotted-line box) is highlighted in the inset (each y-axis division is 2 Hz). Bb, plot of the ratio of firing frequency after 58% (▿) or 67% (▾) I_NaP reduction to control firing frequency, as a function of stimulation intensity.

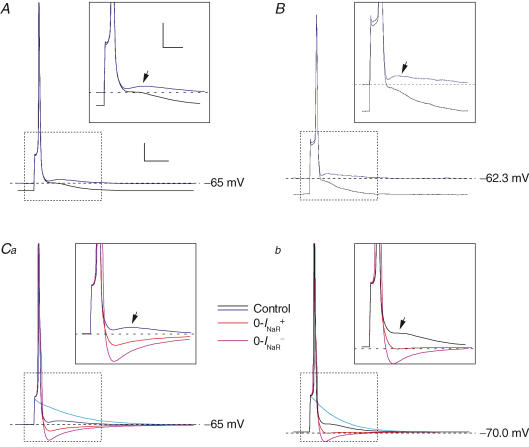
Finally, we tested the ability of the model to reproduce DAPs. Single APs triggered by simulated injection of 0.5 ms depolarizing current pulses under basal conditions were followed by small but clear DAPs (Fig. 11). Starting from a V_bas of −65 mV, the DAP consisted in a true peak following a postspike relative minimum (Fig. 11A, blue tracing). Starting from a more negative V_bas (−70 mV), the DAP consisted in a simple inflection (Fig. 11A, black tracing). The maximal, absolute level reached during the DAP was more positive starting from −65 mV than from −70 mV (−63 versus−65 mV) (Fig. 11A). These properties of the DAP closely resemble those of DAPs experimentally recorded in GCs (compare A with B in Fig. 11). The 0-I_NaR⁺ condition abolished the DAP (Fig. 11C, red tracings), which was replaced by a prompt return to baseline when V_bas was −70 mV (Fig. 11Cb), or a fast AHP at more positive V_bas (Fig. 11Ca). These findings indicate that I_NaR is necessary for DAP generation. In the 0-I_NaR⁻ condition, AP amplitude and duration were increased due to slowed Na⁺-channel inactivation. As a consequence, the postspike AHP was further augmented, due to enhanced activation of repolarizing K⁺ currents (Fig. 11C, violet tracings).

Figure 11. I_NaR determines DAP generation in model GCs.

Each panel shows single APs evoked by injection of 0.5 ms, above-threshold square current pulses. In all panels, black and blue tracings were obtained, under basal (control) conditions, from a V_bas of −70/−71 mV and −65/−62 mV, respectively. Insets show a detail of the tracings corresponding to the region delimited by the dotted-line box in each main panel, and arrows point to the DAPs that follow APs. A, simulated APs obtained from V_bas of either −70 or −65 mV under basal conditions are shown superimposed. B, single APs and DAPs evoked in a real GC (cell C5518) from V_bas of either ∼−62 or ∼−71 mV: note the similarity with the results of computer simulations (A). C, effect of I_NaR suppression obtained by adopting the 0-I_NaR⁺ condition settings (red tracings) or the 0-I_NaR⁻ condition settings (violet tracings) at V_bas of −65 (Ca) and −70 mV (Cb). Light blue tracings represent passive responses to just-subthreshold stimuli. The amplitude of depolarizing current pulses was 106–108 pA (V_bas, −65 mV) or 135–137 pA (V_bas, −70 mV) in all simulated experiments. Calibration bars for main panels, 15 ms, 10 mV. Calibration bars for insets, 8 ms, 8 mV.

Discussion

The present study provides a detailed biophysical and functional characterization of voltage-dependent Na⁺ currents, comprising I_NaT, I_NaP and I_NaR, in cerebellar GCs in situ. The electrophysiological measurements were favoured by the unusually compact electrotonic structure of GCs, which allowed for a precise kinetic analysis of Na⁺ currents. GCs, like other cerebellar neurones, present complex near-threshold behaviours, to which Na⁺ currents have been proposed to give a critical contribution (D'Angelo et al. 1998, 2001). Our experiments and simulations support a significant role for I_NaP in priming AP initiation during near-threshold stimulation, and for I_NaR in boosting the efficiency of repetitive firing and in generating DAPs. The latter effect may be important to explain the tendency of GCs to discharge in bursts and repetitive AP sequences in vivo (Chadderton et al. 2004).

Properties of I_NaT

The major problem affecting Na⁺ current recordings in neurones in situ is the voltage-clamp escape caused by remote localization of Na⁺ channels in the dendrites and axon. Although GCs are among the most electrotonically compact neurones (Silver et al. 1992; D'Angelo et al. 1993, 1995), in most cells we could not fully prevent clamp problems possibly arising from incomplete space-clamp control and Na⁺-channel expression in neuronal processes. In some GCs, however, I_NaT consisted of a well-clamped component only, suggesting that in these cells only channels located in a membrane region electrotonically proximal to the soma were contributing to the recorded current. In such cases, I_NaT showed the voltage dependence and fast kinetics typical of classical neuronal Na⁺ currents. In particular, I_NaT voltage dependence was similar to that observed in cultured GCs (Osorio et al. 2005) in the presence of reverted Na⁺ gradient to render Na⁺ currents non-regenerative and prevent local escape from clamp. To describe the kinetic properties of GC I_NaT, we tentatively applied a classical HH formalism. However, this approach was limited by the fact that proper fitting of I_NaT kinetics required the n exponent to increase with membrane potential (from ∼2 at −45 mV to ∼9 at +10 mV). This finding is anomalous but not surprising, since it is well known that the HH model does not reflect the real mechanisms of Na⁺-channel state transitions. I_NaT inactivation was biexponential, with one time constant in the 4–0.4 ms range and the other in the 10 ms–1 ms range. Biexponential I_NaT decay has also been observed in other central neurones (Huguenard et al. 1988; Sah et al. 1988; Gähwiler & Llano, 1989; Park & Ahmed, 1991; Cummins et al. 1994).

Properties of I_NaP

The persistent Na⁺ current, I_NaP, is widely present in central neurones, but its biophysical properties show some variability in activation threshold, relative amplitude compared to I_NaT, and slow inactivation. In GCs, the permeability underlying I_NaP was half-maximally activated at −55 mV, i.e. 25 mV more negative than I_NaT, and a maximal, steady level was reached at −40 to −15 mV. The voltage range of GC I_NaP activation (−60 to −30 mV) overlapped with the region of Na⁺-dependent inward rectification in the steady-state V–I plot obtained from current-clamp experiments (D'Angelo et al. 1998; see below). The peak amplitude of the I_NaP evoked with long-lasting depolarizing step pulses averaged about −9 pA and represented 1.5–2% of I_NaT peak amplitude. It should be noted that these values could be slightly overestimated, because channel expression in neuronal processes may cause spurious increases in the amplitude of steady-state inward currents under voltage-clamp conditions (White et al. 1995). However, no marked distortion in current voltage dependence is expected (White et al. 1995). I_NaP expression has also been reported for cultured GCs (Osorio et al. 2005). In that case, channels responsible for I_NaP were located in neuronal processes, and I_NaP peak amplitude was greater than in GCs in situ (∼20 pA), which could reflect the prominent process development typical of GC cultures. We also observed that when I_NaP was evoked with slow depolarizing ramps, its amplitude decreased as depolarization rate was reduced. In other neurones (Fleidervish & Gutnick, 1996; Magistretti & Alonso, 1999; Agrawal et al. 2001) this behaviour has been related to the existence of a slow voltage-dependent I_NaP inactivation that proceeds on a time scale of seconds.

Biophysical properties and possible molecular correlates of I_NaR

Perhaps the most intriguing property of GC Na⁺ currents is the expression of a resurgent component, I_NaR (Magistretti et al. 2004; Afshari et al. 2004). The biophysical properties of GC I_NaR were similar to those observed in Purkinje cells and other neurones (Raman & Bean, 1997; Do & Bean, 2003; Cummins et al. 2005), and included a bell-shaped voltage dependence with a peak at −35 mV, and a marked voltage dependence of activation and decay kinetics, both of which showed an abrupt acceleration at potentials negative to −40/−45 mV.

To account for I_NaT, I_NaP and I_NaR in Purkinje cells, Raman & Bean (2001) developed a 13-state allosteric model with five closed states, one open state, six inactivated states, and a ‘blocked’ state accessed from the open state (see Scheme 1). This model implicitly assumes that a single Na⁺ channel is endowed with states explaining a multiplicity of kinetic behaviours. In the model, I_NaP is determined by the equilibrium between open, inactivated, and blocked states. I_NaR is generated by release of channels from the blocked to the open state. Blocking is determined by an intracellular ‘blocking particle’ competing with the classical ‘inactivating ball’ for binding to the open channel. Binding of the blocking particle is voltage independent, whereas unbinding is strongly voltage dependent, probably as an indirect consequence of inwardly directed Na⁺ flow inside the channel upon repolarization (through a mechanism of displacement due to electrostatic repulsion, or mechanical momentum, or both). By preventing the inactivating ball from binding to open channels, the blocking particle would therefore create, upon depolarization, a ‘reservoir’ of non-inactivated channels that would be exploited in repolarization to produce a transient inward current. The relative proportions, voltage dependence, and kinetics of I_NaT, I_NaP and I_NaR in GCs could all be accounted for by the Raman & Bean (2001) model. A more precise correspondence of modelling with experimental currents may require parameterization of the kinetic scheme through the application of specific fitting algorithms (e.g. Vanier & Bower, 1999), and additional data from single-channel recordings.

In Purkinje cells, the presence of I_NaR has been related to the expression of Na_v 1.6 Na⁺ channels (Raman et al. 1997) as a necessary, although not sufficient (Pan & Beam, 1999), requirement. Na⁺ channel α subunits different from Na_v 1.6 (Do & Bean, 2003), including Na_v 1.2 (Rush et al. 2005), have then been shown to also provide a possible molecular substrate for I_NaR in other neurones. GCs do express Na_v 1.6 and Na_v 1.2 mRNA and protein at high levels (Schaller & Caldwell, 2003). More recently, a tight correlation between I_NaR expression and the Na⁺-channel auxiliary β4 subunit (Grieco et al. 2005) has been established. Indeed, a portion of the β4 subunit cytoplasmic tail can act as the ‘blocking particle’ which, according to the Raman-Bean model, competes with the classical ‘inactivating ball’ for binding to the channel's open state. Unlike Purkinje cells, however, GCs do not show high expression levels of β4 subunit mRNA and protein in in situ hybridization and immunohistochemical tests (Yu et al. 2003). Although this does not rule out the presence of functional β4 subunits, it may indicate that molecules other than the β4 subunit determine I_NaR in GCs.

Roles of I_NaP and I_NaR

The impact of a given membrane current on neuronal electrogenesis depends on the specific electrotonic structure and the channel complement of the neurone in which the current is expressed. In some neurones, I_NaP is relatively large (hundreds of pA) and determines processes like oscillations and spike priming (discussed in Magistretti & Alonso, 2002). In GCs, I_NaP has small amplitude, yet it can have a major impact on membrane excitability due to the small size of these neurones and their high input resistance. Indeed, an inward current of 9 pA (the average, peak I_NaP amplitude we observed in GCs) would produce an 18 mV depolarization on a resistance of 2 GΩ (the average GC input resistance at −70 mV, under physiological ionic conditions: D'Angelo et al. 1995, 1998; Brickley et al. 1996). The fact that the voltage range of GC I_NaP activation (−60 to −30 mV) overlapped with the region of Na⁺-dependent steady-state inward rectification observed under current-clamp conditions supports the prediction that a persistent Na⁺ current critically influences GC near-threshold excitability and the rate at which GC membrane potential approaches firing threshold (D'Angelo et al. 1998). Accordingly, our computer simulations indicated that I_NaP has a critical influence in promoting AP firing at low, just-threshold levels of stimulation, whereas the impact of I_NaP on high-frequency firing was much smaller. I_NaP has also been shown to sustain subthreshold membrane potential oscillations and to amplify GC resonance in the theta-frequency range (D'Angelo, 2001).

Because of its property of activating in repolarization after depolarizations able to activate and inactivate I_NaT, I_NaR is more suitable to provide a depolarizing drive following firing of single APs, or during repetitive discharge. The response of Purkinje cells to brief, just-threshold depolarizing pulses, which in most other neurones would trigger single APs, consists in the discharge of doublets or triplets of APs (Raman & Bean, 1997). I_NaR has been proposed to underlie this firing pattern (Raman & Bean, 1997). In GCs, we found that single APs are most frequently followed by evident DAPs that, in ∼80% of cases, show features compatible with a role of I_NaR in their generation. Computer modelling confirmed that I_NaR expression at levels similar to those frequently observed experimentally results in generation of DAPs closely resembling real DAPs. DAPs produced by GCs did not trigger discharge of AP doublets or triplets (except in a single case, data not shown). However, during injection of just-threshold depolarizing steady currents, GC firing is frequently characterized by spike clustering (D'Angelo et al. 1998, 2001). I_NaR-dependent DAPs could contribute to this behaviour, as well as to oscillatory burst firing occurring during partial inhibition of K⁺ currents (D'Angelo et al. 1998). It was recently reported that antidromic stimulation of parallel fibres by brief electrical shocks applied to the molecular layer results in doublets or triplets of APs at the GC soma (Isope et al. 2004), and it was concluded that this behaviour is a consequence of intrinsic excitable properties of GCs. Although the mechanism of spike repetition during antidromic stimulation remains to be established, it is possible that I_NaR contributes to its generation.

Our results also indicate the existence of marked variability in I_NaR amplitude among GCs expressing transient Na⁺ currents of similar size. At the same time, a fraction of GCs did not produce DAPs, and in another cell subset DAPs were generated by a Ca²⁺-, hyperpolarization-dependent mechanism not involving I_NaR. It could thus be hypothesized that heterogeneity in I_NaR expression is a critical factor in determining the variable ability of GCs to generate DAPs at resting potential.

How general the role of I_NaR could be in sustaining DAPs in central neurones is still unexplored. Hippocampal CA1 pyramidal neurones have been found to generate DAPs sensitive to TTx (Jensen et al. 1996; Azouz et al. 1996), that were attributed to I_NaP action. At the time of those reports, however, the existence of I_NaR was not known. In principle, therefore, I_NaR may conceivably contribute to DAP generation also in CA1 neurones. On the other hand, preliminary data suggest that CA1 pyramidal neurones in situ do not express I_NaR (J. Magistretti and L. Castelli, unpublished results), making a role of I_NaP still possible. It is worth remarking that, although the results of our modelling strongly suggest that I_NaR is necessary for DAP generation in cerebellar GCs, they do not rule out a possible contribution of I_NaP to the overall depolarization. Indeed, in the kinetic model we adopted for Na⁺-current simulation, I_NaP is but an aspect of a global Na⁺ current, and it is not possible to suppress its early phases unless I_NaR is also abolished. In fact, I_NaP generation could imply more specialized mechanisms (including modal gating and long-lived burst openings: Alzheimer et al. 1993; Magistretti & Alonso, 2002; Magistretti et al. 2003) that would make it less strictly interconnected with other Na⁺ current components.

The results of our computer simulations also indicated that an additional functional consequence of I_NaR expression in GCs is an increase in firing frequency during sustained depolarization and in the gain of the frequency–stimulation relationship. This is in agreement with what has been found for Purkinje cells (Khaliq et al. 2003). The influence of I_NaR on firing frequency was maximal in the presence of high stimulation levels, and minimal or absent at near-threshold stimulation levels. This behaviour is opposite to that found for I_NaP. Therefore, I_NaP and I_NaR appear to provide cerebellar GCs with two complementary mechanisms for promoting AP firing at different levels of activity.

Distribution of I_NaR and implications for cerebellar function

I_NaR is a Na⁺ current of recent identification. In addition to GCs (this study; Afshari et al. 2004), I_NaR is expressed in other important cerebellar neurones, including Purkinje cells, where it has been originally described (Raman & Bean, 1997), cerebellar unipolar brush cells (Mossadeghi & Slater, 1998; Afshari et al. 2004), and neurones of deep cerebellar nuclei (Raman et al. 2000; Afshari et al. 2004). Preliminary results indicate that I_NaR is also present in Golgi cells (J. Magistretti and E. D'Angelo, unpublished data). Being present in five major cerebellar neuronal types, I_NaR may thus be particularly important for cerebellar function. Subthreshold, persistent Na⁺ currents also have a well-characterized role in setting the excitable properties of Purkinje cells (Llinás & Sugimori, 1980; Raman & Bean, 1999), as well as in GC and Golgi cell functions (D'Angelo et al. 1998, 2001; Forti et al. 2004). What is the reason for expressing such specific Na⁺-current components in so many cerebellar neuronal types? A possible interpretation, based on the role attributed to I_NaR and/or I_NaP in AP conglomeration and bursting (Franceschetti et al. 1995; Raman & Bean, 1997; Parri & Crunelli, 1998; Brumberg et al. 2000), is that the cerebellum privileges spike bursts to communicate, and that this coding property must be maintained throughout the circuit by distributed mechanisms like those provided by I_NaR and I_NaP. GCs are known to produce spike bursts following punctate tactile stimulation (Chadderton et al. 2004), and Purkinje and deep cerebellar nuclei cells also have the ability of conglomerating spikes by exploiting I_NaR (Raman & Bean, 1997; Afshari et al. 2004). Spike bursts are also important for eliciting parallel fibre–Purkinje cell long-term depression (LTD) (Casado et al. 2002). Unfortunately, there is currently no means to inhibit I_NaR or I_NaP selectively in order to directly test their role in cerebellar physiology. Specific network models may help understanding the emergence of I_NaR and I_NaP effects on cerebellar network computation.

Supplemental material

The online version of this paper can be accessed at:

DOI: 10.1113/jphysiol.2006.106682

http://jp.physoc.org/cgi/content/full/jphysiol.2006.106682/DC1 and contains supplemental material consisting of two figures:

Supplemental Figure A

Hodgkin-Huxley (HH) fitting of I_NaT activation

Supplemental Figure B

Effects of manipulations aimed at reducing INaP before and after abolishment of I_NaR in computer simulations.

This material can also be found as part of the full-text HTML version available from http://www.blackwell-synergy.com