Kinetics of force recovery following length changes in active skinned single fibres from rabbit psoas muscle

Abstract

Redevelopment of isometric force following shortening of skeletal muscle is thought to result from a redistribution of cross-bridge states. We varied the initial force and cross-bridge distribution by applying various length-change protocols to active skinned single fibres from rabbit psoas muscle, and observed the effect on the slowest phase of recovery (‘late recovery’) that follows transient changes. In response to step releases that reduced force to near zero (∼8 nm (half sarcomere)⁻¹) or prolonged shortening at high velocity, late recovery was well described by two exponentials of approximately equal amplitude and rate constants of ∼2 s⁻¹ and ∼9 s⁻¹ at 5°C. When a large restretch was applied at the end of rapid shortening, recovery was accelerated by (1) the introduction of a slow falling component that truncated the rise in force, and (2) a relative increase in the contribution of the fast exponential component. The rate of the slow fall was similar to that observed after a small isometric step stretch, with a rate of 0.4–0.8 s⁻¹, and its effects could be reversed by reducing force to near zero immediately after the stretch. Force at the start of late recovery was varied in a series of shortening steps or ramps in order to probe the effect of cross-bridge strain on force redevelopment. The rate constants of the two components fell by 40–50% as initial force was raised to 75–80% of steady isometric force. As initial force increased, the relative contribution of the fast component decreased, and this was associated with a length constant of about 2 nm. The results are consistent with a two-state strain-dependent cross-bridge model. In the model there is a continuous distribution of recovery rate constants, but two-exponential fits show that the fast component results from cross-bridges initially at moderate positive strain and the slow component from cross-bridges at high positive strain.

When a step release is applied to an active skeletal muscle fibre, most of the time taken for force to recover to the original level comprises phase 4, which is the slowest of the force transients described by Ford et al. (1977). The time course of phase 4 in an isometric contraction is roughly similar in frog muscle fibres to the time course of the initial rise of force in a tetanus (Gasser & Hill, 1924; Hill, 1953; Jewell & Wilkie, 1958; Ford et al. 1977), which is probably dominated by the rate of attachment of cross-bridges (Ford et al. 1977). However, phase 4 becomes progressively faster with increasing velocity when a step is imposed during isotonic shortening (Ford et al. 1985) and as the rate of cross-bridge detachment is expected to increase in these circumstances, phase 4 presumably reflects both attachment and detachment.

Many studies have been made of force recovery to the steady isometric level following shortening terminated either by a stop or a large stretch (Gasser & Hill, 1924; Hill, 1953; Jewell & Wilkie, 1958; Ekelund & Edman, 1982; Brenner & Eisenberg, 1986; Brenner, 1988; Swartz & Moss, 1992; Chase et al. 1994; Hancock et al. 1996; Regnier & Homsher, 1996; Wahr et al. 1997; Vandenboom et al. 1998; Burton et al. 2005). A simple two-state model of the cross-bridge cycle in which rates are not dependent on strain predicts that isometric force recovery should be single exponential in form, with a rate constant given by the sum of the apparent rate constants for attachment to, and detachment from, force-generating states (Brenner, 1986). However, it has long been clear that late recovery in response to most length-change protocols, as well as the force rise at the beginning of a tetanus, cannot be described by a single exponential (Ekelund & Edman, 1982; Ford et al. 1985, 1986; Brenner & Eisenberg, 1986; Swartz & Moss, 1992; Chase et al. 1994; Edman et al. 1997; Iwamoto, 1998; Burton et al. 2005), suggesting that this very simple two-state model does not completely explain the mechanical behaviour.

Force redevelopment is more nearly single exponential in form when shortening is terminated by a rapid restretch to the original length (Brenner & Eisenberg, 1986). Recovery is expected to be simpler than in other length-change protocols because (putatively) all cross-bridges must be detached by the large stretch, and reattachment should occur from a simplified distribution, accounting for the single-exponential form of recovery. Brenner & Eisenberg (1986) observed that the recovery could be described by fast and slow components when rapid shortening was terminated by a small stretch, but that a large restretch to the initial length caused recovery to be more single exponential in form. Two components of force recovery have, however, been observed by others even when a large restretch is applied (Swartz & Moss, 1992; Chase et al. 1994). No explanation has been offered for the variable appearance or origins of the different components of force recovery following isometric step release (phase 4) or a period of shortening, either with or without a restretch to the initial length. This issue is addressed here.

In the present work, the components of isometric force recovery were investigated by comparing the effects of several length-change protocols on recovery kinetics that were fitted by multiple-exponential functions. It is shown here that when force recovers from a level near zero, the rate constants of a double-exponential fit are largely independent of the nature of the preceding length changes. The results are interpreted in terms of a simple model in which the fast and slow components arise from strain dependence in the rate constants of cross-bridge attachment into, and detachment from, force-generating states.

Using various biochemical interventions in fibres, we have recently shown that the rate constants of force recovery can be accounted for by two steps in the cross-bridge cycle: ATP hydrolysis and phosphate release (Sleep et al. 2005; Burton et al. 2005). The biochemical scheme presented previously and the results of the present study provide evidence that the fast exponential results largely from cross-bridges detached during shortening by means of ADP release and binding of ATP.

Some of the present results have been reported in preliminary form (Burton, 1997).

Methods

Materials

Fibres were obtained from the psoas major muscle of small adult male Dutch or New Zealand White rabbits. Rabbits (2–2.5 kg) were killed, in accordance with the UK Animals (Scientific Procedures) Act 1986, by overdose of sodium pentobarbitol (150 mg kg⁻¹) administered intraveneously in one ear followed by exanguination. The psoas muscle was rapidly exposed and bathed in a physiological saline solution. Small bundles of muscle fibres from the lateral portion of the muscle were tied to sticks at their in situ length, cut away from the muscle, and gently agitated in skinning solution containing (mm): ATP 7, magnesium acetate 8, potassium propionate 70, EGTA 5 and imidazole 6, with 0.5% Brij 35 detergent for 1–2 h on ice. The bundles were then washed in cold skinning solution without detergent for 5–10 min, and finally placed in fresh skinning solution on ice and used within 3–4 days. Protease inhibitors (phenylmethylsulphonyl fluoride (PMSF, 0.1 mm), leupeptin (8 μg ml⁻¹) and trypsin inhibitor (0.1 mg ml⁻¹)) were added to the skinning and storage solutions.

Fibre handling and apparatus

Single fibres were isolated from bundles in skinning solution and stored as previously described (Burton et al. 2005; Sleep et al. 2005). Single fibres isolated from bundles were used promptly as we invariably observed that relaxed stiffness increased significantly after a few hours in isolation in relaxing solution, even at cold temperatures and in the presence of β mercaptoethanol (βME, 0.1%) and protease inhibitors.

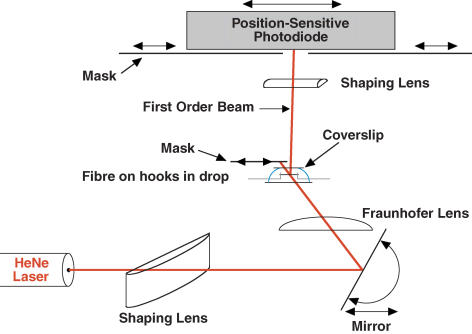
The experimental apparatus was built on an upright, fixed-stage microscope from which the condenser and eyepieces were removed. Fibres were mounted in 40 μl drops of solution held on glass pedestals of the type previously described (Fig. 1; Sleep, 1990). The rotating base was mounted on the condenser rack and pinion to allow adjustment of its height. Additional height adjustment was provided by a spring mount that allowed the entire pedestal assembly and bathing solution to be lowered during rotation. Experiments were done at 5 ± 0.1°C. Temperature was measured by a small (200 μm) thermistor (Thermometrics, Edison, NJ, USA) placed near the fibre and maintained by the flow of a cold mixture of ethylene glycol and water (1: 2, v/v) past the bottom of the rotating mount holding the pedestals. The temperature of the coolant was set by a Peltier-cooled copper block. Evaporation of dry nitrogen gas from a liquid reservoir eliminated moisture on the cold glass surfaces below and above the fibre.

Figure 1. Diagram of laser diffractometer.

The beam from a 5-mW HeNe laser was passed through a shaping lens and Fraunhofer lens (see Methods) via an adjustable mirror that controlled the angle of incidence onto the fibre. The fibre was held in a small drop of solution (40 μl) between a cooled glass pedestal and a glass coverslip by hooks attached to the servomotor and force transducer (not shown). The zeroth-order beam was blocked by a movable mask, while the first-order beam was passed to the photodiode. A shaping lens focused the first-order line down to a spot at the photodiode. Scattered light and lines of higher orders (on the same side as the measured first-order line) were blocked by masks at the photodiode. The fibre was positioned 31 cm from the photodiode and 12.2 cm from the mirror at the position illuminated by the laser (distances orthogonal to fibre axis). Drawing not to scale.

Fibres were attached to the motor and transducer hooks by aluminium foil T-clips crimped onto the ends in the dissecting dish. The clips were cut from aluminium foil using a custom-made punch. T-clips were glued to the hooks with cyanoacrylate (Histoacryl, Braun, Melsungen, FRG; Brenner & Eisenberg, 1986) to minimize movement on the hooks during transfer between solutions and during the large, rapid length steps used in some of the experiments. In most experiments the end of the fibre itself was also glued to the T-clips as this was found to reduce end compliance.

Fibre length (typically 2 mm between the clips) was measured when the fibre was just taut. Fibres were usually not circular in cross-section, so the major and minor axes were measured by rotating the fibre in the dissecting dish using a dissecting microscope at × 50, and cross-section was calculated assuming an elliptical shape. At the beginning of every experiment, sarcomere length (SL) in the relaxed fibre on the experimental apparatus was measured with a × 20 water immersion objective. In some cases, SL was measured directly by using an eyepiece graticule, but more commonly the light diffraction pattern at the back focal plane of the objective was viewed through a phase telescope and the spacing of the two first-order diffraction lines was used to calculate SL. The transmitted illumination was made monochromatic with a green interference fitter (548nm, width at half maximum 20nm), and sharp first-order diffraction lines were produced by removing the condenser and closing down the field aperture so as to collimate the light. An eyepiece graticule was placed in the telescope to measure line spacing. The position of the centroid of the first diffraction order could be assigned with a precision of 15–25 nm sarcomere⁻¹ at an SL of 2.2 μm.

SL during experiments was estimated from the position of the first order of a laser diffraction pattern as previously described (Burton et al. 2005; Sleep et al. 2005) and shown in Fig. 1. The beam from a 5 mW red HeNe laser (05 LHP 151, Melles Griot, Irvine, CA, USA) was focused by two cylindrical lenses before illuminating the fibre. The first (shaping lens) focused the beam onto the fibre to ∼0.7 mm × 0.25 mm, and the second (Fraunhofer lens) was positioned so that its focus was at the photodetector, thus producing far-field conditions and minimizing movements of fine structure arising from fibre translation (Brenner, 1985). The top of the solution was flattened by a coverslip, the vertical position of which was adjusted by the focus control of the microscope. The first-order beam was focused onto a position-sensitive photodiode (LSC 30D, United Detector Technology, Hawthorne, CA, USA) by a third cylindrical lens. The zeroth order was masked at the objective tube above the fibre, and additional off-order scatter was masked at the photodiode (Fig. 1). The lower glass surface of the chamber was kept clean and the fibre positioned ∼1 mm above it in order to reduce spurious interference between diffracted and scattered light, which can shift the apparent centroid of the first order (Burton & Huxley, 1995). The fibre was illuminated at a position where the first order was relatively bright and narrow, indicating good striation order (usually less than 20 nm dispersion in spacing). In addition, translation artefact was minimized by choosing the illuminated position so that (1) adjacent areas had similar first-order patterns, and (2) the illumination was located near to the fixed end of the fibre. SL was calculated using the grating equation with the angle of incidence usually set to the Bragg angle for striations normal to the fibre axis.

A voltage signal proportional to position of the first order of the diffraction pattern was obtained by a divider circuit which calculated the difference of the two outputs of the photodiode divided by their sum. Variation in laser intensity between a level typical of a weak diffraction pattern and saturation of the photodiode caused an error of less than 4% in the estimate of changes in SL. Over a bandwidth of 10 kHz, peak to peak noise in the position signal corresponded to 8 μ at the photodetector or an error in SL of 1 nm. The relationship between the photodiode signal and the position of the diffraction order was calibrated in two ways. In the first, the photodiode was translated along the meridian of the diffraction pattern, thus altering the position illuminated by the first-order beam and hence the voltage output by the photodiode. The masks in the front of the photodiode were removed to ensure that the change in signal was primarily due to movement of the photodiode with respect to the diffraction order rather than the masked background scatter. In the second method, movement of the diffraction order was compared directly to the change in the position signal during length changes imposed on relaxed and active fibres. In cases where the striations became disordered, the background scatter increased at the expense of the diffracted light and recalibration was necessary during the experiment.

The motor used for controlling fibre length was similar to that described by Ford et al. (1977). Small step changes in length (up to about 50 nm (half sarcomere)⁻¹ (nm hs⁻¹)) were complete in ∼0.2 ms and large restretches (about 100 nm hs⁻¹) applied at the end of ramp shortening were complete in 0.4–0.5 ms. Feedback to the servomotor controlling fibre length was obtained either from the motor position signal (PM) or from the position signal of the diffraction order. The gain of the divider output was adjusted so that a change in the SL signal was about the same as that of the PM signal, making the response to the servomotor similar in SL and PM control. Both signals were set to zero when feedback was switched between them so as to minimize length changes during the switch. An active diode switching circuit (Ford et al. 1977) was used to switch out of SL control into PM control when the PM and SL signals did not change together within a preset tolerance. A velocity signal proportional to the rate of change of the PM signal was inverted and added to the feedback in order to provide damping during rapid length changes. The magnitude of the velocity signal was reduced in some experiments in order to underdamp the length change and allow an overshoot and oscillation of a few percent of the fibre length over a period of a few milliseconds (see Fig. 6), thus altering the size and rate of force redevelopment following a large restretch (Burton, 1989). Sequences of length changes were controlled by custom-built circuitry which generated command signals of defined sign and amplitude, rate, frequency, timing, and number of repetitions. The frequency response of the semiconductor strain gauges used (Akers AE801; SensorOne, Sausalito, CA, USA) varied from 1.1 to ∼10 kHz, with higher frequencies obtained by shortening the transducer beam and attaching very small hooks. The motor and tension transducer were mounted on micrometers to allow independent positioning of the hooks in three dimensions or simultaneous translation of both ends of the fibre.

Figure 6. Underdamped restretch or restretch + step release.

Shortening ramps were terminated by step stretches that were underdamped to various extents, causing ‘ringing’ of the servomotor. Force records with ringing amplitude of 0%, 2.8% and 6.2%L_o are shown, with the lowest T_min resulting from the largest ringing. The full amplitude of ringing was not sampled in the computer data, but the actual time courses were recorded separately on an oscilloscope (inset to fibre length graph). Records were in PM control, as underdamping tended to destabilize the feedback loop during the large restretches. Single- and double-exponential functions are shown for the records corresponding to 0% and 6.2% ringing. For the critically damped restretch, where the double-exponential fit is only slightly better than the single exponential (see residuals and double–single difference traces), k_r1 = 6.3 s⁻¹, k_rs = 4.0 s⁻¹, k_rf = 11.2 s⁻¹ and A′_f = 0.62, and for the underdamped restretch, k_r1 = 4.5 s⁻¹, k_rs = 2.4 s⁻¹, k_rf = 10.8 s⁻¹ and A′_f = 0.56. CS = 4.6 × 10³μm², length = 2.45 mm.

For most experiments the signals corresponding to tension, fibre length, and intensity and position of the first-order diffracted beam were recorded. An experimental record usually consisted of two to four sequential blocks consisting of an equal number of samples, but differing in the sampling rate according to the rate of change of the signals during that period. Tension and temperature were recorded on a slow time scale using a strip chart recorder with a high-frequency response.

Experimental protocol

Fibres were mounted on the experimental apparatus in relaxing solution containing (mm): ATP 5, magnesium acetate 7, potassium acetate 50, EGTA 10, imidazole 50 and phosphocreatine 10 with 2 mg ml⁻¹ creatine kinase (ionic strength, 170 mm; pH 7 at 5°C) at low temperature (0.0–0.5°C), and SL was measured as described above. The temperature was raised to 5°C and the fibre was transferred to activating solution containing (mm): ATP 5, magnesium acetate 7, potassium acetate 50, Ca EGTA 10, imidazole 50 and phosphocreatine 10, with 2 mg ml⁻¹ creatine kinase (ionic strength, 170 mm; pH 7 at 5°C). The striation pattern was stabilized by the technique of Brenner (1983) in which cycles of shortening at low force and rapid restretch to the initial length were applied at about 5-s intervals (see Supplemental material, Fig. S4C). Early in the activation, the speed of ramp shortening was adjusted to bring the force to near zero without the fibre going slack. The active fibre was translated through the laser beam to assess striation order as judged from the diffraction pattern, a suitable location was chosen, SL was measured, and the intensity of the laser beam was adjusted to maximize the signal-to-noise ratio of the photodiode signal without saturating it. The gain and offset of the SL signal were adjusted to match that of the PM signal, and the SL signal was then calibrated as described above. The servomotor was then switched into SL control as needed. Test length-change protocols were applied to the active fibre and sampling parameters of the data-acquisition software were adjusted according to the time course of the force response to length changes. Data were acquired during a series of length-change protocols (see Fig. S4C) and the fibre was then either relaxed or another set of active experiments (e.g. using a different length-change protocol) was carried out during the same activation.

Analysis

Force records were fitted by multiple-exponential functions using a Fortran program that incorporated the routines of Provencher (1976) (see http://s-provencher.com/pages/discrete.shtml). The Provencher routine generated its own initial estimates, handled different sampling frequencies in a single record and was able to simultaneously fit one to four exponential terms to the record, ranking them in order of goodness of fit. It was found that the rate constants of the early force transients and the late recovery of isometric force were sufficiently well separated (more than 10-fold) that it was not necessary to include the early transients. The period over which exponential functions were fitted is shown superimposed on experimental records in the Figures. Late recovery after a period of shortening was generally better fitted by two exponentials than by one (Hill, 1953; Brenner & Eisenberg, 1986) on the basis of the residuals of the fit and the standard errors. The improvement in goodness of fit with two rather than one exponential was supported by the signal-to-noise ratios and standard deviations of the fits calculated by the Provencher routines. We also used the difference between single- and double-exponential fits (relative to the magnitude of recovery) as an indicator of the double-exponential nature of force recovery. The amplitudes of these single–double difference curves correlated with the assignment by the Provencher exponential fitting routines of a single or double exponential as the ‘best’ fit based on a comparison of the residuals of the fits using a modified F test. The residuals of single- and double-exponential fits can also be compared, but they include noise in the data which obscures differences between the two fits. Single-exponential fits are also included here because (1) they allow comparison to previous analyses, (2) they provide a single numerical descriptor of ‘overall’ recovery, and (3) they were the only justifiable fits for records showing a small magnitude of recovery or a low signal-to-noise ratio.

Several records were also fitted using another program (Enzfitter, R. J. Leatherbarrow. Elsevier Science Publishers, Amsterdam, 1987) that uses a Marquardt non-linear regression method (Marquardt, 1963). The filted rate constants from the two programs were very similar on average: the ratio of the fast rates calculated by the Enzfitter and Provencher routines was 1.00 ± 0.02 (mean ± s.e.m., n = 25) and the ratio of the slow rates was 0.98 ± 0.02.

No corrections to records that included a stretch were made for passive visco-elastic properties of fibres. Force in relaxed fibres after a ∼10% restretch was only 1–2% of isometric force at the short SLs used here (data not shown; SL ∼2.0–2.4 μm; ratio of relaxed force to active isometric force was 1.4 ± 0.2% for skinned fibres 1–8 days old; n = 7).

Results

To assess differences in force redevelopment reported in previous studies, and to perturb the distribution of cross-bridge states preceding recovery, several length-change protocols were used: (1) isometric step releases and stretches complete in ∼0.2 ms; (2) ‘slack tests’ in which step releases of 3–15% fibre length (L_o) were applied; (3) ramp shortening to a stop over a range of velocities at forces of 2–85% isometric force (P_o); (4) slow ramp shortening terminated by step release; (5) rapid ramp shortening terminated by stretches; and (6) ramp shortening at high velocity terminated by a rapid restretch to the initial length (method of Brenner, 1983). Variations in protocol 6 included small length changes after the restretch, with either (7) a step release or (8) damped oscillations lasting a few milliseconds (Burton, 1989).

Protocol 1 is a small perturbation of the isometric steady-state distribution of cross-bridges (Ford et al. 1974; Cecchi et al. 1986). Protocol 2 was designed to produce a new steady state of cross-bridges with a higher proportion detached and a reduction in attached strain. Protocol 3 is similar in design to Protocol 2, but resulting in cross-bridge distributions and strains intermediate between isometric and rapid shortening. Protocol 4 is a small perturbation of a nearly isometric steady-state distribution for comparison to protocol 1. Protocol 5 was designed to strain attached cross-bridges positively in order to distinguish them from detached cross-bridges during shortening. Protocols 5 and 6–8 forcibly detach cross-bridges in an attempt to elicit synchronous reattachment. Protocol 6 was used to help maintain striation order and isometric force at times during activation when the test protocols were not being applied.

Isometric length steps

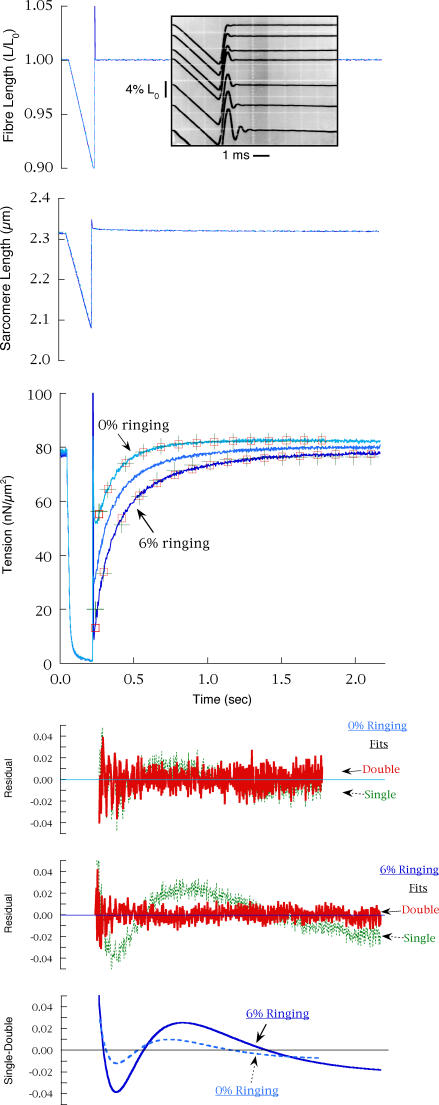
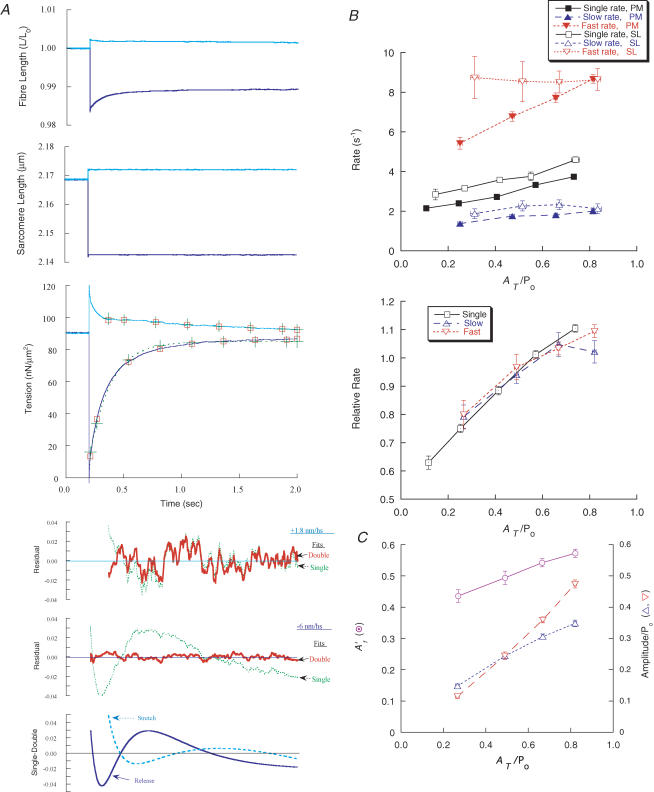
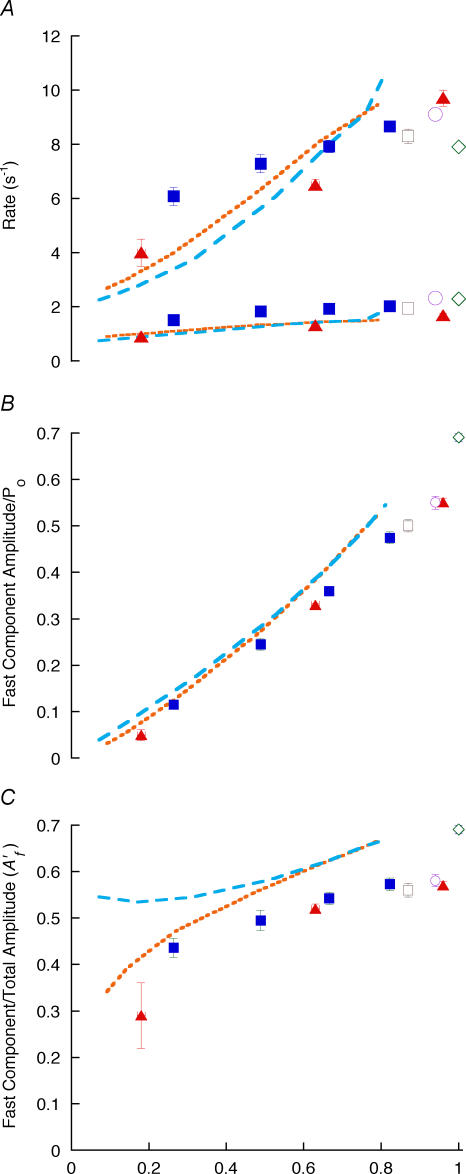
A study was made of the late phase of force recovery (phase 4) following isometric step releases and stretches applied during isometric contraction (Ford et al. 1977). Figure 2A shows records from an experiment in which step length changes were applied to a single fibre under SL control. Double-exponential fits to force recovery were superior to single-exponential fits, as shown by fits superimposed on the force records and by the residuals of the fits. In the largest step releases (∼8 nm hs⁻¹) the rate constants of the slow and fast components were about 2 s⁻¹ and 9 s⁻¹, respectively, and the magnitude of total force recovery (A_T, as defined in Table 1) was about 80%P_o (Table 1), but the rate constants and the relative proportion of the components varied with the size of step (Fig. 2B). The rate constants of the double-exponential fits rose as the magnitude of recovery increased in PM control (t < 0.001; from Student's t- test), whereas the rates in SL control were much more variable and did not show a significant trend (Fig. 2B). Compared with the double-exponential rates, the single-exponential rates were much less variable and rose with recovery in both SL and PM control (t < 0.001). As recovery became larger, there was a greater increase in the amplitude of the fast component (A_f) compared with the slow component (A_s), which caused A′_f (A_f/A_T) to increase (Fig. 2C).

Figure 2. Phase 4 recovery elicited by isometric step length changes.

Step releases and step stretches were applied to an activated fibre in sarcomere length (SL) control. A, records showing fibre length, SL and force for a step release and step stretch. Single- and double-exponential fits (+ and □, respectively) are shown overlaying phase 4 following the release (6 nm hs⁻¹), and phases 3 and 4 following the stretch (1.8 nm hs⁻¹). The single-exponential fit following the release is also indicated by a dashed line (through the + symbols). In the lowest panel, the upper two graphs show the residuals of the fits (dotted lines, single-exponential fits; continuous lines, double-exponential fits). The bottom graph shows differences between the single- and double-exponential fits normalized to recovery magnitude (dashed and continuous lines refer to stretch and release, respectively). The fitted parameters k_r1, k_rs, k_rf and k_s are, respectively, the rate constants of the single, slow rising, fast rising and slowest falling components, and A′_f is the amplitude of the fast component after a release relative to total recovery taken from the double-exponential fit. For the release, k_r1 = 5.5 s⁻¹, k_rs = 2.7 s⁻¹, k_rf = 10.9 s⁻¹ and A′_f = 0.58, and for the stretch, k_r1 = 0.54 s⁻¹, k_s = 1.02 s⁻¹, k_rf = 9.1 s⁻¹ and the ratio of the amplitudes of the rising to falling components = −0.78. Fibre cross-section (CS) = 5.4 × 10³μm², fibre length = 2.3 mm. B, rate constants as a function of total recovery taken from double-exponential fits. Values are means ± s.e.m. The upper graph shows the absolute rate constants for single- (continuous line) and double- (dashed lines) exponential fits. Symbols: (▪,□) single, (▴,▵) slow, and (▾,▿) fast components; filled and open symbols refer to fibre (PM) and SL (SL) control, respectively. In the lower graph, rates at each magnitude of recovery were normalized to that obtained at a reference magnitude for each fibre; SL and PM data combined. The data from 43 fibres were grouped into categories of recovery magnitude with similar n values (∼50 and ∼15 in PM and SL control, respectively). C, as in panel B, but showing amplitudes of the exponential components (▿, A_f/P_o and ▵, A_s/P_o) relative to isometric force (P_o) plotted against A_T/P_o. The proportion of phase 4 in the fast component is shown (⊙A′_f = A_f/(A_f + A_s)). SL and PM data have been combined.

Table 1.

Recovery from near zero force

Shortening protocol	Length control	kr1(s−1)‡	krs(s−1)	krf(s−1)	krf/krs	A′f‡	Recovery (%Po)
Isometric step†	PM	3.7 ± 0.1	2.0 ± 0.1	8.7 ± 0.2	4.5 ± 0.1	0.55 ± 0.01	82 ± 1
		(50,31)	(50,31)	(50,31)	(50,31)	(50,31)	(50,31)
Isometric step†	SL	4.6 ± 0.2	2.1 ± 0.2	8.6 ± 0.6	4.8 ± 0.5	0.64 ± 0.04	83 ± 2
		(28,17)	(26,15)	(26,15)	(26,15)	(26,15)	(26,15)
Slack test	PM	5.1 ± 0.1	2.3 ± 0.04	7.9 ± 0.1	3.5 ± 0.1	0.68 ± 0.01	100 ± 0
		(98,11)	(98,11)	(98,11)	(98,11)	(98,11)	(98,11)
Slow ramp + release	SL	4.1 ± 0.3	2.3 ± 0.1	8.1 ± 0.4	4.0 ± 0.2	0.57 ± 0.0	65 ± 3
		(40,4)	(40,4)	(40,4)	(40,4)	(40,4)	(40,4)
Fast ramp	PM	4.1 ± 0.2	1.7 ± 0.1	9.7 ± 0.3	5.7 ± 0.2	0.57 ± 0.01	98 ± 4
		(18,4)	(18,4)	(18,4)	(18,4)	(18,4)	(18,4)
Ramp–stretch	PM	3.8 ± 0.1	2.0 ± 0.1	8.4 ± 0.2	4.2 ± 0.1	0.56 ± 0.01	87 ± 1
		(22,13)	(20,13)	(20,13)	(20,13)	(20,13)	(20,13)
Ramp−restretch + step	PM	4.3 ± 0.1	2.3 ± 0.1	9.0 ± 0.2	4.0 ± 0.1	0.56 ± 0.01	95 ± 1
		(36,16)	(36,16)	(36,16)	(36,16)	(36,16)	(36,16)
Ramp−restretch + step	SL	5.8 ± 0.5	2.4 ± 0.3	9.6 ± 0.8	4.1 ± 0.3	0.68 ± 0.02	95 ± 1
		(7,5)	(7,5)	(7,5)	(7,5)	(7,5)	(7,5)

Values are means ± s.e.m. Number of force records, fibres given in parentheses.% recovery = (fitted recovery/isometric force) × 100 for double-exponential fits. Amplitudes of exponential components were calculated from the end of the length change. SL, SL control; PM, fibre length control; k_r, rate constant of a fitted exponential component, with subscripts: _r1 = single exponential, _rs = slow rising component and _rf = fast rising component; A′_f = A_f/A_T = A_f/(A_f + A_s) = amplitude of the fast component (A_f) relative to total recovery. For slack tests, the rate constants are averages over all release sizes.

^†T₁, the extreme force reached during the step release, was −0.05 P_o in fibre length control and −0.01 P_o in SL control.

^‡Variations in k_r1 among different protocols are partly a result of variations in A′_f: a small fast component (low A′_f) slows overall recovery (low k_r1).

Table 1 compares exponential fits to force recovery from different fibres under SL and PM control. For step releases the rate constants of single-exponential fits increased by about 25% on average when SL control was used, but this effect can partly be explained by an increase in the relative amplitude of the fast component of recovery. The average rates of the slow and fast components did not depend significantly on the type of length control used. The SL and PM control measurements were usually made on separate fibres, but a direct comparison was made for one fibre during a single activation. When SL control was used, the rate constants of the single, slow and fast components increased by 10%, 17% and 19%, respectively (step releases of 8–14 nm hs⁻¹).

The force response to isometric step stretch consisted of a rise during the stretch, followed by several phases of force decline (Fig. 2A). The rate constant of the slowest phase averaged 0.8 ± 0.05 s⁻¹ (n = 45 records, 18 fibres, stretch magnitude of 3 ± 0.2 nm hs⁻¹). This phase was clearly separated from the faster phases, being over an order of magnitude slower than the next fastest phase (rate constant, 16.6 ± 1.4 s⁻¹).

There was often a pause or slight reversal in force decline after stretches of 1–3 nm hs⁻¹ (phase 3 of Ford et al. 1977), which occasionally was large enough to be distinguished as a rising component by the multiple-exponential fitting routines used here (Fig. 2A). The rate constant of the rising component was 7.5 ± 0.9 s⁻¹ (n = 8, five fibres), similar to the fast rising component of phase 4 after step release (Table 1, PM control).

Shortening to a stop

Stiffness changes little following isometric step releases in intact frog fibres (Ford et al. 1974; Cecchi et al. 1986), suggesting that the number of attached cross-bridges is nearly constant. In contrast, stiffness falls during shortening at high velocity (Ford et al. 1985; Cecchi et al. 1986; Brenner, 1990), so force recovery in that case should at least in part represent a net flux of cross-bridges from detached states to attached, force-generating states.

Force at the start of recovery (T_i) was reduced to zero by applying slack tests in which fibres are completely unloaded (Fig. S1, Supplemental material). The rate constants of double-exponential fits to recovery from slack tests were within 3–20% of those for moderate step shortening (Table 1), and the amplitude of the fast component was 68% of the total. T_i was set to intermediate values by applying ramp shortening. Starting from low force (T_i∼2%P_o), recovery was described by two exponentials with rate constants of 1.7 s⁻¹ and 9.7 s⁻¹ (Fig. 3A and Table 1, A′_f, 0.57). For recovery from low force, the rate constants following ramp shortening and those from step releases are similar. However, when ramp velocity was reduced so that force remained high (80–85%P_o), recovery was closer to a single exponential (Fig. 3A and D), and the rate constant (single exponential, 1.3 s⁻¹) was similar to that of the slow component at low and intermediate forces (1.7 s⁻¹ and 1.3 s⁻¹, respectively). Recovery after shortening at high force was slower than after a step release, which elicited a recovery (A_T) of a similar magnitude.

Figure 3. Ramp shortening to a stop.

A, force records showing recovery following ramp shortening to a stop (shortening = 0.63 L_o, 66–97 nm hs⁻¹, PM control) at three velocities: 0.57, 0.10 and 0.0048 L_o s⁻¹ corresponding to ‘low’, ‘intermediate’ and ‘high’ loads, respectively. Single-exponential fits (+) are shown to recovery following the slowest and fastest ramps; a double-exponential (□) was also fitted to recovery following the fastest ramp, but was not obtained for the slowest ramp because recovery in that case was adequately fitted by a single-exponential (see B and C below). The fits to recovery from intermediate load are omitted for clarity. For the fast ramp, k_r1 = 4.4 s⁻¹, k_rs = 1.8 s⁻¹, k_rf = 9.3 s⁻¹ and A′_f = 0.58, and for the slow ramp, k_r1 = 1.3 s⁻¹. Initial force shown in the graph was higher than at the end of recovery (P_o) due to the longer length before the ramp (2.42 μm versus 2.22–2.28 μm SL, respectively). CS = 4.2 × 10³μm², length = 2.1 mm. B, force records from A shifted so that recovery begins at the same time for all three loads. C, as in B, but with the force records shifted in time so their time courses coincide; a small vertical offset was applied to the force record at high force. D, comparison of force recovery for the three loads plotted with amplitudes normalized to 1.0 and offset to the same start time. Force data are shown as individual points, and fits are shown by continuous lines through the data points with symbols as in A. Recovery at high force was more single exponential in form, as judged by the goodness of fit of a single exponential and the small difference between single- and double-exponential fits.

Force recovery starting at various initial levels can be compared independently of any numeric description by shifting and overlaying the records. The relationships between the traces at three forces from Fig. 3A are illustrated in Fig. 3B and C. It can be seen that the three records overlay one another almost exactly if those that begin at higher initial force are shifted to progressively later times (Fig. 3C). This correspondence shows that recovery from high force is equivalent to the later part of recovery from low force. This similarity cannot result from simple vertical scaling because this does not bring the records into alignment (Fig. 3D).

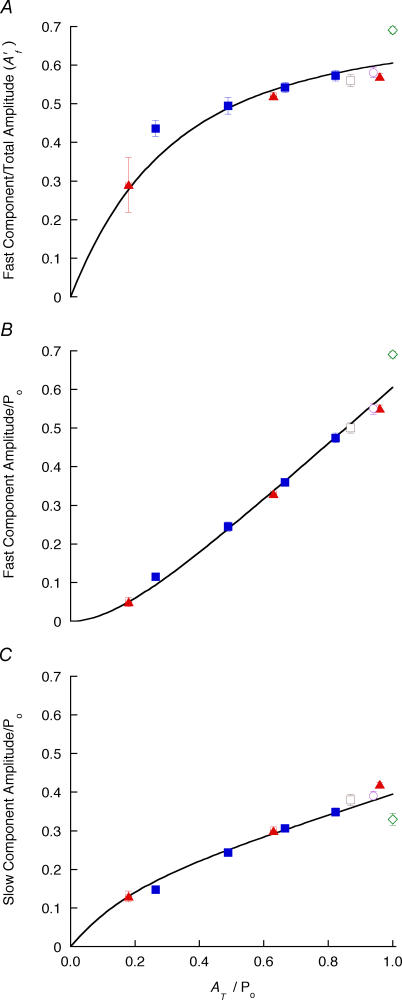
Amplitudes of the exponential components of force recovery

The observations above implied that for ramp shortening to a stop, the amplitude of the fast component was reduced more than that of the slow component as T_i was increased and recovery was reduced, and this was confirmed by the exponential fits in which A′_f fell markedly (Fig. 4A). This was also true of other length-change protocols with slack tests exhibiting the largest fast component (Fig. 4A). The absolute amplitudes of the fast and the slow components (A_f and A_s, respectively) display a roughly linear dependence on total recovery amplitude (A_T) (Fig. 4B and C). Extrapolation of a straight line through each set of points gives a positive intercept on the abscissa for A_f and a negative intercept for A_s (see also Fig. 2C). A possible explanation is that the whole distribution of attached cross-bridges detaches and reattaches more slowly when the force is near isometric, but when the strain is reduced part of the redistribution occurs at a faster rate. If so, the dependence of A_s on A_T can be fitted by an empirical formula such as

where a₁, a₂ and Φ are constants and a₁ + a₂/Φ = 1 (so that A_s → A_T as A_T → 0). The result of a least-squares fit of this function to the points of Fig. 4 is shown as continuous lines using a₁ = 0.27, a₂ = 0.13 P_o and Φ = 0.17 P_o. A_s is the only component at low recovery, whereas at high recovery A_s/A_T approaches a₁ + a₂/A_T = 0.4, and A_f/A_T (= A′_f) approaches 1–0.4 ( = 0.6; cf. Table 1).

Figure 4. Amplitudes of exponential components versus recovery magnitude.

A, amplitudes for double-exponential fits to recovery after ramp shortening to a stop (▴), slack tests (⋄), step releases (▪), ramp + small stretch (□) and ramp−restretch + step release (○). A, A′_f; B and C, amplitudes of fast and slow components, respectively. Continuous lines represent a fitted exponential + line as described in the text. Values are means ± s.e.m.

The value of Φ can be used to calculate an order of magnitude value for the shift in the distribution of cross-bridge strain associated with the increase in A′_f with A_T. Assuming that the length constant (λ) of the shift is given by λ = Φ/k, where k is an apparent cross-bridge stiffness (taken to be ∼0.1 P_o nm⁻¹ from the dependence of T₂ on the size of a step release, where T₂ is the tension reached after the initial rapid recovery phase Huxley & Simmons, 1971), λ∼2 nm, with little additional shift beyond ∼3–4 λ, or 6–8 nm.

The fit of the exponential function for A_s to the experimental points from all the length-change protocols is reasonably good within experimental error, and would imply that there is little difference in the dependence of the relative amplitudes of the two exponential components on the amount of recovery, whatever the experimental origin. However, the points from step releases and from slack tests (A_T = 1) seem to deviate from the curve, and it is shown in the Appendix that this is to be expected from a strain-dependent cross-bridge model.

Force recovery does not depend on the velocity of ramp shortening when T_i is approximately zero

To test whether cross-bridges enter a ‘slow’ state during slow shortening, slow ramps were terminated by a step release that briefly brought force (T₁) to near zero (Fig. S2A). The step release increased the rate of force recovery so that it was not significantly different from that for phase 4 following an isometric step release (Fig. S2B and Table 1). Recovery was also independent of shortening velocity when a ramp was followed by a restretch and T_i was brought to near zero (Fig. S3, see also next section and Fig. 6). These results show that although there is little fast component when recovery occurs from high force at the end of slow shortening, it reappears after a transient reduction in force, and thus attached cross-bridges are not trapped in a slow state.

Stretches at the end of ramp shortening

Another approach to distinguishing the contributions of attached and detached cross-bridges was to terminate shortening ramps with stretches sufficiently large to forcibly detach cross-bridges (Brenner & Eisenberg, 1986), and compare the responses to the effect of small stretches, which are less likely to detach cross-bridges. Step stretches were applied after ramp shortening of 50–80 nm hs⁻¹ at high velocity (P/P_o = 0.05) (Fig. 5). Double-exponential functions could be fitted to recovery following step stretches of 2–75 nm hs⁻¹, whereas larger stretches could only be fitted by single exponentials.

Figure 5. Ramp shortening terminated by step stretches.

A, a series of shortening ramps of constant size and velocity were terminated by step stretches of varying size (5.5, 19, 37, 79 and 148 nm hs⁻¹) as shown in the graphs of fibre length and SL. All of the stretches ended at the same length; the length before the ramp was varied to achieve this and caused a variation in force before the ramp; P_o = 56–58 nN μm⁻² for the five records. Single- and double-exponential functions fitted to the force traces are shown for recovery resulting from the largest (dashed records) and smallest (dotted records) stretches. Fits and residuals are shown as in Fig. 2A. For the largest stretch (148 nm hs⁻¹), k_r1 = 7.6 s⁻¹, k_rs = 4.8 s⁻¹, k_rf = 10.8 s⁻¹ and A′_f = 0.63; for the smallest stretch (5.5 nm hs⁻¹), k_r1 = 3.8 s⁻¹, k_rs = 2.5 s⁻¹, k_rf = 10.2 s⁻¹ and A′_f = 0.55. CS = 6.2 × 10³μm², length = 2.17 mm. B, the dependence of the rate constants on the size of stretch and magnitude of recovery. Data show single (▪), slow (▴) and fast (▾) exponential rate constants. C, as in B, but the data are normalized within each fibre at a recovery magnitude of 60%P_o plotted against observed recovery (force at recovery plateau minus T_min, divided by P_o); change in SL (ΔSL) is taken from the upper graph. It was usually not possible to obtain a double-exponential fit for the largest stretches eliciting the smallest recovery. For the single-exponential fits, n = 5–20 records, and for the double exponentials, n = 5–16 records for each data point; 13 fibres were studied.

When small stretches were used (5.6 ± 0.7 nm hs⁻¹, range 2–14 nm hs⁻¹, n = 20), force prior to recovery (T_min, taken as T_i after a stretch) was low (13%P_o), and recovery was large and well described by a double-exponential function with rate constants of 2.0 s⁻¹ and 8.4 s⁻¹ (Table 1, Ramp–stretch, fibre length control), similar to those reported above for large recovery after isometric steps, slack tests and ramp shortening at high velocity.

When the size of the stretch was increased to > 40 nm hs⁻¹, so that recovery began at higher forces (T_min, ∼60%P_o) and was reduced in magnitude (Fig. 5A), the fitted rate constants increased by about 2 s⁻¹ (Fig. 5B and C). Relative to the rates for small stretches, the slow component increased greatly (∼2-fold), whereas the rate of the fast component increased only slightly (∼20%) (Fig. 5C). This caused the ratio of the fast to slow rate constants to decrease from 4.2 ± 0.2 to 3.0 ± 0.3, so that recovery became more nearly single exponential (residuals and difference plot of single and double exponentials; Fig. 5A). The fitted amplitudes of the fast and slow components were reduced in about the same proportion by large stretch, with the fast component providing 57–63% of the total. Factors that contribute to these apparent changes are examined in the next section.

The effects of large stretches on force recovery might be a function of the large length change itself, or alternatively of the increase in T_min and cross-bridge strain at the beginning of recovery. To distinguish between these possibilities, T_min was increased for a given size of stretch by slowing it from ∼0.3 ms to a few milliseconds (data not shown). For a range of T_min values, the magnitude and rate of recovery was similar to that obtained by varying the stretch size. This result suggests that the kinetics of force recovery following shortening and step stretch depend on cross-bridge strain immediately prior to recovery, rather than on the size of the stretch per se.

Slow decline of force following restretch

One characteristic of the response to a large restretch (60 nm hs⁻¹) at the end of ramp shortening was an overshoot in recovery (Larsson et al. 1993) followed by a slow decline in force that increased with the size of the stretch (Fig. 5A, S4). When T_min was made extremely high (∼90%P_o) by a large restretch (or by slowing the restretch speed), there was an overshoot of about 10–20% of isometric force (Fig. S4B and C) and the slow force decline could be resolved from the force rise by fitting two or three exponentials (Table 2). The rate of the slow fall was 0.4–0.8 s⁻¹, which was similar to the slowest falling component after small isometric stretches described above (0.8 s⁻¹). If the slow falling component is not separated from the rise, the whole recovery is effectively truncated, leading to an increase in rate (Table 2), especially in the slow rising component.

Table 2.

Effect of separating a slow falling component from the force rise after ramp–restretch

Period fitted	No. of exponentials	Single rise kr1 (s−1)†	Slow rise krs (s−1)	Fast rise krf (s−1)	Slow fall ks (s−1)	Overshoot (%Po)	Fall/rise: amplitude ratio	Fast amplitude/total rise (A′f)†	n* (Records, Fibres)
Rise to plateau	1	9.1 ± 0.2	—	—	—	9 ± 1	—	—	45, 15
Rise to plateau	2	6.8 ± 0.2	—	—	0.8 ± 0.10	9 ± 1	0.62	—	44, 15
and slow fall	3	—	3 ± 0.3	10.7 ± 0.6	0.4 ± 0.05	17 ± 0.4	0.40	0.7	18, 7

Symbols are as in Table 1, and in addition k_s = rate constant of the slow falling component. For all records, single, double- and triple-exponential fits were attempted, but in some cases two and/or three components could not be resolved (see Methods).

^†The high A′_f value of 0.7 increases k_r1 after removal of the slow fall (cf. Table 1).

Removal of the slow fall revealed that the amplitudes of both rising components were reduced by a large stretch, but the greatest reduction was in the slow component so that A′_f increased greatly (Table 2). This contributed to an acceleration of overall recovery (k_r1 = 6.8 s⁻¹, Table 2, versus 4–5 s⁻¹ for other protocols, see Table 1).

For records in which the overshoot was small (∼2%P_o), and the slow falling component could not be resolved explicitly, the accelerating effect of a slow falling component was assessed by calculating a record simulated from multiple-exponential functions and fitting it in the same way as the data (Fig. S5). The presence of a slow falling component caused the apparent rate constants of both components of the force rise to increase by ∼0.9 s⁻¹, or 36% and 10% for the slow and fast components, respectively. These results were similar to those observed experimentally. In addition, redevelopment became more single exponential in form as the two apparent rate constants became more similar.

These results show that a large restretch accelerates force recovery because (1) the proportion of recovery in the fast component increases, and (2) the introduction of a slow fall increases the apparent rate of recovery.

Effects of lowering T_min after a large stretch at the end of ramp shortening

The effects of forcible cross-bridge detachment on recovery were assessed by lowering force immediately after large restretches so that T_min was the same as after small step stretches (Fig. 6; cf. Fig. 5). Cross-bridge strain at a given T_min should be comparable in the two protocols as stiffness is little affected by a large restretch (Burton, 1992). T_min was lowered in two ways (Burton, 1989): in the first, the motor movement was underdamped during the restretch (Fig. 6) and in the second, a step release was applied 2 ms after the restretch (Burton et al. 2005). The effects of the two protocols were similar: both decreased T_min and hence increased the magnitude of recovery. As with the data of Fig. 5 in which the size of the stretch was varied, the rate constants of both a single-exponential fit and the slow component of a double-exponential fit were reduced as recovery increased, whereas the rate of the fast component was relatively less affected (Fig. S6A and B). The amplitudes of the two exponential components appeared to change in the same proportion with changes in recovery magnitude (fast amplitude, 55–65% total), but as discussed above (Table 2), a relatively larger effect on the slow rise is probably masked by the presence of a slow falling component (causing an overshoot in recovery, Fig. S6C). The similarity of recovery from a given T_min in the protocols of Figs 6 and 5 suggests that forcible detachment of cross-bridges does not significantly alter recovery kinetics.

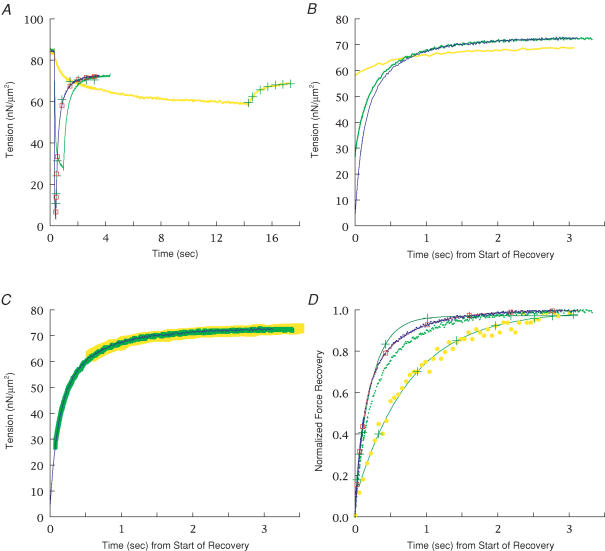
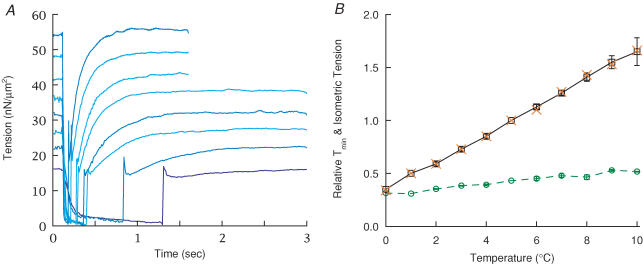
Temperature dependence of force recovery

The effect of temperature on the two rising components following ramp–restretch was studied from 0–10°C during continuous activation. When the temperature was raised, isometric force increased but there was little change in T_min, so the magnitude of force recovery increased both in absolute terms and relative to isometric force (Fig. 7A). The fitted rate constants of the fast and slow components increased with temperature (see Fig. 8), being characterized by Q₁₀ values of 4.5–5 and 2.2–2.5, respectively (Fig. S7A and B, activation energies of 114 and 57 kJ mol⁻¹ obtained from linear regression to Arrhenius plots over a temperature range of 4–9°C, correlation coefficients = 0.90 and 0.91, respectively). The proportion of recovery contributed by the fast component increased with temperature (Fig. S7C), which contributed to a very high Q₁₀ of single-exponential fits (6.6). The linear increase in isometric force over this temperature range (Fig. 7B) has been shown previously (e.g. Zhao & Kawai, 1994).

Figure 7. Force recovery versus temperature.

A, records showing force recovery elicited by ramp–restretch protocol at temperatures from 8°C-1° (l-r) in SL control. Fibre cross-section = 5.2 × 10³μm², length = 2.75 mm, SL = 2.33 μm. The record at 1°C was acquired for 6 s (only 3 s shown). The full magnitude of the force spike during the restretch was not sampled. B, dependence of isometric force and T_min on temperature over the temperature range 0–10°C. Three fibres were studied, with n = 4 (sets of two to three repeats at each temperature) at 2–8°C, n = 2 at 10°C, and n = 1 at 0°C. One fibre was studied in both SL and PM control. Isometric force was defined either as the steady force before the ramp (×) or the offset of a two-exponential fit (□ and continuous line); both were divided by their respective values at 5°C within each fibre and then averaged among fibres. The two measures of force varied in the same way with temperature. The variation in T_min with temperature (○ and dashed line) is shown normalized in the same way, but also multiplied by the mean T_min divided by the offset at 5°C to emphasize its relationship to isometric force and to show its smaller temperature dependence. The restretch was adjusted for critical damping. Many error bars (s.e.m.) are smaller than the symbols.

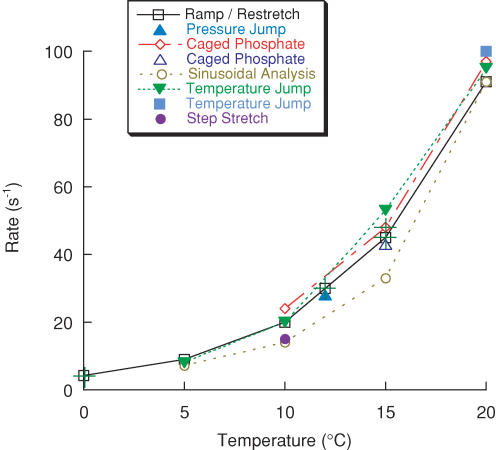
Figure 8. Temperature dependence of related force transients.

The rate constant of the fast component of force recovery elicited by ramp–restretch (□) is compared to force transients elicited by other perturbations over a range of temperatures, including pressure release (‘phase 2’ of Fortune et al. 1994; ▴), caged phosphate (k_pi of Dantzig et al. 1992 (⋄) and Walker et al. (1992) (▵)), sinusoidal analysis (‘process b’ of Zhao & Kawai, 1994; ○), temperature jump (‘phase 2’ of Bershitsky & Tsaturyan, 1992 (▪) and τ_neg⁻¹ of Davis & Rodgers (1995) (▾) and step stretch (‘phase 2b’ of Ranatunga et al. 2002; •). Rate constants shown at more than one temperature are connected by straight lines. Some values have been estimated from Q₁₀ values taken from the data, and these are marked (+). The rate constant of phase 2 of the pressure release response is shown at 12°C (28 s⁻¹, Fortune et al. 1994); the temperature dependence was reported separately (Fortune, 1990), with the Q₁₀ values of their phases 2 and 3 being ∼4.5–5 and ∼2, respectively. The values shown in the graph refer to experiments at low phosphate concentration (∼1 mm). The published temperature-jump data of Davis & Rodgers (1995; τ_neg⁻¹) were obtained at 15 mm phosphate, and are similar to the rate of force recovery elicited by ramp–restretch at that phosphate concentration (Burton et al. 2005), which is ∼1.9-fold higher than reported here. On the assumption that the two types of force response share the same phosphate dependence, their data have been reduced by the same factor to give the data points shown in the graph. The rate of force recovery following ramp–restretch at 20°C was obtained from fibres rapidly activated by release of ATP from a caged precursor (Sleep et al. 2005).

The slow falling component, indicated by an overshoot in force recovery, could not be separated from the force rise in these records and as discussed above it caused an overestimate in the fitted rate constants. This error is greatest at low temperature where the force rise is very small owing to a high T_min, causing the actual Q₁₀ to be greater than that measured. When corrected for the slow component, the rate constant at 5°C is reduced from 3.2 s⁻¹ to 2.3 s⁻¹ (see Supplemental material), yielding a corrected Q₁₀ of ≤ 3.8.

Discussion

Summary of results

The time course of recovery to the isometric level was recorded after a number of interventions designed to alter attached cross-bridge numbers, distribution and strain. Analysis of late recovery curves showed that the majority were not satisfactorily fitted by a single exponential. Most of the records were well fitted by two rising exponentials of about 2–2.5 s⁻¹ (slow component) and 8–10 s⁻¹ (fast component), and the separate nature of the two processes was demonstrated by a difference in their temperature dependence. When a stretch was applied, the decay of force was described by a slow component of about 0.4–0.8 s⁻¹, and following small stretches there was again a rising component of ∼8 s⁻¹. When ramp shortening was followed by a restretch to the initial length, the slow falling component altered the force rise, making it appear faster and more single exponential in form.

Force recovery following an isometric step release might be expected to be different from that following a long period of shortening (slack test or slow ramp) or forcible detachment of cross-bridges (ramp-restretch), because the distribution of cross-bridge states and their strain would be expected to be different at the beginning of recovery. However, when force recovery was made to start from near zero (T_i, ∼0), the kinetics were nearly the same following isometric step release, rapid shortening to a stop, slow shortening (force brought to zero either by step release or by restretch plus ringing, that is, the oscillatory change in length arising from an underdamped motor), or rapid shortening terminated by a large restretch (force brought to zero by subsequent step release). This was true for both the rate constants and amplitudes of force recovery (Table 1). These observations show that, in this case, force recovery does not depend strongly on the amount of time that force was low, or on whether cross-bridges had been greatly strained or forcibly detached.

In contrast to recovery from low force, the rate of recovery did depend on the nature of the preceding length changes when recovery started from an intermediate level. Recovery after a slow ramp had a time course, as described by a single-exponential fit, that was slower than for a fast ramp, and ∼40% slower than for recovery after an isometric step release producing an equivalent initial tension, T_i. The slower time course was associated with a reduction in the amplitude of the fast component. Recovery from a high T_i achieved by applying a step stretch at the end of rapid shortening was faster than recovery from the same T_i following a step release or slow ramp, even when corrected for a slow falling component present after a stretch. This resulted in part from the slow component comprising a relatively smaller proportion of recovery (Fig. S5B and C, and Table 2). These effects of starting from intermediate levels could be reversed by rapidly bringing force to zero at the start of recovery, independent of the velocity of the preceding shortening.

Comparison of force recovery rate to estimated cross-bridge strain

The fast component of recovery was absent after slow ramps, but reappeared when the ramps were terminated by step releases. If this is caused by a reduction in cross-bridge strain per se, then the rate of recovery after shortening and step release should be comparable to that of isometric releases at equivalent cross-bridge strains. When force recovered from near zero, so that average strain was also near zero, the rates were similar. The same comparison for recovery at higher initial force is less straightforward because cross-bridge strain and force do not change in the same proportion during steady shortening (Ford et al. 1985). During shortening at 30%P_o, where stiffness is about 45% of the isometric value (Ford et al. 1985; Brenner, 1990), cross-bridge strain would not be less than about ∼30%/0.45, which equals ∼70% of the isometric value. Following small isometric releases, cross-bridge strain is more closely proportional to force (T₂), as the reduction in stiffness is less (∼12% at T₂ = 80%P_o; Ford et al. 1974; Lombardi et al. 1992). When strain was raised from near zero to 70–90% of the isometric value of strain, the rate of recovery after step releases was reduced to 76% of that at low strain, similar to the reduction observed after steady shortening (69%) (Table 3). These results are not altered when filament compliance is taken into account as all the estimates of strain increase, resulting in similar variations in strain with load. This calculation suggests that the rates after steady shortening and step release were comparable at high strain, providing additional evidence that strain in attached cross-bridges is a determinant of the rate of recovery.

Table 3.

Rate of force recovery for ramps and steps as a function of cross-bridge strain

Length-change protocol	Ti (%Po)	Estimated strain (% isometric)	kr1 (s−1)	kr1(h)/kr1(l) (mean ratio)*	n (records, fibres)	Velocity (nm hs−1 s−1) or step (nm hs−1)
Medium ramp	32 ± 0.7	≳ 70	2.6 ± 0.1	0.69 ± 0.05	18, 4	−99 ± 7
Small release	84 ± 1.3	≳ 90	2.4 ± 0.5	0.76 ± 0.02	24, 8	−2.6 ± 0.2
† Fast ramp	1.9 ± 0.2	≳ 5	4.1 ± 0.2	—	18, 4	−580 ± 42
†Large release	31 ± 2	≳ 40	3.1 ± 0.1	—	34, 8	−8.1 ± 0.5

T_i refers to force at the beginning of recovery, which corresponds to that at the end of shortening for ramps and to T₂ for releases. PM control. Approximate cross-bridge strain estimated from force and stiffness as discussed in the text. k_r1 = rate constant of a single-exponential fit for high force (h) low force (l).

^*Ratio of rate constants at high force (ramps and releases in top two rows, respectively) to those at low force (bottom two rows) calculated for each fibre and then averaged among fibres.

^†T_i was usually restricted to between ∼30% and ∼80%P_o because smaller recovery (high T_i) could not be reliably fitted with a double exponential, and larger step releases (low T_i) caused fibres to go slack and distort the SL signal. This results in higher estimated strain than during a fast ramp at T_i∼2%P_o (strain ≥ 40%versus 5% isometric, respectively), which can explain the lower k_r1 compared to that for a fast ramp (3.1 versus 4.1 s⁻¹). k_r1 for large releases where T_i∼2%P_o(A_t = 0.98 P_o) can be estimated from Fig. 2B by linear regression to the data for PM control, yielding k_r1 = ∼4.3 s⁻¹, which is similar to that for fast ramps (4.1 s⁻¹).

Analysis and modelling of the late recovery phase

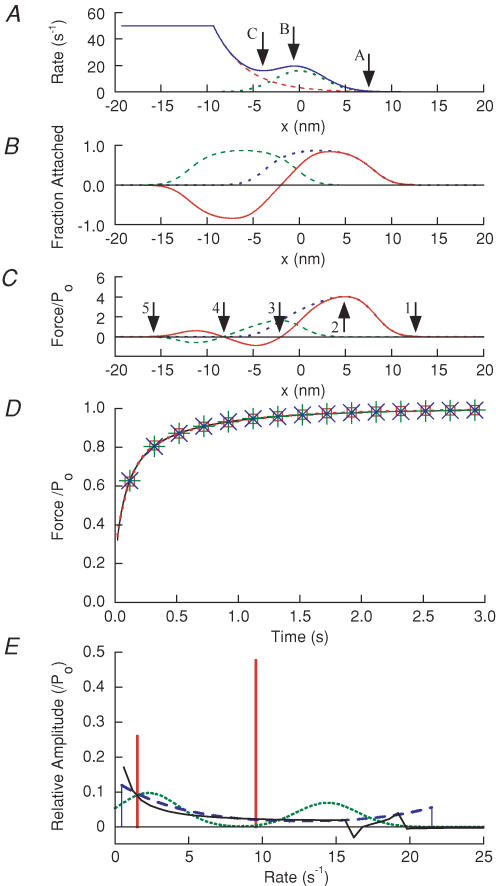
The results are consistent with time courses of force recovery calculated from a simple mechanical model. A two-state Huxley-type model is used in which the attachment rate constant (f) and the detachment rate constant (g) are both functions of cross-bridge strain (Smith & Geeves, 1995). As described in the Appendix (see Figs 10 and 11), the rate components of recovery comprise a continuous distribution, with upper and lower bounds. Fitting two exponentials to recovery curves generated by the model shows that the fast component results predominantly from attachment of cross-bridges at moderate positive strain. Both f and g are comparatively high in this region of strains, but f dominates as it is ∼3-fold larger than g. The slow component is produced by the attachment of cross-bridges at higher strain, where both f and g are low. The model accounts for several experimental observations, including the monotonic reduction in rate constants and the proportion of recovery in the fast component (A′_f) with increased T_i (Fig. 4). Following a simulated isometric step stretch, it produces a small rising component (phase 3) with a rate constant similar to the faster components of phase 4 following a step release; force then falls slowly towards the isometric level with a rate constant similar to that observed experimentally. The model also implies that the experimental data are compatible with a continuous distribution of rate constants, with two exponentials giving a semiquantitative assessment of the breadth of the distribution of rate constants.

Figure 10. Results of fitting a cross-bridge model recovery record.

The record was a shortening step of 8.25 nm hs⁻¹. A, plot of f (dotted line), g (dashed line) and r ( = f + g; continuous line) versus x. B, distribution of attached cross-bridges P(x) with respect to x, in the isometric state (dotted line), immediately after the step (dashed line) and difference ΔP_a between these distributions (continuous line). C, distribution of force F(x) in the isometric state (dotted line), immediately after the step (dashed line) and difference, A(x), between these distributions (continuous line). D force recovery time course calculated from model; symbols as in Fig. 9A. E, amplitude B(r) of exponential components for: model (continuous line), two exponentials (vertical bars), two Gaussian distributions (dotted line) and bounded distribution of exponentials (dashed line). The isometric tension (P_o) and stiffness averaged over all cross-bridges were 1.46 pN and 0.14 pN nm⁻¹, respectively. It should be noted that x is the distance between a cross-bridge and the actin site, and is the strain upon attachment; in the model there is an obligatory force-producing step h so the net strain is x + h.

Figure 11. Dependence on amplitude of recovery of amplitude and rate of exponentials fitted to model data.

Model recovery records from shortening steps and ramps of varying amplitude were fitted with two exponentials. A, plot of fast and slow component rate constants versus amplitude of recovery from steps (dashed line) and ramps (dotted line). B, plot of fast component amplitude versus amplitude of recovery for steps (dashed line) and ramps (dotted line). C, plot of fractional amplitude of fast component versus amplitude of recovery for steps (dashed line) and ramps (dotted line). Corresponding points from experimental data are included for comparison (from Fig. 4).

Relationship to biochemical steps

Recent studies of muscle fibres using alternative metal-nucleotide substrates (Burton et al. 2005) or activated by step increases in ATP concentration (Sleep et al. 2005) suggest that force recovery is controlled by two biochemical steps in the cross-bridge cycle. The first step, ATP hydrolysis, precedes a much faster force-generating transition, and the second step, phosphate release, follows it. The equilibrium constant of the rapid force-generating step can be assumed to depend on cross-bridge strain, and when varied causes simulated force development to vary over a range that includes the two major exponential components observed experimentally. An important feature of the scheme of Sleep et al. (2005) is that the force-generating transition is bounded by two slower biochemical steps assumed to be independent of strain. This sequence of steps ensures that the rate of cross-bridge flux through the force-generating step is constrained within a range governed by the ATP hydrolysis step at low strain and phosphate release at high strain.

Effects of a large restretch

The results of studies of force recovery have been variable partly as a result of variations in T_min (%P_o): 15–30% (Brenner & Eisenberg, 1986), 10% (Chase et al. 1994), 10% (Diffee et al. 1996), 40% (Swartz & Moss, 1992); in intact frog fibres, 24% (Gulati & Babu, 1986), 32% (Bagni et al. 1988); and skinned rat myocardium, 50–60% (Hancock et al. 1996). T_min is sensitive to many factors, including storage time and general condition of fibres, temperature (see Results), [Ca²⁺] and SL (K. Burton & J. Sleep, unpublished results), speed of restretch, amount of shortening before restretch (Burton & Simmons, 1991) and length changes immediately after the restretch (Burton, 1989 and the present study). High force during a restretch and the non-zero value of T_min immediately afterwards suggest that cross-bridges forcibly detached by the large stretch rapidly reattach, and that this process can occur several times during and after the movement through a process of ‘slipping’ to sites at lower strain along the thin filament. Slipping is consistent with the similarity in stiffness measured before and after a large restretch (Brenner & Eisenberg, 1986; Burton, 1992) and high stiffness during rapid lengthening (Lombardi & Piazzesi, 1990) as well as a portion of the transient response to step stretches (Piazzesi et al. 1997). This explanation for the origin of T_min can account for its sensitivity to small rapid length changes immediately after a large restretch, to which some of the variability in the literature can be attributed, for example the low T_min when the restretch is underdamped (10%, Chase et al. 1994) and higher value when critically damped (32%, Bagni et al. 1988).

A large stretch also introduces a slow falling component that varies with T_min and increases the apparent rate constant of recovery, especially that of the slow rising component. The greater increase in the slow component reduced the difference between the apparent rate constants of the two rising components, causing recovery to became more single exponential in form. In contrast, because no falling component was present in the absence of a stretch, the multiple-exponential nature of force recovery was more apparent. The slow fall presumably arises from cross-bridges that have stopped slipping but are still at strains above the normal isometric strain, and hence do not contribute to the rising components. This would account for the smaller amplitudes of the rising components after shortening terminated with a restretch when compared to those without, even when ramp velocity is high in both cases. The amplitude of the fast rising component is reduced less than that of the slow component as T_i increases with larger restretches, whereas the opposite is true when T_i is raised by increasing load during shortening terminated by a stop. These observations could be explained if detached myosin heads contribute primarily to the fast rising component: they are insenstitive to a restretch and thus their contribution is independent of restrech size, whereas there are fewer of them at high load and hence less of a fast rise.

Temperature sensitivity of force recovery

Figure 8 shows rate constants of force transients elicited by various interventions over a range of temperatures, including the ramp-restretch protocol presented here, pressure jump (Fortune et al. 1994), step stretch (Ranatunga et al. 2002), temperature jump (Bershitsky & Tsaturyan, 1992; Davis & Rodgers, 1995), sinusoidal analysis (Zhao & Kawai, 1994) and photolysis of caged phosphate (Dantzig et al. 1992; Walker et al. 1992). These force transients have generally been attributed to the cycling of cross-bridges into force-generating states, the observed rate being the sum of the attachment and detachment rates. It is apparent from Fig. 8 that these rate constants are similar over a large range of temperatures (Q₁₀, 4–5; Fig. S8), although a recent study (Bershitsky & Tsaturyan, 2002) reported a more modest temperature dependence (Q₁₀, ∼3) for a range of temperatures from about 16-33°C.

A notable comparison in Fig. 8 is between the rate of force recovery reported here and the rate of caged-phosphate transients (Millar & Homsher, 1990; Walker et al. 1992). Previous comparisons between these two processes have suggested that the rate of the rapid phase of force decline in response to photolytic release of submillimolar levels of phosphate is faster than the (single-exponential) rate of force recovery in the presence of background levels of phosphate. The origin of this difference has not been clear as both processes have been attributed to attachment and detachment reactions of force-generating cross-bridges. However, the apparent discrepancy can be resolved by using the rate constant of the fast component of recovery after shortening, rather than the rate of a single-exponential fit, indicating that the rates are similar (Fig. 8) and implying that both processes are controlled by the same steps in the cross-bridge cycle.

Zhao & Kawai, 1994 have used sinusoidal analysis to obtain characteristic frequencies of the force response of active fibres, and the corresponding rate constant of one of these, process B, has also been suggested to describe a step governing cross-bridge attachment and a transition into a force-generating state. The reported rate of process B is 70–96% of the rates obtained here for the fast component of force recovery following ramp–restretch over a range of temperatures (Table 1 and Fig. 8). In addition, at 5°C the rate of process B (7.2 s⁻¹) is also similar to the fast rising component of phase 4 observed here (7.7 s⁻¹, PM control, Table 1), as well as to the small pause or reversal in force decline after small step stretches (phase 3).

Conclusions

We have shown that late force recovery from near zero is adequately described by two rising exponential components with rate constants largely independent of the nature of the preceding length changes. The rate of the fast component is similar to those of force transients elicited by perturbations of pressure, temperature, or phosphate or ATP concentration. However, the kinetics of recovery are altered by raising the initial force (T_i), and in that case depend on the length-change protocol used. A restretch after ramp shortening increases T_i, reduces the amplitudes of both exponential components, and introduces a slow falling component which accelerates the force rise and makes it appear more single exponential in form. In the Appendix a model is developed in which the exponential components of late recovery arise from strain dependence in the rate constants of cross-bridge attachment and detachment. The model is compatible with the fast component arising predominantly from attachment of cross-bridges at low positive strain and the slow component from cross-bridges at high positive strain, and can account for the dependence of their rate constants and amplitudes on T_i following step releases and ramp shortening.

Appendix: analysis and modelling of the late recovery phase

Introduction

As described in the main text of the paper, the recovery of muscle fibre force to the isometric level was recorded after several different interventions, including step changes of length and shortening steps. The slow recovery phase was fitted with a number of exponentials using the Provencher routine. Other routines gave closely similar fits for a specified number of exponentials, but the Provencher routine has the advantage that it gives an estimate of the number of exponentials that are needed or can be justified to fit the data. However, it is not at all clear that simple exponentials are the most appropriate functions to use for such an analysis. In most cross-bridge models there is an implicit distribution of the rate constants governing transitions between states, because of a distribution of strain in attached cross-bridges and because rates are expected to be intrinsically sensitive to strain. There may also be complicating effects from non-linear series or filament compliance. It is therefore more likely that recovery curves reflect a distribution of rate constants. There seems to be no a priori way of determining this distribution from the data, and we have instead analysed the data and the data-fitting procedures in a number of different ways to determine what kinds of distribution are consistent with the data.

First, using simulated data, we explored the limits of the Provencher method in distinguishing between two and three discrete-valued exponentials and continuous distributions of exponentials. This showed that fairly broad distributions could go undetected. Second, using the experimental data, we investigated whether other types of function (stretched exponentials, Gaussian distribution of exponentials, or bounded distribution of exponentials) would give satisfactory fits. This approach indicated that, in general, fairly broad distributions fitted the data better than a limited number of discrete exponentials. We did not use this approach routinely partly because it is laborious and partly because simple exponentials are an adequate descriptor of the data for many purposes of analysis and discussion.

Tests of the fitting procedure

As much of the experimental data was fitted well by two (or at most three) exponentials, we generated simulated data consisting of two exponentials with a Gaussian distribution of rates, with added residual noise obtained from the best fits to a data set using the Provencher method. A Gaussian distribution was chosen because the position of a detached cross-bridge may be considered to be undergoing random fluctuations and therefore the range of strains upon attachment to an actin site should follow a Gaussian distribution. In order to test at what level the Provencher routine would detect a deviation from two exponentials, we increased the half-width (σ) of the distributions until the routine suggested the need for an additional exponential.

Much of the experimental analysis shows two exponentials roughly equal in amplitude, with rate constants of about 2 s⁻¹ and 10 s⁻¹, and we generated curves from distributed exponentials centred on these values. We used two approaches: (i) using the same σ for the two distributions, and (ii) using the same fractional σ (i.e. value of σ_f = σ/m) for the two distributions, where m is the mean value. When the distributions became sufficiently broad the Provencher routine signalled that a fit with three exponentials was to be preferred. Using the first approach (same σ), this occurred when σ was ∼1 s⁻¹, and in the second case (same σ_f), σ_f was ∼0.5. We also explored broader distributions as the Provencher routine suggested three exponentials for some data, and showed that the transition to a requirement for four rather than three exponentials occurred when σ was ∼2 s⁻¹ and σ_f was ∼1.

Alternative fits to experimental data

We fitted experimental data using (i) a stretched exponential function, (ii) two Gaussian-distributed rate constants with a single value of σ or σ_f, and (iii) a ‘bounded’ distribution of rate constants. Fitting routines were written in Matlab and used the supplied Simplex routine. In addition to minimizing error, we also looked at the running time-integral of the squared residual to see if there were any longer term deviations.

Stretched exponential

This function has often been used to fit a relaxation time course which is not strictly exponential (e.g. Lee et al. 2001):

This function has the advantage that (essentially) a distribution of rate constants is obtained at the price of a single additional parameter (p) to the basic rate (r), but the function fitted the experimental data much less well than did two exponentials, and we did not pursue it further. The value of p which gave the best least-squares fit was ∼0.7.

Gaussian distribution

The recovery time course is obtained by assuming that exponential recovery (e^−rt) varies in amplitude with respect to the rate constant, r, according to the conventional formula for a Gaussian distribution (where mean value is r_o and half-width is σ), and by integrating with respect to r:

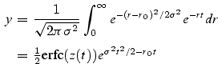where

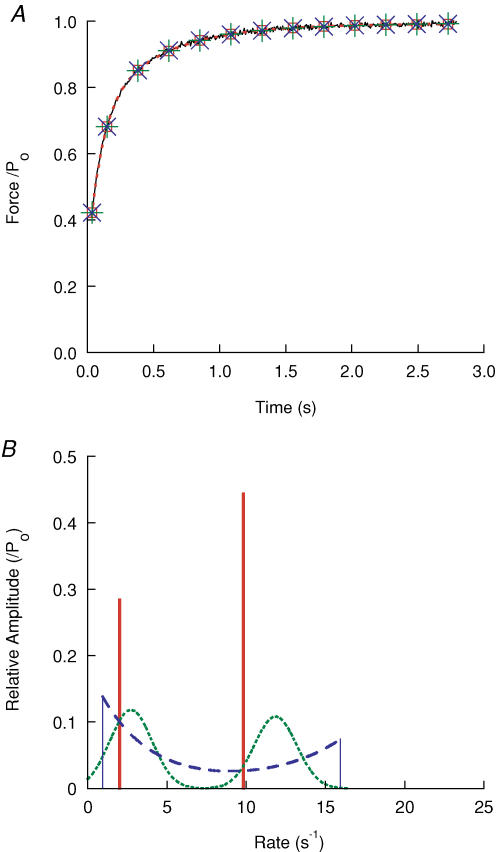
We first tested this function on experimental data that the Provencher routine had fitted with two exponentials (Fig. 9). Using two distributed exponentials, there was an improvement in quality of fit, by a few percent in the sum of errors and more notably in the running time-integral. The width of the distribution varied considerably between different records, and there was a tendency for the width to be narrower the lower the amplitude of recovery. Using a single σ, the best-fit value of σ for recovery after medium to large isometric releases was ∼2 s⁻¹; with a single σ_f, the value was ∼0.5. The result of fitting the recovery after a shortening step is shown in Fig. 9. When fitting experimental data for which the Provencher routine had suggested three exponentials, the quality of the fit using two Gaussian distributions was at least as good as the Provencher fit, and the distributions were about twice as broad as for data for which two exponentials were indicated.

Figure 9. Experimental recovery record fitted with exponential distributions.

A, force recovery following a shortening step of 8.9 nm hs⁻¹ overlaid by two exponentials (□ and dashed line), two Gaussian distributions (+), and bounded distribution of exponentials (×). B, graph of amplitude of component versus rate constant for two Guassian distributions (dotted line), a bounded distribution of exponentials (dashed line and a simple fit of two exponentials (vertical lines).

Bounded distribution of exponentials (BDE)

The third type of distribution was suggested by the distribution of rate constants in the cross-bridge model we used to match the experimental data. The distribution of recovery rates, particularly after recovery from near zero tension, tended to be bounded between two outlying rates, and show a minimum between them. A simple approximation can be found by considering two distributions which decay exponentially away from the boundaries towards the centre. The distribution, bounded by a < r < b, is given by:

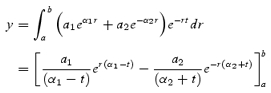where all coefficients are positive and a₂ > a₁.

The fits to experimental data using this function were among the best of all, and the distributions were often quite broad (Fig. 9B). However, it was often difficult to find convincing least-squares minima, even with simulated test data, presumably because of over-determination.

Modelling

As none of the early mechanical transients were analysed in this study, we were able to use a comparatively simple model, one which is confined mainly to the slower rates of recovery. The model (Smith & Geeves, 1995) is based on a two-state Huxley-type cross-bridge model in which the attachment rate constant (f) and the detachment rate constant (g) are both functions of strain (x). The parameters and the values used are as follows. The attachment rate is a Gaussian reflecting thermal motions of cross-bridges around a binding site at x = 0, whether originating from compliance within the cross-bridges themselves or the thick filament backbone. An assumed cross-bridge stiffness of k = 0.56 pN nm⁻¹ generates a maximum value f of 16 s⁻¹ and half-width (σ) of 3.2 nm. It is assumed that an attached cross-bridge goes through an obligatory force-producing step (h = 8.3 nm), so the net strain is x + h. The detachment rate includes a strain-sensitive ADP release step, involving a small (2.1 nm) additional step, and this gives rise to an exponentially increasing detachment rate with decreased positive strain. At high negative values of strain, the detachment rate reached a plateau, with the value of ∼50 s⁻¹ chosen to give the correct value of the maximum shortening velocity. These values were obtained by trial-and-error matching of calculated force recovery time courses to experimental data.

The steady state distribution (the attachment probability P_a(x) or force F (x)) along x of probability of attachment (P_a) and force (F) is calculated in the computer model by matrix inversion, using routines written in Fortran. Recovery to the isometric level after a step or ramp can be calculated by integrating the usual kinetic equations at each x value with respect to time. The model consisted of actin ‘target zones’ separated by 38 nm. In most of the modelling work, for simplicity there was only one actin site in each zone; however, similar results were obtained in a preliminary study using a model in which the target zone consisted of three actin sites.

When only one actin site is available to each cross-bridge, the recovery of force can also be simply calculated from the equilibration at rate (r = f + g), as follows:

(A1)

where A(x) is the difference between final (isometric) tension and the tension immediately preceding recovery for a cross-bridge with strain x. It also follows that

(A2)

where B(r) is the distribution of recovery rates:

(A3)

and x_j(r) is the jth solution of the equation r(x) = r. The recovery time course can be calculated from eqn (A1) or eqn (A3) very rapidly, enabling the use of a least-squares procedure to aid fitting the experimental recovery data. B(r) is the distribution of rate constants, to be compared with the distributions obtained from analytical fits to the experimental data.

We did not attempt to obtain an exact fit of the model to the experimental data; rather, we wished to obtain a semiquantitative simulation of the experimental data to examine the credibility of the analysis based on simple exponential fits, and also to learn about the possible origin of the rate constants found in the experimental data. We therefore obtained approximate fits to a number of records of recovery after large steps using the model, and by a process of iteration also obtained good agreement between the force–velocity relation for the model and experimental data. The resulting dependence of f, g and r on x is shown in Fig. 10A. Plots of P_a(x) and F(x) are shown for the isometric case and immediately after a shortening step. Plots of P_a(x) and its change (ΔP_a(x); final value minus initial value after the shortening step) are shown in Fig. 10B; the corresponding distribution of force change A(x) = (x + h)ΔP_a(x) is shown in Fig. 10C. We then generated model recovery time courses over the range of ramps and steps used in experiments, and analysed them in the same way as the experimental data using fits with two exponentials, two Gaussian distributions and a bounded distribution (Fig. 10D).

Comparison of the distributions of rate constants from the model (Fig. 10E) and from the experimental data (Fig. 9B) shows semiquantitative agreement, and supports the argument that the experimental recovery time courses reflect fairly broad distributions of rate constants. Extending this approach to model steps of varying amplitude showed that the main effect on B(r) was that the distribution became narrower the smaller the step, mainly as a result of a decrease in the upper bound. When the recovery time courses were fitted with two exponentials, the slower of the two components was always close to the lower bound of the calculated B(r). The faster component had a rate constant which was always lower than the upper bound, but gave a proportionate guide to the upper bound.

We used the two-exponential analysis of the model recovery time courses to derive the dependence of exponential amplitudes and rates on recovery after isometric steps and after ramps (Fig. 11). Comparison with the experimental data (taken from Fig. 4 of the main text) shows semiquantitative agreement. The rate constants rise with increased amplitude of recovery, though more steeply than for the experimental data (Fig. 11A). Also, lines fitted to the plots of amplitude of the fast and slow components make intercepts with the ordinate in agreement with the experimental plots (Fig. 11B). However, there are differences: there are signs of a more continuous curvature at high amplitude of recovery in the model data, and a greater relative amplitude for the fast component at low amplitude of recovery followed by only a small increase with increased recovery (Fig. 11C). Lumping together the model data for steps and ramps, as was done for the experimental data, yields values of Φ and λ (describing the lag in rise of the fast component) for the model data that are similar to the values found for the experimental data.

Origin of recovery rates

After shortening steps and during ramps, the distribution P_a(x) of attached cross-bridges (Fig. 10B) is shifted from the isometric position to lower values of x, and during recovery those cross-bridges now at low or negative x values detach and there is net attachment at high values of x. The plot of ΔP_a(x) in Fig. 10B shows where net detachment and attachment occur after a large step release, and the plot of A(x) in Fig. 10C shows where the corresponding gain or loss of force arises. As shown in eqn (A3), it is the product of A(r) and |dx/dr| that gives rise to the plot of B(r) in Fig. 10E.

The peak in the distribution of B(r) at low r in Fig. 10E occurs as a result of attachment of cross-bridges at high x (between arrows 1 and 2 in Fig. 10C) and the corresponding high value of |dx/dr| (arrow A in Fig. 10A), which leads to a large value of |dx/dr|. It is this region that contributes most to the slower of the two fitted exponentials.

B(r) in Fig. 10E falls progressively as r increases in the range 1–15 s⁻¹. This region of B(r) arises from attachment of cross-bridges in the range x∼2–8 nm, corresponding to force at and around the peak at arrow 2 in Fig. 10C; |dx/dr| is relatively small in this region accounting for the decrease in B(r). In the region of r between 15 and 20 s⁻¹, there is a small trough in B(r) followed by a small positive peak. In this region there are overlapping contributions between a positive component from attaching cross-bridges (to the right of arrow 3 in Fig. 10C) and a smaller negative component from the detachment of cross-bridges that are still producing positive force immediately after the step (to the left of arrow 3). The negative component is equivalent to phase 3 of isometric transients. The peak at arrow B and the trough at arrow C in Fig. 10A result in the small negative-going peak at ∼16 s⁻¹ and the small positive peak at ∼19 s⁻¹ in Fig. 10C. The peak and trough effectively cancel each other out when two exponentials are fitted, and the faster of the two exponentials derives mainly from the region of r∼5–15 s⁻¹ (x is ∼4.5–1.7 nm in Fig. 10A) and thus mainly reflects net attachment at low positive values of x.

It is worth noting that while B(r) is dominated by the attachment of cross-bridges as the isometric distribution is re-attained, in the region of B(r) that contributes to the fast component, the rate constant r is dominated by the value of f, because f > g locally, and for the region contributing to the slow exponential component, the rate constant r is determined more equally by the values of g and f, as g > f at x > 7 nm.

There is a further positive peak in B(r) at 50 s⁻¹ deriving from the forcible detachment of negative force-producing cross-bridges lying between arrows 4 and 5 in Fig. 10C (this peak is not shown in Fig. 10E as it was excluded from the subsequent analysis by fitting the time course after 50 ms).

The dependence of rate on the amount of recovery (Fig. 11A) arises in the model as follows. For a small shortening step, the shift in P_a (Fig. 10B) requires that new cross-bridges attach during the recovery predominantly at high values of x, where r is comparatively low; with increase of step amplitude and increased shift of the distribution to lower or negative values of x, cross-bridges attach during recovery also at lower values of x where r is progressively higher. Correspondingly, the slower of the two fitted exponentials becomes faster. A similar argument applies to the width of the distribution, because the larger the step, the further the lower limit of P_a is shifted, encountering higher values of r. An identical argument applies to recovery after ramp shortening at different velocities.

The lag of the amplitude of the fast exponential component with respect to increasing amplitude of recovery, seen most clearly for ramps in both the experimental and model data (Fig. 11B), presumably results from a shift (described by length constant λ) in the edge of the distribution of attached cross-bridges progressively towards lower values of x, the more so the greater the shortening velocity or step size. The lag is then related to the spread of the rising phase of the distribution (Fig. 10B), and thus to the half-width of the distribution of f, which was about 2 nm and similar to the value found for λ (see text associated with Fig. 4). In the case of steps, the shift in the distribution of attached cross-bridges is greater than for the shortening ramp that results in the same amount of recovery, because negatively strained cross-bridges do not have as much time to detach, and therefore the lag effect is less apparent. It is possibly not a coincidence that the σ values of Gaussian distributions of exponentials fitted to the experimental recovery data have values of the same order of magnitude as λ.

After small isometric step stretches, a plot of amplitude versus rate describing the recovery shows two well-separated clusters, one at about 0.5 s⁻¹ corresponding to detachment of highly strained cross-bridges and one at ∼18 s⁻¹ corresponding to attachment (phase 3). These are similar to the rates found for the experimental data. Piazzesi et al. (1997) have suggested that newly attaching cross-bridges can account for phase 3 following a small stretch. No attempt was made to model recovery following a large restretch at the end of shortening as this would require incorporating interactions of myosin heads with multiple actin sites over more than one repeat of the actin helix, which is beyond the scope of the model.

Conclusions from modelling

This analysis has shown that the experimental late recovery data is consistent with a fairly broad distribution of rate constants, though it does not prove that this is the case. Fitting exponentials to recovery data from a simple cross-bridge model with an intrinsically broad distribution of rate constants shows that fitting two exponentials gives a semiquantitative assessment of the breadth of the rate constant distribution. However, using a bounded distribution would be more accurate, but at the price of possible over-determination. In two-exponential fits, the slower exponential reflects attachment of cross-bridges at high values of x, whereas the faster exponential results mainly from attachment at low positive values of x.