Abstract
Outflow facility (C), a ratio of outflow rate (F) to relevant pressure, is an important indication of outflow resistance in the ocular drainage pathway. The higher the C, the lower the outflow resistance. According to the classic Goldmann equation, C=F/(IOP-Pe)(IOP, intraocular pressure; Pe, episcleral venous pressure). Since anterior chamber (AC) perfusions directly measure outflow and are less affected by scleral creep and rigidity or changes in uveal blood content than repeated tonography in living eyes, they are widely used to determine C in living animals or cultured anterior segments from enucleated eyes. Bárány (1964) initially developed the 2-level constant pressure perfusion technique for living monkey eyes to avoid possible influences of changes in eye parameters (e.g., Pe, spontaneous IOP [P0] or aqueous humor formation [AHF]) on C measurements. However, since these eye parameters do not exist in cultured anterior segments, 1-level constant pressure perfusion (Erickson-Lamy et al., 1991) and constant flow rate perfusion (Johnson and Tschumper, 1987) are typically used to determine C in organ culture. Based on different perfusion techniques, two basic formulas derived from the Goldmann equation are used to calculate C: (A) C=(F2-F1)/(P2-P1), which is usually used in 2-level constant pressure perfusion either in living animals or in cultured anterior segments (F1 or F2 represents F at P1 [lower perfusion pressure] or P2 [higher perfusion pressure]); (B) C=F/P, which is usually used in 1-level constant pressure perfusion or constant flow rate perfusion in cultured anterior segments (P, perfusion pressure; Pe is ignored in this formula because it is assumed to be zero in the cultured anterior segments). A comparison of C values calculated using Formula B and the data obtained during 2-level constant pressure perfusion in vivo or in vitro requires the following modifications: C=F1/(P1-P0) or C=F2/(P2-P0) where F1 or F2 is due to the change in pressure from P0 to P1 or P2 (P0 is assumed to be stable during short-term perfusions in vivo and is zero in vitro). C values from the same eye and the same perfusion are often quite different when calculated by the two formulas, since Formula A calculates C for the change in pressure from P1 to P2, whereas Formula B calculates C either for the change in pressure from P0 to P1 or P2 in living eyes or for a given pressure (P1 or P2) in cultured segments. However, the difference has not been clearly stated in previous studies, so that confusion might occur when comparing C values obtained by the two formulas. Additionally, C at different pressures may also be affected by factors physiologically unrelated to the formulas. To determine factors that may affect C values and to evaluate the significance of these factors in aqueous humor dynamics research, we compared C values calculated by Formulas A and B based on some previous perfusion experiments.
1. Aqueous Humor Dynamics Factors
1.1. Living Monkey Eyes
Data used in this section were selected from previous experiments in living cynomolgus monkeys, where F was measured by 2-level constant pressure (∼15/25 mmHg) perfusion of the AC (Bárány, 1964; 1965). All the previous investigations were in accordance with University of Wisconsin and NIH guidelines for animal use, and with the ARVO Statement on the Use of Animals in Ophthalmic and Vision Research. Anesthesia for AC perfusion in the investigations was conducted as described previously (Tian and Kaufman, 2005). To compare CA (C calculated by Formula A) and CB (C calculated by Formula B) or CB1 (CB for P1) and CB2 (CB for P2) in the present study, C was calculated by both Formula A and Formula B per the previously measured F and its corresponding pressure during perfusion (Figure 1).
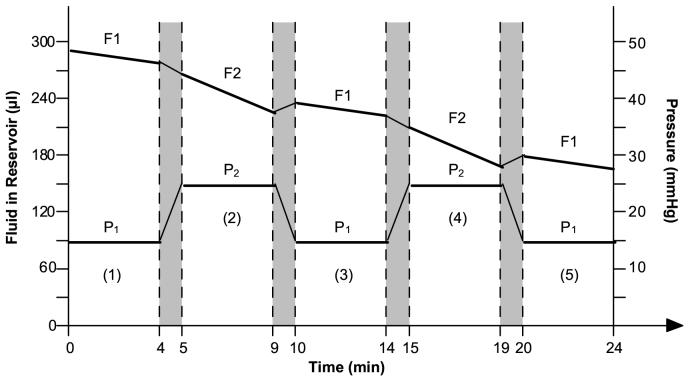
Figure 1.
Illustration for outflow facility calculation methods. The bottom lines represent 2 alternate constant pressures: P1 is the lower pressure; P2 is the higher pressure. The numbers in parenthesis represent the sequential measurement periods. The top lines represent the fluid volume (Q [μl]) in the external reservoir. F represents outflow rate (μl/min). F1 = (Q1 at P1-Q2 at P1)/time [min]; F2 = (Q1 at P2-Q2 at P2)/time [min]; Q1 = Q at the beginning of the measurement; Q2 = Q at the end of the measurement. The dark areas between the dashed lines represent the equilibrium intervals during which the height of the external reservoir is switched and the outflow measurement is stopped.
Formula A:
Uncorrected CA = (F2-F1)/(P2-P1)
Corrected resistance = (1/uncorrected CA) - 0.058 Corrected CA = 1/corrected resistance
Formula B:
Uncorrected CB1 = F1/(P1 - Px)
Corrected resistance = (1/uncorrected CB1) - 0.058
Corrected CB1 = 1/corrected resistance
or
Uncorrected CB2= F2/(P2 - Px)
Corrected resistance = (1/uncorrected CB2) - 0.058
Corrected CB2 = 1/corrected resistancewhere CA is C (outflow facility; μl/min/mmHg) calculated by Formula A; CB1 or CB2 is C calculated by Formula B; 0.058 is the resistance (1/C) of the branched needle used to cannulate the eyes in living animals (the resistance is zero for the inflow through the ports of the organ culture). Px represents Pe (episcleral venous pressure) for the cultured eye (which is assumed to be zero) or represents P0 (spontaneous IOP) for the living eye (which is IOP at 5 min or more after AC cannulation with the external reservoir closed). The 1st CA, CB1 or CB2 was generated from period 1 and/or period 2. Following the 1st value, a new value for CA, CB1 or CB2 was generated every 8 min (excluding the equilibrium intervals) from the next 2 new periods. Note that CA was calculated per every 2 periods in this study in order to allow CA to be compared to CB1 or CB2. In standard C calculations for 2-level constant pressure perfusion, CA values are overlapping averages from 3 measurement periods as described previously (Tian and Kaufman, 2004).
C values for a given eye calculated by Formulas A and B or by Formula B with data obtained at P1 or P2 were quite different. These differences, including the differences between CA and CB1, CA and CB2, and CB1 and CB2, are defined as “ΔCs” in the following text. The corresponding ΔCs differed between eyes. Data in Figure 2, obtained from 2 eyes (Eye X and Eye Y; one each from two cynomolgus monkeys), represented two typical phenomena. In Figure 2a, F1 or F2 in Eye X is greater than that in Eye Y. However, in Figure 2b, CA in Eye X is smaller than that in Eye Y. If we calculate C with Formula B, the C value (e.g., CB1 or CB2) in Eye X becomes greater than or similar to that in Eye Y (Figure 2b). Additionally, CB1 is greater than CB2 in Eye X, but the difference is reversed in Eye Y. It is not quite clear what is responsible for the ΔCs. However, the following factors must be considered.
Figure 2.
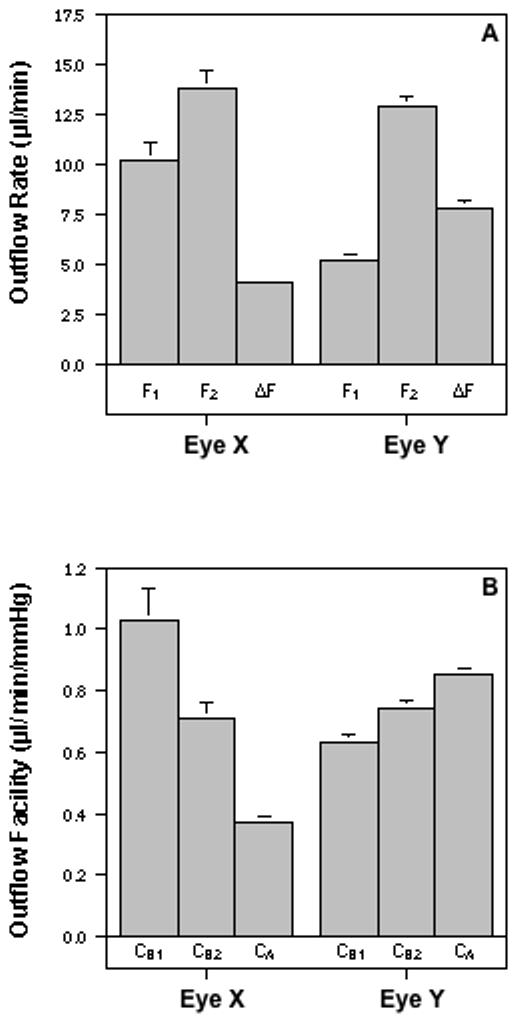
Effect of calculation method on the outflow facility value. Outflow was measured by 2-level constant pressure (15/25 mmHg) perfusion in 2 eyes (Eye X and Eye Y; one each from 2 monkeys). A. The change in flow rate (ΔF) for Eye X is less than for Eye Y even though the flow rates (F1 and F2) at the each of the two pressures (P1 and P2, respectively) are greater for Eye X than for Eye Y. B. Consequently, outflow facility (C) calculated by the two-level method (CA = (F2-F1)/(P2-P1)) is less for Eye X compared to Eye Y. However, C calculated by the one-level method (CB1=F1/[P1-P0] or CB2=F2/[P2-P0]) is greater than CA for Eye X and less than CA for Eye Y. Data, obtained from Eye X or Eye Y, are mean±s.e.m. (μl/min/mmHg for C or μl/min for F) from four to five values collected during a 36-min perfusion of each eye (not including the equilibrium intervals).
Generally, outflow is composed of pressure-sensitive and -insensitive components. In normal living monkeys, trabecular outflow is pressure sensitive and uveoscleral outflow is comparatively pressure-insensitive when IOP is greater than 7 to 10 mmHg (Bill, 1966; 1967). Although, under some circumstances, such as at low pressures (Bill, 1966; 1967), inflammation (Toris and Pederson, 1987), or perhaps after treatment with prostaglandins (Gabelt and Kaufman, 1989), uveoscleral outflow may not be completely pressure insensitive, pressure-insensitive outflow typically represents primarily uveoscleral outflow. During perfusions with living monkeys, the average P0 of pentobarbital-anesthetized monkeys is ∼7 mmHg (Erickson-Lamy et al., 1984). For some individual monkeys or monkeys that had drug-induced ocular hypotension, P0 could be as low as ∼3-5 mmHg (e.g., 2.5 mmHg for Eye X). Based on Bill’s studies (1966; 1967), when the pressure is elevated from P0 to P1 at the beginning of perfusion, uveoscleral outflow will increase pressure-dependently until the pressure reaches a specific point (e.g., 7 -10 mmHg). However, when the pressure is elevated from P1 to P2 during perfusion, the uveoscleral outflow will be no longer pressure sensitive. Therefore, the measured F during perfusion includes both trabecular (pressure-sensitive) and uveoscleral (pressure-insensitive) outflows.
The increased F following pressure elevation from P1 to P2 represents the pressure-sensitive outflow. The greater F (F1 or F2) and smaller difference between F1 and F2 (ΔF in Figure 2a) in Eye X compared to Eye Y indicates that the Eye X has greater pressure-insensitive outflow and smaller pressure-sensitive outflow (Figure 2a). Since pressure-insensitive outflow varies considerably from one animal to another (Bill, 1966), the proportion of pressure-insensitive outflow to total outflow may be different in different monkeys, especially when the monkeys are treated with different agents that may affect trabecular or uveoscleral outflow differently. Therefore, the different pressure-insensitive outflows in Eye X and Eye Y may be due to the fact that the eyes are from different monkeys, they have different P0 values during perfusion and/or they are affected by different treatments. However, for the purposes of the current discussion, we are not concerned with why the 2 eyes have different pressure-insensitive outflows, but rather whether the pressure-insensitive outflow is responsible for ΔCs.
Obviously, Formula A, but not Formula B, excludes the influence of pressure-insensitive outflow on C calculations. Therefore, ΔCs may be due to pressure-insensitive outflow, which is supported by the fact that the ΔCs in Eye Y, which has smaller pressure-insensitive outflow, are smaller than that in Eye X that has greater pressure-insensitive outflow. To further determine if the pressure-insensitive outflow is one of the factors accounting for ΔCs, we calculated C with Formula A and Formula B for the data from 7 monkey eyes that received pilocarpine before and/or during perfusion. Pilocarpine contracts the ciliary muscle, which “spreads” the trabecular meshwork (TM) and Schlemm’s canal by virtue of the muscle’s attachments to these tissues, and in turn increases trabecular outflow or pressure-sensitive outflow (Kaufman and Bárány, 1976). However, the pilocarpine-induced ciliary muscle contraction significantly blocks uveoscleral outflow or pressure-insensitive outflow (Bill and Wålinder, 1966). Therefore, the C calculation by either formula in the pilocarpine-treated eye will not be meaningfully affected by pressure-insensitive outflow. As shown in Figure 3, ΔCs in the pilocarpine-treated eyes are trivial (e.g., CA≈ CB2≈ CB1), which is generally similar to that found with Eye Y but not that with Eye X. This further indicates that pressure-insensitive outflow is one of factors accounting for ΔCs.
Figure 3.
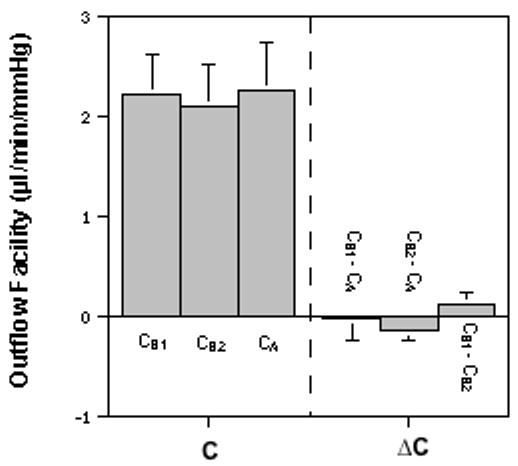
Effect of pilocarpine on calculated outflow facility (C) values. C was measured by 2-level constant pressure (P1/P2; 15/25 mmHg) perfusion in 7 eyes (one each from 7 monkeys) that received a bolus injection of 100μg pilocarpine (5 eyes) or AC exchange and continuous infusion of 400μM pilocarpine (2 eyes) before and/or during perfusion. In contrast to Figure 2, CA≈ CB2≈ CB1 in the pilocarpine-treated eyes, indicating that pressure-insensitive outflow is one of factors accounting for ΔCs. C = outflow facility (CA=[F2-F1]/[P2-P1]); CB1=F1/[P1-P0]; CB2=F2/[P2-P0]); ΔC = difference between Cs as indicated. Data are mean±s.e.m. (μl/min/mmHg) from overall values of 7 eyes. P=NS for difference ≠ 0.0 by the 2-tailed paired t-test.
Another factor that may account for ΔCs is pressure-dependent outflow obstruction. There is evidence that outflow resistance increases as a function of pressure in living animal eyes or enucleated human eyes (Moses, 1977). Van Buskirk (1982) found that pressure-dependent outflow obstruction was related to the collapse of Schlemm’s canal (SC) under pressure. Therefore, one may speculate that pilocarpine may also reduce ΔCs by preventing pressure-induced collapse of SC, similar to what was observed during the lens depression experiments by Van Buskirk (1982). However, Ye et al. (1997) have shown evidence that trabecular outflow resistance may decrease, rather than increase, with increasing pressure (see below). Therefore, further studies are needed to clarify this conflict.
Additionally, the measured F (the rate of fluid flow from the reservoir into the eye; e.g., F1 or F2) during perfusions in living animals does not include AHF. Since drug-induced changes in F are obtained by comparing Fs in contralateral eyes that are assumed to have similar and stable AHF, the lack of AHF in the measured F will not affect the final result. However, if any drug affects AHF unilaterally, the assumption above will be incorrect and the final results may be affected. For instance, during constant pressure perfusion, an increased AHF will result in less fluid flow from the external reservoir into the eye, while a decreased AHF will result in more fluid flow from the reservoir into the eye. In this situation, if C is calculated by Formula B that directly uses F1 or F2, the accuracy of the C value may be affected by the unilateral change in AHF.
Unlike Formula B, Formula A uses ΔF, and the effect of the unilateral change in AHF on F1 or F2 is excluded from the ΔF (assuming that the pressure-dependence of AHF [pseudofacility] and/or the drug-induced unilateral change in pseudofacility is negligible). In this situation, any unilateral change in AHF caused by an agent will not meaningfully affect the CA result in 2-level constant pressure perfusions. This, in conjunction with the fact that Formula A excludes the influence of the pressure-insensitive outflow on C calculations, suggests that 2-level constant pressure perfusion utilizing Formula A is a better technique to determine C in living animals. However, one should realize that CA is calculated based on pressure-sensitive outflow and that lack of an enhancement in CA cannot exclude the possibility of the increase in pressure-insensitive outflow. For instance, Eye X has smaller CA but greater total F than Eye Y as described above. Therefore, changes in total Fs should also be evaluated in this situation.
1.2. Cultured Anterior Segments
C in cultured anterior segments from enucleated eyes is usually determined by 1-level constant pressure perfusion (Erickson-Lamy et al., 1991) and/or by constant flow rate perfusion (Johnson and Tschumper, 1987). To make better comparisons with C in living animals, it may also be determined by 2-level constant pressure perfusion (Hu et al., 2006). In this section, we calculated some previous baseline data, obtained from 2-level constant pressure (∼7/17mmHg) perfusion in 8 cultured anterior segments from enucleated cynomolgus monkey eyes, with Formulas A and B (Figure 1). C values calculated by the two formulas in the cultured eye (CA<CB2<CB1; Figure 4) are similar to what happened in Eye X in vivo (Figure 2b). It is as yet unknown what is responsible for ΔCs in the cultured eye, but AHF and Pe or P0 can be excluded in any situations, because the cultured eye has no AHF and its Pe or P0 is zero.
Figure 4.
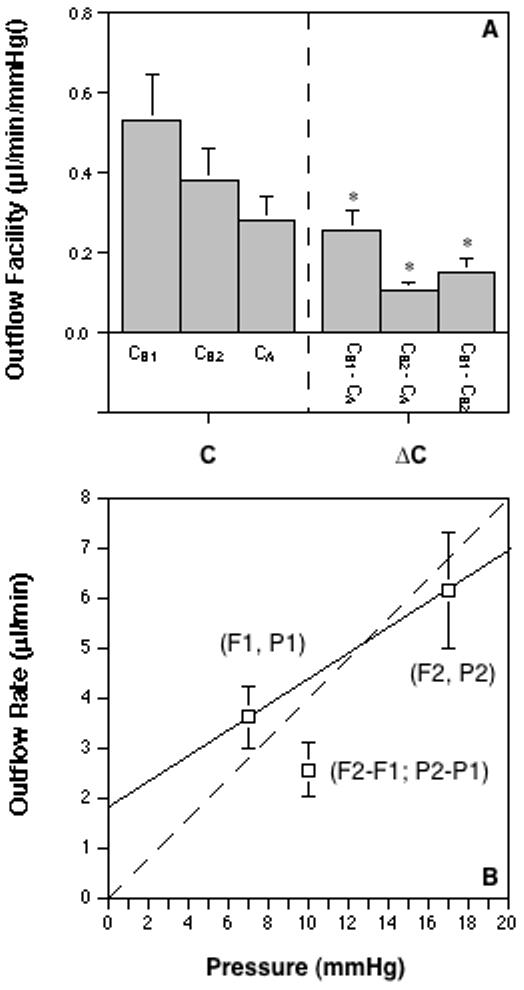
Outflow facility calculations based on monkey organ-cultured anterior segment data. A. Baseline outflow facility was measured by 2-level constant pressure (P1 or P2 = ∼7 or 17 mmHg) perfusion for 36 min (excluding equilibration time) in 8 cultured anterior segments from enucleated monkey eyes. Note that CA<CB2<CB1 in the cultured eye, which is similar to what happened in Eye X in vivo (Figure 2b). C = outflow facility (CA=[F2-F1]/[P2-P1]); CB1=F1/P1; CB2=F2/P2); ΔC = difference between Cs as indicated. Data are mean±s.e.m. (μl/min/mmHg). *P<0.005 for differences ≠ 0.0 by the 2-tailed paired t-test. B. The dashed line represents a theoretical linear relationship between F (outflow rate) and P (pressure). Any intersection of F and P on the dashed line except for the origin will have the same C value. Note that the coordinate for F1 and P1 lies above the dashed line and the coordinate for F2 and P2 or (F2-F1) and (P2-P1) lies below the dashed line, consistent with the relationship between corresponding C values (CA<CB2<CB1). The solid line, a secant between (F1, P1) and (F2, P2) that is not parallel to the dashed line, shows a positive y-intercept of F at pressure 0 and suggests a possible nonlinear relationship between F and P, which may explain ΔCs in the cultured eye.
As discussed in the section of living monkey eyes above, pressure-dependent outflow obstruction may also be a factor affecting C values in the cultured monkey eye (Brubaker, 1975). However, evidence has shown that trabecular resistance might decrease with increasing pressure, because the number and complexity of tight junctional strands in the inner wall of SC decreased and the inner-wall pore formation increased with increasing pressure in the enucleated human eye (Ye et al., 1997). Therefore, it is still not clear if pressure-dependent outflow obstruction in the enucleated human eye is due to a resistance increase in the trabecular drainage pathway. Dijkstra et al. (1996) reported that pressure-dependent outflow obstruction in the enucleated human eye could be due to a pressure-independent outflow shown as a positive y-intercept of the graph of IOP (x) vs F (y). The authors speculated that, although a systematic calibration error of the pressure transducer could result in a positive y-intercept, uveoscleral outflow might be the most likely factor. In the present monkey cultured anterior segment, uveal tissues are completely removed, so that the eye only has partial down-stream uveoscleral outflow routes (e.g., emissarial channels through the sclera). Since the most likely mechanism for pressure-insensitive uveoscleral outflow with increasing pressure may be related to the resistance increase within the ciliary muscle, the supraciliary tissue and the suprachoroid, and between the uveal tissues and the sclera (Bill, 2003), the “uveoscleral outflow” may no longer be pressure-insensitive in an anterior segment where the uvea is absent (Fatt and Hedbys, 1970). Additionally, the pressure-independent positive y-intercept can be excluded in 2-level constant pressure perfusion utilizing Formula A. Recent evidence shows that C, calculated by Formula A in 2-level constant pressure perfusion in the cultured eye, also decreases when pressure levels are elevated (Hu et al., 2006), which indicates that the positive y-intercept may not be the only factor accounting for ΔCs in the cultured eye.
2. Viscoelastic Response
Schlegel et al. (1972) found that the unpressurized enucleated intact human eye consistently showed a large viscoelastic response (stress relaxation) during perfusion, which increased the volume of the eye. A volume increase in the AC will allow some additional fluid to flow from the external reservoir into the eye during perfusion. This fluid flow will be included in the measured F if pressure increases during outflow measurement, but it will not leave the chamber. Therefore, it may be called “pseudo-outflow”. Although pre-equilibration may reduce the viscoelastic response, large changes in pressure after equilibration probably will trigger a new viscoelastic response (Schlegel et al., 1972). In our 2-level constant pressure perfusion, there is a 1 to 2-min interval between outflow measurements at alternate pressures (Figure 1). Since the resistance for inflow (fluid flow from the reservoir into the AC) is either very small or zero, the pressure change from one level to the other or the eye filling/excluding process will be completed within the 1 to 2-min equilibrium. Therefore, “pseudo-outflow” will be largely avoided. However, since the eye wall consists of viscoelastic material rather than elastic material, the strain on the tissue may reach its maximum at an elevated pressure later than the stress. Therefore, after the pressure becomes stable at a new level, the stretch of the eye wall may change a little further (Schlegel et al., 1972). It is unknown yet if this delayed extension-induced volume change of the eye will create an error during outflow measurement and how much, if any, the error will be.
Based on Laplace’s law, the greater the pressure gradient across the eye wall or the larger the radius of the globe, the greater the tissue tension; the thicker the eye wall, the less the tissue tension. Since the present cultured monkey anterior segment has no uveal tissues and, more importantly, since it has thinner sclera than the enucleated human eye, it may have greater tension on its wall than the enucleated intact human globe at a comparable IOP. Additionally, unlike the enucleated whole globe, the cultured anterior segment is an empty shell-like structure, so that its expansion will not be restrained by intraocular tissues. Therefore, although the total volume of the cultured monkey anterior segment is smaller than that of the enucleated whole human globe, the stretch-induced volume change in the former might still be sufficient to affect the C calculation. It is difficult to determine if viscoelastic response is also a factor affecting C calculations in living monkey eyes. The tonicity of the ciliary muscle in a living eye, especially resulting from pilocarpine-induced contraction, may act as an interior force against eye wall expansion. The tonicity of extraocular muscles may act as an exterior force against the eye wall expansion. Also, the orbital pressure of the living eye (3-6 mmHg)(Kratky et al., 1990) may render the pressure gradient across the eye wall in the living eye smaller than that in the enucleated whole eye or the cultured anterior segment at a comparable IOP. Most importantly, the eye wall under physiological conditions may be stronger than that under cultured conditions, especially after several days in culture. A possible redistribution of elastin and collagen in organ cultures will increase the maximal value of tissue distensibility and shift the distensibility peak to lower pressures (Montorzi et al., 2004). All these suggest that the living eye might have less viscoelastic response than the cultured eyes. Further studies are needed to clarify these issues.
3. Summary
Outflow facility (C) values determined by different perfusion techniques and methods of calculation were compared in order to clarify factors accounting for differences between the C values. Outflow data obtained by 2-level constant pressure perfusion in living monkeys or cultured monkey anterior segments were recalculated with formulas utilized in 2-level constant pressure perfusion and 1-level constant pressure or constant rate perfusion studies. Results for both the living monkey eye and the cultured monkey anterior segment showed that C values for a given eye and experimental session were quite different when calculated with the 2 different sets of formulas. The results suggest that the major factor accounting for the difference between the C values in living monkeys is pressure-insensitive or uveoscleral outflow. However, it is not quite clear what is responsible for the difference in cultured anterior segments lacking a uvea. Outflow through the emissarial channels in the sclera in the cultured anterior segment may not affect C values in the same way as uveoscleral outflow because the former may no longer be pressure-insensitive. Viscoelasticity is a potential factor that may affect C measurements in cultured segments more so than in the live monkey eye. Additionally, pressure-dependent outflow obstruction may be a factor affecting C values. This study supports the concept that 2-level constant pressure perfusion of the living monkey eye determines C resulting from pressure-sensitive outflow but not that related to pressure-insensitive outflow. Total outflow rate is a useful indicator for evaluating pressure-insensitive outflow during 2-level constant pressure perfusion in living monkeys. Proper equilibration and avoidance of high pressures are important for minimizing potential effects of viscoelasticity on C measurements during perfusions with organ cultured anterior segments. All these concepts should be taken into consideration when comparing C values obtained using different perfusion techniques.
Acknowledgements
This study was supported by grants from the NIH National Eye Institute (EY02698), Bethesda, MD; Glaucoma Research Foundation, San Francisco, CA; Research to Prevent Blindness, New York, NY; Ocular Physiology Research & Education Foundation, Madison, WI, and Allergan, Inc., Irvine, CA. Authors thank Dr. Ross Ethier for his thoughtful comments.
Footnotes
Address correspondence to: Dr. Baohe Tian, Department of Ophthalmology & Visual Sciences, University of Wisconsin-Madison, F4/319 CSC, 600 Highland Ave., Madison, WI 53792-3220, USA. E-mail Address: btian@wisc.edu
References
- Bárány EH. Simultaneous measurement of changing intraocular pressure and outflow facility in the vervet monkey by constant pressure infusion. Invest. Ophthalmol. 1964;3:135–143. [PubMed] [Google Scholar]
- Bárány EH. In: Rohen JW, editor. Relative importance of autonomic nervous tone and structure as determinants of outflow resistance in normal monkey eyes (Cercopithecus ethiops and Macaca irus); The Structure of the Eye, Second Symposium.. FK Schattauer Verlag, Stuttgart. 1965. pp. 223–236. [Google Scholar]
- Bill A. Conventional and uveo-scleral drainage of aqueous humor in the cynomolgus monkey (Macaca irus) at normal and high intraocular pressures. Exp. Eye Res. 1966;5:45–54. doi: 10.1016/s0014-4835(66)80019-2. [DOI] [PubMed] [Google Scholar]
- Bill A. Further studies on the influence of the intraocular pressure on aqueous humor dynamics in cynomolgus monkeys. Invest. Ophthalmol. 1967;6:364–372. [Google Scholar]
- Bill A. Some thoughts on the pressure dependence of uveoscleral flow. J. Glaucoma. 2003;12:88–89. doi: 10.1097/00061198-200302000-00017. [DOI] [PubMed] [Google Scholar]
- Bill A, Wålinder P-E. The effects of pilocarpine on the dynamics of aqueous humor in a primate (Macaca irus) Invest. Ophthalmol. 1966;5:170–175. [Google Scholar]
- Brubaker RF. The effect of intraocular pressure on conventional outflow resistance in the enucleated human eye. Invest. Ophthalmol. 1975;14:286–292. [PubMed] [Google Scholar]
- Erickson-Lamy K, Kaufman PL, McDermott ML, France NK. Comparative anesthetic effects on aqueous humor dynamics in the cynomolgus monkey. Arch. Ophthalmol. 1984;102:1815–1820. doi: 10.1001/archopht.1984.01040031473026. [DOI] [PubMed] [Google Scholar]
- Erickson-Lamy K, Rohen JW, Grant WM. Outflow facility studies in the perfused human ocular anterior segment. Exp. Eye Res. 1991;52:723–731. doi: 10.1016/0014-4835(91)90024-9. [DOI] [PubMed] [Google Scholar]
- Fatt I, Hedbys BO. Flow of water in the sclera. Exp. Eye Res. 1970;10:243–249. doi: 10.1016/s0014-4835(70)80035-5. [DOI] [PubMed] [Google Scholar]
- Gabelt BT, Kaufman PL. Prostaglandin F2a increases uveoscleral outflow in the cynomolgus monkey. Exp. Eye Res. 1989;49:389–402. doi: 10.1016/0014-4835(89)90049-3. [DOI] [PubMed] [Google Scholar]
- Hu Y, Gabelt BT, Kaufman PL. Monkey organ-cultured anterior segments: Technique and response to H-7. Exp. Eye Res. 2006;82:1100–1108. doi: 10.1016/j.exer.2005.12.004. [DOI] [PubMed] [Google Scholar]
- Johnson DH, Tschumper RC. Human trabecular meshwork organ culture: a new model. Invest. Ophthalmol. Vis. Sci. 1987;28:945–953. [PubMed] [Google Scholar]
- Kaufman PL, Bárány EH. Loss of acute pilocarpine effect on outflow facility following surgical disinsertion and retrodisplacement of the ciliary muscle from the scleral spur in the cynomolgus monkey. Invest. Ophthalmol. 1976;15:793–807. [PubMed] [Google Scholar]
- Kratky V, Hurwitz JJ, Avram DR. Orbital compartment syndrome. Direct measurement of orbital tissue pressure: 1. Technique. Canadian J. Ophthalmol. 1990;25:293–297. [PubMed] [Google Scholar]
- Montorzi G, Silacci P, Zulliger M, Stergiopulos N. Functional, mechanical and geometrical adaptation of the arterial wall of a non-axisymmetric artery in vitro. J. Hypertension. 2004;22:339–347. doi: 10.1097/00004872-200402000-00018. [DOI] [PubMed] [Google Scholar]
- Moses RA. The effect of intraocular pressure on resistance to outflow. Surv. Ophthalmol. 1977;22:88–100. doi: 10.1016/0039-6257(77)90088-1. [DOI] [PubMed] [Google Scholar]
- Schlegel WA, Lawrence C, Staberg LG. Viscoelastic response in the enucleated human eye. Invest. Ophthalmol. 1972;11:593–599. [PubMed] [Google Scholar]
- Tian B, Kaufman PL. Effects of the rho kinase inhibitor Y-27632 and the phosphatase inhibitor calyculin A on outflow facility in monkeys. Exp. Eye Res. 2005;80:215–225. doi: 10.1016/j.exer.2004.09.002. [DOI] [PubMed] [Google Scholar]
- Toris CB, Pederson JE. Aqueous humor dynamics in experimental iridocyclitis. Invest. Ophthalmol. Vis. Sci. 1987;28:477–481. [PubMed] [Google Scholar]
- Van Buskirk EM. Anatomic correlates of changing aqueous outflow facility in excised human eyes. Invest. Ophthalmol. Vis. Sci. 1982;22:625–632. [PubMed] [Google Scholar]
- Ye W, Gong H, Sit A, Johnson M, Freddo TF. Interendothelial junctions in normal human Schlemm’s canal respond to changes in pressure. Invest. Ophthalmol. Vis. Sci. 1997;38:2460–2468. [PubMed] [Google Scholar]