Electron Paramagnetic Resonance Oximetry as a Quantitative Method to Measure Cellular Respiration: A Consideration of Oxygen Diffusion Interference

Abstract

Electron paramagnetic resonance (EPR) oximetry is being widely used to measure the oxygen consumption of cells, mitochondria, and submitochondrial particles. However, further improvement of this technique, in terms of data analysis, is required to use it as a quantitative tool. Here, we present a new approach for quantitative analysis of cellular respiration using EPR oximetry. The course of oxygen consumption by cells in suspension has been observed to have three distinct zones: pO₂-independent respiration at higher pO₂ ranges, pO₂-dependent respiration at low pO₂ ranges, and a static equilibrium with no change in pO₂ at very low pO₂ values. The approach here enables one to comprehensively analyze all of the three zones together—where the progression of O₂ diffusion zones around each cell, their overlap within time, and their potential impact on the measured pO₂ data are considered. The obtained results agree with previously established methods such as high-resolution respirometry measurements. Additionally, it is also demonstrated how the diffusion limitations can depend on cell density and consumption rate. In conclusion, the new approach establishes a more accurate and meaningful model to evaluate the EPR oximetry data on cellular respiration to quantify related parameters using EPR oximetry.

INTRODUCTION

Traditionally, the respiration of cells and cellular components has been determined using polarographic techniques, which use the Clark-type electrode to measure oxygen concentrations. Specifically, the OROBOROS Oxygraph is unique for high-resolution respirometry (HRR) to evaluate mitochondrial function in health and disease, in mitochondrial physiology and pathology, and in the respiration of mitochondria. Respirometry has been used in a variety of applications to monitor oxygen at the extremes of intracellular oxygen limitations to acquire oxygen kinetics (1,2). One primary limitation of this method is the large amount of sample needed, which is typically 2–5 ml. Moreover, additional drawbacks include insensitivity in low pO₂ ranges and the electrode may consume oxygen, causing the repeated measurements of pO₂ to be problematic (2). This technique is suitable in the pO₂ range of 10–100 mmHg but imposes problems with concentrations that deviate beyond this range. As a result, alternatives to this method are being utilized that can provide more sensitivity and accuracy. Magnetic field based methods such as electron paramagnetic resonance (EPR) oximetry (3–5), dynamic nuclear polarization (DNP) based oximetry (6,7), and NMR oximetry (8,9) are currently used as viable alternative methods.

The EPR oximetry technique is based on the paramagnetic distinctiveness of molecular oxygen (10). Using a small amount of sample (∼10 μl), it allows one to determine molecular oxygen from the oxygen-induced EPR line broadening of a suitable paramagnetic probe such as lithium phthalocyanine (LiPc), nitroxides, lithium octa-n-butoxy-substituted naphthalocyanine (LiNc-BuO), etc. (3,11,12). The origin of this technique was based on the principle of the Heisenburg spin-spin interaction between the molecular oxygen and another spin probe. This spin-spin interaction between the molecular oxygen and the spin probe will shorten the relaxation time of the spin probe, causing an increase in the peak-to-peak width in the first derivative EPR spectrum. The line widths of the EPR spectra correlate with oxygen concentrations for soluble probes and pO₂ for particulate probes such as LiPc (13). EPR oximetry can provide real-time, noninvasive, as well as nonperturbing measurements of oxygen. It is distinctive in its potential for high sensitivity in local oxygen measurements (14–17).

When it was first introduced for oxygen measurements, several advantages of this method were highlighted including: the fact that the cells and the spin probe(s) are homogenously distributed throughout the sample tubes and the spin probes do not consume oxygen, allowing low concentrations of O₂ in solutions to be measured (17). To date, this method has been shown to be a useful tool for accurate, repeated measurements of local concentrations of molecular oxygen in the ischemic heart, tumors, cerebral interstitial regions of the brain, and in cell suspensions (4,15,18). When considering accurate EPR oximetry measurements, careful planning is necessary to select the most suitable probe. Both soluble nitroxide-based oximetric probes and insoluble particulate-based probes can be used. A limitation with the soluble nitroxides is that these probes are susceptible to cellular reduction and a progressive decay in signal intensity with time during measurements (19). Although signal intensity is not a major limitation in EPR oximetry where only the line width is used to measure oxygen concentrations, the redox reactions may change the redox equivalence in cells and may even alter the respiration. On the other hand, particulate probes such as LiPc (11,18), chars (20,21), LiNc, and its derivatives (3,22,23) are inert and noninteractive with cells, allowing them to be useful for oxygen measurements. Specifically, LiPc is stable in tissues for extended periods of time. It is insoluble in aqueous solvents and enables high resolution pO₂ measurements in tissues (11,14,15). Typically, the response of the LiPc line shape to pO₂ is not altered under various environments such as pH, temperature, redox conditions, etc. However, the oxygen sensitivity may change or even be lost in some tissues (24,25).

Several studies have demonstrated that the oxygen consumption rate in cellular respiration can be measured using particulate probes such as LiPc in EPR oximetry (3,17,18). Typically, EPR oximetry measurements are performed for a short period of time, where a linear variation of pO₂ with time is observed. The slope of that region is used to quantify the oxygen consumption rate (3). However through other techniques, it is known that there are three distinct phases of cellular respiration (2). Thus far, it has not been established whether EPR oximetry is capable of distinguishing these phases. This is partially due to a lack of proper models to interpret the EPR oximetry data. This poses a serious limitation in applying this technique and extracting meaningful respiration parameters. A major problem in this technique is the O₂ concentration gradient from the cell surface to the bulk (surrounding medium). During EPR oximetry measurements, the sample is kept stationary, which causes oxygen diffusion zones to form as the oxygen is depleted by the respiration. In this work, a new procedure to analyze EPR oximetry data is used where we demonstrate that these diffusion zones have considerable implications for the measured data. Also, we demonstrate that by correcting the diffusion impacts of oxygen, one can extract more significant results.

MATERIALS AND METHODS

Rotenone, stigmatellin, dilithium phthalocyanine (Li₂Pc), and acetonitrile were obtained from Sigma-Aldrich (St. Louis, MO). Tetrabutyl ammonium perchlorate was purchased from ICN Biochemicals (Aurora, OH).

Cell culture

Bovine aortic endothelial cells (BAECs) were obtained from Cell Systems (Kirkland, WA). The BAECs were cultured in CS-C Complete medium (Cell Systems). The growth medium contained JetFuel formulated with growth factor, 10% serum, and antibiotic (gentamycin sulfate). Cells were grown in regular 150-cm² culture dishes coated with attachment factor. Cells were trypsinized and used in experiments when the cultures reached 80–90% confluence.

Cell viability

The cell viability was determined by a NucleoCounter system (New Brunswick Scientific, Edison, NJ) comprising the NucleoCounter automatic cell counter, the NucleoCassette, a cell preparation lysing buffer and a stabilizing buffer, and NucleoView software. Two aliquots of the cell suspension, for nonviable count and the total cell count, were taken. For the total cell count, an equal amount of the lysing buffer and the stabilizing buffer were added to the cell suspension. Each sample was loaded into the NucleoCassette and placed into the NucleoCounter cell counter for analysis. The nonviable count was determined first, followed by the total cell count. Using the NucleoView software, the nonviable, total cell count, viable cell count, and viability were determined.

Oximetry probe

For oximetry measurements, we have used ∼20–30 μm LiPc microcrystals as the oximetry probe. Since the LiPc microcrystals were comparatively larger in the oximetry measurements, the particulates remained in the bulk volume and there was no ingestion by the cells. The probe was synthesized electrochemically, using the established procedure (26). The synthesized microcrystals were subjected to various physicochemical characterizations such as x-ray diffraction (XRD), EPR, microscopy, etc. to ensure the purity of the obtained material. These microcrystals were found to be in the pure λ isoform (or equivalently known as x form), which has been characterized to yield a pO₂-dependent EPR line width.

Measurement of cellular respiration

The oxygen measurements in this study were performed using EPR oximetry (11,14). The EPR line width versus pO₂ calibration curve was constructed using known ratios of premixed O₂ and N₂ gases. The slope of the calibration curve was 5.8 mG/mmHg. Although this calibration curve was constructed using gas mixtures, we have previously demonstrated that this curve is applicable in aqueous solutions as well (11). Thus, by measuring the EPR line width, the pO₂ in the solution can be obtained at any given time.

EPR oximetry experimental setup

The respiration studies have been carried out using an X-band (9.7 GHz) EPR spectrometer, fitted with a TM₁₁₀ microwave cavity. A 50-μl microcapillary tube was used to hold the cells in the horizontal EPR cavity. In a typical experiment, the cell suspension of the required cell density was saturated with room air (pO₂ ≈ 160 mmHg). The cell suspension was incubated for 10 min in a 37°C water bath, and 20 μg of LiPc microcrystals were added to the cells and sampled into 50-μl capillary tubes. The tube was then closed off at both ends using tube sealing clay (Chase Scientific Glass, Rockwood, TN). While sealing, care was taken to ensure that there were no air gaps present inside the tube since such a gap may act as an additional O₂ source. The tube was placed inside the horizontal microwave cavity, and EPR spectral acquisitions of the LiPc were immediately started. During measurements, the modulation amplitude was adjusted to always be less than one third of the line width to avoid modulation-induced broadening. From the EPR line width, the pO₂ in the cell suspension was determined using the standard curve.

Experimental protocol for drug treatments

For each drug treatment, the appropriate concentrations of rotenone (20 μM) or stigmatellin (20 μM) were added to the cell culture and incubated for 30 min. The cells were trypsinized and isolated for respiration measurements. At the time of measurements, cell suspensions with the appropriate concentrations of each drug were incubated at 37°C in a water bath for 10 min and then drawn into the glass capillary tubes for oxygen measurements. The cell densities in this study are expressed as the viable cell counts per milliliter, estimated after the addition of the drug.

Curvefit and data analysis

The EPR spectra, collected during the cellular respiration measurements, were analyzed by fitting the spectral data into a Lorentzian line shape by a least-squares algorithm, using custom-designed software. The correlation coefficient of 0.99 was set as the standard of acceptance of the results. The decrease in pO₂ data was converted into the rate of oxygen depletion by using four-point piecewise differentiation with respect to time. The four-point differentiation was performed using MATLAB 6.1 (The MathWorks, Natick, MA). The simulations and curve fit of the experimental data were carried out using MATLAB 6.1 Curvefit PC (The MathWorks). Data are presented as mean ± SD. Statistical analysis was performed using Student's t-test and one-way ANOVA. The general acceptance level of significance was P < 0.05.

RESULTS

EPR oximetry for cellular respiration: uncharacteristic features

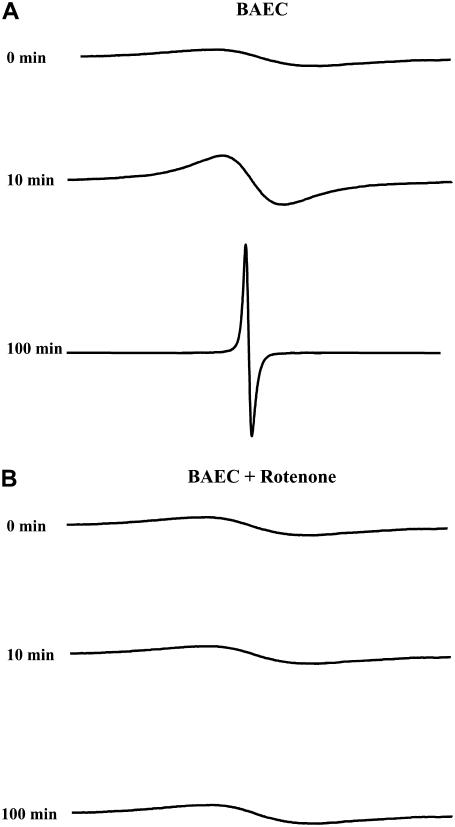
EPR spectra of the suspension of LiPc microcrystals and cells were collected for up to 160 min. As the time increased, the EPR line width decreased due to a continuous depletion of oxygen by the cells, as shown in Fig. 1. The spectra were collected until the line width reached a constant low value of ∼30 mG. To ensure that the oxygen depletion being measured was associated with the mitochondrial respiration, mitochondrial electron transport chain (ETC), inhibitors were used to display their effect on cellular respiration. Rotenone is a complex I blocker, which augments electron leakage from the ETC, and stigmatellin is a complex III inhibitor. Fig. 1 also shows the EPR spectra acquired for ∼2 h in the presence of rotenone (20 μM); stigmatellin (20 μM) had similar results (spectra not shown). In the case of the ETC blockers, there was no significant change in the EPR spectra, suggesting that the oxygen consumption by the cells is inhibited by these agents (Table 1). Within 60 min, there was only an approximate decrease of 10 mmHg for each inhibitor. Thus, it is confirmed that the oxygen consumption measured by EPR oximetry is essentially due to mitochondrial respiration.

FIGURE 1.

EPR spectra for respiration measurements. (A) EPR spectra obtained for LiPc in 50 μl of 5 × 10⁶ cell suspension at various time points. With time, the EPR spectrum narrows down due to the continued depletion of oxygen in the air-tight microtube. (B) Similar to panel A, but with the addition of 20 μM of rotenone. The addition of this ETC inhibitor abolished such a narrowing down.

TABLE 1.

Quantitative analyses of cellular respiration measured by EPR oximetry

		Without O2 diffusion consideration†				With O2 diffusion consideration‡
Cell density (mill/ml)	VO2max* (mmHg/min)	VO2max (mmHg/min)	p50 (mmHg)	p0 (mmHg)	Oxygen affinity (mmHg−1)	VO2max (mmHg/min)	p50 (mmHg)	p0 (mmHg)	Oxygen affinity (mmHg−1)	n
2	1.09 ± 0.10	0.97 ± 0.11	2.34 ± 0.58	0.94 ± 0.14	0.48 ± 0.11	0.95 ± 0.11	1.15 ± 0.24	0.39 ± 0.04	0.96 ± 0.22	3
3	1.47 ± 0.11	1.51 ± 0.09	3.79 ± 0.28	1.11 ± 0.41	0.27 ± 0.02	1.48 ± 0.09	1.85 ± 0.16	0.47 ± 0.18	0.55 ± 0.05	3
5	3.01 ± 0.13	3.82 ± 0.46	5.26 ± 0.60	0.89 ± 0.10	0.20 ± 0.02	3.74 ± 0.46	2.55 ± 0.27	0.36 ± 0.05	0.40 ± 0.04	4
5 +Rotenone	0.32 ± 0.10	−	−	−	−	−	−	−	−	4
5+Stigmatellin	0.21 ± 0.02	−	−	−	−	−	−	−	−	3

The parameters were determined using three different approaches.

^*From the slopes of the linear region of pO₂ versus time plots.

^†Using Eq. 1.

^‡Using Eq. 7; at 1/p50, defined as the oxygen affinity to cytochrome c oxidase of the ETC.

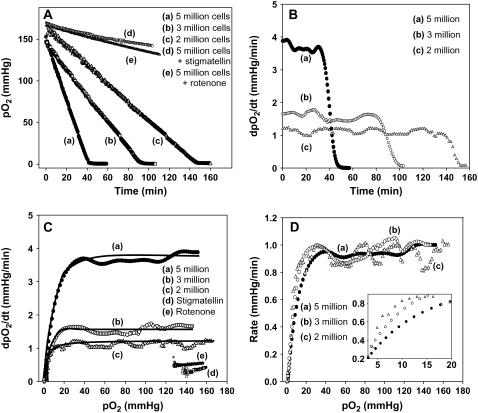
Upon obtaining the EPR spectra, the spectra were analyzed and transformed into pO₂ versus time data using the standard calibration curve, which was constructed using the customary procedure as reported before (11). The obtained results are presented in Fig. 2 A as a function of time for three different cell densities (as well as the ETC inhibitors). In each of the cell density plots, there are three distinctly different regions, namely a linear portion, a curved portion, and a region with no change in pO₂ with time. The slope of the linear region is a measure of the initial rate of O₂ consumption and it represents the pO₂-independent consumption rate. As illustrated in Fig. 2, B and C, the pO₂ versus time data can be converted into rate of depletion (derivative with respect to time; dpO₂/dt) and plotted as a function of time and pO₂, respectively. From Fig. 2, A and C, it is clear that cellular respiration has three different phases: 1) pO₂-independent respiration at high [O₂] concentrations, 2) pO₂-dependent respiration at intermediate concentrations, and 3) cessation of respiration after very low [O₂], where equilibrium is established within the mitochondria (21). This type of behavior has been previously reported in the respiration measurements carried out by HRR methods (2,27). For the first time, we demonstrate that three distinct levels of respiration can be obtained using EPR oximetry.

FIGURE 2.

Respiration of BAECs measured by EPR oximetry. EPR spectra were collected from the cell suspension of various cell densities as displayed in the figure. (A) Change in pO₂ with time for various cell densities and ETC inhibitors, rotenone, and stigmatellin. For a low number of cells, the rate of oxygen consumption was longer. (B) Rate of O₂ depletion with time for various cell densities. (C) Rate of O₂ depletion with pO₂ for various cell densities and ETC inhibitors. The rate of O₂ depletion increased as the cell density enhanced and the ETC blockers greatly attenuated the respiration. Data in the plots were analyzed using Eq. 1 to calculate V_O2max, p₀, and p50. The solid lines in the figure are actual fits (with respect to V_O2max) of the respective data to Eq. 1. In all three cases, R² = 0.98. (D) Normalized plot (with respect to V_O2max) of all cell densities from a single experiment. (Inset) Magnified view of the low pO₂ region, demonstrating that there is a distinct shift in the p50 between the cell densities.

The analysis of data to quantify the relevant parameters was performed using the same approach applied to HRR methods. Each of the three phases can be analyzed from a single run of pO₂-time, using EPR oximetry and adopting the following equation, demonstrated for HRR (2):

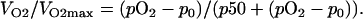(1)

In the above equation, V_O2 is the oxygen consumption rate at a given pO₂, V_O2max is the maximum oxygen consumption rate (steady state), p50 is the concentration at which the V_O2max is reduced to 50%, and the p₀ is the equilibrium pO₂ where pO₂ is very low. The p50 [O₂] is analogous to the K_m values in purified enzymatic reactions. It is an inverse of a measure of the oxygen affinity to cytochrome c oxidase in complex IV of the mitochondrial ETC (28); therefore, the lower the p50, the greater the oxygen affinity.

The data in Fig. 2 C were fit to Eq. 1 and the parameters V_O2max, p50, and p₀ were determined (Table 1). By utilizing the above equation, we were able to quantify levels of respiration for various cell densities. Based on the data we acquired, we noticed considerable differences in comparison to previously reported respiration data. The V_O2max, determined from this approach, agree with the values determined from the slopes of the linear portion. However, although the V_O2max values were comparable to the reported values (2,27), the p50 values were unusually higher in each of the cell densities used. For example, the p50 for human umbilical vein endothelial cells and human neuroblastoma cells has been determined to be 0.6 mmHg and 0.8 mmHg, respectively, for 1.5 million cells (27,29). Also, the p50 for heart mitochondria is 0.26 mmHg, and liver mitochondria have been stated to be 0.43 mmHg (28). Moreover, the oxygen affinity measured in this work has shown a strong dependence on the cell densities used as shown in Table 1 and Fig. 2 D. These two discrepancies illustrate the need for the refinement of Eq. 1 to be suitable for EPR oximetry.

A diffusion model for oxygen consumption in EPR oximetry

One important difference in the case of EPR oximetry compared to respirometry methods is the mass transport limitation in EPR oximetry. In HRR methods, constant stirring of the solution is applied. Thus Eq. 1, originally developed for HRR, does not include any mass transfer rate limitation. However, in the case of EPR oximetry, such stirring is not possible and hence, the mass transport may limit the availability of oxygen near the cell surface. Thus, the above model needs to be modified accordingly to take the O₂ diffusion into account.

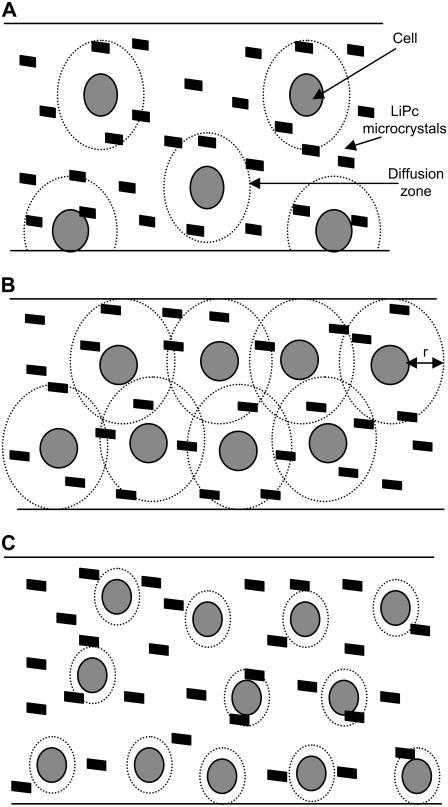
Fig. 3 illustrates the phenomenological conception of the oxygen diffusion limitation. Three different scenarios are depicted in Fig. 3. Fig. 3 A illustrates a condition of low cell density with a higher consumption rate. Thus, diffusion zones develop, but the effective overlap of diffusion zones is negligible. As the time increases, a concentration gradient is developed from the cell surface to bulk, establishing a diffusion zone with radius, r, which increases with time and radial velocity, δ_t, as defined below (30):

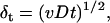(2)

where v is rate of O₂ consumption and D is the diffusion coefficient. As the time increases, the diffusion zone in the spherical shape increases. Thus, the area under such a sphere (A = 4/3πr³) can be defined as follows:

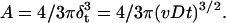(3)

FIGURE 3.

Schematic illustration of the development of diffusion zones and their overlap in LiPc-containing cell suspension in a microtube. (A) Low density of cells in solution with diffusion zones. (B) High density of cells in solution with diffusion zones. (C) High density of cells with less consumption rate. At low cell densities, although the diffusion zones develop, the effective overlap is not appreciable. On the other hand, when the cell density is higher, as shown in panel B, the diffusion zones develop and effectively overlap. In another situation where the cell density is high but the consumption rate is low, the effective overlap of the diffusion zones is once again less, as shown in panel C. These conditions illustrate that the respiration parameters such as oxygen affinity could heavily depend upon the rate and the cell density being used.

The total volume, θ_ex, covered by such diffusion zones is then defined by including the number of cells (N):

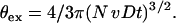(4)

The θ_ex is the fraction of volume covered under the diffusion zones, assuming no overlap is occurring. However, when the cell density is considerably high and/or the rate of consumption is elevated, the diffusion zones develop very fast and these zones overlap, as illustrated in Fig. 3 B. Under such circumstances, the volume under diffusion control can be defined by the Avrami theorem (31) as follows:

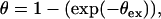(5)

so that Eq. 5 becomes

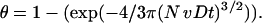(6)

Under these conditions, the radial flux of the oxygen delivered to the cell surface is limited by the linear diffusion of O₂. The conservation of mass in the diffusion zones implies that the amount of oxygen coming into the diffusion zone is consumed by the cell, causing the consumption rate to be dependent on the diffusion rate. Thus, Eq. 1 can be modified, taking into consideration θ, as:

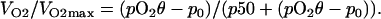(7)

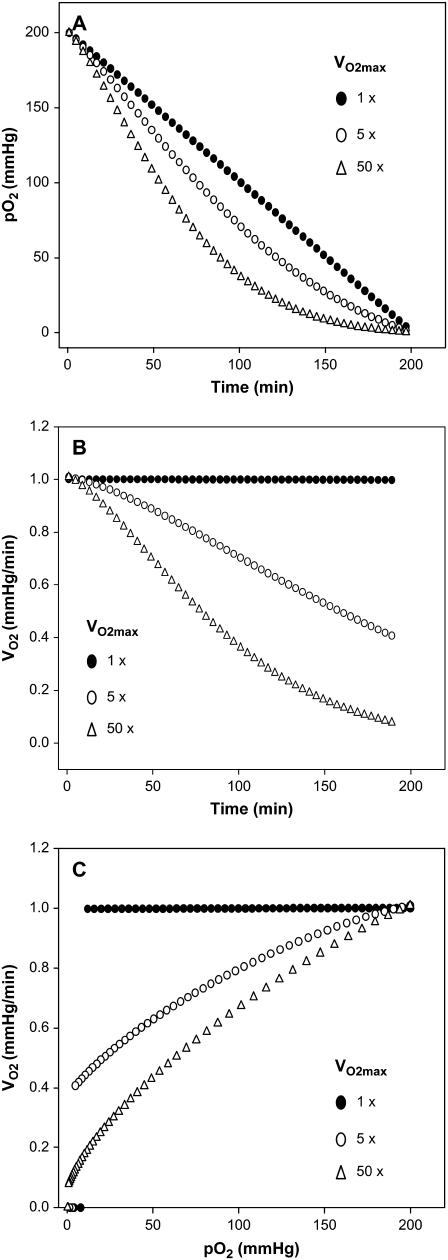
After the appropriate modifications, Eq. 7 was used to simulate normalized pO₂ versus time curves for various V_O2max values. Fig. 4 A shows the effect of V_O2max on the change of pO₂ with time. It can be seen that the increase in the V_O2max changes the shape of the pO₂ versus time curve. At very low V_O2max values, a linear variation in pO₂ is observed, whereas at high V_O2max values a curve is shown. Similarly, an increase in the N value also alters the consumption rate (data not included) because it is directly related to θ. The dependence on θ is better illustrated when these plots are converted into rate versus time plots as shown in Fig. 4 B. As noticed in Fig. 4 B, the consumption rate remains relatively constant when the V_O2max is low—even at longer periods of time. However, when V_O2max is high, the rate decreases with time, clearly demonstrating the V_O2max-dependent consumption rate with respect to time. When compared to HRR, such reliance is not expected because there is no diffusional impact; thus, it is associated with EPR oximetry and other magnetic resonance based oximetry techniques where stirring is not applied. Furthermore, the dependence of V_O2max on pO₂ was also demonstrated as shown in Fig. 4 C. At low V_O2max values, the rate remains the same at low pO₂ ranges. However at high V_O2max values, the rate decreases as the pO₂ decreases. An important implication of this result is that the p50 (and the oxygen affinity to complex IV of ETC) is indirectly associated with the V_O2max, as illustrated in Fig. 4 C. The dependence is uniquely due to the diffusion limitation with EPR oximetry, unlike the polarographic methods where this effect is removed by effective stirring.

FIGURE 4.

Simulation of respiration data using the proposed diffusion model for EPR oximetry. (A) Simulation of the normalized pO₂ with time for various V_O2max, using Eq. 7, (B) Conversion of pO₂ data of panel A into rate of O₂ consumption versus time at various V_O2max values. (C) Rate of O₂ consumption with pO₂. The trends presented in these plots are similar to the measured data, indicating that the proposed model describes the system exactly.

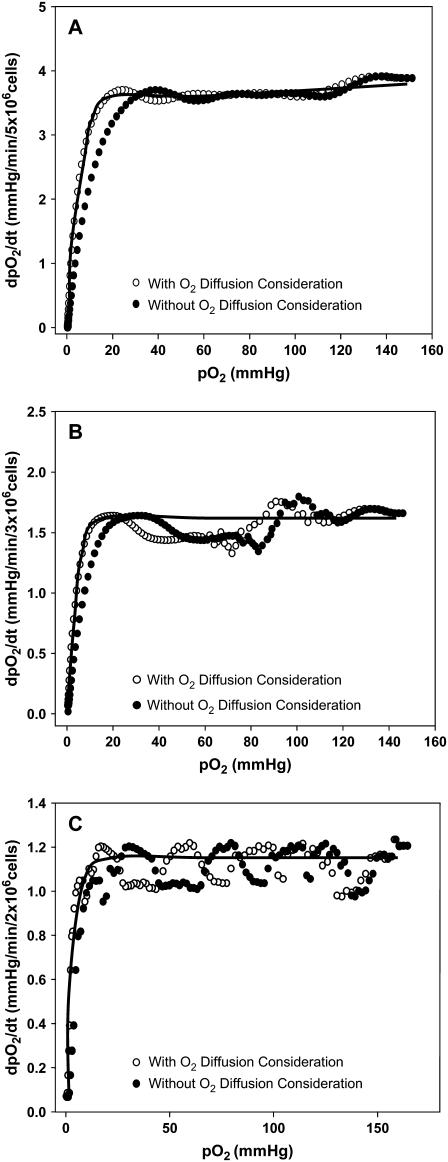
Upon modifying Eq. 1, the experimental data obtained in this work with EPR oximetry were fitted with the new expression, Eq. 7, and the obtained results are summarized in Table 1. The new values from the pO₂ versus time plot were converted into the dpO₂/dt versus pO₂ plot as previously performed with the original expression (Fig. 5). Based on the fit, where R² ≈ 0.98 in all cases, the new values for the p50, V_O2max, and p₀ were acquired. The V_O2max, determined from the new approach at all cell densities, was not significantly different from the values determined either from the slope or from the initial method of fit. However, there was a significant change in p50 and hence the mitochondrial oxygen affinity (Table 1).

FIGURE 5.

Determination of respiration parameters using the initial and the corrected approaches for various cell densities. The respiration data (•) measured for various cell densities were fit with Eq. 1, and the parameters were determined and summarized in Table 1. The same data were corrected for θ (○), using Eq. 7, and the fitted parameter estimations are also summarized in Table 1; (A) 5 million cells, (B) 3 million cells, (C) 2 million cells. The solid line in each of these figures is the actual fit using Eq. 7 with R² = 0.98. At low pO₂ values, there is a leftward shift in the initial model in comparison to the corrected approach, corresponding to a decrease in the p50 value. This shift is larger in higher cell densities.

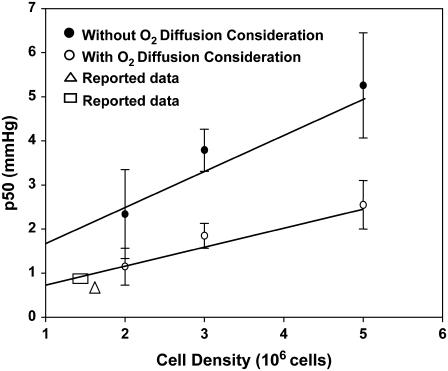
From Table 1 and Fig. 6 (n = 3 for 2 million cells, n = 3 for 3 million cells, and n = 4 for 5 million cells), it is evident that there is an ∼50% decrease in the p50 utilizing this new approach. Upon fitting each data set into the new method, there was a distinct shift to the left (i.e., toward the lower pO₂ side) for each cell density (Fig. 5). Such a shift was obvious at higher cell densities (Fig. 5, A and B). This clearly implies that the diffusion limitation has a direct effect on the p50, while allowing the maximum rate of consumption to remain unchanged. Furthermore, HRR methods (2,27) have assumed that the p₀ value reaches zero. Yet, our approach here reveals that this is not the case. The p₀ value ranges from 0 < p₀ < 1 (Table 1). Fig. 6 also contains p50 values reported in the literature using HRR. They were found to be consistent with the results determined in this work using EPR oximetry.

FIGURE 6.

Dependence of p50 (oxygen affinity) to cell density. The p50 is dependent upon the cell density in the original approach, as well as the new method. However, there is an ∼50% reduction in the p50 when utilizing the refined approach, which is more comparable to the data acquired in polarographic techniques. The reported values (▵, □) agree with our acquired p50 results (24,26). Error bars are the standard deviation from three independent measurements (n = 3).

DISCUSSION

Several studies have been performed to measure mitochondrial oxygen kinetics utilizing polarographic techniques and optical methods such as phosphorescence (27–29). Nonetheless, these systems have several limitations such as requiring a large quantity of sample, a lack of adequate sensitivity, and interferences from other sources (2,32). On the other hand, magnetic field based oximetry methods such as NMR (8,9), DNP-based oximetry (6,7), EPR oximetry (3–5), etc., are currently being used to overcome some of these apparent problems. In view of these techniques, this study reports that EPR oximetry is a useful tool to measure various stages of cellular respiration, similar to HRR. This method provides clear and exact measurements, while having a high sensitivity and only requiring a tiny amount of sample. Several previously reported studies have demonstrated the benefits of this method (3–5,11,15,33); yet, we report two important improvements in the EPR oximetry technique, which have not been previously considered in prior studies. First, the approach here reveals how more precise and meaningful additional results can be acquired by an overall analysis of the obtained data. Second, the current procedure accounts for the diffusion complications in EPR oximetry. This diffusion limitation is a specific problem in unstirred conditions such as magnetic resonance based cellular respiration studies, particularly due to a lack of the sample being mixed. The volume taken in EPR oximetry is very minimal (∼20 μl) and makes it nearly impossible to stir. Conversely, this restriction is neglected in respirometry experiments because the large volume of sample is continuously stirred.

The majority of the reported cellular respiration studies with EPR oximetry show a linear variation of pO₂ with time (3,17,18). This is due to the respiration not being measured until the oxygen is completely depleted. Even any noticeable deviation from this linearity was either neglected or qualitatively interpreted (5,34,35). Although this may be sufficient for determining the oxygen consumption rate, the entire course of oxygen consumption is necessary to calculate other relevant parameters such as the p50. Typically, EPR oximetry experiments are performed for a specific time interval and the rate of oxygen consumption is determined based on the slope of the linear region (3,33). However, we have demonstrated that cellular respiration can be followed using EPR oximetry while attaining the complete consumption of oxygen in the system and many significant parameters. There are three apparent regions in the pO₂ versus time plots, i.e., a linear portion, followed by a curved part, and then a constant value, similar to the results obtained in respirometry methods. These particular areas are easily detected in the dpO₂/dt versus pO₂ plots as illustrated in Fig. 2 for various cell densities. The consumption rates (V_O2max), calculated using the conventional approach, i.e., from the slopes of Fig. 2 A, were found to enhance with an increase in cell density. These values correspond to the plateau regions represented in Fig. 2 C. As the pO₂ decreased, the rate remained relatively the same until it approached around 30 mmHg. At pO₂ values <30 mmHg, the consumption rate decreases, illustrating the pO₂-dependent respiration rates. This is the region reflected as a curve in the pO₂ versus time plots and is described as the pO₂-dependent respiration in cells (Fig. 2 A). Although this type of behavior has been reported in the HRR measurements of oxygen (2,27), we report for the first time that the consumption rate dependence on prevailing pO₂ can be demonstrated in EPR oximetry as well.

Due to the fact that we obtained the rate versus pO₂ data from EPR oximetry, we extended the method to estimate other significant parameters, as achieved with HRR. In the case of the HRR technique, specific phases of cellular respiration are analyzed and numerous parameters such as the V_O2max, p50, and p₀ have been determined based upon Michaelis-Menten kinetics (2). Similarly, we utilized an approach to determine those relevant parameters. Nonetheless, there were some discrepancies in comparison to the established values. The differences were found to arise from the diffusion limitation of oxygen to the cell surface. As pointed out, the theory adopted in this work was developed based on the approaches used for electrocrystallization of metal ions, where the metal ions diffusion was found to influence the measured current features (30). Upon accounting for the diffusion limitation, the values for the respiration parameters turned out to be in agreement with the reported values, illustrating the importance of such a correction. Therefore, the developed method for EPR oximetry is an accurate and alternative way to compute levels of respiration.

In summary, this study utilizes a diffusion model based algorithm to quantify various phases of cellular respiration. Through this technique, we acquired the maximum oxygen consumption rate, the oxygen affinity to cytochrome c oxidase of the ETC (1/p50), and the mitochondrial equilibrium pO₂. To ensure that this respiration was due to the mitochondria, ETC blockers were used, which showed a substantial reduction in the respiration rate (Fig. 2 C and Table 1). Likewise, the approach here provides reliable and reproducible measurements. EPR oximetry offers a dependable, convenient way to measure pO₂ while requiring only a tiny amount of sample, and the probes do not consume oxygen. When utilizing this method, the effect of the diffusion problems and the concentration gradient due to the diffusion layer must be considered and corrected. However, there are some limitations that should be taken into account. Due to the stationary condition of the samples, gravity may cause the cells and the particulate probes to settle down. In such a situation, the cells would be concentrated at the bottom of the microtube lying flat in the resonator, where semispherical diffusion zones may develop into bulk volume instead of spherical zones considered in the approach here.

To address this concern, we performed similar EPR oximetry experiments where the capillary tube was rotated 180° (upside down) within a few seconds between each acquisition, and each acquisition was ∼20 s. Upon analysis of the data, we found that there is no difference between the stationary sample and the sample that was rotated. Thus, settling down did not affect the respiration behavior. However, this may be a potential problem for larger cells such as cardiomyocytes. Second, the oxygen data measured by particulate-based EPR oximetry is from whole volume, as illustrated in Fig. 3. The approach used here does not quantitatively differentiate between the data obtained from the particles present within the diffusion zones and the remaining volume. This may also pose a problem in interpreting the results in some experimental conditions. Thus, further refinement of the approach here may be required, depending upon specific experimental conditions. Despite these limitations, the advancement here highlights the benefits of EPR oximetry and several improvements. This oximetry methodology can be especially valuable to measure p50 and maximum consumption rate in the presence of competitive molecules such as nitric oxide (NO), which is known to reduce the oxygen affinity in the mitochondria. With the suggested corrections and improvements, EPR oximetry provides more meaningful results in cellular respiration studies.