A Guide to Accurate Fluorescence Microscopy Colocalization Measurements

Abstract

Biomolecular interactions are fundamental to the vast majority of cellular processes, and identification of the major interacting components is usually the first step toward an understanding of the mechanisms that govern various cell functions. Thus, statistical image analyses that can be performed on fluorescence microscopy images of fixed or live cells have been routinely applied for biophysical and cell biological studies. These approaches measure the fraction of interacting particles by analyzing dual color fluorescence images for colocalized pixels. Colocalization algorithms have proven to be effective, although the dynamic range and accuracy of these measurements has never been well established. Spatial image cross-correlation spectroscopy (ICCS), which cross-correlates spatial intensity fluctuations recorded in images from two detection channels simultaneously, has also recently been shown to be an effective measure of colocalization as well. Through simulations, imaging of fluorescent antibodies adsorbed on glass and cell measurements, we show that ICCS performs much better than standard colocalization algorithms at moderate to high densities of particles, which are often encountered in cellular systems. Furthermore, it was found that the density ratio between the two labeled species of interest plays a major role in the accuracy of the colocalization analysis. By applying a direct and systematic comparison between the standard, fluorescence microscopy colocalization algorithm and spatial ICCS, we show regimes where each approach is applicable, and more importantly, where they fail to yield accurate results.

INTRODUCTION

From mitosis to apoptosis, almost all cellular processes are regulated through complex interactions between macromolecules such as proteins, lipids, DNA, RNA, and other types of biomolecules. Identification of the major interacting components is an essential step toward understanding the underlying mechanisms that regulate cellular functions. To this end, fluorescence microscopy has proven to be an invaluable tool for in vitro and in vivo studies of molecular interactions, in part due to the advances in fluorescence labeling techniques and commercialization of the laser scanning microscope (LSM). To date, most approaches for measuring interacting cellular constituents using fluorescence microscopy require the analysis of dual color images for the presence of colocalized signal, that is, overlapping signals within images collected on separate detection channels. The measurement of a high degree of colocalization indicates close proximity of the two labeled species, and therefore suggests a nonrandom interaction between them.

Several different approaches to dual color image analysis can be employed to measure the colocalization of biomolecules. The simple overlay of RGB microscopy images for qualitative assessments of colocalization has been, and continues to be, a common practice in many biological studies (1,2). Frequently, images of green and red fluorophores labeling different species are overlapped and assessed for the predominance of yellow pixels in the combined image, which, to a first approximation, indicates the presence of interacting species. Overlaying images is a relatively quick and straightforward method for detecting interactions between molecules, but it is strictly qualitative and can be misleading due to the relatively large size of the optical microscopy diffraction resolution limit relative to the size of the macromolecules of interest.

Numerous strategies have been employed in the past to implement a more quantitative measure of colocalization. For example, the creation of a binary image mask of fluorescein-labeled mitochondria together with images of Texas Red labeled hexokinase, led to the measurement of ∼70% colocalization between the enzyme and the organelle (3). The association of poly(A) RNA with different cytoskeletal elements of human diploid fibroblast cells was quantified by detailed statistical analysis of pixel intensity distributions (4). The analysis of fluorescence intensity second-order histograms was proposed for the characterization of colocalization in dual color fluorescence images, as well any image acquisition artifacts affecting the measurement (5).

More recently, single particle fluorescence imaging techniques were used to quantify colocalization by statistical analysis of either the overlap integral (6), or via estimation of the intermolecular distance by point spread function (PSF) centroid fitting (7,8), for single particles within images. Nevertheless, single particle methods require very sensitive detectors and are not feasible at higher molecular densities where the individual particles cannot be resolved.

The efficiency of fluorescence resonance energy transfer (FRET) is extremely sensitive to short-range separation distances (<10 nm) between two fluorophores with appropriate spectroscopic properties and orientation, and as such, has proven to be an effective measure of interactions in many biological experiments (9,10). The sensitivity of FRET, however, may be a disadvantage in cases where colocalized structures are composed of large protein complexes so that the distance scale may exceed the Förster radius. Although FRET has been effective in measuring interaction distances in cells, the technique is not easily applicable to quantification of the fraction, or numbers, of interacting molecules (11).

Dual color fluorescence cross-correlation spectroscopy (FCCS) is capable of measuring interacting fluorescently tagged macromolecules via temporal cross-correlation analysis of fluorescence intensity fluctuations collected from a small observation volume defined by the beam focus of an excitation laser(s) (12). Intensity fluctuations arising from changes in fluorophore concentration within the beam focus are recorded simultaneously in two channels and correlated in time to reveal transport properties and number densities of interacting and noninteracting species. Image cross-correlation spectroscopy (ICCS) relies on the same principles as FCCS, but utilizes spatial correlation analysis of intensity fluctuations in fluorescence images collected via LSM. It can access transport dynamics on slower timescales (0–10⁻¹⁰ cm²/s) such as those often encountered for cell membrane proteins or immobilized proteins in fixed cells (13,14), and has recently been shown to accurately measure interacting particle densities in single images even at relatively high surface densities of fluorophore (15). ICCS has been applied to living cells by recording both spatial and temporal fluorescence fluctuations in an image time series, although here we focus on the spatial variant of the technique and application to single images (16).

Pearson's correlation coefficient, r_P, is a measure of the covariance between two signals and was first applied to measure colocalization within dual color fluorescence images of biological samples by Manders and co-workers, but was limited to samples with approximately equal number densities detected in each channel (17). To overcome this limitation, Manders and co-workers introduced a method to calculate colocalization coefficients, M1 and M2, which has become the most widespread approach for quantitative colocalization measurements via fluorescence microscopy (18). The authors demonstrated that M1 and M2 were sensitive measures of the degree of colocalization in doubly labeled systems using the analysis of simulation and fixed cell images, and were therefore particularly useful when the two species of interest differed in total number. The correct identification of colocalized pixels pairs is essential to the accurate evaluation of M1 and M2, and is accomplished by defining a threshold value for each detection channel. Specific pixels will contribute to the colocalized signal, only if both channel intensities are above their respective threshold values. For a particular channel, the ratio of the colocalized pixel intensities to the total pixel intensities, define the interacting fraction for that species. Recent work by Costes and co-workers has shown that automatic determination of the colocalization threshold is possible by finding the highest intensity value for which evaluation of r_P for pixels with intensities below this threshold yield an r_P value of zero (19). Their automatic colocalization algorithm proved to be a fast, reliable method for calculating M1 and M2 and eliminated ambiguity in threshold determination. The method, however, was not evaluated at higher particle densities or for different density ratios detected between channels.

Similar spatial correlation techniques that measure r_P as a function of spatial lag in one or two dimensions have been applied previously to dual color images, but did not take full advantage of the information contained within the correlation function (20). Barbarese and co-workers defined a correlation index, γ, to measure the colocalization of protein translation components in oligodendrocytes using such an approach, but did not determine the amount of colocalization with respect to each detection channel. Defining the amount of colocalization present between two images using a single parameter is often difficult to interpret and cannot fully characterize the system.

Although quantitative colocalization algorithms are readily available through many different commercial software packages, the dynamic range and accuracy of these methods has never been well established. In this work, we present a comparison of colocalization measurements using spatial ICCS and automatic determination of the colocalization coefficients, M1 and M2 as a function of the total density, the density ratio between the two detection channels and the interaction fraction. Simulated images were created to control variables such as density and interacting fractions in dual color images, which enabled a systematic comparison of these colocalization methods in two dimensions. From these simulations, the sensitivity and dynamic range of the two techniques were determined. As we demonstrate, commonly used colocalization techniques can have large errors in the measured fraction of interacting molecules when the density reaches moderate levels typical of concentrations encountered in many cellular systems. However, we show that the approaches compliment each other, and taken together, can accurately measure colocalization over a wide range of experimental conditions. ICCS showed much better accuracy in measuring the colocalized fraction when the particle densities detected in the two channels were different, especially when the overall density increased. However, automatic colocalization analysis was capable of measuring lower interaction fractions. We also extended the recent FCCS work of Kim and co-workers for measurement of the distribution of colocalized molecules with variable stoichiometry for application to single, dual color images (21). We show that for simulated images of particles that can bind either one or two ligands, ICCS analysis provides accurate number densities of both types of interacting species (1:1 and 1:2), as well as the binding constant. Finally, we present control colocalization measurements between antibodies adsorbed on a glass substrate as well as colocalization analysis of doubly labeled platelet derived growth factor receptors in fixed AG01523 human fibroblast cells.

THEORY

ICCS

In spatial ICCS, fluorescence intensity excited from a diffraction-limited laser focal volume is collected as a function of space as the laser beam is rastered across the sample to generate an image. For single photon, confocal laser scanning microscopy (CLSM) ICCS, two separate laser lines are usually used to excite two spectrally distinct fluorophores and the fluorescence emission is separated and collected in two detection channels. Intensity fluctuations in detection channel k, are defined as

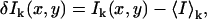(1)

where I(x,y)_k and 〈I〉_k are the intensity at pixel position (x,y) and the average intensity of the image recorded in channel k, respectively. The inverse of the number of particles per beam area (BA) in channel k, including both interacting and noninteracting species, is equal to the square relative fluctuation:

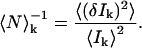(2)

In practice, noise sources contributing to the average intensity of the image prevent a direct calculation of the square relative fluctuation, thus necessitating its indirect evaluation via the zero-lags amplitude of a normalized spatial intensity fluctuation correlation function (Eq. 3). In Eq. 3, the subscripts k and l represent the two separate detection channels and ɛ and η are the corresponding spatial lag variables. Equation 3 is a spatial cross-correlation function when k ≠ l (i.e., two distinct detection channels) and an autocorrelation function when k = l. The zero-lags amplitude of the correlation function, r_kl(0,0), is estimated by nonlinear least-squares fitting to a two-dimensional Gaussian of the form shown in Eq. 4, without weighting the zero-lags point. In Eq. 4, w_xy is the e⁻² laser beam radius, u and v allow for a shift in the central fit peak caused by misaligned laser lines, and r_∞ is an offset to account for possible long-range correlations. In real images, or simulations containing noise contributions, the correlation functions were cropped around the central (zero lags) peak before fitting to reduce the effects of long-range correlations on the nonlinear least-squares fit. In all cases, a region at least 10-times larger than the e⁻² beam radius in the x and y dimensions was included in the fit.

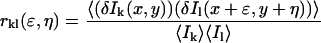(3)

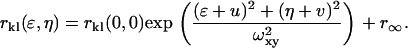(4)

If there is complete spatial overlap of the foci of the two laser beams and no quenching or fluorescence enhancement upon interaction of the two fluorophores, the zero-lags amplitude of the spatial cross-correlation function is directly proportional to 〈N〉_kl, the average number of interacting particles per beam area (22),

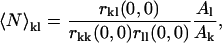(5)

where the number of interacting particles may be determined directly from the fitted amplitudes of the cross-correlation function, the two autocorrelation functions, and the effective areas defined by the focal spots of the two lasers (A_l > A_k = ). The effective area ratio is included in Eq. 5 when the PSFs of the two excitation and detection volumes differ by a small amount (23), and were measured directly from the fitted beam radii for each channel.

For each set of dual color images analyzed, an autocorrelation function is calculated for each channel, along with a cross-correlation function, and each is fit to a two-dimensional Gaussian (Eq. 4) to obtain best fit r₁₁(0,0), r₂₂(0,0), and r₁₂(0,0) values. Colocalization coefficients, defined as the ratio of the number of interacting particles to the total number of particles per beam area for a particular detection channel, are determined using the following equations:

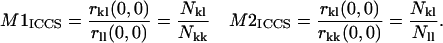(6)

Variable binding stoichiometry

If multiple binding is possible between the two labeled species, then the degree of colocalization can no longer be fully described by just two coefficients. In general, the correlation function amplitude is given by the sum of all fluorescent species contributing in a particular detection channel, weighted by the square of their respective brightness yields (24). After the approach of Kim and co-workers (21), the simplest case of species G (green channel) having two binding sites for species R (red channel), the auto- and cross-correlation function amplitudes have the form shown in Eqs. 7–9 where η_s,k represents the brightness of species s in channel k, N_RFree is the number of unbound species R per beam area, and N(GR_b) is the number of complexes with b particles of R bound to G per beam area:

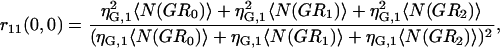(7)

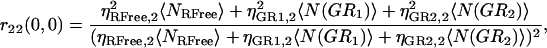(8)

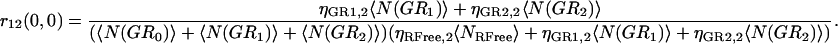(9)

It is assumed that no crosstalk exists between channels, no changes in fluorescence intensity occur upon binding, and that noncooperative binding occurs with equal probability at either site. The distribution of the number of particles with b ligands bound out of n binding sites can be described by the following equation based on the binomial distribution (21):

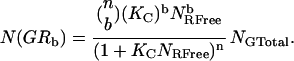(10)

Substitution of Eq. 10 into Eqs. 7–9 leads to three equations with three unknowns that can be readily solved to give the association binding constant, K_c, the number of free species R, and the total number of species G. It should be stressed that the binding constant, K_c, is analogous to the familiar association constant, K_a, in that it represents the concentration ratio of the bound species to that of the product of the two unbound species. In this case, however, K_c is determined from two-dimensional concentration measurements and is therefore not easily comparable to association constants found in the literature for bulk studies in solution. These values can then be used to determine the concentrations of molecules with one ligand bound and those with two ligands bound to fully characterize the interaction between species G and R. This type of analysis can be generalized to systems with any number of binding sites. For derivations of equations and a detailed study of the factors influencing this type of analysis, see Kim et al. (21).

Automatic colocalization

Pearson's correlation coefficient, r_P, is an accurate measure of colocalization when the densities of the two species of interest are approximately equal (17,18). Pearson's correlation coefficient ranges from −1, for perfect anticorrelation, to +1 for perfect correlation between the two variables. For the two channel image data sets, it is calculated as

(11)

where I_k(x,y) and I_l(x,y) are the intensities in detection channel k and l, respectively; the angular brackets indicate an image average of the intensity; and the sum is over all pixels. After the recent work of Costes et al. (19), the colocalization coefficients, M1 and M2, are calculated with automatic determination of the colocalization threshold values, T1 and T2, for each detection channel:

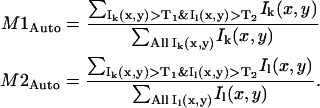(12)

Both I_k(x,y) > T₁ and I_l(x,y) > T₂ must be true for pixel intensities I_k(x,y) and I_l(x,y) to contribute to the sum in the numerator of their respective colocalization coefficient. Pixels below the channel threshold value contribute zero to the sum in the numerator. The colocalization threshold values, T₁ and T₂, were found by first performing orthogonal linear regression on the two-dimensional histogram of pixel intensities (i.e., a plot of I_k(x,y) versus I_l(x,y)) to account for differences in intensity between the two channels. Once the slope, a, and intercept, b, of this line were determined, an initial threshold, T_initial, was chosen and the locations of all pixels below T₁ = T_initial and the T₂ = aT₁+b were found. If the r_P calculated for the pixels below T₁ and T₂ was positive, then the colocalization threshold, T_initial, was lowered incrementally and the process was repeated until the chosen threshold, T_critical, led to r_P = 0 for those pixels below T₁ and T₂. These colocalization thresholds were then used in calculation of M1_Auto and M2_Auto via Eq. 12. This automatic determination of the threshold values and colocalization coefficients was carried out for each set of images analyzed.

MATERIALS AND METHODS

Simulated images

All the computational work, including image simulations, correlation function, and automatic colocalization calculations, was performed using custom-written MatLab 7.0 (The MathWorks, Natick, MA) routines and two toolboxes (Image Processing Toolbox and Optimization Toolbox) running on a personal computer equipped with a 1.5 GHz processor and 512 Mbytes of RAM.

Images were simulated to reflect those obtained by dual color CLSM of fluorescently tagged membrane receptors in two-dimensional cellular membranes and the simulations were run with user set densities and interaction fractions. Three matrices were employed in the image simulations. Matrix C contained the locations of the colocalized particles, with particle positions being generated by randomly choosing both x and y coordinates within a 256 × 256 matrix. At these randomly chosen locations, ones were inserted into the matrix while all other matrix elements were set to zero. It is possible that the same coordinates may be chosen at random more than once, especially at higher particle densities. In this case, the recorded value was the sum of the unity values for each particle located at that position. Matrix C was then convolved with a two-dimensional Gaussian function with an e⁻² radius of five pixels to simulate excitation of point emitters with a focused TEM₀₀ laser beam typical of CLSM imaging. This image size and Gaussian convolution area correspond to sampling of 800 independent spatial fluctuations in each image. Two more image matrices, G and R, with variable particle number were generated in the same fashion as C to represent the noninteracting components imaged in each detection channel. The addition of the colocalized particle matrix, C, to each of the noninteracting particle matrices, G and R, resulted in two images with a known percentage of interaction and fully defined particle densities. The interaction fraction, with respect to channel G, is given by N_C/(Nc + N_G) while that of channel R is given by N_c/(N_c + N_R), where N_i is the number of species, i, per image.

Both ICCS and automatic threshold colocalization determination were then applied to these two images and the results analyzed. Between 20 and 100 images would be generated for each set of simulation parameters so that statistics could be calculated for each colocalization method and their accuracy and precision could be compared.

To study the effects of photon detection shot or counting noise, a noise matrix was added to each image before the colocalization analyses were performed. The noise matrices, U and H, consisted of random numbers with a Gaussian distribution around zero and a standard deviation of one, multiplied by the square-root of the pixel intensity. The standard deviation of this matrix was varied with a scaling coefficient defined as the width factor (WF). The WF represents the ratio of the real signal intensity standard deviation to that of a purely Poisson distribution. Therefore, the intensities, K_x,y and L_x,y, of each pixel (x,y) in the final image set were defined as follows, where a_x,y and b_x,y are the image matrix elements with known interaction fraction as described above:

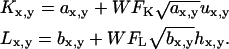(13)

Uniform background noise was investigated by adding different noise matrices, U and H, to each image. For background noise, the noise matrix elements were randomly chosen from the absolute values of a normal distribution with a mean of zero and a standard deviation of one. The standard deviation of the normal distribution was varied with a scaling coefficient to alter the total amount of noise present in the final images. This approach simulates the residual background count left after subtraction of a mean background from each pixel, as is standard practice for image background correction. Using this definition of background noise, the final pixel values in each image were defined as follows:

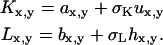(14)

The signal/noise ratio in a simulation image set was then defined as the ratio of the signal (maximum of image matrix A or B) to the standard deviation of the noise (σ). In practice, the signal is calculated as the mean of the most intense pixels to help minimize the artifacts introduced by abnormally bright pixels,

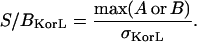(15)

To simulate images resulting from a species with two binding sites for a particular ligand, Eq. 10 was used to calculate the expected distribution of interacting complexes given the single site-binding constant, K_C, the amount of free ligand, L, and the total number of target molecules, M, (the molecule with two binding sites). The x and y pixel coordinates were generated as described above for the free receptor molecules (only channel 1), the free ligand molecules (only channel 2), and the interacting molecules, ML and ML₂, (channels 1 and 2). To generate the image from channel 1, ones were placed at the pixel coordinates of the free target molecules as well as at the locations of all the interacting species. The channel 2 image was generated similarly, by placing ones at the pixel coordinates of the free ligand and the interacting ML species. In addition, twos were placed at the pixel locations of the ML₂ particles to simulate a twofold increase in brightness when two ligands are bound to one target molecule.

Significance test

Calculation of Pearson's correlation coefficient for two uncorrelated images will still lead to non-zero values, which places a fundamental limit on the minimum interaction fraction that can be detected using this type of statistical analysis. Therefore, to test whether automatic colocalization was applicable to a given set of images, the following test was performed as described in previous works (19). Subregions of one image, approximately the size of the Gaussian convolution function (simulating the PSF or beam focus), were randomly permuted in space and then used together with the second, nonpermuted image, to calculate r_P. Two-hundred r_P values were obtained that corresponded to different random permutations of one of the images. If r_P calculated between the two unaltered images was greater than the correlation between 97% of the 200 permuted images, then the images were said to have significant colocalization. The significance test was performed once for each set of simulation conditions to evaluate whether the set conditions (densities, interaction fractions, etc.) would lead to a positive test for the presence of colocalization.

Antibodies

The primary antibody was a monoclonal anti-platelet derived growth factor β-receptor (IgG PDGF-β 4.3 mg IgG/mL) (isotype 2b), and was purchased from Sigma-Aldrich (Cat. No. P7679, St. Louis, MO). The primary antibody binds to an epitope located on the extracellular domain of the PDGF-β receptor and only recognizes human and pig receptors. One of the secondary antibodies used for immunofluorescent staining of the primary IgG was a fluorescein isothiocyanate (FITC) conjugated goat anti-mouse IgG (Fab-specific, Cat. No. F5262, Sigma-Aldrich). It had a protein concentration of 4.7 mg/mL, a dye/protein molar ratio of 5, and showed no binding to the Fc fragment. The other secondary antibody used in these experiments was Alexa Fluor 633 goat anti-mouse IgG_2b (Fc-specific, Cat. No. A-21146, Molecular Probes, Eugene, OR). The Alexa Fluor 633 conjugated antibody had a concentration of 2 mg/mL and a dye/protein molar ratio of 2.

Antibody adsorption on glass

The primary antibody was diluted 1:1000 in phosphate-buffered saline (PBS, pH 7.4) and incubated for 20 min at room temperature on a 35-mm, No. 1.5 glass-bottom microwell dish (P35G-1.5-14-C, MatTek, Ashland, MA). The dishes were then rinsed twice with PBS. Both the FITC and Alexa 633 conjugated secondary IgGs were mixed and diluted 1:1000 in PBS. This mixture of secondary antibodies was then incubated on the microwell dish at room temperature for times ranging from 15 min to overnight.

Control measurements were performed without the presence of primary antibody (i.e., a mixture of fluorescent secondary antibodies was adsorbed on bare glass surface). The spreading of the solution on the surface was greatly reduced and resulted in large clusters of antibody. This was significantly different than samples prepared in the presence of the primary mouse IgG, which resulted in complete spreading on the glass surface and completely uniform secondary antibody distributions.

Cell culture

Human foreskin fibroblasts (AG01523) were purchased from the NIA Aging Cell Culture Repository, Coriell Institute for Medical Research (Camden, NJ). The cells were cultured in Dulbecco's Modified Eagle's Medium supplemented with 10% fetal bovine serum, 4 mM L-glutamine, 100 units/mL penicillin, 0.1 mg/mL streptomycin, and 0.1 mM nonessential amino acids (Gibco, Carlsbad, CA). Cells were maintained in a humidified 5.0% CO₂ atmosphere at 37°C.

Cells were plated on 35-mm microwell dishes (MatTek) and grown for 2–3 days. Cells were incubated with 50 ng/mL of platelet-derived growth factor-BB (PDGF-BB) (R&D Systems, Minneapolis, MN) for 60 min at 37°C to promote clustering of the PDGF-β receptors (25). Cells were rinsed once with PBS and then fixed with 4% (w/v) paraformaldehyde for 20 min at room temperature. Cells were incubated with 0.2% (v/v) Triton X-100 (Sigma-Aldrich) for 5 min at room temperature followed by rinsing three times with PBS. To reduce nonspecific antibody binding, cells were incubated for 30 min with 1% (w/v) bovine serum albumin (BSA) (Sigma-Aldrich) in PBS at room temperature. Cells were then incubated with IgG PDGF-β diluted 1:500 in 1% BSA for 40 min and washed with PBS. Goat anti-mouse IgG FITC conjugate was diluted 1:200 in 1% BSA and incubated 40 min followed by rinsing in PBS. The final step in the labeling process was to incubate the cells for 40 min with goat anti-mouse IgG Alexa 633 conjugate diluted 1:200 in 1% BSA followed by rinsing in PBS. Control samples were prepared in the same manner just described, except labeling with the primary IgG PDGF-β antibody was omitted.

Microscopy

Human foreskin fibroblast cells as well as antibodies adsorbed on glass were imaged using an Olympus FV300 (Olympus America, Melville, NY) confocal laser scanning microscope (CLSM). Simultaneous excitation of FITC and Alexa 633 was provided by the 488-nm line of an Ar ion laser as well as the 633-nm line of a HeNe laser, respectively. Emission from both dyes was collected with an Olympus 60× PlanApo oil immersion objective (NA 1.4). The resulting fluorescence was split with a 570-nm dichroic mirror, and wavelengths between 510 nm and 530 nm were selected using BA510IF and BA530RIF emission filters (Chroma, Rockingham, VT) and detected with a PMT. Longer wavelength emission was collected using another PMT and a LP660 filter (Chroma Technology, Rockingham, VT). The PMT voltages were adjusted such that no pixels were saturated in the image and no threshold was applied. The pixel resolution for cell images was 0.23 μm/pixel while a digital zoom was used to achieve a resolution of 0.058 μm/pixel for images of the antibody on glass.

Mean background intensity levels were calculated from image regions outside of the cells. For the case of antibody adsorption on glass where the entire field of view appeared to contain signal, a region in the middle of the image was deliberately photobleached and the post-bleach mean intensity in that region was used as a measure of background noise. Identical background levels were obtained for control images of primary antibody-coated coverslips in the absence of the fluorescent secondary antibody. All images before ICCS or automatic colocalization analysis were corrected for background noise by subtracting the mean background, plus one standard deviation from all pixels. Bleedthrough between channels was measured by excitation with the 488-nm laser line and collecting the resulting fluorescence in both channels. No detectable cross talk was observed for these experiments.

The CLSM noise-width factor was measured at a particular PMT voltage by recording images of a highly fluorescent slide (Chroma Technology), and then comparing the standard deviation of the image to the square root of the mean.

RESULTS AND DISCUSSION

Simulation results

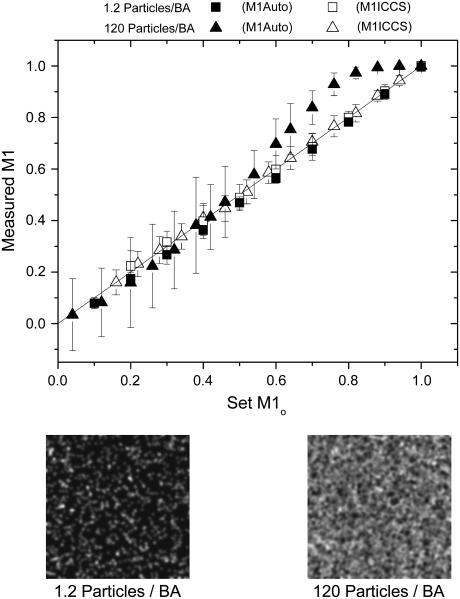
To investigate the detection limits of the colocalization analyses, images were simulated in which the interaction fraction was varied while the total particle densities in channels 1 and 2 were held constant and equal. Results are shown in Fig. 1. Automatic colocalization led to accurate results at low densities for all interaction fractions >3%, which is the detection limit as determined by the colocalization significance test described above (see Fig. 1). At higher densities (∼100 particles/beam area (BA)), automatic colocalization significantly overestimates the amount of interacting particles at large interaction fractions (>60%), but the detection limit remains at 3% (Fig. 1). The standard deviation of the measurement was calculated from the results of 50 simulations under identical conditions for each data point and was seen to increase with increasing particle density. The detection limits of spatial ICCS were significantly greater than those of automatic colocalization, varying from between 15 and 20% as the overall density decreased. The minimum interaction fraction that could be detected by ICCS was determined by successively decreasing the number of interacting particles for a given density until the two-dimensional Gaussian fit of the cross-correlation function failed. A failed fit was defined as more than half of the 50 trials returning a fitted e⁻² beam radius outside a range of ±30% of the simulation input value. It should be noted that to obtain the ICCS detection limits reported, the full correlation function was cropped around the central peak before fitting of the Gaussian function. Excluding long-range correlations (large spatial lag values) led to better fits, especially as the interaction fraction (and density) was decreased. In all cases, the number of points fit was at least six-times that of the e⁻² Gaussian convolution radius to ensure complete decay of the correlation peak. All interaction fractions above the limit of detection led to relative errors of <10% for ICCS for both densities investigated on the 256 × 256 pixel images (Fig. 1).

FIGURE 1.

Measured interaction fractions (M1_Auto and M1_ICCS) as a function of the simulation input interaction fraction for two different particle densities. Each point is an average of 50 image sets with error bars representing the standard deviation of the measurements. BA stands for beam area. Shown below are two example images at densities of 1.2 and 120 particles/BA.

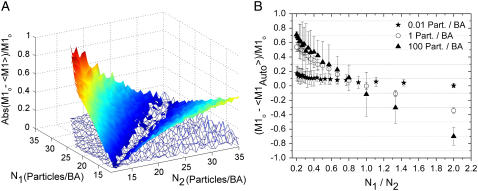
The effect of density on the accuracy of colocalization measurements was investigated by varying the particle density in both channels independently, while fixing the amount of interaction with respect to channel 1 at 50% (Fig. 2). This interaction fraction was chosen as it was above the detection limits and allowed a reasonable range of densities to be explored and still have interacting particles in the simulation images. The pronounced V-shape of Fig. 2 A illustrates the fact that the absolute relative error in M1_Auto was small only when the particle densities in each channel were almost equal. As the density ratio of the two species of particles deviated from one, the absolute value of the relative error in M1_Auto increased dramatically, up to ∼80% when the particle density of channel 1 was only twice that of channel 2. It is important to note that even though the algorithm led to a relative error of 80% in this case, the colocalization significance test, which only gives an indication as to whether or not true colocalization exists, was positive and, therefore, the experimenter would have no way of knowing the result obtained was inaccurate. This is not the case for M1_ICCS, which exhibited a relatively small error over the entire particle density range investigated in these simulations. As shown previously, however, the accuracy of ICCS does depend on the density ratio between channels but to a much lesser extent than automatic colocalization analysis (15). The mean relative error in M1_ICCS was 4% for all density ratios below 10 (the correlation fitting procedure failed above this density ratio). In this limit, the failed fit is due to the correlation between randomly overlapping particles being approximately equal in magnitude to the correlation between truly interacting particles. In this limit, the central zero-lags peak of the spatial cross-correlation function will be approximately equal in magnitude to the background peaks due to statistical correlations that occur at large spatial lags. The ratio between random and nonrandom correlation was only a function of the ratio of the densities between channels (i.e., when one of the interaction fractions is ∼10% or less) and not the total density (data not shown), which allowed ICCS to provide accurate results at high densities even when random overlap appears by eye to dominate.

FIGURE 2.

(A) Plot of the absolute value of the relative error in M1_Auto (solid color) and M1_ICCS (mesh) as a function of set particle density in each detection channel. Relative errors were calculated from the mean of 20 different sets of simulated images with an input M1_o value of 0.5. (B) Plot of the relative error in M1_Auto as a function of the particle density ratio between channel 1 and channel 2. M1_o was set to 0.5 and N₁ was kept constant at either 0.01 particle/BA, 1 particle/BA, or 100 particles/BA while N₂ was varied.

It is not apparent in Fig. 2 A, but the relative error in M1_Auto was a function of the total density as well. This effect is shown more clearly in Fig. 2 B by plotting the relative error in M1_Auto as a function of the particle density ratio between channels for three different densities that span five orders of magnitude. Here, the particle density of channel 1 and M1 (0.5) were kept constant while varying the particle density of channel 2. For densities on the order of 0.01 particles/BA, the relative error in the automatic colocalization measurement was <15% for all density ratios. As the total density increases, the slope of the line increases, which demonstrates an increased sensitivity to the density ratio between channels. The relative error was close to zero at a ratio of one, but increased rapidly for larger and smaller ratios, reaching values of >50% at a density ratio of 1:5 (Ch1/Ch2), when the total density was on the order of one particle/BA. The relative error at this N₁/N₂ ratio rose to even higher values as the total density increased. It should be noted that in all of the results, the relative error in M2 showed the same trends as that of M1 (data not shown).

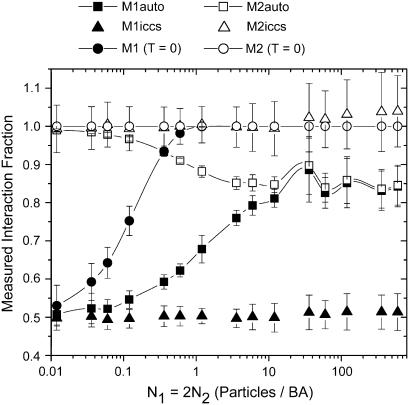
Fig. 3 presents a more detailed view of the density dependence of the colocalization coefficients at a fixed N₁/N₂ ratio of 2, and clearly shows that as the density is increased, M1_Auto and M2_Auto converge to the same value, which is significantly different than the actual set interaction fractions. In Fig. 3, M1_o and M2_o were held constant at 0.5 and 1, respectively, while the particle density was varied. When the density reached one particle/BA, the error in M1_Auto had climbed to ∼35% as shown in Fig. 3 and leveled off at ∼60% at densities >10 particles/BA. At this density ratio, the calculation of M1_ICCS and M2_ICCS was accurate over all densities simulated. Also shown in Fig. 3 is M1 calculated with a colocalization threshold of zero (M1 (T = 0)), which can serve as a first approximation when the contribution from all noise sources is known precisely. In this case, M1 is extremely sensitive to random particle overlap because all pixel pairs are classified as colocalized unless one of the pixels has a value of zero. M1 calculated in this manner classifies all randomly overlapping pixels as colocalized and therefore approached unity very quickly as the density increased. The same trend was observed when evaluating colocalization between two independent images of randomly distributed noninteracting particles using a threshold of zero, in which case, the measured interaction fraction rose steadily until reaching one at a density of ∼0.6 particles/BA (data not shown).

FIGURE 3.

The measured interaction fraction calculated using ICCS, automatic colocalization and automatic colocalization with threshold zero as a function of simulation set particle density. Each point is an average of 100 simulations, and error bars are the corresponding standard deviations. M1_o and M2_o were set at 0.5 and 1, respectively.

A careful consideration of noise contributions that are inherently present in real images is important in any quantitative image analysis method. To simulate the overall uncertainty in photon emission and detection, we introduce a counting noise width factor (WF) that broadens the underlying expected Poisson distribution that governs shot noise. The WF is intended to model the stochastic behavior of photon emission and all the additional sources of noise inherent in photon detection on an analog CLSM system (i.e., signal amplification, digitization, etc.). We do not attempt to model the underlying physical processes but rather simulate the overall statistical result observed in the acquisition of real CLSM images (see Materials and Methods). We also consider a background noise that is uniform across the image and independent of the fluorescence signal in each pixel. The background noise simulates fluorescence intensity that remains after correcting images for noise through mean subtraction of a background, which originates from dark current, autofluorescence, or scattered light. In reality, both counting and background noise are present in real images simultaneously, but have been separated here to examine their contributions individually.

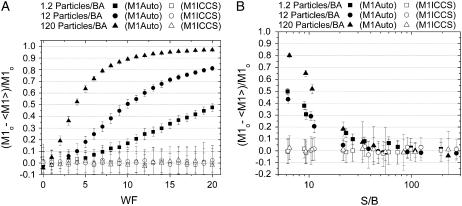
The effect of photon counting noise on automatic colocalization analyses increases as the overall density is increased. This is demonstrated in Fig. 4 A, where the relative error in M1_Auto approaches 1 (i.e., M1_Auto approaches 0), as a function of increasing width factor. As a consequence of the increased noise, r_P goes to zero at very high threshold values, which results in only a small fraction of pixels being identified as colocalized (i.e., above threshold). In contrast, the error in ICCS analysis is small and constant as a function of the width factor for all the densities investigated. Low signal-to-background (S/B) ratios will affect the error in M1_Auto, especially when the overall image density is large as shown in Fig. 4 B. As was seen in the case of counting noise, the S/B ratio has little effect on the accuracy of the interaction fraction measured with ICCS. However, this is not the case for the measured number densities. The error in the particle density measured by ICCS for each channel increases as the S/B decreases, and this effect is more pronounced for higher particle densities. For example, for lower densities (<10 particles/BA) with S/B ratios <10, the error in the measured absolute densities is >20% for ICCS. At this same S/B ratio of 10, but densities >100 particles/BA, the error in the measured absolute channel densities is >60%. Essentially, these errors cancel out when calculating the interaction fraction as long as the background noise in each channel is comparable.

FIGURE 4.

Plot of relative error in measured M1 as a function of the counting noise width factor (WF) (A) and the signal/background ratio of the image (S/B) (B). The densities in each channel are equal and M1_o and M2_o were both set at 0.5. Each point is an average of 50 simulations and the error bars are standard deviations.

The presence of multiple binding sites on a macromolecule of interest will lead to a distribution of interacting species that cannot be fully described by two colocalization coefficients. To distinguish molecules that are associated with one partner from those associated with two, we have applied the FCCS theory of Kim et al. (21) to the ICCS analysis of single, dual color images. Images were simulated to represent binding of either one or two particles with a known distribution and density. Channel 1 was composed of particles in three distinct states: free (i.e., not associated with a particle from Channel 2); associated with one particle from channel 2; or associated with two particles from channel 2. Association was defined by simply placing particles in the same pixel location in both images (see Materials and Methods).

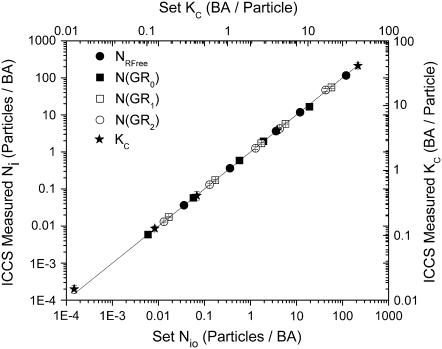
For these sets of simulations, the distribution of interacting particles was determined by Eq. 10 given the total number of channel 1 particles, N_GTotal; the number of free channel 2 particles, N_RFree; and the single-site binding constant, K_C, which was assumed to be the same for both binding sites. To recover the concentrations using ICCS, the fit amplitudes of the cross-correlation function and the two autocorrelation functions were used in Eqs. 7–9 to numerically solve for K_C, N_GTotal, and N_RFree. Once these three values were obtained, the concentrations of the different interacting species were calculated using Eq. 10. The brightness factors, η_s,k, were all set to one except for η_GR2,2, which was set to two. The error associated with ICCS colocalization distribution analysis was small over the density range investigated, as illustrated in Fig. 5.

FIGURE 5.

Plot of measured species number densities and equilibrium binding constant from ICCS distribution analysis as a function of input number density and equilibrium binding constant calculated from the analysis of 50 multiple binding simulation sets with identical settings for each density. Error bars are standard deviations. No counting or background noise was added to these images.

In Table 1, we present a summary of the results described above for the two colocalization methods investigated. The table also includes the sensitivity of the methods to pixel position shifts between images from each channel. Automatic colocalization compares intensity values from identical pixel positions in each channel to determine interaction fractions so it is very sensitive to shifts due to misalignment of the two detection channels. In an ICCS analysis, however, a systematic pixel shift will lead to an equivalent shift in the central peak of the correlation function, which is accounted for in the fitting routine (see Eq. 4). Thus ICCS is capable of accurate measurements even if there are systematic misalignments between the two detection channel images.

TABLE 1.

Automatic colocalization versus ICCS

	Automatic colocalization	ICCS
Colocalization detection limit	3%	10–20%
Applicable density range	N2/2 < N1< 2N2 at 1 particle/BA	N2/10 < N1 < 10N2
	N1 = N2 at 100 particles/BA	For all densities investigated
Variable stoichiometric binding	Not applicable	<10% error
Systematic pixel shift	Sensitive	Not sensitive
Image heterogeneity	Not sensitive	Sensitive

Summary of the performance of automatic colocalization and ICCS in the determination of the amount of colocalization present in dual color simulation images with ∼800 independent fluctuations (BA) sampled per 256 × 256 pixel image.

Experimental results

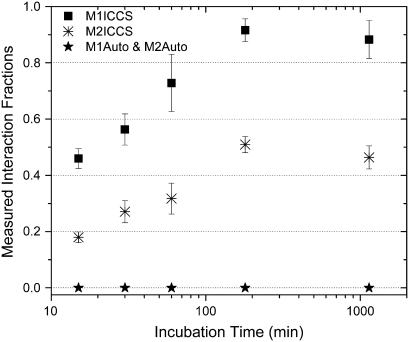
To examine the results of the simulations in the context of real systems with high densities, fluorescent antibodies adsorbed to a glass coverslip were imaged and analyzed for the presence of colocalization. After coating a coverslip with mouse monoclonal anti-PDGF β-receptor IgG, a mixture of secondary anti-mouse IgGs conjugated with either fluorescein isothiocyanate (FITC) or Alexa 633 (Fab- and Fc-specific, respectively) were incubated on the coverslip for varying amounts of time. The calculated colocalization, as measured by either ICCS or automatic colocalization analysis, is plotted as a function of secondary antibody incubation time in Fig. 6. ICCS analysis showed the expected increase in interaction fraction as the incubation time was increased. The overall density was between 100 and 400 particles/BA for each channel and automatic colocalization failed to detect any interactions for this high density sample.

FIGURE 6.

Plot of measured interaction fractions as a function of incubation time for a secondary FITC anti-mouse IgG (Fab-specific), and a secondary Alexa 633 anti-mouse IgG (Fc-specific) incubated on a coverslip coated with mouse monoclonal IgG. Each point is an average of 10 dual color image analyses recorded from different regions of the sample. Error bars are propagated standard errors of the mean.

To estimate the accuracy of these colocalization measurements, the signal was calculated as the maximum image intensity due to the ease at which it can be measured. The signal/noise ratio defined in this manner can be biased if there is an abnormally bright pixel in the image. This may occur as a result of random overlap of multiple molecules, especially at low particle densities. To verify that this was not the case, the mean of the 50 brightest pixels was taken as a measure of the signal and compared to that of using the global maximum as a measure of the signal. Both values were very similar and led to identical accuracies in the measurement. In all cases, it is important to examine the images and their intensity distributions for aberrantly bright features because image correlation methods should not be applied to regions where the spatial distribution is not Poissonian.

At these elevated densities and measured noise levels, the error in ICCS was <10% (S/B₁ = 69–158, S/B₂ = 100–175, and WF₁ = 3.0, WF₂ = 5.9), but automatic colocalization greatly overestimates the colocalization threshold, which leads to a severe underestimation of the interaction fraction (M1_Auto and M2_Auto = 0). The difference in the M1_ICCS and M2_ICCS values are a result of the significantly greater amount of free red species (Alexa 633 IgG) compared t o that of the free green species (FITC IgG). This trend was observed for several different initial concentration ratios between the red and green antibodies for a given incubation time as well as for the PDGF-β labeling on human fibroblasts (see Fig. 7). Control samples were prepared in the absence of the anti-PDGF β-receptor IgG. For the control samples, the spreading of the secondary IgG mixture was significantly reduced and resulted in large clusters of antibody on the glass coverslip, which was considerably different than samples prepared in the presence of the primary antibody.

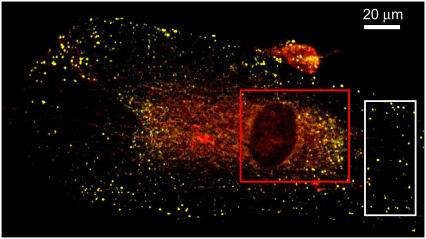
FIGURE 7.

Two-channel overlay RGB image of PDGF-β receptors on human foreskin fibroblast cells immunolabeled with FITC (green) and Alexa-633 (red). The boxes indicate the regions chosen for colocalization analysis. Both methods lead to analogous results in the region indicated by the white box (M1_ICCS = 0.98, M2_ICCS = 1.0, M1_Auto = 0.96, and M2_Auto = 0.94). ICCS fails in the region indicated by the red box due to the edge boundaries of the nuclear region while automatic colocalization works well in this regime (M1_Auto = 0.92 and M2_Auto = 0.35).

Stoichiometric ICCS analysis led to equivalent interaction fractions, i.e., [N(GR₁)+2N(GR₂)]/[N(GR₁)+2N(GR₂)+ N_RFree] and [N(GR₁)+N(GR₂)]/N_GTotal, as those plotted in Fig. 5 that were determined directly from ICCS analysis. This implies that when two binding sites are present on a molecule of interest, ICCS can still be applied to measure the overall interaction fractions. This is due to the fact that a factor of two in the brightness difference between particles detected in a given channel, results in errors of <10% in the recovered number density, regardless of the density ratio between the two species (data not shown). Application of stoichiometric ICCS, however, is advantageous if knowledge of the distribution of bound particles is desired or if the brightness ratio is >2 (i.e., there are more than two binding sites available). In the present experiment, the N(GR₁)/N(GR₂) ratio decreased from 19 to 5 at incubation times of 15 min and 1140 min, respectively.

To compare the two colocalization methods at much lower densities than those described above, the PDGF-β receptor expressed in chemically fixed AG01523 human foreskin fibroblasts was immunolabeled with two distinct fluorophores, FITC and Alexa 633 and imaged by CLSM. A dual color confocal image of the cells is shown in Fig. 7 with boxes to indicate the regions analyzed. In the region outlined by the white box, the density of the receptors (∼0.01 particles/BA) is such that both methods give similar results. After correcting for noise and nonspecific binding of antibodies, the following colocalization coefficients were calculated: M1_ICCS = 0.98, M2_ICCS = 1.0, M1_Auto = 0.96, and M2_Auto = 0.94. We expect these coefficients to be close to one because the cells were pretreated with PDGF-BB to promote clustering of the PDGF-β receptors. The images were corrected for nonspecific antibody binding before the colocalization analyses by subtraction of the mean intensity value of cells labeled in the absence of primary antibody. Some pixels, however, will still contain residual, nonspecific intensity contributions, especially when the measured nonspecific intensity distribution is broad. The red box indicates a region around the nucleus where ICCS analysis fails due to the heterogeneous nature of this part of the cell (edge boundaries). The corresponding correlation function is highly non-Gaussian due to the edges, which prevented fitting for the ICCS analysis. This type of situation is often encountered when the particle distribution in the region of analysis deviates from that of a purely Poisson distribution. If it is not feasible to choose a more uniform area within the cell, then ICCS is no longer a valid method for colocalization analysis and another technique should be used. It should be noted, however, that ICCS does not lead to false-positive results in these situations because the failed fit is readily apparent. On the other hand, automatic colocalization does not require a uniform distribution of labeled species, and successfully located the colocalized pixels for this lower density receptor system (M1_Auto = 0.92, M2_Auto = 0.35).

CONCLUSION

Our study presents a critical comparison of colocalization methods that have been used to analyze fluorescence microscopy images for macromolecular interactions in cells. By applying the analysis methods on simulated image sets, we have been able to establish important guidelines on the accuracy and range of applicability of colocalization measurements in two-dimensional systems. Deviations in the results presented would be expected for nonplanar membranes as studied previously for fluorescence correlation spectroscopy (26). Our results from simulated images as well as control-experiment antibody labeling at high density on glass coverslips demonstrate that widely used colocalization techniques that employ Pearson's correlation coefficient are not applicable for higher densities, which can be important for many biologically relevant situations. We demonstrate that the magnitudes of the number densities of the two labeled species of interest are of the utmost importance in obtaining meaningful quantitative results when using different colocalization techniques. In many ways, the colocalization techniques compared in this study are complimentary, each with their own advantages and disadvantages under different experimental conditions. In systems with interaction fractions <∼10–20%, spatial ICCS fails and the automatic colocalization technique should be used to calculate the amount of interacting particles. Temporal ICCS improves this limit due to increased sampling in time as well as space (data not shown). However, at densities approaching 100 particles/BA and interaction fractions >0.6, automatic colocalization overestimates the interaction fraction and ICCS should be used instead.

A major drawback of automatic colocalization is that when the two labeled species of interest differ in total number, even by a factor of 2, large systematic deviations from the true colocalization fraction are observed. In addition, automatic colocalization is more sensitive to noise than ICCS, especially when the particle density of the image is increased. More importantly, these errors go largely undetected because of the difficulty in determining the validity of the result. ICCS analyses are limited in the same manner but only when the density ratio of the two labeled species is >10. Above this ratio, the method fails, but this is indicated by the shape and the aberrant fitting of the cross-correlation function. Thus, the fitting routine provides a built-in check of the ICCS result.

ICCS analyses on two-dimensional systems can also be performed when there are large shifts between the two observation volumes, which are common occurrences when the two excitation lasers are not perfectly aligned. As long as the shift is equivalent for all pixels, the central peak in the cross-correlation function will simply appear shifted from the zero lag point and accurate results can still be obtained if the fitting procedure includes shift variables.

The major drawback of ICCS is that it requires a relatively uniform spatial distribution of particles within the images to be analyzed. Heterogeneous structures that are larger than the diffraction limit, as well as edge boundaries, can distort the spatial correlation function, which makes the fitting routine difficult to perform. Automatic colocalization, however, is not sensitive to the arrangement of particles and can therefore be used to analyze the colocalization of large structures such as cytoskeletal elements and organelles. Also, unlike the automatic colocalization, application of ICCS to dual color images does not provide information regarding the location of the colocalized pixels, although it can be applied to subregions within a larger image (16).

Due to the importance of colocalization measurements in biology, and the ease of applicability of dual color image analysis algorithms, it is extremely important to understand the errors associated with different colocalization techniques. Automatic colocalization methods, taken together with ICCS, provide a large dynamic range for accurate, quantitative colocalization measurements for a wide range of cellular processes.