Guard Cells Elongate: Relationship of Volume and Surface Area during Stomatal Movement

Abstract

Stomata in the epidermis of photosynthetically active plant organs are formed by pairs of guard cells, which create a pore, to facilitate CO₂ and water exchange with the environment. To control this gas exchange, guard cells actively change their volume and, consequently, surface area to alter the aperture of the stomatal pore. Due to the limited elasticity of the plasma membrane, such changes in surface area require an exocytic addition or endocytic retrieval of membrane during stomatal movement. Using confocal microscopic data, we have reconstructed detailed three-dimensional models of open and closed stomata to precisely quantify the necessary area to be exo- and endocytosed by the guard cells. Images were obtained under a strong emphasis on a precise calibration of the method and by avoiding unphysiological osmotical imbalance, and hence osmocytosis. The data reveal that guard cells of Vicia faba L., whose aperture increases by 111.89 ± 22.39%, increase in volume and surface area by 24.82 ± 6.26% and 14.99 ± 2.62%, respectively. In addition, the precise volume to surface area relationship allows quantitative modeling of the three-dimensional changes. While the major volume change is caused by a slight increase in the cross section of the cells, an elongation of the guard cells achieves the main aperture change.

INTRODUCTION

Opening and closing of stomata is an osmotically driven process. After the accumulation or discharge of K⁺ through K⁺-selective channels, water enters or leaves the cells, respectively. As a consequence, guard cells undergo large changes in turgor pressure and volume (1), which finally result in an opening or closing of the stomatal pore. The considerable and reversible changes in cell volume during stomatal movement must be associated with plastic changes in the surface area of the plasma membrane (PM), because the elasticity (i.e., lysis tension) of biomembranes is limited to only ∼3% (2–4). This is less than the changes in area expected to occur during guard cell movement (5).

The mechanism of changes in surface area in guard cells was examined with the patch-clamp technique using the membrane capacitance as an accurate parameter for surface area (6). Measurements on guard cell protoplasts have shown that an increase in surface area is indeed accomplished by an incorporation of exocytic vesicles into the PM. Endocytic vesicles of about the same size were found to be retrieved for reduction of the surface area during shrinking (7). The involvement of exo- and endocytic vesicle traffic during surface area changes was further supported by experiments in which vesicle trafficking was monitored with fluorescent membrane markers (8). Also, these studies revealed a trafficking of vesicular membrane between the PM and cytoplasmic compartments (9). Furthermore, electrophysiological measurements as well as fluorescent imaging analysis revealed that the vesicles are not only of pure membrane but also carry typical PM ion channels and probably other membrane proteins. These are reversibly inserted into the PM during changes in surface area (9,10).

Although the aforementioned investigations predict that the surface area of guard cells changes due to vesicular incorporation and retrieval, the postulated vesicles were never detected in studies using electron microscopy. To examine this discrepancy, it is necessary to exactly quantify the relevant change in surface area during stomatal movement. This parameter, together with an estimation of the size of the vesicles involved in this process, allows a calculation of the pool size of vesicles involved in reversible changes in surface area. With this number, it will be possible to judge the probability of detecting these vesicles in electron micrographs.

Since intact guard cells are not, due to their cell wall, susceptible to the patch-clamp technique, the parameter in question cannot be obtained electrically. An alternative method is offered by fluorescent confocal microscopy. From a specific labeling of the PM with styryl dyes, it is possible to reconstruct the pseudo surface from three-dimensional (3D) image stacks of stomata. Shope et al. (11) applied this method to achieve quantitative data on volume and surface area changes in guard cells. They were able to relate a general uptake of the endocytic marker FM4-64 in guard cells to surface area and volume changes. However, stomatal movement was forced by intense hyper- and hypoosmotic treatment. In addition, most likely due to the extremely low concentrated FM4-64, Shope and co-workers have seen neither single vesicles nor a constitutive uptake of FM4-64 in the absence of an osmotic change. The heterogeneity of the observed staining pattern between different cells also raises the question whether osmotic force or unspecific uptake caused the distribution of the fluorescent signal.

Here we use high-resolution confocal microscopy in combination with an appropriate semiautomated data processing and 3D reconstruction software to build detailed 3D reconstructions of guard cells of intact stomatal complexes. The question of volume and surface area changes in Vicia faba L. guard cells is examined during physiological stimulated movement of pores under the influence of natural stimuli such as abscisic acid or the fungal toxin fusicoccin. Thereby, we avoided any kind of osmocytosis, which can arise due to osmotic artificial osmotic imbalance (12,13). The data provide a quantitative model for the description of volume and surface area changes during guard cell movement.

MATERIALS AND METHODS

Plant material

Guard cells were investigated on abaxial epidermal strips from 3-week-old leaves of Vicia faba L. cv. Bunyan. The plants were grown at 20°C, 60% relative humidity, 14 h at 300 μE, and 17°C, 70% relative humidity, 10 h in the dark. Epidermal strips were fixed in small dishes with the cuticle facing a coverslip and incubated and investigated in a buffer solution consisting of 10 mM 2-morpholinoethanesulfonic acid (MES, pH 6.1/KOH), 20 mM KCl, and 100 μM CaCl. Cells were checked for cytoplasmic streaming as a viability test before, during, and after each investigation. Trypan blue staining, a commonly used viability test, did not work with intact guard cells (data not shown).

Opening and closing

For 3D analysis of stomatal movement and analysis of membrane recycling, image stacks of identical stomatal complexes were recorded in both closed and open states. Since the osmolarity of the ambient solution does not change in vivo (14), stomata in our study were kept under isoosmotic conditions, except for the slight changes generated by the ion fluxes under control of the guard cells. Dark-adapted stomata (at least 2 h before light period) were imaged (see below) and then opened by adding the fungal toxin fusicoccin to a final concentration of 10 μM for 45 min. This procedure avoids the use of any artificial osmolarities. Analog to the in vivo situation only, the K⁺ gradient acts as a driving force for stomatal opening. After 1 h, the now open stomata were imaged again in fusicoccin-free but dye-containing buffer. Stomata were then induced to close with two stimuli (100 μM abscisic acid and a low potassium concentration of 5 mM), again without changing the osmotic potential of the incubation buffer. Only data of successfully closing stomata were used for further analysis. Since stomata did not close to the same low aperture as dark-adapted, they were not imaged again.

Imaging

Confocal microscopic analysis was carried out using a Leica TCS SP (Leica Microsystems GmbH, Heidelberg, Germany), equipped with a HCX PL APO 63× numerical aperture 1.2 water immersion objective. The PM of guard cells was labeled with FM 2-10 (Invitrogen, Karlsruhe, Germany). The dye was used in a concentration of 20 μM, which in our setup results in a signal/background (S/B) ratio >5 at the PM in each confocal slice. FM2-10 was excited with a two-photon (2P) laser (Spectra-Physics Millenia/Tsunami, Spectra Physics Lasers GmbH, Darmstadt, Germany) at 880 nm. Emission was detected between 530 and 630 nm. The 2P point spread function (PSF) of the microscope was obtained by measuring the diameter of yellow-green fluorescent 0.1 μm FluoSpheres (Invitrogen) at the full width at half-maximum peak height directly next to the guard cells. The lateral and axial dimension of the PSF was 312 ± 33 nm and 1067 ± 50 nm.

Guard cell pairs were imaged as stacks of paradermal images with voxel sizes of 100 × 100 × 480 nm. Considering the resolution behind the cuticle (see also 9 and 15), this voxel size corresponds to a lateral and axial sampling rate of 3.1 and 2.2, respectively. The axial sampling rate has been chosen close to the theoretically required minimum of 2, as stated by the Nyquist-Shannon sampling theorem (16), to obtain 3D stacks with the least number of slices. This maximizes viability and minimizes bleaching without any loss of information.

Images were recorded and stored using the Leica Confocal Software 2.00 (Leica Microsystems GmbH). ImageJ (17) and Huygens 2.0 Professional (SVI, Hilversum, The Netherlands) were used to process the images.

Because excitation is confined to the focal plane, 2P excitation results in a reduced photo bleaching outside the focal volume; however, photo bleaching in the focal plane is higher than with one-photon excitation (18). Nevertheless, 2P excitation greatly limited bleaching and consequently also the production of reactive oxygen species (ROS, data not shown), since the major parts of the whole epidermal peel, i.e., the PM and the cuticle, were always thoroughly stained with fluorophores. Using 2P excitation, cytoplasmic streaming of guard cells was still observed after 50 scans of single planes, whereas at the same time sufficient signal (S/B >5) was achieved for subsequent data analysis. One-photon excitation produced significantly higher S/B ratios but often led to stagnancy of cytoplasmic streaming after recording a stack of images. To further reduce the harmful effects of prolonged imaging, we developed a feedback temperature control system to keep the incubation buffer at 20°C at all times.

Stomatal aperture and pore area

Stomatal aperture and pore area were determined from brightest-point projections of image stacks. Stomatal aperture was measured as the perpendicular distance between the brightly fluorescent cuticular ledges. The pore area was determined by counting pixels fully enclosed by the ledges.

Analysis of 3D image stacks

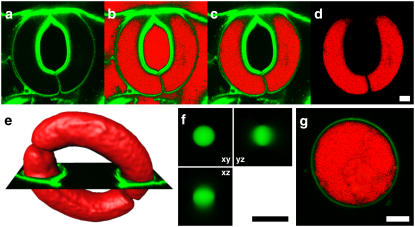
Due to intense staining of all hydrophobic structures of the epidermal peel (cuticle, cuticular ledges, PMs, etc.), it was not possible to directly use the recorded images for 3D reconstructions. All images were therefore preprocessed to get a separate label for the interior volume of guard cells only. A threshold was set for the background, and pixels with a value equivalent to and less than the threshold, which were not located within the guard cells interior, were deleted (Fig. 1, a–d).

FIGURE 1.

3D reconstruction. Preprocessing of image stacks and evaluation of the reconstruction on simple objects. To the original data (a), a threshold was set, and pixels, with a value equivalent to the threshold (b, red pixels), which were not located within the guard cell volume, were removed from the data (c). Finally, the original data were removed (d). An orthoslice (e, green) of the original data was used to verify the expansion of the generated isosurface (e, red) to set the threshold correctly. The method for generating 3D reconstructions was verified on 3D reconstructions of confocal stacks of InSpeck-beads (f) and guard cell protoplasts (g). For both, equatorial slices are shown. Images of FM2-10 labeled guard cell protoplast (g) were processed just as guard cells. Scale bars, 5 μm.

Processed image stacks were further analyzed using Imaris 3.0 (Bitplane AG, Zurich, Switzerland) to reconstruct the 3D models and to obtain volume and surface area values. To calculate the position and control the level of detail of the isosurface, both the intensity threshold and Gaussian filter need to be chosen carefully. The threshold was adjusted such that the joint between the two guard cells was clearly separated. The gap between adjacent guard cell tips at the joint was found to be very constant throughout the data sets (∼600 nm). To further confirm the correct setting, 2D orthoslices of the original data were displayed next to the generated isosurface (Fig. 1 e). Considering the dimensions of the PSF, the sigma of the Gaussian filter was set to 0.5 μm to smooth the data set before calculating the isosurface. The Gaussian filter in Imaris 3.0 is isotropic with respect to the image coordinates.

Calibration of the 3D data analysis with fluorescent beads and guard cell protoplast

To test and calibrate the method for generating 3D reconstructions and to evaluate the robustness of the aforementioned parameter settings, two geometrically simple structures—large fluorescent beads and guard cell protoplasts—were recorded.

InSpeck beads (Invitrogen) were imaged with a voxel size of 40 × 40 × 80 nm (Fig. 1 f). They have, according to the manufacturer, a diameter of 2.5 μm. This size is far beyond the resolution limit and consequently their intensity profile is not a Gaussian distribution. Diameters were therefore estimated as follows: considering that the fluorescence intensity over the structure is even, the intensity profile has a clear plateau. Only at the rims, a sigmoid or “half-Gaussian” intensity profile due to refraction phenomena is found. To estimate the sizes of the test structures, intensity profiles were fit to a semiempirical function (Eq. 1), which is closely related to the Hill function (19), which resembles the features of such a profile. In this case, the distance between the inflection points v and w yields the full width at half-maximum. The remaining fit parameters are y₀ (offset), s (scaling factor), and n, m (steepness of sigmoid rise and fall):

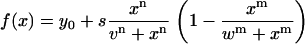(1)

The mean diameter of three beads measured in the axial and lateral direction was 2.59 ± 0.08 μm (d_lateral = 2.53 ± 0.05 μm; d_axial = 2.63 ± 0.05 μm). Analysis of the 3D reconstructions from the beads' image stacks in Imaris 3.0 yielded a mean volume of 9.66 ± 0.56 μm³ and a mean surface area of 22.17 ± 1.16 μm². From these values, diameters were calculated as 2.64 ± 0.05 μm and 2.66 ± 0.07 μm, respectively, assuming the beads to be perfect spheres. The calculated diameters overestimate the diameter determined from the intensity profiles by 2.02% and 2.57%, respectively. Volume and surface area are overestimated by 6.19% and 5.20%, respectively, with respect to values calculated from the directly measured diameters.

To evaluate the method on a biological sample, five guard cell protoplasts were labeled, imaged and processed just as the intact guard cells (Fig. 1 g). Diameters (d) were determined directly from the raw data sets by measuring the cross section at the equatorial plane (d_1–5 = {18.29, 19.39, 20.46, 20.59, 18.47}) and values for volume (V) and surface area (A) were calculated, assuming the protoplasts to be ideal spheres. With respect to these calculated values, volume (V_1–5 = {1061.27, 1187.02, 1349.58, 1281.16, 1089.86}) and surface area A_1–5 = {3202.53, 3820.27, 4377.91, 4755.63, 3262.41}) obtained from the generated isosurfaces were determined with an accuracy of 1.51% and 1.93%, respectively.

Quantification of KAT1∷green fluorescent protein in the plasma membrane of guard cells

Fluorescence was quantified as intensity per plasma membrane area. By carefully adjusting the axial distance between single optical sections to the axial dimension of the PSF (see above), an artificial accumulation in the axial direction was avoided. This approach allows the quantification of the fluorescence intensity slide by slide and subsequently relates it to an area, i.e., the number of slides used in these quantifications.

RESULTS

3D reconstruction of stomatal movement

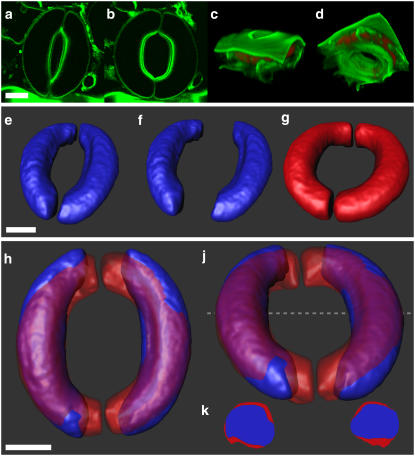
Fig. 2 shows examples of optical sections from the equatorial region of a pair of guard cells stained with FM2-10. The images are from one single stoma in a partially closed and fully open state (Fig. 2, a and b, respectively). The opening, which resulted in an increase in aperture by 7.65 μm (in pore area by 164.7 μm²), was promoted by incubating cells for 45 min in a medium with 10 μM of the fungal toxin fusicoccin. The images show that the cell borders are in both conditions clearly detectable by the fluorescent labeling of the PM.

FIGURE 2.

Optical section and 3D reconstructions of stomata. Optical sections in the equatorial region of the same stomatal complex in the closed (a) and open (b) position are shown. Projections of the preprocessed image stacks show the same stomatal complex from an outer (c) and inner (d) periclinal view. The cell volumes (threshold pixels) are shown in red, autofluorescence and FM2-10 labeling is pseudocolored green. The isosurface of a single stomatal complex is shown in the closed (e) and open (g) position. 3D objects of guard cells of the closed reconstruction were separated to match the aperture of the open reconstruction (f) and overlaid subsequently (h and j). Prominent volume changes obviously occur at the tips of the guard cells. In addition, a volume change can also be attributed to a slight variation in the guard cells cross section (k). The cross sections were obtained at the position marked with a dashed line in j. Scale bars, 10 μm.

To obtain the 3D image of the guard cells, the stomata were scanned in z direction. The resulting image stacks were then used for a 3D reconstruction; 3D projections illustrate the same stomatal complex from the outer and inner periclinal view (Fig. 2, c and d, respectively). Pixels equivalent and less than a set threshold, to discriminate the cell interior from the enclosing structures (PM), are shown in red. FM2-10 labeling is pseudocolored in green.

To obtain quantitative data on surface area and volume for the reconstructed guard cells, data were processed as described in Materials and Methods. This procedure revealed the isosurface of the individual guard cells from the closed and open stomata (Fig. 2, e and g, respectively). From these images the volume and surface area of the individual guard cells was obtained (Table 1). It is interesting to note that in all stomata analyzed, one cell was slightly smaller than the other. On a volume or surface area basis, we found in closed stomata that individual guard cells differed by a factor of 1.12 ± 0.02 or 1.06 ± 0.01, respectively. This small difference was maintained in the open state giving corresponding values of 1.08 ± 0.04 or 1.05 ± 0.03 between the two cells.

TABLE 1.

Quantifications on 3D guard cell objects

	Volume (μm3)	Surface area (μm2)	Aperture (μm)	Pore area (μm2)
Closed	3691.06 ± 478.40	1651.59 ± 126.48	5.97 ± 0.64	123.88 ± 20.35
Open	4603.76 ± 615.76	1899.29 ± 154.25	12.54 ± 0.56	262.14 ± 12.13
Δ (open-closed)	912.70 ± 238.17	247.70 ± 47.08	6.58 ± 0.65	138.27 ± 23.71
Factor (open/closed)	1.25 ± 0.06	1.15 ± 0.03	2.12 ± 0.22	2.17 ± 0.41

The values were obtained from quantifications on 3D reconstructions (volume and surface area, Fig. 2, e and g) and equatorial sections (aperture and pore area, Fig. 2, a and b) of 10 intact guard cells in their closed and open states.

Comparison of the individual guard cells from the closed and open stomata now allows a quantification of the excursion in cell surface and cell volume. For the stoma illustrated in Fig. 2, the analysis revealed that an opening of the pore by 7.65 μm is accomplished by a 1.27 ± 0.08- and 1.17 ± 0.04-fold increase in volume and surface area of the two individual guard cells, respectively. Similar results were obtained from experiments with eight other guard cells. Table 1 shows that a change in aperture by 6.58 ± 0.65 (factor: 2.12 ± 0.22) μm was on average correlated with a 1.25 ± 0.06- and 1.15 ± 0.03-fold increase in cell volume and surface area, respectively.

To analyze the topology of the surface and volume changes, we also examined the spatial distribution of the respective changes during stomatal movement. For this purpose, the guard cells from the same stomata in the open and closed state were inspected in an overlay (Fig. 2, e–j; see also Raschke (5)). For direct comparison, the reconstructed guard cells from the closed stoma (Fig. 2 e) were aligned with those of the open stoma (Fig. 2 f) in such a way that the aperture was the same as in the open stomata. From these images, it immediately occurs that guard cells from the open and closed stomata are most different in the tips regions (Fig. 2, h and j). This suggests that significant volume and surface changes occur at the tips of the guard cells; it fosters the hypothesis that elongation of the guard cells is the main mechanism for volume and surface changes. A close scrutiny of the overlays in a cross section in the center of the cells, however, shows that some volume and surface change also occur along the body of the guard cells in the form of changes of the diameter (Fig. 2 k).

Model for 3D changes during stomatal movement

To distinguish, whether guard cell movement is realized mainly by volume changes at the tips or rather by an overall swelling and shrinking of the entire cell, the data obtained from 3D measurements were fitted to a simple model for guard cells. At first approximation, the geometry of guard cells was therefore described by a half torus with an arc length (h), radius (r), volume (V = πr²h), and a surface area (A = 2πr(r + h)). The equations equal those for a cylinder with a radius (r) and height (h).

Although the arc lengths can also be derived from the confocal images directly (see below), this is not the case for the radii, since guard cells—in a very simplified view—taper toward their tips. Consequently, the radius of a cell is not a single value but rather a function that depends on the distance from the cell's center. However, by fitting the 3D data to a simple 3D model (i.e., a cylinder), we obtain a good approximation for the mean radius along the entire cell body.

In the simple model, the process of guard cell movement is reduced to the question on whether the radius (widening model) or the length (elongating model) of the cylinder changes during volume to surface area changes. Since volume and surface area were the only geometrical parameters obtained for guard cells, the two models are tested by expressing the volume as a function of surface area of a cylinder. The widening and elongating model predict different causal relations between volume (V) and the geometric parameters of the cylinder (h, r) as a function of surface area (A). These relations are described by Eqs. 2 and 3:

(2)

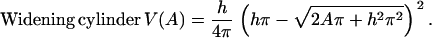(3)

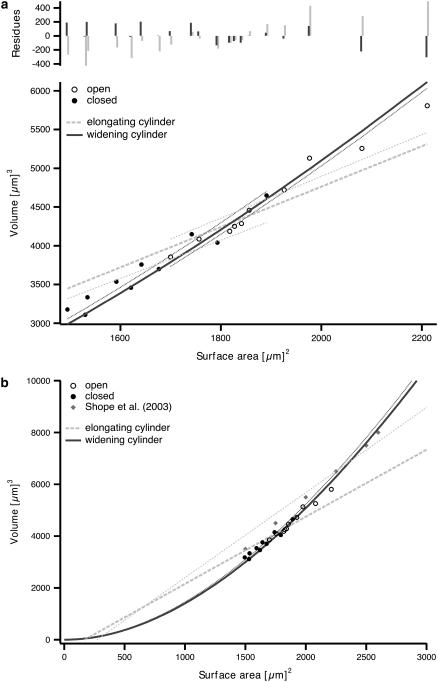
The experimentally measured values for volume were plotted versus the respective surface areas for all individual guard cells (i.e., in their open and closed states) and fitted by both models. The fit results and the residue plot (Fig. 3 a) as well as the correlation coefficients (Table 2) imply that the widening model is superior to the elongation model for describing the entire data set. In contrast to what has been expected from overlays of 3D reconstructions (Fig. 2), the data are not well described by an elongation process. The numerical description of guard cell volume to surface area changes seems to favor a model according to which surface changes occur all along the cell body and lead to an overall thicker cell.

FIGURE 3.

Fits of cylinder models to the 3D data set and their extrapolations. The volume of guard cells being part of closed (•) and open (○) stomata is plotted against their surface area. The elongating (Eq. 2) and widening (Eq. 3) cylinder models were fit to the whole data set (long-dashed light shaded and straight dark shaded lines, respectively). Residues for these fits are shown in the top panel. In addition, the models were fit to data sets of only closed and open stomata separately (elongating cylinder model, short-dashed light shaded lines; widening cylinder model, dotted dark shaded lines) (a). Both the elongating and widening cylinder models were also fit to the combined data set of open and closed stomata of our study (long-dashed light shaded and straight dark shaded lines, respectively) and to the data from Shope et al. (11) (short-dashed light shaded and dotted dark shaded lines, respectively). The fits are extrapolated to values beyond those of the data sets to visualize the (non) linearity (b). Results of the fits are summarized in Table 2.

TABLE 2.

Results of fits to the 3D data sets of guard cell volume and surface area

	Elongating model		Calculated values	Widening model		Calculated values
Data sets	rfit (μm)	R2	rcalc (μm)	hfit (μm)	R2	hcalc (μm)
Closed	4.95 ± 0.10	0.84	4.91 ± 0.31	48.85 ± 0.79	0.93	48.67 ± 2.50
Open	5.39 ± 0.10	0.88	5.33 ± 0.31	51.55 ± 0.71	0.95	51.29 ± 2.10
Open and closed	5.21 ± 0.09	0.88	5.12 ± 0.37	50.45 ± 0.60	0.96	49.98 ± 2.62
Shope et al. (11)	6.57 ± 0.21	0.96	6.29 ± 0.63	48.37 ± 1.97	0.96	46.25 ± 5.24
All	5.63 ± 0.15	0.85	5.39 ± 0.66	49.76 ± 0.69	0.97	49.14 ± 3.63

Values for the radii (r_fit) and heights (h_fit) of guard cells were obtained by fitting the respective (sub)sets of data to the elongating (Eq. 2) and widening (Eq. 3) cylinder models. In addition, values for both parameters were calculated directly (r_calc, h_calc) from the measured values for volume and surface area for each cell individually using Eqs. 5 and 6 and averaged thereafter.

Because of this discrepancy, we fitted both models to the separate data sets of guard cells being part of closed or open stomata only (Fig. 3 a). Hereby we obtained mean values for the lengths (h) and radii (r) of guard cells for both states separately. Additionally, we calculated the radii and lengths, based on the measured values for volume and surface area and a cylinder model. They were first calculated for each cell individually and averaged thereafter. Results of the fitting and calculation procedures are summarized in Table 2.

To calculate the radius (r) and height (h) of a cylinder from its area (A = 2πr (r + h)) and volume (V = πr²h), we need to find the roots of the cubic polynomial (Eq. 4):

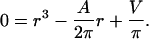(4)

The solution is known as the cubic or Cardano's formula. Only one (Eqs. 5 and 6) out of the three solutions yields real and positive values fulfilling the necessary condition for guard cells, i.e., the radius of the cylinder is smaller than its height (r < h):

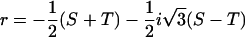(5)

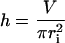(6)

with

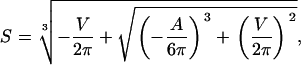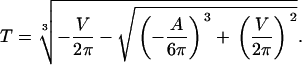Both approaches yield a much more detailed picture about how guard cells accomplish changes in their geometry during stomatal movement. The results clearly suggest that guard cells change their diameter and their length.

To further test the prediction of changes in cell length during stomatal movement, we measured the arc lengths directly in the equatorial sections of the guard cells displayed in Fig. 2. Ten measurements of the arc lengths provided mean values for the two guard cells of 47.97 ± 0.23 μm and 51.73 ± 1.03 μm for the closed and open states, respectively. This confirms that the guard cell movement is indeed correlated also with an elongation of the two guard cells. Calculations for the arc lengths of these particular guard cells yield 46.38 ± 0.48 μm and 49.80 ± 0.82 μm for the closed and open states, respectively. Hence, the calculated values using the cylinder model match the measured values for arc lengths with a precision of 3.52%.

Collectively, the analysis shows that guard cells accomplish changes of cell volume and surface by different changes in diameter and length. Although the absolute variations in length (Δl = 2.62 ± 1.82 μm) clearly exceed those in diameter (Δd = 0.86 ± 0.38 μm), the relative changes in diameter (1.09 ± 0.04) are larger than those in length (1.06 ± 0.04). This small difference, however, causes the observed nonlinear relationship between volume and surface area. More important, the observed changes in diameter (at a constant length) would cause changes in volume and surface area of 1.18 ± 0.13 and 1.14 ± 0.07, respectively, whereas the length changes (at a constant radius) would only account for change in volume and surface area by 1.06 ± 0.06 and 1.03 ± 0.03, respectively.

Hence, on a quantitative basis, the changes in volume and surface area, achieved by the small changes of the cell radius, are more significant than those achieved by the elongation; the reason for this is the elongated shape of the cells (i.e., the ratio between length and radius is ∼10).

Comparison with published data

In a similar analysis on 3D changes of stomatal movement in Vicia faba L. (11), the authors propose a linear relationship between volume and surface area and an increase of the diameter and arc length by equal proportions. This is not in accordance with the results of our study. In our analysis, the quality of fits to combined data sets and fits to separate data sets of closed and open guard cells reveals a clear nonlinear behavior.

To further evaluate the relationship between our data and those published previously (11) we fitted the cumulative data to the two different models. Since the guard cells of Vicia faba L. observed by Shope and co-workers (11) were bigger than those in our study, the combined data set covers a much larger value range to investigate the nonlinear behavior.

Fig. 3 b shows that the nonlinear widening model is best suited to describe the cumulative data. Even more important is the result that a fit to the cumulative data set of our study successfully predicts the values measured by Shope and co-workers (11), whereas the linear elongating model fails to do so. Hence, the nonlinear widening model is sufficient to describe and predict the relationship between volume and surface area during stomatal movement.

Tip concentration of KAT1

Previous work has shown that guard cells accomplish changes of their surface area by an incorporation (increase) and retrieval (decrease) of membrane to and from the PM. Electrophysiological recordings showed that this exo- and endocytic activity results in an increase or decrease respectively in K⁺ channel proteins in the PM (10). The respective cycling of K⁺ channels could also be monitored optically by a dynamic distribution of a fusion construct of the K⁺ inward rectifier KAT1 and green fluorescent protein (GFP) (9).

To further examine whether the observed topology of surface area changes might be reflected in the constitutive trafficking of a plasma membrane protein, we monitored the distribution of KAT1∷GFP fluorescence in guard cells of stomata at steady state (i.e., ∼24 h after transfection) in the absence of any opening or closing stimuli.

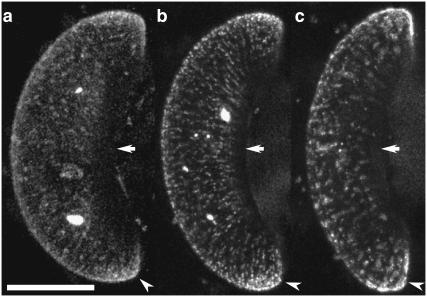
Fig. 4 shows three examples of guard cells that express KAT1∷GFP. Inspection of the images reveals an augmented fluorescence at both tips of the guard cells (Fig. 4, arrowheads, indicate one tip of each guard cell). The total fluorescence in the two tips—on the basis of fluorescence intensity per PM area—is 2.32 ± 0.46 times higher than in PM areas distant from the tips. A similar twofold enhanced fluorescence in the tips of guard cells was observed in 40% out of 20 cells inspected. In the remaining cells, the distribution was less pronounced.

FIGURE 4.

Enhanced localization of KAT1∷GFP to guard cell tips. Brightest-point projections of guard cells expressing KAT1∷GFP reveal an enhanced localization of the channel at the tips of guard cells (a–c, arrowheads indicate one tip of each guard cell). In turn, the channel is not found in the PM at the cuticular ledges (arrows). The distribution of KAT1∷GFP was observed at steady state, i.e., ∼24 after transfection in the absence of any opening or closing stimuli. Scale bar, 10 μm.

DISCUSSION

A still unresolved issue in stomata physiology is the question on the origin and fate of vesicular membrane required for changes in the surface area of guard cells (20). On the basis of our quantitative data, we are now at least able to estimate the minimal number of endo- and exocytic vesicles, which are required for an increase and decrease in PM surface area during stomatal movement. The average difference in surface area between guard cells of open and closed stomata was found to be 247.70 ± 47.08 μm³. This translates into an equivalent of 9734 ± 1850 or 1971 ± 375 vesicles with a diameter of 90 (21) or 200 nm (7), respectively.

Previous transmission electron microscopy (TEM) studies have failed to detect any kind of pools of vesicular membrane in intact guard cells, which were expected to accumulate in the cytoplasm in response to guard cell shrinking. Our data now allow a conservative estimate of the maximal number of vesicles that can be expected in TEM slices as a result of guard cell shrinking: The mean radius and arc length of guard cells in the closed state was found to be 4.91 ± 0.31 μm and 48.67 ± 2.50 μm, respectively (Table 2). Assuming that the cortical cytosol of single guard cells in closed stomata has a mean depth of ∼1 μm (9), we obtain 2444.58 ± 571.76 μm³ for its volume. A perfect, equatorial, and 100 nm thick TEM slice of the entire guard cell would translate into an area of ∼45 × 15 μm. Under the assumption of a homogeneous distribution of endocytosed vesicles in the cytosol, one would expect to find a maximum of only 40 ± 12 or 8 ± 2 vesicles with a diameter of 90 or 200 nm in the cortical cytosol of the entire TEM slice. These calculations assume unrealistic perfect specimen preservation and the complete absence of intracellular fusion events. The latter does not hold true since endocytic vesicles have a tendency to fuse to larger structures (9,12,22). Hence, in reality the number of vesicles per TEM slice is likely to be much lower. This explains why endocytic vesicles, which are anticipated to occur in the cytoplasm upon guard cell shrinking, were not evident in form of vesicle pools in TEM investigations.

3D changes during stomatal movement

Previous investigations on volume to surface area relations in guard cells suggested a linear relationship between the two geometric parameters. This gave no clear-cut indication on the geometry of stomatal movement. Our data now show in combination with those published by others (11) that a nonlinear model indeed best describes the volume to surface area relation. The result of our analysis implies that on a pure numerical basis, an overall widening of the guard cells is sufficient to explain the geometric changes associated with guard cell opening. However, already in the past it was appreciated in microscopic observations (23) that the geometric changes in guard cells cannot be reduced to the changes in only one geometric parameter. It was found that stomatal movement could be divided into two phases, namely a “static” and a “mobile” phase. Guard cells of closed stomata first begin to swell homogenously until the radial oriented cellulose fibrils do not allow a further increase in cell diameter (static phase). A further increase in pressure and volume then results in the dilatation of the tip regions, the most effective change in shape for a change in aperture (mobile phase). A similar biphasic change in guard cell geometry was also put forward by another hypothesis, which explained stomatal movement in the context of a theory for polymer elasticity. By evaluating pressure to volume relations in stomata, Sharpe et al. (24) suggested that guard cells show at the onset of opening an isotropic expansion until their pressure exceeds that of the neighboring cells. Subsequently, expansion becomes anisotropic, i.e., proceeds as elongation. These phases have already been proposed by Ståfelt (25), who termed them “Spannungsphase” (tension phase) and “Motorische Phase” (motor phase).

These qualitative descriptions of stomatal movement are in good agreement with our data. As expected from the aforementioned observations, the geometric measurements on the reconstituted stomata show that guard cells elongate and increase in diameter during stomatal opening. The numerical calculations predict that in this scenario, most of the volume is gained by the swelling of the cells, i.e., by an 18.56 ± 8.96% increase in the cross section. Although the overall elongation of the guard cells (5.50 ± 3.90%) does not contribute much to the volume and surface changes, this “tip growth” nevertheless appears to present the major contribution to the mechanical deformation required for stomatal opening; it provides the force for pushing the two cells apart. This contribution of tip elongation is consistent with previous observations (5) and is well illustrated in the overlay of guard cells from an open and closed stoma. Also the accumulation of K⁺ channels at the tip area is in accordance with the quantitative description of stomatal movement. An expected major contribution of this area to cell surface change implies that the tip areas have a higher degree of membrane turnover than the rest of the cell. If we then consider that the density of KAT1 channels is higher in the vesicular membrane than in the average plasma membrane (10) and that the KAT1 channel has a low lateral diffusion in the membrane (26), a concentration of the channel in the tip areas is even expected.

Collectively, our data conclude that a progressive gain in cell volume during guard cell swelling results in an overall increase in cell diameter. The cell deformation related to this gain in volume, however, has little impact on the pore aperture. The main force for opening of the pore is finally provided by a focal extension of the cells at the guard cell junctions. These small local changes in cell volume are sufficient to deform the guard cells in such a way that the pore opens. Interesting to note is that this scenario is equivalent to the mechanism of stomatal movement in the gramineous type, where the entire mechanism is reduced completely to volume changes in the guard cell tips. Since the gramineous type of stomata is in terms of evolution of the youngest type of stomata, it could be speculated that the mechanism of stomatal movement has been simplified in evolution leaving only the most essential deformation at the tips.