Temperature Effects on DNA Chip Experiments from Surface Plasmon Resonance Imaging: Isotherms and Melting Curves

Abstract

We present an analysis of hybridization experiments on a DNA chip studied by surface plasmon resonance imaging. The reaction constants at various temperatures and for different probe lengths are obtained from Langmuir isotherms and hybridization kinetics. The melting curves from temperature scans are also obtained without any labeling of the targets. The effects of the probe length on the hybridization thermodynamics, deduced from the temperature dependence of the reaction constants as well as from the melting curves, suggest dispersion in the length of the hybridization segments of the probes accessible to the targets. Those are, however, sufficient to suggest efficient point mutation detection from temperature scans.

INTRODUCTION

The recent availability of complete genomic sequences from many organisms coupled with commercial microarray platforms give plenty of opportunity to conduct gene expression analysis (1). However, numerous evidence suggests that the comparison between different platforms is difficult and sometimes produces contradictory results (2–4). Another application of DNA chips, the detection of point mutations with a great medical potential, is far more difficult to conduct since reliable and quantitative results are necessary (5–7). To attain quantitative results, the “solid-surface” or heterogeneous hybridization of DNA on the microarray is needed for a clearer characterization. Recent progress has been obtained on developing a model that takes into account the numerous parameters of the experiments: the probes (length, density, spacers, and grafting procedure), the targets (length, preparation protocols, and hybridization solution), and the hybridization time and temperature (8–16). The thermodynamics of the hybridization reaction also plays an important role in the quantification of the target solution (17–21). The model predictions give guidelines for the different experimental parameters at hand. However, real improvement in the quality of the experiments and the quantification of the results requires experiments in which a direct comparison is made with the theoretical predictions (16,22). The thermodynamics of DNA hybridization in solution has been well known since the 1960s (23–31), but for solid-surface hybridization, as in the DNA chip format, the association of immobilized strands (the probes) with free strands (the targets) in solution occurs at a surface-liquid interface. This modification may sensibly affect the kinetics and equilibrium properties (22).

Our aim in this article is to study in detail the equilibrium and kinetics of hybridization in a simple format of DNA chip and to focus on the temperature dependence. We based our study on two essential techniques: DNA chip fabrication through electropolymerization of oligonucleotide-modified pyrrole and real-time detection of hybridization from surface plasmon resonance (SPR) imaging (33–35). The DNA-chip fabrication technique allows us to control the grafting density and length of the grafted probes, as well as the nature and length of the spacer chains. On the detection side, SPR imaging offers the great advantage of label-free and real-time detection of hybridization (36). The lack of labeling allows us to avoid any effect of the labels on the equilibrium properties of hybridization (37), whereas real-time detection is used to determine the kinetic properties of hybridization. Experimental results on DNA chips are commonly interpreted using the Langmuir model (38–51); however, most of the experiments are done at room temperature and the effects of temperature on the equilibrium or kinetic properties are usually overlooked. The fabrication of a temperature-controlled device allows us to perform constant-temperature experiments as well as temperature scans from room temperature up to 70°C. Temperature effects on hybridization give some information on the thermodynamics of the process, with a possible comparison to hybridization in solution. Melting curves of DNA on a solid support have previously been obtained for optical fibers (52), optical wave guides (53), optical scan arrays (54), and a temperature-gradient assay (55), but with the necessity of labeling the targets or incorporating fluorescent dyes, as in solution melting-curve analysis (56–58). Our approach, coupling SPR imaging and temperature gradient, is original and avoids any labeling of the targets or incorporation of fluorescent dyes in the solution. It is also well adapted for the array format of DNA chips.

The next section focuses on materials and methods used. This is followed by a section on theoretical considerations and experimental constraints imposed to reach conditions where the Langmuir regime is expected. Then, results are presented, starting with an analysis of the kinetics of hybridization followed by isotherms. The effects of temperature and probe length on the kinetic rates and reaction constants are discussed. The thermodynamic parameters for the hybridization reaction at a solid support are obtained by two different routes: from the reaction constants obtained from the isotherms at different temperatures and directly from the melting curves at fixed-target concentration. The results are discussed in the following section, with an emphasis on the role of the probe length and the difference observed between thermodynamic parameters for the reaction on a surface and those for the reaction in solution. This difference may be explained by an effective dispersion in the hybridization segment lengths of the probes due to the entanglement of chains in the matrix of polypyrrole. Finally, some conclusions are presented and possible applications in the detection of point mutations are suggested.

MATERIALS AND METHODS

Probe and target oligonucleotide sequences

All the oligonucleotide (ODN) sequences used in this study are listed in Table 1. The probes have been synthesized by ApiBio (Biomerieux, Grenoble, France). They bear on their 5′ end a 10-thymine spacer and a pyrrole (Py) moiety for the electropolymerization grafting method. The probe lengths have melting temperatures around 30–50°C, which allows us to study the hybridization behavior in a temperature range from 25°C to 70°C. The probes are called PN, with N = 9, 10, 12, and 14 referring to the number of hybridizing bases. We used another sequence, PC, as a positive control.

TABLE 1.

Probe and target sequences

Probes
P14	5′-Py-(T10)-GCC.TTG.ACG.ATA.CA-3′
P12	5′-Py-(T10)-GCC.TTG.ACG.ATA-3′
P10	5′-Py-(T10)-GCC.TTG.ACG.A-3′
P9	5′-Py-(T10)-GCC.TTG.ACG-3′
PC	5′-Py-(T10)-TGG.AGC.TGC.TGG.CGT-3′
Targets
T1	5′-ACA.AAA.TGA.TTC.TGA.ATT.AGC.TGT.ATC.GTC.AAG.GCA.CTC.T-3′
T2	5′-ACG.CCA.GCA.GCT.CCA-3′

The DNA targets were synthesized in our laboratory and purified by HPLC. Two different sequences were used: The first one, T1, is a 40-mer sequence hybridizing specifically with the PN sequences (complementary part in bold characters), and the second, T2, is perfectly matched with the positive control PC. The length of the first target is chosen to improve the sensitivity detection of the SPR method.

Preparation of the DNA chips

The DNA chips are prepared on a glass prism (refractive index n = 1.515) coated with a gold layer (thickness 50 nm), as follows. First, the gold layer is cleaned with a piranha solution and then immersed in a solution containing ethanol and dodecanethiol for ∼20 min at room temperature to create a hydrophobic thiol monolayer. The prism is rinsed with ethanol and deionized water (18.2 MΩ cm). Finally, the DNA spots are fabricated using the pyrrole copolymerization as previously described (33). Briefly, for each probe, we prepare an electropolymerization solution containing 20 mM of pyrrole and 10 μM of pyrrole-modified ODN (Table 1). The probes are then directed to the thiol surface with a μ-pipette and the grafting is realized by an electric pulse of 100 ms at 2 V. The spots obtained with this method are ∼200 μm in diameter, with a thickness of ∼5 nm. From this protocol, the density of probes is estimated to be ∼10 pmol cm⁻² (34).

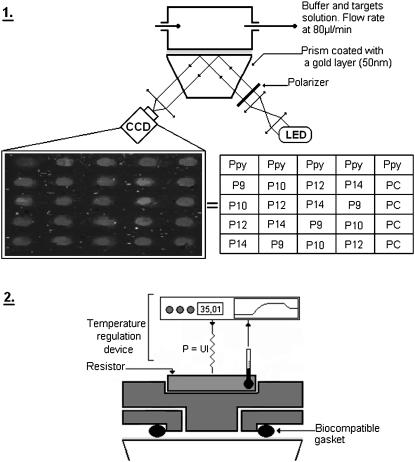
The probes were arrayed in different spots on the prism as indicated in Fig. 1-1. Polypyrrole (Ppy) spots without ODN are used as a negative control whereas spots grafted with PC probes served as a positive control. Each probe sequence is grafted five times (five spots) to control the reproducibility and the dispersion due to the electropolymerization process. The DNA chips are dehydrated and stored at 4°C after use.

FIGURE 1.

(1) Experimental set-up is composed of a LED as the light source (λ = 635nm). The light is polarized in TE or TM mode by a polarizer and it illuminates the functionalized gold layer in contact with the heating flow cell. Reflectivity changes of each spot are followed using a CCD camera monitored by a LabView interface. The inset table gives the positions of each probe sequence grafted onto the gold surface. (2) Schematic representation of the temperature control device. A resistor, integrated in a stainless steel flow cell, is used to heat the cell solution. The electric power of the resistor is regulated in real time to control the variation of the temperature in the cell.

SPR imaging set-up and temperature-control device

A SPR imaging (SPRi) apparatus with an incoherent light source (λ = 635 nm) is used to follow the hybridization kinetics, as described previously (35). This optical method is sensitive to small changes of refractive index near the gold layer (∼200 nm in depth). The transverse magnetic-polarized light is reflected at the gold surface (Fig. 1 1). For a particular angle of incidence in the total internal reflection domain, the photons are coupled to specific free-electron modes of the gold layer. This phenomenon, named surface plasmon excitation, is associated with a loss of reflected light and the optimal coupling angle is particularly dependent on the refractive index near the gold layer.

To achieve the best sensitivity, we choose an angle of incidence that corresponds to the maximum slope of the reflected intensity versus angle (reflectivity range from 20 to 40% for an angle of incidence above the minimum of reflectivity). The SPR images are captured by a CCD camera. A LabView software (GenOptics, Paris, France) allow for real-time averaging of the intensity of the spots to obtain the reflective values.

All the hybridization reactions are done in a home-made heated flow cell of 4 μL (Fig. 1 2). The cell temperature is measured using a negative temperature coefficient resistor and regulated by electrical heating using a PID controller. We are able to regulate the temperature from 25°C to 70°C with 0.05°C precision. A careful degassing of the solution is needed to avoid bubble formation.

Hybridization and denaturation experiments

The hybridization experiments are done in phosphate-buffered saline (Sigma, St. Louis, MO) at 0.35 M of NaCl (sodium dodecyl sulfate) prepared with deionized water. A continuous flow streams on the cell with a flow rate of 80 μL/min. The hybridization is performed by injecting 1 mL of various target concentrations and the kinetics is followed by SPRi for few minutes. The successive injection of a buffer solution without targets allows us to observe the denaturation process. A regeneration step of the DNA chip is achieved using an injection of NaOH at 100 mM for 1 min. Nonspecific adsorption is sometimes observed on the Ppy-spots (ΔR < 0.1%) but never on the PC spots.

Temperature-scan (T-scan) experiments

A home-made LabView interface controls the linear increase of temperature in the cell from 25°C to 70°C. The temperature rate is usually fixed at 1 or 2°C/min to allow for equilibration. To detect the dissociation of the targets from the probes, we perform two successive T-scans. The first one, without injection of DNA targets, is used as a reference. The other one is achieved after the introduction of a fixed target concentration in the cell. The melting curves are then obtained for each spot by subtracting both scans. This procedure removes the temperature dependence of the SPR signal due to the change of refractive index by heating. This change of ∼0.3%/°C has to be compared to the overall signal due to the target hybridization (<1.5% of reflectivity).

THEORETICAL CONSIDERATIONS AND EXPERIMENTAL CONSTRAINTS

The simplest model for DNA hybridization on a chip is the Langmuir kinetic model for adsorption (8,9,14–16). It consists of a reversible reaction between a probe p grafted to the surface and a target t free in solution to form the hybridized probe pt at the surface. Within this model, the fraction of hybridized probes θ on a given spot follows

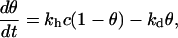(1)

where k_h and k_d are the kinetic rates for hybridization and denaturation, respectively, and c is the concentration of targets in solution. From those rates, the reaction constant K = k_h/k_d can be deduced. When the spot is free from hybridized probes (θ = 0), before the injection of the targets in the solution, the fraction θ reaches its equilibrium value θ_eq(T,c) exponentially when the targets are introduced at a concentration c and a temperature T:

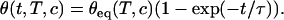(2)

The equilibrium fraction of hybridized probes θ_eq(T,c) and the hybridization timescale τ are given by:

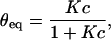(3)

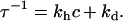(4)

From an equilibrium configuration, removing the targets from the solution allows one to test the denaturation kinetics. The fraction of hybridized probes vanishes exponentially on a timescale 1/k_d:

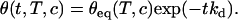(5)

Some experimental conditions are necessary for these behaviors to occur (16). These conditions in turn impose some constraints on the DNA chip fabrication and the sample preparation. The first concerns the target concentration. The target concentration near the surface is assumed to be constant and equal to the bulk concentration during hybridization. Thus, this implies that the effects of diffusion are negligible and that the reaction cell is sufficiently large to contain enough targets compared to the number of probes grafted to the spots. Experimentally, a sufficiently large flow rate (80 μL/min) allows one to avoid diffusive problems and depletion of the target concentration near the surface thanks to convection. Notice that the convection time to renew the solution in the cell (of order 3 s with this flow rate) is a limiting time for the determination of the hybridization timescale. Moreover, the adsorption sites, the probes, need to be identical and without interactions, whether hybridized or not. The grafting of presynthesized probes of identical sequence to the same spot avoids a priori the possibility of dispersion in the probe lengths, as it is inherently produced by in situ synthesis (38). High salt concentration limits the electrostatic interactions by shielding the charges of the DNA chains (14). The use of 0.35 M of NaCl leads to a Debye screening length of 0.7 nm, sufficient to avoid those interactions. The excluded-volume interactions between the probes are controlled by the grafting density (15). Changing the ratio between Py and Py-modified ODN in the grafting solution allows us to control this parameter and thus reduce the interactions. In our experiments, the grafting density, ∼10 pmol cm⁻², corresponds to an average distance between the probes of 4 nm. This is comparable to the span of the probe-spacer chains (the Flory radius R_F = M^3/5a < 4 nm, with a = 0.6 nm the size of a base and M < 24 the number of bases in the probe, taking into account the 10 bases of the spacer). The length of the hybridized segment bN < 4 nm with b = 0.34 nm the basepair contribution of the double helix and N < 14 the number of bases in the hybridizing segment (16). Thus, the probes may be considered mainly isolated whether hybridized or not and the excluded-volume interactions are reduced. The length of the targets is a compromise between higher sensitivity of the SPR detection for longer chains and the possible excluded-volume interactions between the single-stranded tails of the hybridized targets. The choice of 40-base targets is sufficient to avoid overlapping of the tails (<20 bases long), with the advantage of increasing the SPR signal compared to shorter targets. Finally, the hybridization reaction is assumed to occur as a two-state model, hybridized or not, to follow pseudo-first-order kinetics. This is a good approximation if the hybridization segment is sufficiently short (probe length <20 bases). Other hybridization mechanisms, like secondary-structure formation (hairpins), should be avoided. They may affect the kinetic behavior, as well as the equilibrium reaction constant (16,59,60). The sequences of the probes and the targets have been appropriately selected to avoid cross-hybridization and hairpin formation.

Once the reaction constant of the hybridization at the surface is determined from the Langmuir isotherm, an interesting question emerges: how does it compare with the reaction constant for the same reaction in solution? The existence of well-known thermodynamic parameters for the hybridization of short oligonucleotides in solution and the use of nearest-neighbor (NN) models for the calculation of the reaction constant (32) suggest that we should determine the corresponding parameters for the heterogeneous hybridization reaction. Some differences between the two are expected but the difference may be reduced by the use of spacers between the probes and the surface to which they are grafted (16). The use of 10 thymine spacer chains is expected to be sufficient to remove surface effects without introducing excluded-volume interactions.

RESULTS

Preliminary tests

Among the assumptions for the Langmuir kinetic model to apply, the one concerning diffusion effects may easily be confirmed. To achieve this, we measured the flow-rate dependence of the hybridization timescale τ at a fixed target concentration (data not shown). This timescale decreases when increasing the flow rate F before a saturation value is obtained at F > 60 μL/min. Thus, in the following, F is fixed at 80 μL/min to avoid the effects of mass transport and diffusion during the hybridization experiments.

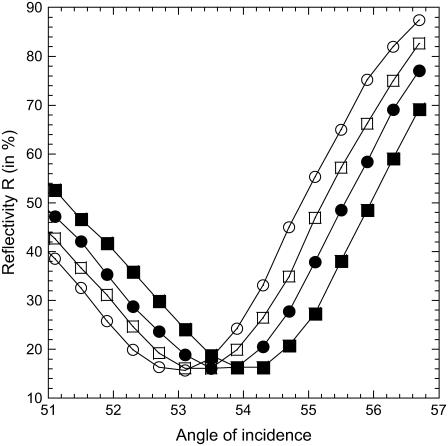
Another assumption concerns temperature effects on SPR measurements. To compare SPR responses at different temperatures, the sensitivity must be the same. To confirm this assumption, we measured the variation of reflectivity R versus the angle of incidence at various temperatures (see Fig. 2 for a spot with probes P14). As expected, the temperature affects the SPR resonance by increasing the angle of minimal reflectivity by 0.04°/°C. However, only slight variations of the slopes are measured in the linear regimes. Thus, the SPR sensitivity changes only slightly with temperature in the reflectivity range between 20% and 40%. In this range, the same variations of SPR signal at different temperatures correspond to the same amount of DNA bound to the surface.

FIGURE 2.

Reflectivity as a function of the angle of incidence for different temperatures (left to right, T = 25, 35, 45, and 55°C). The variation of temperature produces a translation of the SPR resonance curve (∼0.04°/°C) without modification of the sensitivity. The experimental angle of incidence is generally chosen at 55° ± 1° for a reflectivity close to 30%.

Finally, a set of experiments was carried out on the same DNA chip for >1 month. Successive experiments involved hybridizations at fixed temperatures and temperature scans from 25°C to 70°C. By comparing the SPR responses of the DNA chip just after its fabrication and from experiments done 1 month later, we found <10% loss of signal. This confirms the reproducibility of the experiments on the chip, the resistance to high temperatures, and the high level of regeneration.

Hybridization kinetics and equilibrium isotherms

We performed hybridization experiments at different temperatures and target concentrations. The lowest concentration, c = 12.5 nM, allowed us to observe a variation of reflectivity larger than the experimental noise (ΔR = 0.02%) for the lower temperatures. The highest concentration considered was c = 400 nM. For higher values, the hybridization timescale τ is of the same order of magnitude as the time needed to regenerate the reaction cell: V_cell/F = 3 s. Thus, for concentrations >400 nM, we cannot neglect the effects of convection on the hybridization kinetics. The available range of concentrations in those experiments spans nearly two orders of magnitude, 12.5 nM < c < 400 nM. At each temperature, injections of the T1 targets are performed for six different concentrations: c = 12.5, 25, 50, 100, 200, and 400 nM. The kinetic data for both the hybridization and denaturation experiments for each of the probes PN are fitted to the Langmuir kinetic model with two free parameters (Fig. 3):

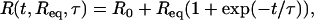(6)

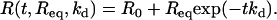(7)

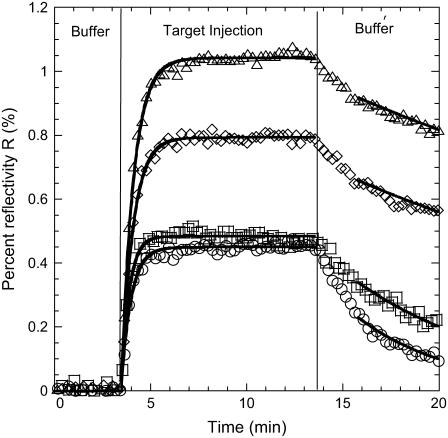
FIGURE 3.

Hybridization curves after the injection of targets at c = 400 nM and denaturation curves obtained after the injection of a buffer solution without targets at T = 32.5°C (○, P9; □, P10; ⋄, P12; and Δ, P14). All the lines are the best fits assuming the Langmuir kinetic model.

For the hybridization experiments, fits to Eq. 6 give an estimation of the equilibrium intensity R_eq and the hybridization timescale τ for each spot. The baseline R₀ is determined separately from the first few minutes before the DNA injection and subtracted from the SPR signal. For the denaturation experiments, fits to Eq. 7 give an estimation of the denaturation rate constant k_d. In principle, the equilibrium intensity R_eq is also determined from this procedure; however, some discrepancies with the R_eq obtained from hybridization are sometimes observed, principally due to a fast initial desorption process (Fig. 3). One possible reason is nonspecific adsorption but we will discuss another explanation later. Finally, notice that only the injections with a signal/noise ratio >5 are used for the fits. This corresponds to a SPR response of R_eq > 0.1% of reflectivity. The hybridization experiments last for a few minutes with an injection of 1 mL of solution and a flow rate of 80 μL/min. This time is, however, sufficient to observe saturation of the SPR signal and to determine directly the equilibrium hybridization content for most of the target concentrations considered (Fig. 3).

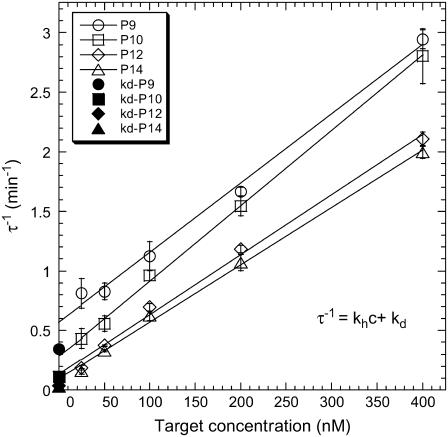
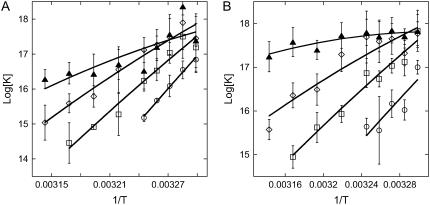
The accuracy of the fits obtained from the kinetic data is not sufficient to confirm the applicability of the Langmuir model, and additional tests are required (61,62). One of these consists of confirming the linear evolution of 1/τ with the target concentration c as predicted by Eq. 4. The different spots with the same probes on a given DNA chip allowed us to estimate average values with their experimental errors. An example obtained at T = 32.5°C is plotted in Fig. 4 and displays excellent linearity of the mean values of 1/τ as a function of concentration. Linear regressions are performed for each probe length, leading to an estimation of the kinetic rates k_h and k_d (Fig. 4). We analyzed the influence of the probe length and the temperature on the rate constants (data not shown) and the deduced reaction constant K(T) = k_h/k_d (see Fig. 6 A). As expected, k_d and K(T) are strongly dependent on those factors, but no obvious effects are observed on k_h. Furthermore, the experimental values k_h ≈ 10⁵ M⁻¹ s⁻¹ obtained in our DNA chip experiments are similar to but systematically larger than those obtained by others (40,48) for hybridization at a surface, and it is <10-fold lower than the usual estimates for hybridization in solution (63). Thus, the DNA chip format considered in our experiments, with a small grafting density of probes to avoid interactions between them, seems to affect the hybridization kinetics only slightly compared to the solution reaction, as we expected (15). Concerning the reaction constant, on one hand, K(T) is found to increase with the probe length, indicating an increased stabilization of the duplex with the number of bases, and on the other hand, a decrease in K(T) is observed for each probe when T increases, indicating temperature destabilization of the duplex. No values are reported above 35°C for P9 and 42.5°C for P10, since the hybridization signal becomes too weak and prevents accurate kinetic rate determination.

FIGURE 4.

Plot of 1/τ (open symbols), obtained from the hybridization curves (Fig. 3), as a function of the target concentration at T = 32.5°C. Error bars correspond to the dispersion between the different spots prepared with the same probe sequence. The solid symbols correspond to the estimation of the rate k_d using the denaturation curves.

FIGURE 6.

Plots of log[K(T)] versus 1/T using kinetics (A) and equilibrium (B) data. The curves correspond to the results of fitting ΔH and ΔS according to Eq. 10, with ΔC_p = −50 cal K⁻¹ mol⁻¹ per basepair.

We compared the values of the denaturation rate constants k_d estimated, respectively, from hybridization kinetics, through the Langmuir behavior of 1/τ, and from denaturation kinetics. These values differ by at least a factor of 2, particularly for P12 and P14 (Fig. 4). This difference can be linked to the difficulty of properly fitting the denaturation processes with a single exponential (Eq. 7). Indeed, at the beginning of the rinsing by the buffer solution, a fast decrease of the SPR signal is observed (Fig. 3), which may be attributable to nonspecific adsorption. This behavior has been observed in other DNA chips by Tawa and Knoll (48). In their case, the fabrication of the spots is based on a sandwich construction with streptavidin-biotin interactions. Another possible explanation is that there is dispersion in the hybridization segments of the probes due to their steric hindrance or to entanglement by the polypyrrole film and the consecutive loss of accessibility. This point will be discussed later in more detail.

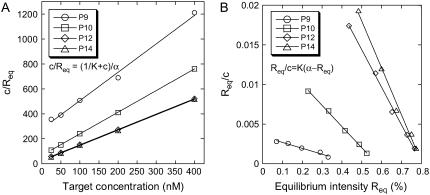
A second determination of the reaction constant K(T) from the dependence of the equilibrium intensity R_eq on the concentration according to Eq. 3 is possible. Because the SPRi response is proportional to the relative surface coverage θ, R_eq = R_maxθ, we considered two different linear regressions to estimate K(T) from equilibrium data:

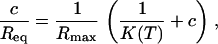(8)

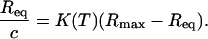(9)

R_max is the intensity for a maximal coverage by the targets (θ = 1), and its value depends on the density of probes on the spot considered. Fig. 5 shows an example of linear regressions at T = 32.5°C using Eq. 8. The linear regression using Eq. 9 is known as Scatchard plot analysis. Its linear trend is not always well defined at high concentration (c = 400 nM) and low temperature, particularly for P12 and P14. Notice also that, in contrast to Fig. 4, we do not present the average values of the different spots with the same probe, since the maximal coverage R_max is different for each spot. The values of the reaction constant as a function of the inverse temperature for the different probe sequences are presented in Fig. 6 B. By comparing the values of K(T) estimated from kinetic and equilibrium data, we observe a good agreement with both values within the error bars. However, the values calculated from the equilibrium data are generally higher than those calculated from the kinetic data. A possible explanation may be an overestimation of R_eq, which leads to an artificial increase of the reaction constant. Indeed, on several spots of PPy, nonspecific adsorption is observed to increase with the target concentration and decrease with the temperature. Therefore, nonspecific adsorption may also exist on other spots even if it was not observed on the PC spots. In a series of experiments performed on another DNA chip free from nonspecific adsorption on PPy spots, the reaction constants calculated at T = 30, 35, and 40°C are in very good agreement for determinations from both the equilibrium and kinetic data (data not shown). A difference in surface charge density due to the electropolymerization grafting may explain the discrepancy in the nonadsorbing behavior.

FIGURE 5.

(A) Plot of c/R_eq as a function of the target concentration for the different probes—P9, P10, P12, and P14—at T = 32.5°C. (B) Plot of R_eq/c as a function of R_eq in the same conditions. For each probe, the reaction constant is determined from a linear fit.

Determination of the thermodynamic parameters

The determination of the reaction constants at different temperatures also gives the opportunity to access the thermodynamic parameters for each probe grafted on the array and to compare these parameters with those expected for the same reaction in solution. The enthalpy ΔH and the entropy ΔS of the hybridization reaction are sometimes considered independent of temperature as a first approximation and may be determined for a given sequence using NN models (32,64,65). In the last 20 years, however, differential scanning calorimetry (DSC) experiments have shown the importance of specific heat changes ΔC_p (66–69). From recent experiments (68–70), values of ΔC_p in the range 0 < −ΔC_p < 100 cal K⁻¹ mol⁻¹ per basepair have been obtained. The temperature range is insufficient and the experimental errors too large to allow determination of the existence and explicit value of ΔC_p on the van't Hoff plots, as mentioned by Miculecky and Feig (71) and Chaires (72). Only DSC experiments would allow its determination. For this reason, we will consider three different values, ΔC_p = 0, −50, and −100 cal K⁻¹ mol⁻¹ per basepair, to estimate its effect on the determination of ΔH and ΔS. In the following, the temperature dependence of the reaction constant

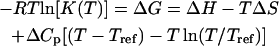(10)

is used to fit the experimental data from van't Hoff plots, with ΔH and ΔS as free parameters. R is the gas constant, T is the temperature in Kelvin, and T_ref = 35°C is the reference temperature. Fig. 6 displays the data for both estimations of the reaction constants as a function of 1/T and the curves obtained by fitting ΔH and ΔS with the value ΔC_p = −50 cal K⁻¹ mol⁻¹ per basepair. Similar curves are obtained with the two other values of ΔC_p. The thermodynamic parameters resulting from the fits with the three different ΔC_ps are listed in Table 2. First, we note that a quasilinear behavior is observed for the P9, P10, and P12 probes. Furthermore, the thermodynamic parameters estimated by kinetic and equilibrium data are in good agreement for those sequences (P9, P10, and P12), as the variation is <30% compatible with the experimental errors for the reaction constants. The effect of the heat capacity changes is within the fitting errors. Nonetheless, the absolute values of ΔH and ΔS decrease with the length of the probes. This peculiar trend is inconsistent with the behavior observed for the reaction in solution or for the thermodynamic parameters obtained from a classical NN model (32,64,65). Indeed, the enthalpy ΔH for duplex formation measures the variation of energy between double- and single-strand states of DNA. Thus, as duplex stabilization increases with the number of hydrogen bonds and base stacking, the absolute value of ΔH increases with the probe length. In the same way, the duplex formation has an entropic cost ΔS compared to the single-strand state, which increases with the probe length. Thus, despite a consistent trend for the reaction constant and the free energy ΔG versus the probe length, the variation of the thermodynamic parameters ΔH and ΔS is clearly unexpected.

TABLE 2.

Thermodynamic parameters obtained from the reaction constants determined through kinetics and equilibrium data with different ΔC_p (in cal mol⁻¹ K⁻¹ per basepair)

Probe		Kinetics		Equilibrium
	ΔCp	ΔH (kJ mol−1)	ΔS (J mol−1 K−1)	ΔH (kJ mol−1)	ΔS (J mol−1 K−1)
P9	0	−262 ± 13	−723 ± 42	−199 ± 63	−516 ± 206
	−50	−267 ± 12	−734 ± 39	−203 ± 63	−532 ± 207
	−100	−271 ± 12	−754 ± 36	−208 ± 64	−547 ± 209
P10	0	−203 ± 17	−523 ± 53	−167 ± 14	−406 ± 44
	−50	−200 ± 17	−514 ± 54	−165 ± 13	−397 ± 44
	−100	−198 ± 17	−507 ± 55	−162 ± 14	−390 ± 44
P12	0	−150 ± 12	−346 ± 40	−108 ± 18	−207 ± 57
	−50	−144 ± 12	−327 ± 38	−102 ± 16	−188 ± 53
	−100	−139 ± 11	−308 ± 37	−97 ± 15	−169 ± 48
P14	0	−87 ± 23	−139 ± 75	−27 ± 6	60 ± 20
	−50	−80 ± 24	−117 ± 78	−20 ± 6	82 ± 18
		−100	−73 ± 25	− 95 ± 82	−13 ± 6	10 ± 19

Another route to determine the thermodynamic parameters is considered looking at the melting curves on each spot from temperature scans in the range 25°C to 70°C (Fig. 7). This method is less time consuming since a single temperature scan at equilibrium is sufficient whereas the previous method needs to obtain the reaction constants from isotherms at different temperatures with each isotherm corresponding to the results of a large set of hybridization experiments. The determination of the melting curves on DNA chips has been obtained in only a few experimental situations (52–55) and only with fluorescence detection. Our approach, based on the SPR signal, is free of fluorescent labeling. The melting curves are fitted to the equation

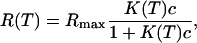(11)

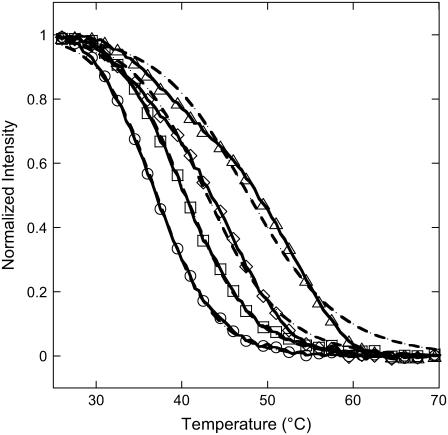
with concentration c = 250 nM and K(T) given by Eq. 10, to estimate the thermodynamic parameters (Table 3). Once again, three different values for ΔC_p were considered. We assume that the hybridization reaction is total below 25°C (intensity R_max normalized to 1) and negligible above 70°C (intensity set to 0). Releasing these constraints leads to similar thermodynamic parameters for each probe sequence. As previously, we observe a good agreement between experimental data and theoretical fits for P9, P10, and P12. Furthermore, the thermodynamic parameters estimated from the temperature scans are consistent with those obtained from the reaction constants, as shown in Table 2. Their unexpected trend is recovered with the melting-curve approach, even though the decrease of the absolute value of the thermodynamic parameters with increasing probe length seems less pronounced in this case. Indeed, as seen in Fig. 7, the melting temperature increases with the probe length, implying stabilization of the duplex; however, the width of the transition also increases. This last behavior is correlated to a decrease in the absolute value of the thermodynamic parameters.

FIGURE 7.

Melting curves (symbols and lines) and theoretical fits with the Langmuir model (dashed lines) for P9 (○), P10 (□), P12 (⋄), and P14 (▵) probes. For each probe, the thermodynamic parameters are estimated from the fit, with ΔC_p = −50 cal K⁻¹ mol⁻¹ per basepair. Melting curves are obtained for each spot of the DNA chip from temperature scans in the range 25°C to 70°C with a temperature rate of 2°C/min.

TABLE 3.

Thermodynamic parameters obtained from the temperature-scan method with different ΔC_p (in cal mol⁻¹ K⁻¹ per basepair)

Probe		Temperature scan
	ΔCp	ΔH (kJ mol−1)	ΔS (J mol−1 K−1)
P9	0	−237 ± 2	−638 ± 6
	−50	−233 ± 2	−626 ± 8
	−100	−231 ± 3	−617 ± 10
P10	0	−213 ± 2	−554 ± 6
	−50	−203 ± 2	−521 ± 8
	−100	−194 ± 3	−492 ± 10
P12	0	−188 ± 4	−468 ± 9
	−50	−167 ± 3	−401 ± 7
	−100	−150 ± 3	−344 ± 7
P14	0	−161 ± 4	−375 ± 13
	−50	−123 ± 3	−255 ± 10
		−100	−93 ± 3	−158 ± 10

The melting curves obtained experimentally with a temperature scan at 2°C/min may reflect out-of-equilibrium behaviors. Scans at lower temperature rates have been produced to check that no rate dependence was observed. Furthermore, temperature cycles have been performed to check for possible hysteresis. The presence of long-term shifts of the SPR signal on the timescale of the cycles prevents a clear conclusion about the establishment of equilibrium conditions. However, the hybridization rate k_h obtained experimentally suggests that a temperature rate of 2°C/min is sufficient.

In conclusion, the melting curves obtained from temperature scans are an alternative to kinetic studies to follow the hybridization thermodynamics of each probe sequence grafted on the DNA chip. This method is simpler and less time-consuming than hybridization experiments, as only one injection is needed. Moreover, we note that the thermodynamic parameters obtained for probe P9 are close to those estimated in solution using the SantaLucia NN model (ΔH = −288.4 kJ/mol and ΔS = −798 J/mol/K) (32,64,65). The discrepancy for longer probes is important and requires an explanation. Importantly, the clear distinction between the melting curves for probes with only one base difference suggests that the effect of a single point mutation may be detected using the temperature scans.

DISCUSSION

The main difference between the experiments performed in solution and those performed on a DNA chip is the fixation of the probes to the surface in the latter case. From a theoretical point of view, the Langmuir kinetic model may explain the hybridization of the targets to the probes in ideal conditions. It means that the effects of diffusion, nonspecific adsorption, and probe-probe interactions may be negligible (16). We studied hybridization kinetics and melting curves in experimental conditions compatible with those constraints. The isotherms seem consistent with the Langmuir model. However, when considering the temperature dependence of the reaction constants or the melting curves, we obtained results for the thermodynamic parameters that were contradictory to those for the reaction in solution, especially the probe length dependence. In the following, we will discuss a possible explanation for this effect.

The gold layer on which the probes are grafted is not perfectly flat but displays some roughness, which can modify the orientation of the probes on the surface. In a similar way, during the pyrrole copolymerization, the grafting of pyrrole and pyrrole-modified ODN does not lead to a monolayer but to a thin spot ∼5 nm in width. Thus, some of the ODN probes may be drawn in the polypyrrole matrix. Those two effects have the same consequence. They reduce the accessibility to the probes by the targets, free in solution. By fixing the probes to the surface, we may create artificially on the spot a broad distribution of their hybridization segment lengths accessible to the targets. This dispersion is inherent in other grafting procedures, like in situ synthesis (38). In our procedure, the grafting of presynthesized probes was done to reduce this effect, but no evidence can be obtained that it was effective. In fact, we will show that such dispersion may explain our experimental results, particularly on the melting curves.

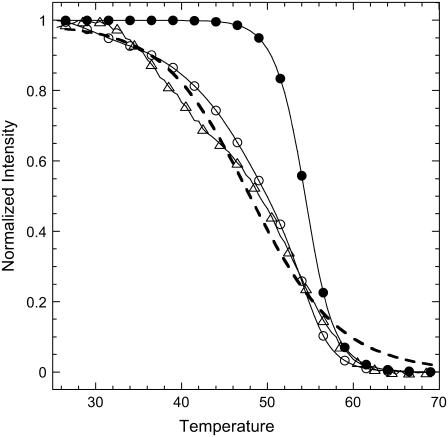
Let us assume that from the N bases in the probe PN grafted to the surface only n ≤ N bases are accessible to hybridization with the targets and the distribution of probes with n accessible bases is P(n). In the following, for simplicity, we consider two sets of probes: the first consists of probes unaffected, with the full length N accessible to the targets, and the second consists of the probes with n < N, which are supposed to have a uniform length distribution. We restrict the length of those affected probes to the range N − 7< n < N. As the stability of the duplex increases with the length of the hybridization segment, the melting temperature of Pn is lower than PN for n < N and the denaturation of both sequences occurs at different temperatures. Thus, for a spot with high dispersion, the shorter sequences denature at lower temperatures, and, as a consequence, during the temperature scans, a broader transition is observed compared to the case without dispersion. These considerations are illustrated in Fig. 8, comparing the melting curves simulated for spots prepared with the P14 probes. The equilibrium surface coverage θ_eq depends on the distribution of lengths P(n) as follows:

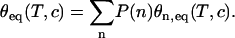(12)

FIGURE 8.

Example of temperature scans simulated for P14 probes in two situations: without (•) and with dispersion in the hybridization segments (○). We observe that the transition is broader in the second situation and compares with the experimental results (▵). The dashed line corresponds to the fit for the thermodynamic parameter determination, with ΔC_p = 0 cal K⁻¹ mol⁻¹ per basepair.

For each length, the relative surface coverage θ_n,eq is assumed to follow the Langmuir kinetic model (Eq. 3). The thermodynamic parameters determined from NN model are used for the reaction constants K(T,n) (32,64,65). Without dispersion, we observe a sharp transition from 50°C to 60°C. On the other hand, assuming the previously described distribution, with a fraction of unaffected probes equal to 60%, the transition is clearly broader, as duplexes with short hybridization segments dissociate at temperatures <50°C. In fact, for the distribution considered, the melting curve is similar to the experimental one. It should be emphasized that this result is obtained with only one free parameter, the fraction of affected probes, since the thermodynamic parameters are determined by the NN model (32,64,65). The same phenomenon of a broader transition is present for the P9 probes but less pronounced (data not shown). Actually, the main difference between probes P9 and P14 is their melting temperatures T_m. Considering P14 probes, T_m is ∼55°C, which implies that the hybridization segments of length 13, 12, or shorter form stable duplexes in the range of temperatures from 25°C to 50°C. In this case, as can be seen in Figs. 7 and 8, the dispersion of hybridization segment lengths has a strong influence on the shape of the transition and, consequently, on the estimation of thermodynamic parameters. In contrast, the melting temperature of probes P9 is ∼35°C and hybridization segments <9 are not stable or only slightly stable in the range 25–35°C. Thus, for a similar fraction of unaffected probes, the effect is weaker for the spot grafted with the smaller probes. This explains why the thermodynamic parameters are consistent with those determined by the NN model for probes P9 but not for P14, as shown in Table 2. Furthermore, the peculiar behavior of the thermodynamic parameters with the probe length can be understood assuming dispersion in the length of the hybridization segment of the probes grafted on the DNA chip.

In addition, from the kinetic point of view, this dispersion can also explain the results obtained for the denaturation process. Indeed, as shown in Fig. 3, we observed a fast decrease of the SPR signal at the beginning of the rising step with the buffer solution. Actually, the denaturation process is described by the following equation:

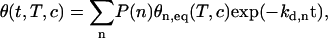(13)

with k_d,n the dissociation rate constant of probes with n accessible bases. This function is quite complex and cannot be fitted by a single exponential if the dispersion is strong. Notice that the initial stage of the dissociation is controlled by the short sequences whose k_d,n are larger. This explains the fast decrease of signal observed at the beginning of the denaturation experiments. Nevertheless, we have to understand how this distribution of lengths acts on the hybridization experiments. As seen before, the Langmuir model is clearly inaccurate to describe the denaturation; however, this model seems adequate to describe the hybridization kinetics, and no obvious effects were observed on the isotherms. Indeed, the hybridization is also described by a quite complex linear system with no obvious analytical solution:

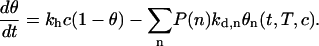(14)

In contrast to the dissociation rate, the hybridization rate k_h is sequence-independent in the first approximation (63). Indeed, the helix formation follows a cooperative zipper mechanism that requires a nucleus of several basepairs to begin with. This means that, after an unfavorable nucleation process, which occurs on three or four bases, the helix grows spontaneously as the zipper is closed. Thus, as the nucleation process is quite independent of the sequence, it is also true for k_h. We performed numerical calculations of Eq. 14 assuming the previously described distribution of lengths, with k_h = 10⁵ M⁻¹ s⁻¹ corresponding to the average hybridization rates obtained experimentally. This rate is also consistent with experimental results in solution. The denaturation rates k_d,n are deduced from k_h and the reaction constants K(T,n). Effective hybridization timescales and equilibrium hybridization contents are deduced from those calculations for the different target concentrations considered in the experiments. Even with >40% of probes affected by the entanglement on the spot, such effective values are still consistent with the Langmuir behavior. Moreover, as we observed with the experimental data, the Scatchard plots lose their linear behavior for target concentrations >400 nM for the simulated data. From the thermodynamic point of view, the van't Hoff law (Eq. 10) seems to be verified and the absolute value of the effective thermodynamic parameters decreases with probe length.

At this stage, it is useful to note the possibility of fitting a distribution of reaction or rate constants as described by Svitel et al. (73). In our case, it would be interesting to extend their model to the distribution of probe length accessible to hybridization. However, such work would require improvements in the experimental data and goes beyond the aim of this study.

CONCLUSION

In this study, we determined the kinetics of hybridization and denaturation in a DNA-chip format for various conditions of target concentration, temperature, and probe length. Our experiments were possible thanks to SPR imaging detection coupled with precise control of temperature in the reaction cell. The conditions of fabrication of the different spots on the chip were chosen to approach applicability conditions for the Langmuir kinetic model. The reaction constants for different temperatures were determined from the dependence on the target concentration of the isotherms and the hybridization timescales, assuming Langmuir behavior. The thermodynamic parameters were deduced from the temperature dependence. A direct comparison with the parameters for the same reaction in solution was only possible for the shorter probes. The spots with longer probes were found to present dispersion of the hybridization segment accessible to the targets.

The accessibility of the probes is fundamental for a correct description of the hybridization on a DNA chip, as it influences the hybridization and denaturation processes in an unusual manner. The kinetics, the reaction constant, and the thermodynamic parameters are altered by the dispersion of the hybridization segments of the probes. The effective reaction constant may be reduced by several orders of magnitude compared to the ideal case, and the effective thermodynamic parameters increase, as their absolute value decreases, with the probe length. Nevertheless, the dispersion effects are reduced by working with shorter probes. A possible way of avoiding the dispersion would be to graft double-stranded DNA chains followed by a denaturation of the duplexes. This method was used by Yao et al. (51) to reduce the density of probes. Unfortunately, the electropolymerization solution contains denaturant, which renders the grafting of double-stranded DNA impossible within those conditions.

As previously mentioned, the existence of different probe lengths is inherent in the in situ synthesis method as used, for example, by Affymetrix (38). Even with a relatively high yield of 98–99% per new base added, the fraction of probes with the perfect length of 25 bases is as low as 60–80% and the effect of dispersion in the probe lengths may not be negligible. However, with this grafting method, the distribution of lengths may simply be deduced allowing for more quantitative determination of the dispersion effect (38). This is of particular importance when considering the Latin square experiments by Affymetrix. Carlon and collaborators (20,21) have shown that those benchmark data could be understood using the Langmuir model with reduced thermodynamic parameters compared to those obtained from NN models for the reaction in solution. This reduction could simply reflect the dispersion of probe lengths, as similar effects were observed in our study.

Controlling the temperature also allowed us to determine the melting curves from temperature scans for the different probes. Using this new technique, the determination of the hybridization reaction thermodynamics is possible in a single experiment. The difference of one or two bases in the length of the probes was shown to shift significantly the melting temperatures. The effect of a point mutation is similar in effect, and recently, this method was successfully applied to detect point mutations in the gene K-ras. The destabilization due to the mutation was sufficient to induce a shift in the melting temperature that was experimentally detectable on the melting curves. Temperature-scanning experiments coupled with SPR imaging techniques may prove very useful for other biological applications.