Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2006 Nov 3;92(3):847–853. doi: 10.1529/biophysj.106.092049

Mechanism for Intein C-Terminal Cleavage: A Proposal from Quantum Mechanical Calculations

Philip Shemella *, Brian Pereira †, Yiming Zhang *, Patrick Van Roey ‡, Georges Belfort †, Shekhar Garde †, Saroj K Nayak *
PMCID: PMC1779973  PMID: 17085503

Abstract

Inteins are autocatalytic protein cleavage and splicing elements. A cysteine to alanine mutation at the N-terminal of inteins inhibits splicing and isolates the C-terminal cleavage reaction. Experiments indicate an enhanced C-terminal cleavage reaction rate upon decreasing the solution pH for the cleavage mutant, which cannot be explained by the existing mechanistic framework. We use intein crystal structure data and the information about conserved amino acids to perform semiempirical PM3 calculations followed by high-level density functional theory calculations in both gas phase and implicit solvent environments. Based on these calculations, we propose a detailed “low pH” mechanism for intein C-terminal cleavage. Water plays an important role in the proposed reaction mechanism, acting as an acid as well as a base. The protonation of the scissile peptide bond nitrogen by a hydronium ion is an important first step in the reaction. That step is followed by the attack of the C-terminal asparagine side chain on its carbonyl carbon, causing succinimide formation and simultaneous peptide bond cleavage. The computed reaction energy barrier in the gas phase is ∼33 kcal/mol and reduces to ∼25 kcal/mol in solution, close to the 21 kcal/mol experimentally observed at pH 6.0. This mechanism is consistent with the observed increase in C-terminal cleavage activity at low pH for the cleavage mutant of the Mycobacterium tuberculosis RecA mini-intein.

INTRODUCTION

Found in more than 250 proteins, inteins are autocatalytic protein elements that undergo N- and C-terminal cleavage reactions as well as a splicing reaction where the cleaved N- and C-exteins are ligated (Fig. 1) (1,2). These reactions are largely dependent on the presence of conserved amino acids mostly located near the N- and C-termini (3–5). The mechanism for intein splicing (or cleavage) is proposed based on mutational analyses and structural information obtained from x-ray crystallography (6–10). Mutational analyses further show that certain highly conserved residues are critical (i.e., their mutation leads to a complete loss of activity), whereas others can accommodate alternative amino acids that change the efficiency or rate of reaction without a complete loss of activity (11–15).

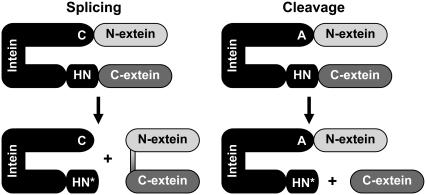
FIGURE 1.

FIGURE 1

Open in a new tab

Intein reactions—splicing and cleavage (after C1A mutation). C, A, H, N, and N* represent cysteine, alanine, histidine, asparagine, and succinimide, respectively.

The cysteine (or serine) at the N-terminus of the intein, when mutated to alanine, eliminates N-terminal cleavage activity, and therefore also inhibits splicing (Fig. 1, right). With this mutation, C-terminal cleavage is isolated, and the peptide bond between the C-terminal of the intein (asparagine) and the N-terminal of the C-extein is cleaved.

Despite significant insights into the intein splicing and cleavage mechanisms obtained from mutational analyses, the details of the component reactions remain to be worked out. It is not even clear what step initiates the splicing or cleavage reactions. Specifically, the origins and movement of protons (16) and the roles of vicinal amino acids or water molecules as proton donors or acceptors during the cleavage reaction are not fully known or understood as illustrated below.

In the experimental study by Wood et al. on the Mycobacterium tuberculosis RecA cleavage mutant mini-intein (ΔI-CM), a decrease in solution pH from 7.5 to 6.0 was found to lead to a significant increase in the rate of C-terminal cleavage (17,18). The higher C-terminal cleavage activity at lower pH for this intein as well as for the Ssp DnaB (19) intein are, however, inconsistent with the currently available details of the mechanism proposed for intein cleavage. For example, Ding et al. have suggested that for the reaction of the Ssp DnaB mini-intein, the F-block histidine acts as a base, deprotonating the nitrogen of the C-terminal asparagine side chain via a vicinal water molecule (20). Experiments on short peptides in solution also show an increased tendency of asparagine to be ionized and to cyclize (leading to succinimide formation) over the pH range of 7.4–13.8 (21–23). For a histidine to act as a base and accept protons, one of its two imidazole side-chain nitrogens must be deprotonated on average. At lower pH, especially below the pKa, histidine is more likely to be present in the doubly protonated state, diminishing its ability to accept protons. Thus, the mechanistic details underlying the increased C-terminal cleavage activity observed in experiments of Wood et al. (17,18) are expected to be different from those proposed by Ding et al. (20).

Based on a combination of semiempirical and first principles computational analyses, here we propose what we believe are new details of the mechanism of asparagine cyclization catalyzed by the cleavage mutant of the M. tuberculosis RecA mini-intein that accounts for an increase in activity of C-terminal cleavage at low pH. These details involve protonation of the nitrogen of the scissile peptide bond by a vicinal hydronium ion (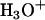Inline graphic). This leads to stretching of that peptide bond due to the loss of π-bond resonance and consequent increase in carbon electrophilicity. Asparagine cyclization and subsequent succinimide formation occur (24), resulting in peptide bond cleavage. Our results are consistent with the experimental observations of Wood et al. that indicate a simple proton-catalyzed reaction (18).

Below we present the details of computational methodology that utilizes available experimental crystal structure information, experimental kinetic data, and mutational analyses, to provide a proposal for mechanistic details of the C-terminal reaction of the cleavage mutant intein. Our proposal highlights the need to account for the local structural information as well as solution conditions (e.g., pH) in formulating details of enzymatic catalysis.

COMPUTATIONAL METHODS

Choice of the system

Given current computational resources, detailed quantum mechanical calculations are limited to small systems (25–29). In the present context, where the mechanism of enzymatic catalysis is of interest, one may choose a large number of atoms (50–100) and perform only a few calculations, or choose a smaller but relevant part of the system, and explore a variety of possible reaction pathways. Inclusion of a larger number of atoms not only adds to the computational expense, but could allow conformational rearrangements that are inconsistent with protein structural context being studied. As a compromise, and based on available crystal structure knowledge, our system includes 25 atoms—the C-terminal asparagine side chain, the backbone atoms of the penultimate histidine and of the cysteine of the C-extein (the dangling bonds are passivated with hydrogen atoms), and one explicit water molecule (see Fig. 2). Additional calculations (not shown) with larger systems containing 45 atoms for limited cases, and a full protein quantum mechanics/molecular mechanics (QM/MM) treatment indicated energetic results similar to the ones presented here with a 25-atom system.

FIGURE 2.

FIGURE 2

Open in a new tab

Computational system containing 25 atoms includes C-terminal asparagine of the intein, backbone atoms of the adjacent amino acids, and a protonated water molecule (panel A). Panel B identifies x, y, and z coordinates used in the exploration of reaction pathways.

Identification of the transition state region

Locating the transition state for biomolecular reactions is a complex problem that requires a search in a multi-dimensional local conformation space using methods such as transition path sampling (30). The computational expense of quantum mechanical calculations, however, prohibits such investigations. Instead, we heuristically choose the constraint minimization procedure based on a two-dimensional space defined by the distances x and y indicated in Fig. 2 (see below and figure captions for details) to locate the transition state region. The precise energy barrier is found by constraining only the y coordinate and relaxing all other internal coordinates.

Semiempirical PM3 (31) calculations were performed using Gaussian code (32) to obtain a two-dimensional potential energy surface in the x-y plane. Geometry optimizations with PM3 are computationally efficient and sufficiently accurate (33). Deficiencies of PM3 with respect to chemical structures, such as the “flattening” of small and medium-sized rings (34), nitrogen atoms with a lone pair having pyramidal geometries (35), and inaccurate hydrogen bonding distances are well known. Nevertheless, PM3 is useful for efficiently scanning many geometries and locating general locations of transition states, as is done here.

Quantitative analysis

The PM3 calculations described above were followed by detailed quantum mechanical calculations along selected values of relevant reaction coordinates. Specifically, we employed first principles density functional theory based on the B3LYP gradient corrected functional (36). We used 6-31G(d,p) basis sets to calculate energies of optimized geometries and compared them with values obtained using larger basis sets (6–311++g(2d,p)) to test for convergence (37). MP2 calculations were conducted to test the accuracy of the B3LYP method for this system, and the energy barrier calculations were consistent. In calculations with a hydronium ion, the three O-H bond distances were constrained to 0.98 Å to avoid spontaneous proton donation observed otherwise.

The polarizable continuum model was used to simulate solvent effects in the detailed calculations (38). Geometry optimizations performed in implicit solvent were compared with similar calculations in the gas phase. The numerical integral equation formalism was used because it allows defining interlocking atomic spheres to represent the extent of the system in solution (a single sphere was put on the hydrogen atoms belonging to the asparagine side-chain nitrogen and to hydrogen atoms of the water molecule) (39). Nondimensional dielectric constants are defined by ɛr ≡ ɛs/ɛo, where ɛo is the vacuum permittivity and ɛs is the static dielectric constant for the dielectric. For the gas phase, ɛr = 1. For water, ɛr = 78.39.

Thermal and entropic contributions calculated with a harmonic approximation for the optimized geometries at the B3LYP/6-31G(d,p) level were combined with the electronic energy to obtain free-energy profiles in the gas phase and in the implicit solvent. Zero point energies were found to differ by between 0.04 and 1.33 kcal/mol, which are within the expected error for the calculation. The approximate entropic components of the free energy include contributions from translational, electronic, rotational, and vibrational degrees of freedom (40,41) and were obtained from frequency calculations at room temperature. Thermal corrections do not include imaginary frequencies of vibrational modes for transition states.

RESULTS AND DISCUSSION

Fig. 2 shows the system considered in our calculations and includes the C-terminal asparagine residue of the intein, and the backbone atoms of the adjacent amino acids, including the scissile peptide bond. In addition, we include a water molecule in the form of a hydronium ion to mimic a low pH environment. Coordinate x in Fig. 2 B represents the distance between the oxygen atom of the water molecule and the hydrogen atom of the asparagine side chain, referred to as the asparagine ionization distance. Coordinate y, the asparagine cyclization distance, is the separation between the asparagine side-chain nitrogen and the peptide carbonyl carbon. Coordinate z represents the length of the scissile peptide bond.

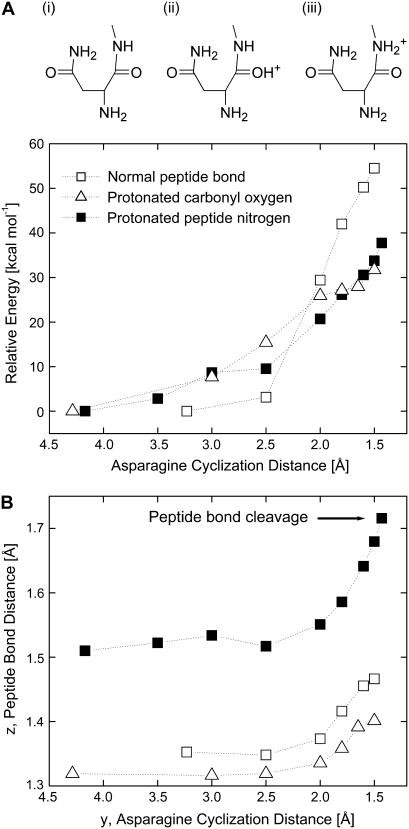
As will be apparent in the discussion below, protonation of the backbone nitrogen of the scissile peptide bond is a necessary first step in the reaction at low pH. To this end, Fig. 3 considers three scenarios corresponding to i), a neutral peptide case in which neither of the atoms are protonated, ii), O-protonation of the carbonyl oxygen, and iii), the N-protonation of the peptide nitrogen (42). Specifically, we study consequences of these three scenarios on the system energy and the equilibrium length of the scissile peptide bond.

FIGURE 3.

FIGURE 3

Open in a new tab

Schematic of the three scenarios considered for asparagine cyclization: i), normal peptide, ii), O-protonation, and iii), N-protonation. Asparagine cyclization energies (panel A) and peptide bond stretching (panel B) versus the asparagine cyclization distance, y, for the neutral peptide bond system (□), for the system where the carbonyl oxygen is protonated (Δ), and where the peptide nitrogen atom is protonated (▪). Gas phase structures are optimized at the B3LYP/6-31G(d,p) level.

In a neutral peptide (scenario i above), the relaxed peptide bond length is 1.35 Å. As asparagine cyclization proceeds (i.e., as y is reduced), the system energy increases significantly (Fig. 3 A). Correspondingly, there is only a slight increase in the peptide bond length, indicating that it remains essentially intact. When the carbonyl oxygen atom is protonated (scenario ii), the relaxed peptide bond length in fact decreases to 1.32 Å, as expected from the increased π-conjugation (or the double bond character of the bond) between C and N. Asparagine cyclization energy (Fig. 3 A) in this case is lower than that for the neutral peptide case; however, the peptide bond is significantly more stable and remains essentially intact as asparagine cyclization proceeds. In contrast, when the peptide nitrogen atom is protonated (scenario iii), the relaxed peptide bond length increases to 1.51 Å, indicating the weakening of that bond. As asparagine cyclization proceeds, that distance increases further and leads to breaking of that bond, resulting from the fact that a doubly protonated nitrogen makes a good leaving group (Fig. 3 B). The cyclization energy (Fig. 3 A) in this case is lower than that for the neutral peptide case and similar to that for oxygen protonation, which does not lead to peptide bond cleavage (see above). Collectively, these preliminary calculations indicate that protonation of the amide nitrogen is an important first step for C-terminal cleavage in low pH environments.

The protonation of the nitrogen of the scissile peptide bond proposed above makes that nitrogen atom transiently doubly protonated. In the broader context of enzymatic catalysis, this proposal is not new. Indeed, in the hydrolysis of a peptide bond by serine proteases, the nitrogen of the scissile peptide bond accepts a proton from the histidine of the catalytic triad (43). In their study of enzymatic reaction catalyzed by the HIV-1 protease, Trylska et al. found that protonation of the amide nitrogen was essential for peptide bond cleavage (44). Similarly, the protonation of the amide nitrogen was found to be the essential step in the hydrolysis of a formamide molecule, which was used as a computational model for peptide bond hydrolysis (45).

Given that the doubly protonated state of the amide nitrogen is a likely starting point of the C-terminal cleavage reaction at low pH, we explored further reaction pathways using semiempirical PM3 calculations, which guided additional high-level quantum calculations. We performed geometry optimizations using the PM3 method for 428 independent points in the two-dimensional space (shown in Fig. 4) based on reaction coordinates x and y (see Fig. 2 B).

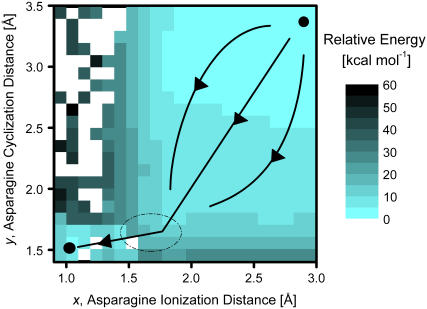
FIGURE 4.

FIGURE 4

Open in a new tab

Potential energy surface obtained from semiempirical PM3 calculations for the N-protonated system. The initial state is located at the top right and the final one at the bottom left. The larger region on the right is relatively featureless and can be sampled by multiple possible paths to the barrier region (dashed ellipse) that all lead to cyclization of asparagine, which is followed by ionization of the asparagine side-chain nitrogen.

The space of reaction coordinates considered in Fig. 4 is broad. The asparagine ionization distance, x, ranges from 0.9 to 3.0 Å (x = 2.0 Å corresponds to a typical hydrogen bond, whereas x = 1.0 Å indicates the deprotonated asparagine side chain and a re-formed hydronium ion). The asparagine cyclization distance, y, ranges from 1.4 to 3.5 Å (y = 3.5 Å is the relaxed distance in the initial state, whereas y = 1.5 Å indicates fully cyclized asparagine). We note that in these calculations the coordinate z (Fig. 2 B) is relaxed and the two original O-H distances in the water molecule were frozen as discussed in the Methods section.

The initial state (x = 3.0 Å, y = 3.5 Å) located on the top right of the plot (Fig. 4) is chosen to be zero for the relative reaction energy. The final products state is located in the bottom left corner (x = 1.0 Å, y = 1.5 Å) and corresponds to cyclized asparagine (succinimide), a re-formed hydronium ion, and a cleaved peptide bond. The path marked by arrows on Fig. 4 indicates the likely path followed by the C-terminal cleavage reaction. Along that path, y is reduced significantly first, and is then followed by a reduction in the value of x. The reduction in y can happen along combinations of paths shown in Fig. 4 because that region of the energy landscape is relatively featureless. In any case, cyclization of asparagine appears to be almost complete before the ionization of the side-chain nitrogen takes place. The barrier region is located near x = 1.6 Å, y = 1.6 Å indicated by the ellipse in Fig. 4 and has energy of ∼25 kcal/mol higher than the reference state. Fig. 4 shows that alternate paths, e.g., in which asparagine ionizes before its cyclization, are highly unlikely as they sample regions of considerably high energies.

We note that PM3 calculations for geometry optimizations do not converge for certain choices of x and y (open squares in Fig. 4). Most of these points are neighbored by points of higher energies, and therefore, should not affect the general conclusions drawn above.

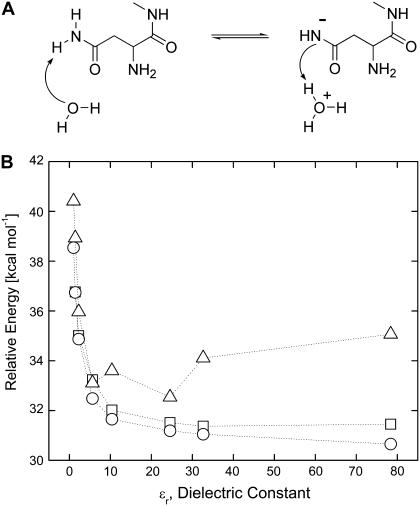
The observation made above that the asparagine cyclization proceeds before the ionization of its side chain is supported independently by high-level quantum calculations at the B3LYP/6-31G(d,p) level. Specifically, we followed the ionization of the asparagine by gradually transferring the proton from the side-chain nitrogen to the vicinal water molecule (Fig. 5 A). These high-level calculations also included effects of the dielectric constant of the local environment, which was assumed to be equal to 1 in the (gas phase) PM3 calculations.

FIGURE 5.

FIGURE 5

Open in a new tab

Energy of ionization of asparagine side-chain nitrogen (panel A) calculated in solvents of different dielectric constants: vacuum (ɛr = 1), argon (ɛr = 1.43), benzene (ɛr = 2.247), chlorobenzene (ɛr = 5.621), dichloroethane (ɛr = 10.36), ethanol (ɛr = 24.55), methanol (ɛr = 32.63), and water (ɛr = 78.39). Each implicit solvent has unique parameters such as radius and density. Gibbs energy is shown by blue triangles. Note that the peptide nitrogen has only one proton in this case. Gas phase coordinates, energy in solvent (○); solvent optimized coordinates, energy (□); and Gibbs free energy (Δ).

Fig. 5 B shows that both the electronic energy (E) and Gibbs free energy (G) for the ionization of the asparagine side chain are rather high, equal to ∼31 kcal/mol and ∼35 kcal/mol, respectively, even in the highly polar medium such as water. The intein active site is expected to have a dielectric constant lower than that of water, and therefore, the relative energy of ionization will be even higher. We note that the asparagine cyclization distance, y, is relaxed in these calculations and does not reduce significantly. Thus, asparagine cyclization will require additional energy. In contrast, as shown later, the side-chain ionization is almost spontaneous once the asparagine side chain has undergone cyclization and formed a succinimide, consistent with the experimental observations of enhanced cleavage at low pH by Wood et al. (17,18).

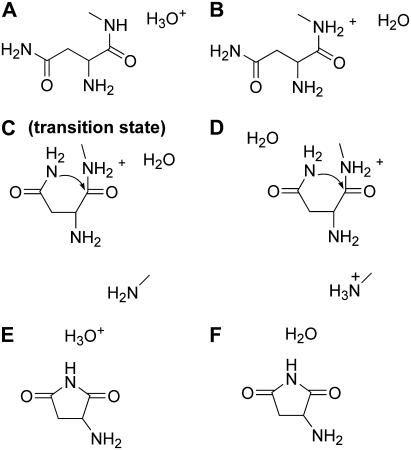
Collectively, the above calculations allow us to propose a somewhat detailed C-terminal cleavage reaction mechanism at low pH, in which six states shown in Fig. 6 are particularly important. Fig. 6 A shows the hydronium ion in the context of the relevant part of our intein system. The second state involves the donation of a proton by the hydronium ion to the peptide nitrogen, resulting in water and N-protonated state (Fig. 6 B). Asparagine cyclization is shown in Fig. 6, C and D, where the asparagine side chain still has two protons. The explicit water molecule is adjacent to the peptide nitrogen in one case (Fig. 6 C) and moves to accept a proton from the forming succinimide in another (Fig. 6 D). The formed succinimide with the proton passed back to the hydronium ion is shown in Fig. 6 E, whereas the final product is shown in Fig. 6 F. Water is re-formed and the extein segment leaves with an NH3 group.

FIGURE 6.

FIGURE 6

Open in a new tab

Important states in the proposed hydronium ion catalyzed asparagine cyclization and peptide bond cleavage mechanism (see text for details).

The vicinal water molecule plays an important role in this mechanism and is used both as an acid (state A → B) and a base (state D → E). Indeed, succinimide with 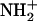Inline graphic is highly acidic due to the resonance effect of amide bonds on either side of that nitrogen. As a result, the nitrogen readily gives a proton to a nearby water molecule (state F).

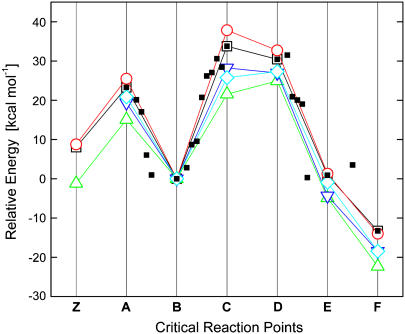
The energies corresponding to the various states (from A to F) presented in Fig. 6 are shown in Fig. 7. State Z in Fig. 7 is shown as a reference. The transition from Z to A corresponds to a positively charged histidine and a water molecule (Z) forming a neutral histidine and a hydronium ion (state A). The energy barrier from B to C/D corresponds to the asparagine cyclization, where the second proton is still attached to the asparagine side chain. Indeed the normal mode corresponding to the single imaginary frequency in state C was in the direction of bond formation, as expected. For this system, the energetics suggest that the nitrogen will give its second proton to water to reform the hydronium ion (Fig. 6 E). As discussed above, in the absence of protonation of the peptide nitrogen (e.g., in the case of a neutral peptide), the asparagine cyclization has a higher barrier.

FIGURE 7.

FIGURE 7

Open in a new tab

Electronic energies and approximate Gibbs free energies for states A through F in Fig. 6 (energies are relative to state B). State Z is shown as a reference and corresponds to a positively charged histidine and a water molecule (Z). Figure key: vacuum optimized coordinates energy (□) and Gibbs free energy (○); water optimized coordinates, energy (Δ); and Gibbs free energy (▿). Single point energies calculated with B3LYP/6-311++g(2d,p) using the coordinates optimized in implicit water without the diffuse functions (◊). Energies of intermediate structures between the states in Fig. 6 optimized in the gas phase (▪) are also shown.

Fig. 7 also highlights the effects of taking into account the dielectric constant of the environment of the active site on intein. As expected, the energy barrier (∼33 kcal/mol) in the gas phase is reduced to ∼25 kcal/mol in implicit solvent having a high dielectric constant. When tested with MP2, the energy barrier was found to be 29.4 kcal/mol at the MP2/aug-cc-pVDZ level. This mechanism was also tested with the 45-atom tripeptide system (histidine-asparagine-cysteine), and the gas phase energy barrier was found to be 28 kcal/mol, with B3LYP/6-311++G(d,p). QM/MM calculations that include more explicit water molecules suggest that the computational energy barrier calculated with B3LYP/6-31G(d,p) is 3–4 kcal/mol lower than the 33 kcal/mol found by the gas phase calculation. Since the crystal structures of active inteins do not include exteins, the conformation of the exteins and N- and C-terminal active sites is unknown. Hence, the intein plus extein system used in the QM/MM calculation will require additional verification to be comparable to precursor inteins used in experiment. The actual dielectric constant of the protein interior is between that of bulk water and vacuum, and hence, our calculations suggest that the energy barrier for C-terminal cleavage lies between 25 and 33 kcal/mol. The experimental value is ∼21 kcal/mol at pH 6.0 (17).

We note that our calculations have several limitations. In the actual intein system, the overall protein structure (including both the intein and exteins) that surrounds the active site provides a significantly greater structural as well as chemical context for the reaction to occur. Also, there will likely be more than one water molecule in the vicinity of the active site that could mitigate the C-terminal cleavage reaction. Our system, in contrast, is significantly smaller due to computational limitations. In addition, our calculations are by necessity static in nature, and ignore the conformational and water exchange dynamics that are important in enzymatic catalysis (46). These types of concerns are shared by most (if not all) quantum calculations of enzymatic reactions. Nevertheless, our calculations provide a plausible mechanism for C-terminal cleavage that could be tested in the future by application of better multi-scale methods and/or detailed experimentation.

CONCLUSIONS

In summary, we present computational analysis of the intein C-terminal cleavage reaction. In particular, we have studied the cleavage mechanism of the M. tuberculosis RecA intein using information from available intein crystal structures and mutagenesis experiments. Part of the intein structure close to the C-terminal reaction site was considered in both gas phase as well as implicit solvent models calculations. Specifically, we performed computationally efficient PM3 calculations to obtain a qualitative understanding of the reaction pathway in the two-dimensional space of reaction coordinates chosen heuristically. More accurate high-level density functional calculations after the PM3 calculations allowed us to propose a detailed mechanism of the C-terminal cleavage at low pH.

Our calculations suggest that N-protonation, protonation of the nitrogen atom of the scissile peptide bond, is the likely starting point of the C-terminal cleavage reaction. A hydronium ion, included in our calculations to mimic a low pH environment, protonates the peptide nitrogen. After N-protonation, the reaction proceeds through asparagine cyclization followed by succinimide deprotonation. The energy barrier of ∼33 kcal/mol for the rate determining step in gas phase reduces to ∼25 kcal/mol in solution, and is close to the value of ∼21 kcal/mol obtained from experiments (18). Our proposed mechanism uses one water molecule, which acts both as an acid and a base, and plays a critical role in the cleavage reaction.

Further work will investigate the importance of the penultimate histidine and first C-extein residue, cysteine, or serine by increasing the system size. The possibility of protonation by histidine is not excluded by the mechanism proposed here. For example, positively charged histidine could donate a proton to the peptide nitrogen via a water molecule; the reaction can then follow steps similar to the ones outlined here.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Acknowledgments

P.S. thanks Caterina Soldano and Dr. Hongwei Liu for help with graphics and figures. We thank Drs. Marlene Belfort and Victoria Derbyshire and their research group for numerous helpful discussions over the past 3 years and a critical reading of this manuscript. We also thank Drs. Henry Paulus, David Wood, Stephan Irle, Gil Amitai, and Dilip Asthagiri for their critical reading of this manuscript.

This work was supported by National Science Foundation grant CTS03-04055-NIRT and National Institutes of Health grant GM44844. Supercomputer time was provided by the National Center for Supercomputing Applications.

References

  • 1.Belfort, M., B. L. Stoddard, D. Wood, and V. Derbyshire. 2005. Homing endonucleases and inteins. In Nucleic Acids and Molecular Biology, 1st ed., Vol. 16. Springer, Berlin, Germany. 233–253.
  • 2.Perler, F. B., E. O. Davis, G. E. Dean, F. S. Gimble, W. E. Jack, N. Neff, C. J. Noren, J. Thorner, and M. Belfort. 1979. Protein splicing elements: inteins and exteins—a definition of terms and recommended nomenclature. Nucleic Acids Res. 22:1125–1127. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Paulus, H. 2000. Protein splicing and related forms of protein autoprocessing. Annu. Rev. Biochem. 69:447–496. [DOI] [PubMed] [Google Scholar]
  • 4.Paulus, H. 2001. Inteins as enzymes. Bioorg. Chem. 29:119–129. [DOI] [PubMed] [Google Scholar]
  • 5.Xu, M. Q., D. G. Comb, H. Paulus, C. J. Noren, Y. Shao, and F. B. Perler. 1994. Protein splicing: an analysis of the branched intermediate and its resolution by succinimide formation. EMBO J. 13:5517–5522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Mizutani, R., S. Nogami, M. Kawasaki, Y. Ohya, Y. Anraku, and Y. Satow. 2002. Protein-splicing reaction via a thiazolidine intermediate: crystal structure of the VMA1-derived endonuclease bearing the N- and C-terminal propeptides. J. Mol. Biol. 316:919–929. [DOI] [PubMed] [Google Scholar]
  • 7.Poland, B. W., M. Q. Xu, and F. A. Quiocho. 2000. Structural insights into the protein splicing mechanism of PI-SceI. J. Biol. Chem. 275:16408–16413. [DOI] [PubMed] [Google Scholar]
  • 8.Klabunde, T., S. Sharma, A. Telenti, W. R. Jacobs Jr., and J. C. Saccettini. 1998. Crystal structure of GyrA intein from Mycobacterium xenopi reveals structural basis of protein splicing. Nat. Struct. Biol. 5:31–36. [DOI] [PubMed] [Google Scholar]
  • 9.Duan, X. Q., F. S. Gimble, and F. A. Quiocho. 1997. Crystal structure of PI-SceI, a homing endonuclease with protein splicing activity. Cell. 89:555–564. [DOI] [PubMed] [Google Scholar]
  • 10.Ichiyanagi, K., Y. Ishino, M. Ariyoshi, K. Komori, and K. Morikawa. 2000. Crystal structure of an archaeal intein-encoded homing endonuclease PI-PfuI. J. Mol. Biol. 300:889–901. [DOI] [PubMed] [Google Scholar]
  • 11.Hiraga, K., V. Derbyshire, J. T. Dansereau, P. Van Roey, and M. Belfort. 2005. Minimization and stabilization of the Mycobacterium tuberculosis recA intein. J. Mol. Biol. 354:916–926. [DOI] [PubMed] [Google Scholar]
  • 12.Chen, L., J. Benner, and F. B. Perler. 2000. Protein splicing in the absence of an intein penultimate histidine. J. Biol. Chem. 275:20431–20435. [DOI] [PubMed] [Google Scholar]
  • 13.Nichols, N. M., and T. C. Evans. 2004. Mutational analysis of protein splicing, cleavage, and self-association reactions mediated by the naturally split Ssp DnaE intein. Biochemistry. 43:10265–10276. [DOI] [PubMed] [Google Scholar]
  • 14.Dassa, B., H. Haviv, G. Amitai, and S. Pietrokovski. 2004. Protein splicing and auto-cleavage of bacterial intein-like domains lacking a C′-flanking nucleophilic residue. J. Biol. Chem. 279:32001–32007. [DOI] [PubMed] [Google Scholar]
  • 15.Amitai, G., B. Dassa, and S. Pietrokovski. 2004. Protein splicing of inteins with atypical glutamine and aspartate C-terminal residues. J. Biol. Chem. 279:3121–3131. [DOI] [PubMed] [Google Scholar]
  • 16.Lyubimov, A. Y., P. I. Lario, I. Moustafa, and A. Vrielink. 2006. Atomic resolution crystallography reveals how changes in pH shape the protein microenvironment. Nat. Chem. Biol. 2:259–264. [DOI] [PubMed] [Google Scholar]
  • 17.Wood, D. W., W. Wu, G. Belfort, V. Derbyshire, and M. Belfort. 1999. A genetic system yields self-cleaving inteins for bioseparations. Nat. Biotechnol. 17:889–892. [DOI] [PubMed] [Google Scholar]
  • 18.Wood, D. W., V. Derbyshire, W. Wu, M. Chartrain, M. Belfort, and G. Belfort. 2000. Optimized single-step affinity purification with a self-cleaving intein applied to human acidic fibroblast growth factor. Biotechnol. Prog. 16:1055–1063. [DOI] [PubMed] [Google Scholar]
  • 19.Mathys, S., T. C. Evans, I. C. Chute, H. Wu, S. Chong, J. Benner, X. Q. Liu, and M. Q. Xu. 1999. Characterization of a self-splicing mini-intein and its conversion into autocatalytic N- and C-terminal cleavage elements: facile production of protein building blocks for protein ligation. Gene. 231:1–13. [DOI] [PubMed] [Google Scholar]
  • 20.Ding, Y., M. Q. Xu, I. Ghosh, X. Chen, S. Ferrandon, G. Lesage, and Z. Rao. 2003. Crystal structure of a mini-intein reveals a conserved catalytic module involved in side chain cyclization of asparagine during protein splicing. J. Biol. Chem. 278:39133–39142. [DOI] [PubMed] [Google Scholar]
  • 21.Geiger, T., and S. Clarke. 1987. Deamidation, isomerization, and racemization at asparaginyl and aspartyl residues in peptides. Succinimide-linked reactions that contribute to protein degradation. J. Biol. Chem. 262:785–794. [PubMed] [Google Scholar]
  • 22.Capasso, S., L. Mazzarella, G. Sorrentino, G. Balboni, and A. J. Kirby. 1996. Kinetics and mechanism of the cleavage of the peptide bond next to asparagine. Peptides. 17:1075–1077. [DOI] [PubMed] [Google Scholar]
  • 23.Capasso, S., L. Mazzarella, A. J. Kirby, and S. Salvadori. 1997. Succinimide-mediated pathway for peptide bond cleavage: Kinetic study on an Asn-Sar containing peptide. Biopolymers. 40:543–551. [Google Scholar]
  • 24.Shao, Y., M. Q. Xu, and H. Paulus. 1995. Protein splicing: characterization of the aminosuccinimide residue at the carboxyl terminus of the excised intervening sequence. Biochemistry. 34:10844–10850. [DOI] [PubMed] [Google Scholar]
  • 25.Blomberg, M. R. A., and P. E. M. Siegbahn. 2001. A quantum chemical approach to the study of reaction mechanisms of redox-active metalloenzymes. J. Phys. Chem. B. 105:9375–9386. [Google Scholar]
  • 26.Wladkowski, B. D., M. Krauss, and W. J. Stevens. 1995. Ribonuclease A catalyzed transphosphorylation: An ab initio theoretical study. J. Phys. Chem. 99:6273–6276. [Google Scholar]
  • 27.Friesner, R. A., and B. D. Dunietz. 2001. Large-scale ab initio quantum chemical calculations on biological systems. Acc. Chem. Res. 34:351–358. [DOI] [PubMed] [Google Scholar]
  • 28.Kahn, K., and T. C. Bruice. 2003. Comparison of reaction energetics and leaving group interactions during the enzyme-catalyzed and uncatalyzed displacement of chloride from haloalkanes. 2003. J. Phys. Chem. B. 107:6876–6885. [Google Scholar]
  • 29.Zhang, X. D., X. H. Zhang, and T. C. Bruice. 2005. A definitive mechanism for chorismate mutase. Biochemistry. 44:10443–10448. [DOI] [PubMed] [Google Scholar]
  • 30.Dellago, C., P. G. Bolhuis, F. S. Csajka, and D. Chandler. 1998. Transition path sampling and the calculation of rate constants. J. Chem. Phys. 108:1964–1977. [Google Scholar]
  • 31.Stewart, J. J. P. 1989. Optimization of parameters for semiempirical methods I. Method. J. Comp. Chem. 10:209–220. [Google Scholar]
  • 32.Frisch, M. J., G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, and J. A. Pople. 2004. Gaussian 03, Revision C.02. Gaussian, Inc., Wallingford, CT.
  • 33.Stewart, J. J. P. 1991. Optimization of parameters for semiempirical methods. III. Extension of PM3 to Be, Mg, Zn, Ga, Ge, As, Se, Cd, In, Sn, Sb, Te, Hg, T1, Pb, and Bi. J. Comput. Chem. 12:320–341. [Google Scholar]
  • 34.Ferguson, D. M., W. A. Gould, W. A. Glauser, S. Schroeder, and P. A. Kollman. 1992. Comparison of ab initio, semiempirical, and molecular mechanics calculations for the conformational analysis of ring systems. J. Comput. Chem. 13:525–532. [Google Scholar]
  • 35.Csonka, G. I. 1993. Analysis of the core-repulsion functions used in AM1 and PM3 semiempirical calculations: Conformational analysis of ring systems. J. Comput. Chem. 14:895–898. [Google Scholar]
  • 36.Becke, A. D. 1993. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98:5648–5652. [Google Scholar]
  • 37.Lynch, B. J., P. L. Fast, M. Harris, and D. G. Truhlar. 2000. Adiabatic connection for kinetics. J. Phys. Chem. A. 104:4811–4815. [Google Scholar]
  • 38.Miertus, S., E. Scrocco, and J. Tomasi. 1981. Electrostatic interaction of a solute with a continuum. A direct utilization of ab initio molecular potentials for the prevision of solvent effects. Chem. Phys. 55:117–119. [Google Scholar]
  • 39.Cancès, M. T., B. Mennucci, and J. Tomasi. 1997. Evaluation of solvent effects in isotropic and anisotropic dielectrics, and in ionic solutions with a unified integral equation method: theoretical bases, computational implementation and numerical applications. J. Chem. Phys. 107:3032–3041. [Google Scholar]
  • 40.Irikura, K. K., and D. J. Frurip. 1998. Computational Thermochemistry: Prediction and Estimation of Molecular Thermodynamics. ACS Symposium Series 677. American Chemical Society, Washington, DC.
  • 41.Ochterski, J. W. 2000. Thermochemistry in Gaussian. Gaussian, Inc., Wallingford, CT.
  • 42.Milner-White, E. J. 1997. The partial charge of the nitrogen atom in peptide bonds. Protein Sci. 6:2477–2482. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Voet, D., J. G. Voet, and C. W. Pratt. 1999. Fundamentals of Biochemistry. Wiley, New York.
  • 44.Trylska, J., P. Grochowski, and J. A. McCammon. 2004. The role of hydrogen bonding in the enzymatic reaction catalyzed by HIV-1 protease. Protein Sci. 13:513–528. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Krug, J. P., P. L. A. Popelier, and R. F. W. Bader. 1992. Theoretical study of neutral and of acid and base-promoted hydrolysis of formamide. J. Phys. Chem. 96:7604–7616. [Google Scholar]
  • 46.Eppler, R. K., R. S. Komor, J. Huynh, J. S. Dordick, J. A. Reimer, and D. S. Clark. 2006. Water dynamics and salt-activation of enzymes in organic media: mechanistic implications revealed by NMR spectroscopy. Proc. Natl. Acad. Sci. USA. 103:5706–5710. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES