VASP Governs Actin Dynamics by Modulating Filament Anchoring

Abstract

Actin filament dynamics at the cell membrane are important for cell-matrix and cell-cell adhesions and the protrusion of the leading edge. Since actin filaments must be connected to the cell membrane to exert forces but must also detach from the membrane to allow it to move and evolve, the balance between actin filament tethering and detachment at adhesion sites and the leading edge is key for cell shape changes and motility. How this fine tuning is performed in cells remains an open question, but possible candidates are the Drosophila enabled/vasodilator-stimulated phosphoprotein (Ena/VASP) family of proteins, which localize to dynamic actin structures in the cell. Here we study VASP-mediated actin-related proteins 2/3 (Arp2/3) complex-dependent actin dynamics using a substrate that mimics the fluid properties of the cell membrane: an oil-water interface. We show evidence that polymerization activators undergo diffusion and convection on the fluid surface, due to continual attachment and detachment to the actin network. These dynamics are enhanced in the presence of VASP, and we observe cycles of catastrophic detachment of the actin network from the surface, resulting in stop-and-go motion. These results point to a role for VASP in the modulation of filament anchoring, with implications for actin dynamics at cell adhesions and at the leading edge of the cell.

INTRODUCTION

Major players in cellular actin dynamics include the polymerization nucleating factors: the actin related proteins 2/3 (Arp2/3) complex (1) and formins (2), which often act in concert with the Drosophila enabled/Vasodilator-stimulated phophoprotein (Ena/VASP) family of proteins (3). Ena/VASP proteins enhance actin dynamics by mechanisms that remain unclear although various functions have been attributed to them, including actin filament nucleation (4), profilin and G-actin recruitment (5,6), anticapping activity (7,8), filament detaching capability (9), and filament bundling (10). Much of what we know about how these and other actin-binding proteins affect actin structure formation and actin-based movement derives from studies performed using in vitro systems, with either Listeria monocytogenes, beads, or vesicles as the substrate for actin polymerization ((11) and references therein).

The role of VASP in cells remains likewise unclear as VASP has been reported to be both a positive and negative regulator of cell motility and adhesion. VASP null fibroblasts show an increase in overall cell motility (8,12), whereas VASP null Dictyostelium shows a decrease in chemotaxis efficiency (13). However, increased adhesion and migration are observed when VASP is specifically removed from integrin adhesion sites by genetic ablation of zyxin in fibroblasts (14). Likewise, VASP null platelets show enhanced aggregation (15). Conversely, either an increase or a decrease in VASP interaction with cell-matrix adhesion sites by altering migfilin levels is detrimental to cell motility (16). In regard to cell-cell contacts, VASP is present there and has been implicated in the actin reorganization accompanying early junction assembly (17–19). All together, these results beg the question as to the role of VASP in the cell, in particular at adhesion sites.

Here we study how VASP affects Arp2/3 complex-catalyzed actin filament formation, using an oil droplet system that more closely mimics a cell membrane than previously used beads or Listeria, which have nonfluid surfaces. We find that the presence of VASP provokes a transition from continuous to jumping motion, concomitant with changes in drop shape and in the actin shell around the drop. We relate these changes to the interplay between the diffusive movement of unbound activators and the convective movement of activators bound to actin filaments on the fluid surface, highlighting the importance of the dynamic attachment of the membrane to the actin network in actin-based processes.

MATERIALS AND METHODS

Proteins and extracts

Glutathione S-transferase (GST) fusions of the VCA fragment of WASP (amino acids 402–503), the PRO domain of ActA (amino acids 235–584), and the ActA-C domain of ActA (amino acids 394–584) were cloned and purified as previously described (20,21). These proteins are called simply VCA, PRO, and ActA-C in the text. Alexa 488-labeled VCA and PRO were prepared following manufacturer's instructions using Alexa Fluor 488 carboxylic acid succinimidyl ester (Molecular Probes, Eugene, OR), at pH 8, followed by dialysis into phosphate buffered saline (PBS) to remove excess label. HeLa cell extract was prepared and supplemented as previously described (22) with the following changes. The total protein concentration was 26 mg/ml by Bradford analysis and the extract was diluted 2:3 or 3:4 with buffer (10 mM Tris, 10 mM EGTA, 2 mM CaCl₂, pH 7.5) before use. Extracts were supplemented with 1 μM actin that included up to 0.5 μM actin-Alexa 594 (Molecular Probes) for epifluorescence and confocal experiments.

Droplet preparation

Oil droplets were formed by sonicating (Misonix Ultrasonic Liquid Processor, Farmingdale, NY) a 10% v/v oil (Isio4)/protein mixture for 10–15 s at 50–100 W. Final protein concentrations in the sonicated mixture were 5.0–6.0 μM VCA and 0.8 μM PRO or ActA-C in PBS. The amount of VCA and PRO on the surface of the droplets is approximately the same as on the surface of hard beads (22), with 6 nm between VCA molecules and 50 nm between PRO molecules, as evaluated by fluorescently labeling the proteins and comparing drop fluorescence to hard bead fluorescence. For a typical reaction, 0.2 μL of the sonicate was mixed with 4–6 μL of extract, placed between slide and coverslip, sealed, and incubated at 23°C for 1–5 h before observation.

Microscopy and immunolabeling

Phase contrast and fluorescence microscopy were performed on an Olympus (Melville, NY) upright microscope with a 100× oil objective. Images were obtained using an intensified charge-coupled device Coolsnap camera (Roper Scientific, Evry, France). Confocal optical sections were taken using a 100× oil objective on a Leica (Wetzlar, Germany) TCS SP2 confocal microscope. The z-series increment was 0.3 μm. Immunolabeling for VASP on droplet surfaces was performed using flowcells composed of two parallel 165 μm-thick spacers overlaid by a coverslip and sealed on two sides with nail polish. Reagents were added, and washes were performed by pipetting on one side of the flowcell and drawing out the liquid on the other side with a piece of Whatman filter paper. Reactions of 40 μL were incubated in the flowcells in a moist chamber, fixed with 1% glutaraldehyde in cytoskeleton buffer (10 mM MES, 150 mM NaCl, 5 mM EGTA, 5 mM MgCl₂, 5 mM glucose, pH 6.1), and then probed with anti-VASP (mouse IgG, BD Biosciences, Le Pont de Claix, France), followed by visualization with anti-mouse Alexa 488 (Molecular Probes).

Analysis of phase contrast and fluorescence images

Time-lapse tracking analyses were performed using Metamorph software. Unless noted otherwise, indicated velocities correspond to the velocity of the centroid of the drop. All indicated drop sizes are the radii of the spheres corresponding to the equivalent prolate volumes of the drops as estimated by Metamorph, using phase contrast or bright field images. The error on the radii is estimated to be ∼1 pixel (±0.1 μm). Elliptical form factors were given by Metamorph and ɛ ratios were calculated by manually fitting circles to the front and the back of drops. Measurements on confocal images were performed using confocal slices that passed through the center of the comet. Thickness measurements on phase contrast and confocal images were taken to be the distance between inflection points in the intensity curves obtained by linescan analysis. Back to front VCA ratios were calculated by performing linescan analysis along the axis of rotation of continuously moving drops and taking the quotient of the two maxima. Likewise, amounts of actin along the sides of drops was measured by performing linescan analysis across the span of the drop, perpendicular to the axis of rotation, and midway between the front and the back of the drop. The average of the maximum intensities was taken. For both linescan analyses, the line width was 0.7 μm and the average intensity across the line width was used. For all data, error bars are ± one standard deviation from the mean. Points without errors bars indicate that a single measurement was taken.

Contour analysis

The experimentally obtained drop shape was digitized, and the (x, y) coordinates of the profile were determined. The digitized drop profile was then smoothed, using a 5–12 pixel window to soften the initial contour. The local radii of curvature at every point along the drop were obtained by differentiation of the smoothed drop profile. A further smoothing step was performed to filter out the high frequency noise. A small region at the very front of the drop was used to determine the radius of curvature, R, in the absence of stress. Results remained unchanged upon reasonable variations of the size of this region, confirming the determination of R. Any other point of the contour was defined by two radii of curvature, 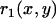, characterizing the curvature in the direction determined by the local tangent of the drop profile, and 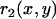, characterizing the curvature in the direction which is perpendicular to the local tangent of the drop profile. (Note that at the front of the droplet, 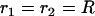.) To obtain the normal stress, 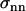, we used Laplace's law comparing the front and each point of the contour of coordinates (x, y), 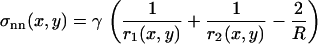, with γ the surface tension of the oil-extract interface, experimentally determined as 4 nN/μm (23). The term 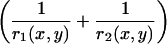represents the total curvature at the point (x, y). Where the actin filaments are pushing on the surface of the drop, they flatten the drop, r₁ and r₂ increase, and the normal stress is negative. Where actin filaments are pulling on the surface, the local curvature is larger than 2/R, and the stress is positive.

RESULTS

VASP-mediated Arp2/3 complex-dependent actin polymerization on oil droplets

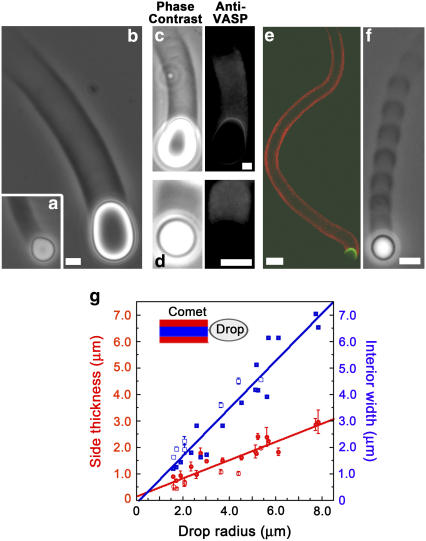
We used two protein fragments, the VCA domain of the Wiskott-Aldrich syndrome protein (WASP) and the PRO portion of the ActA protein from Listeria to recruit the Arp2/3 complex and VASP, respectively, to oil droplet surfaces. Emulsions were prepared by sonicating mixes of VCA and oil, with or without PRO. Using fluorescently labeled proteins, we observed that VCA and PRO bound to the oil droplet surfaces (see below), probably via hydrophobic interactions. When VCA and VCA+PRO-coated droplets were placed in HeLa cell extracts, homogenous actin clouds formed and then the clouds polarized to form comets after 1–3 h of incubation (Fig. 1, a and b). Immunolabeling showed that VASP associated with the entire length of both VCA+PRO and VCA comets and with the surface of VCA+PRO drops under the comet but not with the surface of VCA drops (Fig. 1, c and d, respectively). VCA oil droplets, recruiting only the Arp2/3 complex at their surface, were pear-shaped (Fig. 1 a; (23)) and displayed continuous motion at an average velocity of 0.15 ± 0.07 μm/min, independent of drop size (Supplementary Material, Fig. S1). VCA+PRO droplets, recruiting VASP in addition to the Arp2/3 complex at their surface, were oval-shaped (Fig. 1 b), moved five times faster than drops recruiting the Arp2/3 complex alone, 0.7 ± 0.4 μm/min regardless of drop size (Supplementary Material, Fig. S1), and the comets were partially hollow (Fig. 1 e). When ActA-C, corresponding to the PRO molecule but lacking the VASP binding site, was absorbed to droplet surfaces instead of PRO, the VCA+ActA-C droplets gave the VCA-only phenotype, identical to Fig. 1 a. Depending on the sizes of the drops, up to ∼40% of VASP-recruiting droplets displayed jumping movement, with high- and low-speed phases accompanied by optical density variations in the comet (Fig. 1 f and Table 1). For both continuous and jumping motion, the thickness of the side walls of the comet cylinder was not constant but increased with increasing drop size (Fig. 1 g and Supplementary Material, Fig. S2).

FIGURE 1.

Actin comets form on oil droplets recruiting the Arp2/3 complex and VASP. Phase contrast microscopy of droplets coated with VCA shows a full comet that pinches the drop into a pear shape (a), whereas drops coated with a mixture of VCA and PRO have partially hollow comets and are deformed into an oval shape (b). Immunolabeling of VCA+PRO droplets (c) and VCA droplets (d); left panel: phase contrast and right panel: anti-VASP, shows VASP localization at the surface of VCA+PRO droplets, and a stain throughout the comets on both VCA and VCA+PRO droplets. (e) Comet hollowness is confirmed by confocal microscopy. Actin in red, VCA in green. (f) Phase contrast microscopy shows the striped comet of a jumping droplet. All bars are 2 μm except for the confocal image where the bar is 10 μm. (g) Comet wall thicknesses (red circles) and interior cavity spans (blue squares) as a function of drop radius. Measurements were performed using confocal sections (solid symbols) and phase contrast images (open symbols). Both wall thickness and interior span increase linearly with increasing drop size giving line slopes of 0.3 (correlation factor = 0.91) and 0.9 (correlation factor, 0.95), respectively.

TABLE 1.

Percentage of hopping drops (in relation to the total number of comets, both continuous and jumping) as a function radius

Droplet radius (μm)	% Hopping	Comet count
0–1	43.3	30
1–2	35.2	88
2–3	18.2	55
3–4	14.9	47
4–5	12.2	41
5–6	15.4	26
6–7	7.1	14
7–8	0	8

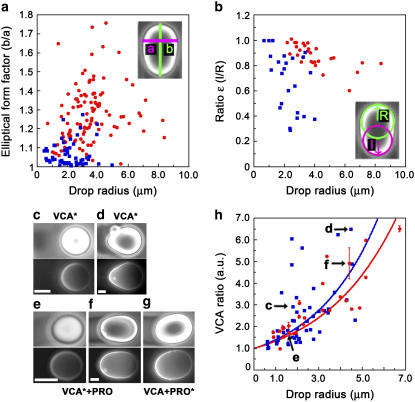
For continuously moving drops, we quantified the shape differences shown in Fig. 1, a and b, using two parameters: the elliptical form factor and the ratio ɛ (Fig. 2, a and b). The elliptical form factor is the length of the long axis divided by the length of the short axis of the drop, and the ratio ɛ is the radius of curvature of the back of the drop (under the comet) divided by the radius of curvature of the front of the drop (schemes, Fig. 2, a and b). These parameters give an evaluation of the extent of drop elongation and asymmetry, respectively. On average, droplets recruiting VASP in addition to the Arp2/3 complex had higher elliptical form factors and ɛ ratios closer to 1 than droplets recruiting the Arp2/3 complex alone, giving the VASP-recruiting drops a kiwi shape as opposed to a pear shape. The decrease in the ɛ ratio and the increase in elliptical form factors with increasing drop size in both the presence and absence of VASP are explained by Laplace's law: large drops have a smaller internal pressure and are thus more easily deformed than small drops.

FIGURE 2.

Droplets recruiting VASP in addition to the Arp2/3 complex are more elongated but less pinched than droplets recruiting the Arp2/3 complex alone, and both drop types accumulate VCA under the comet. (a) Elliptical form factors, calculated by dividing the long axis “b” of the drop by the small axis “a” and (b) Values of the ɛ ratio, calculated by transcribing the front and the back of the drop as circles, and then dividing the radius of the back circle “l” by the radius of the front circle “R”. Both parameters are plotted as a function of radius for drops recruiting the Arp2/3 complex only (blue squares) or VASP in addition to the Arp2/3 complex (red circles). Paired phase contrast (top) and fluorescence (bottom) images of VCA (c,d) and VCA+PRO (e–g) drops undergoing continuous motion. The asterisks in the labels indicate which molecules are fluorescently labeled. Bars 2 μm. (h) Intensities of VCA fluorescence were recorded along the long axis of moving drops, and the intensity under the comet was divided by the intensity at the front of the drop to give the VCA ratio in arbitrary units, which was plotted as a function of drop radius. Droplets coated with VCA alone (blue squares) and droplets coated with VCA+PRO (red circles). The points fit to exponential functions (solid lines) with exponents of 0.34 ± 0.02 μm⁻¹ and 0.30 ± 0.01 μm⁻¹, respectively. Letters on the graph refer to the images (c–f).

Using fluorescently labeled proteins, we visualized the localization of VCA and PRO on droplets undergoing continuous motion (Fig. 2, c–g). We observed that the VCA density at the back of the drop as compared to the front increased with drop radius, showing exponential relations for both VCA+PRO droplets, exponent 0.30 ± 0.01 μm⁻¹, and VCA droplets, exponent 0.34 ± 0.02 μm⁻¹ (Fig. 2 h, red and blue curves, respectively, and images c–f). Fluorescently labeled PRO on VCA+PRO droplets resembled VCA distribution (Fig. 2 g).

Hopping motion of oil droplets

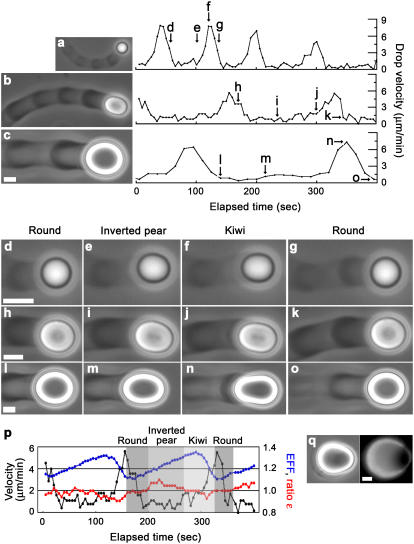
VCA+PRO droplets differ from VCA droplets in their shape, comet morphology, and displacement speed. More importantly, VCA+PRO droplets often displayed hopping motion, whereas VCA droplets never did. To understand how jumping motion could result from the presence of VASP, we did an in-depth study of hopping droplets. Typical jumping droplets of various sizes are shown in Fig. 3, a–c, by phase contrast microscopy with the accompanying velocity cycle measured for the center of mass of the drop. (For movies of drops of Fig. 3, a and c, see Supplementary Material, Videos 1–2.) The maximum and minimum velocities of the center of mass of the droplets were independent of drop size, 6.0 ± 2.0 μm/min and 0.7 ± 0.2 μm/min, respectively. Low-speed phases were associated with dense actin buildup, whereas high-speed phases were characterized by reduced actin accumulation, giving the comets a striped appearance by phase contrast microscopy.

FIGURE 3.

VASP-recruiting droplets in a range of sizes display jumping behavior involving velocity changes, actin density variations in the comet, and shape modulations. Phase contrast microscopy of (a) radius = 1.2 μm, (b) radius = 2.1 μm, and (c) radius = 3.4 μm jumping drops and their accompanying velocity cycles as a function of elapsed time. Arrows on the velocity cycle graphs refer to blowups (d–o) featuring drop deformations at various times of each cycle. (p) A summary of how shape changes are associated with velocity changes, with elliptical form factors (blue) and ɛ ratios (red) plotted as an overlay on a velocity cycle. (q) shows a droplet where the symmetrical actin cloud that precedes comet formation is breaking open, phase contrast (left panel) and fluorescence microscopy using labeled actin (right panel). All bars are 2 μm.

During a velocity cycle, the droplets changed shape, Fig. 3, d–o. The arrows on the velocity graphs indicate where each image was taken, and Fig. 3 p shows traces of elliptical form factor and ratio ɛ over the course of a velocity cycle of the drop shown in Fig. 3 b. Overall, droplets were essentially round coming out of the high-speed phase (ratio ɛ equaled 1 and the elliptical form factor was at a minimum), and they subsequently assumed an inverted pear shape (ratio ɛ > 1). Note that inverted pear shapes were also observed preceding comet formation on droplets (Fig. 3 q). As the low-speed phase progressed, the back of the drop became pinched (ratio ɛ decreased) and the drop also elongated (increasing elliptical form factor). Importantly, only after the elliptical form factor reached a maximum and started to decline did the drop begin accelerating, attaining its maximum velocity and reverting to a round shape.

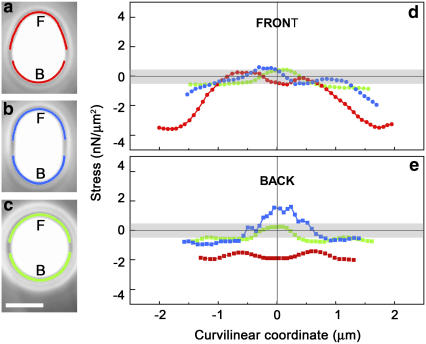
Drop shapes are indicative of the forces exerted by the actin filaments growing on the drop surface, and the force per unit surface, or normal stress, can be estimated by using the Laplace equation, as developed previously (23–25). As such, changes in shape are the signature of a redistribution of forces on the surface. Inverted pear-, kiwi-, and round-shaped drops during a typical jump are shown in Fig. 4, a–c, with the surface stresses plotted as a function of the position along the drop profile (Fig. 4, d and e). (See also Supplementary Material, Video 3.) Compressive stresses are negative, and pulling stresses are positive. The top traces describe the stresses in play along the front of the drops, and the bottom traces along the back halves of the drops. A round drop had a stress that hovered around zero within the error of the measurement at every point along the contour (green curves). For the kiwi shape, compressive stresses developed along the sides of the drop, whereas pulling stresses were evident at the back (blue curves). More importantly, for the inverted pear shape, only squeezing stresses were at work (negative values for the red curves in Fig. 4, d and e) except at the very front of the drop where the stress vanished. As a result of these compressive stresses, the drop was squeezed out the front of the actin pouch, where there was no (or little) actin, reminiscent of symmetry breaking events on droplets (Fig. 3 q).

FIGURE 4.

Analysis of contours indicates that the distribution and magnitude of pushing and pulling normal stresses on the drop vary over the course of a jump. (a–c) Blowups of phase contrast images of inverted pear, kiwi, and round shapes recorded during the velocity jump of a 1.7-μm radius drop and analysis of the stresses developed at the drop surface as a function of position along the contour for the front (d) and the back (e) of the drop. The x coordinate corresponds to the distance along the contour length from the zero position, which is placed at the extreme front and back of the drop (“F” and “B” in a–c). The gray bands in d and e indicate the estimated error in the calculated normal stress, ±0.5 nN/μm², derived from errors in the generation of r₁, r₂, and R values from the smoothed profile (see Materials and Methods). The traces in d and e correspond to stresses in the regions traced out in the same color on the phase contrast images. The gaps in the contours are a result of the smoothing process. Bar, 2 μm.

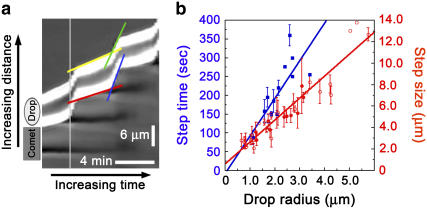
To see how the center of mass measurements compared to the velocities of the front and the back of the drop, we performed a kymograph analysis (Fig. 5 a). During the low-speed phase, the back of the drop moved more slowly than the front due to elongation of the drop, in this case, 1.0 μm/min vs. 1.3 μm/min. The front and the back appeared to jump together (follow the light gray vertical rule in Fig. 5 a) although the back began picking up speed slightly before the front. As the back snapped forward into the round shape, it made up for the difference incurred during the slow phase by moving faster than the front, for this particular jump, 8.0 μm/min vs. 6.1 μm/min. Drops stepped forward one diameter during each cycle, as can be seen in Fig. 5 a (the distance between dark stripes in the comet) and as is quantified for a whole population of jumping drops of different sizes in Fig. 5 b (red curve). In addition, large droplets spent more time performing each cycle, as shown by the linear increase in the time interval (time between two maximum velocities) with increasing drop size (Fig. 5 b, blue curve).

FIGURE 5.

Kymograph analysis of jumps and parameters of the velocity cycle. (a) Kymograph derived from a phase contrast time-lapse acquisition of the drop shown in Fig. 3 c, radius = 3.4 μm. The drop is moving upward, the edges of the drop appear white, and the slopes of the white portions correspond to the velocities of the front and back of the drop. Green and yellow lines depict the front of the drop during the high-speed and low-speed phases, respectively, and blue and red lines mark out the back of the drop during the high-speed and low-speed phases, respectively. Dark stripes behind the drop indicate the high density phases of the comet, which do not extend to the right side of the kymograph due to a change in focal plane of the drop. (b) Step time and step size are dependent on the size of the drop. In blue (squares), the elapsed time between maximum velocity peaks as a function of drop size. The dependence is linear with a slope of 100.4 s/μm (correlation factor = 0.78). In red (circles) the distance between actin-rich stripes as a function of drop radius, measured on phase contrast images (open symbols) and confocal slices (filled symbols). The dependence is linear with a slope of 2.1 (correlation factor, 0.95).

To a first approximation, we can say that during the entire step time the drop was moving at the low-speed velocity of 0.7 μm/min (0.01 μm/s), since the time spent in the low-speed phase greatly exceeded the time spent in the high-speed phase (kymograph, horizontal projection of the yellow and green lines, respectively). The low-speed velocity multiplied by the step time of (100 s/μm) × R (Fig. 5 b, blue curve) therefore gives R as the distance traveled during the low-speed phase, where R is the radius of the droplet. Since the step size is 2 R (Fig. 5 b, red curve, slope 2.1), this means that the droplet traveled a radius length at low velocity and another radius length during the high velocity phase. Indeed, from the kymograph, we can see that the distance traveled during the low-speed phase (vertical projection of the yellow line) is approximately equal to the distance traveled during the high-speed phase (vertical projection of the green line).

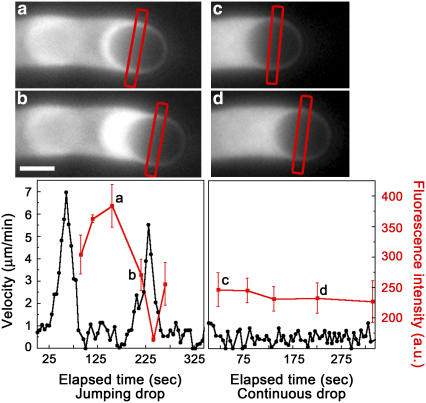
To visualize the waves of actin accumulation at the drop surface during a velocity cycle, we used extract supplemented with fluorescently labeled actin monomers and recorded fluorescence images during jumps (Fig. 6, a and b). A continuously moving drop is shown for comparison (Fig. 6, c and d). The inverted pear in the low-speed phase had more actin along the sides than the kiwi in the acceleration phase, whereas the fluorescence intensity along the sides of the continuously moving drop was almost invariant over the course of the observation. These waves of actin accumulation would be presumed to reflect a redistribution of VCA molecules on the drop surface. To test this, we compared VCA polarization on 2–3-μm radius jumping drops in the low-speed round phase or accelerating kiwi phase and observed no significant differences in VCA distribution (data not shown), indicating that fluctuations were small. In fact, even in the round phase of a jump, the drop is still moving, so we would not expect VCA to be completely homogenous.

FIGURE 6.

Form changes during the velocity cycle of jumping drops are associated with changes in the amount of actin along the sides of the drop, variations that are not observed during continuous motion. Fluorescence microscopy images using labeled actin of a jumping 1.6-μm radius drop in inverted pear form (a) and kiwi form (b) and a continuous 1.7-μm radius drop (c–d). Accompanying velocity cycle graphs for each drop are shown below the images. Fluorescence intensity (red curves, arbitrary units) was measured along the sides of the drop at various times during drop movement using line scans of fluorescence intensity of the center of the drop, perpendicular to the direction of movement. For the images shown, the region where the fluorescence was measured is marked by the red rectangles, and these points are indicated by the small letters in the velocity graphs. The error bars on the fluorescence intensity indicate the standard deviations from the average of the two sides of the drop. Bar, 2 μm.

DISCUSSION

The function of VASP in cell migration and adhesion remains an open question, as different effects have been reported depending on what cell line and organelle are under study. Furthermore, in vitro studies have pointed toward multiple and sometimes contradictory functions for VASP, including actin filament nucleation, G-actin recruitment, profilin recruitment, competition with capping protein, and detachment of Arp2/3 complex branch complexes from activating proteins. Here we use deformable, fluid oil droplet surfaces to study VASP-mediated Arp2/3 complex-catalyzed actin polymerization under conditions that mimic the plasma membrane of the cell, and attempt to shed light on what VASP might be doing in cells.

Immunolabeling for VASP of VCA+PRO oil droplets shows a crescent of stain directly on the surface of the drop, whereas drops coated with VCA alone have no specific surface recruitment of VASP (Fig. 1, c and d). The distribution of VASP on the VCA+PRO drop surface is asymmetric and mirrors the PRO distribution (Fig. 2 g), as expected. In addition, consistent with its F-actin binding properties (4), VASP is present along the entire length of both VCA and VCA+PRO comets and is in fact less intense on VCA+PRO comets because they are hollow. We conclude from this that VASP affects droplet movement only when positioned directly on the surface, close to the VCA molecules, and that similar levels of VASP in the body of the comet do not influence drop motility.

In the presence of VASP at the surface, oil droplets produce partially hollow comets (Fig. 1 e), similar to what we previously observed for hard beads (22). Hollow comets could be explained by monomer diffusion limitation of polymerization at the center of the comet. If this were the case, comet wall thickness would be expected to be constant, whereas we find that the thickness of the side walls of comets increases with increasing drop size (Fig. 1 g), ruling out diffusion limitation.

Hollow comets on kiwi-shaped drops are specifically associated with the surface recruitment of VASP and are not due to the PRO molecule itself. Indeed, when VCA is coadsorbed with ActA-C, which is identical to PRO but lacks the VASP binding site, full comets on pear-shaped droplets were observed, as for VCA-coated droplets. The kiwi shape observed for VCA+PRO droplets results directly from partial comet hollowness since there is little actin at the back of the drop, and therefore the normal (pulling) stresses are small, on the order of 1.5 nN/μm² (data not shown) as opposed to 16 nN/μm² for the normal stress at the rear of a pear-shaped droplet (23). The fact that the normal stress at the back of the kiwi is not zero indicates that actin is still polymerizing there, in agreement with the observation that there is still some fluorescent actin signal in the comet cavity and that VCA molecules are present along the whole back part of the drop.

VCA is concentrated under the comet in the case of both VCA and VCA+PRO droplets (Fig. 2, c–f and h), a situation different from hard beads where VCA molecules are immobilized and symmetrically absorbed. The extent of VCA asymmetry increases exponentially with droplet radius. To understand this dependency, we have to consider how VCA molecules move on a fluid surface during actin-based movement. The asymmetrical distribution of VCA molecules suggests that the VCA molecules are convected (dragged) by the actin filaments that form the comet toward the rear of the drop at a velocity equal to the droplet velocity. However convection alone would give the same VCA distribution for all drop sizes, not the exponential relation that we observe. To explain this, we have to take into account the dynamics of the filament-VCA interaction, in particular the possibility that the VCA molecules can detach from the filaments. Once the VCA molecules detach from a filament, they would be free to diffuse on the droplet surface until they reattach to another filament.

We propose that it is the interplay of convection, unbinding, diffusion, and rebinding that determines the ratio of VCA density between the back and the front of the droplet. In keeping with this, a simple model of this interplay (Supplementary Material, Discussion) predicts an exponential dependence of VCA ratio on drop size, 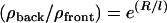, where R is the droplet radius, ρ is the VCA density (proportional to the fluorescence intensity), and ℓ is the characteristic length of the exponential, .

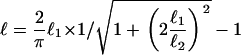The value of ℓ depends on two other characteristic lengths: 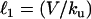, the convection-unbinding length (the distance traveled by a VCA molecule attached to a filament until it detaches) and 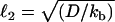, the diffusion-binding length (the distance traveled by a free VCA molecule before it attaches to a filament), where V is the drop velocity, k_u is the rate constant of unbinding, D is the diffusion coefficient of VCA molecules on the drop surface, and k_b is the rate constant of binding. For simplicity, we assume that D is invariant on drop surfaces. The surfaces are saturated by proteins absorbed from the cell extracts (23), and these proteins do not interact with the actin comet and therefore would not create significant gradients in diffusion coefficients or surface tension.

Experimentally the lengths ℓ of the exponential are found to be 3.3 μm and 2.9 μm for VCA+PRO and VCA drops, respectively (the inverse of the exponents 0.30 μm⁻¹ and 0.34 μm⁻¹ in Fig. 2 h). For drop radii larger than ℓ, each small increase in drop size results in a large increase in the VCA density at the back of the drop as compared to the front, producing a slightly steeper curve for VCA drops as opposed to VCA+PRO drops. This is surprising, given the fact that VASP-recruiting drops move fivefold more quickly and therefore would be expected to have a larger convection term (larger ℓ₁), resulting in a higher concentration of VCA under the comet. The velocity effect could be canceled out by an increase in unbinding (k_u) or a decrease in binding (k_b), which would decrease the convection length and increase the diffusion length, respectively. These changes in the association constants translate to a weakening of the attachment of filaments to VCA molecules in the presence of VASP.

This result adds to a growing body of evidence that VASP is not just involved in polymerization enhancement but, in addition, is associated with an overall physical effect of decreasing the attachment of actin filaments to polymerizing proteins acting from a surface. Since attached filaments function as a brake to forward movement, a decrease in attachment results in enhanced motility. The weakening of comet/surface links can also explain the occurrence of hollow comets in the presence of VASP as the weakened links rupture at the center of the comet where pulling forces are highest (22). Furthermore, temperature compensation experiments using mutant Listeria support the idea that VASP affects motility via a de-adhesion effect (26). Under certain conditions, VASP does not enhance actin polymerization in solution but nevertheless catalyzes F-actin production when polymerization-activating proteins are immobilized on a surface (9), again pointing to an effect that is not wholly dependant on polymerization enhancement. Finally, when VASP is enriched at the plasma membrane of cells, the actin network appears to collapse beneath the membrane instead of undergoing sustained protrusion (8), and the filament ends no longer abut the plasma membrane in the direction of movement. All of these independent observations, together with this study, point toward an attenuation of the attachment of growing filaments to polymerization-activating proteins in the presence of VASP.

This result, together with the fact that we only observed hopping motion in the presence of VASP and almost never on hard beads under the same conditions (22), suggested to us that jumping movement was triggered by the conjunction of weakened filament attachment and surface fluidity, as follows. Going through a velocity cycle step by step, just after a peak in velocity, stresses exerted on the surface of the drop are small, and the droplet has a rounded shape with ratio ɛ values of 1, in keeping with the fact that there is little actin around the drop. However since the droplets are in a low Reynolds number situation and inertial effects are therefore negligible, the nonzero velocity of the low-speed phase indicates that there is still some contact between the drop and the actin network. In agreement with this, elliptical form factors only approach 1, indicating that the drops are still slightly elongated, due to residual contact with the actin comet along the droplet sides. Subsequently, actin accumulates almost all around the drop, compressing it, and leading to the inverted pear shape. Convection of actin filaments/VCA molecules toward the rear of the drop then occurs, expelling the drop out the front, as for a symmetry breaking event. The drop assumes a more elongated shape as actin accumulates at the back of the drop, increasing the pulling forces and leading to rupture of the links between the comet and the surface. Detached VCA molecules may diffuse away on the fluid surface, decreasing attachment to the comet still further. Since diminishing the number of links puts even more stress on the existing links, their rupture may proceed in a cascade fashion, leading to a catastrophic breakage of the links and the forward jump of the drop. In keeping with this order of events, we observe that the drop begins to relax (decrease in elliptical form factor), implying link breakage, just before the velocity begins to increase (Fig. 3 p). The jump is sustained until complete loss of contact with the hemispheric pouch of actin, meaning over a distance R. In the absence of VASP, the connection between the actin filaments and the VCA molecules is more robust, and thus jumping is rarely observed.

In the framework of our model and using the distances calculated using Fig. 5 (see Results), we can suggest that the low-speed phase is the convection of actin filaments/VCA molecules toward the rear of the drop, clearing the forward hemisphere of the drop over a distance of R and that the high-speed phase is the expulsion of the drop from the hemisphere of actin that transcribes the back of the drop, thus also giving rise to a distance R. These measurements bring to light fundamental differences concerning previously observed hopping hard beads where jump distance, as well as maximal jump velocities, decreased with increasing bead size (20,27). In the case of hard beads, jumping motion is due to the opposition of the elastic propulsion force and the friction force. Friction develops when the sliding of the actin network toward the rear of the bead during movement is impeded by the attachment between the immobile VCA molecules on the bead surface and the actin filaments (27).

We propose that, in this study, diffusion and convection of VCA, not friction and elasticity, determine step characteristics. We observe waves of actin accumulation along the sides of jumping drops (Fig. 6), indicating that VCA is also moving on the drop surface over the course of a jump. Two other pieces of data also point toward VCA movement during jumps. First, for hard beads recruiting VASP, links break to produce hollow comets (22), but complete rupture is rare, maybe because detached activators cannot diffuse away on the surface. This would predict that if the rupture of the links at the back of droplets is only partial, continuous hollow comets would be observed, and experimentally, it is at this stage of the velocity cycle that jumping drops sometimes become continuous. In support of this idea, the thickness of the sides of the actin pouches during jumping motion were approximately equal to the sides of continuous hollow comets with a similar dependence on droplet radius (Supplementary Material, Fig. S2). A second indication that VCA molecules move during jumps is that jumping events are rare for larger drops (Table 1). In this case, catastrophes may be reduced by the fact that the diffusion length 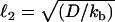is small compared to the portion of the drop under the comet, meaning that the detached VCA molecules cannot diffuse out from under the comet before reattaching.

At a mesoscopic scale, we can explain our results with a convection-unbinding-diffusion-binding model, in conjunction with the idea that VASP weakens the attachment between the comet and the VCA molecules on the drop surface. VASP enhancement of barbed end polymerization (either via nucleation, G-actin/profilin recruitment, or anticapping activity) is probably operational as well; however polymerization enhancement alone does not explain certain aspects of our work. In particular, comet hollowness is difficult to explain by an increase in polymerization efficiency. It is clear from this study that hollowness does not result from diffusion limitation of monomers to the center of the comet. In addition, as pointed out in the discussion of jumping drops, rupture precedes velocity enhancement (the kiwi shape of the drop begins to relax just before the jump takes place). If enhanced polymerization were the cause of rupture, we would expect the opposite sequence of events.

However the molecular basis of VASP de-adhesion activity remains unclear. One possibility is reduced branching of actin filaments in the presence of VASP, as observed in solution (28), on beads (22), and in cells (8). This may lead to a less robust attachment between the actin network and VCA molecules on the drop surface either because filaments are sparser or because VCA interaction with filamentous actin via the Arp2/3 complex is reduced. Another possibility is that VASP acts by catalyzing the detachment of Arp2/3 complex branch structures from polymerization-activating molecules (9), although there is no direct evidence for this, and furthermore VASP does not seem to interact directly with the Arp2/3 complex (29).

CONCLUSION

Overall the results observed here in the presence of VASP are consistent with a model where attachment and detachment of actin filaments to polymerization activators, coupled with diffusion and convection of activators on the surface, governs the growth and collapse of an actin network. Furthermore, the idea that VASP fine tunes the anchoring of the actin cytoskeleton to the cell membrane at the leading edge and at adhesion sites can explain much of what has been observed in cells. This VASP activity may be particularly important in cell-cell adhesions where it has been shown that the link between the cadherin-catenin complex and the underlying actin cytoskeleton is surprisingly dynamic to allow morphogenic changes over the course of development (30).

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.