Abstract
The mechanosensitive channel of small conductance (MscS) is a membrane protein thought to act as a safety valve in bacteria, regulating the release of ions and small solutes when gated by membrane tension under challenging osmotic conditions. The influence of voltage on channel activation and the functional state depicted by the available crystal structure of MscS remain debated. Therefore, in an effort to relate electrophysiological measurements on MscS and properties of the MscS crystal conformation, we report here MscS's response to voltage and pressure as determined by patch-clamp experiments, as well as MscS electrostatics and transport properties as determined through all-atom molecular dynamics simulations of the protein embedded in a lipid bilayer, a 224,000-atom system. The experiments reveal that MscS is a slightly anion-selective channel with a conductance of ∼1 ns, activated by pressure and inactivated in a voltage-dependent manner. On the other hand, the simulations, covering over 200 ns and including biasing electrostatic potentials, show that MscS restrained to the crystal conformation exhibits low conductance; unrestrained it increases the channel radius upon application of a large electrostatic bias and exhibits then ion conduction that matches experimentally determined conductances. The simulated conductance stems mainly from Cl− ions.
INTRODUCTION
Mechanical forces are essential stimuli for living organisms: from cell volume regulation to perception of sound, life relies on mechanosensation. The ultimate and perhaps the most important molecules behind mechanosensation are mechanosensitive channels that widen significantly upon force activation and generate a signal by facilitating transport of solutes across the cell membrane (1–6).
The mechanosensitive channel of small conductance, MscS, is one of such membrane proteins and is thought to act as a safety valve in bacteria, preventing cell lysis upon osmotic shock by opening and closing in response to membrane tension (7–11). MscS-related proteins have been found in bacteria, archea, and plants (12–14). Accordingly, MscS is considered an archetypal mechanosensor. It is one of two mechanosensitive channels structurally known, yet details of its gating mechanism remain unknown. Interestingly, MscS is also voltage-modulated.
The conductance of the fully open channel has been measured in patch-clamp experiments to be ∼1 nS; the channel is slightly anion-selective (7,10) and possesses at least one subconductance state (15). Activation of the channel has been found to be strongly dependent on the rate of pressure applied (11), while inactivation, rather than activation (7), has been found to be voltage-dependent (11,16).
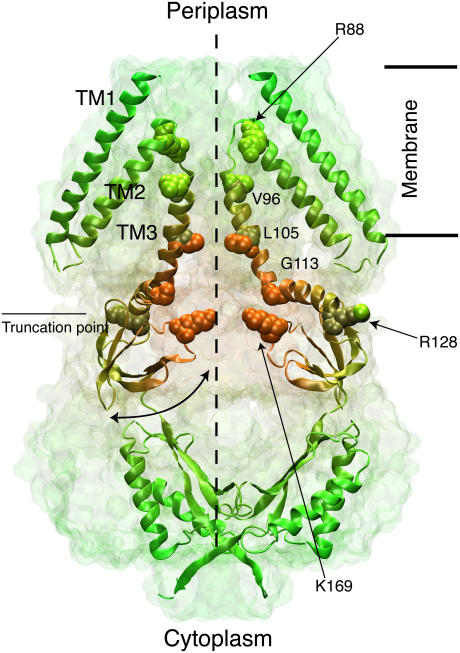
The x-ray crystal structure of Escherichia coli MscS (17), solved at 3.9 Å resolution, revealed a heptameric arrangement of subunits made of three transmembrane helices each (TM1, TM2, and TM3A-TM3B), with the transmembrane pore captured in a putative open state of radius ∼3.3 Å (Fig. 1). The structure features a large, balloon-shaped, cytoplasmic domain with seven side openings and a distal entrance. This large cytoplasmic domain has been suggested to act as a molecular filter (17), to be involved in gating (18–20), and to stabilize the channel (21,22), but actually its function remains unknown.
FIGURE 1.
Architecture of the mechanosensitive channel of small conductance MscS. The crystal structure is shown as a transparent surface with two (out of seven) subunits depicted in cartoon representation (colored for better visualization). The putative location of the membrane is indicated along with the symmetry axis of MscS, and an exit/entrance pathway through one of the cytoplasmic side openings. Charged residues (R88 and K169) located at the entrance of the transmembrane channel and residues forming its narrowest section (L105) are shown in space-filling representation along with residues defining the transmembrane pore (V96 and G113).
Each MscS monomer has 286 amino acids. In the crystal structure the first 26 residues and the last six residues of each subunit were not resolved. Nevertheless, the crystal structure provides an excellent frame of reference to interpret experimental results as well as an essential starting point for simulations that seek to establish MscS's function/structure relationship (23–25). The structure poses a challenge for computational studies, since MscS is a relatively large protein that undergoes considerable, reversible structural rearrangement (11,18,26). Therefore, whether the crystal conformation represents an open, intermediate, inactive, or closed state (27), and how it goes from one state to another, are difficult questions, yet there exists an excellent chance to establish answers by combining experimental and computational approaches.
On the experimental side, replacement of conserved glycine residues by alanine along the pore-lining helices (TM3A) has been shown to increase activation pressure of MscS. A similar effect is observed when conserved alanines are replaced by larger amino acids. Conversely, introduction of glycine residues has been shown to lower the pressure required for gating (28). These results highlight the role in MscS function of hydrophobicity and complementarity of the surfaces of helices forming the pore, suggesting that the glycine-rich region of TM3 plays a “pivotal role” in gating (28). Whether these mutations affect the flexibility of TM3 helices (which present a pronounced kink at Gly113, see Fig. 1) and how concerted movements of TM3 are coupled to peripheral helices (TM1 and TM2) remains to be elucidated. The coupling of the latter helices (TM1-TM2) to lipids has been addressed in an elegant recent study in which hydrophobic residues along them are mutated to asparagine (29). Modification of the hydrophobic lipid-protein interface at both ends of the helices increased the gating threshold of MscS and decreased the viability of cells when subject to osmotic shock (29), pointing out the relevance of membrane-protein interactions for MscS gating. Based on electrophysiological measurements and a reinterpretation of the MscS crystal structure, a gating model of MscS has been put forward by Sukharev and co-workers (11). In this model, the crystal conformation represents an inactive state in which lipids impair coupling between TM1-TM2 and TM3 helices. In the open and closed states, however, these helices are tightly packed, forming either a wide pore or a very compact structure. The latter model of MscS gating, the actual size of the open pore, and the voltage dependence of gating and inactivation remain to be clearly elucidated by experimental means.
On the computational side, two independent all-atom molecular dynamics (MD) studies have shown that the MscS transmembrane pore closes asymmetrically on a nanosecond timescale (30,31). A symmetric closed state has been suggested based on site-directed mutagenesis and computational modeling of only a reduced section of the MscS pore (28). Three computational studies have reported dewetting transitions in the narrowest section of the MscS transmembrane pore as depicted by the crystal (30–32). The computational studies have suggested that the crystal represents an already closed or inactive state (11,32), a “close to conducting” state (31), or a not-fully-open and highly anion selective state (33). The latter study combined all-atom MD with a coarse-grained, particle-based methodology, BioMOCA (34), which simplifies the description of protein, lipids, and solvent, while reaching simulation timescales of microseconds. The BioMOCA methodology and similar widely used simplified approaches (35–39) may introduce systematic errors and all-atom MD simulations of the entire MscS structure are much needed to complement the coarse-grained, i.e., BioMOCA, simulations.
Needless to say, a thorough comparison of computational modeling to conduction and gating properties of MscS unambiguously determined by experiments are invaluable in the quest to relate function and structure of MscS. We present below such comparison suggesting that the available crystal conformation of MscS represents a not-fully-open or inactive conformation, while a modeled conformation may correspond to MscS's open state.
MATERIALS AND METHODS
Electrophysiology
Construct and strain
MscS was cloned in a vector containing an RGS-His6 epitope at the N-terminus (pQE32) and expressed by IPTG induction in an E. coli strain that lacks MscL, MscS, and MscK (MJF465), i.e., provides a genetically clean background. The E. coli strain MJF453 containing genomic MscS was used as well; no significant differences were found while using MscS expressed from the genome or from the plasmid. These strains were kindly donated by I. R. Booth (University of Aberdeen).
Spheroplast patch-clamp
Channel activity was recorded by patch-clamping giant spheroplasts following the method described in Martinac et al. (7). Patch-clamp measurements were done in the inside-out configuration under symmetrical conditions (200 mM KCl, 90 mM MgCl2, 10 mM CaCl2, and 5 mM HEPES) or asymmetrical conditions (100 mM KCl in the pipette/300 mM KCl in the bath, all other salts as above), at pH 6 and room temperature. For both conditions, the bath solution contained 300 mM sucrose to keep spheroplasts intact.
Pipettes were made out of glass capillaries (Sigma, St. Louis, MO: catalog No. P1174), and were fire-polished before use until a resistance between 2 and 2.5 MΩ was reached. Negative pressure on the patch was obtained by applying suction through a syringe and monitored with a homemade piezoelectric pressure transducer. Single-channel and macroscopic currents were sampled at 10 KHz with an analog filter set to 2 KHz. Single channel analyses were done using pCLAMP9 (Axon Instruments, Foster City, CA).
Macroscopic currents were measured using a two-pulse voltage protocol (an initial hyperpolarizing pulse to −65 mV was followed by a set of depolarization pulses up to 60 mV) and at constant negative pressure. The two-pulse voltage protocol reduced the variability in current amplitude due to changes between pressure and voltage pulses and was performed on the same patch with a 3-min interval between sets of pulses (16).
Selectivity of MscS was determined using the experimentally measured reversal potential and the Goldman-Hodgkin-Katz (GHK) equation (40)
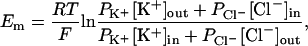 |
(1) |
where Em is the membrane potential, R is the ideal gas constant, T is temperature, F is Faraday's constant, Pion is the ion permeability, [ion]out is the extracellular ion concentration, and [ion]in is the intracellular concentration. The GHK equation used assumes that ions cross the channel independently and the potential drops linearly across the translocation pathway. Hence, the computed selectivity is only an estimate.
The experimental nominal open probability (NPo) was determined using
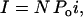 |
(2) |
where I is the macroscopic current, N is the number of identical channels, Po is the channel open probability, and i is the single-channel current at a given membrane potential.
Simulations
Systems
Molecular dynamics simulations were performed on a system containing the entire crystal structure of MscS (Protein Data Bank code 1MXM (17)) embedded in a membrane bilayer formed by 299 POPC lipids solvated in >50,000 explicit water molecules and 200 mM of KCl (altogether a ∼224,000-atom system). Two different starting conformations were assumed. The first conformation (S0) was obtained after ∼4.5 ns of dynamics with backbone atoms restrained to their positions in the crystal (k = 1 Kcal/mol/Å2). The second conformation (S1) was obtained after ∼5 ns of molecular dynamics simulation in which opening was induced by forces applied radially in the x,y-plane to Cα atoms of residues 96–113. In both cases, S0 and S1, all Asp, Glu, Lys, and Arg residues were assumed to be charged, as expected from pKa calculations (see Supplementary Material's Table 3). The sizes of the simulation cell were 108.3 × 111.4 × 178.6 Å3 and 107.9 × 115.3 × 172.1 Å3 for conformations S0 and S1, respectively. Details of the corresponding molecular dynamics simulations leading to S0 and S1 conformations can be found in Sotomayor and Schulten (30) and Sotomayor et al. (33).
Four different modifications of the simulated system were performed as listed in Table 1:
Mutations of amino acids were constructed using the psfgen plugin of VMD (41).
Neutral acetylated N-termini and amidated C-termini were modeled using psfgen as well.
Neutralization of arginine residues was achieved by erasing the Hε atom and redistributing charges among atoms forming the guanidine group (Danilo Gonzales-Nilo, Universidad de Talca, Chile, personal communication, 2005).
An additional, neutral, system containing only the transmembrane domain of MscS (residues 27–128) with neutral termini was simulated; this system was otherwise identical to that containing the entire structure, but featured a wider transmembrane pore (see Results). The size of the simulation cell of the latter system was 108.3 × 111.4 × 164.0 Å3 after equilibration (end of sim15a; see below).
TABLE 1.
Summary of MscS simulations
| Label | tsim (ns) | Voltage (V) | Restraints | Ensemble | MTS | Start | Modifications |
|---|---|---|---|---|---|---|---|
| sim1a | 10 | 0.0 | backbone | NVT | no | S0 | – |
| sim1b | 10 | 0.0 | no | NVT | no | sim1a | – |
| sim1c | 5 | +1.2 | no | NVTM* | no | sim1b | – |
| sim2a | 5 | 0.0 | backbone | NVTM* | no | sim1a | – |
| sim2b | 5 | 0.0 | no | NpTM* | no | sim2a | – |
| sim3a | 4.7 | 0.0 | no | NpTM* | no | sim1a | – |
| sim4a | 10 | 0.0 | backbone | NVT | no | S0 | neutral termini |
| sim4b | 10 | 0.0 | no | NVT | no | sim4a | neutral termini |
| sim5a | 12 | +1.2 | backbone | NVT | no | S0 | – |
| sim5b | 10 | +1.2 | no | NVT | no | sim5a | – |
| sim5c | 5.3 | 0.0 | no | NVT | no | sim5b | – |
| sim5d | 5.6 | 0.0 | no | NpT | no | sim5c | – |
| sim6a | 10 | +1.2 | backbone | NVTM* | no | sim5a | – |
| sim6b | 5 | +1.2 | no | NpTM* | no | sim6a | – |
| sim6c | 3.5 | 0.0 | no | NpTM* | no | sim6b | – |
| sim7a | 12 | −1.2 | backbone | NVT | no | S0 | – |
| sim7b | 4.5 | −1.2 | no | NVT | no | sim7a | – |
| sim8a | 5 | −1.2 | backbone | NVTM* | no | sim7a | – |
| sim9a | 12 | –0.6 | backbone | NVT | no | S0 | – |
| sim9b | 5 | −0.6 | no | NVT | no | sim9a | – |
| sim10a | 9.5 | 0.0 | no | NVTM* | yes | S1 | – |
| sim10b | 9.6 | +0.1 | no | NVTM* | yes | S1 | – |
| sim10c | 9.5 | −0.1 | no | NVTM* | yes | S1 | – |
| sim11a | 3.5 | 0.0 | backbone | NVT | no | S0 | RN46/RN74† |
| sim12a | 5 | 0.0 | backbone | NpT+NVT‡ | yes | S0 | R88Q |
| sim13a | 5 | 0.0 | backbone | NpT+NVT‡ | yes | S0 | K169Q |
| sim14a | 5 | 0.0 | backbone | NpT+NVT‡ | yes | S0 | R88Q/K169Q |
| sim15a | 1 | 0.0 | no | NpT | no | sim5c | truncated§ |
| sim15b | 4.8 | 0.0 | no | NVTM* | no | sim15a | truncated§ |
| sim15c | 4.7 | +1.2 | no | NVTM* | no | sim15a | truncated§ |
| sim15d | 5.4 | −1.2 | no | NVTM* | no | sim15a | truncated§ |
The overall computational effort involved simulations of a system containing ∼224,000 atoms for >200 ns. The constant bias voltage indicated for each simulation is set at the cytoplasmic side of the membrane. Harmonic restraints were applied to indicated atoms using a spring constant of 1 kcal/mol/Å2. Ensembles are denoted according to the thermodynamic quantity held constant (N, number of particles; p, pressure; T, temperature; V, volume). A multiple time step (MTS) algorithm was used when stated (see text). Initial coordinates and velocities were obtained from the last frame of the simulations mentioned in the Start column (see Materials and Methods section for definitions of S0 and S1).
Ensembles labeled with an M indicate that temperature control was applied to heavy atoms of lipids only.
RN: Neutral arginine residue (see text).
These simulations consist of 1 ns of dynamics performed in the NpT ensemble, followed by 4 ns of dynamics performed in the NVT ensemble.
These simulations include residues 27–128 of MscS (see text).
Molecular dynamics
Molecular dynamics simulations were performed using NAMD 2.5 (42), the CHARMM27 force field for proteins and lipids (43), and the TIP3P model for water (44). The simulations are listed in Table 1.
A uniform integration time step of 1 fs was assumed for most of the simulations. However, when stated, a multiple time-stepping (MTS) algorithm (45) was employed in which interactions involving covalent bonds were computed every 1 fs, short-range nonbonded interactions every 2 fs, and long-range electrostatic forces every 4 fs. In all cases a cutoff of 12 Å (switching function starting at 10 Å) for van der Waals interactions was assumed, and the particle-mesh-Ewald (PME) method was used to compute long-range electrostatic forces without cutoff. The density of grid points for PME was at least 1/Å3. All simulated systems were properly neutralized by adjusting the number of ions in the system; periodic boundary conditions were assumed in all cases.
Langevin dynamics was utilized to maintain a constant temperature of T = 300 K, with the damping coefficient set to 1 ps−1 for all heavy atoms in all simulations except those labeled NpTM or NVTM (see Ensemble column of Table 1). In the latter cases, the damping coefficient was set to 1 ps−1 for lipid heavy atoms only and zero for all other atoms, thereby avoiding artificial heating caused by electric fields and artificial viscosity for bulk electrolyte introduced by the Langevin dynamics. Constant pressure simulations at 1 atm were conducted using the hybrid Nosé-Hoover Langevin piston method with a decay period of 200 fs and a damping timescale of 50 fs.
Biasing voltages were applied through a uniform electrostatic field 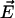 to all atoms of the system along the z axis (perpendicular to the membrane plane) (46,47). The voltage difference V across the simulated cell is
to all atoms of the system along the z axis (perpendicular to the membrane plane) (46,47). The voltage difference V across the simulated cell is
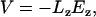 |
(3) |
where Lz is the length of the simulated cell in the z direction. Typical field strengths used for systems starting from conformations S0 and S1 were ±6.7 mV/Å (±1.2 V) and ±0.6 mV/Å (±0.1 V), respectively. Redistribution of mobile charges in the system during equilibration lead to a nonuniform electrostatic potential around the protein. The electrostatic potential was continuous across the boundaries of the simulation cell.
Analysis tools for MD simulations
Coordinates of all atoms of the system were saved every picosecond of simulation for later analysis. Structural deformation of the protein was monitored by computing root mean-square deviations (RMSD) over entire trajectories using VMD (41). The crystallographic structure served as the reference point, and only positions of protein backbone atoms were compared.
Computation of the electrostatic potential φ(r) for different trajectories was carried out using the PME method (42,48,49) through a modified version of the VMD plugin PMEpot. The underlying algorithm solves the Poisson equation
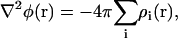 |
(4) |
with ρi(r) being the charge distribution contributed by atom i at position r. The value ρi(r) is approximated by a Gaussian
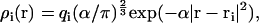 |
(5) |
where qi is the total charge of atom i. Electrostatic potentials were computed using a 135 × 135 × 180 grid (which ensures a density of grid points of at least 1/Å3) and averaged over entire trajectories including all atoms of the system. An Ewald factor of 0.25 Å−1 (width 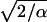 of Gaussian) was chosen and uniform electrostatic field biases were added to potential maps when applicable.
of Gaussian) was chosen and uniform electrostatic field biases were added to potential maps when applicable.
The radius profile of the MscS transmembrane pore along the axis perpendicular to the membrane plane was computed using HOLE (50) for snapshots of the simulated system taken every 100 ps. The default all-atom set of van der Waals radii from AMBER was used and sample planes were spaced uniformly at 0.5 Å in the z direction. Once the radius profile was determined, the minimum value around the constriction zone (Leu105) was employed to construct radius versus time plots.
All densities of ions and water were computed and averaged over stored trajectories using the VMD plugin volmap and a grid spacing of 1.5 Å. Computed densities are stored in a three-dimensional array of voxels used to generate two-dimensional slices of one grid-cell thickness as well as one-dimensional profiles along the channel axis. The number of ions crossing the MscS transmembrane pore was computed for different trajectories with VMD. A crossing event was defined by the passage of an ion from the cytoplasmic to the periplasmic bath or vice versa, with boundaries determined every picosecond by the single-frame average position of Cα atoms of residues Val96 (periplasmic boundary) and Gly113 (cytoplasmic boundary) of all subunits (see Fig. 1). Since the potential drop occurs mainly at the transmembrane pore (see below) and no major electrostatic forces arise in the cytoplasmic openings of MscS, it seems reasonable not to include them in the definition of the crossing region. Ionic currents through the MscS transmembrane pore were then computed by performing a linear fit to the number of crossing events plotted versus time (when applicable). When the number of crossings was too small to perform a reliable fit, the current was estimated using
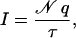 |
(6) |
where 𝒩 is the number of crossing events over a time interval τ. Errors on ionic currents were estimated by assuming a Poisson distribution for permeation events, with the error being 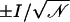 . Although the Poisson probability distribution assumes independent events, which may not be true in the present case, the estimated error provides a good reference when comparing data from different simulations. Conductances (g) were estimated using g = I/V, where V is the electrostatic potential drop across the membrane.
. Although the Poisson probability distribution assumes independent events, which may not be true in the present case, the estimated error provides a good reference when comparing data from different simulations. Conductances (g) were estimated using g = I/V, where V is the electrostatic potential drop across the membrane.
Control simulations of KCl electrolyte
Ten control simulations of a system containing 200 mM of KCl in water (11,703-atom system, 50 Å3) were performed to determine bulk conductivity of KCl as reported in Aksimentiev and Schulten (48). After 1 ns of dynamics in the NpT ensemble (Langevin temperature control was applied to all heavy atoms with a damping coefficient of 1 ps−1, the PME method was employed, and a uniform time step of 1 fs was chosen), three sets of simulations were performed in the NVT ensemble, each set consisting of three simulations (4 ns each) where electrostatic biases of 0, +1.2, and −1.2 Volts were applied. The first set was performed using a Langevin damping coefficient of 1 ps−1, the second set utilized a damping coefficient of 0.1 ps−1, and in the last set the PME method for computation of long-range electrostatic properties was turned off, while the Langevin damping coefficient was set to 0.1 ps−1.
Induced currents and bulk resistivity of the electrolyte were estimated by counting the number of ions that crossed a virtual box (with l = lx = ly = 48.3 Å and lz = 25 Å or lz = 12.5 Å) along the z axis. The number of crossing events, found to be roughly independent of lz, was plotted against time (see Supplementary Material's Fig. 15 B) and currents Ii were determined by corresponding linear fits to the data, yielding I1 = 17.2 nA for the first set, I2 = 20.1 nA for the second set, and I3 = 13.3 nA for the third set. The associated resistivities ρ1 = 0.34 Ωm, ρ2 = 0.29 Ωm, and ρ3 = 0.44 Ωm were computed using the magnitude of the uniform applied electric field E and the measured current density Ji employing the expression
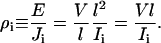 |
(7) |
The experimental conductivity of KCl at 0.1 M and 25°C is κ = 1.28217 S/m, and the estimated experimental resistivity at 0.2 M is ∼0.4 Ωm. Thus, currents computed with the CHARMM force field at 0.2 M are slightly overestimated when using PME and small values for the Langevin damping coefficient, as already reported in Aksimentiev and Schulten (48). Therefore, scaling was applied to ionic currents as specified below.
RESULTS AND DISCUSSION
MscS is a slightly anion-selective, pressure-activated ion channel
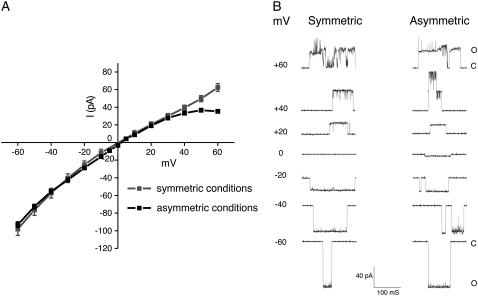
MscS activity was characterized using an E. coli strain lacking MscS, MscL, and MscK channels (9), which ensures that the recorded response corresponds only to that of the recombinant MscS. Patch-clamp experiments were performed on giant-spheroplasts under the inside-out configuration and revealed MscS activity when a gentle pressure (such as −40 mmHg) was applied. The current-voltage relation obtained under these conditions is shown in Fig. 2 A and exhibits a slight rectification for positive membrane potentials, which becomes more evident when using asymmetric conditions. The estimated conductance at 200 mM of KCl is ∼1.16 nS, in agreement with previous electrophysiological measurements of MscS (11,28). Under asymmetric conditions, the reversal potential is estimated to be +2.2 mV, which is small compared to the theoretical reversal potential for a completely selective anion channel (+28.4 mV according to the Nernst equation). Using the GHK equation (see Materials and Methods), the selectivity of the channel is estimated to be PCl+/PK− = 1.19, slightly smaller than the previously reported ratio of ∼1.48 (10). Thus, MscS seems to be only very slightly selective for anions.
FIGURE 2.
Current-voltage relation in symmetric and asymmetric conditions of wild-type MscS under constant pressure as determined by patch-clamp experiments. (A) The current-voltage relation, recorded at a constant pressure of −40 mmHg, shows a slope conductance of ∼1.16 nS in symmetric solutions (200 mM KCl, pH 6.0) and a slope conductance of ∼1.19 nS in asymmetric solutions (100 mM KCl pipette/300 mM KCl bath, pH 6.0). Under these conditions the reversal potential of MscS is ∼2 mV. MscS shows a slight rectification at positive potentials. Mean ± SD are shown. (B) Representative single-channel traces of MscS (in pQE32, see Materials and Methods) expressed in MJF465 (an E. coli strain lacking MscL, MscS, and MscK) were recorded by patch-clamping giants spheroplasts under inside-out configuration. Traces were obtained at the voltage indicated and at a constant pressure of −40 mmHg.
Single-channel traces of MscS activity shown in Fig. 2 B exhibit a behavior that depends on the sign of the applied bias. While MscS remains steadily in an open state at negative membrane potentials, the single channel transitions measured for positive biases are less well defined and more flickery, likely indicating that under these conditions MscS adopts multiple and unstable open conformations.
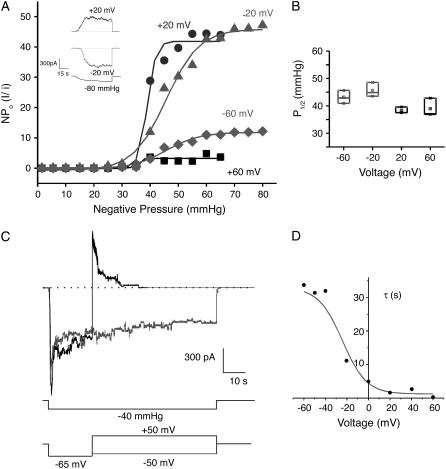
Macroscopic currents and the corresponding nominal open probability of MscS (NPo, Fig. 3 A) seem to indicate that the number of open channels depends on the applied voltage. The higher the magnitude of the voltage applied, the lower the open probability (51). However, this behavior might be caused by differences in the rate of pressure application (see (11)) and/or differences in the total number of channels available in the corresponding patches. Another reason might be associated with the very slow recovery of MscS from inactivation (11,16), coupled with the intrinsic variability of mechanical stimulation of membrane patches (52,53). The midpoint activation value determined from NPo is voltage-independent, as shown in Fig. 3 B, i.e., the pressure required to open MscS does not depend on the applied voltage. In contrast, a two-pulse voltage protocol used to measure macroscopic currents revealed that MscS inactivation depends strongly on the applied bias. Indeed, the decay time-constant for the macroscopic current depends dramatically on the sign of the second voltage pulse (Fig. 3, C and D). The voltage dependence of inactivation appears to be the determinant of channel activity at positive potentials, although the channels also inactivate at negative potentials. The latter result, first reported in Vasquez and Perozo (16), agrees well with data presented in Akitake et al. (11), but differs from previous studies suggesting voltage-independent adaptation (51). The disagreement may be due to differences in the range and/or duration of applied voltages. While voltages utilized in Koprowski and Kubalski (51) did not exceed ±30 mV, the voltage dependence of inactivation observed here arises at voltages larger than ±40 mV (Fig. 3 D).
FIGURE 3.
MscS gating is dependent on tension and modulated by voltage. (A) Macroscopic MscS currents adjusted to a Boltzmann-function fit to the NPo (nominal open probability) versus pressure at different transmembrane potentials. The inset shows macroscopic currents (at least 30 channels in the patch) corresponding to ±20 mV, elicited by an increase in negative pressure up to −80 mmHg. (B) Midpoints of activation (P1/2) plotted against transmembrane voltage (derived from the Boltzmann-function fit shown in panel A) suggest that opening of MscS at different potentials has approximately the same P1/2 value. Mean ± SD are shown. (C) Macroscopic currents obtained from two-pulse protocol experiments under constant pressure reveal the presence of a voltage-dependent inactivation; the rate and extent of inactivation speeds-up significantly with membrane depolarization. (D) Decay time constant τ obtained from fitting a single exponential to the macroscopic records obtained from the two-pulse protocol showing the voltage dependence of the inactivation.
The overall behavior of MscS as determined by patch-clamp experiments reported here agrees well with previous experiments performed using the same E. coli strain (11). This experimental characterization of MscS activity suggests that MscS adopts an open state, a closed state, and an inactive state. Therefore, we asked whether the crystal structure of MscS represents either of such states.
The crystal structure of MscS exhibits low conductance and high anionic selectivity
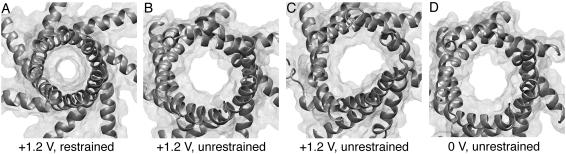
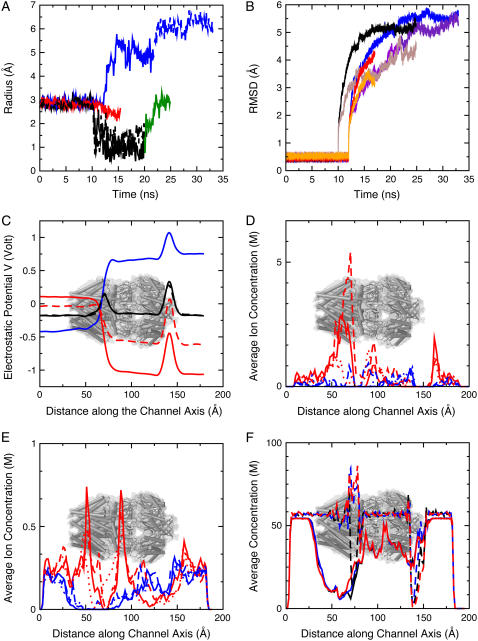
To determine the conduction properties of the MscS crystal structure one needs to invoke simulation. For this purpose two sets of simulations with MscS's backbone atoms restrained to the crystal conformation were performed. A first set of simulations was performed in the NVT ensemble and consisted of four different simulations in which the system was subject to biasing voltages of 0, +1.2, −1.2, and −0.6 V (sim1a, sim5a, sim7a, and sim9a in Table 1, respectively). A second set of simulations of MscS with its backbone restrained consisted of three simulations in which temperature control was applied to heavy atoms of lipids only, to avoid both artificial heating caused by fields and artificial viscosity for bulk electrolyte introduced by Langevin dynamics (sim2a, sim6a, and sim8a, with biasing electrostatic potentials of 0, +1.2, and −1.2 V, respectively). In all cases the transmembrane pore remained in an “open” conformation as observed in the crystal, although side chains, but not backbone atoms, were free to move (see Fig. 4 A with the pore featuring a radius of ∼3 Å in the constriction zone, as quantified in Fig. 8 A).
FIGURE 4.
Top views of MscS's transmembrane pore (residues 96–128) shown in cartoon and transparent surface representations (residues 96–128) at the end of simulations (A) sim5a (+1.2 V, backbone restrained), (B) sim5b (+1.2 V, backbone released), (C) sim6b (+1.2 V, backbone released), and (D) sim5d (0 V, backbone released).
FIGURE 8.
Dynamics and electrostatics of MscS. (A) Time evolution of the radius at the constriction of MscS's transmembrane domain (Leu105) for simulations sim1a-sim1b (solid black), sim4a-sim4b (dashed black), sim5a-sim5b (blue), sim5c-sim5d (dashed blue), sim9a-sim9b (red), and sim1c (green). Harmonic restraints applied to backbone atoms maintained the pore in an open state with a radius of ∼3 Å in simulations sim1a, sim4a, sim5a, and sim9a. A clear decrease in the radius can be observed for simulations in which restraints were released and no biasing potential was applied. (B) Root mean-square deviations for the transmembrane domain of MscS (residues 27–128) during simulations sim1a-sim1b-sim1c (black), sim5a-sim5b-sim5c-sim5d (blue), and sim9a-sim9b (red), as well as for the cytoplasmic domain of MscS (brown, purple, and orange). RMSD values for simulations without bias seem to converge at a rather large value (∼5 Å) after 10 ns of dynamics. (C) Time-averaged electrostatic potential along the symmetry axis of MscS for sim1a (solid black), sim4a (dashed black), sim5a (blue), sim7a (solid red), and sim9a (dashed red). The approximate location of MscS is indicated in this and subsequent plots. (D) Time-averaged ion concentration profile in moles per liter (M) along the symmetry axis of MscS for Cl− (red) and K+ (blue) during simulations sim1a (solid line), sim5a (dashed line), and sim7a (pointed line). (E) Ionic concentrations averaged over time and space (along y axis) shown as in panel D. (F) Time-averaged water oxygen concentration during simulations sim1a (black), sim5a (blue), and sim7a (red). Dashed lines correspond to the concentration profile along the symmetry axis of the channel. The concentration of water in the narrowest section of the channel increases when biasing potentials are applied to the system. Solid lines correspond to time and spatial averages along the y axis (slightly displaced for better visualization). The concentration in bulk is ∼56 M.
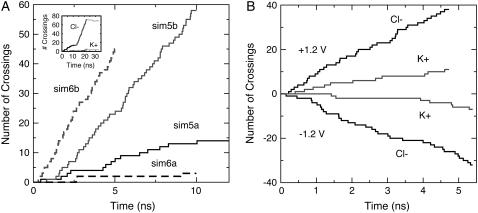
Application of external electrostatic potentials resulted, as expected, in transport of ions through the transmembrane pore. Fig. 5 A shows Cl− permeation events throughout simulations in which a +1.2 V bias was applied while the protein was restrained to its crystallographic conformation (sim5a and sim6a, see Tables 1 and 2). From the data it is evident that the crystal conformation exhibits low conductance and high selectivity for Cl−. Indeed, meaningful conduction was observed only for simulations at +1.2 V and was driven entirely by Cl− ions. The maximum estimated current for the restrained structure is ∼237 ± 61 pA (sim5a), which corresponds to a conductance of ∼198 pS at +1.2 V. If one takes into account the overestimate of bulk KCl conductivity using identical simulation conditions (as described in Materials and Methods), the conductance scales down to ∼169 pS, a value that is small compared to the expected 1 nS conductance of the fully-open channel. Furthermore, reversal of the applied potential to −1.2 and −0.6 V in simulations sim7a, sim8a, and sim9a resulted in negligible ion transport.
FIGURE 5.
Ionic currents through MscS as determined by all-atom MD simulations. (A) Ion crossing events (Cl−) through MscS's transmembrane pore versus time for simulations sim5a (solid black), sim5b (solid gray), sim6a (dashed black), and sim6b (dashed gray). A clear steady-state ionic current driven by chloride ions (enhanced upon release of restraints) is observed for simulations sim5a, sim5b, and sim6b (+1.2 V). The inset shows crossing events during sim5a, sim5b, and sim5c-sim5d (black, gray, and light gray for Cl− and K+ ions). High anionic selectivity is evident, and ions stop crossing the channel when the biasing potential is turned off in sim5c-sim5d (as expected). (B) Ion crossing events in simulations where only the transmembrane domain of a wider conformation of MscS (residues 27–128) was included in the system (sim15c at +1.2 V and sim15d at −1.2 V). Black and gray curves show crossings for Cl− and K+ ions, respectively.
TABLE 2.
Summary of conduction events through MscS
| Label | tsim (ns) | Voltage (V) | K+ +z | K+−z | Cl− +z | Cl−−z |
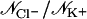 – – |
I pA | I/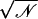 pA pA |
Iscaled pA |
|---|---|---|---|---|---|---|---|---|---|---|
| sim1c | 5 | +1.2 | 0 | 0 | 6 | 0 | large | 192 | 78 | 139 |
| sim2b | 5 | 0.0 | 0 | 0 | 1 | 0 | – | 32 | 32 | 23 |
| sim5a | 12 | +1.2 | 0 | 1 | 14 | 0 | 14 | 237 | 61 | 203 |
| sim5b | 10 | +1.2 | 0 | 4 | 58 | 0 | 14.5 | 1051 | 133 | 893 |
| sim5c-sim5d | 10.9 | 0.0 | 1 | 0 | 2 | 5 | – | 59 | 20 | 50 |
| sim6a | 10 | +1.2 | 0 | 1 | 3 | 0 | 3 | 64 | 32 | 46 |
| sim6b | 5 | +1.2 | 0 | 4 | 45 | 0 | 11.3 | 1586 | 226 | 1150 |
| sim6c | 3.5 | 0.0 | 0 | 0 | 0 | 2 | – | 92 | 65 | 67 |
| sim7a | 12 | −1.2 | 1 | 0 | 0 | 1 | 1 | 27 | 19 | 23 |
| sim7b* | 4.5 | −1.2 | 4 | 0 | 0 | 15 | 3.75 | 676 | 155 | 575 |
| sim10a | 9.5 | 0.0 | 1 | 1 | 2 | 4 | – | 34 | 12 | 25 |
| sim10b | 9.6 | +0.1 | 2 | 2 | 8 | 0 | large | 134 | 38 | 97 |
| sim10c | 9.5 | −0.1 | 0 | 0 | 0 | 4 | large | 68 | 34 | 49 |
| sim15a | 1 | 0.0 | 0 | 0 | 0 | 1 | – | 160 | 160 | 136 |
| sim15b | 4.8 | 0.0 | 0 | 0 | 2 | 1 | – | 33 | 33 | 24 |
| sim15c | 4.7 | +1.2 | 0 | 11 | 38 | 0 | 3.45 | 1656 | 236 | 1200 |
| sim15d | 5.4 | −1.2 | 7 | 0 | 0 | 32 | 4.5 | 1086 | 192 | 787 |
Simulations are labeled as in Table 1. Ion-crossings (as defined in Materials and Methods) are indicated for all simulations in which at least one ion crossed MscS's transmembrane pore. Conduction events are labeled as +z for an ion going from the periplasmic to the cytoplasmic bath and −z for an ion going in the opposite direction. Selectivity can be estimated from the ratio of the number of permeation events for each ion, 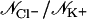 . Ionic currents were determined as indicated in Materials and Methods for simulations that showed Ohmic behavior (sim5a, sim5b, sim6b, sim15c, sim15d) or by simply dividing the total number of permeation events by the corresponding simulation time. An error for ionic currents can be estimated from I/
. Ionic currents were determined as indicated in Materials and Methods for simulations that showed Ohmic behavior (sim5a, sim5b, sim6b, sim15c, sim15d) or by simply dividing the total number of permeation events by the corresponding simulation time. An error for ionic currents can be estimated from I/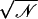 . The values presented in the last column are scaled according to estimated KCl bulk conductivities as indicated in the main text.
. The values presented in the last column are scaled according to estimated KCl bulk conductivities as indicated in the main text.
The integrity of the pore was compromised during this simulation and ions permeated through interstitial openings between TM3A helices.
The small currents and strong rectification observed for negative biasing potentials contrast with the experimental data showing only a weak rectification that becomes more apparent under asymmetrical conditions (Fig. 2 A). The discrepancy may be a consequence of the large voltages used in the simulations, since the maximum current flowing through the channel is limited by free diffusion of ions being supplied to the periplasmic and cytoplasmic ends of the pore (40), as discussed in Spronk et al. (31). However, the same behavior was observed in BioMOCA simulations of the MscS crystal conformation lasting 100 ns each and using smaller biases of ±50 mV and ±100 mV (33) (see comparison below). Moreover, crude estimates of MscS's conductance presented in Sotomayor and Schulten (30) and Anishkin and Sukharev (32) agree well with the observed behavior. Overall, different computational results (obtained in some cases from independent groups) seem to converge to the same conclusion (30,32,33,39).
What determines then the strong selectivity seen in the prior (33) and present simulations given the fact that electrophysiological measurements do not show such selectivity? Averaged electrostatic potentials, shown for each of the restrained simulations in Fig. 6 and Supplementary Material's Fig. 9, along with distribution of ions and density of water molecules throughout the simulation cell, described below, partially answer this question.
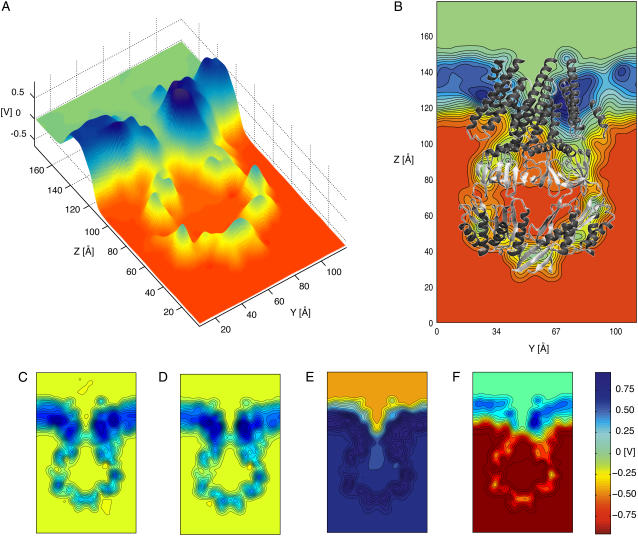
FIGURE 6.
Averaged electrostatic potential of MscS as determined through all-atom MD simulations and the PME method. (A) Three-dimensional surface showing the electrostatic potential of MscS averaged over 10 ns of simulation (sim9a) in which the protein backbone was restrained to its original crystallographic conformation and a biasing potential of −0.6 V was applied to the simulated system. The surface corresponds to the electrostatic potential of a slice perpendicular to the membrane plane passing through the center of the channel. (B) Two-dimensional contour plot of the electrostatic potential shown in panel A. The crystal structure (shown in cartoon representation) is superimposed as a reference. Twenty contour lines are drawn over the range of voltages of the corresponding data set. All values above or below the scale limits (see color bar) are shown at the same level. (C) Electrostatic potential (as in panel B) averaged over 10 ns of simulation in which the protein backbone was restrained and no biasing potential was applied (sim1a). (D) Electrostatic potential averaged over 10 ns of simulation in which the protein backbone was restrained, no biasing potential was applied, and N- and C-termini were modeled as neutral entities (sim4a). (E) Electrostatic potential averaged over 10 ns of simulation in which the protein backbone was restrained and a biasing potential of +1.2 V was applied to the simulated system (sim5a). (F) Electrostatic potential averaged over 10 ns of simulation in which the protein backbone was restrained and a biasing potential of − 1.2 V was applied to the simulated system (sim7a).
Electrostatic potential maps of restrained MscS
Electrostatic potential maps were computed for simulations in which the backbone of MscS was restrained to its crystal conformation (simulations sim1a, sim2a, sim5a, sim6a, sim7a, sim8a, and sim9a). The most interesting feature of the computed electrostatic potentials without bias is a positive barrier (+320 mV) observed along the transmembrane pore (see Figs. 6 C and 8 C). The barrier arises in a hydrophobic region of low water concentration and explains the accumulation of Cl− ions observed in the vicinity of this region (Fig. 7 A), as well as the ion selectivity described below. Several simulations were carried out to investigate the electrostatic barrier. Termini were neutralized (sim4a), different sets of charged residues were mutated (R88Q in sim12a, K169Q in sim13a, and R88Q/K169Q in sim14a), and arginine residues located in the transmembrane domain were neutralized (sim11a, R46/R74), the latter simulation motivated by recent experimental and theoretical results suggesting that arginine residues in a low dielectric environment may not be charged (54) (Danilo Gonzales-Nilo, Universidad de Talca, Chile, personal communication, 2005). As documented in the Supplementary Material, mutation K169Q showed a major effect on the barrier.
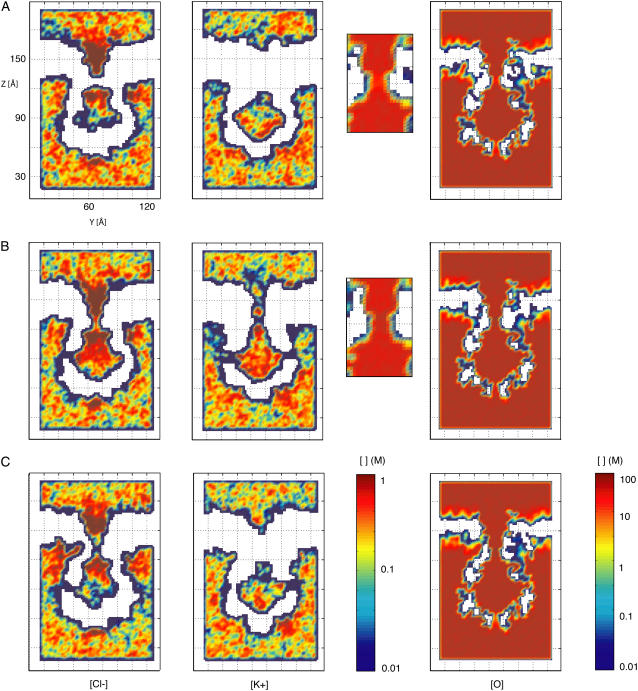
FIGURE 7.
Two-dimensional slices showing Cl−, K+, and water oxygen concentrations for different all-atom MD simulations. Concentrations are plotted in moles per liter (M) on a logarithmic scale. All values above or below the scale limits are shown at the same level. (A) Average concentrations for a 10-ns MD simulation in which the protein backbone was restrained and no biasing potential was applied to the system (sim1a). A clear separation in the distribution of Cl− and K+ is observed, but conduction of ions through the transmembrane pore did not occur. The water oxygen concentration is reduced at the narrowest sections of the transmembrane (see inset) and cytoplasmic distal pore. (B) Average concentrations over 10 ns from an MD simulation in which the protein backbone was restrained and a biasing potential of +1.2 V was applied to the system (sim5a). While the Cl− density shows a rather flat profile along the transmembrane pore, the K+ ion density is clearly reduced at the narrowest sections. For both Cl− and K+ ions, transport occurs through the side openings of MscS's cytoplasmic domain. The water density at the narrowest section of the pore is larger than that observed when no biasing potential is applied (see panel A). (C) Average concentrations over 10 ns of MD simulation in which the protein backbone was restrained and a biasing potential of −1.2 V was applied to the system (sim7a). No conduction of K+ ions is observed through the transmembrane pore, since the only permeation event reported for K+ (see Table 2) occurred outside of the time-window used for averaging. An increased penetration of Cl− ions through the cytoplasmic side of the membrane is discernible.
An even larger electrostatic barrier (+530 mV) is observed across the distal “bottom” (oriented as in Fig. 1) entrance of the cytoplasmic domain. This entrance is hydrophobic and features few water molecules; it is far from the location of the potential drop observed when biasing potentials are applied and, therefore, should not play a direct role in ion transport. Side openings in the cytoplasmic domain exhibit smaller or almost nonexistent electrostatic barriers to ions.
In addition to the features described above, all the computed electrostatic potentials were found to be flat in bulk electrolyte, to exhibit a focused drop across the transmembrane pore of MscS when external biases were applied, and to be positive within proteinaceous and lipidic regions.
The flat potential in bulk electrolyte suggests that simulation times (5–12 ns) were long enough for ions to reach a stationary state. Moreover, despite the large voltages applied during our simulations, the membrane did not break apart, but functioned as an effective barrier for ions and water molecules.
Positive values of the electrostatic potential (∼+800 mV) in the lipid region, observed in all simulations, are consistent with the membrane dipole potential caused by lipid headgroups and surrounding water molecules. First postulated to explain experiments in which hydrophobic anions readily permeated across membrane bilayers (in contrast to structurally analogous hydrophobic cations) (55–58), positive membrane dipole potentials have been observed in multiple all-atom, explicit-solvent molecular dynamics studies (48,59–64) and mixed implicit/explicit solvent Poisson computations (65). Positive values of the electrostatic potential in protein domains have been reported earlier as well and attributed to the distribution of charges in the backbone dipoles (66).
Ion and water densities in simulations of restrained MscS
The distribution of ions around MscS was not completely uniform and exhibited an accumulation of Cl− ions at the periplasmic and cytoplasmic ends of the MscS transmembrane pore in the absence of biasing potentials (Fig. 7 A), consistent with the electrostatic potential maps described above. Potassium ions, on the other hand, accumulated in the distal zone of the cytoplasmic domain (Fig. 7 A).
From the distribution of ions it can be confirmed that permeation events did not occur across the transmembrane domain unless biases were applied (compare Fig. 7, A–C). Indeed, upon application of electrostatic biases, Cl− ions were observed to permeate the transmembrane pore, while K+ ions did so more rarely, as clearly seen in the corresponding density plots (Fig. 7, B and C), which also show how ions permeate through the protein's cytoplasmic side openings. During these simulations, Cl− ions were observed to temporarily bind to a pocket formed by residues 83–98 of adjacent subunits at the periplasmic entrance of the channel, directly involving Arg88 and Thr93, the latter residue causing a gain of function phenotype when mutated to Arg (21) (the simulations are shown in Supplementary Material's movies). An unusual increase in the Cl− concentration in the cytoplasmic boundary of the membrane (at the interface with the protein) is observed for simulations with a negative biasing potential; ions indeed penetrated hydrophobic crevices of the protein.
Only a single potassium ion was observed to permeate the restrained channel in simulations sim5a, sim6a, and sim7a. The positive ion used chloride ions as a ladder to climb across the transmembrane pore, a behavior reflected also in an unusual peak in the K+ ion density at the center of this region.
Is water distributed homogeneously throughout the simulation cell? This question is relevant since hydration may affect conduction through MscS. The average water density is uniform throughout bulk regions and in the interior of MscS's cytoplasmic domain (∼56 M, see Fig. 7 and Fig. 8 F). However, a drastic reduction in water density can be observed along the transmembrane pore and at the distal “bottom” entrance of the cytoplasmic domain. The reduction in density is consistent with observed dewetting transitions in hydrophobic pores (30–32,67–69) and disappears when a large electrostatic bias is applied. The latter effect is very similar to that reported in Dzubiella et al. (70) for ion transport through generic hydrophobic nanopores. In addition, Spronk et al. (31) presented compelling evidence suggesting that hydration of the pore is indeed favored by application of an electrostatic potential and the energetics of water molecule orientation within the transmembrane pore. However, only simulations of hydrophobic pores with and without ions and subject to small electrostatic fields will demonstrate if dewetting transitions are totally eliminated, and whether this is caused by the action of the electrostatic potential itself (71), or is a consequence of movements of ions and their respective hydration shells.
Overall, the simulations of MscS restrained to its crystal conformation show consistent electrostatic potential maps as well as ionic and water distributions depicting a channel with small conductance and high selectivity for anions over cations.
Wider conformations of MscS match experimentally determined conductance but remain anion-selective
Properties of MscS described above correspond to those of a structure restrained to its crystal conformation. Release of restraints lead to dramatic changes in the MscS transmembrane domain conformation. Indeed, when restraints were released under equilibrium (no bias) conditions, the channel closed asymmetrically (simulations sim1b, sim3a, and sim4b, discussed in the Supplementary Material), while release of restraints in the presence of sufficiently strong electric fields resulted in a wider transmembrane pore (simulations sim5b and sim6b).
Widening of MscS transmembrane pore
Surprisingly, release of restraints applied to backbone atoms while the protein was subject to large and positive electrostatic biases lead to channel conformations that feature a transmembrane pore wider than the one depicted by the crystal structure (sim5a, compare Fig. 4, A and B). Widening proceeded by straightening of TM3A-TM3B helices (which partially established contact with peripheral helices TM2) and is likely caused by forces arising from ions and water rushing through the transmembrane domain. Salt-free simulations should clarify whether ions, water, or charges in the protein itself are responsible for opening.
The increase in pore size seems to be larger than that reported in Spronk et al. (31), and has a direct impact on the magnitude of the ionic currents through the channel, as discussed below. The radius of MscS's constriction zone during 22 ns of simulation (sim5a and sim5b) is shown in Fig. 8 A (solid blue curve). The increase in magnitude upon release of restraints is evident, reaching a steady value of 5 Å. A second set of control simulations (sim6a and sim6b), in which release of restraints was performed while an NpTM ensemble was adopted, resulted in the same qualitative behavior, i.e., an increase in size of the transmembrane pore (see Fig. 4 C and Supplementary Material's Fig. 16 A, red curve). Thus, widening of the MscS pore seems to be a rather robust event.
Widening was only observed when positive biases were applied to the system, resulting in Cl− ions permeating from the periplasmic to the cytoplasmic bath. A large negative bias prevented closure (−1.2 V, sim7b), but negative ions permeated hydrophobic crevices in the transmembrane zone of MscS and the integrity of the pore (residues 96–113) was compromised, with water and ions pouring through contact regions of adjacent TM3A helices. It is not clear if this kind of behavior will result in a disordered pore and whether poor packing of lipids around the protein or steric/electrostatic barriers in the transmembrane pore are its cause.
A second simulation with a smaller negative electrostatic bias was performed as well (−0.6 V, sim9a-sim9b). MscS's transmembrane pore remained intact, and a less dramatic tendency to close upon release of restraints was observed in the time evolution of the computed constriction radius (see Fig. 8 A, red curve).
Are ionic currents through the wider conformation of MscS as produced through a positive bias larger than those observed for MscS in its crystal conformation? A clear increase in the number of ions permeating the pore (sim5b and sim6b; shaded lines in Fig. 5 A) was observed. Although selectivity for anions remained almost absolute (see Table 2 and inset in Fig. 5 A), the estimated ionic currents (1051 ± 133 pA and 1586 ± 226 pA; 893 pA and 1150 pA after bulk correction) are consistent with conductances of 876 pS and 1322 pS (744 pS and 958 pS) at + 1.2 V, close to the experimentally determined conductance of MscS of ∼1000 pS as reported here and elsewhere (11,28). Turning off the applied bias resulted in a negligible backward current (sim5c-sim5d, see Table 2), and ionic currents for negative biases were small and likely unrealistic, since ions and water leaked through perforations between adjacent TM3A helices (sim7b).
The RMSD for simulations in which biasing potentials were applied (sim5a-sim5b and sim9a-sim9b) are shown in Fig. 8 B and seem to converge at rather large values (<6 Å). Indeed, the simulations of MscS described above and in previous studies (30,31) show an extremely flexible protein. Whether this is an intrinsic property of MscS, reflects possible faults in the crystal structure, or is caused by artifacts of our computational methods, remains to be elucidated.
Overall, computed ionic currents indicate that the MscS pore, as depicted by the crystal structure, does not correspond to a fully-open state with an observed conductance of 1 nS, but slightly wider conformations may do so. The high selectivity observed here for anions remains in relative disagreement with experiments. We ask then, whether the cytoplasmic domain is, at least in part, responsible for such anionic preference.
Role of cytoplasmic domain in selectivity and transport
Previous BioMOCA simulations (33) showed that the cytoplasmic domain has a minor impact on the selectivity of the narrower crystal structure conformation. However, the impact of the cytoplasmic domain on conduction through a wider transmembrane pore was not probed in Sotomayor et al. (33). Thus, four additional all-atom simulations (sim15a-d) were performed to determine how ion conduction through a wider conformation of MscS is affected by the presence/absence of its cytoplasmic domain. Coordinates from the last frame of simulation sim5c (featuring a wide transmembrane pore obtained upon release of restraints while a positive bias was applied) were used to build a system in which protein residues 129–280 were deleted and termini neutralized (see Materials and Methods). The deletion cut off the major part of MscS's cytoplasmic domain, eliminating entirely the domain's putative filtering function. This in silico deletion was made even though our experiments show that MscS channels lacking the cytoplasmic domain impair cell growth, perhaps because of an increase in tension sensitivity or a decrease in MscS's filtering capabilities when spontaneous and sporadic openings occur in the resting E. coli membrane (see Supplementary Material's Fig. 20).
The resulting system (see Supplementary Material's Fig. 17) was equilibrated for 1 ns (sim15a) and then three simulations were performed applying biases of 0, +1.2 and −1.2 V (sim15b, sim15c, and sim15d, respectively). In all cases the transmembrane pore remained in a wide-open state reflecting the irreversibility of the opening transition on a nanosecond timescale. Although the timescale of these simulations are three orders-of-magnitude or more shorter than those explored through patch-clamp experiments, these irreversible conformational changes may explain residual currents observed after pressure had been turned off, as reported in Akitake et al. (11) (see discussion in the Supplementary Material).
Fig. 5 B shows the corresponding ion permeation events resulting in currents of 1656 ± 236 pA (1200 pA after bulk correction) at +1.2 V and 1086 ± 192 pA (787 pA) at −1.2 V (see Table 2). The currents are slightly larger than those measured when the cytoplasmic domain was present (sim5b and sim6b) and rectification for negative biases is less significant (the pore's integrity is conserved and all ions permeated through the lumen of the pore). Selectivity for anions decreased in both cases (from a ratio of ∼14 to a ratio of ∼4 chloride per potassium ions), being now closer to the slight anion selectivity observed in experiments. Indeed, the electrostatic barrier seen in simulations with restrained MscS is absent (see Supplementary Material's Fig. 18). This could be caused by neutralization of termini (unlikely, as discussed in the Supplementary Material), the absence of residue Lys169 at the cytoplasmic entrance, and most importantly, the wider conformation used. Comparison of the electrostatic potential maps computed for the wide conformation of MscS with and without the cytoplasmic domain (Supplementary Material, Figs. 18 and 19) suggest that the latter two facts explain the observed MscS selectivity. Nevertheless, the number of potassium ions permeating the channel remains lower than expected from experiments (the experimental ratio of chloride per potassium ions is 1.2–1.5). Perhaps even wider conformations of the pore, neutralization of arginines in wider conformations, or incorporation of missing residues at the N-termini could lead toward the low selectivity observed in experiments. It is also entirely possible that the cytoplasmic part of the reported crystal structure differs from its native conformation. In any case, the conformation adopted by the cytoplasmic domain has a direct impact on the magnitude and character of the ionic currents transported through MscS.
Comparison to coarse-grained, particle-based models
The outcome of all-atom molecular dynamics simulations presented here should be compared to recently published work on the electrostatic properties of MscS (33), where a coarse-grained, particle-based method, BioMOCA (34), was employed to determine MscS's electrostatic potential, ionic densities, and transport properties. Similar simplified models are widely employed in the investigation of ion channel properties (35–38,72) and, therefore, the comparison is highly relevant. As mentioned in the introduction, both methodologies offer much needed complementary views of MscS and, in the present case, converge to the same qualitative conclusions. Indeed, BioMOCA simulations indicated that 1), conformations similar to those of the crystal structure exhibit low conductance, whereas wider conformations match experimentally determined conductances; 2), all conformations studied exhibit high selectivity for Cl− ions; 3), rectification at high voltages is opposite to what is observed in experiment; and 4), there is a separation in the distribution of anions and cations inside and in the immediate vicinity of MscS's cytoplasmic domain. These conclusions agree well with the present findings.
Although ionic distributions between the two simulation approaches also agree well, details of the electrostatic potential for the crystal conformation do differ. Positive electrostatic potential barriers observed in all-atom MD simulations along the transmembrane pore and the cytoplasmic opening, distal to the transmembrane channel, are narrower and higher (up to five times) than those observed in BioMOCA simulations. The positive potential observed within lipid regions in all-atom MD simulations is not reproduced in BioMOCA simulations, likely due to the absence of explicit interfacial water molecules, as reported in Lin et al. (65).
To perform a more rigorous comparison of transport properties, three additional all-atom MD simulations were carried out (sim10a, sim10b, and sim10c) in which a structure previously simulated with BioMOCA (labeled open3 in (33), and S1 in this work; see Supplementary Material's Fig. 13 A) was simulated at 0, +100, and −100 mV.
BioMOCA simulations performed on conformation S1 over 100 ns using a 200 mM concentration of KCl showed 127 ion-crossing events when a +100 mV electrostatic bias was applied, and 57 crossing events for a bias of −100 mV (estimated conductances of 2 ± 0.18 nS and 0.9 ± 0.12 nS, respectively). The number of crossing events during all-atom MD simulations sim10b and sim10c (lasting ∼9.5 ns each) were 8 for +100 mV and 4 for −100 mV (Table 2 and Supplementary Material's Fig. 15 A), in good agreement with BioMOCA simulations, in particular, when one takes into account that the effective radius of MscS's transmembrane pore during simulations sim10a, sim10b, and sim10c decreased from ∼7 to ∼5.5 Å (see Supplementary Material's Figs. 13 and 15 B), and ionic currents determined using BioMOCA are likely overestimated because of the use of a uniform diffusion coefficient (estimated conductances in this case are 1.3 ± 0.47 nS and 0.67 ± 0.34 nS, respectively). The electrostatic potential maps for these simulations are shown in the Supplementary Material's Fig. 14 and exhibit a particularly interesting feature: the positive electrostatic barrier seen at the constriction zone of the crystal conformation is absent in this wider state of MscS and is shifted toward the cytoplasmic domain.
Overall, both methods, all-atom MD and BioMOCA, complement each other by providing a detailed view of MscS at short timescales (all-atom MD), and a less detailed view, but with significantly improved statistics, at long timescales (BioMOCA). It is important to stress that the detailed view provided by all-atom MD simulations is essential and both methodologies need to reinforce each other, since unexpected dynamical effects, possibly caused by electrostatic fields or water hydrodynamics, like widening of MscS's pore upon application of electrostatic potentials and the dewetting transitions, cannot be neglected (as they are in a BioMOCA approach) for an analysis of ion channels.
CONCLUSIONS
Computational models are an ideal tool for the investigation of structure/function relationships in proteins. Ion channels, in particular, represent a relevant example in which modeling can assist in the quest to determine functional states depicted by crystallographic structures as well as functionally relevant motions involved in transport and gating.
Electrophysiological experiments presented here and elsewhere indicate that MscS should be found in at least three different conformations (7,10,11): an open state, which exhibits a conductance of 1 nS and is slightly anionic-selective; a closed state, which should readily open in response to membrane tension; and an inactive state, which is populated in a voltage-dependent manner and in which the channel does not respond to external stimuli. Multiple intermediate conformations of so-called subconductance states observed in patch-clamp experiments at positive potentials (see Fig. 2 and (15)) may exist as well. The experimental data presented here clarifies some of the inconsistencies found in the MscS literature, particularly about the influence of voltage in activation and inactivation transitions. Based on this unambiguous characterization of MscS, a combination of theoretical and experimental tools to probe the available crystallographic structure of MscS seems to be a good strategy to determine what functional state this structure represents and to model the remaining conformations of MscS.
All-atom MD simulations of MscS described above, along with previous work focusing on gating and stability of MscS (30) as well as MscS's electrostatic properties (33), reveal dynamical and permeation properties of the entire crystal structure of MscS in its nativelike environment spanning timescales from tens to hundreds of nanoseconds. While most of the previous studies on ion channels have focused on computing the potential of mean force (35,73), we have used a direct approach that mimics the experimental conditions by applying an electric field to all atoms of the system (48). Such realistic simulations enable measurements of ionic currents that can be readily compared to experimental ionic currents determined through patch-clamp experiments. The method used here also provides electrostatic maps that can be used to determine the relevance of electrostatic interactions for ion translocation. Moreover, by using a realistic all-atom model, water structuring along the channel, thought to be relevant for ion translocation (70,73), can be readily monitored as well.
The simulations suggest that the conformation depicted by the crystal structure of MscS (17) represents an intermediate or inactive state, since its conductance is small and it is highly selective for anions. On the other hand, closed states, obtained upon release of restraints applied to the backbone of the structure in the absence of tension or external biases, are evidently nonconducting. Tension as well as large voltage can partially reopen the channel. The latter result is unexpected, since voltage is supposed to mediate inactivation and does not open the channel by itself.
Even more unexpected is the observed widening of MscS's transmembrane domain upon release of restraints while a large electrostatic bias is applied. The wider conformation is stable, exhibits straighter TM3 helices and a large conductance matching the value determined by experiments, but remains highly anion-selective. Simulations of this wider conformation without the entire cytoplasmic domain showed a less dramatic anionic selectivity, moderate rectification for negative potentials, and an overall good, although not perfect, agreement with experimental results. One could speculate then that not only does MscS's transmembrane domain need to be wider to represent a fully open channel, but also that ionizable residues in TM1 and TM2 helices need to be uncharged (54) and/or part of the cytoplasmic domain does need to move apart or undergo a conformational change upon channel opening. The function of the cytoplasmic domain itself remains unclear: ions are readily transported through its multiple side openings, while small solutes such as glutamate may not do so.
Induced permeation of ions through MscS, as observed in our simulations, also reveal interesting properties that might lead to more general principles of ion conduction in wide pores. The rectification in ionic currents observed in the simulations seems to arise both from the geometric arrangement of the MscS transmembrane pore (a funnel-like shape with the widest side oriented toward the periplasm) and the electrostatics of the pore. The latter has also a clear impact in selectivity and ion concentration at the entrances of the MscS pore. The more positively charged the pore, the greater the concentration of anions and the larger the corresponding ionic current. As observed in the simulations presented here, when the pore is wide enough, the increased concentration of anions around the pore seems to provide a dynamic and rather chaotic “ladder” that can be used by potassium ions to climb through an otherwise positive and repulsive pore. Thus, attention may be placed in future modeling on ion-ion interactions in confined environments and the effect of other charged species, such as Mg2+.
Consistent results observed in different computational studies, performed in some cases by independent groups using different methodologies, suggest that the computational characterization of MscS presented here is robust. Even the study of Spronk et al. (31), which uses a different MD engine and force field and concludes that the crystal conformation is more nearly that of an open, conducting state of the channel, is consistent with our results in that they observe high selectivity for anions, their restrained structure representing the crystal conformation exhibits low conductance, they observe a strong rectification at the high voltages probed, and their simulations show widening of the channel upon release of restraints when electrostatic fields are applied.
The simulations also raise many questions that still require answers. Is the N-terminal domain responsible for selectivity? Are the simulations capturing only partial structural rearrangements due to limited time sampling? Does the occluded state observed in simulations represent a closed or inactive state? What is the conformation adopted by the cytoplasmic domain upon channel opening/closing? Can the cytoplasmic domain be used to gate the channel? Are subconductance states selective for anions? Do they play a functional role?
Modeling of the missing N-terminal domain, along with microsecond timescale MD simulations combined with improved crystallographic studies and other experimental techniques that report the state of the protein in its native environment (such as electron paramagnetic resonance spectroscopy) will be needed to answer the questions raised above. Such studies will elucidate with more certainty structural models for the closed, inactive, and open conformations of MscS and, thereby, bridge the gap between electrophysiological measurements and simulations of MscS reported here.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
We thank Boris Martinac, D. Marien Cortes, Julio Cordero-Morales, Alek Aksimentiev, Danilo Gonzales-Nilo, Jordi Cohen, and members of the Perozo, Roux, and the Urbana Theoretical and Computational Biophysics groups for helpful discussions. The molecular images in this article were created with the molecular graphics program VMD (41).
This work was supported by funds of the National Institutes of Health to K.S. (NIH grant No. P41 RR05969 and NIH grant No. 1 RO1 GM067887) and to E.P. (NIH grant No. GM063617). The authors also acknowledge computer time provided by the National Science Foundation NRAC grant No. MCA93S028.
M. Sotomayor and V. Vasquez contributed equally to this work.
References
- 1.Hamill, O. P., and B. Martinac. 2001. Molecular basis of mechanotransduction in living cells. Physiol. Rev. 81:685–740. [DOI] [PubMed] [Google Scholar]
- 2.Perozo, E., and D. C. Rees. 2003. Structure and mechanism in prokaryotic mechanosensitive channels. Curr. Opin. Struct. Biol. 13:432–442. [DOI] [PubMed] [Google Scholar]
- 3.Sukharev, S., and D. P. Corey. 2004. Mechanosensitive channels: multiplicity of families and gating paradigms. Sci. STKE. 219:Re4. [DOI] [PubMed]
- 4.Kung, C. 2005. A possible unifying principle for mechanosensation. Nature. 436:647–654. [DOI] [PubMed] [Google Scholar]
- 5.Anishkin, A., and C. Kung. 2005. Microbial mechanosensation. Curr. Opin. Neurol. 15:397–405. [DOI] [PubMed] [Google Scholar]
- 6.Perozo, E. 2006. Gating prokaryotic mechanosensitive channels. Nat. Rev. Mol. Cell Biol. 7:109–119. [DOI] [PubMed] [Google Scholar]
- 7.Martinac, B., M. Buechner, A. H. Delcour, J. Adler, and C. Kung. 1987. Pressure-sensitive ion channel in Escherichia coli. Proc. Natl. Acad. Sci. USA. 84:2297–2301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Berrier, C., A. Coulombe, C. Houssin, and A. Ghazi. 1989. A patch-clamp study of ion channels of inner and outer membranes and of contact zones of E. coli, fused into giant liposomes. FEBS Lett. 259:27–32. [DOI] [PubMed] [Google Scholar]
- 9.Levina, N., S. Totemeyer, N. R. Stokes, P. Louis, M. A. Jones, and I. Booth. 1999. Protection of Escherichia coli cells against extreme turgor by activation of MscS and MscL mechanosensitive channels: identification of genes required for MscS activity. EMBO J. 18:1730–1737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sukharev, S. 2002. Purification of the small mechanosensitive channel of Escherichia coli (MscS): the subunit structure, conduction, and gating characteristics in liposomes. Biophys. J. 83:290–298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Akitake, B., A. Anishkin, and S. Sukharev. 2005. The dashpot mechanism of stretch-dependent gating in MscS. J. Gen. Physiol. 125:143–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kloda, A., and B. Martinac. 2002. Common evolutionary origins of mechanosensitive ion channels in archaea, bacteria and cell-walled eukarya. Archaea. 1:35–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pivetty, C. D., M. R. Yen, S. Miller, W. Bartlett, Y. Tseng, I. R. Booth, and M. H. J. Saier. 2003. Two families of mechanosensitive channel proteins. Microbiol. Mol. Biol. Rev. 67:66–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Haswell, E. S., and E. M. Meyerowitz. 2006. MscS-like proteins control plastid size and shape in Arabidopsis thaliana. Curr. Biol. 16:1–11. [DOI] [PubMed] [Google Scholar]
- 15.Shapovalov, G., and H. A. Lester. 2004. Gating transitions in bacterial ion channels measured at 3 μs resolution. J. Gen. Physiol. 124:151–161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vasquez, V., and E. Perozo. 2004. Voltage dependent gating in MscS. Biophys. J. 86:545A. [Google Scholar]
- 17.Bass, R. B., P. Strop, M. Barclay, and D. C. Rees. 2002. Crystal structure of Escherichia coli MscS, a voltage-modulated and mechanosensitive channel. Science. 298:1582–1587. [DOI] [PubMed] [Google Scholar]
- 18.Edwards, M. D., I. R. Booth, and S. Miller. 2004. Gating the bacterial mechanosensitive channels: MscS a new paradigm? Curr. Opin. Microbiol. 7:163–167. [DOI] [PubMed] [Google Scholar]
- 19.Koprowski, P., and A. Kubalski. 2003. C termini of the Escherichia coli mechanosensitive ion channel (MscS) move apart upon the channel opening. J. Biol. Chem. 278:11237–11245. [DOI] [PubMed] [Google Scholar]
- 20.Grajkowski, W., A. Kubalski, and P. Koprowski. 2005. Surface changes of the mechanosensitive channel MscS upon its activation, inactivaction and closing. Biophys. J. 88:3050–3059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Miller, S., W. Bartlett, S. Chandrasekaran, S. Simpson, M. Edwards, and I. R. Booth. 2003. Domain organization of the MscS mechanosensitive channel of Escherichia coli. EMBO J. 22:36–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Schumann, U., M. Edwards, C. Li, and I. R. Booth. 2004. The conserved carboxy-terminus of the MscS mechanosensitive channel is not essential but increases stability and activity. FEBS Lett. 572:233–237. [DOI] [PubMed] [Google Scholar]
- 23.Tieleman, D. P., P. C. Biggin, G. R. Smith, and M. S. Sansom. 2001. Simulation approaches to ion channel structure-function relationships. Q. Rev. Biophys. 34:473–561. [DOI] [PubMed] [Google Scholar]
- 24.Roux, B., and K. Schulten. 2004. Computational studies of membrane channels. Structure. 12:1343–1351. [DOI] [PubMed] [Google Scholar]
- 25.Gumbart, J., Y. Wang, A. Aksimentiev, E. Tajkhorshid, and K. Schulten. 2005. Molecular dynamics simulations of proteins in lipid bilayers. Curr. Opin. Struct. Biol. 15:423–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Miller, S., M. D. Edwards, C. Ozdemir, and I. R. Booth. 2003. The closed structure of the MscS mechanosensitive channel. J. Biol. Chem. 278:32246–32250. [DOI] [PubMed] [Google Scholar]
- 27.Anishkin, A., and S. Sukharev. 2005. Explicit channel conductance: can it be computed? Biophys. J. 88:3745–3761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Edwards, M. D., Y. Li, S. Miller, W. Barlett, S. Black, S. Dennison, I. Iscla, P. Blount, J. U. Bowie, and I. R. Booth. 2005. Pivotal role of the glycine-rich TM3 helix in gating the MscS mechanosensitive channel. Nat. Struct. Mol. Biol. 12:113–119. [DOI] [PubMed] [Google Scholar]
- 29.Nomura, T., M. Sokabe, and K. Yoshimura. 2006. Lipid-protein interaction of the MscS mechanosensitive channel examined by scanning mutagenesis. Biophys. J. 91:2874–2881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sotomayor, M., and K. Schulten. 2004. Molecular dynamics study of gating in the mechanosensitive channel of small conductance MscS. Biophys. J. 87:3050–3065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Spronk, S., D. E. Elmore, and D. A. Dougherty. 2006. Voltage-dependent hydration and conduction properties of the hydrophobic pore of the mechanosensitive channel of small conductance. Biophys. J. 90:3555–3569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Anishkin, A., and S. Sukharev. 2004. Water dynamics and dewetting transitions in the small mechanosensitive channel MscS. Biophys. J. 86:2883–2895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sotomayor, M., T. A. van der Straaten, U. Ravaioli, and K. Schulten. 2006. Electrostatic properties of the mechanosensitive channel of small conductance MscS. Biophys. J. 90:3496–3510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.van der Straaten, T. A., G. Kathawala, A. Trellakis, R. S. Eisenberg, and U. Ravaioli. 2005. BioMOCA—a Boltzmann transport Monte Carlo model for ion channel simulation. Mol. Sim. 31:151–171. [Google Scholar]
- 35.Roux, B., T. Allen, S. Berneche, and W. Im. 2004. Theoretical and computational models of biological ion channels. Q. Rev. Biophys. 37:15–103. [DOI] [PubMed] [Google Scholar]
- 36.Kurnikova, M. G., R. D. Coalson, P. Graf, and A. Nitzan. 1999. Relaxation algorithm for 3-D Poisson-Nernst-Planck theory with application to ion transport through the Gramicidin A channel. Biophys. J. 76:642–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Corry, B., S. Kuyucak, and S.-H. Chung. 2000. Tests of continuum theories as models of ion channels. II. Poisson-Nernst-Planck theory versus Brownian dynamics. Biophys. J. 78:2364–2381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gillespie, D., W. Nonner, and R. S. Eisenberg. 2002. Coupling Poisson Nernst Planck and density functional theory to calculate ion flux. J. Phys. Condens. Matter. 14:12129–12145. [Google Scholar]
- 39.Vora, T., B. Corry, and S.-H. Chung. 2006. Brownian dynamics investigation into the conductance state of the MscS channel crystal structure. Biochim. Biophys. Acta Biomembr. 1758:730–737. [DOI] [PubMed] [Google Scholar]
- 40.Hille, B. 2001. Ionic Channels of Excitable Membranes, 3rd Ed. Sinauer Associates, Sunderland, MA.
- 41.Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD—visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- 42.Phillips, J. C., R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale, and K. Schulten. 2005. Scalable molecular dynamics with NAMD. J. Comput. Chem. 26:1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.MacKerell, A. D., Jr., D. Bashford, M. Bellott, R. L. Dunbrack, Jr., J. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, I. W. E. Reiher, B. Roux, M. Schlenkrich, J. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- 44.Jorgensen, W. L., J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
- 45.Grubmüller, H., H. Heller, A. Windemuth, and K. Schulten. 1991. Generalized Verlet algorithm for efficient molecular dynamics simulations with long-range interactions. Mol. Simul. 6:121–142. [Google Scholar]
- 46.Crozier, P. S., D. Henderson, R. L. Rowley, and D. D. Busath. 2001. Model channel ion currents in NaCl-extended simple point charge water solution with applied-field molecular dynamics. Biophys. J. 81:3077–3089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Aksimentiev, A., J. B. Heng, G. Timp, and K. Schulten. 2004. Microscopic kinetics of DNA translocation through synthetic nanopores. Biophys. J. 87:2086–2097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Aksimentiev, A., and K. Schulten. 2005. Imaging α-hemolysin with molecular dynamics: ionic conductance, osmotic permeability and the electrostatic potential map. Biophys. J. 88:3745–3761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Essmann, U., L. Perera, M. L. Berkowitz, T. Darden, H. Lee, and L. G. Pedersen. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
- 50.Smart, O., J. Goodfellow, and B. Wallace. 1993. The pore dimensions of Gramicidin A. Biophys. J. 65:2455–2460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Koprowski, P., and A. Kubalski. 1998. Voltage-independent adaptation of mechanosensitive channels in Escherichia coli protoplasts. J. Membr. Biol. 164:253–262. [DOI] [PubMed] [Google Scholar]
- 52.Gil, Z., S. D. Silberberg, and K. L. Magleby. 1999. Voltage-induced membrane displacement in patch pipettes activates mechanosensitive channels. Proc. Natl. Acad. Sci. USA. 96:14594–14599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zhang, P. C., A. M. Keleshian, and F. Sachs. 2001. Voltage-induced membrane movement. Nature. 413:428–432. [DOI] [PubMed] [Google Scholar]
- 54.Cymes, G. D., Y. Ni, and C. Grosman. 2006. Probing ion-channel pores one proton at a time. Nature. 438:975–980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Liberman, Y. A., and V. P. Topaly. 1969. Permeability of biomolecular phospholipid membranes for fat-soluble ions. Biofizika. 14:452–461. [PubMed] [Google Scholar]
- 56.Haydon, D. A., and V. B. Myers. 1973. Surface charge, surface dipoles and membrane conductance. Biochim. Biophys. Acta. 307:429–443. [DOI] [PubMed] [Google Scholar]
- 57.Flewelling, R., and W. Hubbell. 1986. Hydrophobic ion interactions with membranes. Thermodynamics analysis of tetraphenylphosphonium binding to vesicles. Biophys. J. 49:531–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Flewelling, R., and W. Hubbell. 1986. The membrane dipole potential in a total membrane potential model: application to hydrophobic ion interactions with membranes. Biophys. J. 49:541–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Zhou, F., and K. Schulten. 1995. Molecular dynamics study of a membrane-water interface. J. Phys. Chem. 99:2194–2208. [Google Scholar]
- 60.Feller, S. E., R. W. Pastor, A. Rojnuckarin, S. Bogusz, and B. R. Brooks. 1996. Effect of electrostatic force truncation on interfacial and transport properties of water. J. Phys. Chem. 100:17011–17020. [Google Scholar]
- 61.Essman, U., and M. L. Berkowitz. 1999. Dynamical properties of phospholipid bilayers from computer simulation. Biophys. J. 76:2081–2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Mashl, R. J., H. L. Scott, S. Subramaniam, and E. Jakobsson. 2001. Molecular simulation of dioleoylphosphatidylcholine lipid bilayers at different levels of hydration. Biophys. J. 81:3005–3015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Saiz, L., S. Bandyopadhyay, and M. L. Klein. 2002. Towards an understanding of complex biological membranes from atomistic molecular dynamics simulations. BSR. 22:151–173. [DOI] [PubMed] [Google Scholar]
- 64.Böckmann, R. A., A. Hac, T. Heimburg, and H. Grubmüller. 2003. Effect of sodium chloride on a lipid bilayer. Biophys. J. 85:1647–1655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Lin, J.-H., N. A. Baker, and J. A. MacCammon. 2002. Bridging implicit and explicit solvent approaches for membrane electrostatics. Biophys. J. 83:1374–1379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Gunner, M. R., M. A. Saleh, E. Cross, A. ud-Doula, and M. Wise. 2000. Backbone dipoles generate positive potentials in all proteins: origins and implications of the effect. Biophys. J. 78:1126–1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Beckstein, O., and M. S. P. Sansom. 2003. Liquid-vapor oscillations of water in hydrophobic nanopores. Proc. Natl. Acad. Sci. USA. 100:7063–7068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Beckstein, O., and M. S. P. Sansom. 2004. The influence of geometry, surface character, and flexibility on the permeation of ions and water through biological pores. Phys. Biol. 1:42–52. [DOI] [PubMed] [Google Scholar]
- 69.Hummer, G., J. C. Rasaiah, and J. P. Noworyta. 2001. Water conduction through the hydrophobic channel of a carbon nanotube. Nature. 414:188–190. [DOI] [PubMed] [Google Scholar]
- 70.Dzubiella, J., R. J. Allen, and J.-P. Hansen. 2004. Electric field-controlled water permeation coupled to ion transport through a nanopore. J. Chem. Phys. 120:5001–5004. [DOI] [PubMed] [Google Scholar]
- 71.Vaitheeswaran, S., J. Rasaiah, and G. Hummer. 2004. Electric field and temperature effects on water in the narrow nonpolar pores of carbon nanotubes. J. Chem. Phys. 121:7955–7965. [DOI] [PubMed] [Google Scholar]
- 72.Chen, D. P., J. Lear, and R. S. Eisenberg. 1997. Permeation through an open channel. Poisson-Nernst-Planck theory of a synthetic ionic channel. Biophys. J. 72:97–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Peter, C., and G. Hummer. 2005. Ion transport through membrane-spanning nanopores studied by molecular dynamics simulations and continuum electrostatics calculations. Biophys. J. 89:2222–2234. [DOI] [PMC free article] [PubMed] [Google Scholar]