Mechanical Unfolding of RNA: From Hairpins to Structures with Internal Multiloops

Abstract

Mechanical unfolding of RNA structures, ranging from hairpins to ribozymes, using laser optical tweezer experiments have begun to reveal the features of the energy landscape that cannot be easily explored using conventional experiments. Upon application of constant force (f), RNA hairpins undergo cooperative transitions from folded to unfolded states whereas subdomains of ribozymes unravel one at a time. Here, we use a self-organized polymer model and Brownian dynamics simulations to probe mechanical unfolding at constant force and constant-loading rate of four RNA structures of varying complexity. For simple hairpins, such as P5GA, application of constant force or constant loading rate results in bistable cooperative transitions between folded and unfolded states without populating any intermediates. The transition state location (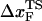) changes dramatically as the loading rate is varied. At loading rates comparable to those used in laser optical tweezer experiments, the hairpin is plastic, with 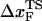being midway between folded and unfolded states; whereas at high loading rates, 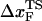moves close to the folded state, i.e., RNA is brittle. For the 29-nucleotide TAR RNA with the three-nucleotide bulge, unfolding occurs in a nearly two-state manner with an occasional pause in a high free energy metastable state. Forced unfolding of the 55 nucleotides of the Hepatitis IRES domain IIa, which has a distorted L-shaped structure, results in well-populated stable intermediates. The most stable force-stabilized intermediate represents straightening of the L-shaped structure. For these structures, the unfolding pathways can be predicted using the contact map of the native structures. Unfolding of a RNA motif with internal multiloop, namely, the 109-nucleotide prohead RNA that is part of the φ29 DNA packaging motor, at constant value of r_f occurs with three distinct rips that represent unraveling of the paired helices. The rips represent kinetic barriers to unfolding. Our work shows 1), the response of RNA to force is largely determined by the native structure; and 2), only by probing mechanical unfolding over a wide range of forces can the underlying energy landscape be fully explored.

INTRODUCTION

The discovery of self-splicing catalytic activity of ciliate Tetrahymena thermophila ribozyme (1,2) and subsequent findings that RNA molecules play an active role as enzymes (3) in many cellular processes have revolutionized RNA research. Just as for protein folding, the structures and functions of RNA enzymes (ribozymes) are linked. As a result, the RNA folding problem—namely, how a nucleotide sequence folds to the native state conformation—is important in molecular biology. Several studies from a number of groups (4–9) have shown that, under in vitro conditions, ribozymes have rugged energy landscapes. Despite significant advances in our understanding of how ribozymes fold, several outstanding issues remain, which can be addressed using single molecule experiments (4–10).

Thermodynamic and kinetic measurements in ensemble and single-molecule florescent energy transfer experiments are typically made by varying the concentration of counterions. Recently, using the laser optical tweezer (LOT) setup, mechanical force has been used to trigger folding and unfolding of RNA molecules at a single-molecule level (11,12). Mechanical force, applied to a specific position of the molecule, induces sequence- and structure-dependent response, which is reflected in the force-extension curve (FEC) that is usually fit using the worm-like model (13,14). The stability of RNAs is inferred by integrating the FECs. For simple motifs, such as hairpins, it has been shown that the stability of the native structures can be accurately measured using mechanical unfolding trajectories that exhibit multiple transitions between the folded and the unfolded state when the force is held constant (11). Similarly, thermodynamics of ribozymes can also be obtained using the nonequilibrium work theorem (15,16).

Mechanical force has also been used to probe unfolding and refolding kinetics of RNA. The cooperative reversible folding of hairpins has been shown by monitoring the end-to-end distance (R), a variable conjugate to the mechanical f, as a function of time. This procedure works best when RNA folding is described using two-state approximation. For multidomain ribozymes, the folding/unfolding kinetics is complex and new tools are required to interpret the kinetic data. In a pioneering study, Onoa et al. (12) showed that the rips in FECs for the L-21 derivative of Tetrahymena thermophila ribozyme (T. ribozyme), composed of multiple domains, are a result of unfolding of individual intact domains that are stabilized in the native state by counterion-dependent tertiary interactions.

The single molecule studies show that the response to mechanical force is a powerful tool to analyze the underlying principles of RNA self-assembly. The extraction of unfolding pathway using FECs alone is not easy, especially when the ribozyme is composed of multiple domains (12). To decipher the unfolding pathways of T. ribozyme, Onoa et al. (12) did a series of experiments in which FECs of different independently folding subdomains were used to interpret the order of unfolding of the substructures. In RNA, there is a clear separation in the free energies associated with secondary and tertiary interactions. Thus, the FEC for a multidomain ribozyme is, to a first approximation, the union of the FECs for the individual domains. Such a strategy can be used to assign a rip of FEC to the unfolding of a particular subdomain as long as the contour lengths of two different unfolded motifs are not similar. Moreover, it is known that the precise response of RNA to force depends not only on the sequence and the native structure but also on how the force is applied (17,18). Single-molecule experiments can be performed in different modes that includes either force-clamp (f is in constant) (11,19) or force-ramp (f varies in a time-dependent manner) (18,20). Theoretical studies have proposed models for obtaining a number of experimentally measurable quantities including FECs for RNA (21–23). Computational studies have shown, using RNA hairpin as an example, that the kinetics of unfolding and force-quench refolding as well the nature of unfolding depend on the magnitude of f and the loading rate (r_f) (17,24). These studies show that it is important to complement the single-molecule studies with computations that can reliably resolve key issues that are difficult to address in experiments.

In this article, we probe the forced-unfolding dynamics of RNA molecules using a simple model. Because these simulations can be used to directly monitor structures in the transition from folded to the fully stretched states, unfolding pathways can be unambiguously resolved. We introduce the self-organized polymer (SOP) model for RNA that is based only on the self-avoiding nature of the RNA and the native structure. We apply the SOP model to probe forced-unfolding of a number of RNA structures of varying complexity. Many of the subtle features of the variations in the mechanical unfolding as a function of f and r_f can be illustrated using P5GA, a simple RNA. For example, we show that the dramatic movements in the location of the unfolding transition state occur as r_f (or f) is varied. Applications to structures of increasing complexity (TAR RNA, prohead RNA from domain IIa of the Hepatitis C virus, φ29 DNA bacteriophage motor) show that discrete intermediates can be populated in force-ramp and force-clamp simulations over a certain range of forces. Our results show that the response of RNA to force is largely dependent on the architecture of the native state. More importantly, we have established that the characterization of the energy landscape requires using force values (or loading rates) over a wide range.

METHODS

Model

Our goal is to construct a model for obtaining mechanical folding and unfolding trajectories for simple RNA hairpins to large ribozymes. The model has to be realistic enough to take into account the interactions that stabilize the native fold, yet simple enough that the response to a wide range of forces and loading rates can be explored. To this end, we introduce a new class of versatile coarse-grained self-organized polymer (SOP) model that is particularly well suited for single-molecule force spectroscopy applications of large ribozymes and proteins. The SOP model can be used to probe the response of mechanical force that is applied by means of force-clamp (constant force), force-ramp, and force-quench. The reasons for using SOP model in force spectroscopy applications are the following.

1. Forced-unfolding and force-quench refolding lead to large conformational changes. For example, upon application of constant force, the end-to-end distance of the RNA changes by ∼(10–100) nm, depending on the size of RNA. Currently, single molecule experiments (laser optical tweezer or atomic force microscopy) cannot resolve structural changes below a few nm. As a result, details of the rupture of hydrogen bonds or local tertiary contacts between specific bases cannot be discerned from FEC or the dynamics of R alone. Because only large changes in R (the variable that is conjugate to force) are monitored, it is not crucial to include details of the local interactions such as bond-angle and various dihedral angle potentials.

2. We had shown, in the context of mechanical unfolding of proteins, that many of the details of unfolding pathways can be accurately computed by taking into account interactions that stabilize the native fold (25). Based on this observation, accurate predictions of unfolding forces and the location of the unfolding transition states were made for a number of proteins with β-sandwich, α/β, and α-helical folds. Our previous study (25) also suggested that it is crucial to take into account chain connectivity and attractive interactions that faithfully reproduce the contact map of a fold.

3. Electrostatic interactions are pivotal in RNA. However, under physiological condition, counterion concentration is large enough to effectively screen the electrostatic repulsion between the phosphate groups. Thus, due to effective screening (small Debye length), the repulsive electrostatic potential between phosphate groups is effectively short-ranged.

With the above observations in mind, we propose the SOP model for RNA that retains chain connectivity and favorable attractive interactions between sites that stabilize the native fold. Each interaction center represents the center of mass of a nucleotide. In terms of the coordinates {r_i, i = 1, 2, …N} of RNA with N nucleotide, the total potential energy in the SOP representation is

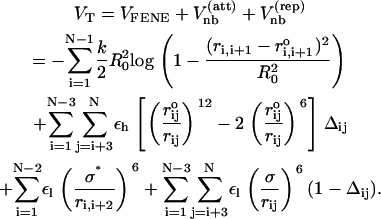(1)

The first term is for the chain connectivity. The finite extensible nonlinear elastic potential (26) is used with k = 20 kcal/(mol × Å²), R₀ = 0.2 nm, and r_{i, i+1} is the distance between neighboring beads interaction centers i and i + 1, 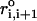is the distance in the native structure. The use of finite extensible nonlinear elastic potential is more advantageous than the standard harmonic potential, especially when considering forced-stretching because the fluctuations of r_{i, i+1} are strictly restricted around 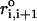with variation of ±R₀. The Lennard-Jones potential is used to account for interactions that stabilize the native topology. Native contact is defined for the pair of interaction centers whose distance is <R_C ≤ 1.4 nm in the native state for |i − j| > 2. If i and j sites are in contact in the native state, Δ_ij = 1, otherwise Δ_ij = 0. We used ε_h = 0.7 kcal/mol for the native pairs, ε_l = 1 kcal/mol for nonnative pairs. In the current version, we have neglected nonnative attractions that will not qualitatively affect the results because, under tension, such interactions are greatly destabilized. To ensure the noncrossing of the chain, we set σ = 7 Å. Only for i, i + 2 pairs we set σ* = 3.5 Å to prevent the flattening of the helical structures when the overall repulsion is large. There are five parameters in the SOP force field (k, R₀, ε_h, ε_l, and R_c) (27). Of these, the results are sensitive to the precise values of ε_h/ε_l and R_c. We have discovered that the quantitative results are insensitive to R_c as long as it is in the physical range that is determined by the RNA contact maps. In principle, the ratio ε_h/ε_l can be adjusted to obtain realistic values of forces. For simplicity, we choose a uniform value of ε_h for all RNA constructs. Surprisingly, the SOP force field, with the same set of parameters, can be used to obtain near-quantitative results for RNA molecules of varying native topology.

The time spent to calculate Lennard-Jones forces scales as 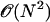. Drastic savings in computational time can be achieved by truncating the forces due to the Lennard-Jones potential for interaction pairs with r_ij > ( 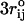or 3σ) to zero. We refer to the model as the self-organized polymer (SOP) model because it only uses the polymeric nature of the biomolecules with the crucial topological constraints that arise by the specific fold. For probing forced-unfolding of RNA (or proteins) it is sufficient to include attractive interactions only between contacts that stabilize the native state (see Eq. 1). We believe none of the results will change qualitatively if this restriction is relaxed, i.e., if nonnative interactions are also taken into account.

Simulations

Using the SOP model, we simulated the mechanical unfolding and refolding of various RNA structures from a simple hairpin to a large ribozyme (N ≈ 400). To simulate force-ramp experiments, we pull a harmonic spring (k_s = 28 pN/nm), which is attached to the 3′ end of molecule at a constant speed (v). The time(t)-dependent force acting on the 3′ end is 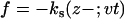, where z is z^th coordinate of the 3′ end. In force-clamp simulations a constant force is applied to one end of the molecule while the other end is fixed. Finally, in force-quench computations the force on the molecule is reduced to the final value to initiate mechanical refolding. In both the force-clamp and force-quench setups the dynamics of the linker (usually hybrid RNA/DNA handles) is not relevant; however, depending on the characteristics of the linkers, the dynamics of linker may play an important role in the force-ramp experiments (24).

Timescales

Since a typical value for the mass of a nucleotide, m ∼ 300–400 g/mol, the average distance between the adjacent nucleotides in the SOP representation of RNA is a ≈ 5 Å, ε_h = 0.7 kcal/mol, and the natural time is 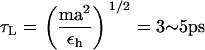. We use τ_L = 4.0 ps to convert simulation times into real times. To estimate the timescale for mechanical unfolding dynamics, we use a Brownian dynamics algorithm (28,29), for which the natural time for the overdamped motion is 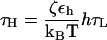. We used 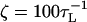in the overdamped limit, which approximately corresponds to the friction constant of a nucleotide in water.

The equations of motion in the overdamped limit are integrated using the Brownian dynamics algorithm. The position of a bead i at the time t + h is given by

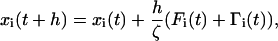(2)

where 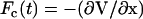; the Newtonian force acting on a bead is i; and Γ(t) is a random force on i^th bead that has a white noise spectrum. The autocorrelation function for Γ(t) in the discretized form is

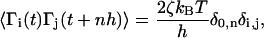(3)

where δ_{0, n} is the Krönecker delta function; n = 0, 1, 2, …; and all the force simulations are performed at T = 300 K. For the integration time step h = 0.1 τ_L, the 10⁶ integration time steps in the overdamped limit (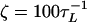) are 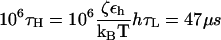with τ_L = 4 ps, ε_h ≈ 0.7 kcal/mol, and k_BT ≈ 0.6 kcal/mol. The system composed of RNA and the spring is extended along the force direction by δx every 10⁴ τ_H = 0.47 μs integration time steps. We chose δx = 0.003 nm, so that the pulling speed, 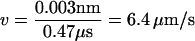, for h = 0.1 τ_L. To maintain numerical stability, neither h nor δx should be too large.

Contact map

In RNA with simple native structures, force-induced unfolding pathways can be qualitatively predicted from the native structure. To rationalize the simulated unfolding pathways it is useful to construct RNA contact maps. We generated the contact maps (Figs. 2, 4, and 5) using the definition of native contact. More precisely, we generated a matrix 𝒬 where matrix elements are

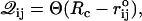(4)

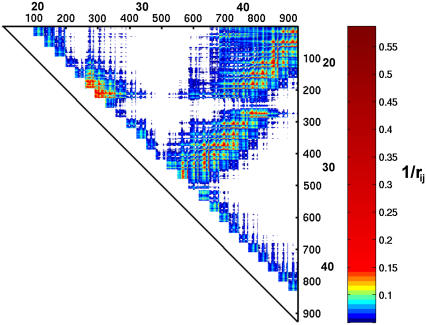
where 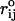is the distance between two nucleotides in the SOP representation of the native fold. Representing the native RNA using only the center of mass of each nucleotide as the interaction center is a drastic simplification. To ascertain whether the SOP representation misses any essential feature of the RNA structure we also generated the distance map using the heavy atom (C, N, O, P) coordinates. The coarse-grained model captures the important interactions on length scales, i.e., >∼0.7 nm. For example, the SOP contact map (Fig. 4 C) and the distance map (Fig. 1) of 1uud are similar.

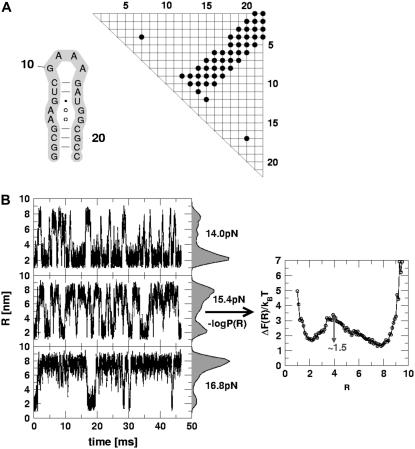
FIGURE 2.

(A) The secondary structure of P5GA hairpin and its contact map. (B) The time-dependent fluctuations of P5GA hairpin between the folded (R ≈ 1.5 nm) and unfolded (R ≈ 8 nm) states. The end-to-end distance changes spontaneously between two values. The force-clamped dynamics of the P5GA hairpin is probed for ∼45 ms. The histograms P(R) at f_c = 14.0, 15.4, and 16.8 pN are shown. The free energy profile ΔF(R) as a function of R for f_c = 15.4 pN on the right shows two-state behavior.

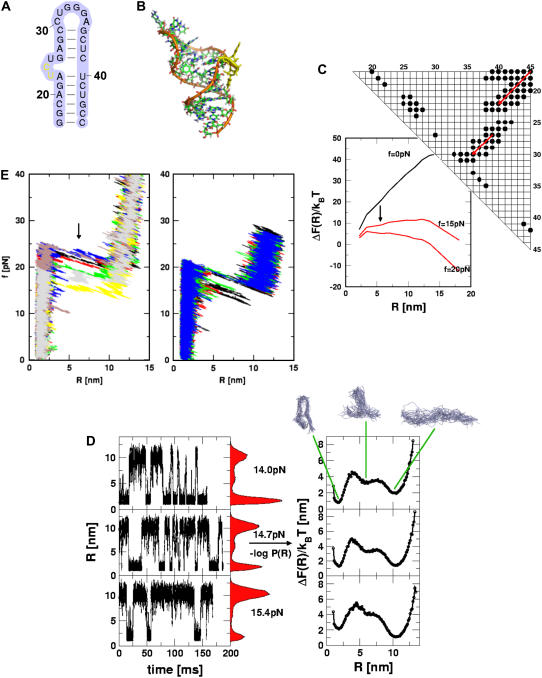
FIGURE 4.

Analysis of force-induced transitions in TAR RNA hairpin. (A) Secondary structure. (B) In the three-dimensional structure, the nucleotides (i = 23, 24) in the bulge are in yellow. (C) The contact map and the energy profile at three values of f. The plot suggests the presence of one intermediate at R ∼ 6 nm when f ≠ 0. (D) The results of force-clamp simulations at f_c = 14 pN, 14.7 pN, and 15.4 pN. The dynamics of R is probed for 150 ms and the histograms P(R) are given in the shaded color. The corresponding free energy profiles computed using ΔF(R)/k_BT = −log P(R) are shown on the right. The structures that correspond to the three basins of attraction are displayed at the top. (E) FECs at the loading rates, 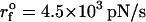(k_s = 0.7 pN/nm, v = 6.4 μm/s) (left) and 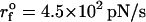(k_s = 0.7 pN/nm, v = 0.64 μm/s) (right) for a number of molecules. The arrow in the left panel is the signature of a kinetic intermediate, which is absent when r_f is reduced.

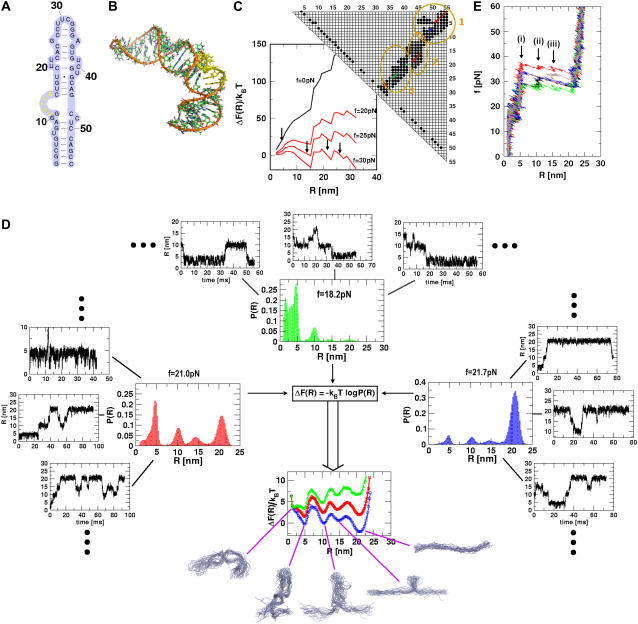
FIGURE 5.

Force-induced transitions in domain IIa of HCV IRES RNA. (A) Secondary structure. (B) The nucleotides (i = 12–16) in bulge in the three-dimensional structure are in yellow. (C) The contact map and the associated energy profile as a function of R at three values of f_c. The three clustered regions are encircled for clarity. The presence of three metastable intermediates at R ∼ 5, 15, 22, and 28 nm is indicated by arrows. (D) The results of force-clamp simulations at f_c = 18.2, 21.0, and 21.7 pN. The multiple dynamical transitions in the hairpin is probed by following the time-dependence of R. For each force, the transitions, which are probed for 800-ms duration in 10 trajectories, are shown for three molecules. The distributions P(R) averaged over time and the initial conditions (the dots indicate seven other trajectories) are shown next to the displayed trajectories, and the free energy profile ΔF(R) is shown below. The colors in the ΔF(R) profiles are the same as in P(R) at each force. The structures of the intermediates, the native conformation, and the unfolded structures are explicitly shown. (E) FECs at the loading rate, 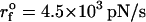(k_s = 0.7 pN/nm, v = 6.4 μm/s) for three trajectories. The arrow indicates the kinetic intermediates.

FIGURE 1.

The distance map for TAR RNA (PDB code 1uud). The distance (r_ij [Å]) between all the heavy atoms (C, N, O, P) are computed for the nucleotides (|i − j| > 2 with r_ij < 2 nm). The scale on the right gives the inverse of distances (1/r_ij) in color. Small rectangular lattices corresponds to the nucleotide unit. The index for the heavy atoms is labeled in small typeface on the i and j axes, and the index of the nucleotides (i = 17–45) is labeled using a large typeface. Upon coarse-graining using the SOP model, we obtain the contact map in Fig. 4 C.

Dynamics of rupture of contacts

The dynamics of RNA unfolding is monitored using a number of variables including the time-dependence of R and the number of nucleotide-dependent native contacts Q_i(t) that remain at time t. We define 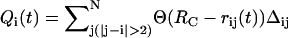, where R_C is the cutoff distance for native contacts; r_ij(t) is the distance between i and j^th nucleotide; and Δ_ij = 1 for native contact, otherwise Δ_ij = 0. If a certain subdomain of the molecule is disrupted and loses its contacts, the extension of the molecule suddenly increases and the mechanical force exerted on the end of the molecule drops instantly. These molecular events are reflected as rips in the FEC. When the time-dependence of the force f(t) or the end-to-end distance R(t) is directly compared with Q_i(t) using t as a progressive variable to describe unfolding, the direct correlation between sudden drops (sudden increase) in the value of f(t), (R(t)), and Q_i(t) enables us to unambiguously identify the structures involved in the dynamics of rupture of contacts at the nucleotide level.

RESULTS AND DISCUSSION

Mechanical unfolding of the secondary structural elements of RNA

The stability of RNA molecule in the native state can be approximated as the sum of interactions 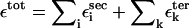where 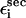and 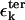are interactions that stabilize the secondary and tertiary structures, respectively, i refers to the number of secondary structural elements, and k labels the tertiary contacts that may be mediated by counterions. The contributions from the tertiary interactions are small compared to the energetics associated with the secondary interactions (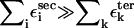). Because of the stability gap between the secondary and the tertiary interactions the analysis of FEC for RNA can be independently made domain by domain. The hairpin stacks, which can vary in the length and sequence, are among the simplest structural motifs. Additional structural complexity in RNA arises due to the presence of hairpin loops, bulges, internal loops, and internal multiloops. The remarkable structural diversity of RNA secondary structures allows us to probe the sequence and fold-dependent energy landscape using force as a perturbation. Here, we discuss the force spectroscopy of relatively simple RNA motifs using four examples. Many aspects of the physics of mechanical unfolding of RNA, such as the shifts in the transition-state locations as r_f is changed, can be understood using these simple structural motifs as examples.

Force-induced transitions in a simple hairpin (P5GA)

Liphardt et al. (11) showed that the P5ab hairpin, the construct in which P5c stem-loop and the A-rich bulge in P5a are removed from the P5abc subdomain in T. ribozyme, reversibly folds in an all-or-none fashion upon application of constant force. The equilibrium between the native basin of attraction (NBA) and the unfolded basin of attraction (UBA) can be shifted by altering the value of the constant force, f_c. To probe the two-state behavior of hairpins under force we used a smaller 22-nt hairpin, P5GA (Protein Data Bank (PDB) id: 1eor) (17,30). For the P5GA hairpin, simulations over a wide range of forces can be performed in reasonable times. The topologically simple hairpin has a single tetra-loop and nine consecutive basepairs. In an earlier study (17) we showed, using a minimal three-interaction site (TIS) model in which each nucleotide is represented by three sites, that the dynamical behavior of P5GA under tension is qualitatively similar to P5ab. The much simpler SOP representation of P5GA allows us to probe exhaustively the folding and unfolding kinetics of the hairpin that is manipulated by force-ramp, force-quench, and force-clamp.

Constant force

The hallmark of P5ab (11) and P5GA (17), when a constant force is applied to either the 3′ or the 5′ ends, is the observation of bistable kinetics. When a constant f_c is applied to the 3′ end, P5GA makes transitions (Fig. 2 B) between the UBA (R ≈ 8 nm) to the NBA (R ≈ 2 nm). At f_c = 14.0, 15.4, and 17.5 pN, a large number of transitions occur over 45-ms duration, which suggests that the hairpin dynamics is effectively ergodic. As in our previous study (17), the equilibrium constant between the folded and unfolded hairpin calculated using a long mechanical unfolding trajectory coincides with an independent ensemble average calculation, i.e., time averages are roughly equivalent to ensemble averages. When f_c = 14 pN, the residence time in the NBA is much greater than in the UBA while, at f_c = 16.8 pN, the UBA is preferentially populated (Fig. 2 B). The population of P5GA in the NBA changes when f_c is varied, as can be seen in the histogram (P(R)) of the end-to-end distance R (Fig. 2). At f_c = 15.4 pN, which is slightly above the midpoint of the NBA ↔ UBA transition, several jumps between the NBA and UBA are observed. The P(R) distribution reflects the bistable nature of the landscape. The free energy profile with respect to R is computed using ΔF(R) = −k_BT log P(R). From P(R) at f_c = 15.4 we can obtain the free energy of stability of the folded hairpin with respect to the unfolded state using ΔG ≈ f_cΔR_UF where ΔR_UF is the distance between the folded and unfolded states of P5GA. Using ΔR_UF ≈ 6 nm, we find that ΔG ≈ 13 kcal/mol. The Vienna RNA package (31), which uses entirely different free energy parameters for RNA, gives ΔG ≈ 12.8 kcal/mol. This comparison shows that the SOP model can, for simple structures, give accurate results for stability. At f_c = 15.4 pN, the transition barrier is ∼1.5 k_BT. The UBA is more populated at this value of f_c. The observed transition times are much shorter than the residence times in each basin of attraction, which is also a reflection of the underlying cooperativity of the all-or-none of nature of hopping between UBA and NBA.

Qualitatively similar results were observed in our previous study using the three-interaction site (TIS) model (17). However, the values of the midpoint of the force was approximately a factor-of-two smaller in the TIS model than in the SOP model. Despite the large differences in the nature of the force fields, the overall results are robust, suggesting that it is the underlying native structure determining the nature of the force-induced transitions in simple RNA. Indeed, for simple structures the mechanism of forced unfolding in RNA helices are imprinted in the contact map (Fig. 2 A), which is a two-dimensional representation of the folded hairpin (Methods). The clustered band in the contact map suggests that P5GA should unfold when a critical number of stacking interactions are unzipped. Thus, the contact map for P5GA (and presumably P5ab) is consistent with the observed two-state kinetics. As the architecture of the native state becomes more complex, it becomes difficult to anticipate the unfolding mechanism using the contact map alone (see below).

Force-ramp

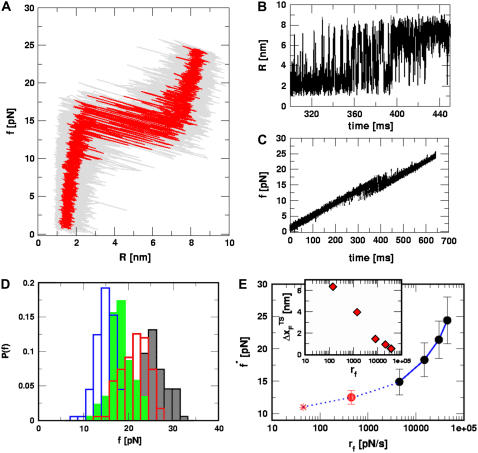
We also performed force-ramp simulations by subjecting the P5GA hairpin to a continuously changing force, i.e., varying the loading rate (Methods). The simplicity of the SOP model allows us to use values of r_f that are comparable to those used in laser optical tweezer (LOT) experiments. At 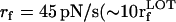), the force-extension curves show a transition to the UBA at f ∼ 13 pN (Fig. 3 A). As the force dynamically increases, we observe bistable fluctuations in the FEC between the NBA and the UBA just as when force is held constant (Fig. 3 A). The conformational fluctuations between the two states are unambiguously seen in the time-dependence of the end-to-end distance (R(t)) (Fig. 3 B). As time progresses, the force is ramped up, resulting in global unfolding (R ≈ 8 nm) for t > 400 ms (Fig. 3 B). During the timescale of simulation, we find frequent and sharp transitions between the UBA and the NBA (Fig. 3 B).

FIGURE 3.

Force-ramp unfolding of P5GA hairpin. (A) An example of FEC at the loading rate r_f = 45 pN/s (k_s = 0.07 pN/nm, v = 0.64 μm/s). The data points are recorded every 50 μs (gray), but for better illustration the running average is displayed every 500 μs (red). (B) The end-to-end distance (R) as a function of time. (C) Time-dependence of f. The loading rate r_f = df/dt is nearly a constant. (D) Distribution of unbinding forces from 100 trajectories at four loading rates 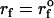, , 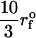, 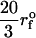and 10 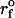((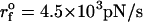k_s = 0.7 pN/nm, v = 6.4 μm/s)). The red star is the rupture force value (f* = 12.5 pN) at r_f = 45 pN/s. (E) Plot f*, the most probable unfolding force, as a function of r_f. The position of transition state 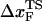is computed using 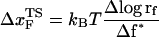. The inset shows the variation of 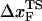as a function of r_f.

The location of the unfolding transition state 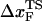for proteins and RNA is often estimated from force-ramp experiments using the variation of the most probable rupture force with r_f ([f*, log r_f] plot). The loading rate, r_f = df(t)/dt, and can be accurately estimated from the slope of the time-dependence of f(t) as a function of time. The slope of f(t) as a function of t (Fig. 3 C) is nearly the same as r_f ≈ k_s × v, where v is the pulling speed. Strictly speaking, r_f = k_eff × v with 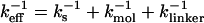and k_s, k_mol, and k_linker are the spring constants of the optical trap, the RNA molecule, and linker, respectively. Typically k_s ≪ k_mol, k_linker, thus k_eff ≈ k_s (32). Throughout the article, we obtain the loading rate using r_f = k_sv.

From the force distributions, computed at four different loading rates (Fig. 3 D), we observe that the most probable rupture force (f*) does not increase logarithmically over a wide range of loading rates (Fig. 3 E). Only if the range of r_f is restricted, f* changes linearly with log r_f (33). The location of the transition state (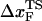) is usually calculated using 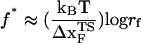(33), which may be reasonable as long as r_f range is small. However, the [f*, log r_f] plot is highly nonlinear (Fig. 3 E). If we use linear regression to analyze the [f*, log r_f] plot then 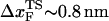for the distance between the NBA and the transition state. The small value of 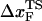is a consequence of the large variation of 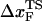as r_f is changed (17,34). If the loading rate is varied over a broad range, the r_f-dependence of 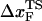is manifested as a pronounced convex curvature (24) in the [f*, log r_f] plot (Fig. 3 E). Based on the equilibrium free energy profile F(R) as a function of R (17), we expect that, for P5GA, 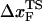≈ 3 nm if r_f is small. Indeed, from the constant force simulation results in Fig. 2 B we find 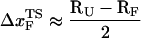. Thus, the slope of [f*, log r_f] should decrease ( 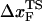increases) as r_f decreases. To illustrate the dramatic movement in the transition state, we have calculated 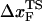using f* values for two consecutive values of r_f. For example, using f* ≈ 12.5 pN at r_f = 450 pN/s and f* ≈ 14.9 pN at r_f = 4.5 × 10³ pN/s (a value that can be realized in atomic force microscopy experiments), we obtain 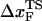≈ 4.0 nm. From the values of f* at five values of r_f, we find that 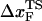can move dramatically (Fig. 3 E). In particular, we find that 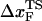changes by nearly a factor of 10 as the loading rate is decreased to values that are accessible in LOT experiments (see inset in Fig. 3 E). Because of the nearly logarithmic variation of 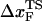on r_f over a narrow range of r_f, we do not expect 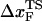to change appreciably if r_f is lowered from 45 pN/s to ≈5 pN/s. At high r_f or f_c, the unfolded state is greatly stabilized compared to the folded state. From Hammond's postulate (35), generalized to mechanical unfolding (24), it follows that, as f_c increases, 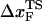should move closer to the native state. The simulations are, therefore, in accord with the Hammond's postulate.

Force-induced transition in hairpins with bulges, internal loops—TAR RNA (PDB id: 1uud)

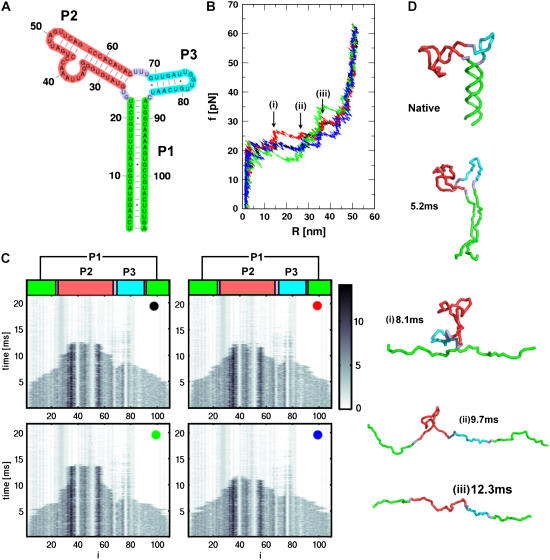
The presence of bulges or internal loops contributes to the bending of the stiff helical stack. The enhanced flexibility enables formation of intramolecular tertiary contacts or facilitates RNA-protein interactions. Base-sugar and base-phosphate as well as base-base contacts are found in these structural elements in the native structure. For example, the base group of U23 in HIV-1 TAR RNA (PDB code 1uud (36), Fig. 4 A), protrudes away from the hairpin stack and makes tertiary contacts with i = 38–41 (see three-dimensional structure in Fig. 4 B). The inherent flexibility in the bulge region also facilitates interaction with ligands (37,38).

To probe the effect of the U23C24U25 bulge (Fig. 4 A) on mechanical unfolding, we performed force-ramp and force-clamp simulations. The time-dependence of R at f_c = 14 pN (NBA is the preferred state) shows multiple transitions. Unlike in P5GA some of the transitions to UBA involves a small pause in intermediate values of R(5–8) nm, which is suggestive of a short-lived intermediate. Force-clamp simulations also show that R fluctuates between 2 nm (NBA) and 10 nm (UBA). In addition, there is a signature for an intermediate with R between (5 and 8) nm. The free energy profile ΔF(R) shows that there is a high free energy intermediate centered at R ≈ 6 nm that is metastable with respect to the NBA and the UBA. At f_c = 14 pN, the intermediate is less stable than the UBA and the NBA. It is likely that the instability of the intermediate state might make it difficult for experimental detection. As force is increased to f_c (= 14.7 pN), which is very close to the critical value at which the stabilities of the folded and stretched states are nearly equal, the residence times in the NBA and UBA are similar (see middle panel in Fig. 4 D). The P(R) distribution and ΔF(R) as a function of R show that f_c = 14.7 pN is close to the critical value. Interestingly, at f_c = 14.7 pN, the shallow high free energy intermediate is less pronounced than at f_c = 14.0 pN (Fig. 4 D). When force is further increased to f_c = 15.4 pN, the intermediate becomes essentially a part of the UBA. When the hairpins are unzipped, the presence of bulges and internal loops contributes to the formation of the intermediate state when tertiary contacts between these bulges and the rest of the structure are disrupted. In the predicted intermediate, the first six basepairs (Fig. 4 A) and additional contacts associated with these nucleotides are ruptured (see the representative structures in Fig. 4 D).

The contact map for TAR RNA has two “clusters” (Fig. 4 C): one at the upper-right corner that is associated with the lower hairpin stack, and the other (nucleotides 25–31) that represents the structure from the bulge to the apical end. As the lower stack unfolds, the force propagation goes along the diagonal for the upper cluster to the lower cluster (Fig. 4 C). We can qualitatively predict the kinetic barriers that oppose forced-unfolding at high r_f using the contact map computed from the native structure (Fig. 4 C). If hairpin unfolding occurs in a sequential unzipping manner, then we expect (upon applying force to the 3′ end) the structure to disrupt along the direction specified by the series of red arrows in Fig. 4 C. We predict that, upon disruption of the first basepair (G17C45), the other contacts involving G17 and C45 ((17,39), (17,40), (17,41), (17,42), (17,43), (17,44), (17,45), (18,45), (19,45), and (20,45)) should spontaneously break (upper cluster). Similarly, upon rupture of the G18-C44 basepair, the contacts associated with these nucleotides are disrupted (lower cluster). Therefore, the contact map suggests that rupture should occur as force propagates along the diagonal direction (red arrows in Fig. 4 C). When the contacts associated with the lower clusters unravel, a high energy intermediate is populated (Fig. 4 C). Only detailed simulations can reveal the stability and lifetime of the intermediate.

The free energy profile as a function of R can also be computed from the contact map using 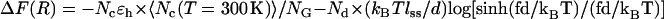, where 〈N_c(T = 300 K)〉 is the average number of contacts at temperature T = 300 K at zero force, and N_G is the corresponding quality in the PDB structure. The first term is the energetic contribution arising from N_c surviving contacts and the second term accounts for the entropy arising from the segment in which N_d contacts are disrupted. The energetic contribution using N_d and the entropy is given by the product of N_d and the entropy associated with the freely jointed chainlike model. We used Kuhn length d ∼ 2.0 nm, and the effective nucleotide length of single-strand RNA, l_ss ∼ 0.59 nm. The chain extension is given by R = R₀ + N_dl_ss, where R₀ is the end-to-end distance in the folded state. In the presence of constant force, the free energy profile tilts to UBA. The free energy profile ΔF(R) at f_c ≈ 17 pN is suggestive of an intermediate R ≈ 6 nm, whereas at higher force, the signature of the intermediate disappears (see also Fig. 4 D). Since we approximated the conformational entropy using the freely jointed chain model in this exercise, the estimate for the equilibrium critical force does not coincide with the SOP simulations, which shows that the freely jointed chain model does not estimate the entropy of the finite-sized RNA structures. Nevertheless, for simple hairpins, the number of kinetic barriers or kinetic intermediates can be predicted using this simple analysis based only on the knowledge of native contact topology. More recently, Cocco et al. (23) have proposed a similar scheme using the Monte Carlo simulations on the sequence-dependent free energy profile computed with the Turner's thermodynamic rule (39). A similar analysis was previously used to estimate equilibrium-unbinding force for proteins (40).

The FECs obtained using force-ramp simulations at r_f = 4.5 × 10³ pN/s (Fig. 4 E) also show that one intermediate is present. At this value of r_f, the presence of an intermediate occurs as a rip in the FECs (indicated using an arrow) at f ≈ 23 pN. However, when r_f is lowered by a factor of 10 (see right panel in Fig. 4 E), there is no signature of a rip at f ≈ 15–17 pN that corresponds to a pause in a high free energy metastable intermediate. As time increases, the global unfolding are preceded by fluctuations between metastable intermediates to the folded state, and TAR RNA unfolds in an all-or-none manner at a force of ∼20 pN. The picture that emerges from force-ramp simulations—namely, the presence of an intermediate at high r_f and its absence at low r_f—is completely consistent with constant force simulations. The r_f-dependent rupture of RNA structures is a general property of self-organized molecules, which we explore fully using physical arguments and simulations of ribozymes (see below).

HCV IRES domain II

We consider mechanical unfolding of the 55-nt domain IIa of the Hepatitis C Viral (HCV) genome whose NMR structure (41) is known (PDB code: 1p5m). The secondary structure map of the hairpin contains bulges and is capped by the UUCG tetraloop at the apical end (Fig. 5 A). The domain IIa oligonucleotide adopts a distorted L-shaped structure (41) (Fig. 5 B) with a relatively flexible hinge bulge (A53–A57) that is stabilized by Mg²⁺. Just as for the TAR RNA, the number of plausible kinetic intermediates (in the appropriate force regime) in the NBA → UBA transition and the range of force and R values over which they occur can be anticipated using the contact map, which reflects the nature of the native fold. The contact map (Fig. 5 C) shows that it can be partitioned into three distinct clusters that are spatially adjacent. Upon application of force to the 3′ end, the rupture of contacts associated with nucleotides G1 and C55 occurs and force propagates diagonally (see upper-right corner of Fig. 3 C). There is a change in the structure of the contact map, with the breaking of contacts involving the basepair (A8–U49) that signal the formation of the first intermediate. As a result, force propagates along the diagonal associated with second cluster. Upon disruption of A8U49, basepair force propagates along the diagonal of the subcontact map (blue line in Fig. 5 C). The second intermediate is populated when all the base contacts involving this substructure unravel. Similarly, for 1p5m, we expect population of the third intermediate, which opposes forced unfolding associated with substructure-involving contacts associated with the nucleotides near the vicinity of the green line in Fig. 5 C.

Explicit force-clamp simulations confirm that there indeed are three intermediates associated with mechanical unfolding of 1p5m. We generated 10 unfolding trajectories for a cumulative 800 ms at f_c = 21 pN. As indicated approximately by the energy profile (Fig. 5 C), we find multiple transitions between the structures that are revealed as plateaus in R(t) (Fig. 5 D). Not all the possible transitions are explicitly observed in all the trajectories. This observation may be a reflection of the intrinsic heterogeneity or stochastic nature of fluctuations. By averaging the residence time in each basin of attraction over time and the initial conditions, we obtain P(R) and the associated free energy profile (Fig. 5 D). The NBA → UBA occurs through a sequence of three intermediates. The barrier separating the UBA and the first intermediate (R ≈ 5 nm) is larger than the subsequent ones. All the intermediates, whose populations are f_c-dependent (see below), are metastable with respect to NBA and UBA. The predicted intermediates can be detected experimentally provided they are long-lived. If the lifetime of the metastable intermediate is too short, then a high time resolution would be required. An identical unfolding pathway is also found in force-ramp simulations (Fig. 5 E) in which we find, in many trajectories, three rips that represent the kinetic intermediates. The forces at which these intermediates are populated are higher because the loading rate is large. The structures that are populated along the unfolding pathway (Fig. 5 D) are in accord with the predictions based on the secondary structure and contact maps.

Just as found explicitly for TAR RNA, the intermediates may not be populated at lower f_c or r_f values. From the energy profile in Fig. 5 C, we find (approximately) that the energy associated with a putative intermediate at R ≈ 10 nm (see Fig. 5 D) is ΔF(R ≈ 10 nm) ≈50 k_BT ≈ 200 pN × nm. Thus, the smallest value of f required to transiently populate the R ≈ 10 nm intermediate is f_i ≈ ΔF(R ≈ 10 nm)/10 nm ≈ 20 pN. Only if f exceeds 20 pN, can these intermediates be significantly populated. At these forces, the predicted intermediates are metastable with respect to both UBA and NBA. Their experimental detection would depend on their lifetimes. Unless relatively high time resolution is used in experiments, for practical purposes, mechanical unfolding of domain IIa of the HCV IR2S RNA might follow two-state behavior. This simple consideration and the simulations might explain the apparent absence of intermediates in the recent constant-force LOT experiments on TAR RNA performed at f < 15 pN.

Three-way junction prohead RNA (pRNA)

The next level of complexity in the secondary structural RNA motif is the one that contains an internal multiloop. We choose the prohead RNA (PDB code 1foq (42)) which is part of the φ29 DNA packaging motor. In the context of the motor, pRNA assembles as a pentamer with each monomer consisting of two stem-loops that are separated by an internal multiloop (Fig. 6 A). Even at this level of complexity, it becomes difficult to predict the kinetic barriers associated with force-induced unfolding using the contact map alone. For the 109-nucleotide RNA, we generated four mechanical force-ramp unfolding trajectories (Fig. 6 B). The mechanical unfolding of the structure exhibits multiple rips signaling the presence of kinetic barriers separating the NBA and UBA (Fig. 6 B). The four different FECs, colored in black, red, green, and blue, are distinct. Variations in the rip dynamics from molecule to molecule may reflect the heterogeneous nature of the unfolding pathways. Upon force-ramp, unfolding of the pRNA begins at R ∼ 2 nm in all the trajectories (Fig. 6 B). The FEC in red has three rips at R ≈ 15, 28, and 38 nm, while the FEC in green has only one rip at R ≈ 38 nm. For pRNA, which is structurally more complex than the simpler three-way junction (e.g., P5abcΔA; see (11)), the details of the unraveling mechanism are difficult to extract using the FECs alone. To unambiguously extract the unfolding pathways we have calculated the time-dependence of nucleotide-dependent rupture (Fig. 6 C) of individual contacts (Methods).

FIGURE 6.

(A) The secondary structure of 109-nucleotide pRNA. (B) The four FECs of pRNA at 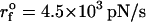(k_s = 0.7 pN/nm, v = 6.4 μm/s). (C) The rupture history of pRNA (Q_i(t)) corresponding to FECs in panel B. Here Q_i(t) is the number of contacts that the nucleotide i has at time t. The scale on the right represents the number of contacts associated with the i^th nucleotide. Darker shades have a larger number of contacts than the lighter shades. (D) Structures of pRNA at each stage of unfolding, as time progresses, is illustrated. Structures in i–iii are associated with kinetic barriers in the red trajectory in panel B.

Because of the additional stem-loop that branches out of the internal multiloop (Fig. 6 A), there are potentially two routes by which the unfolding of pRNA can proceed. One is P1 → P3 → P2, and the other is P1 → P2 → P3. We can rule out the unfolding pathways such as P2 → P1 → P3 or P3 → P2 → P1, because of the directional nature of the applied mechanical force. It should be stressed that such pathways can emerge if force is applied at points other than the ends of the chain. Using the time evolution of the native contact of the i^th nucleotide, Q_i(t), we unambiguously pin-down the time series of the rupture of individual contacts upon force-ramp (Fig. 6 C). The rupture pattern of the individual contacts in all the trajectories is very similar (Fig. 6 C), despite seeming differences in the FECs. From Fig. 6 C, it is clear that the nucleotides in P1-unravel (Q_i(t)) associated with these nucleotides are zero for t > 5 ms) early (t ∼ 5 ms), which signals the first event in pRNA unfolding. Subsequently, Q_i(t) for i ∼ (70–85) are disrupted. This shows that the smaller stem-loop in P3 opens, forming a cusp at R ∼ 15 nm in the FEC. The bigger stem-loop with the large bulge in P2 follows the opening of P3, which is manifested as a rip near R ∼ 35 nm in the FEC. Thus, the unfolding pathway for pRNA is P1 → P3 → P2. Depending on the trajectory, not all the three rips are detected in the FECs, although the unfolding pathway defined by the subdomains is not altered. The sequence of structural changes that accompany the unfolding of pRNA for the trajectory in red in Fig. 6 B is shown in Fig. 6 D. Force-ramp simulations of pRNA show that, even when the native structure is not too complex, it is difficult to predict the nature of kinetic barriers without detailed dynamical simulations or experiments. It would be interesting to test these predictions using LOT experiments.

CONCLUSIONS

We have used the self-organized polymer representation of a variety of RNA structures to predict their mechanical unfolding trajectories. Constant force and force-ramp simulations show that dramatic changes in the force profiles take place as the loading rates and the values of the force are varied. If the force is varied over a wide range, then regions of the energy landscape that cannot be accessed in conventional experiments can be probed. However, to realize the full utility of the single molecule force spectroscopy, it becomes necessary to use force in distinct modes (constant force, force-ramp, and other combinations) along with reliable computations that can mimic the experimental conditions as closely as possible. The simulations of RNA, with diverse native structures, using the SOP model illustrate the structural details in the unfolding pathways that are experimentally accessible. It is remarkable that the simple, native-state-based SOP model can quantitatively predict the FECs for a number of RNA molecules with varying degree of structural complexity. We conclude the article with the following additional remarks.

Transition state movements show changes from plastic to brittle behavior

The small size and simple architecture of RNA hairpins has allowed us to explore their response to force over a range of r_f that spans four orders of magnitude. The lowest r_f value is close to those used in LOT experiments. A key prediction of our simulations is that the location of the transition state for P5GA moves dramatically from ∼6 nm at low r_f to ∼0.5 nm at high r_f (see inset to Fig. 3 E). The large value of 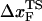at low r_f suggests that P5GA is plastic while the small 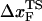at high r_f is suggestive of brittle behavior. The mechanical properties of RNA structures can be drastically altered by varying the loading rate, which is reminiscent of the changes in the visco-elastic behavior of polymeric materials that changes with frequency. The transformation from plastic to brittle behavior can be captured by the fragility index (34), used to describe mechanical unfolding of hairpins. Although we have discussed the r_f-dependent movement of the transition states using P5GA as an example, we predict that this result is general and should be observed in other RNA structures as well.

The predicted movement in the transition state as a function of r_f might help resolve the apparent differences in the estimated values of 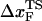in proteins using laser optical tweezer (LOT) and atomic force microscopy (AFM) experiments. The typical value of 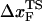for a number of proteins using AFM is approximately 0.5 nm (43), whereas 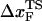for RNase H (44) (the only protein that has been experimentally studied using the LOT setup) is ∼6 nm. We believe that such a large difference is not merely due to changes in native topology and stability, which undoubtedly are important. Rather, it is due to the variations in r_f. The value of r_f in LOT is typically <10 pN/s, whereas r_f in AFM varies from (100–1000) pN/s. Our findings here suggest that the different loading rates used in the two setups might explain the large differences in the values of 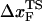. Thus, it is important to perform experiments on a given protein using both LOT and AFM setups to sort out the loading-rate-dependence of the location of the transition state.

Forced-unfolding pathways for simple RNA are encoded in the contact map

From the contact map it is possible to visualize the directions along which the applied tension propagates. As illustrated using simple RNA structures, the unfolding pathway depends on the direction of tension propagation and local structural stability. Using the contact map alone one can anticipate the most probable unfolding pathways. Here, we have shown that for P5GA, TAR RNA, and HCV IRES domain II it is possible to get a qualitative picture of forced-unfolding using the reduced representation of RNA structures in the form of contact maps. However, as the structural complexity increases and a number of alternate unfolding pathways become possible, the simple native-structure-based method alone is not always sufficient in predicting how a particular structure unravels. Such is the case in the unfolding of the three-way junction prohead RNA studied here at constant r_f.

Limitations of the SOP model

The SOP model is remarkably successful in reproducing the unfolding pathways of complex ribozymes in a realistic fashion. Surprisingly, for both proteins (27) and RNA, the SOP model is quite successful in predicting the nature of unfolding pathways. The unfolding dynamics of proteins, as well as RNA, with size exceeding 250 residues or nucleotides, can be conveniently simulated on a PC in a few days with the simulation condition used in this article (r_f ≈ 10²−10⁵ pN/s). Quenching the force to zero drives the stretched state of molecule close to the native state (27), which allows us to map the folding pathways starting from different initial conditions. The SOP model consisting of the polymeric nature and the minimal characteristics of RNA architecture is reasonable in visualizing the forced-unfolding and force-quench refolding dynamics of RNA molecules. We believe that, when accompanied with the experimental analysis, the SOP model can serve as a useful tool that provides insights into the folding/unfolding process of large macromolecules. However, as with all models, there are certain limitations of the SOP model that prevent us from making quantitative predictions of the measurable force-extension curves, especially for large RNA. The sequence and/or the counterion effect are not explicitly taken into account in the SOP model. The neglect of explicit counterions in the simulations fails to capture their specific coordination with RNA, which in turn leads to an underestimate of the local stability of the folded structure. Hence, in applying the SOP model to investigate structures in which counterion-mediated tertiary interactions determine local structures, ε_h should be varied. Despite the obvious limitations, it is clear that the SOP model is powerful enough to provide insights into the structures and pathways that are explored upon application of force. The model cannot only be used as a predictive tool (as shown here with explicit applications on systems for which experiments are not currently available) but also can be used to interpret experimental results.