Abstract
Multiple tethers are very likely extracted when leukocytes roll on the endothelium under high shear stress. Endothelial cells have been predicted to contribute more significantly to simultaneous tethers and thus to the overall rolling stabilization. We therefore extracted and quantified double tethers from endothelial cells with the micropipette aspiration technique. We show that the constitutive parameters (threshold force (F0) and effective viscosity (ηeff)) for double-tether extraction are twice those for single-tether extraction and are remarkably similar for human neonatal (F0 = 105 ± 5 pN; ηeff = 1.0 ± 0.1 pN·s/μm) and adult (F0 = 118 ± 13 pN; ηeff = 1.3 ± 0.2 pN·s/μm) dermal microvascular, and human umbilical vein (F0 = 99 ± 3 pN; ηeff = 1.0 ± 0.1 pN·s/μm) endothelial cells. Additionally, these parameters are also independent of surface receptor type, cytokine stimulation, and attachment state of the endothelial cell. We also introduce a novel correlation between the cell-substrate contact stress and gap width, with which we can predict the apparent cell-substrate separation range to be 0.01–0.1 μm during leukocyte rolling. With a biomechanical model of leukocyte rolling, we calculate the force history on the receptor-ligand bond during tether extraction and predict maximum stabilization for the double simultaneous tether extraction case.
INTRODUCTION
During the inflammatory response, leukocytes roll stably in vivo despite dramatic variations in wall shear stress. Capture and rolling of leukocytes on the endothelium is controlled in part by the kinetics of selectins and their glycoprotein ligands expressed on apposed cell surfaces (1–5). Stable rolling, characterized by lesser variation in rolling velocity and longer bond lifetimes, has been attributed to cellular mechanical features like microvillus extension and tether extraction from the rolling cell in flow-chamber studies (6–8). A possible modulation mechanism suggesting changes in tether number and architecture has been shown to explain the lesser variation (or apparent plateau) observed in neutrophil rolling velocity with increasing wall shear stress (7).
Single-tether extraction from erythrocytes, neutrophils, neuronal growth cones, outer hair cells, T-lymphocytes, endothelial cells, and liposomes (9–15) has been well characterized and the following relationship between the pulling force (F) and tether growth velocity (Ut) has been determined to hold in the physiological range of tether extraction rates (16),
 |
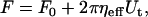(1) |
where F0 is the threshold force that is determined by the membrane tension, membrane bending stiffness, and adhesion energy between the membrane and cytoskeleton, and ηeff is the effective viscosity that is determined by the membrane viscosity, interbilayer slip, and membrane slip over the cytoskeleton (11).
Our recent study shows that double tethers extracted from leukocytes have approximately doubled the threshold force and effective viscosity (15), the two parameters used to characterize tether extraction in the physiological range. In another study, we showed that simultaneous tethers from both neutrophils and endothelial cells are likely extracted when neutrophils roll on the endothelium (12). Endothelial cells, with a fourfold lower effective viscosity relative to neutrophils, contribute much more to the composite tether length (12). Since multiple tethers can be extracted from neutrophils at high shear rate (7), it is likely that multiple simultaneous tethers can be extracted under similar conditions. As a consequence, the force drop on the receptor-ligand bond would be much more dramatic in the case of double simultaneous tethers compared to double neutrophil tethers or just single tethers from the neutrophil. Thus, it is obvious that double-tether extraction from the endothelium is a much more vital component in leukocyte rolling stability and hence needs to be examined in more detail. However, it remains to be investigated whether sufficient membrane materials would be available to facilitate double- or multiple-tether extraction from endothelial cells in addition to leukocytes. Although multiple tethers have been extracted from endothelial cells with atomic force microscopy (AFM), no correlation between the pulling force and tether growth velocity was given for multiple tethers (17).
Leukocytes exhibit site-specific mechanisms for translocation to sites of injury or infection (18,19). Thus, different interacting receptor-ligand pairs may be expected to promote rolling and capture of leukocytes depending on the type of vasculature. For instance, previous studies have investigated functional differences between HUVECs (human umbilical vein endothelial cells) and HDMECs (human dermal microvascular endothelial cells) with respect to upregulation of adhesion molecules in response to cytokine or PKC (protein kinase C) stimulation and expression of surface antigens (20–24). This partly explains different mechanisms of cell trafficking in different regions of the microvasculature. However, whether differences in signaling pathways and adhesion-molecule expression would affect mechanical properties with respect to tether extraction is unknown. One of our previous studies suggests similarity in effective viscosity and threshold force for single-tether extraction from three distinct endothelial cell lines (25). One of the objectives of this study is to examine this similarity in the context of double-tether extraction.
We therefore investigate and characterize double-tether extraction from endothelial cells in this study. We employ the micropipette aspiration technique (MAT) and use antibody-coated beads as the force transducer, as in the case of single-tether studies conducted earlier (12,25). The primary objectives of the study described here are to show that sufficient membrane materials are available for double-tether extraction from endothelial cells and to subsequently obtain and compare constitutive relations describing double-tether extraction from three distinct endothelial cell lines: HUVECs, and human neonatal and adult dermal microvascular endothelial cells (HDMECs-n and HDMECs-a, respectively). Additionally, we introduce a novel correlation between the contact stress and the cell-substrate apparent gap width for leukocyte rolling on protein-coated substrates, and utilize this in a biomechanical model to predict the force history on the receptor-ligand bond during leukocyte rolling.
MATERIALS AND METHODS
Endothelial cell culture and preparation
HUVECs and HDMECs (adult and neonatal) were purchased from Cambrex Biosciences (Walkersville, MD) and were cultured in 60-mm petri dishes or six-well culture plates with endothelial growth medium for HUVECs and microvascular endothelial growth medium for HDMECs, also obtained from Cambrex Biosciences. The cells were detached with 5 mM EDTA. For the experiments with suspended cells, detached cells were directly resuspended in CO2-independent medium and then transferred into the experimental chamber. For the experiments with attached cells, detached cells were cultured on Thermanox coverslips (NUNC, Naperville, IL), which were mounted on the side wall of the experimental chamber as described previously (12). For experiments with cytokine-stimulated endothelial cells, the cultured HUVECs and HDMECs were then treated with either 10 ng/ml tumor necrosis factor-α (TNF-α; R&D Systems, Minneapolis, MN) for 4 h or with 10 ng/ml of interleukin 1-β (IL1-β; R&D Systems) for 6 h. Thereafter, the experimental chamber was washed and refilled with CO2-independent medium supplemented with 0.1% bovine serum albumin.
Bead and micropipette preparation
Mouse anti-human monoclonal antibodies were purchased from two sources: anti-CD29 and anti-CD62E were from BD Pharmingen (San Diego, CA), and anti-CD31 and anti-CD54 were from R&D Systems. Goat antimouse antibody-coated latex beads (∼8 μm in diameter; Sigma, St. Louis, MO) were washed twice in phosphate-buffered saline (PBS, pH 7.4) and incubated with mouse anti-human antibodies (anti-CD29, anti-CD62E, anti-CD31, or anti-CD54) for 1 h at 37°C. The beads were washed twice and resuspended in PBS before use. The bead diameter in solution was determined by dividing the optical diameters (measured with bright-field microscopy) by a correction factor (26). Glass micropipettes of the desired diameter (∼8 μm in diameter) were prepared and backfilled with 1% bovine serum albumin and PBS as described previously (12). The micropipette diameter was determined with differential interference contrast microscopy and divided by a correction factor (26). In this study, the gap between the bead and micropipette was ∼0.1 μm on average.
Tether extraction
Tether-extraction experiments were conducted as described previously in the single-tether-extraction study (12). Essentially, latex beads coated with mouse antibodies to receptors expressed on endothelial cells were used as the force transducer of the MAT. The schematic for tether extraction from suspended and attached HDMECs-n is shown in Fig. 1. Briefly, the force transducer (antibody-coated bead) was aspirated into a micropipette that has a diameter almost identical to the bead diameter. A positive pressure was then used to move the bead transducer close to the cell. Once contact was established between the bead and the cell, an aspiration pressure was used to pull the bead away from the cell. In comparison to our previous study (12), the contact time in this case was increased to facilitate double-tether extraction. This process was repeated ∼50 times per cell-bead pair at each aspiration pressure (Δp). The whole experiment was recorded on either an S-VHS videotape or a DVD for postanalysis. The increased contact time between the bead transducer and the cell facilitated a high adhesion frequency, thus favoring multiple bond formation and multiple-tether extraction (27,28).
FIGURE 1.
(a) Microscopic view of the MAT schematic for tether extraction from suspended HDMECs with two-micropipette manipulation. The right pipette, holding the HDMEC-n, is not shown. (b) Microscopic view of the MAT schematic for tether extraction from surface-attached HDMECs-n with single-micropipette manipulation.
Data analysis
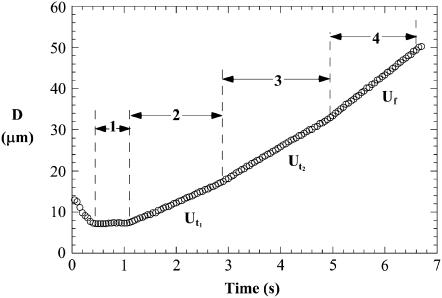
The tether-extraction experiments were analyzed as described previously (12). Briefly, the tether-extraction movies were transmitted through a monochrome frame grabber onto a Windows PC and the region of interest was tracked with a computer program to obtain the time-displacement data of the bead in ASCII format. The tether-growth (Ut) and corresponding free-motion (Uf) velocities of the bead were then obtained by linear regression. Two tether-growth velocities corresponding to a single (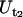
)- and a double-(
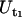) tether-extraction event were obtained in this case. A typical tracking curve for the bead transducer is shown in Fig. 2. The force imposed on the bead transducer (F), corresponding to double-tether extraction, can be calculated by (10)
 |
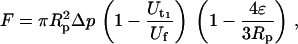(2) |
where Δp is the aspiration pressure inside the left micropipette of radius Rp and ɛ is the minimum gap width between the bead and pipette wall.
FIGURE 2.
A double-tether event tracked with the single particle tracking technique. D, displacement of the bead (force transducer). The slopes yield the tether and free-motion velocities of the force transducer in the pipette. Changes in the bead velocity for a double-tether event are marked as 1–4, the contact, double tether, single tether, and free motion, respectively, of the force transducer.
Statistical analysis
The threshold force and effective viscosity values were obtained by linear regression between the tether force (F) and the tether growth velocity (Ut), for a total of 22 different cases of double-tether extraction from three distinct endothelial cell lines. A t-test or an analysis of variance (ANOVA) was employed to investigate differences between the effective viscosities (slope/2π; ηeff) obtained from the slopes of linear regressions for each case (see Table 4) (29). Similarly, the t-test (two regressions) or the Tukey test (multiple regressions) was employed to check for differences in values of the threshold force (intercept; F0) obtained for different cases (see Table 4) (29).
TABLE 4.
Statistical comparison between HUVECs, HDMECs-a, and HDMECs-n to test for significant parameter differences
|
p-value
|
|||||
|---|---|---|---|---|---|
| Receptor | Cell state | Cell lines* | Statistic | ηeff | F0 |
| CD31 | Suspended | A and C | t-test | 0.49 | 0.54 |
| CD29 | Suspended | A and C | t-test | 0.85 | 0.73 |
| CD54 | Suspended† | A–C | ANOVA and Tukey | 0.71 | >0.05 |
| CD62E | Suspended† | A–C | ANOVA and Tukey | 0.93 | >0.05 |
| CD31 | Attached | A and C | t-test | 0.95 | 0.47 |
| CD29 | Attached | A and C | t-test | 0.87 | 0.94 |
| CD54 | Attached† | A–C | ANOVA and Tukey | 0.34 | >0.05 |
| CD62E | Attached† | A–C | ANOVA and Tukey | 0.13 | >0.05 |
Parameters tested include effective viscosity (ηeff; ANOVA or t-test), threshold force (F0; Tukey or t-test ), and p-value.
Cell lines A–C represent HUVECs, HDMECs-a, and HDMECs-n, respectively.
Cytokine-stimulated endothelial cells.
Calculation of the force drop due to tether extraction
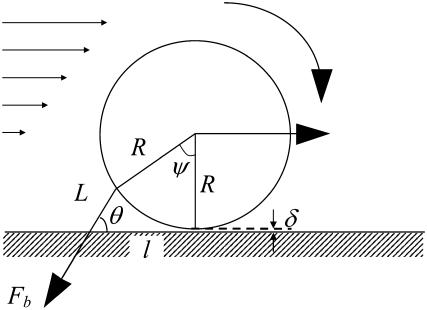
The constitutive relationship for tether extraction can be utilized in a biomechanical model of cell rolling to predict the force history on the receptor-ligand bond connecting the tethers. The model utilized earlier (12,30) was valid only for the limiting case where the cell was in contact with the substrate (31). In such a case, the motion of the cell was constrained (i.e., the translation and rotational velocities were close to zero, even though a finite ratio existed between the two, as predicted by the lubrication theory). If a finite gap was assumed between the cell and substrate, the effect of hydrodynamic resistances to translational and rotational motion of the cell could be incorporated and a more realistic model could be utilized to predict the force history on the receptor-ligand bond. The geometry of the model was similar to the one proposed earlier, with the introduction of a gap, δ, and an additional angular parameter, ψ, as illustrated in Fig. 3. The composite tether length was defined as L, the moment arm as l, the radius of the leukocyte as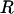 
, the apparent gap between the leukocyte and the substrate as δ, and the two angular parameters that describe the vertical and horizontal orientation of the tether as ψ and θ, respectively. The direction of fluid flow was from left to right. The equations describing the instantaneous geometry of the model were obtained as
 |
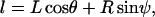(3) |
 |
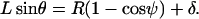(4) |
FIGURE 3.
A biomechanical model of cell rolling. This figure was modified from Shao et al. (30). The composite tether length is represented by L, the moment arm by l, the radius of the rolling cell by R, the bond force by Fb, and the gap between the cell and the substrate by δ. The direction of flow is from left to right.
The parameters and geometry equations were differentiated with time to obtain the following kinematic relations describing the motion of the leukocyte:
 |
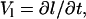(5) |
 |
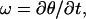(6) |
 |
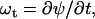(7) |
 |
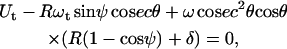(8) |
 |
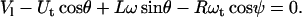(9) |
The force and torque on the cell can be expressed as linear functions of the velocity (31). The coefficients for these linear functions are weak functions of the cell-substrate gap and are denoted by hi. Analytical expressions for these hydrodynamic resistance functions, hi, were obtained from Zhao et al. (32). Assuming that the rolling cell achieves mechanical equilibrium almost instantaneously, the following equation was obtained for the force balance in the horizontal (flow) direction (32–34):
 |
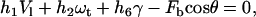(10) |
where γ is the shear rate and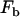 
is the force on the bond. A torque balance around the center of the cell (32–34) yielded
 |
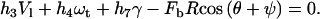(11) |
The equations describing tether extraction from the leukocyte and endothelial cell may be expressed as
 |
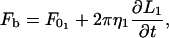(12) |
 |
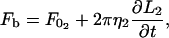(13) |
where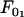 
and 
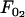represent the threshold forces 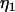and 
and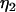 
represent the effective viscosities for tether extraction (single or double) from the leukocyte and endothelial cell, respectively. These parameters, in the case of HUVECs and HDMECs-n, were obtained by averaging threshold forces and effective viscosities obtained with different surface receptors (provided no significant difference exists between the parameter values from different receptors). The rate of growth of the simultaneous tether may be expressed as the sum of rates of growth of the individual tethers:
 |
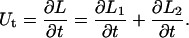(14) |
Radii of 4.25 μm for the neutrophil and 3.75 μm for the T-lymphocyte were assumed. An initial tether length of 0.35 μm, corresponding to the natural length of a microvillus, was assumed in all the calculations. The initial values of the angular parameters (θ, ψ) were calculated by simultaneously solving the equations describing the geometry of the cell (Eqs. 3 and 4) and force and torque balance at the initial state (Eqs. 10 and 11 with Vl = 0 and ωt = 0).
The force drop and tether lengths were calculated by solving Eqs. 8–14 simultaneously. The following four cases were examined in the current study: neutrophil-HUVEC and T-lymphocyte-HDMEC-n simultaneous double tether, and neutrophil and T-lymphocyte double tether alone. The calculation was repeated for shear rates of 100, 270, and 450 s−1 for each of the above cases. For all these calculations, a constant gap of 0.01 μm was assumed between the leukocyte and substrate. To verify whether the force history depends on the cell-substrate gap, the calculations were repeated with a range of predicted cell-substrate separations from 0.01 μm to 0.1 μm at shear rates of 100 and 450 s−1 for the case of single simultaneous tether extraction from the HUVEC and neutrophil (see Appendix). An optimized time step of 0.1 ms was used for all calculations and the computations were performed with MATLAB (The MathWorks, Natick, MA) by Euler's method. The force drop for the first 1 s was calculated assuming that the receptor-ligand bonds do not dissociate during this time frame. Further, it was assumed (based on tether extraction results and observations in this study) that sufficient membrane materials were available to extract tethers and that double simultaneous tethers were extracted in parallel from distinct locations on apposing cell surfaces.
RESULTS
Double-tether extraction from HUVECs and HDMECs
Our earlier study showed that single-tether extraction from HUVECs is independent of surface receptor type on the cell surface, attached or suspended state of the cell, and cytokine stimulation (12). We have also shown that the same holds true for single-tether extraction from HDMECs (25). In this study, we employed similar methodology to extract double tethers from three distinct endothelial cell lines. As shown in Fig. 2, double-tether extraction is indicated by two consecutive changes in the bead velocity, the first due to the decrease from two tethers to one and the second to the complete rupture of the adhesion.
In general, tethers are only tens of nanometers in diameter when they are extracted from normal endothelial cells, so it is difficult to observe them directly using conventional microscopic techniques. However, when tethers are extracted from endothelial cells using antibody-coated beads as the force transducer, tether diameter will increase if we allow the extracted tethers to retract back to the cell body. As shown in Fig. 4, after a relatively slower motion of the bead (compared to its free motion in the absence of tethers) was observed and the bead moved ∼70 μm inside the pipette, the suction pressure was released and set to zero. As a consequence, the bead retracted back to the cell due to the elastic energy stored in the tether and cell body. Fig. 4 clearly shows that two tethers were extracted, and from distinct locations on the cell surface. Later, we found that the bead tracking curve showed that the tether pulling force and tether growth velocity in this case agree with a double-tether extraction event shown in Fig. 2. Therefore, double tethers were indeed extracted from endothelial cells.
FIGURE 4.
Observation of double tethers extracted from an HDMEC-a with an anti-CD31-coated bead as the force transducer. The observation shown was captured during retraction of the two tethers after suction pressure on the bead was set to zero. Note that the two tethers are drawn from distinct locations on the cell surface.
Double-tether extraction from HUVECs is independent of receptor type, TNF-α stimulation, and cell attachment state
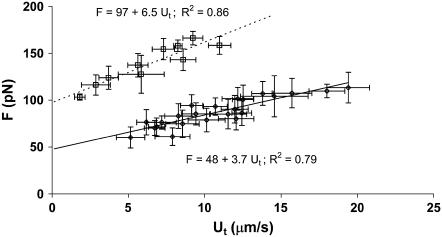
We extracted double tethers from unstimulated suspended and surface-attached HUVECs with beads coated with antibodies to CD31 or CD29, two receptors expressed constitutively on the cell surface. We also extracted double tethers from TNF-α-stimulated suspended or attached HUVECs using anti-CD54- or anti-CD62E- coated beads as force transducers. Shown in Fig. 5 is the correlation between the threshold force and effective viscosity for double- and single-tether extraction from stimulated attached HUVECs with anti-CD54-coated beads as the force transducer. The threshold force and effective viscosity for all the cases obtained from HUVECs are summarized in Table 1. Statistical analysis shows no significant difference between the effective viscosities and threshold forces for all the cases studied. Therefore, it can be concluded that double-tether extraction from HUVECs is independent of surface receptor type, TNF-α stimulation, and attachment state.
FIGURE 5.
The correlation between the pulling force and tether-growth velocity when double tethers were extracted from attached HUVECs with anti-CD54-coated beads. The correlation for single-tether extraction is also drawn for comparison (25).
TABLE 1.
Summary of parameters for double-tether extraction from HUVECs
| Receptor | F0 (pN) | ηeff (pN·s/μm) | R |
|---|---|---|---|
| Suspended and unstimulated HUVECs | |||
| CD29 | 101 ± 7 | 0.93 ± 0.18 | 0.96 |
| CD31 | 98 ± 6 | 0.82 ± 0.13 | 0.93 |
| Suspended and TNF-α-stimulated HUVECs | |||
| CD54 | 96 ± 12 | 1.03 ± 0.26 | 0.85 |
| CD62E | 103 ± 8 | 1.03 ± 0.24 | 0.90 |
| Attached and unstimulated HUVECs | |||
| CD29 | 99 ± 10 | 1.06 ± 0.21 | 0.89 |
| CD31 | 101 ± 7 | 1.09 ± 0.20 | 0.90 |
| Attached and TNF-α-stimulated HUVECs | |||
| CD54 | 97 ± 7 | 1.03 ± 0.16 | 0.93 |
| CD62E | 97 ± 6 | 0.99 ± 0.13 | 0.95 |
ηeff, effective viscosity; F0, threshold force; R, 68% confidence limits and correlation coefficients (29).
Double-tether extraction from ECs is independent of IL1-β treatment and EC lineage
Endothelial cells isolated from different regions within the vasculature might exhibit different mechanical properties with respect to tether extraction, so we extracted double tethers from adult and neonatal HDMECs (HDMECs-a and HDMECs-n). For unstimulated cells, beads coated with antibodies against CD31, CD29, and CD54 were used as force transducers. For stimulated cells, beads coated with antibodies against CD54 and CD62E were used as force transducers. We first stimulated HDMECs-a with TNF-α. After we found that TNF-α did not affect tether extraction from HDMECs-a as found in HUVECs, we chose a different proinflammatory cytokine, IL1-β, to stimulate HDMECs-n. The results from all these experiments are summarized in Tables 2 and 3. Statistical analysis again shows no significant difference between the threshold force and effective viscosity for all cases within each cell type, so double-tether extraction does not depend on IL1-β treatment. This conclusion is consistent with our previous findings in single-tether extraction from HDMECs (25).
TABLE 2.
Summary of parameters for double-tether extraction from stimulated HDMECs-a
| Receptor | F0 (pN) | ηeff (pN·s/μm) | R |
|---|---|---|---|
| Suspended and TNF-α-stimulated HDMECs-a | |||
| CD54 | 103 ± 7 | 1.15 ± 0.15 | 0.89 |
| CD62E | 131 ± 13 | 1.04 ± 0.28 | 0.85 |
| Attached and TNF-α-stimulated HDMECs-a | |||
| CD54 | 113 ± 8 | 1.35 ± 0.18 | 0.74 |
| CD62E | 125 ± 13 | 1.53 ± 0.31 | 0.95 |
ηeff, effective viscosity; F0, threshold force; R, 68% confidence limits and correlation coefficients (29).
TABLE 3.
Summary of parameters for double-tether extraction from HDMECs-n
| Receptor | F0 (pN) | ηeff (pN·s/μm) | R |
|---|---|---|---|
| Suspended and unstimulated HDMECs-a | |||
| CD29 | 105 ± 10 | 0.99 ± 0.22 | 0.91 |
| CD31 | 104 ± 10 | 0.98 ± 0.23 | 0.92 |
| CD54 | 107 ± 11 | 0.91 ± 0.26 | 0.84 |
| Suspended and IL 1-β-stimulated HDMECs-n | |||
| CD54 | 105 ± 12 | 0.94 ± 0.23 | 0.89 |
| CD62E | 103 ± 15 | 0.92 ± 0.32 | 0.85 |
| Attached and unstimulated HDMECs-n | |||
| CD29 | 100 ± 5 | 1.03 ± 0.12 | 0.94 |
| CD31 | 94 ± 6 | 1.04 ± 0.12 | 0.94 |
| CD54 | 109 ± 6 | 0.96 ± 0.14 | 0.92 |
| Attached and IL 1-β-stimulated HDMECs-n | |||
| CD54 | 113 ± 14 | 0.94 ± 0.34 | 0.74 |
| CD62E | 105 ± 6 | 1.11 ± 0.16 | 0.95 |
ηeff, effective viscosity; F0, threshold force; R, 68% confidence limits and correlation coefficients (29).
To investigate whether double-tether extraction from endothelial cells depends on cell lineage, we compared the results from all three distinct endothelial cell lines (HUVECs, HDMECs-a, and HDMECs-n; summarized in Tables 1–3). No statistical difference was found for the threshold force and effective viscosity among all three cell lines for the cases outlined in Table 4.
Double-tether extraction doubles the effective viscosity and threshold force
For all the cases we have studied, the effective viscosity and threshold force values are approximately twice those for single-tether extraction from HUVECs (12) and HDMECs (25). This can be seen clearly in Table 5, so it may be concluded that 1), double-tether extraction from endothelial cells doubles the threshold force and effective viscosity (i.e., doubles the resistance to tether flow); and 2), tether extraction from endothelial cells is a local phenomenon where two tethers are independent of each other if they are extracted simultaneously. An n-fold increase may therefore be expected for the case of extracting n parallel tethers, as long as sufficient membrane materials are available.
TABLE 5.
Summary of the ratios of effective viscosity (ηeff) and threshold force (F0) obtained from double-/single-tether extraction from HDMECs-n, HDMECs-a, and HUVECs
|
F0 (double/single)
|
ηeff (double/single)
|
|||||
|---|---|---|---|---|---|---|
| Receptor | HUVECs | HDMECs-n | HDMECs-a | HUVECs | HDMECs-n | HDMECs-a |
| Suspended and unstimulated cells | ||||||
| CD29 | 1.9 ± 0.3 | 1.9 ± 0.4 | 1.9 ± 0.6 | 2.1 ± 0.9 | ||
| CD31 | 2.0 ± 0.3 | 1.9 ± 0.4 | 2.1 ± 0.7 | 2.1 ± 0.9 | ||
| CD54 | 1.9 ± 0.5 | 1.9 ± 1.0 | ||||
| Suspended and cytokine-stimulated cells | ||||||
| CD54 | 2.1 ± 0.6 | 1.9 ± 0.5 | 1.9 ± 0.5 | 2.1 ± 1.0 | 1.9 ± 1.0 | 1.9 ± 0.6 |
| CD62E | 2.0 ± 0.3 | 1.9 ± 0.6 | 2.0 ± 0.6 | 2.1 ± 0.9 | 1.8 ± 0.5 | 2.0 ± 0.5 |
| Attached and unstimulated cells | ||||||
| CD29 | 1.9 ± 0.4 | 1.9 ± 0.3 | 2.0 ± 0.8 | 2.0 ± 0.6 | ||
| CD31 | 2.0 ± 0.3 | 2.0 ± 0.4 | 2.0 ± 0.6 | 2.0 ± 0.6 | ||
| CD54 | 1.8 ± 0.3 | 2.0 ± 0.7 | ||||
| Attached and cytokine-stimulated cells | ||||||
| CD54 | 2.0 ± 0.4 | 1.9 ± 0.4 | 1.9 ± 0.4 | 1.8 ± 0.5 | 1.6 ± 0.9 | 2.0 ± 0.5 |
| CD62E | 1.8 ± 0.3 | 1.8 ± 0.2 | 1.9 ± 0.5 | 2.3 ± 0.8 | 2.0 ± 0.5 | 2.4 ± 0.5 |
Effect of double tethers on the adhesive bond force during leukocyte rolling
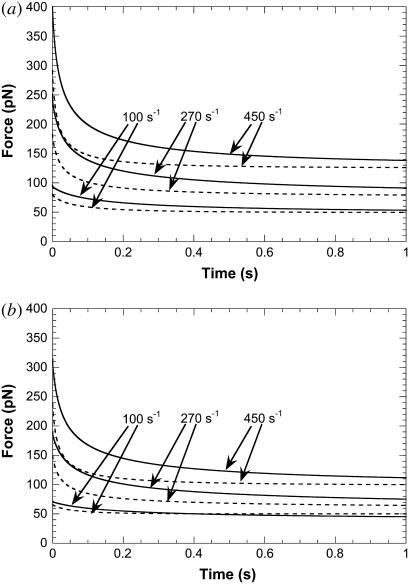
With the constitutive relationship between the threshold force and effective viscosity for double-tether extraction from endothelial cells and leukocytes, we can predict the instantaneous force on the adhesive bonds with the leukocyte rolling model described earlier. Typical shear rates of 100, 270, and 450 s−1 were used for this prediction. The dotted lines in Fig. 6, a and b, show the force history for two cases of simultaneous double-tether extraction from endothelial cells and leukocytes: 1), HUVECs and neutrophils, and 2), HDMECs-n and T-lymphocytes. The solid lines represent the force history if double tethers are only extracted from the neutrophil or T-lymphocyte. In all cases, the plotted values correspond to the force on a single-tether bond (i.e., the force on the double-tether bonds divided by 2). It is obvious that the instantaneous force on the receptor-ligand bond is smaller for the case of simultaneous double-tether extraction from the leukocyte and endothelium (relative to double-tether extraction from the leukocyte alone) and the difference becomes more prominent with increasing shear rates. The expected prolongation in the adhesive bond lifetime would thus be the maximum for the case of simultaneous double-tether extraction, followed by double-tether extraction from the leukocyte alone, then by single simultaneous tether extraction, and finally by single-tether extraction from the leukocyte alone (12). Thus, simultaneous multiple tethers would be expected to yield maximum stability to the rolling leukocytes on the endothelium.
FIGURE 6.
(a) The decrease in the bond force over time determined at shear rates of 100, 270, and 450 s−1 (from bottom to top). The dotted line represents the case of double simultaneous tether extraction from both neutrophils and HUVECs, whereas the solid line represents the case of double-tether extraction from the neutrophil alone. In both cases, the force drop on a single bond is shown. (b) The decrease in the bond force over time determined at shear rates of 100, 270, and 450 s−1 (from bottom to top). The dotted line represents the case of double simultaneous tether extraction from both T-cells and HDMECs-n, whereas the solid line represents the case of double-tether extraction from the T-cell alone. In both cases, the force drop on a single bond is shown.
Effect of the cell-substrate gap on the adhesive bond force during leukocyte rolling
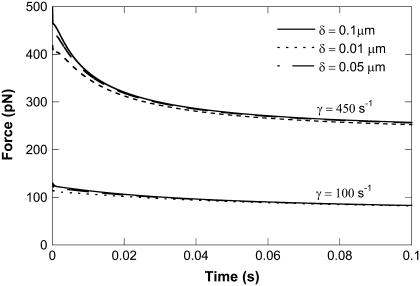
Even at the same shear rate during leukocyte rolling, the cell-substrate gap may affect the force history of the adhesive bond. To examine this effect, we first estimated the range of cell-substrate gap under physiological conditions of leukocyte rolling and then repeated the prediction described above. The evolution of the bond-force history was calculated for the case of simultaneous single tethers (one tether from the HUVEC and the other from the neutrophil with the adhesive bond in the middle) (12). We found that the cell-substrate gap was between 0.01 and 0.1 μm, as described in the Appendix. With this range of apparent gap, the force history of the adhesive bond during single simultaneous tether extraction (neutrophil-HUVEC) was calculated at two different shear rates (100 and 450 s−1) (Fig. 7). It is obvious that the force history only depends on the cell-substrate gap weakly at the shear rate of 100 s−1 and it does not change dramatically even at the shear rate of 450 s−1. Thus, it may be concluded that the force drop on the adhesive bond during leukocyte rolling is only a weak function of the cell-substrate gap, which does not remarkably influence rolling stability.
FIGURE 7.
Effect of cell-substrate gap (δ = 0.01, 0.05, 0.1 μm) on the calculated force history for the case of neutrophil-HUVEC single simultaneous tether extraction at shear rates of 100 and 450 s−1.
DISCUSSION
Single and double tethers extracted from leukocytes can dramatically reduce the force on the adhesive bond during leukocyte rolling on the endothelium. However, our recent study of endothelial tether extraction (12) clearly showed that tether extraction from HUVECs had a much more pronounced effect on the rolling stability. Therefore, in this study, we explored whether sufficient membrane materials were locally available for extraction of double tethers from endothelial cells and its implication on leukocyte rolling stability.
With the MAT, double tethers were extracted from three distinct human endothelial cell lines: HUVECs, HDMECs-a, and HDMECs-n. The results for the constitutive parameters (effective viscosity and threshold force) showed no significant difference within any of the cell lines investigated. Moreover, a comparison for different cases (Table 5) among different cell lines also showed no significant difference for the threshold force and effective viscosity calculated from linear regressions. The conclusions drawn here are similar to those established for single-tether extraction from HUVECs in our earlier study (12) and for single-tether extraction from HDMECs (25). Thus, double-tether extraction from endothelial cells can also be concluded to be independent of the surface receptors expressed on the cell, cytokine stimulation, and attachment state of the cell. Moreover, for each of the cell lines studied here, the effective viscosity and threshold force for double-tether extraction were found to be approximately twice those for single-tether extraction. Consequently, multiple tethers can be expected to be local and behave simply as multiple occurrences of the single tether, provided a membrane reservoir exists for multiple-tether flow.
Double tethers extracted in this study were identified from a change in the velocity of the force transducer. When multiple tethers were extracted with the AFM (17), they were identified from some stepwise changes in the force magnitude. Sun et al. obtained a smaller pulling force (∼29 pN) when they extracted tethers from endothelial cells at 3 μm/s (17). In our study, this force is ∼60 pN at the same pulling velocity. This discrepancy may be because different adhesion schemes (nonspecific and specific) were used in these two studies to impose pulling forces on the cell membrane. It may be also because the pulling forces imposed by the AFM and MAT were loaded with different rates initially. The location where a tether was extracted might have also contributed (we usually extracted tethers from the region close to the nucleus), since the cell membrane is not a uniform homogeneous material. In our study, the effective viscosity decreased after one adhesive bond was broken (compare regions 2 and 3 in Fig. 2). This implies that, compared with single-tether extraction, the additional resistance in double-tether extraction is not due to alterations in the underlying cellular architecture and is purely a viscous flow phenomenon. This interpretation is supported by previous observations showing that tether extraction involves membrane flow and tethers lack F-actin inside (35). Tether extraction also does not significantly or observably alter the shape of the cell, suggesting the role of cortical architecture (cytoskeleton) in preserving the integrity of the cell during membrane flow. Moreover, a dual change in the velocity of the transducer was rarely observed if the contact time between the bead and cell was decreased significantly and the occasional single tethers thereby extracted under the same conditions were shown to have the same viscosity as observed in the single-tether phase of double-tether extraction (region 3 in Fig. 2). Thus, no increase in the resistance to tether flow (36) was observed, suggesting the presence of an excess membrane reservoir in endothelial cells. In this sense, they are just like leukocytes, which store excess membrane lipids in their microvilli. In one instance, the extracted double tethers were allowed to retract back to the cell before the adhesive bonds were broken (Fig. 4), which clearly shows that two tethers were extracted locally from distinct locations on the endothelial cell surface and there was no observable competition for available lipids. Hence, it can be concluded that double tethers are extracted as a consequence of two receptor-ligand bonds being formed in the contact area.
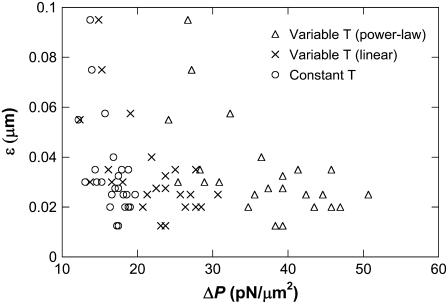
The impingement forces and the ensuing neutrophil deformation against a stationary bead were used to estimate the contact stress, which was then used to estimate the gap width between the cell and substrate (see Appendix). The gap was found to be between 0.05 and 0.1 μm for the contact forces between 150 and 250 pN. For the case of single simultaneous tether extraction from the neutrophil and HUVEC, the peak value of the contact force can be approximated as 430, 250, and 110 pN at the shear rates of 450, 270, and 100 s−1, respectively. Thus, the contact stress in this case may be expected to lie between 20 and 50 pN/μm2, assuming that the contact area increases from ∼5 μm2 to ∼8 μm2 with increasing impingement force, following the trend observed in the impingement experiment described in the Appendix. The apparent gap width for this range of contact stress would be expected to fall between 0.01 and 0.1 μm (Fig. 8). Our experimental studies on neutrophil impingement over a stationary bead show a small increase in contact stress with increasing impingement force. Thus, at relatively high shear rates, the apparent gap between the rolling cell and substrate would approach the lower limit of 0.01 μm. The force history of the adhesive bond during leukocyte rolling as a consequence of tether extraction was calculated for the range of cell-substrate gap estimated above. Although a small difference exists in the initial force history for different cell-substrate gaps, the overall stability may be expected to be similar at different gaps for all the cases considered. The initial difference is not substantially affected at higher shear rates and thus it may be reasonable to state that the cell-substrate gap does not dramatically affect leukocyte rolling stability on the endothelium. Since the force history is relatively invariable as a function of this separation, the stability achieved by increased cell deformability and contact area may be solely due to increased probability of multiple bond formation (37) and subsequent tether extraction.
FIGURE 8.
Correlation between the contact stress (ΔP) and apparent gap (ɛ) between the neutrophil and the micropipette estimated for three models of cortical tension.
Double tethers extracted from leukocytes have been shown to exhibit similar mechanical properties and confer stability by a force-drop mechanism (15). We utilized the constitutive relationships obtained for endothelial cells in this study and the leukocytes from earlier studies (10,15) to predict the force drop in the event of simultaneous double-tether extraction and compared it to double-tether extraction from the rolling leukocyte alone. The biomechanical model of cell rolling (Fig. 3) showed that the force on the receptor-ligand tether bond was significantly lowered upon simultaneous double-tether extraction relative to double-tether extraction from the leukocyte alone. The endothelial cell tether, being the major contributor to the composite tether due to an ∼4-fold lower effective viscosity relative to the passive leukocyte, is therefore the major contributing factor for leukocyte rolling stabilization. Simultaneous multiple tethers would therefore be expected to cause a significantly higher instantaneous force drop, eventually increasing the bond lifetime to facilitate firm adhesion or firm arrest of the leukocyte on the endothelium. The current mechanism is applicable to a nearly spherical leukocyte rolling on inflamed or noninflamed endothelium. Since the rolling in vivo is orchestrated by a diverse microenvironment, the mechanical properties of the endothelium may be altered upon treatment with other inflammatory mediators and a different stabilization mechanism may be expected to operate. These potential effects and the consequences of membrane depletion in the event of multiple tethers remain to be investigated in the future.
CONCLUSIONS
We have shown for the first time we know of that double tethers extracted from endothelial cells isolated from three distinct vascular sources were not different in the threshold force and effective viscosity. Statistically similar mechanical properties of HUVECs and HDMECs suggest universal mechanical stabilization mechanisms for leukocytes rolling on the endothelium. Both effective viscosity and threshold force are doubled in the event of double-tether extraction from ECs, indicating that double-tether extraction is a local phenomenon and enough membrane materials are available to thwart the competition between double tethers for lipids. Double-tether extraction is also independent of cytokine stimulation of EC, attachment state of EC, and surface receptor type expressed on the EC. Moreover, the force drop on the receptor-ligand bond is much more pronounced in the event of simultaneous double-tether extraction than double-tether extraction from the leukocyte alone.
Acknowledgments
This work was supported by the National Institutes of Health (R01 HL069947).
APPENDIX: THE CELL-SUBSTRATE GAP DURING LEUKOCYTE ROLLING
When a neutrophil rolls on the endothelium (Fig. 3), a vertical compressive force (Fc) will develop between them. This force coupled with cell deformability determines the gap width (δ) between them. If we could establish a correlation between the contact stress (Fc divided by the contact area) and δ, then the range of δ can be estimated from the contact stress experienced by the leukocyte during its rolling.
In a previous study where a neutrophil was aspirated into a micropipette completely (38), a correlation was established between the cell-pipette diameter ratio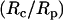 
and the apparent gap width (ɛ) or separation between the cell and glass pipette surface. In this appendix, we will relate 
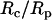to the contact stress and obtain a correlation between the contact stress and ɛ.
Neutrophils have been shown to exhibit a static cortical tension (Trest) in their passive state (39–41). Micropipette aspiration of neutrophils has also been shown to increase the apparent surface area due to smoothing of the numerous folds and projections (microvilli) (40,42). This increase in the apparent surface area can be easily determined using volume conservation for a neutrophil that is completely aspirated into a micropipette,
 |
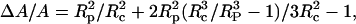(A1) |
where A is the original apparent surface area, ΔA is the change, Rc is the original cell radius, and Rp is the micropipette radius.
The cortical tension of the cell inside the micropipette changes as a function of ΔA either linearly (39,41) or according to a power-law relationship (43). Thus, if the resting cortical tension of the neutrophil is assumed to be 23.5 pN/μm and the apparent membrane expansion modulus (Kapp) is 39 pN/μm, the new cortical tension can be estimated according to the linear model as
 |
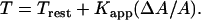(A2) |
Alternatively, the new cortical tension can also be calculated from the power-law model proposed by Drury and Dembo (41) as
 |
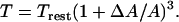(A3) |
For a neutrophil that is completely aspirated into a micropipette, assume the contact stress imposed on the neutrophil by the micropipette is ΔP. Balancing the forces in the radial direction of the micropipette will yield the relationship between the contact stress and cortical tension as
 |
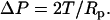(A4) |
Consequently, ΔP can be calculated for each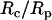 
from Eqs. A1–A4 and a correlation between ΔP and ɛ can be established as shown in Fig. 8. This correlation can thus be utilized to estimate the cell-substrate gap during leukocyte rolling if the contact stress is known.
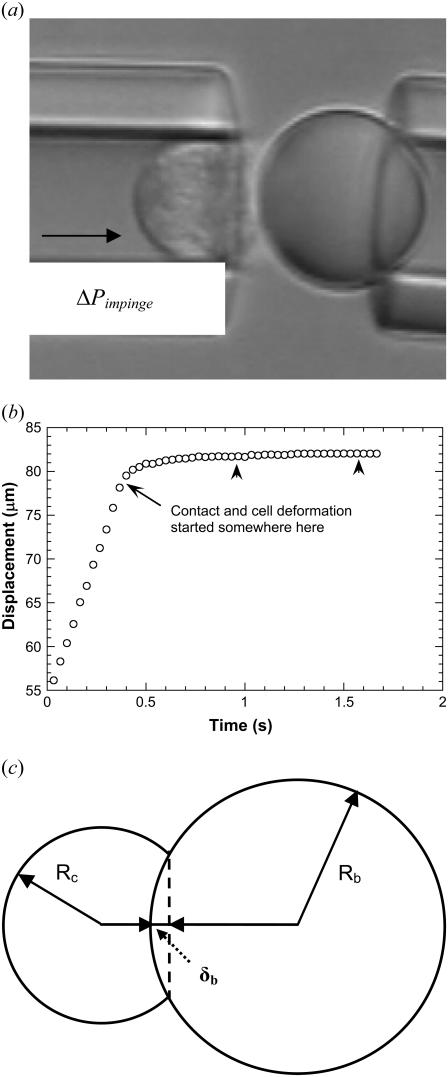
It is possible to determine the range of the contact stress by subjecting the neutrophil to different impingement forces and measuring the cell deformation in a micropipette experiment, the schematic of which is illustrated in Fig. 9 a. After the impingement forces were imposed on the neutrophil inside the micropipette by applying positive or outward pressures (ΔP), as indicated in Fig. 9 a, the neutrophil underwent a small deformation. The contact area of the neutrophil-bead pair was estimated by tracking the motion of the neutrophil with a single particle-tracking algorithm that had a resolution of ∼5 nm and quantifying the subsequent cellular deformation.
FIGURE 9.
(a) Microscopic view of the setup used to impinge a neutrophil (left) on a stationary bead (right) by applying a known outward pressure (ΔPimpinge). (b) Tracking of the neutrophil as it impinges the bead. The two smaller arrowheads mark the region used for averaging to approximate the final position of the neutrophil after deformation. (c) Geometry of the neutrophil (radius Rc) as it impinges on the bead (radius Rb). The deformation or indentation depth (δb) was used to calculate the macroscopic contact area (Eq. A7).
A typical tracking curve is shown in Fig. 9 b. The initial linear portion represents the approach of the neutrophil toward the bead under the known constant positive pressure. The approximate contact point (start of the cell deformation) is marked in Fig. 9 b. The cell deformation approached a plateau eventually and the final point was determined by taking the average of points representing the plateau (Fig. 9 b, small arrowheads). The accurate starting point was determined by fitting the region from the approximate start of the cell deformation to the plateau with
 |
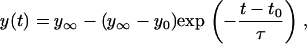(A5) |
where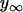 
represents the final equilibrium position of the neutrophil, y0 is the approximate starting position, t0 is the approximate start time of impingement and τ is a parameter that represents the characteristic time of the cell deformation. After we fitted Eq. A5 with the experimental data (a three-parameter fit), the total depth of impingement was quantified as 
.
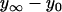The macroscopic contact area was then estimated in terms of the bead radius (Rb) and the deformation (δb) shown in Fig. 9 c. The geometric details for calculating δb from the total neutrophil deformation are illustrated in Lomakina et al. (44). The contact stress from the impingement force and the macroscopic contact area were obtained:
 |
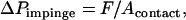(A6) |
 |
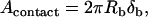(A7) |
where F is the impingement force calculated from Eq. 2 for a known pipette radius (Rp) and positive pressure (ΔP) in the pipette.
With several different positive pressures, the contact stress (ΔPimpinge) was determined as 39 ± 10, 35 ± 9, 35 ± 12, and 30 ± 11 pN/μm2, corresponding to the impingement forces of 234, 205, 175, and 146 pN, respectively. With the correlation shown in Fig. 8, the range for the cell-substrate gap (ɛ) can be predicted to lie within 0.05–0.1 μm for the range of contact stresses measured in this study. However, a gap of 0.01 μm (lower limit for the expected range of cell-substrate gap) was used in the biomechanical model since the peak contact stresses would be expected to lie between 20 and 50 pN/μm2 if the shear rates are between 100 and 450 s−1 during leukocyte rolling.
References
- 1.Alon, R., S. Chen, K. D. Puri, E. B. Finger, and T. A. Springer. 1997. The kinetics of L-selectin tethers and the mechanics of selectin-mediated rolling. J. Cell Biol. 138:1169–1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chen, S., and T. A. Springer. 2001. Selectin receptor-ligand bonds: formation limited by shear rate and dissociation governed by the Bell model. Proc. Natl. Acad. Sci. USA. 98:950–955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ley, K. 1996. Molecular mechanisms of leukocyte recruitment in the inflammatory process. Cardiovasc. Res. 32:733–742. [PubMed] [Google Scholar]
- 4.Springer, T. A. 1990. Adhesion receptors of the immune system. Nature. 346:425–434. [DOI] [PubMed] [Google Scholar]
- 5.McEver, R. P. 2002. Selectins: lectins that initiate cell adhesion under flow. Curr. Opin. Cell Biol. 14:581–586. [DOI] [PubMed] [Google Scholar]
- 6.Park, E. Y., M. J. Smith, E. S. Stropp, K. R. Snapp, J. A. DiVietro, W. F. Walker, D. W. Schmidtke, S. L. Diamond, and M. B. Lawrence. 2002. Comparison of PSGL-1 microbead and neutrophil rolling: microvillus elongation stabilizes P-selectin bond clusters. Biophys. J. 82:1835–1847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ramachandran, V., M. Williams, T. Yago, D. W. Schmidtke, and R. P. McEver. 2004. Dynamic alterations of membrane tethers stabilize leukocyte rolling on P-selectin. Proc. Natl. Acad. Sci. USA. 101:13519–13524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yago, T., A. Leppanen, H. Qiu, W. D. Marcus, M. U. Nollert, C. Zhu, R. D. Cummings, and R. P. McEver. 2002. Distinct molecular and cellular contributions to stabilizing selectin-mediated rolling under flow. J. Cell Biol. 158:787–799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hochmuth, R. M., H. C. Wiles, E. A. Evans, and J. T. McCown. 1982. Extensional flow of erythrocyte membrane from cell body to elastic tether: II. Experiment. Biophys. J. 39:83–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shao, J.-Y., and R. M. Hochmuth. 1996. Micropipette suction for measuring piconewton forces of adhesion and tether formation from neutrophil membranes. Biophys. J. 71:2892–2901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hochmuth, R. M., J.-Y. Shao, J. Dai, and M. P. Sheetz. 1996. Deformation and flow of membrane into tethers extracted from neuronal growth cones. Biophys. J. 70:358–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Girdhar, G., and J.-Y. Shao. 2004. Membrane tether extraction from human umbilical vein endothelial cells and its implication in leukocyte rolling. Biophys. J. 87:3561–3568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Li, Z., B. Anvari, M. Takashima, P. Brecht, J. H. Torres, and W. E. Brownell. 2002. Membrane tether formation from outer hair cells with optical tweezers. Biophys. J. 82:1386–1395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Waugh, R. E., and R. G. Bauserman. 1995. Physical measurements of bilayer-skeletal separation forces. Ann. Biomed. Eng. 23:308–321. [DOI] [PubMed] [Google Scholar]
- 15.Xu, G., and J.-Y. Shao. 2005. Double tether extraction from human neutrophils and its comparison with CD4+ T-lymphocytes. Biophys. J. 88:661–669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Schmidtke, D. W., and S. L. Diamond. 2000. Direct observation of membrane tethers formed during neutrophil attachment to platelets or P-selectin under physiological flow. J. Cell Biol. 149:719–729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sun, M., J. S. Graham, B. Hegedus, F. Marga, Y. Zhang, G. Forgacs, and M. Grandbois. 2005. Multiple membrane tethers probed by atomic force microscopy. Biophys. J. 89:4320–4329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Springer, T. A. 1995. Traffic signals on endothelium for lymphocyte recirculation and leukocyte emigration. Annu. Rev. Physiol. 57:827–872. [DOI] [PubMed] [Google Scholar]
- 19.Springer, T. A. 1994. Traffic signals for lymphocyte recirculation and leukocyte emigration: the multistep paradigm. Cell. 76:301–314. [DOI] [PubMed] [Google Scholar]
- 20.Lelkes, P. I., V. G. Manolopoulos, M. Silverman, S. Zhang, S. Karmiol, and B. R. Unsworth. 1996. On the possible role of endothelial cell heterogeneity in angiogenesis. In Molecular, Cellular and Clinical Aspects of Angiogenesis. M. E. Maragoudakised, editor. Plenum Press, New York. 1–17.
- 21.Mason, J. C., H. Yarwood, K. Sugars, and D. O. Haskard. 1997. Human umbilical vein and dermal microvascular endothelial cells show heterogeneity in response to PKC activation. Am. J. Physiol. Cell Physiol. 273:C1233–C1240. [DOI] [PubMed] [Google Scholar]
- 22.Petzelbauer, P., J. R. Bender, J. Wilson, and J. S. Pober. 1993. Heterogeneity of dermal microvascular endothelial cell antigen expression and cytokine responsiveness in situ and in cell culture. J. Immunol. 151:5062–5072. [PubMed] [Google Scholar]
- 23.Swerlick, R. A., K. H. Lee, L. J. Li, N. T. Sepp, S. W. Caughman, and T. J. Lawley. 1992. Regulation of vascular cell adhesion molecule 1 on human dermal microvascular endothelial cells. J. Immunol. 149:698–705. [PubMed] [Google Scholar]
- 24.Swerlick, R. A., K. H. Lee, T. M. Wick, and T. J. Lawley. 1992. Human dermal microvascular endothelial but not human umbilical vein endothelial cells express CD36 in vivo and in vitro. J. Immunol. 148:78–83. [PubMed] [Google Scholar]
- 25.Chen, Y., G. Girdhar, and J.-Y. Shao. 2006. Single membrane tether extraction from adult and neonatal dermal microvascular endothelial cells. Am. J. Physiol. Cell Physiol. In press. [DOI] [PubMed]
- 26.Shao, J.-Y., and J. Xu. 2002. A modified micropipette aspiration technique and its application to tether formation from human neutrophils. J. Biomech. Eng. 124:388–396. [DOI] [PubMed] [Google Scholar]
- 27.Piper, J. W., R. A. Swerlick, and C. Zhu. 1998. Determining force dependence of two-dimensional receptor-ligand binding affinity by centrifugation. Biophys. J. 74:492–513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shao, J.-Y., and R. M. Hochmuth. 1999. Mechanical anchoring strength of L-selectin, β2 integrins, and CD45 to neutrophil cytoskeleton and membrane. Biophys. J. 77:587–596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zar, J. H. 1999. Biostatistical Analysis. Prentice Hall, Upper Saddle River, N.J.
- 30.Shao, J.-Y., H. P. Ting-Beall, and R. M. Hochmuth. 1998. Static and dynamic lengths of neutrophil microvilli. Proc. Natl. Acad. Sci. USA. 95:6797–6802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Goldman, A. J., R. G. Cox, and H. Brenner. 1967. Slow viscous motion of a sphere parallel to a plane wall: II. Couette flow. Chem. Eng. Sci. 22:653–660. [Google Scholar]
- 32.Zhao, Y., S. Chien, and S. Weinbaum. 2001. Dynamic contact forces on leukocyte microvilli and their penetration of the endothelial glycocalyx. Biophys. J. 80:1124–1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tissot, O., A. Pierres, C. Foa, M. Delaage, and P. Bongrand. 1992. Motion of cells sedimenting on a solid surface in a laminar shear flow. Biophys. J. 61:204–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Yago, T., J. Wu, C. D. Wey, A. G. Klopocki, C. Zhu, and R. P. McEver. 2004. Catch bonds govern adhesion through L-selectin at threshold shear. J. Cell Biol. 166:913–923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Raucher, D., T. Stauffer, W. Chen, K. Shen, S. Guo, J. D. York, M. P. Sheetz, and T. Meyer. 2000. Phosphatidylinositol 4,5-bisphosphate functions as a second messenger that regulates cytoskeleton-plasma membrane adhesion. Cell. 100:221–228. [DOI] [PubMed] [Google Scholar]
- 36.Raucher, D., and M. P. Sheetz. 1999. Characteristics of a membrane reservoir buffering membrane tension. Biophys. J. 77:1992–2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Spillmann, C. M., E. Lomakina, and R. E. Waugh. 2004. Neutrophil adhesive contact dependence on impingement force. Biophys. J. 87:4237–4245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shao, J.-Y., and R. M. Hochmuth. 1997. The resistance to flow of individual human neutrophils in glass capillary tubes with diameters between 4.65 and 7.75 μm. Microcirculation. 4:61–74. [DOI] [PubMed] [Google Scholar]
- 39.Albarran, B., H. P. Ting-Beall, and R. M. Hochmuth. 2000. Effect of surface area change on cortical tension in passive neutrophils. Biophys. J. 78:187A. (Abstr.) [Google Scholar]
- 40.Evans, E., and A. Yeung. 1989. Apparent viscosity and cortical tension of blood granulocytes determined by micropipette aspiration. Biophys. J. 56:151–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Needham, D., and R. M. Hochmuth. 1992. A sensitive measure of surface stress in the resting neutrophil. Biophys. J. 61:1664–1670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Schmid-Schönbein, G. W., Y. S. Yuan, and S. Chien. 1980. Morphometry of human leukocytes. Blood. 56:866–875. [PubMed] [Google Scholar]
- 43.Drury, J. L., and M. Dembo. 2001. Aspiration of human neutrophils: effects of shear thinning and cortical dissipation. Biophys. J. 81:3166–3177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lomakina, E. B., C. M. Spillmann, M. R. King, and R. E. Waugh. 2004. Rheological analysis and measurement of neutrophil indentation. Biophys. J. 87:4246–4258. [DOI] [PMC free article] [PubMed] [Google Scholar]