Charge Structure and Counterion Distribution in Hexagonal DNA Liquid Crystal

Abstract

A hexagonal liquid crystal of DNA fragments (double-stranded, 150 basepairs) with tetramethylammonium (TMA) counterions was investigated with small angle neutron scattering (SANS). We obtained the structure factors pertaining to the DNA and counterion density correlations with contrast matching in the water. Molecular dynamics (MD) computer simulation of a hexagonal assembly of nine DNA molecules showed that the inter-DNA distance fluctuates with a correlation time around 2 ns and a standard deviation of 8.5% of the interaxial spacing. The MD simulation also showed a minimal effect of the fluctuations in inter-DNA distance on the radial counterion density profile and significant penetration of the grooves by TMA. The radial density profile of the counterions was also obtained from a Monte Carlo (MC) computer simulation of a hexagonal array of charged rods with fixed interaxial spacing. Strong ordering of the counterions between the DNA molecules and the absence of charge fluctuations at longer wavelengths was shown by the SANS number and charge structure factors. The DNA-counterion and counterion structure factors are interpreted with the correlation functions derived from the Poisson-Boltzmann equation, MD, and MC simulation. Best agreement is observed between the experimental structure factors and the prediction based on the Poisson-Boltzmann equation and/or MC simulation. The SANS results show that TMA is too large to penetrate the grooves to a significant extent, in contrast to what is shown by MD simulation.

INTRODUCTION

In biological cells, phages, and globules, DNA is often tightly packed in a liquid-crystalline fashion. The thermodynamics of such a compacted structure is largely determined by the free energies of confinement and electrostatic interactions (1–3). Intense theoretical work over the last 40 years suggests that multivalent counterions induce attraction between DNA molecules and play a central role in stabilizing the congested state. Recent advances in the physics of strongly interacting charged systems go beyond the framework of classical mean-field theories that always predict a repulsive interaction between like-charged polyelectrolytes. It is now well established that fluctuation-induced dynamic correlation of cations shared by different polyanions gives rise to an attractive electrostatic force that can explain experimental aggregation (4–6), and the idea of a strongly correlated 2D liquid of adsorbed ions, similar to a Wigner crystal, has been proposed (7,8). Detailed structural information on the charge ordering of ions at the macromolecular surface can be obtained by small-angle neutron and/or x-ray scattering (SANS and SAXS, respectively). In a SAXS study on cytoskeletal filamentous actin, counterion charge density waves along the F-actin were observed (9). In the case of DNA, scattering studies have focused on the radial density profile of counterions away from the DNA axis (10–13). To the best of our knowledge, charge ordering of counterions in dense DNA liquid crystal has never been investigated before by similar scattering methods.

Persistence-length (50-nm) DNA fragments in water or salt solutions show at least two first-order transitions from the isotropic, through the cholesteric, to the hexagonal phase, if the DNA volume fraction is increased (14,15). Here, we report SANS experiments on a hexagonal liquid crystal of DNA fragments (150 basepairs) with monovalent tetramethylammonium (TMA⁺) counterions and no added salt. The density of our samples is just above the critical boundary for the transition from the cholesteric to the hexagonal phase, with an interaxial spacing between the DNA molecules of R = 4 nm (16). The hexagonal phase is characterized by long-range order in the orientation of the DNA molecules, as shown by the typical fanlike polarized light microscopy textures. The actual range of the position order in the transverse plane perpendicular to the DNA molecules is unknown. For much longer DNA molecules (with a contour length of ∼100 persistence lengths) and higher packing fractions, high-resolution x-ray scattering experiments have shown local hexagonal structure and an increase in correlation length from ∼5 to 8 neighboring molecules once the interaxial spacing increases from 2.4 to 2.75 nm. The counterintuitive increase in correlation length with increasing interaxial spacing is thought to be related to the chiral nature of the DNA molecule (17). If we extrapolate these results to the spacing for our system, R = 4 nm, a correlation length in transverse-position order of ∼15 neighbors is obtained.

The scattering is sensitive to the set of spatial Fourier transforms of the solute density correlation functions, i.e., the partial structure factors. An advantage of the SANS approach is the possibility for contrast variation to blank or highlight certain components in a mixture of DNA, solvent, and counterions. SANS methods based on variation of the isotopic composition of the solvent have made it possible to determine individual DNA, DNA-counterion, and counterion partial structure factors in persistence-length DNA-fragment solutions with TMA⁺ counterions (11). It was seen that by optimizing some of the geometric parameters, the classical Poisson-Boltzmann (PB) or modified Poisson-Boltzmann (MPB) theory gives a good description of the counterion distribution around the DNA molecule (12). In this contribution, these investigations are done for the same DNA fragments, but at higher concentration in the hexagonal liquid crystal. In particular, we will focus on the charge structure and counterion distribution at a distance scale on the order of the interaxial spacing in the intervening space between the DNA molecules.

Supplementary to the scattering, we will also investigate the counterion distribution by Monte Carlo (MC) and full-atomic-scale molecular-dynamics (MD) computer simulations (18–21). In contrast to the classical PB or MPB theories, the MD simulations take into account a molecular description of the solvent water molecules and give, in principle, a complete picture of hydration. Furthermore, MD simulation contains a detailed atomic description of DNA and counterions. To mimic the liquid crystalline structure, we have simulated nine double-stranded DNA decamers in hexagonal arrangement and with periodic boundary conditions in both the transverse and longitudinal directions. A link of the 5′ and 3′ ends of the decamers ensures that infinitely long DNA molecules are simulated. From a 20-ns simulation, we extract information about the fluctuations in inter-DNA distance, the counterion distribution, and the range of charge fluctuations. The radial counterion profile will also be determined with a MC simulation of seven charged rods in a hexagonal arrangement. The information obtained from the computer simulations will then be used for the further analysis and interpretation of the SANS data, to arrive at a consistent picture of the charge structure and counterion distribution in the liquid crystal.

SCATTERING ANALYSIS

From intensities to structure factors

The structure factors describing the density correlations of DNA and counterions (TMA⁺) are obtained from SANS. It is convenient to consider the nucleotides and counterions as the elementary scattering units. Since the liquid crystals were prepared without adding low-molecular-weight salt, the macroscopic nucleotide concentration exactly matches the counterion concentration: ρ_n = ρ_c = ρ. The liquid crystal can accordingly be considered as a three-component system, i.e., DNA nucleotides, counterions, and water solvent. It was checked that the intensities on the two-dimensional, planar detector were isotropic due to the mosaic spread, so the liquid crystals are not macroscopically aligned with respect to the incident beam. The coherent part of the solvent-corrected and isotropically averaged intensity is given by the sum of three partial structure factors describing the density correlations among DNA and counterions:

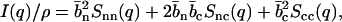(1)

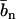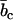with the nucleotide and counterion scattering length contrasts and , respectively. Momentum transfer q is defined by the wavelength λ and scattering angle θ between the incident and scattered beam according to 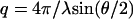. The partial structure factors 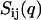are the spatial Fourier transforms of the nucleotide and counterion density correlation functions

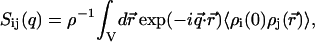(2)

with i and j = n and c. In the absence of inter-DNA interactions, the partial structure factors 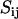are normalized to the number of nucleotides per DNA molecule at q = 0. In an H₂O/D₂O solvent mixture, the scattering length contrast is given by

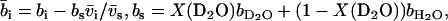(3)

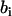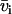with X(D₂O) the D₂O mole fraction of the solvent. The solute (i) and solvent (s) have scattering lengths and and partial molar volumes and 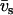, respectively. In our SANS experiments, the DNA and counterion structure factors are obtained from the intensities by contrast variation in the water, i.e., by adjusting the solvent scattering length .

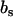Number and charge structure factor

The structure of the DNA liquid crystal can be described in terms of the partial structure factors S_ij(q) with i and j = n and c, but certain linear combinations of these functions are of more physical interest (22). The number structure factor

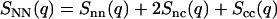(4)

is the Fourier transform of the correlation function pertaining to correlations in the sum of the local DNA and counterion densities, ρ_N = ρ_n + ρ_c, and is closest in significance to the single structure factor of a one-component (or one-solute) system. It shows a maximum at wavelengths on the order of the inverse correlation distance of the assembly of DNA and counterions. The charge structure factor

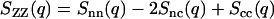(5)

describes the correlations in the difference of the local DNA and counterion densities ρ_Z = ρ_n − ρ_c (i.e., the charge). In particular, the effects of strong charge ordering reflect themselves in a sharp peak at wave lengths on the order of the inverse screening length. The charge structure factor should obey the Stillinger-Lovett sum rules (23). In the q → 0 limit the charge structure goes to zero because of overall charge neutrality. By expanding Eq. 5 up to the second power of q, one obtains the second moment of the charge density pair correlation, which is a definition of the screening length. For high q values, the charge structure factor decreases with increasing q, because the internal structure of the charge carriers is probed.

Comparison of the number and charge structure factors thus gives information about the extent of the local charge versus total density correlations. As we will see below, the counterions are strongly ordered and correlated with the DNA molecules. In the case of the existence of a distinct double-layer structure and the absence of significant charge fluctuations at larger length scales, the partial structure factors can be further evaluated with the cell model.

Cell model

The requirement for applying the cell model is that the DNA chain is locally rodlike over a length far exceeding the double-layer thickness and bearing a sufficiently large number of charges. The DNA molecule with the longitudinal axis projected nucleotide repeat distance A = 0.171 nm is placed along the z axis of a coaxial cylinder of radius r_cell. The cell radius is determined by the nucleotide concentration ρ_n through 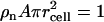. In the longitudinal direction (along the DNA axis), the nucleotide and counterion distributions are assumed to be uniform while perpendicular to this axis, the corresponding densities are given by the radial concentration profiles and 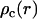, respectively. A self-consistent charge distribution can be obtained using the cell model and the solution to the PB equation. We will also determine the radial distribution of the counterions with MD simulation of an assembly of nine DNA molecules in hexagonal arrangement.

Within this range of momentum transfer the scattering is sensitive to correlations over distances of the order of the double-layer thickness and the effects of finite contour length and flexibility are negligible. The partial structure factors can then be expressed as a product of terms involving the radial profiles and a term related to the structure of an equivalent solution of DNA molecules with vanishing cross-section

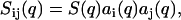(6)

with the cylindrical Fourier (Hankel) transformation of the radial profile

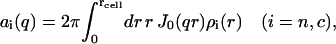(7)

and J₀ denotes the zero-order Bessel function of the first kind (12,24). The term 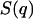, which describes inter-DNA interference, can be eliminated by taking the ratios of the partial structure factors according to

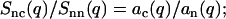(8)

and

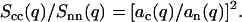(9)

From the full set of partial structure factors, information on the radial counterion density profile can hence be obtained without a model of inter-DNA correlations.

Net charge fluctuations of the cell are required to be minimal, i.e., the DNA charge should be compensated within a distance on the order of half the interaxial spacing at all times. Furthermore, in the derivation of Eq. 6 small ion-density fluctuations about the average radial profile are ignored. These fluctuations give an additional scattering contribution to the counterion structure factor S_cc only. The cross term S_nc is expected to be unaffected due to the heterodyne interference between the amplitudes scattered by the DNA and the counterions (25–27). The latter condition will be checked below by a comparison of S_nc/S_nn, as directly obtained from MD simulation, with the ratio of the Hankel transforms of the radial profiles.

The factorization of the structure factors according to Eq. 6 is important for the data analysis procedure. The structure factor of an equivalent solution of DNA molecules with vanishing cross section, S(q) is positive definite, since it represents a scattered intensity (i.e., a squared amplitude). As a result of the factorization, the intensities in Eq. 1 can be expressed in terms of two factors 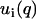rather than three partial structure factors S_ij(q) (i and j = n and c)

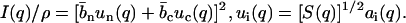(10)

As shown in previous work on more dilute samples of the same DNA fragments, explicit use of Eq. 6 in the data analysis procedure according to Eq. 10 is consistent with a model-free three-parameter fit of all partial structure factors (12). The concomitant reduction in number of adjustable parameters results in improved statistical accuracy in the derived structure factors. For this data set, we found likewise that the model-free three-parameter fit gives the same results, albeit with larger uncertainty.

Radial profiles

The transform Eq. 7 can be further evaluated using analytical expressions of the radial densities. If the radial DNA density is assumed to be uniform for 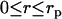, and given by 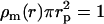and zero for 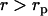, with r_p the DNA radius, one obtains

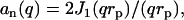(11)

with J₁ the first-order Bessel function of the first kind. The DNA cross-section might also be described by a Gaussian radial density profile with second moment 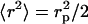. In this range of momentum transfer, the Hankel transform of such Gaussian profile is very similar to Eq. 11, and the radius r_p can be interpreted as a cross-sectional radius of gyration of the DNA molecule.

The radial counterion density profile 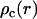will be obtained from MD/MC simulation as well as the analytic solution of the PB equation in the cell model (28–30). In the MD simulations, which include ionic correlation effects, the radial counterion profiles are obtained from a full atomic description. In the PB approach, the counterions are treated as pointlike particles, and the effect of counterion radius including an effective hydration shell is taken into account through a distance of closest approach. Besides the cell radius, the structural parameters are the distance of closest approach between the counterion center of mass and the DNA spine-axis r_c, and the linear charge density parameter ξ = Q/A, Q being the Bjerrum length 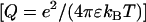. The distance of closest approach, cell radius, and nucleotide (charge) repeat distance were fixed at the same values as obtained from fitting of the structure factors to the SANS data in previous work of more dilute DNA-TMA samples, with values listed in Table 1. The distance of closest approach is not necessarily equal to the DNA radius r_p; rather, one expects a slightly larger value due to counterion size and intermediate hydration shell.

TABLE 1.

Geometric parameters of DNA

A	rp	rc	rcell	Lp	L
0.171	0.8	1.4	2.0	50	54

Values are given in nanometers. A, spine-axis projected repeat distance; r_p, cross-sectional DNA radius of gyration; r_c, distance of closest approach to the DNA spine axis; r_cell, cell radius (0.74 mol nucleotides/dm³); L_p, persistence length; and L, contour length.

MATERIALS AND METHODS

Isolation of DNA fragments

DNA fragments were obtained by micrococcal nuclease digestion of calf thymus chromatin (31). After precipitation in cold 2-propanol, the DNA pellet was dried under reduced pressure at room temperature. The DNA was brought to the salt-free sodium form by dissolving it in a buffer of 50 mM NaCl, 24 mM EDTA and by extensive dialysis against water (purified by a Millipore system with conductivity <1 × 10⁻⁶ Ω⁻¹ cm⁻¹). To avoid denaturation, care was taken that the DNA concentration did not drop below 3 × 10⁻³ mol nucleotide/dm³. The differential molecular weight distribution was monitored by size exclusion chromatography (SEC) with light-scattering detection. Further SEC fractionation resulted in a relatively monodisperse mononucleosomal DNA eluent fraction with weight-average molecular weight M_w = 104,000 (157 basepairs) and M_w/M_n = 1.14. The ratios of the optical absorbencies A₂₆₀/A₂₈₀ = 1.91 and A₂₆₀/A₂₇₀ = 1.21 indicate that the material is essentially free of protein and phenol, respectively. DNA with TMA⁺ counterions was prepared by pouring a Na-DNA solution through a cation exchange resin (AG 50W X8, Biorad, Hercules, CA). Atomic absorbance spectroscopy showed that the residual sodium content in TMA-DNA (without salt) is <1%. The hypochromic effect at 260 nm exceeds 35%, which confirms the integrity of the double helix. The material was freeze-dried and the residual water content was determined by infrared spectroscopy.

Concentrations were determined by weight, using the water content in the freeze-dried materials, and checked with ultraviolet spectroscopy. A set of samples were prepared with 0.74 mol nucleotide/dm³ TMA-DNA (i.e., without added simple salt). This concentration is just above the melting concentration of the hexagonal phase (16). We have checked with polarized light microscopy that our samples exhibit the characteristic fanlike textures pertaining to a hexagonal molecular arrangement (14). For contrast variation, the samples were prepared in 0, 41, 64, and 99% D₂O. The solvent compositions were determined by weight and checked with infrared spectroscopy as well as by the values for transmission. Scattering-length contrasts were calculated using Eq. 3 and the parameters in Table 2 and are collected in Table 3. The DNA scattering length has been calculated using the values reported by Jacrot (32) and according to the calf-thymus base composition A/G/C/T/5-methylcytosine = 0.28:0.22:0.21:0.28:0.01. Reference solvent samples with matching H₂O/D₂O composition were also prepared. Standard quartz sample containers with 0.1-cm (for samples in pure H₂O) or 0.2-cm path length were used.

TABLE 2.

Partial molar volumes and scattering lengths

Solute	(cm3/mole)	bi (10−12 cm)
DNA	172	9.772 + 2.020X
TMA+	84	−0.89
H2O	18	−0.168
D2O	18	1.915

X denotes the D₂O mole fraction (effect of exchangeable hydrogen). The partial molar volume of the nucleotide is based on the specific volume of calf thymus NaDNA at 298 K, 0.50 ml/g (45), the average molecular weight per mole of nucleotide 330, and subtracting the (negative) partial molar volume of the sodium counterion, −6.6 ml/mole.

TABLE 3.

Scattering length contrast

Solvent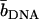
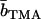H2O	11.4	−0.1
41% D2O	4.1	−4.1
64% D2O	−0.2	−6.4
99% D2O	−6.5	−9.8

Values are given in 10⁻¹² cm.

Small-angle neutron scattering

Small-angle neutron scattering experiments were done with the PAXY diffractometer, situated on the cold source of the high neutron flux reactor at the Laboratoire Léon Brillouin (LLB, Gif sur Yvette, France), CEN de Saclay. The temperature was kept at 293 K. The samples were measured with the PAXY instrument in two different experimental configurations, but with constant wavelength of 0.5 nm. In the first configuration, the effective distance between the sample and the planar square multi-detector (S-D distance) was 1.2 m. This allows for a momentum transfer range of 0.5–3.6 nm⁻¹. The counting time per sample or solvent was ∼4 h. In the second configuration, the S-D distance was 3.2 m. Here, the momentum transfer ranged from 0.3 to 1.4 nm⁻¹, with a counting time of ∼7 h/sample. Data correction allowed for sample transmission and detector efficiency. The efficiency of the detector was taken into account with the scattering of H₂O. It was checked that the scattering patterns on the two-dimensional, planar detector were isotropic, so that the liquid crystals are not macroscopically aligned with respect to the incident beam. Absolute intensities were obtained by reference to the attenuated direct beam and the scattering of the pure solvent with the same H₂O/D₂O composition was subtracted. It was observed that the reference solvents do not show significant scattering in the range of momentum transfer used in this study. Finally, the intensities were corrected for a small solute incoherent scattering contribution.

Molecular dynamics and Monte Carlo simulation

Molecular dynamic simulations were done using a 30°-inclined parallelogram simulation cell, which contains either a single or nine identical DNA decamers in the B-form. We used a randomly selected sequence of 10 basepairs (G5AAGAGGCTA3-C3TTCTCCGAT5) neutralized with 20 TMA⁺ counterions (the box with nine DNA molecules hence contains 180 counterions). We also did a supplementary run in which a single DNA molecule with sodium counterions was simulated. The AMBER (version 98) force field was used to model the DNA (33) and the nonstandard force-field parameters of TMA (in particular, partial charges, bond lengths, and bond angles) were then derived employing the AMBER strategy of force-field development. The 10985 water molecules were described with the TIP3P model (34). The long-range electrostatic interactions were treated by the fast particle-mesh Ewald summation method, whereas the temperature was controlled around 300 K with Berendsen temperature coupling (35,36). During the simulation, the volume of the box was kept fixed. The GROMACS simulation software with a time step of 2 fs was used (37,38). All MD simulations were done on a cluster of dual processor Intel Pentium III PCs, equipped with the Linux operating system. In the initial configuration, the nine DNA molecules were put on a hexagonal grid and the counterions were randomly distributed in the space between the DNA molecules. The simulation was equilibrated for 1 ns, after which 20 ns production runs were carried out. All distribution functions and statistical averages were calculated using the atomic and molecular coordinates stored during the production runs.

Monte Carlo simulation was done for seven DNA molecules arranged in a periodic hexagonal cell. The DNA molecule was modeled as an infinitely long cylinder of radius 1 nm with either uniform charge or a “phosphate group” charge located on the surface according to the B-form. Each phosphate group has a charge −e and a soft repulsive 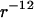potential with effective radius σ = 0.2 nm. The TMA counterion was modeled as a charged sphere with radius 0.4 nm and also with a repulsive 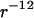potential. In the MC simulation, a sequence of 30 basepairs was used with 420 counterions to neutralize the DNA charge. The long-range electrostatic interaction was treated with the Ewald summation. Two million MC steps were done, of which the last 1.4 million steps were collected to produce the radial counterion distribution. More details about the MC procedure can be found in Lyubartsev and Nordinskiöld (18), and Korolev et al. (19,20).

RESULTS AND DISCUSSION

Molecular dynamics and Monte Carlo simulations

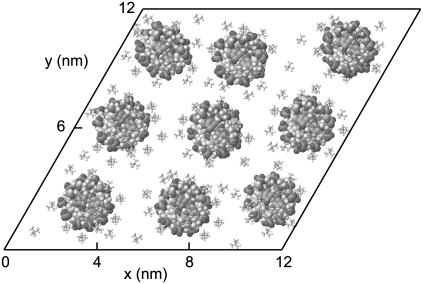
To investigate the effect of inter-DNA interactions on the structure, we did a MD simulation of an assembly of nine DNA molecules with TMA⁺ counterions. The average interaxial spacing between the molecules in the transverse plane was set to 4.0 nm, in accordance with the experimental condition in the SANS experiment. To impose the hexagonal structure, we used a 30°-inclined parallelogram simulation box with periodic boundary conditions in the transverse and longitudinal directions. Periodic boundary conditions in the longitudinal direction, together with a link of the 5′ and 3′ ends of the decamers, ensure that infinitely long DNA molecules are simulated. Notice that the periodicity along the longitudinal axis matches the helical twist of the DNA molecule (10 base pairs/turn). Furthermore, the connectivity of the decamers set by the periodic boundary condition inhibits bending fluctuations with wavelengths exceeding the longitudinal repeat distance of the simulation box, 3.4 nm. A snapshot of the transverse cross section at the center of the simulation box is shown in Fig. 1.

FIGURE 1.

Snapshot of the 30°-inclined simulation box containing nine DNA molecules in a hexagonal arrangement.

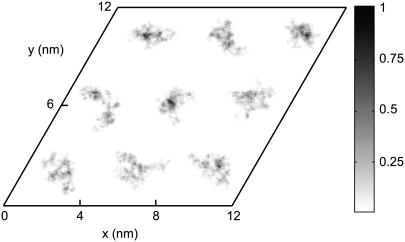
To verify the imposed hexagonal structure, we monitored the positions of the DNA spine axes during the 20-ns simulation. The DNA density is given by the fractional time a DNA molecule is located at a certain position per unit area. As can be seen in Fig. 2, the DNA molecules fluctuate about their positions, but the overall hexagonal structure is preserved. To quantify the fluctuations, we calculated the mean value, the standard deviation, and the autocorrelation function of the time-dependent interaxial spacing 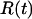between every DNA pair. The autocorrelation functions show an oscillatory decay with a characteristic correlation time of ∼2 ns, which is an order of magnitude shorter than the total duration of the simulation, 20 ns (data not shown). The mean values are all equal to the preset spacing R = 4.0 nm within a root mean-square standard deviation of 0.34 nm. In this context, it is of interest to compare the standard deviation in the interaxial spacing with an estimation of the root mean-square transverse fluctuations based on a theory of undulation-enhanced electrostatic interactions (39). In this theory, the DNA chain with persistence length P undulates within its confinement with an undulation parameter u and characteristic deflection length 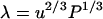. For TMA-DNA hexagonal liquid crystal with interaxial spacing of 4.1 nm, u and λ take the values 0.39 and 2.0 nm, respectively (16). The deflection length is significantly shorter than the longitudinal repeat distance of the simulation box, 3.4 nm, which indicates that the influence of the periodic boundary condition on the bending fluctuations is moderate if not insignificant. Accordingly, the standard deviation in the interaxial spacing, as obtained from the MD simulation, compares favorably with the theoretical value of the undulation parameter.

FIGURE 2.

Density of DNA in the transverse plane as monitored during a 20-ns simulation. The density profile was obtained with 0.05-nm and 0.05-ps spatial and time resolution, respectively (20,000 samples). The gray scale is the fractional time a DNA molecule is located at a certain position per unit area.

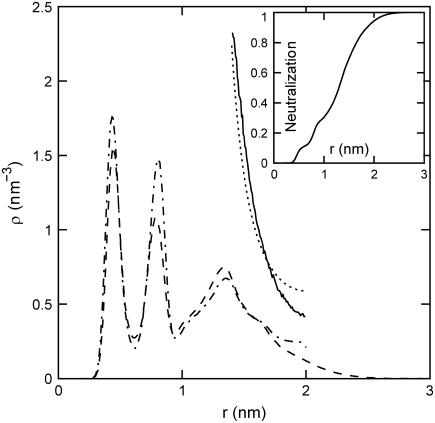
During the 20-ns simulation, the counterions diffuse through the simulation box and do not stay in close proximity to a particular DNA molecule. Although a large fraction of the counterions is accommodated within the grooves, their typical residence time is a few nanoseconds, after which they move on to “sample” another DNA molecule or a different region of the same DNA molecule. However, we did not perform a diffusion and/or residence-time analysis, but rather focused on the average radial density profiles since they are relevant for the interpretation of the SANS data. The radial counterion profile was calculated by time-averaging the fraction of counterions at a certain distance away from the spine axis of their nearest DNA molecule. Due to fluctuations in inter-DNA distance, the latter distance can exceed half the average interaxial spacing, 2.0 nm (the cell boundary). The result is displayed in Fig. 3, together with the result pertaining to the simulation of a single DNA molecule in a parallelogram simulation box. Simulation of nine molecules does not give a profile qualitatively different from the one obtained from the simulation of a single DNA molecule. More than 95% of the counterions are within 2.0 nm of the spine axis (see inset) and the concentration at the cell boundary is close to zero. Accordingly, the effect of inter-DNA distance fluctuations on the radial counterion density profile is small.

FIGURE 3.

Radial counterion profiles of TMA⁺ in the nine- and single-DNA-molecule (dashed and dash-dotted lines, respectively) MD simulations. The solid line refers to the MC simulation of charged rods in a hexagonal arrangement. The dotted line represents the solution to the PB equation in the cell model. (Inset) Integrated charge compensation as a function of the distance away from the DNA molecule obtained from the MD simulation with nine DNA molecules.

The two strong peaks in the radial density at ∼0.4 and 0.8 nm show that a large fraction of the counterions are accommodated inside the minor and major grooves of the DNA molecule. It was checked with a supplementary simulation of a single DNA molecule with sodium counterions that the considerable penetration of the grooves by the counterions is not due to the specific properties of TMA. Specific binding of ions inside the grooves, which is to a large extent determined by the hydration structure, have been reported before in MD studies of the alkali ionic environment of DNA and also for polyamine charged amine group association to hexagonally ordered DNA (18,40,41). However, these MD studies were done for DNA at much lower concentration and for alkali ions they showed a much smaller integral charge per phosphate inside the grooves than observed in this work.

In Fig. 3, we have also included the radial counterion density profile resulting from the PB equation using the structural parameters in Table 1. In the PB framework, potentially important ion correlation effects are neglected. To estimate these effects, we also obtained the radial profile with a MC simulation of seven charged rods in a hexagonal arrangement and with periodic boundary conditions in the longitudinal and transverse directions. The linear charge density of the rods was set to comply with DNA and the simulation system did not include added salt. We have done MC simulations with a uniform, smeared-out charge distribution, as well as with a helical charge distribution following the double-helical structure of the phosphate groups. The resulting radial counterion profiles for these two different models are almost the same and we present the results pertaining to the uniform charge density model only. As in the case of the MD simulation, the interaxial spacing was set to 4 nm, but here, the positions of the rods are fixed. The diameter of the rods and the counterions were set at 2 and 0.8 nm, respectively, so that the distance of closest approach of the counterion center of mass to the DNA spine axis is 1.4 nm. As can be seen in Fig. 3, the profiles predicted by the PB and MC approaches are similar, although the MC simulation predicts a somewhat lower counterion concentration at larger distances away from the DNA. Because the distance of closest approach is set to 1.4 nm, it is obvious in the PB calculation as well as the MC simulation that the predicted profiles do not exhibit any ions at distances corresponding to groove binding. Furthermore, with the chosen parameters, it is inevitable that the PB calculation and the MC simulation predict a higher counterion concentration at the cell boundary compared to the molecular-dynamics simulation results.

SANS data analysis

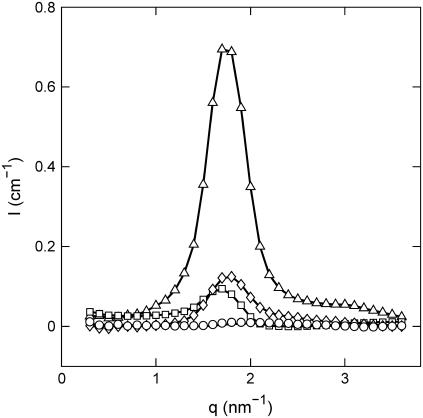
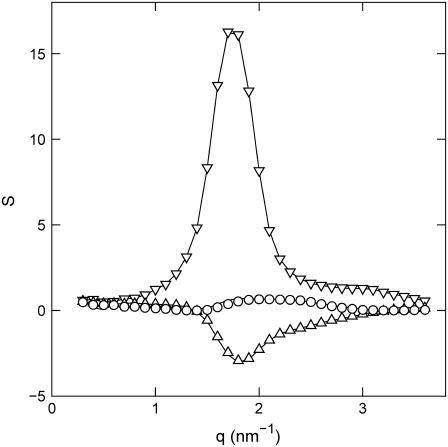
For simple salt-free solutions, all ions come from the DNA and there are three molecular components only: solvent, DNA nucleotides, and counterions. The solvent is treated as a uniform background, and a description of the structure thus requires three partial structure factors. The DNA, DNA-counterion, and counterion partial structure factors can be obtained from the scattered intensities of samples with different contrast length parameters. The two-dimensional scattering patterns were isotropic, which means that the samples are randomly oriented with no macroscopic orientation with respect to the incident beam (isotropic mosaic spread). Fig. 4 displays the intensities with contrast-matching in the water. Notice that in H₂O the counterions have very small scattering-length contrast with respect to the one pertaining to DNA and the intensity is proportional to the DNA structure factor (Table 3). The same applies for 63% D₂O solution, but here the DNA is blanked and the scattering is proportional to the counterion structure factor. For the sample in 41% D₂O, the scattering-length densities of the nucleotide and counterion are equal in magnitude, but opposite in sign. Under this zero average contrast condition, the scattered intensity is directly proportional to the charge structure factor. With four experimental intensities and three unknown partial structure factors per set, the data is overdetermined and the partial structure factors can be derived by orthogonal factorization in a least-squares sense (i.e., a three-parameter fit to four data points for every q value). The structure factors resulting from the three-parameter fit are shown by the lines in Fig. 5.

FIGURE 4.

Experimental SANS intensities versus momentum transfer. The H₂O/D₂O solvent composition is 0% (triangles), 41% (diamonds), 64% (circles), and 99% (squares) D₂O. The lines represent a two-parameter fit in which the partial structure factors are optimized.

FIGURE 5.

DNA ( 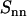, upside-down triangles), DNA-counterion ( 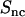, triangles), and counterion ( 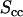, circles) partial structure factors in 0.74 mol nucleotides/dm³ TMA-DNA liquid crystal obtained from the two-parameter fit. The lines are the structure factors resulting from the model-free three-parameter fit.

The accuracy of the derived partial structure factors can be improved in the framework of the cell model. In this case, the partial structure factors can be expressed as a product of terms involving the radial profiles and a term describing the structure factor of an equivalent solution of DNA molecules with vanishing cross section. As shown by Eq. 10, the intensities can then be expressed in terms of two unknown functions, 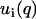, rather than three partial structure factors S_ij(q) (i and j = n and c). With a nonlinear least-squares procedure, the two factors u_i(q) were fitted to the data and the partial structure factors were reconstructed according to 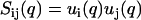. The fitted intensities and the derived partial structure factors are given by the curves in Fig. 4 and the symbols in Fig. 5, respectively. Now, the statistical accuracy has improved and the partial structure factors agree with the results obtained from the model-free three-parameter fit. This agreement seems to justify our use of the cell model, as was already suggested by the results of MD computer simulation. Notice that the two-parameter fit does not require the specification of any structural parameters such as the cell radius or the distance of closest approach; the only condition is the applicability of the factorization of the structure factors into cross-sectional form-factor terms and a term describing intermolecular interaction (Eq. 6). The factorization of the structure factors has been applied in previous work on more diluted DNA solutions (12) and has recently been suggested for the scattering analysis of two-dimensional hexagonal liquid crystal of cylinders as well (42).

The DNA structure factor shows a strong interaction peak at q_m = 1.8 nm⁻¹. For a hexagonal unit cell, the peak position is related to the interaxial spacing between the DNA molecules 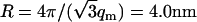. This value is in agreement with the value based on the DNA concentration. In previous work, it has been shown that the hexagonal phase melts if R exceeds 4.1 nm. Accordingly, the density of the liquid crystal is just above the critical boundary pertaining to the transition from the hexagonal to the cholesteric phase (16). The width of the peak is close to the instrumental resolution, which is primarily determined by the 10% spread in wavelength. Due to the resolution broadening, the higher-order peak at 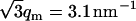is not resolved and takes the form of a shoulder. From these low-resolution experiments, no information can be deduced about the range of the hexagonal position order. The counterion structure factor also displays a maximum, but with much weaker and broader intensity and at higher values of momentum transfer. Finally, the DNA-counterion structure factor exhibits a broad negative minimum, which is related to the shell-like ordering of the ions around the DNA molecule. However, before we continue to discuss the behavior of the partial structure factors, we will present the number and charge structure factors. These structure factors allow us to estimate the range of the charge fluctuations and provide additional justification for the use of the cell model.

Number and charge structure

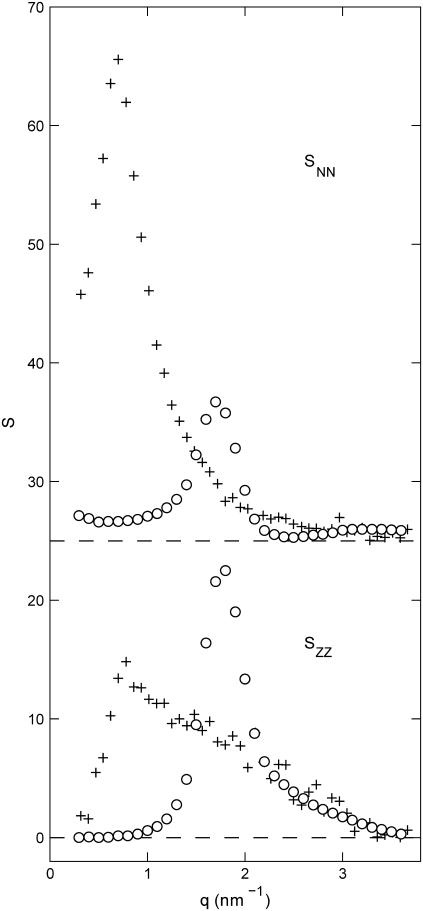
The number and charge structure factors are displayed in Fig. 6. We have also included the corresponding structure factors pertaining to an isotropic solution of the same DNA fragments more than seven times diluted. In the liquid crystal, both the number and charge structure factors show a peak at q_m = 1.8 nm⁻¹, and hence, the corresponding correlation lengths are the same as the one for the DNA density. As in the case of the DNA structure factor, the widths of the peaks are close to the instrumental resolution. A striking result is that the order in peak intensities in the number and charge structure is reversed from the isotropic to the hexagonal phase. The peak in the number structure factor decreases in intensity with increasing concentration, which is related to the q⁻¹ scaling of the form factor of the rodlike assembly of DNA and counterions. However, the peak in the charge structure factor becomes sharper and increases in intensity from the isotropic phase to the liquid crystal. This clearly shows the stronger ordering and confinement of the counterions in the intervening space between the DNA molecules.

FIGURE 6.

Number ( 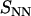, top) and charge ( 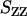, bottom) structure factors of liquid-crystalline (circles) and isotropic (plus signs) TMA-DNA solutions. The DNA concentrations are 0.1 and 0.74 mol nucleotides/dm³ for the isotropic and liquid-crystalline solutions, respectively. For clarity, 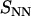has been shifted upward by 25 units.

The charge and number structure factors also behave markedly differently in the lower q range in front of the peak. In the q → 0 limit, the number structure factor is related to the osmotic compressibility, whereas the charge structure goes to zero because of overall charge neutrality (22). As seen in Fig. 6, the charge structure factor of the liquid crystal is already close to zero for q values that are, say, <1 nm⁻¹. This shows unambiguously that charge fluctuations exceeding a length scale on the order of the interaxial spacing or, in other words, beyond the cell volume are vanishing small. We argue that the strong confinement of the counterions as shown by the MD simulations, the consistency of the SANS data analysis, and the behavior of the charge structure factor justify the use of the cell model for the further analysis of the partial structure factors.

DNA-counterion and counterion partial structure

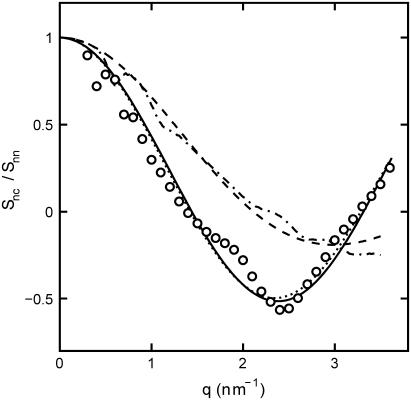
Like the DNA structure factor, the DNA-counterion and counterion structure factors are influenced by the strong inter-DNA interference in the liquid crystal. In the framework of the cell model, the latter interference can be eliminated by taking the ratio of the partials according to Eqs. 8 and 9. To verify this approach, we have calculated 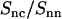according to Eq. 2 and time-averaging (20 ns) of the atomic coordinates from our MD simulation of nine DNA molecules. The corresponding result is displayed in Fig. 7. According to Eq. 8, 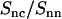should equal the ratio of the Hankel transforms of the radial counterion and nucleotide density profiles, respectively. We have thus calculated the Hankel transforms of the MD radial counterion and nucleotide density profiles, and their ratio is also displayed in Fig. 7. The transform of the nucleotide profile 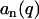, as obtained from the atomic scale model, was found to be very close to that calculated with Eq. 11 and r_p = 0.8 nm. The ratios pertaining to the MD simulation and the Hankel transforms of the radial profiles are similar, which shows that inter-DNA interference is indeed largely suppressed in 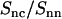(in the low q-range, the oscillatory behavior is due to finite-box-size effects). Furthermore, the close agreement shows that the DNA-counterion cross term 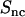is indeed unaffected by counterion fluctuations about the average profile, due to the heterodyne interference between the amplitudes scattered by DNA and the counterions. The fact that the cross-correlation is determined by the mean-field approximation, even if the counterions are strongly fluctuating, has also been shown by MD simulation of a charged, spherical colloidal particle with explicit counterions (27).

FIGURE 7.

Ratio of the DNA-counterion and DNA partial structure factors 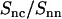. The dash-dotted line represents the ratio as obtained from the MD simulation. The dotted, dashed, and solid lines represent the ratio in Eq. 8 calculated with the structural parameters in Table 1 and radial counterion profiles resulting from the solution to the PB equation, MD simulation, and MC simulation, respectively. Notice that the ratios pertaining to the PB and MC approaches are almost indiscernible. The circles refer to the experimental SANS results.

The experimental DNA-counterion structure factor divided by the DNA structure factor 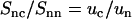is also displayed in Fig. 7. By taking the ratio according to Eq. 8, the strong inter-DNA interaction peak is largely, if not completely, suppressed. The experimental 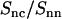is clearly different from that obtained from MD simulation; its minimum at q = 2.5 nm⁻¹ is more negative and shifted toward lower q values. This shows that in reality the counterions are distributed over larger distances away from the spine axis of the DNA molecule than shown by the MD simulation. The ratio in Eq. 8 was also calculated using the radial counterion profile resulting from the solution to the PB equation, as well as MC simulation of seven charged rods in a hexagonal arrangement (for profiles see Fig. 3). The corresponding Hankel transforms are almost indiscernible and fair agreement with the experimental data is now observed. The shift of the predicted ratio toward lower q values compared to the MD result is primarily due to the larger distance of closest approach of the counterion center of mass to the DNA spine axis r_c = 1.4. This value for r_c was also obtained in similar experiments at lower DNA concentration in the isotropic regime (11,12,24). Despite the fair overall agreement, the experimental data deviate from the PB and MC predictions in an oscillatory manner. Besides incomplete suppression of inter-DNA interference, a possible explanation for these small deviations is ionic correlation along the DNA molecule in register with the phosphate moieties. These longitudinal ion correlations are not captured by the PB approach, since their ion distributions do not vary along the DNA axis. The dash-dotted line in Fig. 7, obtained from Eq. 2 and the full three-dimensional spatial ion distribution from MD, on the other hand, does capture the longitudinal variation in counterion density. It is thus of interest to note that despite the shift of the 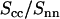curve obtained from MD as compared to the SANS data, the MD curve does exhibit an oscillatory dependence on q. This supports the interpretation that the oscillatory behavior is at least partly due to counterion density variation along the DNA axis.

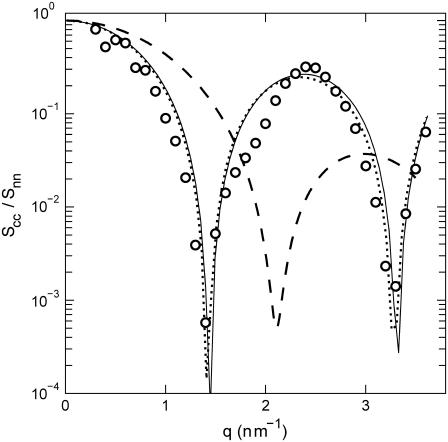
Because the intensities are analyzed according to Eq. 10, the ratio of the counterion and DNA structure factors 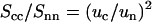does not carry more information than what is already known from the cross term. For the sake of completeness, we display the experimental ratio 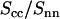in Fig. 8 in semilogarithmic representation. The experimental data show two sharp minima, which are nicely reproduced in the theoretical curve calculated according to Eq. 9, the structural parameters in Table 1, and the radial counterion profile resulting from the solution to the PB equation and/or MC simulation. The corresponding curve calculated with the MD profile is clearly shifted to values of momentum transfer that are too high. This again shows that in the MD simulation, the counterions appear to be much closer to the DNA spine axis than indicated by the SANS data.

FIGURE 8.

Ratio of the counterion and DNA partial structure factors 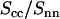. The dotted, dashed, and solid lines represent the ratio in Eq. 9 calculated with the structural parameters in Table 1 and radial counterion profiles resulting from the solution to the PB equation, the MD simulation, and MC simulation, respectively. Notice that the ratios pertaining to the PB and MC approaches are almost indiscernible. The circles refer to the experimental SANS results.

The distance of closest approach r_c between the counterion center of mass and the DNA spine axis agrees with the physical extent of the DNA molecule (with cross-sectional radius of gyration r_p = 0.8 nm), hydration shell, and counterion size. For instance, in TMACl solutions with similar cation concentrations, intermolecular correlations about TMA⁺ start rising at ∼0.36 nm and peak at ∼0.46 nm from the central nitrogen atom (43). If the TMA⁺ counterion is drawn into close contact with the DNA phosphates with a concurrent displacement of hydration water, r_c is expected to take a value of ∼1.4 nm. The optimized distance of closest approach in the analysis of the SANS data agrees with the maximum in the radial MD profile pertaining to counterions that do not penetrate the grooves (see Fig. 3). However, the MD simulation also shows that ∼50% of the TMA⁺ counterions are accommodated at smaller distances and/or inside the grooves. The SANS results show that, for relatively bulky TMA counterions, the groove penetration is not significant, since penetration of the counterions inside the grooves would push the minima in DNA-counterion and counterion partial structure factors toward higher values of momentum transfer. The MD prediction of the relatively large fraction of TMA⁺ counterions in the grooves may correlate with the fact that the calculated free energy of hydration of the methyl group in the force field is overestimated by a value of 2.6 kJ/mol, as compared to experimental data (44). We are currently making an effort to improve the force field.

CONCLUSIONS

With a view to characterize the structure of a dense, hexagonal DNA liquid crystal we simulated an assembly of nine DNA molecules in hexagonal arrangement. We also performed SANS experiments to obtain the structure factors pertaining to the DNA and counterion density correlations. The MD simulations showed that the inter-DNA distance fluctuates with a correlation time of a∼2 ns and a root mean-square standard deviation of 8.5% of the interaxial spacing. The value of the standard deviation agrees with a theoretical estimation of the transverse fluctuations based on undulation-enhanced electrostatic interactions in a hexagonal polyelectrolyte gel (39). The MD simulation also showed a distinct double layer structure with >95% of the counterions distributed within half the interaxial spacing away from the DNA spine axis. By comparison of the radial counterion profiles obtained from a one- and a nine-DNA-molecule simulation, it was seen that the effect of inter-DNA distance fluctuations on the counterion distribution is small. Furthermore, the MD simulation showed considerable penetration of the grooves by TMA counterions.

Motivated by the strong correlation between counterions and DNA as observed in the MD simulation, the SANS data were analyzed within the framework of the cell model. The DNA structure factor shows a strong interaction peak at a momentum transfer in agreement with the interaxial spacing between the molecules based on density and hexagonal structure. The width of the peak is, however, close to the instrumental resolution and from such low-resolution scattering experiments no information can be derived about the range of the position order. Information on the effects of the liquid-crystalline confinement on the number and charge (i.e., the sum and difference, respectively, of DNA and counterion) density correlation was obtained from the number and charge structure factors. The number structure factor shows a strong decrease in peak intensity from the isotropic to the liquid-crystalline phase, due to the 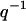scaling of the scattering of the rodlike assembly of DNA and counterions. In contrast to the behavior of the number structure factor, the charge structure factor becomes sharper and increases in intensity with an increase in DNA density. This shows the stronger ordering of the counterions in the more confined intervening space between the packed DNA molecules. Furthermore, charge fluctuations at longer wavelengths exceeding the interaxial spacing are vanishing small, which shows that electroneutrality is achieved within the primitive cell.

The counterion distribution was further investigated by an analysis of the DNA-counterion and counterion partial structure factors. These structure factors are also influenced by the strong inter-DNA interference, but this can be eliminated by dividing the relevant partials by the DNA structure factor. The results show that in the MD simulation the counterions appear to be too close to the DNA spine axis. Fair agreement is observed between the experimental structure factors and the prediction based on the radial counterion profile as obtained from the PB equation as well as MC simulation and a distance of closest approach of the counterion center of mass to the spine axis of 1.4 nm. Residual deviations may be due to ionic correlation along the DNA molecule in register with the phosphate moieties, which is not captured by the PB and MC approaches. The DNA-counterion and counterion partial structure factors are fairly sensitive to the distance of closest approach, whereas the effects of the actual shape of the profile and the counterion concentration variation at the cell boundary are minimal. The optimized distance of closest approach agrees with the physical extent of the DNA molecule, hydration shell, and counterion size as shown by the MD profile for those ions which do not penetrate the grooves of the DNA molecule. It is also in the range of the values reported for polyamines in isotropic samples of the same DNA fragments (12).