Distortion product otoacoustic emissions measured as vibration on the eardrum of human subjects

Abstract

It has previously not been possible to measure eardrum vibration of human subjects in the region of auditory threshold. It is proposed that such measurements should provide information about the status of the mechanical amplifier in the cochlea. It is this amplifier that is responsible for our extraordinary hearing sensitivity. Here, we present results from a laser Doppler vibrometer that we designed to noninvasively probe cochlear mechanics near auditory threshold. This device enables picometer-sized vibration measurements of the human eardrum in vivo. With this sensitivity, we found the eardrum frequency response to be linear down to at least a 20-dB sound pressure level (SPL). Nonlinear cochlear amplification was evaluated with the cubic distortion product of the otoacoustic emissions (DPOAEs) in response to sound stimulation with two tones. DPOAEs originate from mechanical nonlinearity in the cochlea. For stimulus frequencies, f₁ and f₂, with f₂/f₁ = 1.2 and f₂ = 4–9.5 kHz, and intensities L₁ and L₂, with L₁ = 0.4L₂ + 39 dB and L₂ = 20–65 dB SPL, the DPOAE displacement amplitudes were no more than 8 pm across subjects (n = 20), with hearing loss up to 16 dB. DPOAE vibration was nonlinearly dependent on vibration at f₂. The dependence allowed the hearing threshold to be estimated objectively with high accuracy; the standard deviation of the threshold estimate was only 8.6 dB SPL. This device promises to be a powerful tool for differentially characterizing the mechanical condition of the cochlea and middle ear with high accuracy.

The exquisite sensitivity, frequency selectivity, and dynamic range of hearing are defined by a mechanical amplifier in the cochlea (1). Should this amplifier be damaged, for example by sound overstimulation, ototoxic substances, aging, disease, or genetic defects, the result is sensorineural hearing loss. Although we are beginning to understand the underlying mechanisms of cochlear amplification (2–5), we are a long way from a clinically applicable, differential diagnosis of the functional state of the amplifier components. Perhaps the greatest problem is that the cochlea, being embedded in the temporal bone in humans, is not directly accessible for examination.

To date, there exists only one noninvasive method to diagnose the functional state of the cochlear amplifier: otoacoustic emissions (OAEs). OAEs are sound-pressure signals that are recorded in the ear canal but generated in the cochlea and transmitted retrograde by the middle ear to its input at the eardrum, where they are emitted as sound (6). Since their discovery almost 30 years ago by David Kemp (6), the OAEs have been used routinely in the clinic for an objective diagnosis of the cochlear amplifier (7, 8). However, in their present clinical application, OAEs provide only dichotomous information as to whether the amplifier is normal or impaired.

The clinical use of OAEs promises to change as more understanding is gained about their generation processes (see refs. 9 and 10 for recent reviews). At the moment, the most widely studied OAE is the cubic distortion product (DP) of the OAE (DPOAE), which is generated when stimulating with two tones (of frequency f₁ and f₂). Although the underlying mechanisms remain largely unknown (e.g., refs. 11–13), there is strong evidence that DPOAEs, at least at low sound intensities, derive from two different regions along the cochlea (14), with a different mechanism being involved at each region (15–18): the distortion-source emission and the reflection-source emission. The distortion-source emission appears to result from nonlinear interaction of the two primaries near and apical to the f₂ place, yielding the cubic distortion component of frequency 2f₁ − f₂, which is directed both backward to the cochlear input and forward apically along the cochlea.^† The forward wave is coherently reflected within the tuned region at the 2f₁ − f₂ place. This reflected wave, called the reflection-source emission, is sent backward to the cochlear input. The two backward waves sum to yield the DPOAE. The quasiperiodic, so-called fine structure of the DPOAE appears to derive from constructive and destructive interference between these backward waves (15). Recently, Boege and Janssen (19) showed that, under certain stimulus conditions, the cubic DPOAE can be used objectively to predict auditory threshold at f₂.

Instead of only using sound pressure measurements to assess the patency of the cochlear amplifier in humans, it has been proposed that vibration measurements of the eardrum, in particular at the umbo, might provide more reliable information (20), particularly at high frequencies where correctly calibrated sound fields are notoriously difficult to achieve (5, 21, 22). The most modern technology employs a laser Doppler vibrometer (LDV) to measure eardrum vibrations in human subjects (20, 23–30). The LDV is a heterodyne interferometer where the instantaneous frequency of the interferometric signal is shifted in direct proportion to the velocity of the vibrating object (31, 32).

Although our early experiments provided initial evidence for a cochlear mechanical component in the frequency response of the umbo (20), more recent studies by others (25, 30) have found no difference between umbo vibration in normal hearing subjects and in patients with sensorineural hearing loss. The problem with these latter studies is that they are conducted at sound pressure levels (SPLs) of 80–100 dB, where the cochlear amplifier is effectively short-circuited (3). Although our experiments were performed at lower sound intensities of ≈60 dB SPL (20), where there are some remnants of nonlinear cochlear amplification (3), even our LDV was far too insensitive to measure vibrations near auditory threshold. It is in the low-amplitude region below ≈40 dB SPL that the cochlear amplifier produces extraordinary sensitivity and frequency selectivity.

The main problem with umbo vibration measurements in human subjects is one of measurement sensitivity. Stimulus levels of 60 dB SPL produce umbo displacements of ≈1 nm below 1 kHz (20, 23–30). However, vibration measurements of <1 nm on the eardrum are difficult to perform in human subjects because the poor signal-to-noise ratio (SNR), due to poor optical reflection and extraneous noise such as heart beat, breathing or swallowing, necessitates inordinately long averaging times. Therefore, although vibration measurements at the umbo are proving to be very useful clinically for the differential diagnosis of middle-ear ossicular chain disorders (20, 25–27), attempts to gain information about cochlear function by performing umbo vibration measurements in human subjects have generally not been successful.

Here, we report on techniques that begin to solve these problems. These techniques allow evaluation of the status of the mechanical amplifier in the cochlea and its relationship to hearing threshold. For this purpose we developed a more sensitive LDV with background noise levels of <1 pm for umbo vibration measurements of >1 kHz. This LDV allows measurement of DPOAEs as vibration of the umbo. We find that the vibration DPOAEs yield estimates of auditory threshold that are more accurate than hitherto achieved with pressure DPOAEs.

This device, with its high sensitivity (0.3 pm/$\sqrt{\text{Hz}}$ above 1.5 kHz for vibrating objects with 0.9% reflectivity), has general application for optically based scanning devices for which measuring time is at a premium, such as in optical coherence tomography.

Results

Vibration data are presented here for 20 subjects for stimulus frequencies of 0.2–10 kHz and SPLs of 20–65 dB. The levels are well below the acoustic reflex threshold of 86 ± 3 dB SPL ipsilaterally, averaged over the usual four test frequencies (0.5, 1, 2, and 4 kHz) [see supporting information (SI) Text] in the 20 subjects. According to standard clinical audiometry (SI Text), 15 subjects had normal auditory thresholds (a ≤20-dB hearing level), three had a mild sensorineural hearing loss (21–25 dB) at high frequencies (6–10 kHz), and two showed a mild sensorineural hearing loss (21–25 dB) exclusively at 10 kHz. Immediately after the vibration measurements, pure-tone psychoacoustic thresholds were measured with fine frequency resolution (100 Hz) by using automatic Békésy audiometry (SI Text). The duration of the recording session for vibration and Békésy threshold measurements was ≈1 hr.

Linearity of the Eardrum Vibration Response.

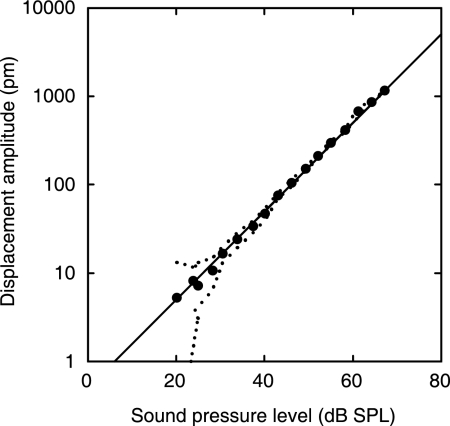
The vibration response of the umbo to a single tone was approximately a linear function of sound pressure down to at least 20 dB SPL (Fig. 1). Any deviation from linearity was <2 dB (mean deviation, 0.6 dB in Fig. 1) and could not be distinguished from noise (Fig. 1, dotted line). This linear eardrum response implies that the input impedance of the cochlea, the mechanical load to the middle ear (33), is linear, at least down to a SPL of 20 dB.

Fig. 1.

Dependence of umbo displacement amplitude on SPL for single-tone stimulation (3.5 kHz) measured for an open sound field. The linear regression line of unity slope (1 dB/dB) indicates that the measured umbo response is linear. The dotted lines delineate the maximum noise level in the 100-Hz sidebands adjacent to the stimulus frequency. A reflector was not placed on the umbo. (Subject identifier: JT.)

Vibration DPOAEs on the Eardrum.

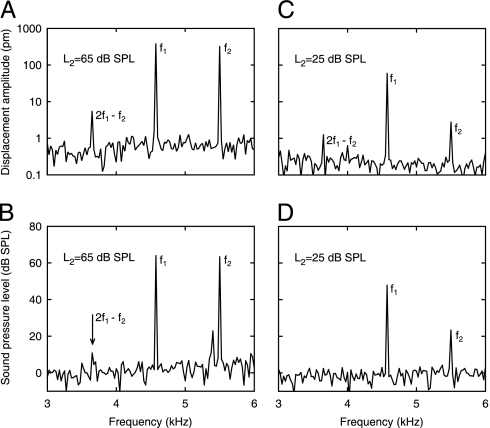
Inspite of the cochlear input impedance being linear, nonlinear cochlear amplification can be addressed by means of OAEs. Fig. 2 shows amplitude spectra of the LDV signal and the corresponding probe-microphone signal for two-tone stimulation at two sets of stimulus levels (L₂ = 25 and 65 dB SPL). Vibration and sound pressure were measured simultaneously in an open sound field. Notice that the cubic DP at 2f₁ − f₂ = 3.7 kHz is clearly visible for the umbo vibration (Fig. 2 A and C); their displacement amplitudes are 1.3 and 5.6 pm, respectively, for L₂ = 25 and 65 dB SPL. Across subjects (n = 20), DPOAE displacement amplitudes were no more than 8 pm. Here, one should be reminded that because L₁ is assigned according to the paradigm L₁ = 0.4L₂ + 39 dB (Materials and Methods), the 45-dB change of L₂ produces only a 21-dB change in total SPL. This dependence of L₁ on L₂ was chosen because it has been shown that with decreasing L₂ maximum DPOAE levels are achieved when using an increasing separation of the primary-tone levels, L₁ − L₂ (19). Maximization of DPOAE level is thought to occur when the primary tone responses at the f₂ place on the basilar membrane are approximately equal, which in turn is achieved by accounting for the different compression of the two primaries at this place (19).

Fig. 2.

Amplitude spectra of umbo displacement (A and C) and sound pressure (B and D) for two-tone stimulation with f₂ = 5.5 kHz and f₁ = 4.6 kHz, measured simultaneously for an open sound field. (A and B) L₂ = L₁ = 65 dB SPL. The DP at 2f₁ − f₂ presents displacement amplitude of 5.6 pm on the umbo and SPL of 10.8 dB (arrow). (C and D) L₂ = 25 dB SPL and L₁ = 49 dB SPL. The umbo displacement amplitude is 1.25 pm at 2f₁ − f₂; the sound pressure is not detectable there. A reflector was placed on the umbo. (Subject identifier: AS.)

The DPOAE sound level for the higher level stimulus (Fig. 2B, L₂ = L₁ = 65 dB SPL) was 10.8 dB SPL; a pressure DPOAE was not detectable for the lower level stimulus (Fig. 2D, L₂ = 25 dB SPL and L₁ = 49 dB SPL).

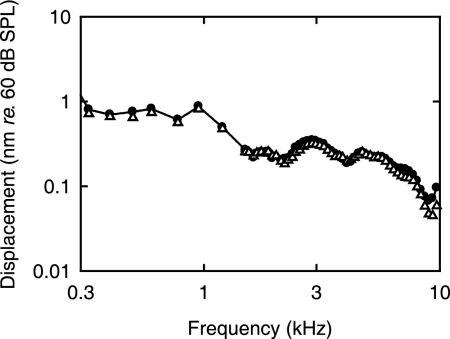
Fig. 3 illustrates the frequency response of the umbo relative to a SPL of 60 dB per frequency point. Because the relationship between stimulus sound pressure and umbo displacement is linear (Fig. 1), a single-tone sound stimulus of 10.8 dB SPL at 3.7 kHz would, according to the data shown in Fig. 3, result in an umbo displacement of only 0.8 pm. In contrast, for two-tone stimulation, the DPOAE displacement associated with a DPOAE SPL of 10.8 dB was 5.6 pm (Fig. 2A), or 17 dB higher than the value of 0.8 pm. This larger value is simply a result of the DPOAE signal being generated in the cochlea.

Fig. 3.

Displacement amplitude responses of the umbo expressed for a SPL of 60 dB. Responses were measured before (●) and 30 min after (▵) measuring the DPOAE responses. Notice that the reproducibility is better than 1 dB up to 7 kHz. DPOAE data from this subject are shown in Fig. 2.

Noise Levels for OAE Experiments.

In all subjects, we were able to obtain vibration measurements with a noise level of better than 1 pm (e.g., Fig. 2 A and C). Because the vibration experiments were conducted in an open sound field, the noise floor for sound pressure was relatively high, being ≈0 dB SPL for all subjects (e.g., Fig. 2 B and D). Thus, for example, referring to Fig. 2, a pressure DPOAE was not found in the open sound field for the lower-level stimulus (Fig. 2D, L₂ = 25 dB SPL and L₁ = 49 dB SPL) simply because it was buried in the noise; the expected value was −2.2 dB SPL based on middle-ear linearity (e.g., Fig. 1). Therefore, in general, we did not use the DPOAE pressure in the open sound field for further analysis, because in the majority of cases it showed insufficient SNR. Instead, we used DPOAE pressures measured in a closed sound field (DP2000; Starkey, Eden Prairie, MN) (Materials and Methods). This sound system had a noise floor typically between −25 and −35 dB SPL.

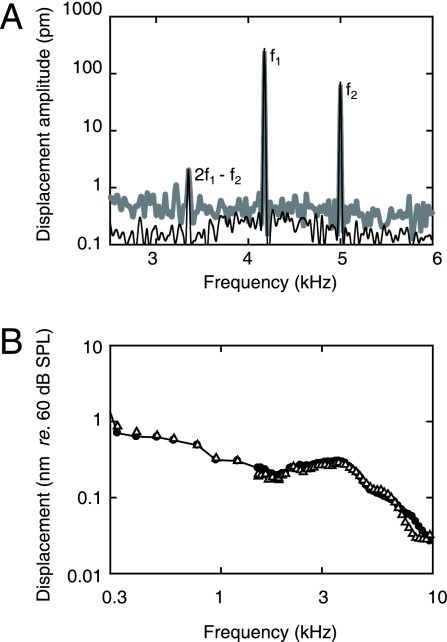
Although we usually (for 17 of 20 subjects) placed a reflector on the umbo to improve vibration SNR (Materials and Methods), control experiments indicated that the vibration responses were not affected (<1 dB). An example is shown in Fig. 4, for which the measurements on the first day were made on a natural reflecting point situated on the edge of the umbo corresponding to the tip of the light reflex. Twenty-four hours later, measurements were made from a reflector placed on the umbo. Apart from the expected improvement in SNR due to the reflector (up to 10 dB, Fig. 4A), the responses almost superimpose.

Fig. 4.

Reproducibility of umbo vibration responses from one day to the next, with and without placement of a reflector. The measurements on the first day were made without placement of a reflector on the umbo, whereas a reflector was placed for the measurements 24 h later. (A) Amplitude spectra for two-tone stimulation with f₂ = 5.0 kHz, f₁ = 4.2 kHz, L₂ = 55 dB SPL, and L₁ = 61 dB SPL. The gray shaded line represents measurements without reflector placement on the first day. The black line represents measurements with reflector placement 24 h later. Notice that (i) all three signals superimpose and (ii) there is a (small) improvement of SNR with the reflector (up to 10 dB below 3.6 kHz). (B) Displacement amplitude responses of the umbo expressed for a SPL of 60 dB. The measurements shown are without reflector placement on the first day (●) and with reflector placement 24 h later (▵). Notice that the reproducibility is better than 1 dB up to 7 kHz. (Subject identifier: SK.)

Reproducibility.

The reproducibility of the vibration measurements was extraordinarily high, for measurements repeated both within the hour (Fig. 3) and after days (Fig. 4).

For amplitude frequency responses to single-tone stimulation (Figs. 3 and 4B), the reproducibility was better than (i) 1 dB up to 7 kHz and (ii) 4 dB up to 10 kHz.

To quantify the reproducibility of DPOAE experiments over days, we examined, for the same (intended) primary levels, the ratio of vibration amplitudes at 2f₁ − f₂ and f₂ (V_DP/V₂) for each of the 2 days. We found a mean difference between the two vibration amplitude ratios of 1.6 dB (n = 9, 35 ≤ L₂ ≤ 65 dB SPL, 4 ≤ f₂ ≤ 5.5 kHz) and 6 dB in the high-frequency band (n = 5, 35 ≤ L₂ ≤ 65 dB SPL, 8 ≤ f₂ ≤ 9.5 kHz). Second, we examined the ratio V_DP/L₂ for each of the 2 days. We obtained a mean difference between the two amplitude ratios of 1.4 dB (n = 9, 4 ≤ f₂ ≤ 5.5 kHz) and 12.5 dB (n = 5, 8 ≤ f₂ ≤ 9.5 kHz). The differences at high frequencies, even in the open sound field and with a probe microphone fairly close to the eardrum (6 mm in this case), is almost certainly due to calibration errors arising from standing waves between the probe tip and eardrum (5, 20, 22).

Estimated DP Threshold.

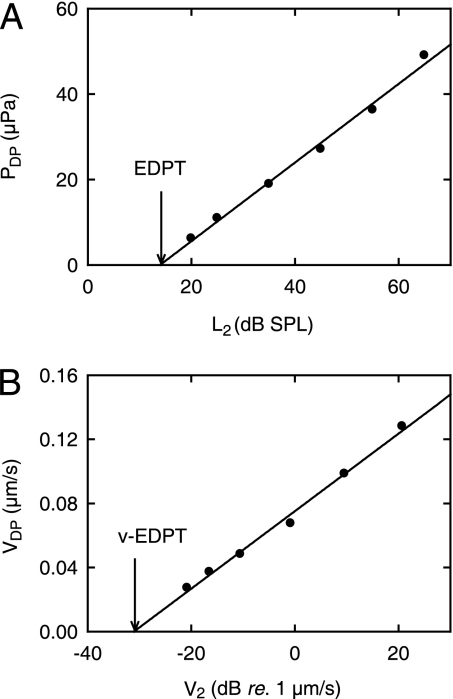
DPOAE umbo velocity (V_DP) and DPOAE sound pressure (P_DP) were nonlinearly dependent on velocity (V₂) and pressure (P₂) at the frequency, f₂, of the second primary tone. Fig. 5 shows an example of the dependence, whereby sound pressures in Fig. 5A are for a closed sound field and umbo velocities in Fig. 5B are for an open sound field. Notice that V_DP and P_DP are plotted as functions of the logarithm of velocity and pressure at f₂. Clearly, these input/output (I/O) functions show that V_DP and P_DP are directly proportional to 20log(V₂ re. 1 μm/s) and L₂ = 20log(P₂ re. 20 μPa),^‡ respectively, over a range of at least 40 dB (r² = 0.99). Across subjects, the mean slopes of these velocity and pressure I/O functions were, respectively, 2.7 ± 1.0 nm·s⁻¹·dB⁻¹ re. 1 μm/s (30 I/O functions) and 1.2 ± 0.5 μPa/dB SPL (116 I/O functions), without obvious frequency dependence (4 ≤ f₂ ≤ 9.5 kHz).

Fig. 5.

Dependence of DPOAEs on primary stimulus level. (A) DPOAE sound pressure (P_DP) as a function of SPL (L₂) at the stimulus frequency, f₂, of the second primary tone. Pressures were measured in a closed sound field. (B) DPOAE umbo velocity (V_DP) as a function of umbo velocity (V₂) at f₂. Velocities were measured in an open sound field. The stimulus parameters were as follows: f₂ = 5.5 kHz, f₁ = 4.6 kHz, L₂ = 25–65 dB SPL, and L₁ = 0.4L₂ + 39 dB. The lowest measured pressure amplitude at 2f₁ − f₂ = 3.7 kHz is 6 μPa, or −10.5 dB SPL. The lowest measured vibration amplitude at 2f₁ − f₂ = 3.7 kHz corresponds to a displacement amplitude of 1.18 pm. (A) The intersection of the regression line (r² = 0.99, slope = 0.92 ± 0.04 μPa/dB SPL) with the abscissa (arrow) yields the so-called (19) EDPT = 14 dB SPL. (B) Correspondingly, the intersection of the regression line (r² = 0.99, slope = 2.42 ± 0.10 nm/s/dB re. 1 μm/s) with the abscissa (arrow) yields the v-EDPT = 0.0272 μm/s. A reflector was placed on the umbo. (Subject identifier: AS.)

This type of logarithmic dependence for pressure DPOAEs was reported originally by Boege and Janssen (19) and replicated by Gorga et al. (34). In the original report (19), the value of L₂ for which the sound pressure of the DPOAE is equal to zero is called the estimated DP threshold (EDPT). It was found by linear extrapolation of the I/O function to the L₂ axis. The value for the example in Fig. 5A (14 dB SPL) is indicated by the arrow. The importance of the EDPT lies in its ability to provide an objective estimate of auditory threshold at f₂. By analogy, we define the velocity EDPT (v-EDPT) as the umbo velocity at f₂, which yields V_DP = 0 (Fig. 5B, arrow).

To test whether the v-EDPT might provide a better estimate of auditory threshold than the EDPT derived from closed-field pressure measurements, we calculated the SPL at f₂ that would be required to yield this value of v-EDPT. This level was calculated from the experimentally determined linear dependence of umbo velocity on sound pressure, both of which were measured simultaneously in the open sound field. To allow direct comparison with the data of Boege and Janssen (19), we adopted their data acceptance criteria (SI Text). Accordingly, 116 of the 136 pressure I/O functions and 30 of the 40 velocity I/O functions were used for further analysis.

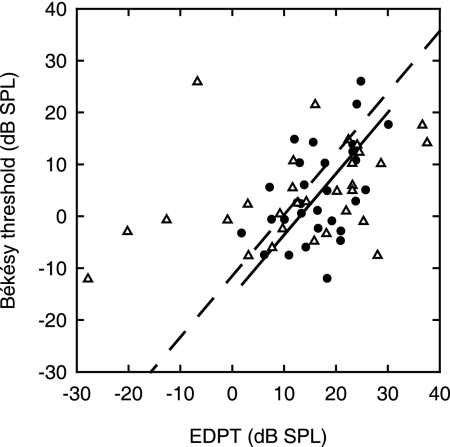
Fig. 6 shows the Békésy thresholds and the EDPTs as derived from the conventional (19) pressure measurements in closed sound field and as derived from the umbo vibration measurements in open sound field. To allow direct comparison of the accuracy of the two EDPT estimators of threshold, the EDPTs are included in Fig. 6 only if the pressure and vibration EDPTs were estimated from the same set of primaries. The scatter in the vibration EDPTs is considerably smaller than for the pressure EDPTs. Thus, linear regression for the vibration EDPTs yielded a statistically significant (99.8%)^§ slope (0.68 ± 0.22 dB/dB; regression line not illustrated); whereas, for the pressure EDPTs, a statistically significant slope (90%) was not detected. The standard deviation of the thresholds from the regression line (which is not shown) for the vibration EDPT estimator was 7.9 dB.

Fig. 6.

Békésy threshold as a function of the EDPT. The measurements shown are for EDPT derived from conventional pressure in a closed sound field (▵) and for EDPT derived from umbo vibration measurements in an open sound field. n = 30 I/O functions from 14 subjects; f₂ = 4–9.5 kHz. Regression lines for both the sound (dashed line) and the vibration (solid line) data have fixed slopes at 1.18 dB/dB, equal to the value derived by Boege and Janssen (19) for pressure DPOAEs. Their data set contained 4,236 points and exhibited a standard deviation of the Békésy thresholds from the regression line of 10.9 dB SPL. Here, the standard deviation of the Békésy thresholds from the regression line is 16.7 dB SPL for the sound pressure and 8.6 dB SPL for the umbo vibration measurements.

To further quantify the difference in accuracy between the two estimators and to allow comparison with the data in ref. 19, we refitted the two sets of data with the slope held constant at the value of 1.18 dB/dB reported in ref. 19 for the pressure EDPTs. In choosing this slope, we are tacitly assuming that it is more representative of the true value because, compared with our data set, (i) their data set was much larger (4,236 I/O functions) and (ii) their range of measured thresholds was larger (70-dB range). The standard deviation from the regression line (Fig. 6) for the vibration EDPT estimator was approximately half that for the pressure EDPT estimator, being 8.6 and 16.7 dB SPL, respectively.

If we now repeat this regression analysis on all of our pressure EDPT data from a closed sound field (116 I/O functions), we find a standard deviation of 11.2 dB SPL from the regression line of fixed slope of 1.18 dB/dB (SI Fig. 7 and SI Text). This deviation compares favorably with the result of 10.9 dB SPL reported in ref. 19. That is, our closed sound-field pressure data replicate the original observation of Boege and Janssen (19) and provide confidence in our experimental protocol.

Discussion

Laserinterferometric Measurement of Umbo Vibration and Estimation of Auditory Thresholds.

The results show that reliable measurement of picometer-sized vibrations of the umbo near hearing threshold are indeed possible up to high frequencies (10 kHz) in human subjects. The range of DPOAE displacement amplitudes (1–8 pm) is consistent with that expected from DPOAE vibration measured at the DPOAE place on the basilar membrane of laboratory animals (SI Text).

The range of stimulus intensities (20–65 dB SPL) used in our experiments is within the linear and nonlinear ranges of the cochlear amplifier (3). The lower bound was defined by the SNR achievable with our LDV system. The upper bound was chosen to be much less than the measured and expected (35) acoustic reflex threshold (85–95 dB SPL). Importantly, the middle-ear response and, therefore presumably the cochlear input impedance, were found to be linear down to the 20-dB SPL measuring limit. This finding is consistent with evidence from DPOAE sound-pressure experiments (36) and cochlear modeling (5, 37),^¶ which suggest that the cochlear input impedance is independent of sound intensity. Less directly, it is also consistent with the results of intracochlear fluid pressure and basilar membrane velocity measurements (38).

It is astonishing that the auditory thresholds estimated from the umbo v-EDPT values, using an algorithm originally proposed for ear-canal pressure measurements (19), show an 8-dB smaller standard deviation of the threshold estimate compared with that derived from our pressure EDPT values from a closed sound field. Moreover, this standard deviation for the v-EDPT estimator (8.6 dB SPL) is no more than 5 dB greater than that for standard Békésy audiometry (standard deviation of 4 dB). Here, it is important to emphasize that the Békésy algorithm yields a subjective measure of auditory threshold, whereas the EDPT algorithm yields an objective measure. The accuracy of the vibration technique compared with the pressure technique for estimating auditory threshold was not expected because (i) the SNR of the umbo vibration measurements was generally less than that for the conventional sound pressure measurements (typically 20 dB smaller); (ii) the measurement time was longer (typically 150 s instead of 6 s for a DPOAE); and (iii) the conventional sound pressure measurements and the Békésy threshold measurements were made in a closed sound field, whereas the pressure values to which the velocity measurements are referenced were made in an open sound field (near the eardrum).

In our view, the most probable reason for the success of this technique is that, even with state-of-the-art equipment, closed-field sound-pressure measurements are more prone to have calibration artifacts, especially at high frequencies (5, 20, 22).

Perspectives.

Measurement of vibration DPOAEs in human subjects opens the way to improved strategies for characterizing and diagnosing the function of the middle ear and the cochlea. Thus, in addition to its application to indirectly assessing cochlear mechanics, the vibration DPOAEs could be used to evaluate part of the middle-ear transfer function, because the umbo velocity relative to ear-canal pressure can now be measured directly in both the forward and the reverse directions in vivo. This type of measurement is of considerable interest because the forward and reverse transfer functions are not identical (39, 40). By applying parametric changes to the middle-ear impedances, e.g., by manipulating acoustic reflex or static pressure (e.g., ref. 41), it is reasonable to expect that ratios between several impedances can be measured accurately to support differential diagnosis of middle-ear and cochlear pathologies.

Finally, it is important to mention that, in principle, it is possible to improve the sensitivity of the vibrometer by 30–50 dB and, thus, even further improve the auditory threshold estimate.

Conclusion

We have designed and used a LDV to detect picometer-sized vibrations of the human umbo in the presence of relatively large ambientally induced noise movements, such as heart beat, breathing, or swallowing. We have adapted the EDPT method, originally described for pressure DPOAEs (19), to umbo vibration DPOAEs and provided an extremely accurate estimate of auditory threshold. Measurement of vibration DPOAEs provides possibilities for the differential diagnosis of conductive and sensorineural hearing loss.

Materials and Methods

Subjects.

Twenty young, healthy adults without medical history of ear diseases, were accepted for the study. The age of the subjects varied between 20 and 30 years (mean age, 24.4 years); there were 17 females and 3 males. The subjects had “normal” hearing as indicated by standard audiometric tests (SI Text). Informed written consent was obtained from each subject. The study was approved by the Ethics Committee of the University of Tübingen.

Sound-Field Assessment of DPOAE.

The subjects were mainly selected according to their sound-field DPOAE levels at the cubic difference frequency, 2f₁ − f₂. The DPOAEs were recorded with a commercial system (DP2000; Starkey, Eden Prairie, MN) under closed-field conditions. As an initial screening step, 2f₁ − f₂ levels were first measured over a wide frequency range, with f₂ = 1–10 kHz, in 500 Hz steps; the ratio f₂/f₁ was held constant at 1.2. The two primary tone levels were L₂ = 55 dB SPL and L₁ = 61 dB SPL. L₁ was chosen according to the scissors paradigm: L₁ = 0.4L₂ + 39 dB (42). Then, I/O functions were measured for f₂ selected in the range 4–9.5 kHz; L₂ was 20–65 dB SPL. This frequency range was chosen because it yielded velocity DPOAEs with the largest SNR. Up to nine I/O functions were measured in each subject and a total of 136 for all subjects. Of these, 40 I/O functions having DPOAE levels at 2f₁ − f₂ greater than 0 dB SPL for at least three different levels of the primary tones (typically L₂ = 65, 55, and 45 dB SPL) served for comparison with the DPOAE vibration measurements.

Measurements of DPOAE fine structure (see the Introduction) were performed around the frequencies selected for the DPOAE I/O functions to avoid later making vibration measurements at local minima in either the sound-field or the vibration DPOAE I/O functions. The instrument used to assess the fine structure was an AmDis-OAE (Hortmann Neuro-Otometrie, Neckartenzlingen, Germany). These measurements were performed with the same parameters as for the preliminary DP-gram assessment: L₂ = 55 dB SPL, L₁ = 61 dB SPL, and f₂/f₁ = 1.2, and f₂ was chosen in accordance with the frequency of the I/O measurement (4–9.5 kHz). For f₂ = 4–5.5 kHz, f₂ was swept in 10-Hz steps in a range of 70 Hz below and above the I/O frequency; whereas, for f₂ = 6–9.5 kHz, f₂ was swept in 15-Hz steps and covered a region of 100 Hz below and above the I/O frequency. The DPOAE I/O function measurement was repeated at a suitable frequency offset if the fine structure showed that the initial measurement had been performed near a local minimum.

Vibration Measurement System.

The vibration measurement set-up consists of a custom-built LDV (SI Text) employing a conventional heterodyne interferometer (43), for which all optical and electronic parts were tailored to the problem of measuring picometer-sized vibrations in the presence of large, extraneous movements in the order of 0.1 mm (e.g., heart beat, breathing, or swallowing). The LDV, including the custom-built demodulator, achieves a maximum sensitivity of 0.3 pm/$\sqrt{\text{Hz}}$ for acoustic frequencies of >1.5 kHz when measured on a mirror, the reflectivity of which was reduced to 0.9% by means of a neutral density filter.

Vibration Measurements.

Measurements of vibration DPOAEs were performed unilaterally (n = 20 ears). The ear to be examined was chosen according to the criterion specified for the pressure DPOAE described above (Sound-Field Assessment of DPOAE). Sound pressure was delivered free field and measured 2–4 mm from the ear drum (SI Text). To improve SNR for vibration measurements, a small light reflector with surface dimensions of 0.5 × 0.5 mm² and weighing between 40 and 50 μg was placed on the umbo (n = 17 ears). The reflector was custom-made by gluing a piece of 3M reflective tape on a piece of surgical silicone strip of 0.13-mm thickness with silicon glue. The silicon strip prevented “irreversible” clinging of the reflector to the umbo. The reflector was placed on the umbo and removed after the experiment with a fine suction needle. Control experiments with direct focusing on unloaded eardrums (n = 3) gave no indication of reflector-induced artifacts in the frequency spectra or I/O functions up to 7 kHz; amplitude differences were <1 dB (Results). The SNR improvement due to the reflector was up to 30 dB. In the other three ears, the reflector was not used because the measurements could be performed on a natural reflecting point situated on the edge of the umbo, corresponding to the tip of the light reflex.

Angle correction for the orientation of the laser beam relative to the surface normal of the umbo was not performed; the angle was estimated to be 35–50°.

For determination of the frequency response of the umbo vibration, the sound stimulus was a multitone complex with equal amplitude but a randomly and uniformly distributed phase at each frequency point (20). The complex was divided into two parts to avoid sound overexposure. One multitone complex covered the low-frequency range of 0.2–2 kHz and contained 3.1 frequencies per octave, with 65 dB SPL per frequency point. The second multitone complex covered the (partially overlapping) high-frequency range of 1.5–10 kHz and contained 9.1 frequencies per octave, with 50 dB SPL per frequency point. Data in each of the two frequency ranges were collected, depending on SNR, from 20 or 40 nonsequential time windows 40 ms long (SI Text).

For DPOAE vibration measurements, the stimulus parameters were f₂ = 4–9.5 kHz, f₂/f₁ = 1.2, L₂ = 20–65 dB SPL, in 10 dB steps, and L₁ = 0.4L₂ + 39 dB. Depending on SNR, 200–500 nonsequential time windows were recorded for one DPOAE measurement. A DPOAE measurement usually required 2–3 min, depending on handling time and extraneous noise, for example from heart beat, breathing, or swallowing. I/O functions had at least three data points.

All amplitudes are given as rms values.

Abbreviations

DP

distortion product

OAE

otoacoustic emission

DPOAE

DP of the OAE

EDPT

estimated DP threshold

v-EDPT

velocity EDPT

I/O

input/output

LDV

laser Doppler vibrometer

SNR

signal-to-noise ratio

SPL

sound pressure level.