Unraveling the three-metal-ion catalytic mechanism of the DNA repair enzyme endonuclease IV

Abstract

Endonuclease IV belongs to a class of important apurinic/apyrimidinic endonucleases involved in DNA repair. Although a structure-based mechanistic hypothesis has been put forth for this enzyme, the detailed catalytic mechanism has remained unknown. Using thermodynamic integration in the context of ab initio quantum mechanics/molecular mechanics molecular dynamics, we examined certain aspects of the phosphodiester cleavage step in the mechanism. We found the reaction proceeded through a synchronous bimolecular (A_ND_N) mechanism with reaction free energy and barrier of −3.5 and 20.6 kcal/mol, in agreement with experimental estimates. In the course of the reaction the trinuclear active site of endonuclease IV underwent dramatic local conformational changes: shifts in the mode of coordination of both substrate and first-shell ligands. This qualitative finding supports the notion that structural rearrangements in the active sites of multinuclear enzymes are integral to biological function.

The complexity and variety of enzymatic reactions is astonishing, arising from a delicate interplay of many interactions, such as hydrogen bonding, electrostatics, steric effects, polarization, and charge transfer among others (1–3). Rationalizing the origins of the remarkable catalytic power of enzymes has been a long-standing challenge for both experimental and theoretical chemical biology. Advances on the theoretical front have been based on the advent of quantum mechanics (QM)/molecular mechanics (MM) methods (4), allowing the consistent treatment of the entire enzyme/substrate/solvent system. More recently, these have been coupled to ab initio molecular dynamics techniques (5, 6), which have made possible the introduction of dynamical, many-body, and polarization effects into simulation models of unprecedented size and sophistication.

Herein, we have focused specifically on a trinuclear zinc metalloenzyme, endonuclease IV (endo IV), involved in DNA repair. Despite its remarkable stability, DNA under normal physiological conditions is subject to a variety of reactions that could potentially lead to loss of vital genetic information (7). To cope with the problem of genomic instability, cells have evolved elaborate mechanisms for DNA repair. DNA repair systems can be classified into several broad pathways, such as direct damage reversal, base excision repair (BER), nucleotide excision repair, mismatch repair, and double-strand break repair (8). The pathway most commonly used to remove incorrect or damaged bases is BER. BER can be conceptually divided into two sequential steps. The first damage-specific step is carried out by a variety of DNA N-glycosylases (9) that hydrolyze the glycosydic bond between the damaged base and the deoxyribose sugar. Removal of the damaged base by an appropriate glycosylase leads to the formation of an apurinic/apyrimidinic (AP) site. AP sites are the central intermediate in BER and are highly cytotoxic. Therefore, they have to be eliminated in the second stage of BER (8, 10), which is generic and involves nicking of the damaged DNA strand by an AP endonuclease enzyme upstream of the AP site. Subsequent extension of the resulting 3′ OH terminus by a DNA polymerase, accompanied by AP lyase excision of the AP site leads to the completion of the repair process.

Endo IV from Escherichia coli belongs to one of two conserved 5′ AP endonuclease families that exist in biology (10–12). In Saccharomyces cerevisiae, the major AP endonuclease (APN-1) (13) is an analog of endo IV. The availability of recent high-quality crystal structures (11) for the enzyme and its complex with abasic DNA determined at 1- and 1.5-Å resolution has opened the possibility for a detailed structure-based investigation of the mechanism for this nuclease, which also carries quite general mechanistic implications for other multinuclear hydrolytic enzymes such as P1 nuclease and phospholipase C(2). A schematic representation of the reaction catalyzed by endo IV is shown in Fig. 1. Outstanding mechanistic questions include: (i) the origin of the nucleophile initiating the reaction; (ii) the nature of phosphodiester bond cleavage reaction, concerted versus stepwise, associative, or dissociative; (iii) the extent of dynamical rearrangements in the trimetal cluster on a time scale commensurate with the chemical transformation; and (iv) the role of the metal ions, first-shell ligands, and protein environment in stabilizing the transition state.

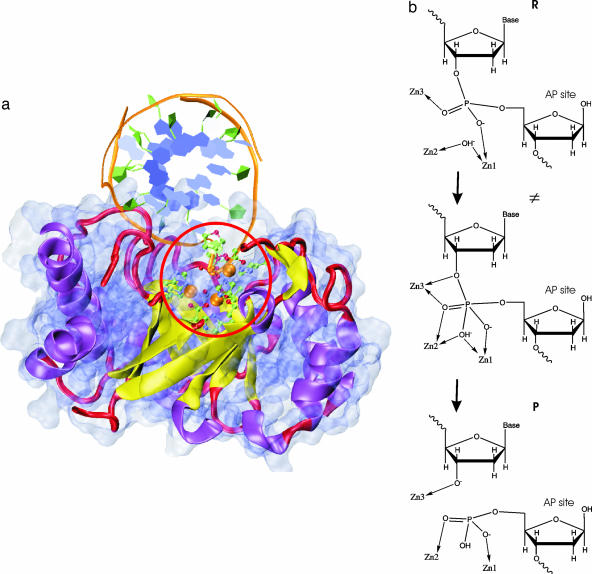
Fig. 1.

Endo IV structure and schematic mechanism. (a) QM/MM model of endo IV: the QM subsystem is in ball-and-stick representation and highlighted by a red circle; the enzyme and DNA substrate are in cartoon representation (color-coded according to secondary structure) along with a van der Waals surface for the protein atoms. A cut-plane through the protein was used to reveal the trinuclear active site. (b) Schematic representation of the mechanism. Zinc coordination distances for the reactant (R), transition state (TS; ξ = 0) and product (P) are included in supporting information (SI) Table 1.

Results and Discussion

To establish the origin of the catalytic nucleophile, we turned to two models of the active site (Fig. 1), reflecting the two alternatives: a metal-bridging water molecule (A) versus a metal-bridging hydroxide ion (B). Direct ab initio molecular dynamics (QM/MM) simulation of model A revealed proton transfer events from the bridging water molecule to a favorably positioned glutamate residue (Glu-261). Facile deprotonation through Glu-261 (Fig. 2) is indicative of the fact that the three metal ions in the active site of endo IV are capable of electrostatically stabilizing a hydroxide ion in that position. The small barrier for this process leads us to suggest that early proton transfer in the active site of endonuclease VI is responsible for generating a nucleophilic hydroxide species, which subsequently initiates the attack on the scissile POP′ bond. Kinetically, that result would imply the existence of a fast equilibration step in the mechanism preceding the rate-limiting phosphodiester cleavage step:

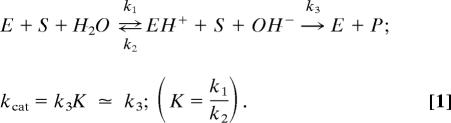Because such a preequilibration step is not expected to significantly affect the overall kinetics, subsequent analysis and constrained dynamics runs were based on model B. This decision is, of course, based on the underlying assumption that the free energy of taking the proton to bulk solvent would not influence the overall energetics, which cannot be ascertained by the present simulations.

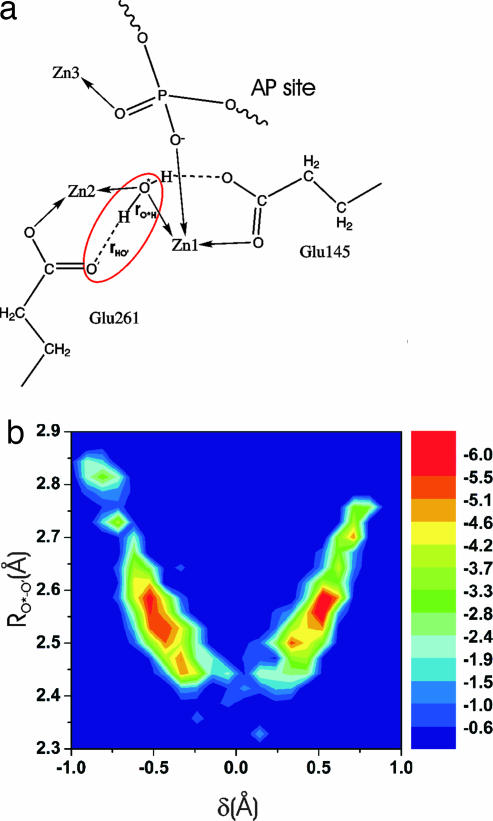
Fig. 2.

Proton transfer in the endo IV active site. (a) A schematic representation of the process (for model A). It is useful to analyze proton mobility in terms of simple, yet representative, internal coordinates such as the asymmetric stretch δ = (r_O*–H − r_H–O′) and the distance R_O*–O′. To quantify the process we constructed a 2D histogram, reflecting the joint probability P(R_O*–O′, δ) to observe a particular value of the proton displacement coordinate δ and a particular value of R_O*–O′ in our trajectory. From it we obtain an effective free energy surface (units in kcal/mol) by using the relation F = β⁻¹lnP(R_O*–O′, δ). Here β is 1/k_BT where k_B is the Boltzmann constant and T is the absolute temperature in K. Analogous repeated proton transfer events were reported for the binuclear active site of arginase (23). Unlike the case of arginase where the bridging water molecule was found to be more stable, the effective free energy profile (shown in b) appears to be an almost symmetric double well, indicating comparable stability for the protonated and deprotonated forms. This result could be rationalized by the large electrostatic stabilization arising from having three metal centers and the fact that zinc tends to shift the pK_a of metal-bound water more than manganese or magnesium.

A three-metal-ion mechanism (10, 11) has been proposed for endo IV-mediated phosphate ester cleavage. The nature of the transition state in enzymatic phosphoryl transfer has been a contentious issue (14). Enzymes apparently can use either associative or dissociative mechanisms; however, the extent to which an active site can influence the nature of the transition state has been a subject of much debate. We used the method of constraints to effect a reactive transition by forcing the system to follow a representative intuitive reaction coordinate ξ. The free energy profile resulting from thermodynamic integration along ξ is plotted in Fig. 3. It is evident from the computed potential of mean force that the reaction follows an A_ND_N mechanism, proceeding through a pentacoordinated trigonal bipyramidal transition state. The averaged lengths for the apical phosphorus–oxygen bonds (r_O*–P and r_P–O′) in the transition state structure were 2.04 Å, indicating that nucleophilic addition occurred synchronously with dissociation of the leaving oxyanion group. The reaction is concerted with no intermediates of appreciable stability. Experimental k_cat values for endo IV-mediated phosphodiester hydrolysis are in the range of 5.6–18 min⁻¹ (15), which translates into ΔG^≠ of ≈19 kcal/mol. The barrier estimated from our simulations appears to be 20.6 ± 0.44 kcal/mol and compares favorably to experiment within the accuracy of ab initio density functional theory methods. The reaction was also found to be exergonic by about −3.5 ± 0.95 kcal/mol, in reasonable agreement with a −5.3 kcal/mol experimental estimate of ΔG°′ for hydrolysis of a DNA phosphodiester bond in T4 DNA ligase (16). Although the statistical error in calculating the individual potential of mean force points is small (as reflected in the error bars), we note the existence of additional systematic error arising from nonequilibrium hysteresis effects (SI Fig. 5 and SI Table 2). The collapse of the pentacoordinated transition state leads to stereochemistry inversion at the phosphorus atom. All three zinc ions were found to closely associate with the transition-state complex (through coordination to the oxygen atoms of the phosphate group and the incoming nucleophile) and thus actively participated in catalysis (Fig. 3). Releasing the constraint at the end of the trajectories with ξ values 0.0, 0.1, 0.2, and 0.3 Å led to the reactant state. For trajectories with ξ = −0.1, −0.2, and −0.3 Å the system relaxed to the product state, confirming the notion of a transition state at the top of the barrier (Fig. 3) and no intermediate.

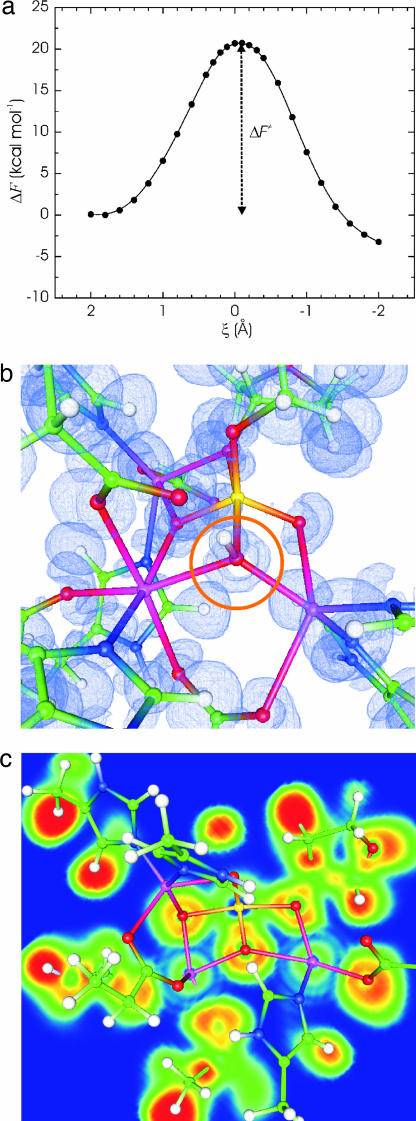
Fig. 3.

Phosphodiester cleavage reaction: potential of mean force (PMF) profile, transition state structure, and ELF isosurface. (a) The PMF profile for the phosphodiester cleavage reaction is shown. The reaction coordinate ξ is defined as: ξ = (r_O*–P − r_P–OP′). Here, r_O*–P and r_P–OP′ are the distances between the electrophilic P atom, O* is the oxygen atom of the nucleophilic hydroxide, and OP′ is the displaced oxygen atom of the substrate. (b) Displayed is the calculated transition state structure for ξ = 0 along with an ELF isosurface at contour level 0.82. (c) ELF contour profile drawn through the plane of the Zn1, Zn2, and OP′ atoms is shown.

An important question pertaining to catalysis by multinuclear enzymes is what is the exact role of the metal centers in transition-state stabilization. We used the atoms-in-molecules (AIM) method (17) to partition the QM subsystem valence electron density for a number of snapshots taken from the constrained trajectories for different values of the control parameter ξ. By adding the nuclear and core-electron contributions we obtained AIM-derived charges on the QM atoms. The charges on the three metal ions (Zn1, Zn2, and Zn3) were 1.27 ± 0.0062, 1.26 ± 0.0046, and 1.34 ± 0.0041 (SEM), respectively. These were essentially invariant, changing by <0.149, 0.073, and 0.071, respectively, during the reactive transformation. The changes are comparable to the expected charge fluctuations in a dynamic environment and do not follow a trend as ξ is varied (see also SI Table 3). To rationalize this result we analyzed the electron localization function (ELF) (18, 19) along the mechanistic path. A snapshot of the transition-state structure at ξ = 0 with an ELF contour profile is displayed in Fig. 3. The ELF indicates spatial regions where electron pairs are most likely to be found. The decrease in the value of ELF in the region between the phosphate oxygen atoms and the Zn ions indicates the largely ionic character of the coordination bond between them, which minimizes charge transfer. Thus, we conclude that pure electrostatic stabilization has a comparatively larger contribution relative to charge transfer effects in endo IV catalysis.

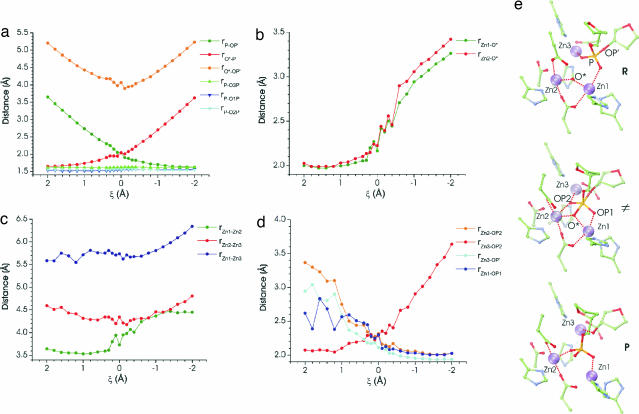
Stable binding of the substrate and metal cofactors and the need to undergo dynamic transformations during catalysis are two, sometimes, opposing requirements that multinuclear enzymes have to satisfy. In Fig. 4 we outline the changes occurring in the trimetal cluster as the reaction proceeds. It is evident that the trimetal cluster undergoes significant structural reorganization in the course of the reaction. This fact underscores the advantage of computational models that explicitly account for the protein dynamics and the flexibility of the active site. First, we comment on the evolution of the coordinates directly involved in phosphoryl transfer and note the gradual decrease in the average O*-P bond length, mirrored by an increase in the POP′ bond. The average r_O*–O′ distance has a minimum at ξ = 0 as expected for phosphoryl transfer with partially associative character. The equatorial OP distances undergo little change and have values close to 1.60 Å. The average intermetal distances r_Zn2–Zn3 and r_Zn1—Zn3 (Fig. 4c) reflect an overall contraction of the metal cluster in the transition state relative to both the reactant and product states. The ensemble average Zn1–Zn2 distance varies from ≈3.5 to ≈4.4 Å along the reaction coordinate reflecting a shift from a μ-1,1 coordination of the OH⁻ ion in the Michaelis complex to a μ-1,3 coordination of the phosphate group in the product. Our calculations support a mechanism in which the hydroxide ion initiates the nucleophilic attack directly from the μ-1,1 bridging position. Two arguments (20, 21) have been advanced that counter this proposal: (i) the fact that the lone electron pairs on the oxygen atom are engaged in coordination with the two metals would render them unavailable for initiating an attack on the phosphate group and (ii) a bridging hydroxide moiety would be unreactive because of decreased nucleophilicity. Thus, it would follow from these arguments that although a bridging hydroxide ion would form more readily, a terminal OH⁻ moiety should be the active form of the nucleophile and would have to form transiently before the nucleophilic attack. From Fig. 4b we conclude that this is not the case: the O* atom remains practically equidistant from Zn1 and Zn2 up to and even beyond the transition state, which ensures an optimal “in line” geometry for the transition-state structure (O*–P–OP′ angle of 159.5 ± 4.84° (SD) in the reactant state and 170.49 ± 3.86° (SD) in the transition state). The ELF shows that the three lone pairs around O* are in a delocalized ring structure around the OH bond axis (Fig. 3b). This pattern indicates a lack of preferred directionality in bonding to O* and a capacity to accommodate additional coordination partners. We conclusively show that an attack originating from a metal-bridging position leads to reasonable energetics for the reaction. This finding supports the notion that the bridging OH⁻ is sufficiently nucleophilic and negates the second argument. Fig. 4d details the changes in the phosphate coordination pattern as the reaction proceeds. Briefly, we observe that the phosphodiester group of the substrate is initially bound to Zn1 and Zn3 through two of the nonbridging oxygen atoms (O1P and O2P). During the reaction the initially labile binding of O1P to Zn1 increases (the r_O1P–Zn1 bond decreases from ≈2.5 to ≈2.0 Å) and O2P switches coordination from Zn3 to Zn2. This process frees a coordination site on Zn3, which then becomes available to the departing oxygen atom OP′. Thus, Zn3 helps to electrostatically stabilize the developing negative charge on the leaving group [as proposed in the original mechanism (10, 11)] only at the final stage of the reaction. The originally proposed three-metal-ion mechanism tends to emphasize the role of the Zn²⁺ ions, while assigning primarily supportive role to the protein residues. Here, we show that the first-shell aspartate and glutamate ligands, apart from serving as a scaffold for the catalytic metal centers, display considerable flexibility (22) and accommodate the above changes in substrate coordination by minimal compensatory moves. In particular, we observe shifts of Glu-145 from a bidentate (μ-1,3 bridging) to monodentate mode and a carboxylate shift in Asp-229. Glu-261 also exhibits considerable motion to accommodate the departure of the O* atom from its μ-1,1 bridging position at the end of the reaction. Thus, the flexibility of the first-shell carboxylates plays an important role in promoting fast catalytic turnover.

Fig. 4.

Ensemble averaged structural parameters along the reaction coordinate. (a) Phosphorus–oxygen distances within the DNA phosphate group. (b) Distance between the oxygen atom on the metal-bridging hydroxide and Zn1 or Zn2 ions. (c) Intermetal distances. (d) Zinc coordination distances of the phosphate moiety. (e) Zinc coordination pattern in the reactant (Top), transition state (Middle), and product (Bottom) structures. OP′ denotes the leaving group oxyanion; O* is the oxygen atom of the nucleophile; P is the phosphorus atom of the scissile phosphate group; and OP1, and OP2 are the two equatorial oxygen atoms coordinated to the Zn1 and Zn2 ions, respectively.

In the crystal structure of the endo IV product complex (11) the phosphate group was seen occupying an asymmetrically bridging position between Zn1 and Zn2 (d_O–Zn1 of 2.01 Å and d_O–Zn2 of 2.48 Å), whereas μ-1,3 coordination pattern was suggested by the simulation. This seeming contradiction can be easily resolved by considering the proton affinities of the products. Based on the difference in pK_a the proton residing on the phosphate group has to be shuttled to the leaving oxyanion group. This subsequent step in the catalytic cycle has to be taken into account by the simulation. Therefore, after switching the protonation state on these two groups, we carried out unconstrained ab initio molecular dynamics on a model of the product complex for an additional picosecond. The model relaxed to reflect the experimentally observed coordination pattern with the phosphate oxygen in a μ-1,1 position (SI Fig. 6) and a reduced Zn1–Zn2 distance as expected for a bridging ligand.

The analysis presented here emphasizes the significant level of complexity involved in enzymatic catalysis by multinuclear enzymes even when the underlying chemical transformation is relatively straightforward. At the same time certain universal patterns regarding the multiple mechanistic roles of the metal cofactors emerge. First, the metal ions play a role in generating the reactive nucleophile. This process involves precise positioning of a carboxylate ligand to deprotonate an exogenous water molecule and orient the resulting hydroxide for an in-line attack. Deprotonation is further facilitated by the combined electrostatic effect of two zinc ions (Zn1 and Zn2), necessitating a relatively close distance between them. The second role of the metals is to accommodate and electrostatically stabilize the more compact partly associative transition state. Hence, an overall contraction of the trimetal cluster is observed. Finally, a metal cofactor (Zn3) is responsible for stabilizing the developing charge on the leaving group toward the end of the reaction. To effectively carry out these roles, the active site rearranges dynamically, a finding, that underscores the crucial importance of flexibility for the reactive transition.

Materials and Methods

The simulations were performed with CPMD version 3.9 (www.cpmd.org) at ambient conditions by using a QM/MM algorithm where both QM and MM parts of the system were coupled at the boundary region through bonded and nonbonded terms via a fully Hamiltonian coupling scheme (24). The QM subsystem consisted of 132 quantum atoms for model A and 131 for model B (three zinc ions, all first-shell ligands, substrate, and nucleophile, water in model A or hydroxide ion in model B) in a box of dimensions 18.26 × 18.73 × 20.60 Å, using the BLYP functional (25, 26), Troullier–Martins pseudopotentials (27), a Γ-point plane wave expansion of the valence orbitals up to 70 Ry, and fictitious electronic mass of 700 a.u. All QM hydrogen nuclei were treated as classical particles with the mass of the deuterium isotope. Because nuclear quantum effects are not included in our simulation, the only effect of this replacement is to allow an increased time step, while preserving the results from equilibrium sampling. For zinc the nonlocal part of the pseudopotential was integrated numerically by using a Gauss-Hermite quadrature, otherwise the Kleinman–Bylander scheme (28) was applied. The entire system contained 37,573 atoms in total, including the protein, 15-bp DNA substrate, solvent, and counterions. The AMBER force field parameters (29) were used for the MM subsystem.

The systems corresponding to models A and B were set up and equilibrated first with classical molecular dynamics. The initial structures were based on the 1.55-Å resolution structure of endo IV in complex with abasic DNA (Protein Data Bank ID code 1QUM). The active site was modified with the program Sybyl to create a model for the uncleaved substrate. Thus, neither the reactant nor the product geometry directly corresponds to the x-ray structure. In the model, the Zn1 ion was coordinated by His-69, His-109, Glu-145, and the bridging hydroxide ion; Zn2 was coordinated by Glu-145, Asp-179, Glu-261, His-216, and the bridging hydroxide ion; Zn3 was coordinated by Asp-229, His-231, His-182, and an equatorial oxygen atom of the DNA phosphodiester backbone. The XLeap module of the AMBER 7.0 program was used to add hydrogen atoms, counterions, and preequilibrated solvent with a distance of at least 8 Å from the protein to the edge of the simulation box [11,080 TIP3P (30) water molecules were added in total]. Fifty Na⁺ and 19 Cl⁻ ions were used to neutralize the overall charge of the protein/DNA complex and mimic physiological salt concentration. Neutral protonation state was used for all histidine residues, and the choice of protonated nitrogen atom (Nδ or Nε) was decided by examination of the hydrogen-bond network. The scissile phosphate group of the abasic site carried a charge of −1. Because a reliable MM force field is not available for the Zn-containing active site, the side chains of metal-coordinating residues Glu-261, His-231, Asp-229, His-182, Asp-179, Glu-145, His-109, and His-69 and the DNA abasic site phospate group and the three zinc ions (Zn1, Zn2, and Zn3) were constrained during the classical equilibration.

The system was minimized for 1,000 steps to remove unfavorable contacts, brought to a temperature of 300 K over 50,000 steps of dynamics at constant volume, and equilibrated for 1 ns in the isothermal-isobaric ensemble (NPT) at 1 atm (1 atm = 101.3 kPa) and 300 K. The long-range electrostatic interactions were treated by using the smooth particle mesh Ewald algorithm (31). For the nonbonded short-range interactions we used a cutoff of 12 Å with a switching function between 10 and 12 Å. The bonds between hydrogen and heavy atoms were constrained with the SHAKE algorithm (32), which permitted an increased integration time step of 2 fs, while maintaining control over the conserved quantities. The r-RESPA multiple time step method (33) was used with a 2-fs time step for bonded, 2 fs short-range for nonbonded, and 4 fs for long-range electrostatic forces. The equilibration runs were performed with the program NAMD 2.5 (34) using the AMBER parm99 forcefield parameters (29).

The classical equilibration was followed by 1 ps of QM/MM equilibration. Dynamics simulations on the model systems were performed with a time step of 0.125 fs (5 a.u.) in the NVT ensemble. We have used constrained molecular dynamics to enforce the reaction, through the use of a control parameter ξ defined as: ξ = (r_O*–P − r_P–OP′). Here, r_O*–P and r_P–OP′ are the distances between the electrophilic P atom, O* is the oxygen atom of the nucleophilic hydroxide, and OP′ is the displaced oxygen atom of the substrate. The constraint was linearly added to the CP Lagrangian according to the blue moon ensemble method (35). The values of ξ were varied in increments of 0.2 Å from −2.0 to 2.0 Å (0.1 Å in the interval −0.4 to 0.4 Å), and constrained trajectories of length ≈3 ps (≈1 ps of equilibration and 2 ps of production dynamics) were obtained for each discrete value of the control parameter. Error bars were calculated by integrating along ξ the SEM in the force at each constrained point.

Abbreviations

QM

quantum mechanics

MM

molecular mechanics

endo IV

endonuclease IV

BER

base excision repair

AP

apurinic/apyrimidinic

ELF

electron localization function.