Abstract
We explore the question of what are the best ligands for macromolecular targets. A survey of experimental data on a large number of the strongest-binding ligands indicates that the free energy of binding increases with the number of nonhydrogen atoms with an initial slope of ≈−1.5 kcal/mol (1 cal = 4.18 J) per atom. For ligands that contain more than 15 nonhydrogen atoms, the free energy of binding increases very little with relative molecular mass. This nonlinearity is largely ascribed to nonthermodynamic factors. An analysis of the dominant interactions suggests that van der Waals interactions and hydrophobic effects provide a reasonable basis for understanding binding affinities across the entire set of ligands. Interesting outliers that bind unusually strongly on a per atom basis include metal ions, covalently attached ligands, and a few well known complexes such as biotin–avidin.
Although an elegant analysis exists of the optimum kinetic performance of enzymes (1), estimation of maximal ligand binding has been addressed in a more limited way (2, 3). In this communication, we examine both empirical and theoretical bounds on the free energy of ligand binding. We conclude that maximal free-energy contributions per nonhydrogen atom are ≈−1.5 kcal/mol (1 cal = 4.18 J) across a wide variety of macromolecule–small molecule interactions. The empirical data also reveal a significant trend to smaller contributions per atom as the relative molecular mass of the ligand increases. These observations, drawn from a diverse collection of natural and synthetic ligands, can be used to guide drug-design strategies and explore evolutionary relationships. They also have implications for protein engineering and protein folding. Important exceptions to these generalizations are covalently bound ligands, interactions with metal ions, and a few interactions with small anions.
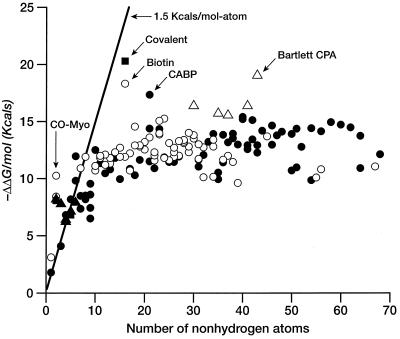
We begin our discussion with a summary of empirical equilibrium data on the free energy of ligand binding. We will assume, for convenience, the “biochemical” reference state: aqueous solutions at 300 K, pH = 7, all other concentrations at 1 M, although no effort has been made to correct the literature data. In Table 1, we have collected dissociation constants or IC50 values of a diverse set of strongly bound ligands. These have been converted to ΔΔGbinding (Eq. 1) and are plotted against that number of nonhydrogen atoms per molecule in Fig. 1.
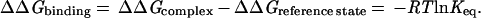 |
1 |
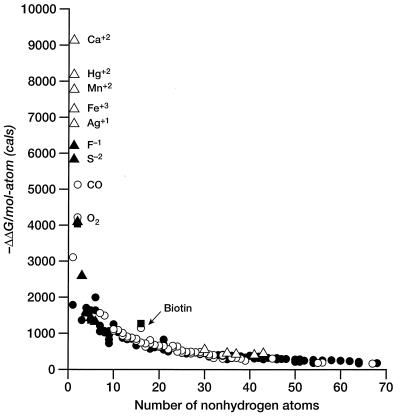
If we ignore simple cations and anions, the data show a sharp improvement in binding free energy until ≈15 heavy atoms per molecule. The ΔΔGbinding of the tightest-binding ligands then plateaus at ≈−15 kcal/mol (i.e., picomolar dissociation constants). The initial slope is approximately −1.5 kcal/mol per atom. We next plot the free energy of binding per heavy atom (ΔΔg) by dividing ΔΔG by the number of nonhydrogen atoms (Fig. 2). In displaying the data in this fashion, we are attributing the entire intermolecular interaction to the ligand, alone. This is a useful representation for our purposes because we do not always have the information required to identify interactions between specific atoms in the ligand and the target. Others have used the same presentation (4). It is immediately apparent (Table 1, Fig. 2) that the largest binding interactions per atom are associated with metals, small anions, and ligands that form covalent bonds. The strongest nonmetallic complexes from natural or synthetic ligands do not exceed −1.5 kcal/mol complex per heavy atom. It is also clear from Fig. 2 that there is a strong tendency for the contribution per atom to decrease as the number of atoms increase. The slope of this curve is ≈.01 kcal/mol per atom.
Table 1.
Experimental binding affinities of selected ligands
| No. of atoms | Ligand | Target | Type* | −log K1† | Ref. |
|---|---|---|---|---|---|
| 1 | Ca2+ | Amino transferase | IM | 6.70 | 5 |
| 1 | Hg2+ | Uroporphy synthase | IM | 6.00 | 5 |
| 1 | Mn2+ | Inositol phosphatase | IM | 5.70 | 5 |
| 1 | Fe3+ | Hydroxylase | IM | 5.30 | 5 |
| 1 | Ag+ | Arylformamidase | IM | 5.00 | 5 |
| 1 | F− | Phosphotransferase | IA | 4.55 | 5 |
| 1 | S2− | Peroxidase | IA | 4.28 | 5 |
| 1 | Xe | Myoglobin | L | 2.30 | 6 |
| 1 | NH3 | Meamine glutamate transferase | I | 1.79 | 5 |
| 2 | Carbon monoxide | Myoglobin | L | 7.52 | 7 |
| 2 | Oxygen | Myoglobin | L | 6.18 | 7 |
| 2 | Cyanide | Methane oxygenase | IA | 6.00 | 5 |
| 2 | Hydroxylamine | Glycerol oxidase | IC | 5.92 | 5 |
| 3 | Azide | Glycerol oxidase | IA | 5.70 | 5 |
| 3 | Ethylamine | Protease I | I | 3.00 | 5 |
| 4 | Thioacetamide | Methane monooxygen | I | 5.00 | 5 |
| 4 | NO3− | Carbonate deydratase | IA | 4.70 | 5 |
| 4 | Vanadate | Phytase | IA | 4.55 | 5 |
| 5 | Thiosemicarbazide | Methane monooxygen. | I | 6.00 | 5 |
| 5 | SO42− | Creatine kinase | IA | 5.22 | 5 |
| 5 | Iodoacetamide | Methyl transferase | IC | 5.00 | 5 |
| 6 | Putrescine | Spermine synthase | I | 8.77 | 5 |
| 6 | Aminooxyacetic acid | Aminotransferase | I | 7.19 | 5 |
| 6 | Oxalate | Lactate dehydrogenase | IA | 5.80 | 5 |
| 7 | α-Aminobutyid acid | Neuromanidase transmitter | L | 8.00 | 2 |
| 7 | l-Cysteine | Serine acetyl transferase | I | 6.22 | 5 |
| 7 | Aminomethiozolidine | Methyl transferase | I | 5.40 | 5 |
| 8 | Muscimol | α-aminobutylicacid agonist | L | 8.73 | 2 |
| 8 | Bromopyrimidone | Cytosine deaminase | I | 6.24 | 5 |
| 8 | Phosphonoacetic acid | DNA polymerase | I | 6.00 | 5 |
| 9 | Acetopyruvate | Acetoacetate decarboxylase | I | 7.00 | 5 |
| 9 | Methyl iodotyrosine | Tyrosine monooxygenase | I | 6.30 | 5 |
| 9 | Nitrooxazolidinone | Aldehyde dehydrogenase | I | 5.46 | 5 |
| 9 | Benzamidine | Trypsin | I | 4.77 | 8 |
| 10 | Allopurinol | Xanthine oxidase | I | 9.17 | 2 |
| 10 | Acetylcholine | Cholinergic receptor | L | 8.14 | 2 |
| 10 | Cabachol | Cholinergic receptor | L | 7.85 | 2 |
| 11 | Diethyl pyrocarbonate | Ca2+ transmitter | L | 8.80 | 5 |
| 11 | Dopamine | α, β-androgen receptor | L | 8.65 | 2 |
| 11 | Mercapto oxoglutaric | Isocitrate dehydrogenase | I | 8.30 | 5 |
| 12 | Norepinephrine | Adrenergic agonist | L | 8.88 | 2 |
| 12 | Nicotine | Nicotinic receptor | L | 8.22 | 2 |
| 12 | Hydroxybenzyl-Me3NR4 | Acetycholiesterase I | I | 7.68 | 5 |
| 13 | Tiamenidine | α-Adrenergic agonist | L | 8.66 | 2 |
| 13 | Serotonin | 5-Hydroxy tryptamine receptor | L | 8.30 | 9 |
| 13 | Benzyl mercaptopropionate | Carboxypeptidase | I | 7.96 | 5 |
| 14 | Guanabenz | α-Adrenergic receptor | L | 9.02 | 2 |
| 14 | Methylenpenicillanic | β-Lactamase | I | 8.85 | 5 |
| 14 | Captopril | Carboxypeptidase | I | 8.70 | 5 |
| 15 | Aminoclonidine | L | 9.32 | 2 | |
| 15 | Guanfacine | α-Adrenergic agonist | L | 8.73 | 2 |
| 15 | Isatin derivative | Rhino protease | I | 7.30 | 10 |
| 16 | Acetophenone der. | ACEsterase | IC | 14.89 | 11 |
| 16 | Biotin | Streptavidin | L | 13.43 | 8 |
| 16 | Naphazoline | Adrenergic | L | 8.73 | 2 |
| 17 | Melatonin | Melatonin receptor | L | 8.96 | 12 |
| 17 | Guanine derivative | Purine nucleoside phosphorylase | I | 7.96 | 4 |
| 17 | piperoxan | antihyper. receptor | L | 7.85 | 2 |
| 18 | Iodomelatonin | Melanin receptor | L | 10.68 | 12 |
| 18 | Alprenolol | β-adrenergic receptor | L | 9.47 | 2 |
| 18 | Phosphoramidon | Metalloproteinase | I | 7.55 | 5 |
| 19 | Vesamicol | Vesamicol receptor | L | 9.47 | 13 |
| 19 | Propranolol | β-adrenergic receptor | L | 9.39 | 2 |
| 19 | Trimethoprim der | Dihydrofolate reductase | I | 8.53 | 14 |
| 20 | Estradiol | Steroid receptor | L | 9.69 | 2 |
| 20 | Melatonin derivative | Melatonin receptor | L | 9.68 | 12 |
| 20 | Vesamicol derivative | Vesamicol receptor | L | 9.20 | 13 |
| 21 | 2-Carboxyl arabinitol bisphosphate | Ribulose carboxylase | I | 12.72 | 15 |
| 21 | 4-Carboxyl arabinitol bisphosphate | Ribulose carboxylase | I | 10.55 | 15 |
| 21 | Triprolidine | Histamine antagonist | L | 9.98 | 2 |
| 21 | Trimethoprim | dihydrofolate reductase | I | 8.44 | 2 |
| 22 | Amitriptylinoxide | Antidepressant | L | 9.02 | 2 |
| 22 | Mazindol derivative | Dopamine transporter | L | 8.82 | 16 |
| 22 | Indolyl ethyl amines | 5-Hydroxy tryptamine receptor | L | 8.49 | 17 |
| 22 | Isatin derivative | Rhino protease | I | 8.00 | 10 |
| 23 | Vesamicol der. | VR | L | 11.05 | 13 |
| 23 | Neuraminic acid der. | Sialidase | I | 10.52 | 18 |
| 23 | Melatonin der. | melamin receptor | L | 10.24 | 12 |
| 23 | Vesamicol der. | VR | L | 10.17 | 13 |
| 24 | Vesamicol der. | VR | L | 11.19 | 13 |
| 24 | Isatin der. | Rhino protease | I | 8.70 | 10 |
| 24 | Methadone | Narcotic | L | 8.66 | 2 |
| 25 | Melatonin der. | Melamin receptor | L | 9.62 | 12 |
| 25 | Corticosterone | Steroid receptor | L | 8.51 | 2 |
| 25 | Isatin der. | Rhino protease | I | 8.40 | 10 |
| 26 | Aldosterone | Steroid receptor | L | 9.32 | 2 |
| 26 | Haloperidol | Antipsychotic | L | 9.02 | 2 |
| 26 | Yohimbine | α-2 adrenergic receptor | L | 8.73 | 2 |
| 26 | Isatin der. | Rhino protease | I | 8.40 | 10 |
| 27 | Vesamicol der. | VR | L | 9.74 | 13 |
| 27 | Dexetimide | Anticholinergic | L | 8.80 | 2 |
| 27 | Dehydrosinefungin | mRNA Me trans. | I | 8.74 | 5 |
| 28 | Vesamicol der. | VR | L | 9.82 | 13 |
| 28 | Indoyl ethyl amines | 5-Hydroxy tryptamine receptor | L | 9.70 | 17 |
| 28 | Prazosin | α1-adrenergic agonist | L | 9.62 | 2 |
| 29 | Spiperone | L | 10.27 | 2 | |
| 29 | Ketanserin | Serotonin antagonist | L | 9.39 | 2 |
| 29 | Dextromoramide | Analgesic | L | 9.02 | 2 |
| 30 | Peptide phosphonates | Carboxy peptidase | IM | 12.00 | 19 |
| 30 | Domperidone | Dopamine antagonist | L | 10.13 | 2 |
| 30 | Etorphine | Narcotic | L | 9.91 | 2 |
| 31 | Carboxamide derivative | 5-Hydroxy tryptamine receptor | L | 9.54 | 20 |
| 31 | Benzodiazepine derivative | Integrin antagonist | L | 8.60 | 21 |
| 31 | Budesonide | Glucocorticoid receptor | L | 8.54 | 22 |
| 31 | Flavin mononucleotide | Cytochrome b reductase | I | 8.10 | 5 |
| 32 | Serotonin dimer | 5-Hydroxy tryptamine receptor | L | 9.34 | 9 |
| 32 | Cyclic urea | HIV protease | I | 8.85 | 23 |
| 32 | Hoechst 33258 | DNA | L | 7.41 | 24 |
| 33 | Methotrexate | Dihydrofolate reductase | I | 9.70 | 8 |
| 34 | Cyclic-aza isostere | HIV protease | I | 10.21 | 25 |
| 34 | Buprenorphine | narcotic | L | 9.83 | 2 |
| 34 | Pimozide | antipsychotic | L | 9.39 | 2 |
| 34 | Hoechst 33342 | DNA | L | 7.44 | 24 |
| 35 | Peptide phosphonates | Carboxypeptidase | IM | 11.52 | 19 |
| 35 | Argatroban | Thrombin | I | 7.72 | 8 |
| 35 | Peptide derivative | Thermolysin | I | 7.29 | 8 |
| 36 | Cyclic-aza isostere | HIV protease | I | 10.15 | 25 |
| 36 | Benzodiazepines | Integrin | L | 8.55 | 21 |
| 36 | Cyclic urea | HIV protease | I | 8.37 | 23 |
| 37 | Peptide phosphonates | Carboxypeptidase | IM | 11.40 | 19 |
| 37 | Cyclic-aza isostere | HIV protease | I | 9.31 | 25 |
| 37 | Benzodiazepines | Integrin | L | 8.80 | 21 |
| 38 | Hydroxypyrone | HIV protease | I | 10.22 | 26 |
| 38 | Cyclic urea | HIV protease | I | 9.92 | 23 |
| 38 | Benzodiazepines | Integrin | L | 8.40 | 21 |
| 39 | Cyclic sulfone | HIV protease | I | 9.52 | 27 |
| 39 | Benzodiazepines | Integrin | L | 7.05 | 21 |
| 40 | Cyclic-aza isostere | HIV protease | I | 11.30 | 25 |
| 40 | Hydroxy pyrone | HIV protease | I | 11.16 | 26 |
| 41 | Peptide phosphonates | Carboxypeptidase | IM | 12.00 | 19 |
| 41 | Cyclic urea | HIV protease | I | 9.48 | 23 |
| 41 | Cyclic sulfone | HIV protease | I | 9.22 | 27 |
| 42 | Hydroxypyrone | HIV protease | I | 11.10 | 26 |
| 42 | Cyclic urea | HIV protease | I | 9.85 | 23 |
| 43 | Peptide phosphonates | Carboxypeptidase | IM | 13.96 | 19 |
| 43 | Cyclic urea | HIV protease | I | 9.48 | 23 |
| 43 | Cyclic sulfone | HIV protease | I | 9.00 | 27 |
| 44 | Cyclic urea | HIV protease | I | 10.41 | 28 |
| 45 | Serotonin dimer | 5-Hydroxy tryptamine receptor | L | 10.05 | 9 |
| 46 | Cyclic urea | HIV protease | I | 10.75 | 28 |
| 46 | Cyclic urea | HIV protease | I | 9.51 | 23 |
| 47 | Zaragozic acid A | Squalene synthase | I | 10.11 | 29 |
| 48 | Cyclic urea | HIV protease | I | 10.35 | 28 |
| 50 | Cyclic urea | HIV protease | I | 10.20 | 28 |
| 50 | Hydroxyethyl amine derivative | Cathepsin D | I | 7.85 | 30 |
| 51 | Zaragozic acid B | Squalene synthase | I | 10.54 | 29 |
| 51 | Combichem hydroxyethyl amine derivative | Cathepsin D | I | 8.05 | 30 |
| 52 | Cyclic urea | HIV protease | I | 9.37 | 28 |
| 54 | Cyclic urea | HIV protease | I | 10.57 | 28 |
| 54 | Combichem hydroxyethyl amine derivative | Cathepsin D | I | 7.23 | 30 |
| 55 | Peptide-based | Thrombin receptor | L | 7.40 | 31 |
| 56 | Cyclic urea | HIV protease | I | 10.37 | 28 |
| 56 | Peptide-based | Thrombin receptor | L | 7.92 | 31 |
| 58 | Cyclic urea | HIV protease | I | 10.96 | 28 |
| 60 | Cyclic urea | HIV protease | I | 10.80 | 28 |
| 62 | Cyclic urea | HIV protease | I | 10.62 | 28 |
| 64 | Cyclic urea | HIV protease | I | 10.07 | 28 |
| 64 | Acetyl-CoA | Acetyl-CoA carboxylase | I | 8.00 | 5 |
| 67 | Peptide-based | Thrombin receptor | L | 8.10 | 31 |
| 68 | Stearyl-CoA | Acetyl-CoA carboxylase | I | 8.89 | 5 |
I, inhibitor; IM, metal ion inhibitor potential chelator in metalloprotein; IA, small anionic inhibitor; IC, potential covalent interaction; L, ligand (agonist or antagonist).
In most cases, Ki values were taken directly from the literature; however, some IC50 values have been used. Although the differences are small for purposes of this paper, original publications should be consulted for accurate thermodynamic data.
Figure 1.
Free energy of binding (in kcal/mol) for ligands and enzyme inhibitors plotted as a function of the number of nonhydrogen atoms in the ligand. See Table 1. A line with slope of 1.5 kcal/mol and an intercept of 0 is included as a visual aid to analysis. ▵, Metal ions or metalloenzymes; ▴, small anions; ○, natural ligands; ●, enzyme inhibitors.
Figure 2.
Free energy of binding per atom (in cal/mol per atom) for ligands and enzyme inhibitors plotted as a function of the number of nonhydrogen atoms in the ligand. Symbols are as described in Fig. 1.
Whereas there are certainly caveats concerning individual data points and uncertainties of reference state and experimental conditions, the empirical trends in the experimental data are clear. It is, however, much more difficult to establish limits based on theoretical grounds. Typical contributions to the free energy of binding include hydrogen bonding, the hydrophobic effect, van der Waals forces and electrostatic interactions (Eq 2; ref. 32).
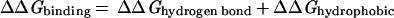 |
2 |
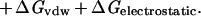 |
Any such list is necessarily incomplete, and each term is a complex function of enthalpic and entropic factors so that decomposition in this way may have only heuristic value (32). Thus, we have elected to focus on the empirical free energy trends in Figs. 1 and 2 and to compare them with theoretical estimates of important individual terms.
The interaction of two monovalent ions in van der Waals contact is −100 kcal/mol in vacuum or in crystals (33). This interaction is greatly diminished in water, leading to free energies of association near zero for ion pair formation. Many of the common ionizable groups in biological systems (e.g., guanidinium, carboxyl, phosphate) have the formal charge distributed across several heavy atoms. The contributions to overall affinity from electrostatic interactions are obviously important for small ligands where large affinities per atom are seen for the selective binding of small anions and cations. However, larger ligands generally have only a few formal charges per molecule, and the electrostatic groups in the binding region are increasingly buried and desolvated by the rest of the ligand. Thus, all things being equal, a given electrostatic interaction would provide a less favorable interaction in a larger ligand. Furthermore, many large, tight-binding ligands have no formal charges. Thus, although electrostatic interactions have a critical role to play in specific complexes, they do not, by themselves, offer a general explanation of the binding data.
We can estimate the maximum number of hydrogen bonds per molecule by using the number of polar atoms per total number of atoms. Whereas the fraction of polar atoms is quite high for a few small, tight complexes (e.g., biotin–avidin and carboxyl arabinitol bisphosphate/ribulose disphosphate carboxylase, Fig. 2), for larger ligands, this fraction approaches 0.15–0.20, perhaps because of the need for a balanced composition to insure water/lipid solubilities (34). Furthermore, there are many examples among HIV protease inhibitors for which the affinity is poorly correlated with the number of hydrogen bonds (35). It seems unlikely that any simple accounting for the number of hydrogen bonds is broadly predictive of the strength of ligand–receptor complexes.
Instead, we suggest that the general behavior of ligand binding over this wide range of ligands is determined by a combination of van der Waals and hydrophobic interactions as well as by factors unrelated to the thermodynamics of binding.
Maximal contributions of van der Waals terms can be readily estimated on a very simple, solvent-free model. In this model, ligand and receptor atoms are arrayed on a cubic lattice of spacing dlat = 2 × r, where r is the van der Waals radius. The strongest interactions are for a single point ligand, well buried in “receptor” lattice. The model gives a maximal value of ≈8.5ɛ where ɛ is the well depth, typically ≈0.15 kcal for a front-row atom (36, 37), yielding ≈−1 kcal/mol per atom. As the number of ligand atoms increases, “self-shielding” reduces the average contribution per atom because of the strong r−6 dependence of the force field. Limiting average interactions per atom are geometry-dependent: a completely buried long linear ligand gives a value of 6.5ɛ; a extended planar ligand ≈4ɛ, and a compact completely buried cubic ligand 3ɛ. If the ligand structure is only partially buried, smaller values are found. If we assume that the receptor site is preformed (3, 38), requiring no reorganization of either the site or the ligand, and we continue to ignore solvation, we can equate the full enthalpic term from the force field with the (maximal) free energy of interaction. Thus, van der Waals terms can yield substantial maximal interactions per atom that decrease as more atoms are added to the ligand. However, these maximal values are based on a vacuum reference state and might be significantly reduced with an aqueous reference state. It might be argued that desolvation terms should almost exactly compensate for ligand–receptor interactions, yielding little or no net binding. Two factors enhance ligand–receptor interactions compared with ligand–water interactions: the hydrophobic effect (see below) and the high atom density in macromolecules arising from polymer covalency. Protein densities, for example, are 30–40% higher than the density of water (39), leading to a 50–70% higher density of nonhydrogen atoms (based on an approximate protein empirical composition of C4NO). Effects of this size could readily yield significant net van der Waals contributions to the free energy of binding, even in the presence of strong ligand–solvent interactions. In addition, Myamoto and Kollman (38) have noted, on the basis of free energy calculations, that part of the hydrophobic effect arises from the repulsive van der Waals free energy of a nonpolar solute in water because of the larger contribution from the r−12 than the r−6 term.
Hydrophobic interactions can be estimated based on the (maximal) buried surface area or by converting free energy of transfers to a per heavy atom basis, yielding ≈850 cal⋅mol−1⋅carbon atom−1 (40). This value is at the lower end of the range of the 25–75 cal/Å2 contribution for buried surface area—the subject of continued research activity (41–43). If there were no site reorganization, these quantities would augment the van der Waals terms, leading to a limit of ≈−2 kcal⋅mol−1⋅heavy atom−1 for the strongest interactions in a rigid, completely buried site. (38). Although these limits are consistent with experiment, the dependence on molecular size is less than is seen empirically in Figs. 1 and 2. For simple ligand geometries, both van der Waals and hydrophobic terms should change in proportion to the surface/volume ratio. For simple geometries, the ratio reduces as n−1/3 where n is the number of atoms, a smaller dependence than shown in Fig. 2.
We conclude that a combination of van der Waals and hydrophobic terms provides the right magnitude to bound the experimental results, but the simplest models do not readily explain the nonlinearity of ligand interactions as a function of molecular size. Rather than exploring more complex models, we suggest that there are other reasons for this trend. Most of the data in Table 1 are from natural ligands or synthetic enzyme inhibitors. Ligands that bind much more tightly than picomolar may be selected against either by nature or by the pharmaceutical industry for a number of reasons. First, the kinetic dissociation time of femtomolar ligands is measured in years (19)! Long ligand lifetimes might well have unintended consequences. Furthermore, issues of solubility, clearance, and the cost of analoging would also tend to limit the pursuit of tighter-binding ligands in the higher molecular weight range (44). Thus, it may be that very high affinity ligands are sought neither by nature nor by medicinal chemists. If so, the experimental data underrepresent maximal attainable affinities for large ligands.
DISCUSSION
If we use these ideas to design small, high-affinity ligands, our analysis suggests the use of covalent bonds, the use of metal-containing (e.g., ref. 45) or organometallic moieties, strategies for generating buried compensating charges (46), and a better understanding of the clear outliers amongst the small ligands (e.g., biotin, carboxyl arabinitol bisphosphate). Simple models of van der Waals terms lead to molecular geometries with branched extended architectures, such as often seen for protease inhibitors (47), as a way to maximize surface/volume ratios. The limits presented in this paper, coupled with functional group analysis (2), can be used to assess ligands throughout the discovery process. This procedure is well suited to evaluate “build up” methods that construct composite molecules either through direct linkages (48–50) or combinatorial methods (30). It is encouraging to note that subnanomolar binding can, in principle, be achieved with ligands containing as few as 7–10 atoms. Such affinities have often been observed in systems containing 10–20 atoms (Table 1).
The inverse problem of assessing the quality of a potential binding site is more complex. A rough estimate is available by simply counting the number of atoms that are directly accessible on the surface of the site. However, knowledge of the precise shape of the pocket and detailed complementary chemical interactions (46) would seem to be required for an accurate calculation.
Although our discussion has centered on small molecule ligands, it is plausible that the maximal affinities in macromolecular systems have similar limits on a per-atom basis. The general nonlinearity with ligand size needs to be explored. One strong exception to nonadditivity is found in base pairing in DNA and RNA, where the local interactions can be accumulated in a linear manner over a very large number of bases.
In summary, the upper boundaries to the data shown in Figs. 1 and 2 can be used as one measure of how a particular ligand or family of ligands compares to other systems of the same size. Because these curves lie below our estimates of the maximal theoretical contributions, and especially because of the pronounced nonadditivity in binding for larger ligands, there is a large unexplored region of increased affinity. However, as noted above, maximal affinity is frequently not the only goal or even the most important goal in a design strategy.
Acknowledgments
We thank Jack Kirsch, Juan Alvarez and Geoff Skillman for helpful discussions. Research support from the National Institute of General Medical Sciences to I.D.K. and P.A.K. is gratefully acknowledged.
References
- 1.Knowles J R. Nature (London) 1991;350:121. doi: 10.1038/350121a0. [DOI] [PubMed] [Google Scholar]
- 2.Andrews P R, Craik D J, Martin J L. J Med Chem. 1984;27:1648–1657. doi: 10.1021/jm00378a021. [DOI] [PubMed] [Google Scholar]
- 3.Miyamoto S, Kollman P A. Proc Natl Acad Sci USA. 1993;90:8402–8406. doi: 10.1073/pnas.90.18.8402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.DeWitte R, Shakhnovich E. J Amer Chem Soc. 1996;118:11733–11744. [Google Scholar]
- 5.Zollner H. Handbook of Enzyme Inhibitors. Basel, Switzerland: Weinheim; 1989. [Google Scholar]
- 6.Ewing G J, Maestas S. J Phys Chem. 1970;74:2341–2344. doi: 10.1021/j100705a018. [DOI] [PubMed] [Google Scholar]
- 7.Parkhurst L. Annu Rev Phys Chem. 1979;30:503–546. [Google Scholar]
- 8.Rarey M, Kramer B, Lengauer T, Klebe G. J Mol Biol. 1996;261:470–4889. doi: 10.1006/jmbi.1996.0477. [DOI] [PubMed] [Google Scholar]
- 9.Halazy S, Perez M, Fourrier C, Pallard I, Pauwels P J, Palmier C, John G W, Valentin H-P, Bonnafous R, Martinez M. J Med Chem. 1996;39:4920–4927. doi: 10.1021/jm960552l. [DOI] [PubMed] [Google Scholar]
- 10.Webber S E, Tikhe J, Worland S T, Fuhrman S A, Hendrickson T F, Matthews D A, Love R A, Patrick A K, Meador J W, Ferre R A, et al. J Med Chem. 1996;39:5072–5082. doi: 10.1021/jm960603e. [DOI] [PubMed] [Google Scholar]
- 11.Nair H K, Lee K, Quinn D M. J Am Chem Soc. 1993;115:9939–9941. [Google Scholar]
- 12.Spadoni G, Stankov B, Duranti A, Biella G, Lucini V, Salvatori A, Fraschini F. J Med Chem. 1993;36:4069–4074. doi: 10.1021/jm00077a010. [DOI] [PubMed] [Google Scholar]
- 13.Rogers G A, Kornreich W D, Hand K, Parsons S M. Mol Pharmacol. 1993;44:633–641. [PubMed] [Google Scholar]
- 14.Dunn W J, III, Hopfinger A J, Catana C, Duraiswami C. J Med Chem. 1996;39:4825–4832. doi: 10.1021/jm960491r. [DOI] [PubMed] [Google Scholar]
- 15.Schloss J V. J Biol Chem. 1988;263:4145–4150. [PubMed] [Google Scholar]
- 16.Houlihan W J, Boja J W, Parrino V A, Kopajtic T, Kuhar M J. J Med Chem. 1996;39:4935–4941. doi: 10.1021/jm960288w. [DOI] [PubMed] [Google Scholar]
- 17.Barf T A, Boer P d, Wikström H. J Med Chem. 1996;39:4717–4726. doi: 10.1021/jm9604890. [DOI] [PubMed] [Google Scholar]
- 18.von Itzstein M, Dyason J C, Oliver S W, White H F, Wu W-Y, Kok G B, Pegg M S. J Med Chem. 1996;39:388–391. doi: 10.1021/jm950294c. [DOI] [PubMed] [Google Scholar]
- 19.Kaplan A P, Bartlett P A. Biochemistry. 1991;30:8165–8170. doi: 10.1021/bi00247a011. [DOI] [PubMed] [Google Scholar]
- 20.Norman M H, Navas F, III, Thompson J B, Rigdon G C. J Med Chem. 1996;39:4692–4703. doi: 10.1021/jm9603375. [DOI] [PubMed] [Google Scholar]
- 21.Samanen, J. M., Ali, F. E., Barton, L. S., Bondinell, W. E., Burgess, J. L., Callahan, J. F., Calvo, R. R., Chen, W., Chen, L., Erhard, K., et al. (1996) J. Med. Chem.39. [DOI] [PubMed]
- 22.Ashton M J, Lawrence C, Karlsson J-A, Stuttle K A J, Newton C G, Vacher B Y J, Webber S, Withnall M J. J Med Chem. 1996;39:4888–4896. doi: 10.1021/jm9604639. [DOI] [PubMed] [Google Scholar]
- 23.Lam P Y S, Ru Y, Jadhav P K, Aldrich P E, DeLucca G V, Eyermann C J, Chang C-H, Emmett G, Holler E R, Hodge C N, et al. J Med Chem. 1996;39:3514–3525. doi: 10.1021/jm9602571. [DOI] [PubMed] [Google Scholar]
- 24.Harapanhalli R S, McLaughlin L W, Howell R W, Rao D V, Adelstein S J, Kassis A I. J Med Chem. 1996;39:4804. doi: 10.1021/jm9602672. [DOI] [PubMed] [Google Scholar]
- 25.Sham H L, Zhao C, Stewart K D, Betebenner D A, Lin S, Park C H, Kong X-P, Kempf D J, Plattner J J, Norbeck D W, et al. J Med Chem. 1996;39:392–397. doi: 10.1021/jm9507183. [DOI] [PubMed] [Google Scholar]
- 26.Thaisrivongs S, Skulnick H I, Turner S R, Strohbach J W, Tommasi R A, Johnson P D, Aristoff P A, Judge T M, Gammill R B, Watenpaugh K D, et al. J Med Chem. 1996;39:4349–4352. doi: 10.1021/jm960541s. [DOI] [PubMed] [Google Scholar]
- 27.Kim C U, McGee L R, Krawczyk S H, Harwood E, Harada Y, Swaminathan S, Bischofberger N, Chen M S, Cherrington J M, Xiong S F, et al. J Med Chem. 1996;39:3431–3434. doi: 10.1021/jm960340o. [DOI] [PubMed] [Google Scholar]
- 28.Wilkerson W W, Akamike E, Cheatham W W, Hollis A Y, Collins R D, DeLucca I, Lam P Y S, Ru Y. J Med Chem. 1996;39:4299–4312. doi: 10.1021/jm9602773. [DOI] [PubMed] [Google Scholar]
- 29.Bergstrom J D, Kurtz M M, Rew D J, Amend A M, Karkas J D, Bostedor R G, Bansal V S, Dufresne C, VanMiddlesworth F L, Hensens O D, et al. Proc Natl Acad Sci USA. 1993;90:80–84. doi: 10.1073/pnas.90.1.80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kick E K, Roe D C, Skillman A G, Liu G, Ewing T J A, Sun Y, Kuntz I D, Ellman J A. Chem Biol. 1997;4:297–307. doi: 10.1016/s1074-5521(97)90073-9. [DOI] [PubMed] [Google Scholar]
- 31.Bernatowicz M S, E, Klimas C, Hartl K S, Peluso M, Allegretto N J, Seiler S M. J Med Chem. 1996;39:4879–4887. doi: 10.1021/jm960455s. [DOI] [PubMed] [Google Scholar]
- 32.Dill K A. J Biol Chem. 1997;272:701–704. doi: 10.1074/jbc.272.2.701. [DOI] [PubMed] [Google Scholar]
- 33.Atkins P W. Physical Chemistry. San Francisco: Freeman; 1982. [Google Scholar]
- 34.Lipinski C A, Lombardo F, Dominy B W, Feeney P J. Adv Drug Del Rev. 1997;23:3–25. doi: 10.1016/s0169-409x(00)00129-0. [DOI] [PubMed] [Google Scholar]
- 35.Holloway M, Wai J, Halgren T, Fitzgerald P, Vacca J, Dorsey B, Levin R, Thompson W, Chen L, deSolms S, et al. J Med Chem. 1995;38:305–317. doi: 10.1021/jm00002a012. [DOI] [PubMed] [Google Scholar]
- 36.Cornell W D, Cieplak P, Bayly C I, Gould I R, Kollman P A. J Amer Chem Soc. 1995;117:5179–5197. [Google Scholar]
- 37.Kaminski G, Jorgensen W. J Phys Chem. 1997;100:18010–18013. [Google Scholar]
- 38.Miyamoto S, Kollman P A. Proteins Struct Funct Genet. 1993;16:226. doi: 10.1002/prot.340160303. [DOI] [PubMed] [Google Scholar]
- 39.Kuntz I D, Crippen G M. Int J Peptide Protein Res. 1979;13:223–228. doi: 10.1111/j.1399-3011.1979.tb01872.x. [DOI] [PubMed] [Google Scholar]
- 40.Tanford C. The Hydrophobic Effect. New York: Wiley; 1973. , Chap. 2. [Google Scholar]
- 41.Dill K A. Science. 1990;250:297–298. doi: 10.1126/science.2218535. [DOI] [PubMed] [Google Scholar]
- 42.Sharp K A, Nicholls A, Fine R F, Honig B. Science. 1991;252:106–109. doi: 10.1126/science.2011744. [DOI] [PubMed] [Google Scholar]
- 43.Cheng Y-K, Rossky P J. Nature (London) 1998;392:696–698. doi: 10.1038/33653. [DOI] [PubMed] [Google Scholar]
- 44.Ajay, Walters W P, Murcko M A. J Med Chem. 1998;41:3314–3324. doi: 10.1021/jm970666c. [DOI] [PubMed] [Google Scholar]
- 45.Katz B A, Clark J M, Finer-Moore J S, Jenkins T E, Johnson C R, Ross M J, Luong C, Moore W K, Stroud R M. Nature (London) 1998;391:608–612. doi: 10.1038/35422. [DOI] [PubMed] [Google Scholar]
- 46.Chong L T, Dempster S E, Hendsch Z S, Lee L-P, Tidor B. Protein Sci. 1998;7:206–210. doi: 10.1002/pro.5560070122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kim E, Baker C, Dwyer M, Murcko M A, Rao B G, Tung R D, Navia M A. J Am Chem Soc. 1995;117:1181–1182. [Google Scholar]
- 48.Eisen M B, Wiley D C, Karplus M, Hubbard R H. Proteins. 1994;19:199–221. doi: 10.1002/prot.340190305. [DOI] [PubMed] [Google Scholar]
- 49.Bohacek R, McMartin C. J Am Chem Soc. 1994;116:5560–5571. [Google Scholar]
- 50.Shuker S B, Hajduk P J, Meadows R P, Fesik S W. Science. 1996;274:1531–1534. doi: 10.1126/science.274.5292.1531. [DOI] [PubMed] [Google Scholar]