Fast marching methods for the continuous traveling salesman problem

Abstract

We consider a problem in which we are given a domain, a cost function which depends on position at each point in the domain, and a subset of points (“cities”) in the domain. The goal is to determine the cheapest closed path that visits each city in the domain once. This can be thought of as a version of the traveling salesman problem, in which an underlying known metric determines the cost of moving through each point of the domain, but in which the actual shortest path between cities is unknown at the outset. We describe algorithms for both a heuristic and an optimal solution to this problem. The complexity of the heuristic algorithm is at worst case M·N log N, where M is the number of cities, and N the size of the computational mesh used to approximate the solutions to the shortest paths problems. The average runtime of the heuristic algorithm is linear in the number of cities and O(N log N) in the size N of the mesh.

Consider a problem in which we are given a speed function F(x) > 0 defined in a domain x ∈ Rⁿ. We are also given a collection of points (“cities”) X_i ∈ Rⁿ. The goal is to find the shortest roundtrip path that touches each city only once. Here, the speed function F(x) represents the inverse of the cost associated with passing through that point.

If the speed function F(x) = 1, then the metric is Euclidean, and the shortest path between any pair of cities is the straight line connecting them. In this case, all of the edges (both their positions and weights) of the graph connecting the cities are known, and the problem quickly reduces to the well known (but nonetheless NP-hard) traveling salesman problem (see, for example, ref. 1).

However, in the case of a non-constant speed function, both the actual path and time required to travel between any pair of cities is unknown. A large collection of physical problems fall into this category, including finding optimal paths to navigate terrain with various speeds and obstacles while reaching a given number of fixed stations.

This problem can be thought of as having two parts: first, to find the shortest path between cities with a nonconstant metric; and second, to find the solution to the traveling salesman problem with known edges and weights. One algorithm to find the shortest path is given by the fast marching method, which is an algorithm to solve the Eikonal equation on a approximation mesh that discretizes the continuous problem. At the same time, there are many algorithms to find both optimal and near-optimal solutions to the traveling salesman problem. This suggests two distinct approaches to our problem:

1. Use the fast marching method to find the shortest path between all pairs of cities, and then let the time required for each path serve as input to the traveling salesman problem.

2. Couple the two algorithms, so that optimal paths between pairs of cities are created “on the fly” as needed.

We will investigate both approaches.

Fast Marching Methods for Computing the Shortest Paths

Here, we review some work on fast marching methods to compute the shortest path between points under a nonconstant metric.

Dijkstra's Method and Optimal Paths.

Consider a discrete optimal trajectory problem on a network. Given a network and a cost associated with each node, the global optimal trajectory is the most efficient path from a starting point to some exit set in the domain. Dijkstra's classic algorithm (2) computes the minimal cost of reaching any node on a network in O(N log N) operations. Since the cost can depend on both the particular node and the particular link, Dijkstra's method applies to both isotropic and anisotropic control problems. The distinction is minor for discrete problems but significant for continuous problems. Dijkstra's method is a “one-pass” algorithm; each point on the network is updated a constant number of times to produce the solution. This efficiency comes from a careful use of the direction of information propagation and stems from the optimality principle.

We briefly summarize Dijkstra's method, since the flow logic will be important in explaining fast marching methods. For simplicity, imagine a rectangular grid of size N, where the cost C_ij > 0 is given for passing through each grid point x_ij. Given a starting point, the minimal total cost U_ij of arriving at the node x_ij can be written in terms of the minimal total cost of arriving at its neighbors:

To find the minimal total cost, Dijkstra's method divides mesh points into three classes: Far (no information about the correct value of U is known), Accepted (the correct value of U has been computed), and Considered (adjacent to Accepted). The algorithm proceeds by moving the smallest Considered value into the Accepted set, moving its Far neighbors into the Considered set, and recomputing all Considered neighbors according to Eq. 1. This algorithm has the computational complexity of O(N log N); the factor of log N reflects the necessity of maintaining a sorted list of the Considered values U_i to determine the next Accepted mesh point. More efficient implementation can be obtained by using other sorting data structures.

Continuous Control: Methods for Solving the Eikonal Equation.

Consider now the problem of continuous optimal control; here, we assume that the cost C is now a function C(x,y) defined throughout the domain, and the goal is to find the optimal path from a starting position to an exit set. As the mesh becomes finer and finer, Dijkstra's method does not converge to the continuous solution, since it produces the solution to the partial differential equation max(|u_x|,|u_y|) = h·C, where h is the grid size (see ref. 3). As h goes to zero, this does not converge to the desired solution of the continuous Eikonal problem given by [u_x² + u_y²]^1/2 = C.

Ordered Upwind Solvers for Continuous Isotropic Control.

Nonetheless, algorithms that produce convergent approximations to the true shortest path for nonconstant metrics can be obtained by using Dijkstra's method as a building block. The first such algorithm was due to Tsitsiklis (4), who obtains a control-theoretic discretization of the Eikonal equation, which then leads to a causality relationship based on the optimality criterion. Tsitsiklis's algorithm evolved from studying isotropic min-time optimal trajectory problems, and involves solving a minimization problem to update the solution. Tsitsiklis's algorithm uses Dijkstra-like ideas to order and sort the update procedure, and has the same O(N log N) operation count.

A finite difference approach, based again on Dijkstra-like ordering and updating, was developed by Sethian (5, 6) for solving the Eikonal equation. Sethian's fast marching method evolved from studying isotropic front propagation problems and involves an upwind finite difference formulation to update the solution. Both Tsitsiklis's method and the fast marching method start with a particular (and different) coupled discretization, and each shows that the resulting system can be decoupled through a causality property. In the particular case of a first-order scheme on a square mesh, the resulting quadratic update equation at each grid point is the same for both methods. We refer the reader to these references for details on ordered upwind methods for Eikonal equations, as well as to ref. 7 for a detailed discussion about the similarities and differences between Tsitsiklis's method and the fast marching method. More recently, Sethian and Vladimirsky have built a class of ordered upwind methods, based on Dijkstra-like methodology, for solving the more general class of optimal control problems in which the speed/cost function depends on both position and direction, which leads to a convex Hamilton–Jacobi equation. See ref. 7 for details.

We now briefly discuss the finite difference approximations behind fast marching methods.

Fast Marching Method Update Procedure.

We approximate the Eikonal equation

where F(x) is the given speed function at point x in the domain. We replace the gradient by an upwind approximate of the form

where we have used standard finite difference notation: this approximate was suggested by Rouy and Tourin (8).

The fast marching method is as follows. Suppose at some time the Eikonal solution is known at a set of Accepted points. For every not-yet-accepted grid point with an Accepted neighbor, we compute a trial solution to the above quadratic Eq. 2, using the given values for u at accepted points, and values of ∞ at all other points. We now observe that the smallest of these trial solutions must be correct, since it depends only on accepted values which are themselves smaller. This “causality” relationship can be exploited to efficiently and systematically compute the solution as follows.

First, tag initial points as Accepted. Then, tag as Considered all points one grid point away and compute values at those points by solving Eq. 2. Finally, tag as Far all other grid points. Then the loop is:

1. Begin loop: Let Trial be the Considered point with smallest value of u.

2. Tag as Considered all neighbors of Trial that are not Accepted. If the neighbor is in Far, remove it from that set and add it to the set Considered.

3. Recompute the values of u at all Considered neighbors of Trial by solving the piecewise quadratic equation according to Eq. 2.

4. Add point Trial to Accepted; remove from Considered.

5. Return to top until the Considered set is empty.

This is the fast marching method given in ref. 5. Helmsen (9) compares a similar algorithm with a volume-of-fluid approach for photolithography simulations; Malladi and Sethian (10) apply the fast marching method to image segmentation. The key to an efficient implementation of the above technique lies in a fast heap algorithm to locate the grid point in set of trial values with the smallest value for u.

Algorithms for the Optimal Solution

We now present two options for finding the optimal solution to the continuous traveling salesman problem: by optimal, we mean the shortest closed path that passes through all cities. The first approach is to use the fast marching method to calculate the shortest path between each pair of cities to generate the complete graph, and then use an optimal algorithm for the traveling salesman problem. The second approach is to embed the fast marching method into the actual construction of the optimal path. This latter approach can reduce runtime at the cost of some additional storage; results on both approaches are discussed.

The Discrete Traveling Salesman Problem on a Complete Graph: Optimal Solution.

We begin with a brief description of the discrete traveling salesman problem in which positive weights (cost) on a discrete graph are known. The problem is NP-complete: one straightforward method for constructing the optimal solution is given by branching. Define a “partial path” as a continuous route along the adjacent edges between consecutive cities in the path, with an associated total cost for visiting all cities in the path. Define a “complete path” to be a closed partial path that includes all cities. If a partial path P ends at a city C, we can define a “branch” of P as the continuation of P beyond C to any neighbor of C not included in the partial path P. We can systematically create all possible paths that exclude revisitation by starting at any city and then looping through branching until all complete paths have been found: the optimal one is then selected by comparison. Thus, the algorithm is the following. At each city, construct a partial path containing only that city. For each partial path, construct all possible branches, which yields a new set of partial paths and associated costs. Repeat until all partial paths have become complete paths, and then select the one with the smallest associated cost. The total runtime is of this algorithm is M!, where M is the number of cities.

Coupling the Fast Marching Method and Optimal Traveling Salesman Problem Solution Algorithm.

We now give two algorithms for computing optimal solutions to the continuous traveling salesman problem.

Algorithm A: branching.

The most straightforward technique to couple the fast marching method and the optimal algorithm for the traveling salesman problem is to first calculate the graph connecting each city with all other cities: this will assign a cost to each edge, and the resulting graph can be given to the optimal algorithm for the traveling salesman problem. On a computational mesh of size N, the fast marching method finds the optimal path from a given point to each of N points in time O(N log N). Starting M such calculations (one for each starting city) produces the complete graph in O(MN log N), and hence the total compute time is O(M! + MN log N).

Algorithm B: efficient branching.

The solution to the traveling salesman problem on the given graph dominates the runtime in the above algorithm: the labor of computing the graph itself using the fast marching method is negligible. However, computing the shortest path between every possible pair of cities may be unnecessary, and savings may be realized by embedding the path construction with the optimal traveling salesman problem solution. Here, we present an algorithm designed to build-up partial paths, ordered by cost, until one finally becomes a complete path. By construction, no other complete path or partial path can be shorter.

The key idea is the introduction of a time step to control the branching of the partial paths. This allows for an ordering of the partial paths, such that each path that is created during that time step has a cost greater than any created during a previous time step and a cost less than any created during the next time step. We look for the first time step in which one or more paths is completed: the cheapest will be optimal.

Consider a domain that contains all of the cities and discretize into a mesh^† of size N. Choose a time step dt. Set the clock time T = 0. We assume that there are M cities.

• T = 0: At each of M cities, initialize a fast marching method, where the only accepted point is the city itself.

• Begin Loop:

  • {Advance each fast marching method until all Considered points have values greater than T.
  • {For each fast marching method, build an edge from the base city to each city reached during this time period and build a partial path consisting of that edge.
  • {For each partial path P that ends at city i, suppose there is a partial path Q connecting city i to a city j such that the total cost of connecting P and Q is less than T + dt. Then, if there is no revisitation or it is a complete path, create path P + Q.
  • {Check if any partial path is complete, if one or more is completed, choose one with minimum cost and Exit.

• Set T = T + dt; Return to Loop.

Here, the condition for looping has changed from calculating all complete paths to calculating one complete path. It is straightforward to check that the obtained path is indeed optimal. One does not need to calculate all complete paths or even construct the complete graph of all possible links; in general, however, it is typically computed. The amount of work saved using algorithm A vs. algorithm B depends on the ratio of partial paths of associated cost less than the optimal path compared with the partial paths of associated cost greater than the optimal path: this ratio varies widely across problems.

Heuristic Algorithms

We now focus on producing algorithms for the continuous traveling salesman problem that produce near-optimal solutions: more efficient algorithms can be developed with a slight relaxation of the optimality requirement. First, we note that our problem of a continuous traveling salesman problem contains within it a triangle inequality, namely that if T(A, B) is the time it takes to travel from A to B for two cities A and B, then T(A, C) ≤ T(A, B) + T(B, C), since this is satisfied by any set of geodesics under the assumed slowness field. Thus, we may couple the fast marching method to Christofides's algorithm (11), which is a polynomial approximation algorithm in the case of an underlying triangle inequality. Christofides's algorithm has an upper bound of producing a path of cost 1.5·OPT, where OPT is the cost of the optimal path. Christofides's use of the minimum spanning tree lends itself to a union with the fast marching method through the use of Kruskal's algorithm (12). This union of algorithms allows for an approximate solution of 1.5·OPT of the continuous traveling salesman problem.

Christofides's Algorithm.

Christofides's algorithm involves a series of simple polynomial time steps. The first is the calculation of the minimum spanning tree. Then comes the calculation of a perfect matching among the cities of the minimum spanning tree with an odd number of edges in the minimum spanning tree. These two graphs, the minimum spanning tree and the perfect matching, are then merged to create one undirected graph. With this composite graph, a Eulerian path is found through the graph. The desired approximation solution is then the removal of revisitation from this Eulerian path, resulting in a solution at most 1.5·OPT.

In more detail, the steps of Christofides's algorithm are as follows.

The Minimum Spanning Tree.

For the first step of creating the minimum spanning tree, Kruskal's algorithm (12) can be used. A spanning tree is a set of edges between cities such that any pair of cities is connected through a subset of those edges. The cost of a spanning tree is the summation of the cost of all edges in the spanning tree. The tree that minimizes this cost is the minimum spanning tree. An efficient algorithm for calculating the minimum spanning tree on any given connected graph is Kruskal's algorithm, which runs in time O(E log E), where E is the number of edges in the graph. Kruskal's algorithm orders the edges in increasing cost and then recursively either adds the edge to the tree or discards it. If the edge does not redundantly connect a city to the tree, it is added. When the tree spans all cities, this then is the minimum spanning tree and is returned by Kruskal's algorithm.

The Perfect Matching.

Given the minimum spanning tree, Christofides then calculates a perfect matching among the cities with an odd number of edges in the minimum spanning tree. Here, a perfect matching is matching in which every city is adjacent to exactly one edge of the matching. Christofides's algorithm allows for this perfect matching to have one city with no edge in the matching. These edges used in the perfect matching must not also be used in the minimum spanning tree.

Composition and the Hamiltonian Path.

With the composition of the minimum spanning tree and the perfect matching, all that remain are graph traversal algorithms to calculate the Eulerian path and then the subsequent Hamiltonian path. The composition graph is formed simply by adding all edges of the perfect matching and the minimum spanning tree. The Eulerian path over the composite graph is simply a path that visits each edge of the graph once. One algorithm to create this path is to randomly progress from a city along a non-bridge edge to another city and delete the traversed edge from the graph: here, a bridge edge is an edge whose deletion results in a disconnected set of edges. The Eulerian path is then the order in which these edges are deleted from the graph.

The remaining step is then the transformation of the Eulerian path into the approximate solution. The Eulerian path generates a list of the order in which the cities are visited. This list generally contains multiple visits of cities. Christofides's method turns this list into a Hamiltonian path by progressing through the list, visiting only cities that had not previously been visited. Christofides's algorithm simplifies the list by starting at the beginning, and as it progresses along removes cities from the list that have previously been visited earlier in the list. This produces the desired Hamiltonian path within 1.5·OPT, where OPT is the cost of the optimal path.

Coupling the Fast Marching Method to Christofides's Algorithm.

The fast marching method can be coupled with Christofides's algorithm during two stages: the calculation of the minimum spanning tree and the perfect matching. The remaining steps of Christofides's algorithm run efficiently on the previously generated information from the fast marching method.

Coupling the Fast Marching Method and Kruskal's Algorithm.

The coupling we produced with the fast marching method and Kruskal's algorithm starts the fast marching method from each city. Through the use of a time step, identical to the one used in algorithm B, the edges between cities are ordered in ascending order. As an edge is created from the fast marching methods, it is put through the loop of Kruskal's algorithm. If the addition of that finishes the minimum spanning tree, the various fast marching methods pause and the algorithm progresses to the perfect matching.

Combining the fast marching method with Kruskal's algorithm is advantageous, since the fast marching method produces the edges of the complete graph in ascending order. The largest amount of work done in Kruskal's algorithm is the sorting of the graph's edges into ascending order. This removal of the sort cost cuts down the runtime of Kruskal within Christofides's from E log E to E. Additionally, Kruskal's algorithm recurses through the sorted edges of the graph: once the minimum spanning tree is calculated, the rest of the untouched sorted edges are ignored. This allows the fast marching method to stop calculating edges whenever the minimum spanning tree has been calculated, removing the need for the fast marching method to calculate the complete graph in all but the worst case.

Coupling the Fast Marching Method and a Perfect Matching Algorithm.

There are two possible methods to couple the fast marching method to producing a perfect matching. The first is similar to coupling the fast marching method to Kruskal's algorithm. Resume the time-stepped fast marching method from each of the cities to be in the perfect matching. At each time step, check whether a perfect matching without any edges from the minimum spanning tree exists. The second is to resume the fast marching method from the point where it stopped during calculation of the minimum spanning tree and calculate the complete graph for the cities to be matched.

Performance and Results

Timings.

In Table 1, we show the results^‡ of varying the number of cities on the three different algorithms: (i) branch, which is algorithm A and produces the optimal solution; (ii) efficient branch, which is algorithm B and produces the optimal solution; and (iii) adaptive Christofides, which uses a heuristic approach to produce a near optimal solution. In the numbers below, we computed average times over 20 different runs of randomly placed cities: the calculations were performed on a fixed mesh with 1,225 nodes.

Table 1.

Time in seconds on a 1,225-node mesh with random placement of cities

Cities	Branch	Efficient branch	Heuristic
2	0.007971	0.009923	0.009337
3	0.011875	0.015291	0.011777
4	0.015453	0.020333	0.013859
5	0.020008	0.025376	0.017015
6	0.025376	0.031069	0.021407
7	0.034323	0.041155	0.019097
8	0.101341	0.061651	0.026319
9	0.796741	0.205285	0.028727
10	8.681845	0.813008	0.033249
11	107.1124	3.351421	0.036698
12	1440.468268	18.69935	0.028239
13	inf	57.21878	0.032013
14	inf	(116.0744*)	0.037609
15	inf	inf	0.036795

*Average was taken of instances that finished; approximately half of the inputs failed to finish in under 30 min.

In Table 2, we show the results of varying the number of cities on the branch, efficient branch, and adaptive Christofides algorithms. Here, cities are uniformly distributed along the boundaries of two concentric circles. The calculation is performed on a fixed mesh with 12,250 nodes.

Table 2.

Time in seconds on a 122,500-node mesh with placement of cities around 2 concentric circles

Cities	Branch	Efficient branch	Heuristic
2	0.008784	1.31272	1.287344
3	0.013664	2.063264	1.508896
4	0.016592	2.782576	1.765584
5	0.0244	3.488224	2.01056
6	0.027328	4.276832	2.261392
7	0.03904	5.21184	3.432592
8	0.103456	6.169296	4.628192
9	0.794464	7.263392	5.808176
10	8.576112	9.383264	6.969616
11	105.938942	20.973264	7.441024
12	1429.103149	90.990528	7.289744

In Table 3, we show the results of varying the number of mesh nodes in the fast marching method on the branch, efficient branch, and adaptive Christofides algorithms. Here, cities are placed along the boundaries of two concentric circles. We examine the performance dependence of the fast marching part of the algorithm. The timings show that the results are essentially linear in the number of mesh points.

Table 3.

Time in seconds for 10 cities placed randomly

Grid nodes	Efficient branch	Heuristic
900	0.826282	0.017373
18,496	1.501869	0.555539
36,100	3.082989	1.298796
53,824	3.882918	1.81061
71,289	5.018787	2.803853
88,804	6.56809	3.36258
106,929	7.766276	4.116443
124,609	9.007699	5.213141
142,129	10.08169	6.485109
160,000	11.66066	6.793611

Nodes are increased linearly at a rate of 17,600.

Results.

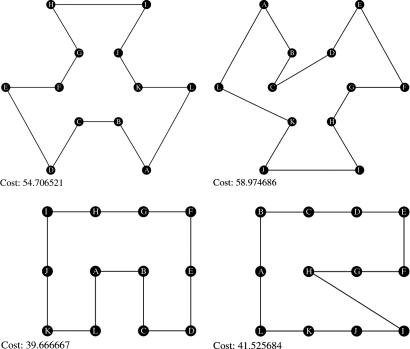
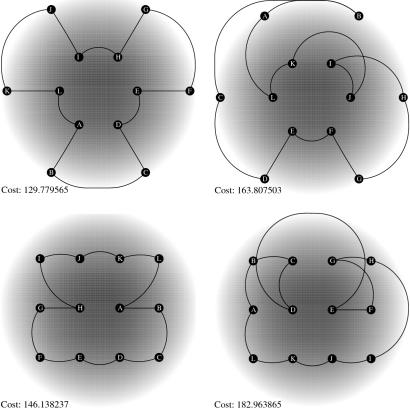
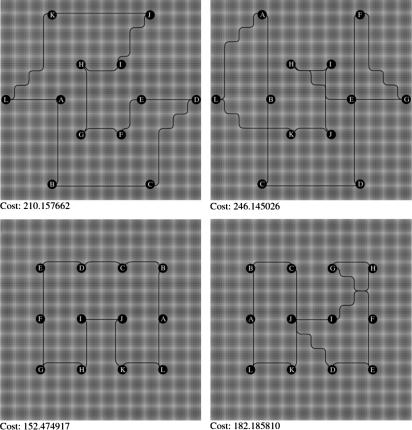
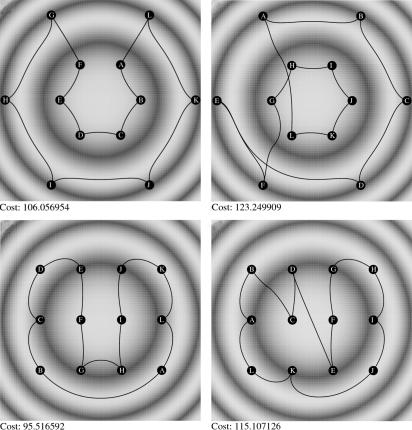
Here, we show a sequence of results, comparing obtained results for both the optimal path algorithm and the heuristic near-optimal Christofides's algorithm. In Figs. 1–4, we show a gray-scale background, in which the darker the region, the slower the speed function background metric. The left column shows results from the optimal fast marching–branching algorithm, and the right column shows results from the heuristic fast marching–Christofides's algorithm. The top row is for a configuration of cities in two concentric circles, and the bottom row shows cities in a rectangular lattice.

Fig. 1.

Constant speed function. (Left) Coupled fast marching–optimal algorithm (cost: Upper = 54, Lower = 39). (Right) Coupled fast marching Christofides's (cost: Upper = 58, Lower = 41).

Fig. 2.

Speed function proportional to radius. (Left) Coupled fast marching–optimal algorithm (cost: Upper = 129, Lower = 146). (Right) Coupled fast marching Christofides's (cost: Upper = 163, Lower = 182).

Fig. 3.

Checkerboard speed function. (Left) Coupled fast marching–optimal algorithm (cost: Upper = 210, Lower = 152). (Right) Coupled fast marching Christofides's (cost: Upper = 246, Lower = 182).

Fig. 4.

Double sinusoidal speed function. (Left) Coupled fast marching–optimal algorithm (cost: Upper = 106, Lower = 95). (Right) Coupled fast marching Christofides's (cost: Upper = 123, Lower = 115).

Fig. 1 shows results for a uniform speed function. As expected, the shortest path between each pair of cities is a straight line. Fig. 2 shows a radially symmetric speed function, with monotonically decreasing speed as one approaches the center at the origin. Fig. 3 shows a checkerboard speed function, and Fig. 4 shows a double sinusoidal speed function. Over all results, the average computed cost for modified Christofides's is 1.45 times that of the optimal algorithm.