Noise can play an organizing role for the recurrent dynamics in excitable media

Abstract

We analyze patterns of recurrent activity in a prototypical model of an excitable medium in the presence of noise. Without noise, this model robustly predicts the existence of spiral waves as the only recurrent patterns in two dimensions. With small noise, however, we found that this model is also capable of generating coherent target patterns, another type of recurrent activity that is widely observed experimentally. These patterns remain essentially deterministic despite the presence of the noise, yet their existence is impossible without it. Their degree of coherence can also be made arbitrarily high for wide ranges of the parameters, which does not require fine-tuning. Our findings demonstrate the need to reexamine current modeling approaches to active biological media.

It is now firmly established that excitability is one of the main dynamical principles behind a variety of biological functions. Spatially distributed excitable systems, or “excitable media,” are an important class of excitable systems whose main biological function is long-range signal transmission through self-sustained waves of activity (1–10). A canonical example of excitability is the ability of nerve cells to transmit pulses of electrical activity in the form of action potentials (4). Perhaps, the most well known example of excitable media in biology is the heart tissue, which relies on electrical couplings between excitable cells (2). On the other hand, many mechanisms of excitability exist in tissues that are mediated by different chemical messengers, notably, extracellular calcium (6, 11), ATP (9), and peptide growth factors (7, 10, 12). In single-cell organisms, such as social amoeba Dictyostelium discoideum, excitability may arise as an emergent property of a large population of cells (5, 13). Even on the level of single cell, excitable dynamics can be seen as, e.g., waves of intracellular calcium (8, 14, 15). Because of this widespread occurrence in biology, nonliving excitable media, such as the Belousov–Zhabotinsky reaction, catalytic surface reactions, excitable semiconductor systems, etc., have also attracted considerable interest (3).

The social amoeba D. discoideum, which is arguably one of the best-studied model organisms exhibiting excitability (see ref. 5 and references therein), is a good case in point. When Dictyostelium cells are starved, they begin to emit pulses of cAMP, a chemoattractant, which are then relayed to more distant cells by radially divergent waves or spiral waves of cAMP signaling. The established wave pattern then initiates a movement of cells toward the origin of the wave, resulting in cell aggregation; these cells will later differentiate to form sophisticated fruiting bodies and complete the organism's life cycle. Detailed experimental studies of the patterns of cAMP signaling reveal the standard phenomenology (1–3, 16) of a 2D excitable medium (5, 17–19). The basic questions these experiments raise, which are common to studies of all excitable systems, are about the origin of wave pattern initiation and selection.

The basic paradigm of an excitable dynamical system involves the existence of a fast excitatory variable with threshold-like dynamics coupled to a slow recovery variable responsible for the relaxation of the system back to the quiescent state (1, 2, 16). Excitable media are obtained by coupling such dynamical units locally in an excitatory fashion. This setup provides a basic module that robustly accounts for the phenomenon of wave propagation in excitable media, and, in particular, explains the existence of spiral waves (1, 2, 16). On the other hand, this minimal setup does not account for wave initiation and, in particular, fails to explain the existence of target patterns, another commonly observed pattern in excitable media (1–3, 5, 8, 9, 20, 21).

In reality, excitable systems are always noisy (15, 18, 22). Most of the time the noise simply perturbs the dynamics and does not significantly affect the observed behavior. Occasionally, small noise can have a large effect on the system by triggering rare events. In excitable media, these rare events can lead to nucleation of radially divergent waves, with the resulting waves appearing sporadically at random spatial locations and propagating through the medium (23, 24). The randomness in the time and location of these nucleation events will, therefore, make the observed wave patterns essentially incoherent. Let us note that upon increasing the strength of the noise some degree of coherence may appear because further nucleations are less likely during the refractory period (25–27). However, it is important to realize that the strength of the noise required to maintain this type of activity needs to be sufficiently high. As a result, unless the parameters are tuned in a way that the system is near a bifurcation threshold, it is not possible to control the degree of the pattern's coherence in this situation (for a more detailed explanation in the space-independent case, see ref. 28).

We found, however, that under certain conditions the situation may change in a qualitative way. Remarkably, instead of making the system behave in an incoherent fashion, the noise actually leads to the emergence of a highly regular spatiotemporal pattern. Furthermore, the degree of the pattern's coherence is under control and can be made as high as desired by a suitable choice of the parameters in a broad range that does not require fine-tuning. In other words, noise can generically result in the formation of a spatiotemporal pattern that is essentially deterministic, yet the noise is required and serves as a control parameter for the observed pattern. Specifically, we show that in an excitable medium the noise can spontaneously create regions that periodically emit radially divergent waves that organize themselves into target patterns. The noise here plays a truly constructive role by producing a new type of nonrandom behavior, fundamentally absent in the system without the noise.

To demonstrate this point, we performed numerical simulations of a model excitable medium driven by small-amplitude Gaussian white noise. We were motivated by the experiments on Dictyostelium by Lee and coworkers (17–19), who studied the initiation and evolution of the cAMP signaling patterns under various conditions. Our model is a coarsely discretized version of a stochastic partial differential equation with the Brusselator-like kinetics (29) and diffusive excitatory coupling:

Here, u(x, y, t) and v(x, y, t) are the excitatory and recovery variables, respectively, α is the ratio of the time scales of excitation and recovery, η(x, y, t) is white noise in time with short spatial correlation, ε is the noise amplitude (assumed to be small), f(u, v) = 1 + Au²v − (1 + A)u − Bu⁵ and g(u, v) = Au − u²v are the nonlinearities (A and B are parameters), Δ is the 2D Laplacian, and u_t = ∂u/∂t, etc. (see SI Text for details). A crucial assumption, which lies at the core of the standard excitability paradigm, is that there exists a strong separation between the time scales of the excitatory and the recovery variables; in the model, this corresponds to the assumption that α ≪ 1. If this condition is satisfied, the model is capable of supporting propagating waves in a wide range of parameters in the absence of the noise, i.e., when ε = 0.

We now present our findings. Our main result is the demonstration of an autonomous self-organized periodic wave source in an ideally homogeneous system, whose existence is caused entirely by noise (Fig. 1). To achieve this, we specified an initial condition in the form of a bell-shaped distribution of the recovery variable v and a uniform subthreshold distribution of u and simulated Eq. 1 (for details, see Fig. 1 legend). At first, the recovery variable v increased uniformly, with the highest value in the center. When it reached a certain critical value, a wave was initiated in the center of the system and propagated outward in a radial fashion, resetting the recovery variable to a lower value.

Fig. 1.

An autonomous self-organized periodic wave source generated by noise. Results of the numerical solution of Eq. 1 with α = 0.01, ε = 0.05, A = 0.7, B = 6.4 × 10⁻⁵, and h = 3.16 are shown. The system is discretized by finite difference on a 800 × 800 grid with reflecting boundary conditions. Red pixels denote the regions where u > 5, and the gray scale shows v (white is v = 1, black is v = 0, with various shades of gray showing v in between). The system is initially seeded with u = 0.5, v = 0.05 + 0.65 exp(−((x − 400 h)² + (y − 400 h)²)/(200 h)²), a bell-shaped distribution of the recovery variable. Note that the initial values of v are all below the deterministic threshold for firing. After a number of cycles a steadily oscillating pattern in which waves are initiated periodically in the center of the system is established. Once initiated, these waves propagate radially outward, generating a characteristic target pattern. The pattern persisted for as long as the simulation could be run. The snapshots are taken after ≈100 periods [see supporting information (SI) Movies 1–10]. Notice the characteristic formation of the nuclei ahead of the wave, which are then absorbed by the oncoming wave front; this is strongly reminiscent of the observations of cAMP signaling in Dictyostelium populations (19). We emphasize that this pattern is impossible in the same model in the absence of the noise.

As the system recovered, v remained the highest at the center, so at some later time the cycle repeated. After many such cycles a clearly visible target pattern emerged (see Fig. 1). This pattern maintained its coherence and was not destroyed by the noise (for several periods of the well formed wave source, see SI Movies 1–10). Moreover, the threshold value of the recovery variable was found to always remain below the value of v at which an individual excitable unit will fire in the absence of the noise. Therefore, it is indeed the noise that initiated the waves via nucleation, which is clearly seen in Fig. 1 and SI Movie 1. Note that a characteristic feature of the dynamics is nucleation of new sources right ahead of the main wave front, which are then absorbed by the oncoming wave (compare with ref. 19).

Furthermore, we found that the amplitude of the noise rather sensitively controls the parameters (such as amplitude and frequency) of the wave source. Upon decreasing the noise amplitude, the frequency of the source goes down and, at the same time, firing becomes less regular, until at some critical level of the noise the target pattern is no longer sustained (with firing occurring sporadically at random locations). On the other hand, upon increasing the noise amplitude, firing occurs more frequently, but at the same time the pattern starts to lose its coherence when the noise is no longer weak.

We next investigate how this mechanism can generate spatiotemporal patterns in a more realistic setting and the effect of wave resetting. Fig. 2 shows the results of a simulation in which the initial states of the units are taken to be identical. We also added a small smoothly varying subthreshold inhomogeneity [i.e., such that no spontaneous oscillations that could serve as heterogeneous pacemakers (30) would occur anywhere in the absence of the noise] to the parameter A (see SI Text). This inhomogeneity only plays a role at late stages. One can see that after an initial incubation period, waves start to appear at random locations throughout the system. Once initiated, they propagate, leaving a refractory region behind. Then, by the same mechanism as in Fig. 1, the new waves are initiated at the locations of the previous nucleations. After some transient, the system gets filled with many competing wave sources that oscillate almost in synchrony. Here is where the effect of the slowly varying inhomogeneity becomes important. The frequency of the sources at different locations becomes slightly different, so after a while the source with the highest frequency takes over the whole system (see Fig. 2). This finding is consistent with the observations of a variety of excitable systems (1, 3, 16). We point out, however, that a strongly localized heterogeneity will have a similar effect, so our finding is not inconsistent with the observations of the Belousov–Zhabotinsky reaction (1, 20, 31).

Fig. 2.

Establishment of a target patter in a more realistic setting, in which a slowly varying heterogeneity was added to the control parameter A (for details, see SI Text). Results of the numerical solution of Eq. 1 (see Fig. 1 for more explanation) with the same parameters as in Fig. 1 (except for A), with uniform initial conditions are shown. The system is discretized by finite difference on a 400 × 400 grid, with reflecting boundary conditions. Initially, multiple nucleation events occur, leading to the formation of many competing wave sources, oscillating nearly in synchrony. Because of the presence of the heterogeneity, some of the sources have higher frequency, so after several periods the source with the highest frequency entrains other sources and takes over the whole system. Note the increased regularity of the observed wave pattern.

On the other hand, if the initial distribution of the recovery variable varies significantly on a sufficiently large spatial scale, as in Fig. 3, the outcome can be quite different. Here, as a result of a wave nucleation, broken wave fragments are created, which then curl up and eventually transform into pairs of counterrotating spirals. Wave sources are also created in this situation; however, because of their lower frequency, they become entrained by the spiral later on. Thus, under this type of initial conditions spirals can be the usual outcome.

Fig. 3.

Large variations in the initial conditions may lead to the formation of spirals. Results of the numerical solution of Eq. 1 with the same parameters as in Fig. 2 (see Fig. 1 for more explanation) are shown. The system is discretized by finite difference on a 400 × 400 grid, with reflecting boundary conditions. In contrast to Fig. 2, the initial condition for v is taken to vary significantly in space. As a result of the initial wave nucleation, the wave front runs into regions that did not yet sufficiently recover and are still incapable of supporting waves; as a result, the front breaks up. The torn-up wave segments then curl up to form pairs of counterrotating spiral waves. Following the experimental protocol of ref. 19, at t = 1,500 we reset the values of u to a suprathreshold value (for details, see SI Text). Soon after, all activity was abolished; after a while, however, waves started to reappear at the locations where the medium was most recovered. The wave fronts forming as a result became disconnected; eventually, a different spiral wave pattern took over the entire system. Note that resetting u to a higher value abolished the spiral pattern altogether, reestablishing the target pattern seen in Fig. 2 (see SI Text).

To further investigate the formation of the spirals, we reproduced the resetting protocol of ref. 19 by uniformly increasing the value of the excitatory variable above the threshold at t = 1,550 (see Fig. 3 and SI Movie 8). As a result, after a large global excursion the activity was wiped out; however, after some time the pattern reappeared and evolved into one spiral that overtook the transient wave sources. On the other hand, by applying a larger reset to the value of u, we were able to extinguish the spiral pattern completely and obtain a target pattern as in Fig. 2 instead (results not shown). Let us point out the striking similarity of the basic phenomenology of the experiments of refs. 9, 15, and 17–19 with our findings.

The appearance of noise-induced deterministic wave patterns is consistent with the mechanism of self-induced stochastic resonance discovered in ref. 32 (see also ref. 33). We first explain the mechanism in the setting of stochastic ordinary differential equations, i.e., when the spatial derivative in Eq. 1 is set to zero, and the solutions of these equations have no spatial variation, u ≡ u(t), v ≡ v(t). Because of the strong time-scale separation between u and v the system spends most of the time in the small vicinity of the slow manifold [the stable branch of the u-nullcline, where f(u, v) = 0 and ∂f(u, v)/∂u < 0]. In the presence of noise, however, the system's trajectory can be kicked out of the basin of attraction of the slow manifold by a noise-activated event. The excitable nature of the system ensures that such an event will result in a large excursion away from the slow manifold. For ε ≪ 1, the likelihood of this excursion on a small fixed time interval [t₀, t₀ + Δt] is proportional to the Arrhenius factor exp(−ΔV(v(t₀))/ε)Δt, where ΔV(v(t₀)) is the effective “energy” barrier (34). In the case when η is a delta-correlated Gaussian white noise the barrier height as a function of v is given explicitly by (35):

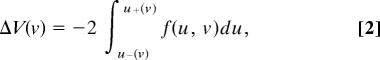where u₋(v) is a point on the slow manifold and u₊(v) is a point on the boundary of the basin of its attraction.

As the system creeps up along the slow manifold toward the equilibrium point (u₀, v₀), this likelihood rapidly increases, because the barrier ΔV(v) is a monotonically decreasing function of v. In fact, if one fixes Δt = O(α⁻¹), the time scale of the slow deterministic motion of the recovery variable, then one can see that this likelihood becomes large when v reaches a critical value v*, satisfying the equation ΔV(v*) = β, where β = εlogα⁻¹, provided that one chooses β = O(1), while α, ε ≪ 1. So, in the limit α, ε → 0 with β fixed a large excursion will happen with probability one when v reaches v* from below. If, after the excursion, the system always lands at the same point on the slow manifold (determined by v*), this will result in an establishment of a bona fide limit cycle (32). We note that while the deterministic characteristics (e.g., the period, etc.) of the limit cycle is controlled by the value of β, the degree of its coherence is controlled by ε and thus can be made as high as desired by choosing ε and α small enough, provided that β = εlog α⁻¹ is fixed. In practice, the systems is already very close to the asymptotic limit and coherence is very high when α ≲ 10⁻².

This picture carries over locally to the stochastic partial differential equation (Eq. 1), except now the role of a noise-activated barrier-crossing event is played by a nucleation event. Assume that the recovery variable v = v(x, y, t) varies smoothly on the spatial scale O(α⁻¹). Then, for any point (x₀, y₀) one can introduce a “local” nucleation rate in the fixed neighborhood of that point, provided the size L of this neighborhood lies in the range 1 ≪ L ≪ α⁻¹, where v is nearly constant. Once again, the probability of a nucleation event in such a neighborhood during the time interval [t₀, t₀ + Δt] is proportional to exp(−ΔV(v(x₀, y₀, t₀)/ε) Δt, where now:

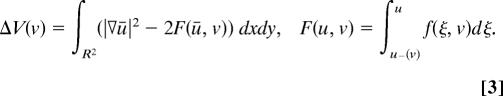Here v is assumed to be constant and ū is the droplet solution of the equation (the lowest energy saddle point of the energy functional in Eq. 3) (36):

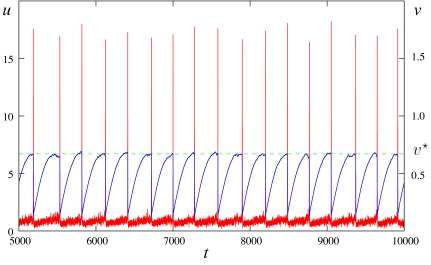
As before, in an excitable medium one expects that the barrier height ΔV(v) is a decreasing function of the recovery variable v. Hence, the nucleation rate will be maximal at the point (x₀, y₀) where v is largest, and by the same argument as in the spatially independent case, with probability one a radially divergent wave will be nucleated at (x₀, y₀) in the limit α, ε → 0, with β = εlog α⁻¹ = O(1) fixed, whenever v(x₀, y₀, t) = max_(x,y)v(x, y, t) = v*, where v* solves ΔV(v*) = β. In the wake of the wave v recovers on the slow time and, correspondingly, large spatial scale, making re-emergence of another wave at (x₀, y₀) after a deterministic O(α⁻¹) time possible. We further corroborated this scenario numerically from the simulation data shown in Fig. 1. In Fig. 4, we plot the trajectory of the system at point (x₀, y₀), which in this case is the center of the computational domain. One can see that a wave is nucleated in the neighborhood of this point at regular time intervals whenever v(x₀, y₀, t) reaches the critical value of v* ≃ 0.67, consistent with the above explanation. The value of v* observed in the simulations is in good agreement with the theoretical estimate based on the self-induced stochastic resonance mechanism (see SI Text).

Fig. 4.

The time series of u(x₀, y₀, t) (red line) and v(x₀, y₀, t) (blue line) in Fig. 1 is shown, where (x₀, y₀) is the point at the center of the computational domain. Observed is a localized version of self-induced stochastic resonance. The dashed green line shows the average jump-off value of v = v*.

Lastly, let us comment on the importance of our findings for modeling. It is commonly accepted that to explain a coherent dynamic, such as oscillations, etc., in a biological system, one needs to construct a deterministic model, described by a system of differential equations, that possesses such a dynamic; noise is considered largely irrelevant (1, 2, 37). Our results, however, suggest that proper account of the noise can be indispensable for interpreting the observations, even if the noise appears to be “small.” Specifically, we were able to demonstrate that the observed essential phenomenology (16) of excitable media can be robustly reproduced within the basic fast excitation/slow recovery paradigm of excitable media, if the effect of small noise is accounted for, with no further assumptions about the existence of pacemakers. These assumptions are inevitable when modeling excitable media with purely deterministic equations (1–3, 16, 31).