Structure of the light-harvesting bacteriochlorophyll c assembly in chlorosomes from Chlorobium limicola determined by solid-state NMR

Abstract

We have determined the atomic structure of the bacteriochlorophyll c (BChl c) assembly in a huge light-harvesting organelle, the chlorosome of green photosynthetic bacteria, by solid-state NMR. Previous electron microscopic and spectroscopic studies indicated that chlorosomes have a cylindrical architecture with a diameter of ≈10 nm consisting of layered BChl molecules. Assembly structures in huge noncrystalline chlorosomes have been proposed based mainly on structure-dependent chemical shifts and a few distances acquired by solid-state NMR, but those studies did not provide a definite structure. Our approach is based on ¹³C dipolar spin-diffusion solid-state NMR of uniformly ¹³C-labeled chlorosomes under magic-angle spinning. Approximately 90 intermolecular CC distances were obtained by simultaneous assignment of distance correlations and structure optimization preceded by polarization-transfer matrix analysis. It was determined from the ≈90 intermolecular distances that BChl c molecules form piggyback-dimer-based parallel layers. This finding rules out the well known monomer-based structures. A molecular model of the cylinder in the chlorosome was built by using this structure. It provided insights into the mechanisms of efficient light harvesting and excitation transfer to the reaction centers. This work constitutes an important advance in the structure determination of huge intact systems that cannot be crystallized.

Photosynthesis is the primary energy source for all living organisms. Chlorophyll–protein complexes capture light energy in most photosynthetic systems. Their structures are well known (1, 2). However, there are other light-harvesting devices called chlorosomes, which contain bacteriochlorophyll (BChl) assemblies. No protein is present in the BChl assemblies in sharp contrast to the light-harvesting chlorophyll–protein complexes mentioned above. Chlorosomes are found only in green sulfur bacteria and green filamentous bacteria. They catch weak light in an environment (3). A green sulfur bacterium species found in a deep-sea hydrothermal vent (4), for example, uses the dim light of geothermal radiation for photosynthesis. The atomic structure of chlorosomes has not been determined, which has impeded structure-based study of their functions. Because the design of chlorosomes is completely different from that of other light-harvesting devices, elucidation of their structure provides insight into the light-harvesting mechanism involved.

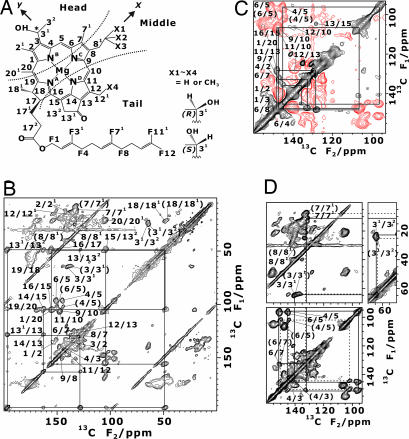
Freeze-fracture electron microscopy revealed that chlorosomes were oblong bodies filled with several rod-shaped elements and were attached to the cytoplasmic side of cell membranes (5, 6). The rod elements of Chlorobium limicola, the target of this work, are composed of BChl c. Light energy captured by BChl c in the rod elements is transferred to the reaction centers in the cytoplasmic membrane through BChl a in baseplate proteins (7). The BChl c molecule has two stereoisomers and homologues as shown in Fig. 1A. The (3¹R)-BChl c isomer is the major component (≈90%) in the rod elements (8) in C. limicola. A series of investigations have indicated that the BChl c assembly formation involves an intermolecular coordination bond between the 3¹-hydroxyl group and the Mg atom and a hydrogen bond between the coordinated 3¹-hydroxyl and 13¹-carbonyl groups (9–11).

Fig. 1.

Two-dimensional MAS ¹³C¹³C dipolar correlation NMR spectra of uniformly ¹³C-labeled chlorosomes from C. limicola are shown. (A) Chemical structure of BChl c isomers is shown. Numbers with prefix F are carbon atoms in the farnesyl chain. BChl c has two stereoisomers with chirality at the 3¹ position and homologues with different side chains at C8 and C12 as shown on the right. The head, middle, and tail parts are also indicated. The z-axis is perpendicular to the ring plane. (B) Two-dimensional ¹³C correlation spectrum with an rf-driven recoupling mixing time of 1.28 ms is shown. (C) Two-dimensional ¹³C correlation spectrum with a SPC-5 mixing time of 1.1 ms is shown. The red lines stand for negative contour levels. (D) Displayed are the connectivities of the doublet signals shown in a part of the 2D ¹³C NMR spectrum in B. Two individual connectivities for signals a and b are shown by solid and dashed lines, respectively, from C7¹ to C3¹, and are indicated by assignments with and without parentheses.

Structure determination of the BChl c assembly in chlorosomes has been a long-standing problem. Because chlorosomes do not form crystals, x-ray diffraction does not provide sufficient constraints for such determination. Proposed assembly structures based on NMR data can be classified into two major models. The solid-state NMR study by Nozawa and coworkers (12–15) presented an antiparallel-chain model composed of stacked piggyback dimers. The piggyback dimer is formed through the two intermolecular coordination bonds with Mg so that the z directions defining the ring orientations (Fig. 1A) are parallel to each other. Balaban et al. (11, 16) and van Rossum et al. (17) interpreted the solid-state NMR data as monomer-based parallel-chain stacking. Mizoguchi et al. (8) also proposed a monomer-based parallel-chain model on the basis of NMR investigations on BChl c aggregates in solution.

Magic-angle-spinning (MAS) solid-state NMR can provide atomic structural information for huge structures. However, it is difficult to obtain a large number of distances from uniformly ¹³C-labeled molecules. In this study, we have acquired distance constraints from direct dipolar couplings by complete polarization-transfer matrix analysis of ¹³C spin diffusion. The obtained ¹³C¹³C distances were assigned to specific intramolecular and intermolecular spin pairs in a BChl c assembly simultaneously with structure optimization. This iterative procedure (18, 19) provided the structure of the BChl c assembly at atomic resolution.

Results

Signal Assignments for BChl c in Chlorosomes.

We have assigned the resonances based on the dipolar couplings between carbons connected by a covalent bond (20). Fig. 1B presents a 2D ¹³C dipolar correlation spectrum of uniformly ¹³C-labeled C. limicola chlorosomes obtained under an rf-driven recoupling pulse sequence (21). The cross-peaks can be followed along the covalent bonds from C13¹ to C17 as shown by the solid lines in Fig. 1B. For instance, carbonyl carbon C13¹ at 196.0 ppm gives a cross-peak with C13 at 127.8 ppm on the vertical line in Fig. 1B. The next carbon, C14, appears at 162.4 ppm on the horizontal line in Fig. 1B. The rf-driven recoupling sequence gives weak cross-peak intensities near the diagonal line in Fig. 1B owing to the low recoupling efficiency. In contrast, double-quantum (DQ) dipolar recoupling sequence SPC-5 (22) gives peaks almost independently of the chemical-shift difference in the selected region. The aliphatic diagonal region of a 2D ¹³C DQ dipolar correlation spectrum is presented in Fig. 1C. The overlapping cross-peaks for C9/C10 and C11/C10, for example, were assigned based on the connectivity with the cross-peaks of C9/C7 and C11/C13, respectively. Thus, we have assigned all carbon signals in the BChl c ring and the farnesyl chain [supporting information (SI) Table 2]. The well resolved signals with linewidths of ≈1 ppm caused by chemical shift dispersion in Fig. 1 B–D indicate that the BChl c assemblies in the chlorosomes assumed a unique well defined structure. Some cross-peaks were observed to form doublets (Fig. 1D and SI Table 2). The doublets will be assigned on the basis of the determined structure in Discussion.

Polarization-Transfer Matrix Analysis of Cross-Peak Intensities in Spin Diffusion Spectra.

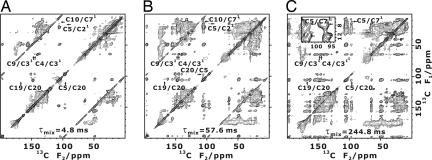
We have obtained distance information from the proton-driven spin diffusion (23, 24) caused by ¹³C¹³C dipolar interactions. 2D spin diffusion experiments on uniformly ¹³C-labeled chlorosomes were performed with a series of mixing times, τ_mix = 0.0, 1.1, 4.8, 11.2, 25.6, 57.6, 115.2, and 244.8 ms (Fig. 2).

Fig. 2.

Two-dimensional proton-driven spin diffusion ¹³C¹³C dipolar correlation NMR spectra of uniformly ¹³C-labeled chlorosomes. (A) τ_mix = 4.8 ms. (B) τ_mix = 57.6 ms. (C) τ_mix = 244.8 ms. Cross-peaks between the two sets of sequentially connected signals are shown in C Inset. Arrows indicate cross-peaks whose intensities are shown in Fig. 3 A–D.

We have obtained polarization-transfer rates caused only by direct dipolar couplings by transfer matrix analysis. Spin diffusion can be characterized by matrix R in

Here matrix M(τ_mix) gives the peak intensities for C1-C20, C2¹, C3¹, C3², C7¹, C8¹, C12¹, C13¹, C13², C18¹, and C20¹. Weaker signals for doublets were ignored because they do not cause deviation in the calculated distances by more than ≈10%. Experimental peak intensities are caused by both direct and relayed polarization transfer mechanisms, but R gives the rates caused by the direct dipolar couplings (25). Thus the determination of R provides the distance information only from direct dipolar couplings. This procedure is especially important for uniformly ¹³C-labeled molecules where the polarization transfer is dominated by strong dipolar couplings between ¹³C spins bonded covalently.

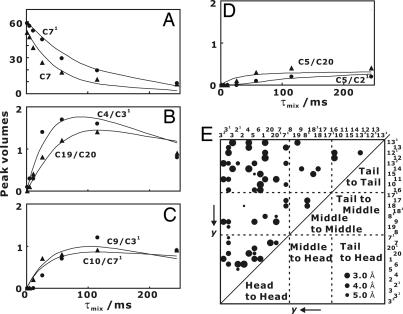
Polarization-transfer matrix R was determined by minimizing the difference between the signal intensities calculated with Eq. 1 and the experimental intensities obtained from the peak volumes. Typical build-up curves are presented in Fig. 3 A–D, together with best-fit calculated curves. The large increase at the beginning of mixing can be ascribed to direct magnetization transfer. A small increase after a lag time, as shown for the C5/C2¹ cross-peak (Fig. 3D), is caused by indirect magnetization transfer and does not contribute to R.

Fig. 3.

Build-up curves for ¹³C¹³C spin diffusion. Experimental (symbols) and simulated (lines) cross-peak intensities are presented. (A) Intensities of diagonal peaks for C7¹ (●) and C7 (▴). (B) Cross-peaks C4/C3¹ (●) and C19/C20 (▴). (C) Cross-peaks C9/C3¹ (●) and C10/C7¹ (▴). (D) Cross-peaks C5/C2¹ (●) and C5/C20 (▴). (E) Experimental ¹³C¹³C distance map for r_j,k^eff calculated from the polarization-transfer matrix on the BChl c assembly. Carbons are arranged in the order of the y coordinate defined in Fig. 1A. The diameters of circles are inversely proportional to the distances as shown by examples.

Simultaneous Structure Calculation and Cross-Peak Assignments for Distance Correlations.

To determine the assembly structure from the distance constraints for R_j,k in R, we must identify molecules l and m that spins j and k belong to, respectively. In general, the polarization transfer for R_j,k is caused by more than one CC dipolar couplings. It is not unusual that intramolecular and intermolecular spin pairs for j and k contribute to R_j,k. We have taken these contributions into account below.

Internuclear distances were calculated by using the perturbation theory on the ¹³C spin diffusion under MAS at spinning frequency ω_R (26). The initial build-up rate R_j,k for the direct polarization transfer can be expressed as

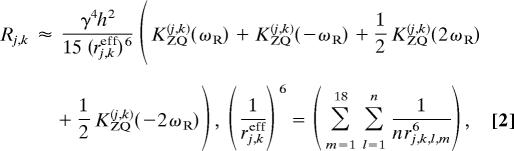where K_ZQ^(j,k) and r_j,k,l,m are the zero-quantum (ZQ) lineshape function and the distance between spin j in molecule l and spin k in molecule m, respectively. Integer n is the number of nonequivalent molecules in a unit lattice. The ZQ lineshape functions were estimated from the observed single-quantum lineshapes of relevant ¹³C signals without ¹H decoupling as described in Methods. The validity of this approximation was confirmed by 68 intramolecular distances for pairs of carbons connected by one or two covalent bonds. The distances calculated with this method agreed with known distances with a SD 25%.

At first, the distances for ¹³C pairs separated by more than three covalent bonds in BChl c were tentatively assigned to intermolecular distances. These spin pairs include the three correlation types: head–head, head–tail, and tail–tail correlations. These correlations give r_j,k^eff as shown in Fig. 3E and SI Table 3. Here, head and tail stand for the portions around C3 and C13 in BChl c, respectively (Fig. 1A). The correlations with ¹³C spins in the middle part were not used because these correlations do not contribute to the building of the initial assembly models as described below.

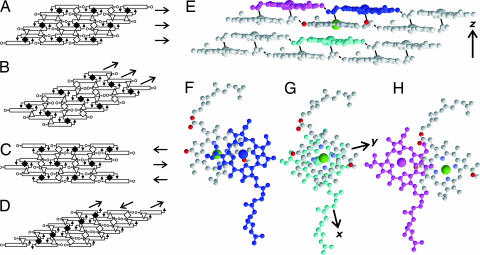
We have assigned a carbon pair to a specific BChl c intermolecular spin pair by referring to model assembly structures. This is similar to structure-based NOE assignments on protein NMR (18, 19). The initial assembly models are assumed to form planar structures as shown in Fig. 4 A–D, where farnesyl chains stick out of the plane. The farnesyl chains disrupt the interaction in the x direction in Fig. 4G when BChl molecules are stacked with coordination bonds between Mg and C3¹-OH as reported (9–11). Thus BChl c molecules would stabilize the planar structure. Planar stacking models were generated by using two translational symmetry operations on a two-dimer or a four-monomer unit. The structures having the head–head, head–tail, and tail–tail correlations are satisfied only by the four models: parallel-dimer layers, uneven-dimer columns, antiparallel-dimer layers, and antiparallel-monomer columns (Fig. 4 A–D and SI Fig. 6). Here, the BChl c ring in the model is allowed to take either orientation of the molecule that flips by 180° along the axis including Mg and C3¹. In this structure optimization, we excluded structures not expressed by the models in Fig. 4 A–D such as a model consisting of monomers and dimers. Such complicated structures would cause signal splitting and broadening due to chemical shifts. The possibility of those structures can be eliminated because the resonance lines are not broadened by more than ≈1 ppm.

Fig. 4.

BChl c assembly models satisfying head–head, head–tail, and tail–tail contacts and the structure of the BChl c assembly determined under ¹³C¹³C distance constraints. (A) Parallel-dimer layers. (B) Uneven-dimer columns. (C) Antiparallel-dimer layers. (D) Antiparallel-monomer columns. Arrows in the structure indicate the coordination bonds between C3¹OH and Mg. Open rectangles represent BChl c rings. , ◇, and ▵ stand for the head–head, tail–tail, and head–tail contacts, respectively. The arrows on the right of A and C and those at the top of B and D indicate layers and columns, respectively. (E) A side view of the structure of the BChl c assembly. Solid and broken lines represent coordination and hydrogen bonds, respectively. Oxygen atoms are colored red. (F) A top view of the piggyback dimer. (G) A top view of the interdimer full stacking at the center of E. (H) A top view of the intercolumn contact between neighboring dimers. The coordinates of BChl c molecules are given in the legend to SI Fig. 7.

Structures were optimized by simulated-annealing molecular dynamics under the intermolecular distance constraints except for the correlations with ¹³C spins in the middle part. The assignment was revised to a new one after this optimization if the new intermolecular spin pair for r_j,k^eff gave a shorter distance. Each of the intermolecular CC distances, r_j,k^eff, for the middle–middle, middle–tail, and middle–head correlations was also assigned to a single spin pair that gave the shortest CC distance in the assembly structure. The second simulated annealing was performed with the corrected assignments. This cycle of assignment and structure optimization was iterated until convergence of the structure was attained.

After obtaining the optimized structures based on r_j,k^eff, we adopted new distance constraints r_j,k,l,m computed from distances in the optimized structure, r_j,k,l,m^cal as r_j,k,l,m = r_j,k^eff · (r_j,k,l,m^cal/r_j,k^cal), with

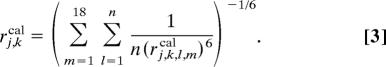Namely, R_j,k was ascribed to more than one dipolar coupling. Intramolecular dipolar couplings at l = m were also considered at this stage. Distances, r_j,k,l,m, < 7 Å were used for the constraints. All of the optimal structures for the dimer-based models converged to structures consisting of piggyback dimers in the previous optimization. Thus we set the number of nonequivalent molecules, n, to 2 for the dimer structure models in Fig. 4 A–C. The monomer-based model was optimized under n = 1. The BChl c assembly structure was refined by simulated annealing under these revised distance constraints. This cycle of the assignment and structure optimization was iterated until the convergence was attained.

The resultant statistics for the final structure are summarized in Table 1. The final structure that best satisfied the distance constraints was derived from the parallel-dimer layers (Fig. 4 E–H). It exhibited half less violations in the distance constraints than the structures optimized for the other three models. The average rmsd for the 10 lowest-energy structures of 200 calculations (see SI Fig. 7) was 0.20 ± 0.06 Å for the chlorin backbone.

Table 1.

NMR and refinement statistics for calculated structures

Statistics	Parallel-dimer layers	Uneven-dimer columns	Antiparallel-dimer layers	Antiparallel-monomer columns
NMR distance constraints
Total intermolecular C–C constraints*	94	96	102	81
Constraints in class −3.5 Å	63	70	70	55
Constraints in class 3.5–4.5 Å	21	20	20	22
Constraints in class 4.5–5.5 Å	6	4	8	2
Constraints in class 5.5–7.0 Å	4	2	4	4
Structure statistics
Violations, mean and SD
Distance constraints, ņ	0.9 ± 1.0	1.6 ± 1.1	1.6 ± 1.6	1.7 ± 1.6
Distance constraints ± 50%, Ň	0.2 ± 0.4	0.6 ± 0.7	0.8 ± 1.2	0.8 ± 1.1
Deviations from idealized geometry
Bond lengths, Å	0.01	0.01	0.01	0.01
Bond angles, °	0.6	0.6	0.6	0.6
Average pairwise rmsd, ŧ
Heavy	2.99 ± 0.63	3.03 ± 0.64	3.41 ± 0.70	6.21 ± 2.07
Backbone	0.20 ± 0.06	0.19 ± 0.05	0.63 ± 0.27	3.26 ± 1.82

*The numbers of the distance constraints for the stacking molecules in the central part in the optimized assembly structure consisting of 18 molecules.

^†Average values of differences between experimental distances r_j,k,l,m and those in optimized structures, r_j,k,l,m^opt.

^‡Averages of the deviations from the error bounds defined by r_j,k,l,m^opt − 1.5r_j,k,l,m (for 1.5r_j,k,l,m < r _j,k,l,m^opt), 0 (for 0.5r_j,k,l,m ≤ r_j,k,l,m^opt ≤ 1.5r_j,k,l,m), and 0.5r_j,k,l,m − r _j,k,l,m^opt (for r _j,k,l,m^opt < 0.5r_j,k,l,m).

^§Pairwise rmsd was calculated for the 10 lowest-energy structures of 200 calculations.

To confirm the significance of the NMR violations in determining the structure, we performed a nonparametric Mann–Whitney test for the differences between the distance determined from R and that in the optimized final structure, r_j,k,l,m − r_j,k,l,m^cal. This test indicated that the final structure shown in Fig. 4 E–H agreed with the experimental distance constraints better than the other three optimized structures at a confidence level of 99% (see SI Table 4).

Fig. 4F shows the head–head contact in the piggyback dimer with the stacking distance along the z axis, d_p^z, 3.0 Å, and Mg–Mg distance in the xy plane, d_xy^Mg-Mg, 5.6 Å. The head–tail contact in Fig. 4G shows fully overlapping stacking at d_p^z = 3.2 Å and d_Mg-Mg^xy = 1.2 Å. Fig. 4H illustrates the tail–tail contact with partial overlap at d_p^z = 3.8 Å and d_Mg-Mg^xy = 9.2 Å. It should be noted that an intercolumn hydrogen bond between C3¹OH and C13¹O can be formed in this structure as shown in Fig. 4E.

Discussion

Structure of the BChl c Assembly.

This high-resolution structure of the BChl c assembly in intact chlorosomes was determined by distance analysis using solid-state NMR. A variety of structural models have been proposed based on the results of visible absorption and NMR spectroscopy of artificial aggregates and chlorosomes (12, 16, 17). Recent models were constructed based mainly on a few distance constraints and chemical shifts such as ring current shifts in solid-state NMR spectra (27, 28). It is difficult to assign the chemical shifts to structural factors in the stacking BChl c complex. Thus, solid-state NMR could not provide a definitive structure so far. This problem has been solved by our solid-state NMR methodology developed for uniformly ¹³C-labeled chlorosomes. Approximately 90 distance constraints for direct dipolar couplings were obtained by the polarization-transfer matrix analysis of the spin-diffusion experiments. Every effective CC distance r_j,k^eff was ascribed to dipolar couplings at specific intramolecular and intermolecular CC distances simultaneously with structure optimization.

The obtained structure comprised the piggyback dimer-based parallel layers unlike the well known monomer-based structures (1, 10). This structure includes the important structural elements established in previous investigations (1, 9–11). The two stacking modes, piggyback dimer and full interdimer stacking shown in Fig. 4 F and G, together with the intercolumn hydrogen bonds (Fig. 4E) would stabilize the huge BChl c assembly without the support of proteins.

There are two sets of correlated peaks a and b in the spectra for signal assignments (Fig. 1D and SI Table 2). The doublets were explained by either a bilayer model (17) or the coexistence of two kinds of assembly structure (27) in the previous solid-state NMR works. However, similar doublets observed in solution NMR studies were ascribed to the piggyback-dimer structure based on absorption spectra, ring current shifts, and NOEs (13, 29, 30). The signals of the dimer can split because the two molecules are not equivalent owing to the lack of 2-fold symmetry. The correlation coefficient between the chemical-shift differences for 33 carbon resonances in the chlorosomes and the solution was 0.63, indicating a significant positive correlation. The intensity ratio observed for solids was almost 1:1 as for solutions (13, 29, 30). The volume intensity ratio of the two components, a to b, was 0.5:0.5 for the C5/C6, C20/C19, C7/C7¹, and C18/C18¹ cross-peaks and 0.6:0.4 for the C3¹/C3² and C5/C4 cross-peaks. Note that the height ratios for the signals were ≈0.7:0.3 despite the 1:1 volume ratios. The resemblance between the intensity ratios for the chlorosomes and the BChl c solution is consistent with the piggyback-dimer structure determined in this work. This dimer structure is also supported by the observation of cross-peaks between the two sets of correlated peaks at the C5/C7¹ correlation in the spin-diffusion spectra (Fig. 2C). This head—head correlation indicates that two BChl c molecules stack at a distance less than ≈5 Å, as shown in Fig. 4F. Here, each of the molecules is responsible for one set of signals.

Excitation Transfer in Chlorosomal Antennas Based on Parallel-Dimer Layers.

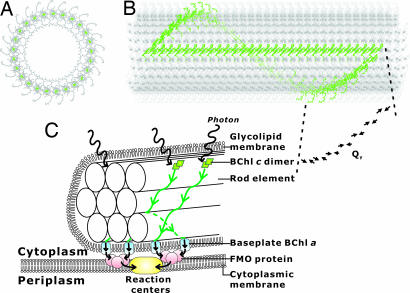
We have built a chlorosomal rod element structure based on parallel-dimer layers (Fig. 4 E–H) under the requirements based on the results of the solid-state NMR and electron microscopy. Electron microscopy showed that chlorosomes of C. limicola have rod-like elements with a diameter of ≈10 nm (5, 6). This rod architecture can be formed by 14.5° rotation of the BChls in the neighboring columns about the vector connecting the Mg atoms in the lower BChl molecules of the dimers in the columns (Fig. 4 F and G). This structure increased the NMR violation (>50%) in Table 1 by only 0.1 Å and did not disrupt the intercolumn hydrogen bonds. This rod element consists of 25 columns parallel to the rod axis and has an outer diameter 9.5 nm without farnesyl chains (Fig. 5A and B). This rod has spiral layers formed by dimers as shown in Fig. 5B. The ring planes in the layers are inclined by 42° from the rod axis. The direction of the ring plane is determined by the rotation axis for the formation of the cylinder. This inclination fulfills the requirement caused by the linear and circular dichroism of the Q_y band (10, 31–33). This rod model is also consistent with the x-ray powder diffraction pattern. Major diffractions were observed at ≈0.45, 0.94, and 1.17 nm for Chlorobium tepidum chlorosomes (34). The diffractions at 0.45 and ≈0.94 nm can be ascribed to the repeats along the long axis of the rod at distances between the planes. The intensity at ≈1.17 nm would be caused by repeats of the columns.

Fig. 5.

A rod element structure built with the parallel dimer layers shown in Fig. 4 E–H. (A) A top view. Magnesium atoms are colored dark green. Columns perpendicular to the page are arranged on the circumference. (B) A side view. The cylindrical structure consists of ≈1,500 molecules. A single spiral layer and a single column are colored green. A layer consisting of 25 dimers makes one spiral rotation. Twenty-nine full stacking dimers (Fig. 4 F and G) constitute the green column along the cylinder axis. The arrows represent the Q_y transition dipole moments of BChls. The Q_y transition dipolar vectors form an angle of 46° with the cylinder axis and an angle of 236° with the radius vector connecting Mg and the cylinder axis. (C) Schematic representation of the excitation energy transfer in a chlorosome. The green lines with arrows indicate the paths of the excitation transfer along the spiral layers to the baseplate shown in B. The model structure was taken from ref. 46.

The rod structure based on the determined assembly structure provides the basis for elucidation of the light-harvesting mechanism. The assembly without proteins allows 3D organization of pigments for the purpose of capturing the low-density photons as excited states. The rod containing the inclined Q_y transition dipole moments shown in Fig. 5B can catch incoming photons from all directions. The pigment arrangement on the surface of an optically hollow cylinder also enhances light harvesting by increasing the area for light absorption. This 3D structure contrasts with 2D assemblies consisting of Chl rings of light-harvesting complexes, LH1 and LH2, in plasma membranes (1, 2). The dimer formation and strong interdimer stacking would contribute to the red shift and broadening of the Q_y band mainly caused by Q_y–Q_y dipolar couplings, leading to more efficient absorption of solar light of longer wavelength than BChl c monomers. Chlorosomes containing the cylinders have a size much larger than the exciton in length. Thus chlorosomes can accommodate multiplex excitons generated efficiently for their size. These structural elements make chlorosomes useful antennas for capturing weak light (3).

The rod element structure has spiral layers as shown in Fig. 5B. The Q_y transition dipole of BChl c that governs the excitation transfer is almost parallel to the layers. This arrangement would transfer the excitation preferably along the spiral layers as theoretically shown for a cylinder consisting of monomer layers (33). The cylinder we proposed is built from dimers having antiparallel Q_y transition dipoles as shown by arrows in Fig. 5B. An analogous BChl arrangement is found in the inner ring B850 of an LH2 antenna complex from the purple bacterium Rhodopseudomonas acidophila (2). The inner ring consists of nine dimeric BChl a units with antiparallel Q_y dipoles (1, 35). The B850 ring and the spiral layer have similar Mg–Mg distances of ≈9.5 Å and Q_y dipole orientations. The excitation is transferred in LH2 on a subpicosecond time scale mainly by the exciton mechanism (35–38). This similarity in the arrangement of Q_y transition dipoles also supports the rapid excitation transfer along the spiral layers. Such fast excitation transfer along the spiral layer expedites the interrod transfer to BChl a in baseplates, leading to the reaction centers, as shown in Fig. 5C (7, 32, 39).

In conclusion, a high-resolution molecular structure of the BChl c assembly in the chlorosome was determined by ¹³C dipolar correlation solid-state NMR. The chlorosome structure built with the assembly provided insights into light harvesting under low-density photons: the high-density cylindrical arrangement of BChls c enables both efficient light absorption and excitation transfer to the reaction centers. The high-density cylindrical arrangement makes the pigment architecture completely different from those in light-harvesting protein complexes. The similar arrangements of Q_y transition dipoles for the assembly in chlorosomes and the B850 ring in LH2, however, suggest a common excitation transfer mechanism in the two systems. The present study marks important advances in both the atomic structure analysis of the BChl c assembly and solid-state NMR methodology. Quantitative distance analysis of the spin diffusion in solid-state NMR was shown to be a powerful method for structure determination of huge intact systems that cannot be crystallized.

Methods

Preparation of Uniformly ¹³C-Labeled Chlorosomes.

C. limicola f. sp. thiosulfatophium was grown at 27°C in a tank illuminated with two 20-W fluorescent neon lamps under anaerobic conditions (40). All of the carbons were uniformly ¹³C-labeled with NaH¹³CO₃ (99% ¹³C; MassTrace, Woburn, MA) in growth medium. The cells were washed with a buffer solution (10 mM KH₂PO₄/10 mM sodium l-ascorbate/2 M NaSCN) at pH 7.4 and then disrupted three times with a French press. The supernatant was purified by sucrose density gradient centrifugation according to the reported method (41). We collected the fraction that gave no absorption bands for the Fenna–Matthews–Olson (FMO) protein, the BChl a protein, and BChl c monomers, as crude chlorosomes. It was diluted with 50 mM Tris·HCl buffer and then centrifuged to remove sucrose and FMO protein. The pellet of intact chlorosomes was transferred to a 4-mm MAS rotor.

NMR Experiments.

NMR spectra were recorded on an Infinity-plus 500 spectrometer (Varian, Palo Alto, CA) equipped with a double-resonance MAS probe for a 4-mm rotor at a ¹³C resonance frequency of 125.7 MHz. 2D rf-driven recoupling (21) and SPC-5 (22) ¹³C¹³C dipolar correlation spectra and 2D proton-driven ¹³C spin-diffusion spectra (23, 24) were recorded under MAS at 10°C. The sample spinning frequency was 12.5 kHz (11.0 kHz for SPC-5) within a precision of 10 Hz. The details are given in SI Text.

Polarization-Transfer Matrix Analysis for Distance Constraints.

Spin-diffusion spectra were analyzed to obtain ¹³C¹³C distances. Signal intensity matrices were constructed from the volume intensities of cross-peaks in the spin-diffusion spectra. These matrices were fitted to Eq. 1. Overlapping signals were deconvoluted to measure the intensities. The polarization-transfer matrix, R, 30 × 30 in size, was determined with a FORTRAN program for the nonlinear least-squares method by using the Levenberg–Marquardt algorithm. The initial R was estimated linearly from experimental signal intensities with a short mixing time (25).

Conversion to Distances.

Distance constraints were determined from R_j,k as described in Results. The zero-quantum lineshape function was calculated as

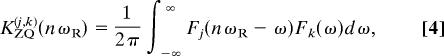where F_j(ω) is the single-quantum (SQ) dipolar lineshape function of spin j under CH couplings. The linewidths for F_j(ω) were determined primarily from the experimental SQ lineshapes obtained with a 2D chemical-shift resolved CH dipolar spectrum (26).

Structural Calculations.

The structures were calculated for 18 (3¹R)-, 8-propyl, 12-ethyl-BChl c molecules by using the standard simulated-annealing protocol, anneal.inp, in CNX (Accelrys, San Diego, CA) (42). When the complex is formed from 18 molecules, the molecules in the central part can be surrounded by other molecules so as to satisfy the distance constraints at a backbone rmsd of 0.2 Å, as shown in Table 1. Thus a further increase in the number of molecules would not improve the accuracy of the structure in the central part. The potentials for BChl c were defined by referring to parameter files for chlorophyll a stored in the Hetero-compound Information Center (Uppsala University, Uppsala, Sweden) (43) and CHARMm (44). The oxygen of 3¹-OH was assumed to coordinate to the Mg atom of a neighboring molecule at a distance of <2.7 Å. In the parallel-dimer layers, the hydrogen-bond distance between 13¹O and 3¹-O(H) was restricted to 2.7–2.8 Å, and that between 13¹O and 3¹-(O)H to 1.7–1.8 Å in the final stage. Structural parameters were obtained from the stacking molecules in the central part in the optimized assembly structure consisting of 18 molecules. The details are given in SI Text. The graphics in Figs. 4 E–H and 5 were prepared with RASMOL (45).

Abbreviations

BChl

bacteriochlorophyll

MAS

magic angle spinning.