Photoselected electron transfer pathways in DNA photolyase

Abstract

Cyclobutane dimer photolyases are proteins that bind to UV-damaged DNA containing cyclobutane pyrimidine dimer lesions. They repair these lesions by photo-induced electron transfer. The electron donor cofactor of a photolyase is a two-electron-reduced flavin adenine dinucleotide (FADH⁻). When FADH⁻ is photo-excited, it transfers an electron from an excited π → π* singlet state to the pyrimidine dimer lesion of DNA. We compute the lowest excited singlet states of FADH⁻ using ab initio (time-dependent density functional theory and time-dependent Hartree–Fock), and semiempirical (INDO/S configuration interaction) methods. The calculations show that the two lowest π → π* singlet states of FADH⁻ are localized on the side of the flavin ring that is proximal to the dimer lesion of DNA. For the lowest-energy donor excited state of FADH⁻, we compute the conformationally averaged electronic coupling to acceptor states of the thymine dimer. The coupling calculations are performed at the INDO/S level, on donor–acceptor cofactor conformations obtained from molecular dynamics simulations of the solvated protein with a thymine dimer docked in its active site. These calculations demonstrate that the localization of the ¹FADH⁻* donor state on the flavin ring enhances the electronic coupling between the flavin and the dimer by permitting shorter electron-transfer pathways to the dimer that have single through-space jumps. Therefore, in photolyase, the photo-excitation itself enhances the electron transfer rate by moving the electron towards the dimer.

Cyclobutane pyrimidine dimer (CPD) photolyases bind to CPD lesions of UV-damaged DNA and repair them by photo-induced electron transfer (ET) (see refs. 1–3 for reviews). The electron donor cofactor of a photolyase is a two-electron-reduced flavin adenine dinucleotide (FADH⁻). FADH⁻ transfers an electron to the protein-bound CPD lesion of DNA upon photo-excitation with 350- to 450-nm light. This ET step initiates the cleavage of the dimer bonds and the repair of the lesion (conversion to two pyrimidine monomers). FADH⁻ can be excited either directly by absorption of a photon, or indirectly from the chromophore cofactor of photolyase. The latter acts as an antenna molecule, absorbing light and transferring its energy to FADH⁻ via dipole–dipole interactions. The chromophore is either methenyltetrahydrofolate in folate class photolyases or 8-hydroxy-7,8-didemethyl-deazariboflavin (8-HDF) in deazaflavin class photolyases.

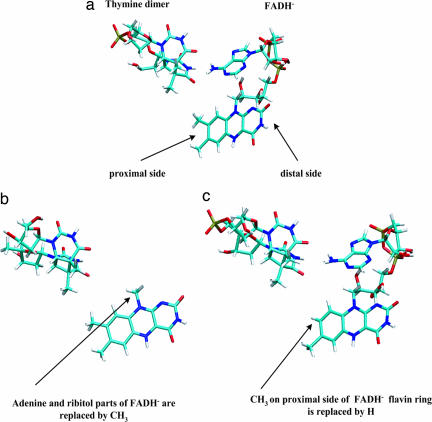
Structures of both folate and deazaflavin class photolyases are known from x-ray crystallography (4–6). Only the most recent structure is a complex between the photolyase and DNA (a DNA oligomer that contains a cyclobutane thymine dimer analog; ref. 6). The protein is bound to the DNA oligomer at the location of the dimer lesion, and the dimer lies inside the protein's active site [a binding mode also suggested by biochemical, fluorescence, and NMR experiments (1–3, 7–9), and investigated in several computational studies (10–14)]. In the active site, the dimer is adjacent to FADH⁻ (6). The C4 carbonyl groups of the dimer's 5′-T and 3′-T form hydrogen bonds with the amino N6 of the adenine portion of FADH⁻. Furthermore, the C4 carbonyl in 3′-T is adjacent to the C8 methyl group of the flavin moiety of FADH⁻ (4 Å) (Fig. 1a).

Fig. 1.

Diagram showing donor and acceptor molecular structures. (a) Pyrimidine dimer–FADH⁻ geometry taken from an MD snapshot of solvated E. coli photolyase with a thymine dimer docked in the active side. (b) The modified flavin cofactor obtained by deleting the ribytol and adenine moieties of FADH⁻ and replacing them by a methyl group at the C1′ position. (c) The modified flavin cofactor obtained by deleting the C8 methyl group on the proximal side of the flavin ring with a hydrogen.

The ET reaction that initiates dimer repair, ${}^1\text{FADH}^{-\ast }+\text{Pyr-Pyr}\stackrel{e-}{\to }{\text{FADH}}^{·}+{\text{Pyr-Pyr}}^{·-}$, involves the transfer of an electron from an excited singlet π → π* state of FADH⁻, at a rate of the order of 100⁻¹ psec⁻¹. Stuchebrukhov and coworkers (13, 14) performed detailed analysis of this ET reaction mechanism. Using docking and molecular dynamics simulations, they predicted the location of the dimer relative to FADH⁻ that was later observed in the crystal structure (6). They also calculated the electronic structure of the donor and acceptor states of the FADH⁻–dimer system, and the donor–acceptor electronic coupling, using the extended-Hückel method and tunneling current analysis (15). They predicted that ET takes place by a tunneling mechanism that does not involve protein (non-FADH⁻) intermediates. The experimental evidence supports this mechanism (see refs. 1–3 for reviews).

In refs. 13 and 14, the π → π* electron donor state of FADH⁻* was taken to be the (extended-Hückel) lowest occupied molecular orbital (LUMO) of the flavin ring. This LUMO has most of its electron amplitude localized on atoms C4, O4, and C10, i.e., on the side of the ring that is furthest away from the dimer (hereby denoted the distal side, Fig. 1a). For this donor state, the computed rms tunneling matrix element is on the order of 10⁻³ eV. Furthermore, tunneling current calculations showed that the main ET path to the dimer begins in the C4, C10, N10 region of flavin, continues with a through-space jump to the adenine ring (from C1′–H of flavin to C6–N6 of adenine), and ends with a second through space jump from the adenine to the dimer (N6 of the adenine ring to the C4 carbonyl groups of 5′-T and 3′-T in the dimer) (13, 14). Therefore, the adenine ring is described as acting as a superexchange bridge between the distal side of the flavin moiety of FADH⁻ and the dimer lesion (13, 14).

Here, we reexamine the subject of the donor-state localization on the flavin ring, and we investigate how this localization influences the flavin–dimer electronic coupling and the ET pathways. We first compute the lowest excited singlet states of FADH⁻ using ab initio [time-dependent Hartree–Fock (TDHF) (16) and time-dependent density functional theory (TDDFT) (17, 18)], and semiempirical (INDO/S configuration interaction; refs. 19 and 20) methods. The calculations show that the lowest π → π* singlet states of FADH⁻ that are localized on the flavin moiety have most of their amplitude on the benzene side of the flavin ring, adjacent to the dimer (hereby denoted the proximal side, Fig. 1a). To analyze the electronic coupling between FADH⁻ and the dimer, we compute the conformationally averaged tunneling matrix elements between empty dimer orbitals and the donor state of FADH⁻ (the lowest π → π* singlet state). The coupling calculations are performed at the INDO/S level using MD simulations of the protein with a thymine dimer docked in its active site.

To explore the structure of the ET pathways between the donor and the dimer acceptor states, we also perform tunneling matrix element calculations using modified flavin cofactors as donor molecules, constructed by pruning FADH⁻. The modifications of FADH⁻ are performed in such a way so as to erase either adenine mediated ET pathways (that always contain at least two through-space jumps) or the more direct C8-methyl mediated pathways (that contain one through-space jump). In one kind of structure modification, the ribytol and adenine moieties of FADH⁻ are deleted and replaced by a methyl group at the C1′ position (Fig. 1b). These deletions eliminate all ET pathways through the adenine ring. In the other kind of modification, we replace the C8 methyl group on the proximal side of the flavin ring with a hydrogen (Fig. 1c). The hydrogen atoms of the C8 methyl group are close to the C4 carbonyl of 3′-T of the dimer (Fig. 1a). Therefore, their deletion diminishes the strength of the direct ET pathways between the flavin and the dimer that contain single through space jumps.

We find that the above chemical modifications of FADH⁻ do not appreciably change the character and relative energies of the lowest π → π* singlet states of the flavin ring. Therefore, we use the same type of electron donor state for the modified cofactors as we did for the full FADH⁻ (i.e., the lowest singlet π → π* state of the flavin ring localized on its proximal side). Furthermore, the conformational averaging of the tunneling matrix elements for the modified cofactors is performed using MD snapshots created as follows. For each snapshot of the FADH⁻–dimer subsystem obtained from the original protein–dimer simulations, we delete the FADH⁻ atoms and perform the atom replacements described above (Fig. 1) without perturbing the positions of the remaining FADH⁻ atoms, nor the conformation of the adjacent dimer. Therefore, the conformationally averaged matrix elements with the flavin cofactor of Fig. 1b used as the donor are computed using dimer–flavin ring trajectories that are identical to the dimer–ring trajectories of the original simulations. A similar approach is used for the other cofactor (Fig. 1c), in which case the MD trajectories used to compute matrix element averages differ from the full FADH⁻–dimer trajectories only for four atoms (the C8 methyl group). For FADH⁻ and the modified flavin cofactors, we analyze the magnitudes of the donor–acceptor coupling fluctuations in terms of the coherence parameter (21–24).

Results and Discussion

Excited-State Electronic Structure Calculations.

The aim of the excited-state calculations is to identify the lowest π → π* singlet state of FADH⁻, which we take to be the electron–donor state for the ET reaction: ${}^1\text{FADH}^{-\ast }+\text{Pyr-Pyr}\stackrel{e-}{\to }{\text{FADH}}^{·}+{\text{Pyr-Pyr}}^{·-}$. Because of the large size of FADH⁻ and the need to calculate its excited states in different geometries, it is practical to use single-reference quantum-chemical methods (25, 26). These include TDDFT, TDHF theory, and semiempirical methods (such as INDO/S configuration interaction singles, CIS). To gauge the reliability of our calculations, we used all of these methods and sought robust predictions. We performed the electronic-structure calculations on several molecular geometries derived from different protein–FADH⁻–dimer MD conformations. Furthermore, each calculation was performed in the solvation environment of the protein's active site (including active site residues, water, and the thymine dimer), whose total charge was varied.

In the 300- to 500-nm range, the observed absorption spectrum of Escherichia coli photolyase with only the FADH⁻ cofactor (no methenyltetrahydrofolate chromophore; ref. 1) has a maximum of ε ≈ 3 × 10⁴ (M⁻¹ cm⁻¹) at λ = 300 nm, dropping to a minimum value of ε_min ≈ 5 × 10³ (M⁻¹ cm⁻¹) at λ_min ≈ 340 nm. For longer wavelengths, the absorption spectrum has a secondary maximum of ε_max ≈ 6–7 × 10³ (M⁻¹ cm⁻¹) at λ_max ≈ 365 nm. Absorption vanishes as λ approaches 500 nm. Because we are only interested in the lowest singlet excited state of FADH⁻, the relevant region of the spectrum for our calculations is the low-maximum region centered at λ_max ≈ 365 nm.

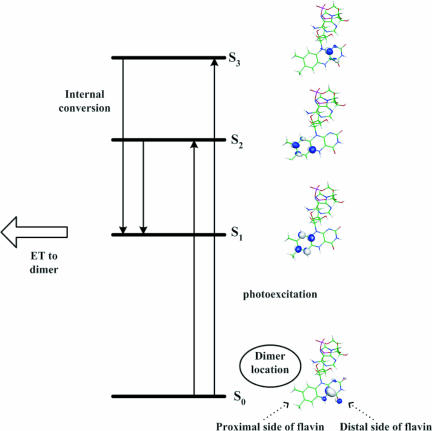
The INDO/S calculations predict that the two lowest singlet excited states of FADH⁻ (S₁ and S₂ of Fig. 2) are of π → π* character, and they involve the displacement of electron amplitude from the distal side to the proximal side of the flavin ring. S₁ and S₂ have dipole moments 12.9 D and 13.1 D relative to ground state, respectively. At higher energies, there is also a π → π* singlet excited state (S₃ in Fig. 2) that retains the electron amplitude on the distal side of the flavin ring (with dipole moment of 1.6 D relative to the ground state), and π → π* states that displace electron amplitude from the distal side of the flavin ring to the adenine ring. S₁ has negligible oscillator strength and cannot be related to the experimental absorption spectrum. S₂ has observable oscillator strength and an absorption wavelength slightly beyond the low maximum of the experimental spectrum (predicted f = 2–3 × 10⁻¹, λ = 390–400 nm). S₃ has the highest oscillator strength and absorption wavelength smaller than λ_min ≈ 340 nm (predicted f = 4.0–4.5 × 10⁻¹, λ = 320–330 nm). The flavin to adenine π → π* states have negligible oscillator strengths. The ranges of the reported wavelength and oscillator-strength values reflect different results from the MD snapshots and the total solvation charges that were tested. The INDO/S calculations allow us to identify the low maximum in the experimental absorption spectrum with the S₂ excited state, because the predicted wavelengths for S₂ are the closest to the experimental λ_max ≈ 365 nm among the S_n wavelengths. Importantly, the INDO/S oscillator strength of S₂ for the majority of the FADH⁻ MD conformations (f = 0.2) corresponds to ε ≈ 6 × 10³ (M⁻¹ cm⁻¹), which is approximately the experimental value of ε_max ≈ 6–7 × 10³ (M⁻¹ cm⁻¹).

Fig. 2.

Diagram showing photo-excitation of the ¹FADH⁻ ground state to the ¹FADH⁻* S₂ and S₃ excited states. Relaxation to the lowest ¹FADH⁻* S₁ excited state is followed by ET to the dimer.

The TDDFT/BHandHLYP calculations compute the 10 lowest singlet excited states of FADH⁻. They predict flavin-flavin π → π* excitations that are similar to the INDO/S S₁ and S₂, and low-lying flavin-adenine π → π* excitations (the S₃ type state lies beyond the energy range of the 10 lowest singlets). For S₁ and S₂, the TDDFT wavelengths are slightly smaller (by 10–20 nm) than the INDO/S values. The oscillator strength for S₂ is of the order of 10⁻¹ (as in INDO/S), and the strengths for S₁ and the flavin–adenine excitations are negligible. TDHF greatly underestimates the absorption wavelengths (this is a known shortcoming of the method; ref. 25).

In conclusion, Fig. 2 summarizes the state scheme for the lowest flavin–flavin π → π* excitations of solvated FADH⁻ that emerges from the semiempirical and ab initio TDDFT calculations, and is consistent with the experimental absorption spectrum of FADH⁻ in photolyase. This scheme is also consistent with early semiempirical analysis of flavin spectra and with flavin spectroscopic data (refs. 27–29 and references therein). The excitations shown in Fig. 2 are properties of the flavin moiety of FADH⁻, and they are not determined by the solvation environment of the protein active site (we observe the same state ordering and electron localization for the modified cofactors of Fig. 1 b and c, and for FADH⁻ in vacuum).

Upon photo-excitation, we expect that the high-oscillator-strength S₂ and S₃ states will be populated, with S₃ having greater population than S₂. The rate of the photo-induced ET reaction is ≈200⁻¹ psec⁻¹ (30). For excited states with highly overlapping vibrational levels, (as in the flavin-localized excited states), the time scale of S_n → S₁ relaxation is of the order of 1 psec or less. There is evidence from time-resolved absorption and fluorescence experiments on flavin compounds (31, 32) that the internal conversion rate in the π* singlet excited state manifold is a few hundred femtoseconds to 1 psec. Therefore, before ET, we expect that the donor excited state has relaxed to S₁ and is localized on the proximal side of the flavin ring, adjacent to the dimer.

The observation in our calculations of low-lying flavin–adenine π → π* singlet excited states raises the question of whether the donor electron density may be localized on the adenine ring before the ET reaction to the dimer. Because the oscillator strength of these states are very low compared to S₂ and S₃, we do not expect appreciable population of the adenine ring upon photo-excitation. Adenine can only be populated if it accepts the excited electron from the flavin (i.e., through a resonant tunneling or hopping mechanism) before ET from FADH⁻ to the dimer. Recent femtosecond time-resolved spectroscopy of the ET reaction ${}^1\text{FADH}^{-\ast }+\text{Pyr-Pyr}\stackrel{e-}{\to }{\text{FADH}}^{·}+{\text{Pyr-Pyr}}^{·-}$ in E. coli photolyase has excluded this possibility (30). There is no observation of ET to adenine in that experiment, even in the absence of the dimer. The absence of a real adenine intermediate supports the prediction of Stuchebrukhov and coworkers (13, 14) that ET takes place by a single superexchange step.

Tunneling Matrix Element Calculations.

Having concluded that the electron donor state for the photo-induced ET reaction is localized on the proximal side of the flavin ring, we now explore how this state couples to the dimer electron-accepting orbitals. The donor–acceptor electronic coupling may arise from the tunneling matrix element between the donor state and any empty thymine dimer state that becomes nearly resonant with the donor state.

As mentioned in the Introduction, we examined three donor cofactors (the full FADH⁻ molecule and the modified cofactors of Fig. 1). For each cofactor, and for the different donor molecular orbital (MO)–acceptor MO pairs, we computed the conformational averages 〈T_DA〉 and 〈T_DA²〉, using dimer-FADH⁻ MD snapshots from the MD simulations of photolyase with the thymine dimer docked in its active site. The computations of the tunneling matrix element were performed at the INDO/S level, and were based on Green's function (33) and energy splitting methods (34). In all computations with the Green's function approach, we examined the tunneling energy dependence of our results.

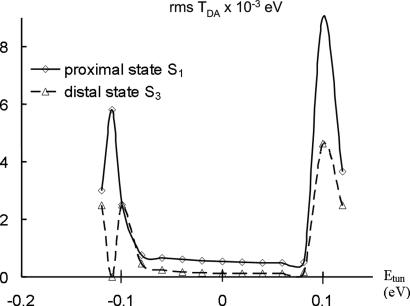
Fig. 3 is derived from a thymine dimer–full FADH⁻ calculation, where we show the tunneling-energy dependence of $T_{DA}^{(rms)}=\sqrt{\langle T_{DA}^2\rangle }$ for two different choices of the donor state: first, the excited MO of S₁ (proximal side of the flavin) and second, the excited-MO of S₃ (distal side of flavin) (see Fig. 2). Although we propose that S₁ is the actual donor for the ET reaction ${}^1\text{FADH}^{-\ast }+\text{Pyr-Pyr}\stackrel{e-}{\to }{\text{FADH}}^{·}+{\text{Pyr-Pyr}}^{·-}$, we use both MOs as donors in order to probe the tunneling-energy dependence of the coupling and to locate bridge resonances. T_DA is calculated with the Green's function method and the conformational averages of the coupling are computed from 100 MD snapshots separated by 1-psec time intervals. Furthermore, for each donor MO, the plotted T_DA^(rms) values are averages of four T_DA^(rms) values involving different acceptor MOs. The four acceptor MOs are empty orbitals of the thymine dimer that are closest in energy to the donor orbital. The solid line in the plot refers to the S₁ donor and the dotted line to S₃. For a wide range of tunneling energies, each T_DA^(rms) remains approximately constant. Sharp changes in T_DA^(rms) are observed only around E_tun ≈ ±0.1 eV, but these E_tun regions are not physically relevant because the D and A MO energies in the MD simulations fluctuate within the flat region of the plot [the sharp increase in T_DA^(rms) at E_tun ≈ ±0.1 eV indicates that these E_tun values are near-resonant with bridge electronic states]. The flat behavior of T_DA^(rms) in the physically relevant energy range, regardless of the localization of the donor state on the flavin, is consistent with a tunneling mechanism for the ET step from the flavin to the dimer. Fig. 3 also shows that T_DA^(rms) for the proximal D state (S₁) is about four times greater than T_DA^(rms) for the distal D state (S₃) for all tunneling energies in the physical range. This difference in T_DA^(rms) magnitudes reflects the different localizations of the S₁ and S₃ states with respect to the thymine dimer.

Fig. 3.

The tunneling energy dependence of $T_{DA}^{(rms)}=\sqrt{\langle T_{DA}^2\rangle }$ for two different choices of donor state: the excited MO of S₁ (proximal side of flavin), and the excited MO of S₃ (distal side of flavin), both shown in Fig. 2.

We now analyze the electronic coupling pathways between the proposed donor state for the photo-induced ET reaction (S₁ of Fig. 2) and the thymine dimer acceptor states. The semiempirical and ab initio calculations described above showed that there are low-energy adenine-localized virtual MOs that could act as superexchange bridge orbitals that couple the donor and the acceptor states. We investigate this possibility by comparing the electronic couplings computed using the full FADH⁻ molecule (Fig. 1a) to the couplings computed using the modified cofactors shown in Fig. 1 b and c.

Table 1 shows T_DA^(rms) and the coherence parameter R_coh = 〈T_DA〉²/〈T_DA²〉 values for the thymine dimer–full FADH⁻ cofactor pair (R_coh measures the magnitude of the coupling fluctuations compared to the average coupling; ref. 21). The values of T_DA^(rms) and R_coh shown in the table are averages over four D–A MO pairs where the D MO is the π* orbital of S₁ (Fig. 2), and the A MOs are empty orbitals of the thymine dimer that are closest in energy to D. T_DA is computed using the Green's function method with E_tun equal to 0.04, 0.06, and 0.08 eV. These values of E_tun correspond approximately to the average energies of the D–A pairs mentioned above, and they are located in the flat region of Fig. 3. The T_DA^(rms) and R_coh averages were computed using 100 MD snapshots separated by 1 psec time intervals (similar values for T_DA^(rms) were obtained by averaging over 100 MD snapshots separated by 1 fsec time intervals). The results in Table 1 show that the rms tunneling matrix element between the proximal D state and the thymine dimer is of the order 5 × 10⁻⁴ eV. Further, the coherence parameter is less than 0.1, indicating large fluctuations of the tunneling matrix element with respect to structural changes (i.e., σT_DA ≫ 〈T_DA〉).

Table 1.

rms T_DA and coherence parameter for the dimer with full FADH⁻ (Fig. 1a)

Etun, eV	TDA(rms), eV	Rcoh
0.08	5.11 × 10−4	0.075
0.06	4.78 × 10−4	0.056
0.04	4.83 × 10−4	0.049

$T_{DA}^{(rms)}=\sqrt{\langle T_{DA}^2\rangle }$ and R_coh = 〈T_DA〉²/〈T_DA²〉 for the thymine dimer–FADH⁻ pair (Fig. 1a) as a function of tunneling energy (Green's function method). T_DA^(rms) computed with the energy splitting method is 2.76 × 10⁻⁴ eV.

Tables 2 and 3 show T_DA^(rms) and R_coh for the thymine dimer with the modified flavin cofactors of Fig. 1 b and c, respectively. The D orbitals used in these calculations are very similar to S₁ in Fig. 2, (the calculations are based on the Green's function method). A comparison of T_DA^(rms) for the thymine dimer–FADH⁻ system (Table 1) to T_DA^(rms) for the thymine dimer-modified flavin cofactor systems (Tables 2 and 3) shows that the tunneling matrix element for the proximal donor state is not much affected by the deletion of the adenine-mediated pathways (Table 2). It is, however, reduced by a factor of 4–5 by the deletion of the methyl-mediated pathways (Table 3). These observations indicate that the electronic coupling between the proximal donor state of FADH⁻ and the dimer acceptor states is mediated mostly by the C8 methyl group that is on the proximal side of the flavin ring, next to the dimer. The proximity of the excited donor state to the C8 methyl group results in the adenine moiety not being an essential mediator of the donor–acceptor electronic coupling.

Table 2.

rms T_DA and coherence parameter for the dimer with the cofactor of Fig. 1b

Etun, eV	TDA(rms), eV	Rcoh
0.08	5.16 × 10−4	0.07
0.06	5.48 × 10−4	0.03
0.04	5.74 × 10−4	0.04

$T_{DA}^{(rms)}=\sqrt{\langle T_{DA}^2\rangle }$ and R_coh for the system of Fig. 1b (Green's function method). T_DA^(rms) computed with the energy splitting method is 2.5 × 10⁻⁴ eV.

Table 3.

rms T_DA and coherence parameter for the dimer with the cofactor of Fig. 1c

Etun, eV	TDA(rms), eV	Rcoh
0.08	1.28 × 10−4	0.09
0.06	1.13 × 10−4	0.03
0.04	1.15 × 10−4	0.03

T_DA^(rms) and R_coh for the system of Fig. 1c (Green's function method). T_DA^(rms) computed with the energy splitting method is 8.93 × 10⁻⁵ eV.

The three systems in Tables 1–3 have essentially the same donor–acceptor MO pairs and average donor–acceptor distances but different ET pathways and electronic couplings. Their coherence parameters R_coh = 〈T_DA〉²/〈T_DA²〉 are very small (<0.1). If we increase the donor–acceptor distance by changing the nature of the donor state (by choosing as D the excited MO of S₃ in Fig. 2), the ET pathways change and T_DA^(rms) is reduced. However R_coh remains the same order of magnitude as before. The small value of the coherence parameter in these systems indicates large fluctuations in the donor–acceptor electronic coupling with geometry. In all cases considered, both the donor state and the thymine acceptor state are delocalized over several atoms that are “connected” by through space interactions. This geometry gives rise to multiple rapidly fluctuating pathways that can interference destructively and constructively depending on subtle aspects of the molecular conformation. The changing interference patterns caused by molecular motion lead to large fluctuations in the tunneling matrix element. The small R_coh values observed for FADH⁻–dimer ET in photolyase are similar to those reported for solvent-mediated ET reactions in small C-clamped molecules (22), for ET in azurin (23), and for the BPh → Q_A ET reaction in the bacterial photosynthetic reaction center (24). The common feature of these different ET systems is the existence of multiple destructively interfering pathways that include through space and hydrogen bond couplings.

Conclusions

We have used molecular dynamics simulations and electronic structure analysis to show that the excited donor state associated with the ET reaction ${}^1\text{FADH}^{-\ast }+\text{Pyr-Pyr}\stackrel{e-}{\to }{\text{FADH}}^{·}+{\text{Pyr-Pyr}}^{·-}$ in E. coli DNA photolyase is localized on the side of the FADH⁻ flavin ring proximal to the pyrimidine dimer. The localization of the donor excited state enhances the donor–acceptor coupling and the direct through-space ET pathways between FADH⁻ and the dimer. Our calculations indicate that the donor–acceptor coupling is of the order of 5 × 10⁻⁴ eV. If we assume that the ET reaction is activationless (14, 15) with a reorganization energy of ≈1 eV, the predicted room temperature ET rate is 230⁻¹ psec⁻¹. This value is close to the experimental rate of (170 psec)⁻¹ for ET to a thymine dimer lesion (in E. coli photolyase; ref. 30). It should be noted, however, that it is difficult to estimate the reorganization energy of the reaction because there is substantial solvent reorganization of the active site upon photo-excitation (30).

The donor state used here is assumed to be the lowest-energy π → π* singlet localized on the flavin ring of FADH⁻ (as experiment excludes localization on adenine; ref. 30). Higher π → π* singlet states that are populated upon photo-excitation are expected to relax rapidly to this state. The lowest flavin π → π* singlet of FADH⁻ involves a large displacement of electron density across the flavin ring, from the pyrimidine to the benzene ring side adjacent to the docked thymine dimer. This type of transition is consistent with the experimental absorption spectrum of E. coli photolyase, and it is a property of the flavin ring that is not altered by the protein environment surrounding FADH⁻. The electron-density displacement upon photo-excitation creates a large dipole moment that should cause substantial solvent reorganization of the active site. Recent time-resolved experiments have observed such photo-induced solvent reorganization (30).

For the proposed donor state, we performed ET pathway analysis on a large number of MD conformations to see whether the adenine moiety of FADH⁻ acts as a virtual intermediate for the ET step. We found that the adenine is not essential to tunneling because an electron of the excited state on the benzene side of the ring can tunnel to the dimer through the adjacent C8-methyl group that is in direct through-space contact with the dimer. It is difficult, however, to completely rule out superexchange contribution from adenine, because low-probability conformational fluctuations may provide secondary superexchange pathways through this moiety. We believe that a more important role for the adenine moiety in FADH⁻ is to stabilize the observed dimer–FADH⁻ conformation sterically inside the active site, and to anchor the dimer to FADH⁻ by forming adenine–dimer hydrogen bonds (6, 30). This stabilized conformation places the dimer next to the benzene side of the flavin ring. Therefore, the protein can utilize the electron displacement characteristic of the lowest flavin π → π* transition to direct the electron towards the dimer and to enhance the donor–acceptor coupling.

Computational Methods

MD Simulations.

The MD simulations were performed on E. coli photolyase (Protein Data Bank ID code 1DNP; ref. 4). The initial conformation of the docked thymine dimer in the protein active site was obtained from refs. 13 and 14. In all MD simulations, we used the Amber 8.0 program (35, 36) and the AMBER force field (37). The dimer and FADH⁻ partial charges were calculated at the Hartree–Fock level using Gaussian 98 (38) and a 6–31 G(d) basis set. Partial charges were fitted using the RESP procedure (39–41). For FADH⁻ and the thymine dimer Amber force-field potential types were assigned in the same manner as in refs. 10 and 11. The MD was performed with a constant pressure (NpT) ensemble, Langevin thermostat, periodic boundary conditions, and full electrostatics particle mesh Ewald calculation (42). The structure was solvated with a TIP3P water box of dimensions 95 × 75 × 75 A. Na⁺ ions were added to neutralize the system. Crystallographic water molecules within 5 Å of FADH⁻ were retained. After initial energy minimization of 5,000 steps, with harmonic constraints imposed on the protein backbone and on the FADH⁻ and dimer heavy atoms, we followed with 300-psec MD using the same harmonic constraints. The structure was then equilibrated for 500 psec at 300 K without constraints. After the equilibration procedure, MD was performed for 100 psec. During the production run, the relative positions of FADH⁻ and the dimer were stable, and the rmsd fluctuations were within 1 Å. Conformational snapshots were saved every 1 psec.

Excited-State Electronic Structure Calculations.

FADH⁻ contains π-electrons in regions of space that are spatially separated, i.e., at the opposite sides of the flavin ring (distal and proximal sides in Fig. 1a), and in the adenine moiety. Therefore, some of its π → π* excitations may contain charge transfer (CT) character. Generally, for CT excitations of extended π-systems, single-reference ab initio methods can be inaccurate (e.g., refs. 25, 26, and 43–45). In many cases, a semiempirical method parameterized for excited states, such as INDO/S CIS, may be a dependable approach for the computation of the energy spectrum in a large molecule (e.g., refs. 43 and 44). To gauge the reliability of our calculations, we used all of the methods above, INDO/S CIS, TDDFT, and TDHF, and sought robust predictions.

For FADH⁻, we performed the electronic structure calculations on several molecular geometries derived from different protein–FADH⁻–dimer MD conformations (separated by 20–80 psec). Each calculation was performed both in vacuum and in the solvation environment of the protein's active site (represented by Amber force-field atomic charges). The solvation environment included the active site residues 222, 234–239, 271, 338, 341, 344, 372, 374, and 378 of E. coli photolyase, the thymine dimer, 47 water molecules, and Na⁺ ions used for charge neutralization in MD. The Na⁺ ions were used in the electronic structure calculations to vary the total charge of the system so that FADH⁻ is either fully neutralized (total charge 0), or it has an effective charge of −1 (total charge −1). Finally, to probe the effect of the adenine moiety on the π → π* excitations of FADH⁻ that are localized on the flavin ring, we also performed the ab initio and semiempirical calculations on the modified flavin cofactor of Fig. 1b that does not contain the ribytol and adenine moieties. For the INDO/S CIS calculations, we used the program of ref. 46, and for the ab initio calculations, we used the program Gaussian03 (47). The dipole moments of the FADH⁻ ground state and of the singlet excited states denoted S₁, S₂, and S₃ were calculated using the program of ref. 46.

The TDDFT and TDHF calculations computed the 10 lowest singlet excited states of FADH⁻ using the 6–31+G(d) basis set. Compared to the B3LYP functional (48, 49), the BHandHLYP functional (50) gave the most dependable results, predicting absorption wavelengths close to the INDO/S values that were robust with respect to changes in molecular size (i.e., FADH⁻ versus the flavin cofactor of Fig. 1b).

Tunneling Matrix Element Calculations.

The electronic-coupling calculations were performed at the INDO/S level using the Harlem program (51) and two different computational approaches. In one approach (the “Green's function method”), the tunneling matrix element between the donor MO (D) and the acceptor MO (A) is T_DA(E_tun) = {E_tunS̃ − G̃(E_tun)⁻¹}_D,A, where G̃ (S̃) is the Green's function (overlap) matrix for the entire donor–acceptor cofactor system, and E_tun is the tunneling energy (33). In the other approach (the “energy splitting method”), the donor and acceptor MOs are brought into resonance by application of an external electric field Ē along the donor–acceptor axis (34). The eigenvalues/vectors of the Hamiltonian are computed as a function of the electric-field strength in order to identify minimum energy splittings between eigenvalues (at resonances between coupled MOs). T_DA is taken as half the minimum energy splitting created by the resonance of the eigenstates that originate from the initial donor and acceptor MOs. We also performed exploratory INDO/S calculations of T_DA for several snapshot geometries using the generalized Mulliken–Hush (GMH) approach (52). This analysis indicates that the electronic couplings calculated with the Green's function method and the GMH method are very similar.

Abbreviations

TDHF

time-dependent Hartree-Fock

TDDFT

time-dependent density functional theory

CIS

configuration interaction singles

ET

electron transfer.