Inferring the Cellular Origin of Voltage and Calcium Alternans from the Spatial Scales of Phase Reversal during Discordant Alternans

Abstract

Beat-to-beat alternation of the action potential duration (APD) in paced cardiac cells has been linked to the onset of lethal arrhythmias. Both experimental and theoretical studies have shown that alternans at the single cell level can be caused by unstable membrane voltage (V_m) dynamics linked to steep APD-restitution, or unstable intracellular calcium (Ca) cycling linked to high sensitivity of Ca release from the sarcoplasmic reticulum on sarcoplasmic reticulum Ca load. Identifying which of these two mechanisms is the primary cause of cellular alternans, however, has remained difficult since Ca and V_m are bidirectionally coupled. Here, we use numerical simulations of a physiologically detailed ionic model to show that the origin of alternans can be inferred by measuring the length scales over which APD and Ca_i alternans reverse phase during spatially discordant alternans. The main conclusion is that these scales are comparable to a few millimeters and equal when alternans is driven by APD restitution, but differ markedly when alternans is driven predominantly by unstable Ca cycling. In the latter case, APD alternans still reverses phase on a millimeter tissue scale due to electrotonic coupling, while Ca alternans reverses phase on a submillimeter cellular scale. These results show that experimentally accessible measurements of Ca_i and V_m in cardiac tissue can be used to shed light on the cellular origin of alternans.

Numerous experimental studies have shown that isolated cardiac cells, when paced rapidly or pharmacologically stressed, exhibit a beat-to-beat alternation in both the action potential duration (APD) and the intracellular Ca transient (Ca_i) (1,2). This phenomenon of “alternans” has been widely studied and has been linked to various cardiac rhythm abnormalities. In fact, several clinical studies have shown that the detection of a beat-to-beat alternation in the T-wave morphology, which is a manifestation of APD alternans at the cellular level, is strongly correlated with the risk of sudden cardiac death (3). Furthermore, APD alternans has been shown to form spatially discordant alternans, where different regions on the surface of the heart alternate out-of-phase (4), thereby dynamically forming a heterogeneous substrate for reentry. All these studies suggest a central role of alternans in the genesis of cardiac arrhythmias.

Despite extensive theoretical and experimental work on this subject (1,5,6), pinpointing the cellular origin of alternans experimentally in multicellular tissue has remained difficult. Two leading cellular mechanisms of alternans have been considered. Firstly, alternans has been attributed to steep APD restitution, where APD restitution is itself governed by the kinetics of ion channels that control the dynamics of transmembrane voltage (V_m). Here, the mechanism for alternans can be described as a period-doubling instability of the V_m dynamics (7,8), which in turn drives Ca_i transient alternans via the L-type Ca channels and the sodium-calcium exchange current, which interacts with the Ca cycling machinery. In this scenario, Ca transient alternans is slaved to APD alternans. Secondly and more recently, alternans has been attributed to a period-doubling instability of Ca cycling driven by a steep relationship between the amount of Ca release from the sarcoplasmic reticulum (SR) and the SR Ca load. In this case, alternans is driven predominantly by the period-doubling instability of the Ca cycling dynamics, with APD alternans simply a secondary response due to the influence of the amplitude of the Ca transient on the Ca-sensitive ion channels that modulate the APD. The existence of a dynamical instability of Ca cycling independent of an instability of V_m dynamics linked to steep restitution is clearly demonstrated by experiments (9,10) where alternans of intracellular Ca_i can occur even though the membrane V_m is clamped to a periodic waveform.

Identification of the cellular origin of alternans is essential for understanding cardiac arrhythmogenesis. However, since V_m is bidirectionally coupled to Ca cycling via ion channels which are both Ca- and V_m-sensitive, it is generally difficult to assess to what degree the period-doubling instability driving alternans is linked to APD restitution, unstable Ca cycling, or both. Pacing a single cell with a periodic-clamped AP waveform can in principle shed light on the origin of alternans, but this procedure cannot be implemented in organ level experiments where alternans has been directly linked to arrhythmias. In such experiments, local measurements of the timecourse of the V_m and Ca_i transient do not suffice to reveal the primary driver of the instability. In this letter, we introduce a novel approach to show that the spatial distribution of APD and Ca_i transient alternans in cardiac tissue can be used to unmask the underlying cellular origin of alternans. Using numerical simulations in a physiologically detailed ionic model, we show that by measuring the length scales over which alternans of Ca and APD change phase during spatially discordant alternans, it is possible to reliably infer which component of the system is the primary driver for alternans.

We modeled a 3-cm one-dimensional strand of homogeneous tissue using the standard cable equation 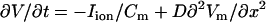, where C_m = 1 μF/cm² is the transmembrane capacitance, D = 5 × 10⁻⁴ cm²/ms is the effective diffusion coefficient of V_m in cardiac tissue, and I_ion is the total membrane ionic current density modeled after the canine action potential model of Fox et al. (5), which is coupled to a model of Ca cycling of Shiferaw et al. (6). The currents implemented in the model are described in Sato et al. (11). The detailed parameters used in this study are given in the Supplementary Material. An important feature of this ionic model is that alternans of Ca_i and APD can be induced by either APD restitution or unstable Ca cycling. The steepness of APD restitution is controlled here by the time constant of recovery of the L-type Ca channel, denoted by τ_f. Increasing τ_f steepens APD restitution and promotes repolarization alternans (7,8). On the other hand, unstable Ca cycling can be induced, independently of V_m, as shown both theoretically (6,12) and experimentally (10), by increasing the sensitivity of SR Ca release on SR Ca load. In this case, the key parameter controlling the onset of alternans is the slope of the curve relating SR Ca release versus SR Ca load at high load, which is denoted here by the parameter u.

The cable was stimulated from the left-most end at a fixed pacing cycle length (BCL) of 280 ms. At this BCL, spatially discordant alternans form due to steep CV restitution (13,14). In our ionic model, steep CV restitution can be induced by increasing the time constant of recovery of the sodium current (see Supplementary Material). Once spatially discordant alternans is formed, we compute the spatial distribution of Ca alternans using 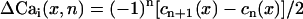, where n is the beat number and c_n(x) is the peak of the Ca_i transient measured at position x along the cable. The factor of (−1)ⁿ was introduced such that the amplitude of alternans does not change sign at every beat. Similarly, the spatiotemporal distribution of APD alternans is measured using .

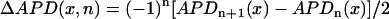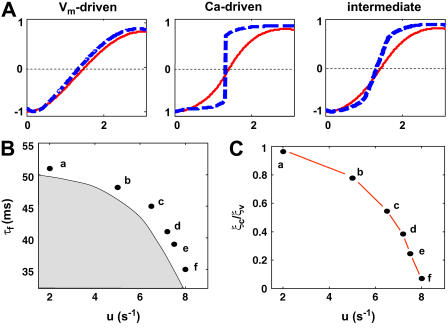
Fig. 1 A shows the steady-state spatial distribution of ΔCa_i and ΔAPD after the induction of discordant alternans, for a range of model parameters. When alternans is V_m-driven, the length scale over which Ca_i and APD alternans changed phase was similar (approximately a few millimeters). On the other hand, when Ca was the primary driver for the instability, Ca_i alternans changed phase over a much shorter scale (<0.015 cm) than that of APD alternans (∼1 cm). Thus, the underlying mechanism for the instability is directly related to the spatial scale of phase reversal of Ca and APD alternans.

FIGURE 1.

(A) Normalized spatial distribution of alternans on a 3-cm cable for a range of instability parameters. Blue denotes ΔCa_i and red ΔAPD. (B) Stability boundary for a cable paced at 280 ms. (C) Scale ratio τ_C/τ_v for the indicated points in panel B. The parameters used in panel A correspond to points a, f, and c, respectively, on the parameter space shown in panel B.

To investigate in more generality the relationship between the cellular mechanism of alternans and the spatial scales of phase reversal during discordant alternans, we studied the spatial distributions of APD and Ca alternans along the cable as a function of the two aforementioned parameters τ_f and u for a fixed BCL of 280 ms. Fig. 1 B shows the stability boundary that separates stable (shaded region) and unstable regions (open region) without and with alternans, respectively, in a plane where the vertical and horizontal axes correspond to increasing degree of V_m-driven (τ_f) and Ca-driven (u) instability, respectively. Here, we have chosen parameters such that a larger Ca_i transient promotes a larger APD and cellular alternans is electromechanically concordant as commonly observed experimentally. This choice corresponds to the case where the bidirectional coupling of calcium and voltage is termed positive in the scenario outlined by Sato et al. (11). To compute the scale over which alternans changes phase, we fitted a hyperbolic tangent function to the spatial distribution of Ca and APD alternans, respectively. The width of the fitted function to the APD and Ca alternans pattern is denoted by ξ_V and ξ_C, respectively. In Fig. 1 C, we plot the ratio ξ_C/ξ_V for the points on the stability diagram labeled a–f. From this graph, we see that the ratio of scales was roughly 1 for V_m-driven alternans due to steep APD restitution, i.e., in the region of parameter space when τ_f was large and u was small. In contrast, ξ_C/ξ_V becomes vanishingly small in the region of parameter space when alternans was due predominantly to unstable Ca cycling, i.e., where τ_f was small and u was large. This is also true for the case of negative coupling where alternans is electromechanically discordant (results not shown), with the added ingredient that discordant alternans can be initiated without CV restitution in this case (11). These results demonstrate a direct relationship between the ratio of the spatial scales of phase reversal during spatially discordant alternans and the underlying mechanism driving the instability to alternans.

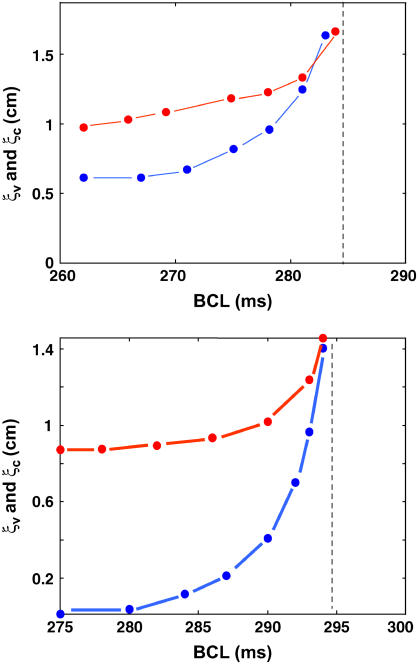
We note that ξ_C/ξ_V could also approach unity in the case where alternans was due predominantly to an instability of Ca cycling, but only for a relatively narrow range of BCL (∼5 ms) close to the onset of alternans. At more rapid rates, away from onset, ξ_C and ξ_V were markedly different in the case when the alternans was Ca-driven as shown in Fig. 2. Therefore, while measurements of the spatial scales of phase reversal provide a powerful means to infer the underlying cause of alternans, these measurements should generally be performed over a large enough range of BCL.

FIGURE 2.

Length scales for V_m-driven and Ca-driven alternans, close to the onset of instability. The top graph corresponds to V_m-driven alternans, with, u = 2 s⁻¹ and τ_f = 51 ms. Bottom graph is Ca-driven, u = 8 s⁻¹ and τ_f = 35 ms. For both graphs, red corresponds to ΔAPD and blue to ΔCa_i. The dashed vertical lines denote the BCL onset for alternans.

The relationship between the ratio of scales and the cellular instability mechanism can be understood intuitively as follows. For V_m-driven alternans, the Ca_i transient amplitude is graded by the L-type Ca current, which is larger for a longer APD. Moreover, the Ca_i transient amplitude in a given cell is not significantly influenced by the Ca transient amplitude of adjacent cells due to the slow diffusion of Ca between cells. Thus, the Ca_i transient amplitude passively tracks the APD (which itself controls the L-type Ca current amplitude) of each cell. For Ca-driven alternans, however, the Ca_i transient alternans can change phase over very short, even subcellular, distances due to the slow diffusion of Ca, but the APD cannot follow this abrupt change due to electrotonic coupling. This argument should be valid in higher dimensions, since it relies only on single cell properties, and the fact that V_m diffuses much faster than Ca. The main difference being that the scale separating out-of-phase regions should be measured along a line normal to the line (two dimensions) and plane (three dimensions) separating these regions.

In conclusion, we have shown that measurements of the spatial scales of phase reversal of Ca_i and APD alternans during spatially discordant alternans can be used to infer whether alternans are due predominantly to an instability of Ca or voltage dynamics. This represents a novel approach to unambiguously determine the underlying mechanism for alternans, using experimentally accessible measurements of V_m and Ca_i on the surface of the heart.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.