The Effect of Translocating Cylindrical Particles on the Ionic Current through a Nanopore

Abstract

The electric field-induced translocation of cylindrical particles through nanopores with circular cross sections is studied theoretically. The coupled Nernst-Planck equations (multi-ion model, MIM) for the concentration fields of the ions in solution and the Stokes equation for the flow field are solved simultaneously. The predictions of the multi-ion model are compared with the predictions of two simplified models based on the Poisson-Boltzmann equation (PBM) and the Smoluchowski's slip velocity (SVM). The concentration field, the ionic current though the pore, and the particle's velocity are computed as functions of the particle's size, location, and electric charge; the pore's size and electric charge; the electric field intensity; and the bulk solution's concentration. In qualitative agreement with experimental data, the MIM predicts that, depending on the bulk solution's concentration, the translocating particle may either block or enhance the ionic current. When the thickness of the electric double layer is relatively large, the PBM and SVM predictions do not agree with the MIM predictions. The limitations of the PBM and SVM are delineated. The theoretical predictions are compared with and used to explain experimental data pertaining to the translocation of DNA molecules through nanopores.

INTRODUCTION

We consider two compartments separated by an electrically insulating membrane equipped with a single pore (Fig. 1). One of the chambers contains a dilute solution of rigid cylindrical, charged particles. In the presence of an appropriate potential difference between the two chambers, particles translocate electrophoretically from one chamber to the other and affect the ionic current through the pore. Through the particles' effect on the ionic current, one hopes to detect the presence of particles inside the pore as well as obtain information on the particles' characteristics. This phenomenon has been utilized in Coulter Counters (1,2) for particle counting and cell sorting and in various biosensors in which specific binding events increase the apparent diameter of the particles (3).

FIGURE 1.

A schematic depiction of the computational model.

Recently, there has been a growing interest in mimicking nature's ionic channels and utilizing nanopores to obtain information on individual molecules such as proteins, DNA, and RNA. Earlier workers utilized nanopores formed by proteins in a lipid bilayer membrane to form “molecular-scale” Coulter counters (see (4) for a review). With the advent of nanofabrication, various groups (4–16) fabricated synthetic nanopores and nanotubes and used these solid-state, nanopore “microscopes” to measure the effect of the translocating molecules on the ionic current through the pore. The experimental studies demonstrated that the ionic current during translocation depends on the voltage bias across the nanopore (6–10,13,14), the length and the cross-sectional area of the molecules (6,8–14,27), the thickness of the membrane (6), the pore size (6,12–15), and the electrolyte bulk concentration (7,9,15,16). When the solvent contains a high salt concentration (thin electric double layer), typically “current blockade” is observed (6–12). When the bulk ionic concentration is reduced, both current blockade and current enhancement are observed during a single molecule translocation (13,14). When the bulk ionic concentration is low, current enhancement is often observed (15,16). The objectives of this article are to improve the understanding of these diverse phenomena through continuum simulations and to provide a predictive tool to estimate the effect of translocating molecules on ionic currents.

To better understand the effect of the electric double layer on the ionic current during the translocation process, we study theoretically the translocation of a rigid, cylindrical particle with a fixed surface charge through a nanopore as a function of the solution's bulk concentration, the particle's and pore's sizes, the particle's location, and the electric field intensity. To this end, we solve the Nernst-Planck, Poisson, and Stokes equations (the MIM model) for the ion concentration in the pore, the particle's velocity, and the ionic current. The results of this model are compared with the predictions of frequently used, simplified models based on the Poisson-Boltzmann equation (PBM) and on the Smoluchowski slip velocity (SVM).

The article is organized as follows. Mathematical Model details the multi-ion model (MIM) that accounts for the polarization of the electric double layer; the nonlinear, Poisson-Boltzmann model; and a model based on the Smoluchowski slip velocity (17). Numerical Methods describes the numerical procedures and code validation. Results and Discussion provides the results of the calculations pertaining to the ionic current when a cylindrical particle translocates axisymmetrically through the pore. The theoretical predictions are compared with experimental observations. This is followed by Conclusions.

MATHEMATICAL MODEL

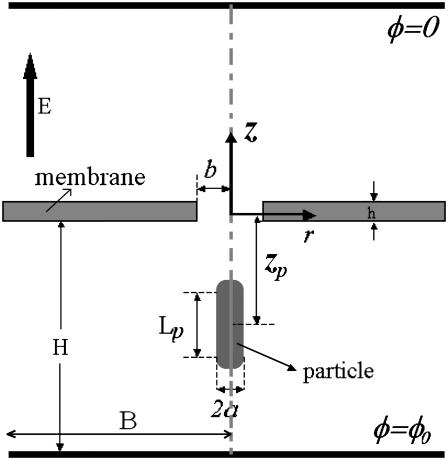
Consider a charged, cylindrical particle of radius a and length L_p, having two hemispherical caps of radius a at both ends (Fig. 1). The particle is submerged in an electrolyte solution. The solution is confined in a vessel that is separated by an electrically insulating membrane of thickness h into two reservoirs, each of radius B and height H. The membrane is equipped with a single pore of radius b ≪ B and has a uniformly distributed surface charge of density σ_m.

We define a cylindrical coordinate system with radial coordinate r and axial coordinate z. The origin of the coordinate system is at the pore's center. The surfaces |z| = H and r = B are sufficiently far from the pore to have little effect on the translocation process of the particle through the pore. The surfaces |z| = H are permeable to fluid flow and maintained at uniform equal pressures. The electrolyte solution at |z| = H is neutral and has its bulk concentration. The surfaces z = H and z = −H are, respectively, maintained at uniform potentials φ(r,H) = 0 and φ(r,−H) = φ₀. The surface r = B is insulated, free of charge, and impermeable to fluid flow.

A cylindrical particle is initially placed with its axis coinciding with the pore's axis. The location of the particle's center of mass is denoted as z_p. The particle's surface is uniformly charged with charge density σ_p.

The potential difference φ₀ induces an electric field that causes the particle to migrate axially and translocate through the pore. Due to symmetry, the particle's center of mass will move along the z axis (r = 0). We wish to determine the particle's velocity and the ionic current through the pore as functions of the particle's location, the magnitude of the potential φ₀, the geometry, and the solution's composition.

We assume that the continuum equations provide a reasonable description of the physics associated with the translocation process, and we focus on steady-state conditions. Below, we will use a number of models that are applicable for various ranges of problem parameters. The first model, dubbed the multi-ion model (MIM), consists of the Nernst-Planck equations and accounts for the effect of the external electric field and convection on the ions' concentration field. The second model assumes that the ions obey the Boltzmann distribution. This model is based on the Poisson-Boltzmann equation (PBM). The third model does not account for the ion distribution explicitly, but rather replaces the effect of the electric double layer with a slip velocity at charged surfaces. We refer to this model as the Smoluchowski velocity model (SVM).

The multi-ion model (MIM)

The multi-ion model (MIM) consists of the ion conservation equations, Poisson's equation, and the hydrodynamic equations for a viscous, incompressible fluid. Assuming quasi-steady state and no chemical reactions, the ionic conservation for species i requires that the flux (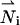) is divergence-free:

(1)

In the above,

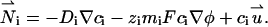(2)

D_i is the molecular diffusion coefficient, c_i is the ionic concentration, m_i is the ion mobility, z_i is the valence, F is the Faraday constant, and 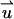is the flow velocity. The first, second, and third terms in Eq. 2 correspond, respectively, to diffusion, migration, and convection. In the above, we assume that the diffusion coefficients and mobilities are uniform throughout the domain and neglect confinement effects. The potential φ satisfies the Poisson equation

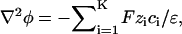(3)

where ɛ is the fluid's dielectric constant. Here, we assume that ɛ is uniform. The summation carried over K species represents the net charge density in the solution.

Since typically the Reynolds number associated with electrophoretic flows is very small, we neglect the inertial terms in the Navier-Stokes equation, and model the fluid motion with the Stokes equation,

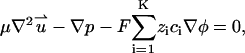(4)

and the continuity equation for an incompressible fluid,

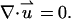(5)

In the above, p is the pressure and μ is the fluid's dynamic viscosity. The first, second, and third terms in Eq. 4 represent, respectively, the viscous, pressure, and electrostatic forces.

To complete the mathematical model, we need to specify the appropriate boundary conditions. The boundary conditions associated with the electric field are φ(r,H) = φ(r,−H) −φ₀ = 0, specified electric charge densities on the particle's and the membrane's surfaces, and insulation condition 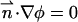at r = B, where 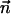is an outwardly-directed unit vector normal to the surface. The boundary conditions associated with the Nernst-Planck equation include specified concentrations at the top and bottom boundaries c_i(r,H) = c_i(r,−H) = 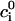and zero flux at all impermeable surfaces,

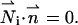(6)

The boundary conditions for the flow field are specified pressures at the top and bottom boundaries

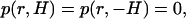(7)

zero velocities at all solid boundaries other than the particle's surface, and

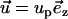(8)

on the particle's surface. In the above, u_p is the vertical velocity of the particle's center of mass. The velocity u_p is determined by requiring the total force in the z direction (F_T) acting on the particle

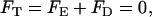(9)

where

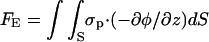(10)

and

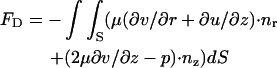(11)

are, respectively, the electrostatic and hydrodynamic forces acting on the particle. S is the particle's surface; u and v are, respectively, the r and z components of 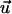; and n_r and n_z are, respectively, the r and z components of 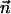. In the above, we assume that the induced charges in the particle are negligible compared to the assigned surface charge σ_p.

The current density

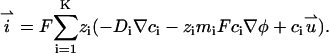(12)

By integrating the Eq. 12 over the cross-sectional area of the pore, we obtain the total current through the pore.

The Poisson-Boltzmann model (PBM)

When the external electric field (potential ψ) is weak relative to the field induced by the surface charges (potential ϕ), one can employ the classical treatment (17) of electrophoresis, which assumes that the electric field can be described as a linear superposition of the potentials ψ and ϕ, i.e., φ = ψ + ϕ, and that the ions' concentrations satisfy the Boltzmann distributions

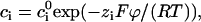(13)

where R is the universal gas constant, T is the temperature, and 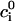is the bulk (far field) concentration of the ion of type i. The potential associated with the surface charges is given by the Poisson-Boltzmann equation:

(14)

Along the particle and membrane surfaces, the potential ϕ satisfies, respectively,

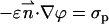(15)

and

(16)

At all other solid boundaries, 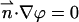and ϕ(r,−H) = ϕ(r,H) = 0. The external electric potential satisfies the Laplace equation

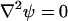(17)

with ψ(r,−H) − φ₀ = ψ(r,H) = 0 and 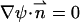at the surfaces of the particle and the membrane.

The corresponding Stokes equation becomes (18)

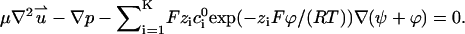(18)

The boundary conditions for the flow field are the same as in the MIM.

The Smoluchowski velocity model (SVM)

When the thicknesses

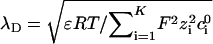(19)

of the electric double layers adjacent to the particle and the membrane are very small, it is not practical to resolve the electric double layer with numerical simulations. Instead, the motion of the liquid next to the particle and the solid boundaries is approximated with the Smoluchowski electroosmotic slip velocity. In other words, when (a/λ_D) ≫ 1, the difference between the fluid's velocity at the “edge” of the electric double layer and the particle's velocity at any point on the particle's surface is given by the slip velocity 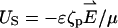, which is independent of the particle's shape (19). In the above, the zeta-potential ζ_p on the particle's surface corresponds to the potential ϕ in the PBM, and it relates to the surface charge by the formula (20):

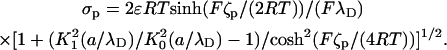(20)

In the above, K₀ and K₁ are, respectively, the zero-order and the first-order modified Bessel functions of the second kind. The applied electric field is 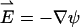, where ψ was defined by Eq. 17.

In the framework of the SVM approximation, the particle and its adjacent double layer are considered as a single entity, and the fluid motion outside the electric double layer is described by the Stokes equation without any electrostatic body forces:

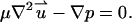(21)

In other words, all the electrodynamic effects induced by the surface charges are incorporated in the slip velocity boundary conditions. The liquid's velocities adjacent to the particle and membrane surfaces are, respectively,

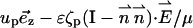(22)

and

(23)

In the above, I is the unitary tensor, and ζ_m is the zeta-potential of the pore's surface. According to Newton's third law, the total force acting on the particle together with its adjacent electric double layer is

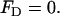(24)

Equation 24 is used to determine the unknown particle's velocity u_p.

The multi-ion model accounts for the deformation and the polarization of the electric double layer, and it is valid for all thicknesses of the electric double layer. The PBM neglects the deformation of the electric double layer due to convection and polarization and assumes that the ions satisfy the Boltzmann distribution. The PBM model does not require one to compute the ionic concentration fields; consequently, it reduces significantly the computational complexity. One would expect that the PBM would provide reasonable predictions when the external electric field is relatively small compared to the electric field induced by the surface charges. Both the MIM and PBM require one to determine the electric double layer. When the thickness of the electric double layer is very small (λ_D ≪ a,b), it is impossible to provide a sufficiently fine mesh to resolve the electric double layer, and the SVM provides a great simplification in the computational effort. Below, we will compare the predictions of the various models. An agreement between the MIM, PBM, and SVM in the limiting cases when all three are applicable will provide us with a means to verify the numerical code.

Dimensionless form of the various mathematical models

In what follows, we consider a binary, symmetric electrolyte such as KCl aqueous solution (z₁ = 1 and z₂ = −1). It is convenient to normalize the various variables. We use the bulk concentration c₀ as the ion concentration scale, RT/F as the potential scale, the pore's radius b as the length scale, U₀ = c₀RTb/μ as the velocity scale, and μU₀/b as the pressure scale. The dimensionless governing equations of the multi-ion model are

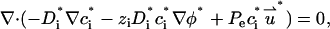(25)

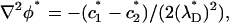(26)

and

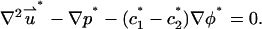(27)

Variables with superscript * are dimensionless. In the above, 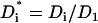, 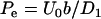is the Peclet number, and 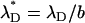is the dimensionless thickness of the electric double layer. The dimensionless current density normalized with 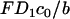is

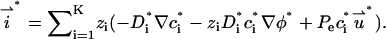(28)

Similarly, the dimensionless equations of the PBM are

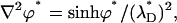(29)

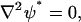(30)

and

(31)

The dimensionless momentum equation for the SVM is

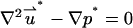(32)

with the slip velocity boundary conditions

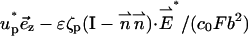(33)

and

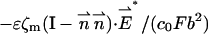(34)

on the particle's and membrane's surfaces, respectively.

NUMERICAL METHODS

The solution process is complicated by the fact that the particle's velocity u_p is not known a priori and needs to be obtained as part of the solution. In the next two subsections, we describe briefly the algorithms used to obtain the particle's velocity. The section concludes with a brief description of code verification.

Determination of the particle's velocity with MIM

In the MIM, the ion mass transport and the momentum transport are coupled. The flow field affects the ionic concentration through convection, and the ionic concentration affects the flow field through the electrostatic force. To determine the particle's velocity, we need to solve the force balance Eq. 9. We start with an initial guess u_p = 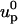for the particle's velocity, and compute the various fields and forces. The resulting forces are not likely to satisfy the force balance Eq. 9, and it is necessary to correct the initial guess. To compute the correction δu_p, we use the Newton-Raphson algorithm:

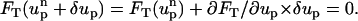(35)

The process is repeated with 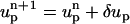until the changes in the computed velocity are insignificant. This process typically converges within fewer than five iterations.

Determination of the particle's velocity with PBM and SVM

In the PBM and SVM, the equations for the electric field are decoupled from the momentum equation and can be solved without knowledge of the particle's velocity u_p. Furthermore, the momentum equation is linear, and one can use superposition. To this end, we decompose the velocity field into the electroosmotic-induced velocity field (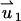) and particle-induced velocity field ():

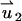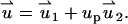(36)

The pressure field is decomposed in a similar way:

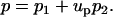(37)

In the PBM, 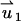satisfies Eq. 18 with zero (nonslip) velocity at all solid boundaries. The second velocity component 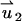satisfies Eq. 18 without the electrical body force. The value 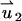satisfies unit velocity boundary condition on the particle's surface (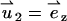) and zero (nonslip) velocity at all other solid boundaries. The particle's velocity is determined from the force balance:

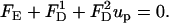(38)

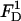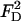In the above, and are, respectively, the z-direction hydrodynamic drag forces on the particle resulting from the flows 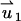and 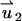. We use a similar technique to determine the particle's velocity in the SVM.

Code verification

The computations were carried out with the finite-element, multiphysics program FemLab (COMSOL AB, Stockholm, Sweden). We used a nonuniform grid with a higher concentration of elements in the electric double layer regions. We verified that the numerical solutions were convergent, independent of the size of the finite elements, and satisfied the various conservation laws. The total electric current was computed at the lower and upper surfaces and through the pore's cross section. All three current values agreed within 0.01%.

The predictions of the MIM, PBM, and SVM were compared and found to be in excellent agreement in the limiting cases when all three models are valid. See Thin Electric Double Layer for additional details.

We have performed several tests to ensure the validity of the MIM solutions. In one instance, we calculated the coaxial electrophoretic motion of a spherical particle of radius a in a long cylindrical tube of radius b when the thickness of the electric double layer is significant. Fig. 2 compares the results of our calculations (circles) with the approximate solution of Ennis and Anderson (22) (solid line) that was derived using the Poisson-Boltzmann equation and the method of reflections. The figure depicts the normalized velocity of the sphere as a function of the radii ratio a/b when a/λ_D ≈ 1, ζ_m = 0, and ζ_p = 1 mV. The velocity of the sphere is normalized with U_ep = ɛζ_pE_z/μ. When a/b < 0.2, the MIM solution (circles) agrees well with the approximate analytical solution (solid line). When a/b increases, the precision of the reflection method deteriorates and so does its agreement with the numerical solution.

FIGURE 2.

Relative mobility of a sphere moving coaxially in a long cylindrical tube as a function of the ratio of the sphere and the tube radii. The ζ-potentials along the surfaces of the sphere and the cylindrical pore are, respectively, 1 mV and 0. The value a/λ_D ≈ 1. The solid line and symbols correspond, respectively, to the approximate analytical solution of Ennis and Anderson (22) and to the MIM predictions.

RESULTS AND DISCUSSION

In this section, we present the results of our numerical computations and compare them with experimental data. All the available experimental data pertains to the translocation of single- and double-stranded DNA molecules. The structure of the DNA molecule is considerably more complex than that of the rigid, cylindrical particle that we are considering here. Nevertheless, as we shall see below, our simple model captures many of the phenomena observed in the experiments. This may be due, in part, to the large persistence length of the double-stranded DNA, ∼50 nm, which is much larger than the pore's radius and height, and which allows us to consider the DNA as a rigid object.

In experiments, one typically measures the ionic current (I) as a function of time as the particle translocates through the pore. ΔI = I–I_b is the deviation of the current from the base current I_b when the particle is far from the pore. We define the normalized current deviation χ = ΔI/I_b, and we will present many of our results in the form of χ as a function of the particle's location 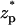, where .

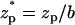Thin electric double layer

First, we investigate the case of a thin EDL. We consider a pore of radius b = 5 nm and membrane thickness h = 5 nm. The particle's radius a = 1 nm and its length L_p = 20 nm. The particle carries a surface charge of density σ_p = 7.65 × 10⁻³ C/m², and the membrane is not charged (σ_m = 0). The two reservoirs have heights H = 60 nm and radii B = 40 nm, and are filled with 1 M KCl solution at 300 K. The magnitudes of H and B are chosen large enough so that further increases in H and B had little effect on the computational results, but small enough so as not to tax computer memory too heavily. A bias potential of φ₀ = 120 mV is imposed across the top and bottom boundaries. The positively charged particle is driven toward the cathode (in the positive z direction).

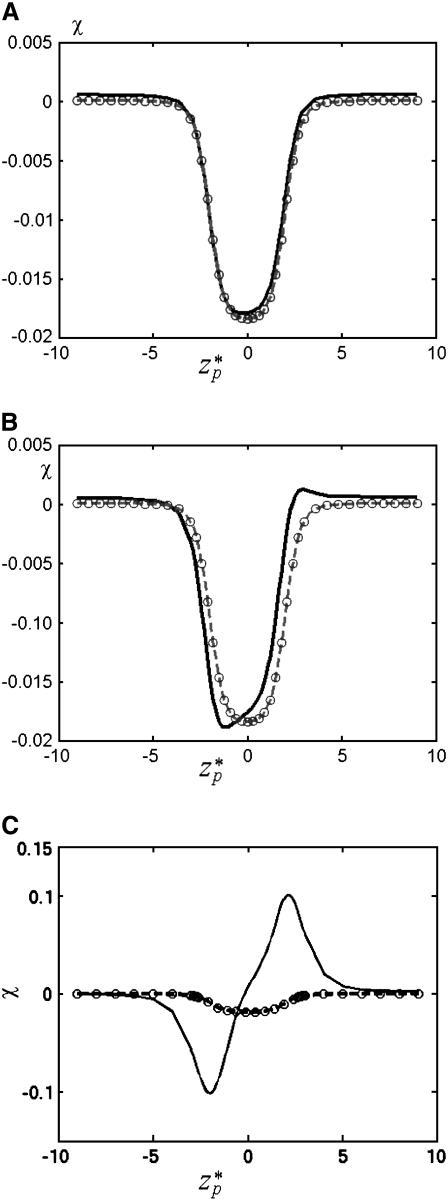
Fig. 3 A depicts the relative ionic current deviation χ as a function of the particle's location 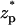when the bulk ion concentration c₀ = 1 M. The corresponding electric double layer thickness is λ_D = 0.3 nm. It is convenient to express the thickness in terms of the gap width. Accordingly, we define α = λ_D/(b−a). Here, α = 0.078. The solid line, dashed line, and circles correspond, respectively, to the predictions of the MIM, PBM, and SVM. When the particle is far from the pore, the ionic current is nearly at its unperturbed free pore value (χ ∼ 0). As the particle translocates through the pore, χ decreases, attains a minimum (χ_min ∼ −0.018) when 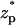∼ 0, and then increases again. This reduction in the ionic current is known as blockade-current.

FIGURE 3.

The ionic current deviation χ as a function of the dimensionless particle's location 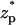when (A) c₀ = 1 M, σ_p = 7.65 × 10⁻³ C/m², (B) c₀ = 0.1 M, σ_p = 7.65 × 10⁻³ C/m², and (C) c₀ = 0.01 M, σ_p = 3.06 × 10⁻² C/m². Note a = 1 nm, b = 5 nm, L_p = 20 nm, H = 60 nm, B = 40 nm, φ₀ = 120 mV, and σ_m = 0. The solid line, dashed line, and circles represent, respectively, the MIM, PBM, and SVM predictions.

Many authors (2,12,23) attribute the current reduction to the particle's presence in the pore reducing the cross-sectional area available to the ionic current flow and thus increasing the electric resistance by ΔR_S. Accordingly, the resistance

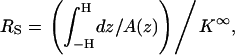(39)

where A(z) is the cross-sectional area available for current flow, and K^∞ is the bulk solution conductivity and

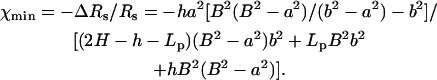(40)

In our case, Eq. 40 yields χ_min ∼ −0.03, which greatly underestimates the MIM's prediction. This discrepancy can be attributed to the fact that Eq. 39 does not account for the intensification of the electric field in the gap between the particle and the pore. In fact, the increase in the electric field's intensity is likely to compensate for most, if not all, of the blockade-effect. The actual reduction in the ionic current is a result of edge effects. Not surprisingly, when the current reduction is estimated from the solution of the Laplace equation for a conductive medium with the same bulk conductivity as our electrolyte solution and the corresponding geometry, one finds χ_min ∼ −0.018.

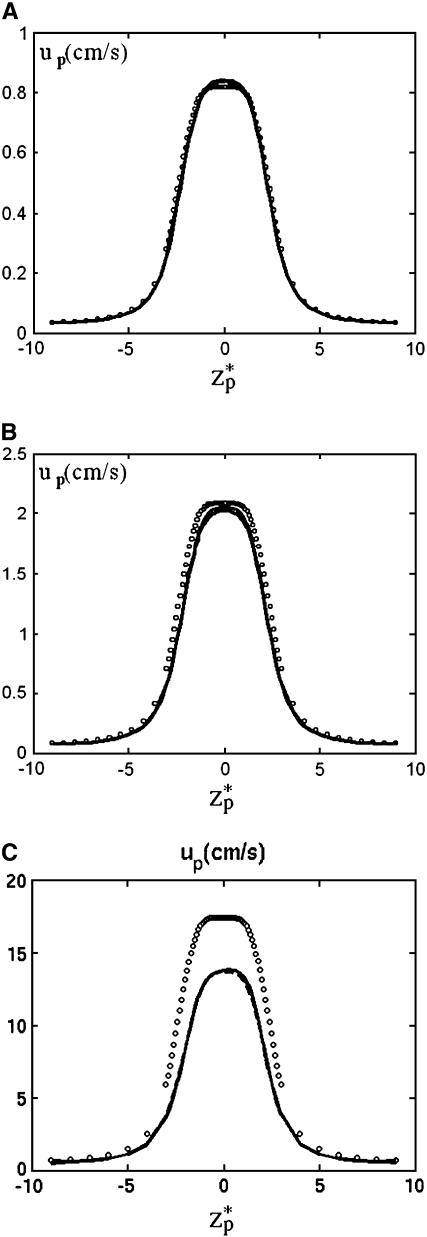
Fig. 4 A depicts the corresponding particle's velocity (cm/s) as a function of the dimensionless location of the particle's center of mass 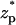. As the particle approaches the pore, the electric field's magnitude increases and so does the particle's velocity. The particle attains its maximum velocity when 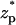= 0. The solid line, dashed line, and circles correspond, respectively, to the predictions of the MIM, PBM, and SVM. Since α ≪ 1, the presence of the particle in the pore does not alter significantly the ion distribution inside the pore, and the results of the three models are in good agreement. Thus, under the above conditions, the SVM is applicable.

FIGURE 4.

The translocation speed of the particle as a function of the particle's location 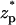when (A) c₀ = 1 M, (B) c₀ = 0.1 M, and (C) c₀ = 0.01 M. The simulation parameters are the same as in Fig. 3. The solid line, dashed line, and circles represent, respectively, the results of MIM, PBM, and SVM.

The computational efficiency of the SVM facilitates the simulation of the translocation of relatively long particles with thin electric double layers. Next, we use the SVM to simulate the experiments of Li et al. (6). The experimental setup consisted of 0.3-mm high chambers with a radius of 1.5 mm, a nanopore of 1.5-nm radius and 5-nm thickness, and a 120-mV potential bias across the electrodes. The 3-kb translocating dsDNA with an approximate radius of 1 nm, a length of 1 μm, and an aspect ratio of 10³ was submerged in a 1 M KCl and 10-mM TRIS-HCl buffer (pH = 8.0, and α ∼ 0.08). Given the large disparity of length scales, we simulated a reduced size chamber of 0.6-μm height and 0.3-μm radius. Numerical experiments indicated that increases in the chamber's size beyond the dimensions specified above had an insignificant effect on the calculations' results. The large aspect ratio of the particle also presented a computational challenge. Therefore, we simulated a cylindrical particle (with two spherical caps) with a radius of 1 nm and a length of 50 nm (≫pore thickness of 5 nm). We will show in The Effect of the Particle's Length that once the particle's length exceeds a certain threshold, both χ_min and the particle's maximum velocity are insensitive to the particle's length. The calculated base current I_b = 1730 pA, the blockade current is 1100 pA, χ_min = −0.36, and the average particle velocity is 0.81 cm/s. The experimental ionic current as a function of time is qualitatively similar to Fig. 3 A, which depicts the ionic current as a function of the particle's location (in the interest of space, we did not reproduce a figure depicting current as a function of time). In the experiment, the base current was 1430 ± 20 pA, the blockade current was 1310 ± 15 pA, χ_min = −0.084 ± 0.02, and the average velocity was 0.85–1.13 cm/s. The computational results are of the same order of magnitude as the experimental observations. The deviations between the experimental observations and the theoretical predictions can be attributed, in part, to the complexity of the DNA molecule, which was not captured in the numerical simulations and, in part, to underestimation of the pore's size (23). The reported pore geometry is interpreted from transmission electron microscope images. These images are, however, two-dimensional projections of the pore and capture the smallest dimensions of the pore along its length. In fact, the nanopores are often elliptical in cross section rather than circular, and typically have a conical shape along their length. Hence, the reported pore dimensions are an underestimate of the pore's true dimensions, and therefore the experimental |χ_min| is smaller than the computed one. The fact that the measured translocation velocity is nearly the same as the predicted one indicates that the translocation process is governed by a balance between the electrostatic and viscous forces and that, in this case, the entropic effects associated with the coiling of the molecule do not play a significant effect. This is perhaps due to the persistence length of the molecule being much larger than the pore's diameter, the stretching of the molecule in the electric field, and the molecule being relatively short.

Thick electric double layer

Fig. 3 B depicts χ as a function of 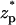when the bulk ion concentration c₀ = 0.1 M, λ_D = 0.97 nm, and α = 0.24. All other conditions are as in Fig. 3 A. The solid line, dashed line, and circles correspond, respectively, to the predictions of the MIM, PBM, and SVM. The PBM and SVM predictions are in excellent agreement; but they deviate somewhat from the MIM's predictions. The PBM and SVM predict only current blockade and are similar to Fig. 3 A while the MIM predicts current blockade along most of the particle's path, but current enhancement when 2.4 < 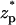< 4. This difference is due to the electric double layer significantly affecting the ion distribution inside the pore. The particle's locations at the current minimum and maximum correspond, respectively, to the upper and lower ends of the particle coinciding with the center of the pore. The behavior depicted in Fig. 3 B is similar to the experimental observations of Heng et al. (14). When they were measuring the ionic current of 100 bp dsDNA translocating through a 3.5-nm diameter pore (1 M KCl concentration and 200 mV bias), Heng et al. observed (Fig. 3 in their article) that the ionic current had a “positive spike” immediately before the particle cleared the pore—quite similar to the one depicted in Fig. 3 B. The continuum simulations are also in agreement with the results of the Aksimentiev et al. (13) molecular dynamics simulations. However, to reduce the time of the simulations, the molecular dynamic simulations were carried out at much larger electric field intensities than those used in the experiments.

The current elevation becomes more pronounced as the thickness of the electric double layer increases. This effect is exemplified in Fig. 3 C, which depicts χ as a function of 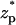when c₀ = 0.01 M, λ_D = 3.08 nm, σ_p = 3.06 × 10⁻² C/m², and α = 0.77. The solid line, dashed line, and circles correspond, respectively, to the predictions of the MIM, PBM, and SVM. The predictions of the PBM and SVM are qualitatively similar to the ones depicted in Fig. 3 A and consist only of a current blockade. The predictions of the MIM are, however, markedly different. Witness that as the particle enters the pore, the current declines, attains a minimum at 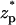∼ −2, increases, attains its undisturbed (free pore) value at 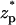∼ 0, increases further above the base current, attains a maximum value at 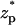∼ 2, and then declines back to the base current as the particle clears the pore.

To better understand the reasons for the current enhancement, Figs. 5 and 6 depict, respectively, the distributions of the dimensionless ionic concentrations of K⁺ (c₁) and Cl⁻ (c₂) when the particle is below (a, z_p = −12.5nm), inside (b, z_p = 0), and above (c, z_p = 12.5 nm) the pore. When the positively charged particle enters the pore, the concentration of the co-ions c₁ around the particle (Fig. 5) decreases below and the concentration of counterions c₂ (Fig. 6) increases above the bulk concentration. When the particle is below the pore (Fig. 6 A), the co-ions' z-direction concentration gradient in the pore is negative and the concentration gradient of the counterions is positive. The resulting diffusion induces current in the negative z direction, enhancing the blockade-effect and reducing the ionic current through the pore. In contrast, when the particle is above the pore (Fig. 6 C), the diffusion contributes to an increase in the ionic current. This enhancement appears to more than compensate for the blockade-effect. This contribution to the ionic current is significant only when the electric double layer is relatively thick.

FIGURE 5.

The distribution of the dimensionless ionic concentration of K⁺ (c₁) when the particle is below the pore, z_p = −12.5 nm (A); in the pore, z_p = 0 (B); and above the pore, z_p = 12.5 nm (C). The simulation parameters are the same as in Fig. 3 C.

FIGURE 6.

The distribution of the dimensionless ionic concentration of Cl⁻ (c₂) when the particle is below the pore, z_p = −12.5 nm (A); in the pore, z_p = 0 (B); and above the pore, z_p = 12.5 nm (C). The simulation parameters are the same as in Fig. 3 C.

Fig. 7 depicts the diffusion, migration, and convection contributions to the ionic current as functions of 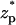. Since the convection's contribution is very small, the magnitude of the convection-induced current was multiplied by a factor of 10× to enhance visibility. The dominant migration current remains positive during the particle's translocation. The alteration in the migration current's magnitude due to the particle's presence in the pore is of the same order of magnitude as the diffusive current. The direction of the diffusive current depends on the particle's location. When the particle's center of mass is below/above the pore's center, the diffusive current is negative/positive. The total current results in a blockade and a hilltop due to, respectively, the offset and contribution of the diffusive current.

FIGURE 7.

The ionic currents from diffusion (solid line), migration (dashed line), and convection (dashed-dot line) as functions of the particle's location 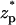. The conditions are the same as in Fig. 3 C.

Since neither the PBM nor the SVM account for the variations in the concentration field, both models fail to predict the current enhancement.

Fig. 4, B and C, respectively depict the particle's velocity as a function of 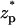for c₀ = 0.1 M and 0.01 M. The solid line, dashed line, and circles correspond, respectively, to the predictions of the MIM, PBM, and SVM. As the bulk concentration decreases (the electric double layer's relative thickness increases), the discrepancy between the MIM predictions and the SVM predictions increases. The PBM predictions are in good agreement with the MIM predictions. In all cases, the particle attains its maximum velocity when its center of mass is located at the center of the pore. For the conditions of Fig. 4 C, the particle's velocity increases nearly linearly as a function of the potential difference φ₀, u_p,max ∼ 0.4 φ₀. As the ion concentration decreases and the thickness of the electric double layer increases, so does the maximum velocity of the particle. When c₀ = 1 M, 0.1 M, and 0.01 M, the maximum velocity u_p,max ∼ 0.85, 2, and 13.8 cm/s.

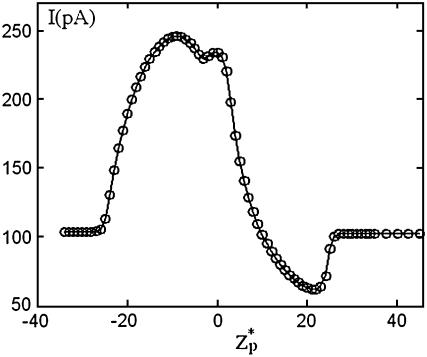
In yet another experiment, Chang et al. (15) recorded the ionic current during the translocation of a 200-bp dsDNA through a silicon oxide nanopore with a radius of 2.2 nm and a thickness of 50 nm. The particle's translocation was induced by a potential bias of φ = 200 mV. Their chamber was filled with 0.1 M KCl solution with 2 mM Tris buffer with pH ∼ 8.5. Under these conditions, the silicon oxide pore is expected to carry a negative charge (24) of ∼−0.0095C/m². The surface charge density of the dsDNAs (6) is estimated at −0.15 C/m². The ratio α ≈ 0.88 suggests that it is necessary to use the MIM to simulate the experiment. In the simulations, we specified σ_p = −0.015C/m² and σ_m = −0.0095 C/m². Fig. 8 depicts the computed ionic current as a function of the dimensionless particle's location (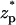). In the simulations, H = 150 nm, B = 40 nm, L_p = 60 nm, and the other parameters are consistent with Chang et al.'s data. As in Chang et al.'s experiment, throughout most of the translocation process, the ionic current is above the base value. Although the simulation results are in qualitative agreement with the experimental data, there are significant differences in the current's magnitude. In the simulations, the current changed from the open pore value of 100 pA to the maximum value of 240 pA while the corresponding values in the experiment were, respectively, 75 pA and 90 pA. The difference between the predicted and measured open-pore currents may be due to differences between the modeled and the actual pore's dimensions (see earlier discussion) and possibly due to an unmodeled potential drop at the electrodes' buffer interface. Current enhancement was also observed by Fan et al. (16). We will discuss their experimental data later in The Effects of Buffer and Surface Charge Concentrations.

FIGURE 8.

The ionic current through the pore as a function of the particle's location 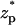. Note a = 1 nm, b = 2.2 nm, h = 50 nm, L_p = 60 nm, H = 150 nm, B = 40 nm, φ₀ = 200 mV, c₀ = 0.1 M, σ_p = −0.15 C/m², and σ_m = −0.0095 C/m². The simulation parameters are consistent with the experimental conditions of Chang et al. (15).

The effect of the particle's length

Next, we investigate the effect of the particle's length on the ionic current. Figs. 9 and 10 depict χ₀ as a function of the particle's normalized length (L_p/h) when a = 0.5 nm, h = 5.2 nm, φ₀ = 120mV, σ_p = −0.0637 C/m² (approximate surface charge density of a single strand DNA molecule), σ_m = 0, z_p = 0, and the solution concentration c₀ = 1 M. The subscript 0 in χ₀ indicates that χ is evaluated at z_p = 0. In Fig. 9, H = 36 nm, B = 18 nm, b = 0.9 nm, and α = 0.75. In Fig. 10, H = 200 nm, B = 100 nm, b = 5 nm, and α = 0.07. The solid line with diamonds and the dashed line with circles correspond, respectively, to MIM and SVM predictions.

FIGURE 9.

The current deviation χ₀ as a function of the particle's length. Note a = 0.5 nm, b = 0.9 nm, h = 5.2 nm, H = 36 nm, B = 18 nm, φ₀ = 120 mV, c₀ = 1 M, σ_p = −0.0637 C/m², and σ_m = 0. The solid line with diamonds and the dashed line with circles represent, respectively, the results of the MIM and SVM.

FIGURE 10.

The current deviation χ₀ as a function of the particle's length when the radius of the pore is 5 nm. All other conditions are the same as in Fig. 9. The solid line with diamonds and the dashed line with circles represent, respectively, the results of the MIM and SVM.

When α = 0.75 (Fig. 9), the MIM model predicts that as L_p increases, χ₀ initially decreases (current blockade), attains a minimum at ∼L_p/h ∼ 0.5, and then increases to eventually attain positive values (current enhancement). Once L_p/h > 2, χ₀ increases very slowly as L_p is further increased. This slow increase can be attributed to the increasing length of the electric double layer with its excess ion concentration. In contrast, the SVM (thin electric double layer) predicts only current blockade. As L_p increases, the SVM-predicted χ₀ (dashed line) decreases and attains an asymptotic value once L_p/h > 1.8. In other words, further increases in the particle's length have a negligible effect on the ionic current.

When α = 0.07 (Fig. 10), as the length of the particle increases, the MIM predicts that χ₀ decreases, attains a minimum at L_p/h ∼ 2, and then increases slowly. The qualitative behavior is similar to that depicted in Fig. 9. The SVM predicts that χ₀ decreases and eventually attains an asymptotic value when L_p/h > 4.

The prediction that the increase in the particle's length beyond ∼2h has a minimal effect on |χ₀| is consistent with Meller et al.'s (10) measurements. They reported two distinct regimes: when L_p < h, |χ₀| increased as L_p increased; and when L_p > h, χ₀ was nearly independent of L_p. Interestingly, despite the relatively large value of α (∼0.75) in some of their experiments, Meller et al. observed only current suppression and no current enhancement (under circumstances when others observed current enhancement with double-stranded DNA). One possible reason for the difference between our predictions and Meller et al.'s experiments is that the single-strand DNA has much smaller persistence length than the double-stranded DNA, and is less likely to mimic the rigid cylinder simulated here.

The effects of buffer and surface charge concentrations

The ionic conductivity can be decomposed into bulk conductivity and a contribution from the “surface conductance” (25,26).

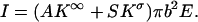(41)

In the above, A is a shape-factor that describes the reduction in the ionic current due to the presence of the particle in the pore. A is a function of the aspect ratio (a/b) and of the length of the particle (when the particle is short). S = 2(a+λ_D)/b² is the ratio of the circumference of the electric double layer and the pore's cross-sectional area. K^∞ and K^σ are, respectively, the bulk conductivity (in AV⁻¹ m⁻¹) and the surface conductivity of the electric double layer (in AV⁻¹). The base current when the particle is far from the pore, 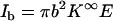, results only from the bulk conductivity of the electrolyte (assuming a thin electric double layer at the pore's surface). Therefore, the normalized current deviation is

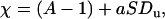(42)

where 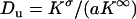is the Dukhin number (25). The first term results from the disturbance induced by the particle. The second term represents the current elevation resulting from the excess of ions in the electric double layer, and it depends both on the electric double layer's thickness and on the particle's surface charge.

The surface conductivity can further be decomposed into two parts,

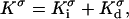(43)

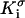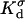where and are, respectively, the surface conductivities of the Stern layer and the diffuse layer. In our simulations, we do not account for ion diffusion in the Stern layer, and we take 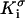= 0. When the electrolyte is 1:1 with equal diffusion coefficients, the concentration obeys the Boltzmann distribution, and the zeta-potential is small (26):

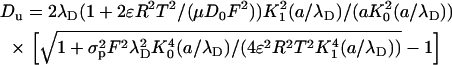(44)

The diffusion coefficients of the ions K⁺ and Cl⁻ are nearly identical. D₀ = 2 × 10⁻⁹ m²/s. The above expression is valid only when 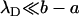. When the electric double layer's thickness and/or the surface charge increase, so does the Dukhin number.

Eq. 42 suggests that there is a critical Dukhin number,

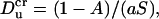(45)

which corresponds to χ = 0. When 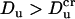, χ > 0 and current elevation occurs, 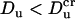, χ < 0 and current suppression is observed.

To examine the effect of bulk solution concentration on the ionic current, we computed χ₀ as a function of the bulk solution concentration (c₀). Fig. 11 depicts χ₀ as functions of c₀ (upper section) and 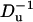(lower section) when a = 1 nm, b = 5 nm, h = 5 nm, L_p = 20 nm, H = 60 nm, B = 40 nm, σ_p = −0.15 C/m², σ_m = 0, and φ₀ = 120 mV. The hollow circles and the solid line correspond, respectively, to the results of the MIM simulations and the predictions of Eq. 42. When the bulk concentration is low, the electric double layer is relatively thick, the Dukhin number is large, and χ₀ > 0 (current elevation). As the concentration increases, the thickness of the electric double layer and the Dukhin number decrease and so does χ₀. When the bulk concentration c₀ = 0.46 M, D_u = 1.19, and χ₀ = 0. Further increases in the bulk concentration (reductions in the Dukhin number) lead to current suppression (χ₀ < 0). Similar trends are featured by the approximate expression Eq. 42, albeit the agreement between the approximation and the full numerical solution is poor. The discrepancy between simulation and theory can be attributed to the assumptions of small ζ-potential (ζ_pF/(RT) ≪ 1) and thin electric double layer (α = λ_D/(b–a) ≪ 1) for the Eq. 42. In our simulation, the large surface charge σ_p yields large zeta-potentials of the particle. For example, when c₀ = 2 M, ζ_pF/(RT)∼1.6. As the concentration increases, the value of α decreases and so does the discrepancy between the MIM results and the analytical predictions.

FIGURE 11.

The relative current deviations χ₀ as functions of the bulk concentration C₀ (upper) and 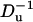(lower). Note a = 1 nm, b = 5 nm, 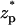= 0, L_p = 20 nm, H = 60 nm, B = 40 nm, φ₀ = 120 mV, σ_p = −0.15 C/m², and σ_m = 0. The solid line represents the approximate solution from Eq. 42, and the circles are the MIM results.

The theoretical predictions of Fig. 11 are consistent with the experimental observations of Fan et al. (16), who measured the ionic current as a function of the bulk solution concentration when double-stranded DNA translocated in a silicon oxide tube. At high salt (KCl) concentrations (i.e., c₀ = 2 M), current blockade was observed. At relatively low bulk concentrations (i.e., c₀ = 0.5 M), current enhancement was observed.

To examine the effect of the particle's surface charge σ_p, we fixed σ_m and varied σ_p from zero to −0.4 C/m². Fig. 12 depicts the relative current deviation χ₀ as a function of σ_p (upper image) and as a function of 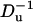(lower image) when a = 1 nm, b = 2.2 nm, h = 50 nm, L_p = 60 nm, H = 150 nm, B = 40 nm, φ₀ = 200 mV, c₀ = 0.1 M, α ≈ 0.78, and σ_m = −0.009 C/m². The above parameters were selected to mimic Chang et al.'s (15) experiment. The symbols and solid line represent, respectively, the MIM solution and the approximate Eq. 42. Since α in Fig. 12 is relatively large, we do not expect the approximate Eq. 42 to provide a good prediction of χ₀ for large surface charges. As Eq. 42 is valid only for small ζ-potentials, we depicted the approximate expression only in the range −0.1 C/m² < σ_p < 0. Witness that as |σ_p| decreases, the discrepancy between the simulation and theory decreases. When |σ_p| < 0.05 C/m², the Eq. 42 provides a good approximation for the MIM results. When |σ_p| is small, the excess concentration in the electric double layer is relatively small and current suppression (χ₀ < 0) is observed. When the magnitude |σ_p| increases, the excess concentration in the electric double layer and the Dukhin number increase and we observe ionic current enhancement (χ₀ > 0).

FIGURE 12.

The current deviations χ₀ as a function of the surface charge density on the particle (upper) and as a function of 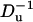(lower). Note a = 1 nm, b = 2.2 nm, 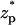= 0, h = 50 nm, L_p = 60 nm, H = 150 nm, B = 40 nm, φ₀ = 200 mV, C₀ = 0.1 M, and σ_m = −0.009 C/m². The solid line represents the approximate solution from Eq. 42, and the circles are the MIM results.

Fig. 13 depicts the particle's speed 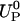, calculated with the MIM when z_p = 0, as a function of σ_p (upper section) and as a function of 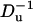(lower section) under the same conditions as in Fig. 12. Since the particle is negatively charged, it is expected to migrate toward the anode (in the negative z direction). This is, indeed, the case as long as σ_p < σ_m. When σ_p is close to the value of σ_m, the particle's velocity goes to zero. When 0 > σ_p > σ_m, the electroosmotic flow induced by the membrane's surface charge will drive the particle away from the pore (positive translocation speed), and the particle will not translocate.

FIGURE 13.

The translocation speed of the particle as a function of the surface charge density on the particle (upper) and as a function of 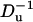(lower). All the conditions are the same as in Fig. 12.

Finally, Fig. 14 divides the parameter space spanned by λ_D and |σ_p| into a region in which current elevation (χ₀ > 0) and current suppression (χ₀ < 0) are observed. The solid and dashed lines correspond, respectively, to the predictions of the approximate formula Eq. 42 and the results of the MIM calculations. In Fig. 14, a = 1 nm, b = 5 nm, L_p = 20 nm, H = 60 nm, B = 40 nm, φ₀ = 120 mV, and σ_m = 0. The approximate solution underestimates the values of λ_D corresponding to χ₀ = 0. This is due to the assumption used in Eq. 42 that the thickness of the electric double layer is much smaller than the width of the gap between the particle and the pore.

FIGURE 14.

The dependence of the relative current deviation χ₀ on the surface charge density and the electric double layer's thickness. Note a = 1 nm, b = 5 nm, 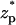= 0, L_p = 20 nm, H = 60 nm, B = 40 nm, φ₀ = 120 mV, and σ_m = 0. The solid and dashed lines represent, respectively, the predictions of Eq. 42 and the MIM results.

CONCLUSIONS

Using a multi-ion model that accounts for the polarization of the electric double layer, we computed the effect of a translocating, cylindrical particle on the ionic current through a pore. When the electric double layer is thin (high bulk solution concentration), current blockade is typically observed. The magnitude of the current blockade is roughly proportional to the cross-sectional area of the particle, and the duration of the blockade is proportional to the length of the particle. The blockade's amplitude is independent of the particle's length as long as the particle is longer than the pore. When the membrane's surface charge is of the same sign and same magnitude (or larger) as the particle's surface charge, the electroosmotic flow induced by the pore's surface charge will prevent the particle from translocating and the particle will not go through the pore. When the electric double layer is thin, predictions based on the Poisson Boltzmann model and the Smoluchowski's slip velocity model are in good agreement with the results of the multi-ion model.

When the electric double layer is thick, the excess ion concentration inside the electric double layer and the polarization of the double layer contribute significantly to the ionic current. As a result, one may observe either both current depression and elevation or current enhancement alone during the translocation process. Models based on the Poisson-Boltzmann equation and the Smoluchowski velocity fail to predict the current enhancement phenomenon and are not appropriate for simulating a particle's translocation under the conditions of a thick electric double layer.

The theoretical predictions were compared and qualitatively agreed with experimental observations for the translocation of double-stranded DNA molecules through synthetic nanopores. When the cylindrical particles were endowed with similar charge distributions to those of DNA molecules, the predicted electrophoretic velocity was in good agreement with experimental measurements. This suggests that DNA translocation is dominated by a balance between electric and viscous forces.

In our simulations, we used exclusively a continuum model. A few studies found discrepancies between continuum model and Brownian Dynamics model predictions for transport through ionic channels and concluded that the continuum model is not appropriate when the Debye length (λ_D) exceeds the pore's radius and when the number of ions in the pore is very small (28,29). In our case, however, the number of ions is an order-of-magnitude larger than in the above studies. Moreover, studies of ion transport in synthetic nanopores reveal a remarkable agreement between the experimental data and continuum model predictions under conditions when the pore's smallest dimension ranged from 0.1 to 1 Debye lengths (30–33). MIM continuum theories have also been successful in predicting ionic currents through ionic channels (34). Finally, our continuum-based predictions are in good qualitative agreement with experimental data for DNA translocation and with predictions of molecular dynamics simulations (13). Hence, it appears that the MIM model captures the essential physics of the translocation process. The quantitative differences between the simulations and the experiments can be attributed to the complex geometry of the synthetic pore, which was not duplicated in the numerical simulations.