Abstract
Structural barriers to wave propagation in cardiac tissue are associated with a decreased threshold for repolarization alternans both experimentally and clinically. Using computer simulations, we investigated the effects of a structural barrier on the onset of spatially concordant and discordant alternans. We used two-dimensional tissue geometry with heterogeneity in selected potassium conductances to mimic known apex-base gradients. Although we found that the actual onset of alternans was similar with and without the structural barrier, the increase in alternans magnitude with faster pacing was steeper with the barrier—giving the appearance of an earlier alternans onset in its presence. This is consistent with both experimental structural barrier findings and the clinical observation of T-wave alternans occurring at slower pacing rates in patients with structural heart disease. In ionically homogeneous tissue, discordant alternans induced by the presence of the structural barrier arose at intermediate pacing rates due to a source-sink mismatch behind the barrier. In heterogeneous tissue, discordant alternans occurred during fast pacing due to a barrier-induced decoupling of tissue with different restitution properties. Our results demonstrate a causal relationship between the presence of a structural barrier and increased alternans magnitude and action potential duration dispersion, which may contribute to why patients with structural heart disease are at higher risk for ventricular tachyarrhythmias.
INTRODUCTION
When paced at a rapid rate, cardiac cells typically exhibit repolarization alternans, where successive action potentials alternate between having long and short duration. In tissue, where many cells are coupled together, such cellular alternans may occur in different spatial patterns. One type of pattern is spatially concordant alternans, where the tissue everywhere exhibits the long action potential on one beat and everywhere the short action potential on the next beat. A second type of pattern is spatially discordant alternans, where (at least) one region is out of phase and exhibits a long action potential when another region exhibits a short action potential.
Alternans can induce gradients of repolarization across the heart, particularly during spatially discordant alternans. Repolarization gradients, in turn, are a known substrate for cardiac arrhythmias (1–5). One way in which an arrhythmia may be initiated is through unidirectional block, which can occur when a long action potential has left the tissue in one region with too little recovery time for the next wave to propagate, whereas a neighboring region, having had an action potential of shorter duration, allows for propagation of the wave. Evidence of causality between repolarization alternans and the onset of arrhythmias has been demonstrated in experiments (6–11) and in computer simulations (10,12,13).
Action potential alternans is manifest on the surface electrocardiogram (ECG) as T-wave alternans (TWA). In patients with structural heart disease, alternans occurs at slower pacing rates than in healthy people (14–18). This indicates a potential problem for these patients, since the occurrence of TWA at relatively slow rates is a predictor of ventricular tachyarrhythmias and sudden cardiac death (17,19–23), possibly due to the mechanistic link described above.
It has been hypothesized that the decreased TWA threshold in patients with structural heart disease is due to the presence of structural barriers (e.g., fibrosis or scar tissue due to a prior myocardial infarction (“heart attack”)), which impede propagation of the action potential across the heart. Indeed, in vitro studies have shown that the presence of a structural barrier reduces the threshold for discordant alternans (7). The proposed mechanism for this threshold reduction is a decoupling by the barrier of regions of tissue with different intrinsic ionic properties, regions that exist as part of the apex-base heterogeneity across the epicardium (7). However, the exact mechanism of this decoupling is not known.
The duration of the action potential is strongly dependent on the duration of the recovery period (the diastolic interval (DI)) before the action potential, in that the action potential tends to shorten when the diastolic interval shortens. This property is known as action potential duration (APD) restitution. A similar relationship is characteristic of the conduction velocity (CV) of a propagating wave; this is known as CV restitution.
Previous modeling studies have shown how discordant alternans may arise during constant pacing in homogeneous tissue due to APD restitution and CV restitution (13,24). However, several experimental studies have indicated that spatial heterogeneity may promote discordant alternans (6,8,9,11,25). Indeed, it is well known that electrophysiological properties are not homogeneous throughout the ventricles. There are intrinsic differences in ionic properties (e.g., ion-channel densities) in isolated cells or tissue slices from different regions of the ventricles, e.g., across the ventricular wall, between the apex and the base, between the left and the right ventricle, and between the posterior and the septal walls of the left ventricle (26).
In this study we investigate the effects of the presence of a structural barrier on the onset of alternans in tissue with and without intrinsic ionic heterogeneity, simulating the apex-to-base gradient in expression levels of certain potassium channels. A simulation study is particularly well suited to investigate the effects of ionic heterogeneity in the mechanism of discordant alternans, since one cannot straightforwardly eliminate it experimentally. In particular, using modeling, we address the hypothesis that the threshold for discordant alternans is reduced in the presence of a structural barrier and that this is due to decoupling of intrinsically heterogeneous tissue. Furthermore, we quantify the effects of the structural barrier on the repolarization gradient and discuss how our findings may contribute to explaining the increased risk of arrhythmias in patients with a prior myocardial infarction.
METHODS
Mathematical model
Recent experimental studies have indicated that alternans is caused by instabilities in intracellular Ca2+ handling (27–32). We have therefore used the combined Shiferaw et al. and Fox et al. (the Shiferaw-Fox) model, presented in Shiferaw et al. (33), for our simulations. This model includes the ionic membrane currents of Fox et al. (34), plus a comprehensive intracellular Ca2+ handling system (35), which can become unstable during fast pacing. Parameters that were varied in previous studies (33,35) were fixed here at u = 9, γ = 0.2, τf = 30 ms, and τq = 20 ms. With these parameter values, the transition from no alternans to (electromechanically concordant) alternans in a space-clamped model cell is predominantly driven by instability of the Ca2+ dynamics (33). This is most likely also the case in the spatially extended two-dimensional (2D) sheets in our simulations.
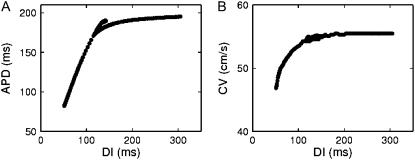
Since the CV restitution curve of the Shiferaw-Fox model is very flat (decreases by ∼5% with 16-fold decrease in DI), we have multiplied the time constant of the slow inactivation variable of the sodium current (τj) by a factor of five, as done for other models (e.g., Qu et al. (13)), to slow down recovery from inactivation and incorporate CV restitution. The APD and the CV restitution curves obtained in a one-dimensional (1D) cable are shown in Fig. 1. For comparison, see, e.g., Fig. 1 of Qu et al. (13), in which discordant alternans was investigated without structural barriers.
FIGURE 1.
APD (A) and CV (B) restitution curves in the Shiferaw-Fox model. Data points were obtained from the middle of 1.5-cm-long homogeneous cable, using a dynamic (S1S1) restitution protocol.
The model code is available as Supplementary Material.
Geometry
The model tissue was designed to mimic the experimental setup of Pastore and Rosenbaum (7). Since those experiments were carried out with “frozen heart” preparations (the myocardium under the mapping region is frozen from the endocardium, leaving a 0.8-mm thin rim of viable epicardial tissue (7)), we use a 2D sheet. The sheet size was set to 1.5 × 1.5 cm2, which approximates the mapping region in Pastore and Rosenbaum (7). The sheet was anisotropic, with the fiber direction parallel to the x axis. This was achieved by setting the diffusion coefficient in the x direction (Dx = 1.0 cm2/s) equal to four times that in the y direction (Dy = 0.25 cm2/s).
Sheets were normally paced from a small square of 0.06 × 0.06 cm2 centered on the bottom edge of the sheet. In some simulations (see the section Effects of changing the stimulus site), sheets were paced from an equally sized area centered on the left or the right edge of the sheet. In all cases, the stimulus duration was 0.5 ms and the stimulus amplitude −150 pA/pF, corresponding to ∼1.5 the diastolic threshold.
Ionic heterogenity
In several species, including dog (36) and guinea pig (37,38), the APD is shorter at the apex than at the base. In canine hearts this gradient in APD correlates with the densities of the transient outward potassium current (Ito) and the slow delayed rectifier current (IKs) being lower at the base than at the apex (both by a factor of two) (36). In the model, ionic heterogeneity was included by introducing a gradient in the horizontal direction in the maximal conductances of Ito and IKs. These conductances were varied linearly from 2/3 of their nominal values at the left edge of the sheet to 4/3 of their nominal values at the right edge of the sheet to give a twofold variation across the sheet. This variation results in a gradient of APD of 30 ms/cm at a basic cycle length (BCL) of 340 ms, very similar to the values reported for guinea pig (32 ms/cm at 400 ms (37) and ∼30 ms/cm at 300 ms (38)).
Structural barrier
The structural barrier is modeled as a rectangular piece of inexcitable tissue surrounded by no-flux boundaries to mimic the well-defined scar that was obtained experimentally by burning the tissue with a laser (7). Because of these no-flux boundary conditions, the structural barrier does not function as a current sink. The structural barrier measured 0.21 × 1.02 cm2 and was placed in the middle of the sheet. The structural barrier is a macroscopic obstacle in the sense that it is ∼3 times the space constant in the direction perpendicular to the barrier. As such, the structural barrier removes the coupling between tissue on either side of it, i.e., it decouples different regions of tissue.
Numerical integration
The equations were solved using an operator splitting method (39) with forward Euler integration of both operators. We used a fixed time step for the partial differential equation of Δtmax = 0.025 ms, and an adaptive time step for the ordinary differential equations varying between Δtmax/20 and Δtmax using the criterion of Qu and Garfinkel (39). The space step was fixed at Δx = 0.015 cm. No-flux boundary conditions were used. The activation and inactivation variables were computed from their analytic formula (40). To increase computation speed, lookup tables were used for evaluation of the voltage-dependent rate constants or steady-state values and time constants. These tables were built with 0.1-mV increments in voltage; linear interpolation was used to compute intermediate values.
Data analysis
APD was defined as the time between the crossing of −80 mV on the upstroke of the action potential and the crossing of −80 mV during repolarization. In the Shiferaw-Fox model, this corresponds to ∼85% repolarization. The local cycle length (CL) was defined as the time between the crossing of −80 mV on the upstroke of two successive action potentials. DI was defined as CL-APD. Dispersion of APD and CL was calculated as the standard deviation of the spatial distributions. Alternans was said to be present when the difference between two successive APDs exceeded 1 ms anywhere in the sheet.
RESULTS
To separate the effects of the structural barrier from the effects of the intrinsic ionic heterogeneity, we investigated four different situations: ionically homogeneous tissue in the absence of and in the presence of a structural barrier (see the section Ionically homogeneous tissue, below), and ionically heterogeneous tissue in the absence of and in the presence of a structural barrier (see the section Ionically heterogeneous tissue).
Ionically homogeneous tissue
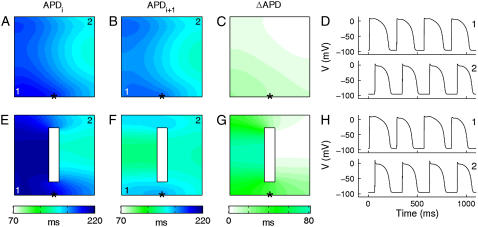
In an ionically homogeneous sheet, the Shiferaw-Fox model exhibits APD alternans when paced at a rapid BCL. This occurs both in the presence and absence of a structural barrier. An example is shown in Fig. 2 for BCL = 250 ms. In the absence of a structural barrier, there is a gradient in APD, even though the tissue is homogeneous (Fig. 2, A and B). This nonuniformity of APD is partly due to differences in electrotonic load (due to wavefront curvature and no-flux edge effects): e.g., APD is longer at the stimulus site (*) where the load is large. This type of nonuniformity also occurs in the absence of alternans (41–43). Indeed, the spatial distribution of the action potential with the long duration (APDi) is very similar to that during normal, nonalternating rhythm at longer values of BCL.
FIGURE 2.
APD alternans in ionically homogeneous sheets without (A–D) and with (E–H) a structural barrier. (A–C) Spatial distribution of APD of even beat (APDi; A) and odd beat (APDi+1; B) and difference between successive beats (ΔAPD; C) in tissue without a structural barrier. (D) Voltage waveforms obtained from two different locations (marked “1” and “2”) in the sheet without a barrier. (E–H) Same as for A–D but in tissue with a structural barrier. A and E, B and F, and C and G are pairwise on the same color scale. Asterisks indicate stimulus site. BCL = 250 ms.
During alternans, CV restitution effects also contribute to the APD gradient as previously described (13,24). Suppose the tissue at the stimulus site has a long APDi alternating with a short APDi+1. Then DIi (the DI after APDi) is short and DIi+1 long so that APDi + DIi = APDi+1 + DIi+1 = BCL at the stimulus site. Due to CV restitution, the short DIi causes a slower CVi+1. The slowed conduction of the next AP causes an increase in DIi far from the stimulus site, which in turn increases APDi+1 and CLi far from the stimulus. The opposite situation occurs after the long DIi+1. Thus gradients in APD arise such that the long APDi decreases as the wave propagates across the tissue and the short APDi+1 increases, thereby causing the alternans magnitude (ΔAPD = APDi − APDi+1) to decrease away from the stimulus site (Fig. 2 C). In the presence of a structural barrier these gradients in APD are slightly enhanced (Fig. 2, E–G). In particular, APD is increased behind each of the far corners of the barrier due to an increase in the electrotonic load for the propagating wavefront (43).
If the gradients in APD are steep enough and the tissue sufficiently large, APDi+1 becomes larger than APDi far from the stimulus site and spatially discordant alternans arises (13,24). Fig. 3 shows an example of discordant alternans at BCL = 280 ms. The figure shows APD profiles of two successive action potentials parallel to and in close proximity (0.45 mm) of the structural barrier (solid curves). At the distal end of the barrier, at a distance of ∼1.25 cm from the stimulus site, the APD profiles cross, showing the existence of spatially discordant alternans. The discordance arises in this case because the APD of the odd beat is longer behind the structural barrier than it is in the absence of the barrier (dashed curves; compare lower solid to lower dashed curve) due to an increase in the electrotonic load. Whereas the wavefront is approximately rectilinear when it propagates along the structural barrier, it becomes convex behind the barrier. Hence, we find that APD is increased where the wave is convex, in accordance with previous studies (44,45).
FIGURE 3.
Discordant alternans in homogeneous sheet with structural barrier. (A) Successive APD profiles along the y axis (parallel to the structural barrier) in a homogeneous sheet without (dashed lines) or with a structural barrier (solid lines). The profiles are taken at a distance of 0.6 cm from the edge of the sheet, i.e., in the case of a structural barrier, 0.45 mm from the edge of the barrier. Thick line indicates the position of the barrier. (B) Closeup of APD node in A. BCL = 280 ms.
Fig. 3 thus shows a situation where discordant alternans is induced by a source-sink mismatch that changes the curvature and the APD of the propagating wave. The reason discordant alternans occurs at this BCL of 280 ms and not at the faster BCL of 250 ms (Fig. 2) is that due to APD restitution, ΔAPD is smaller at the longer BCL (only a few ms behind the structural barrier) so that a small increase in the duration of the shorter APD is sufficient to induce discordant alternans. In this case, discordant alternans does not require intrinsic ionic heterogeneity to be present.
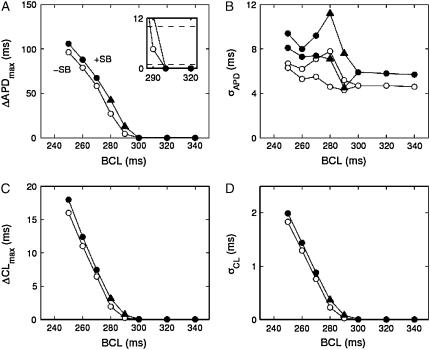
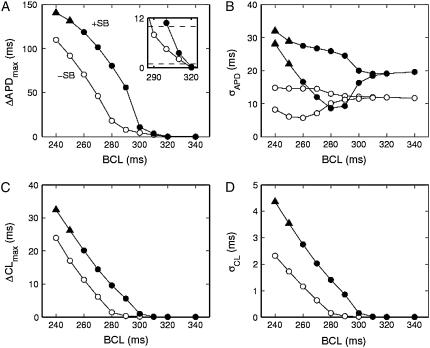
A summary of the types of dynamics occurring at different values of BCL for homogeneous tissue with and without the structural barrier is shown in Fig. 4. For BCL values of 300 ms and longer there is no alternans (i.e., ΔAPD < 1.0 ms) with (solid symbols) or without (open symbols) the structural barrier (Fig. 4 A). Without the structural barrier there is concordant alternans at values of BCL between 290 ms and 250 ms (○), whereas there is 2:1 conduction block for BCL = 240 ms (not shown). In contrast, in the presence of a structural barrier, there is discordant alternans (▴) for values of BCL of 290 ms and 280 ms, there is concordant alternans for BCL values of 270 ms to 250 ms (•), whereas at 240 ms there is 2:1 conduction block.
FIGURE 4.
Alternans magnitude and dispersion in homogeneous sheets. (A) Maximum difference in APD between two successive action potentials. Inset shows magnification of onset of alternans. (B) Dispersion of APD. Two values of σAPD are shown at each BCL because the dispersion of the even beats differs from that of the odd ones during alternans (the short APs are in general more uniform). (C) Maximum difference in CL between two successive action potentials. (D) Dispersion of CL. The alternation in σCL is tiny and not visible on the scale of the figure. Solid symbols indicate the presence of a structural barrier, and open symbols indicate its absence. Triangles indicate discordant alternans. “+SB” indicates presence of structural barrier, “−SB” indicates its absence.
The spatial dispersion of APD (σAPD) tends to grow with decreasing BCL and is slightly larger when the structural barrier is present (Fig. 4 B), as seen in Fig. 2. Likewise, the maximum difference in CL of two successive beats (ΔCL; Fig. 4 C) and the dispersion of CL (σCL; Fig. 4 D) are slightly increased by the presence of the barrier.
Ionically heterogeneous tissue
Given that cellular ion-channel expression is not uniform throughout the myocardium, we sought to investigate the effects of ionic heterogeneity on the dynamics of the tissue both in the presence and in the absence of a structural barrier. As our 2D sheet models the epicardium, where apex-base gradients in several ionic currents cause a gradient in APD (36–38), we included linear gradients in the conductances of Ito and IKs parallel to the fiber direction and perpendicular to the structural barrier (see Methods).
Concordant alternans
The spatial APD distribution at BCL = 280 ms in the presence of ionic heterogeneity but in the absence of a structural barrier is shown in Fig. 5, A and B. Because Ito and IKs are both repolarizing currents and because both are decreased in the left side of the sheet but increased in the right side, APD is longer toward the left side and shorter in the right side of the sheet. The alternans is spatially concordant with a fairly smooth and small ΔAPD (Fig. 5, C and D).
FIGURE 5.
Concordant APD alternans in ionically heterogeneous sheets without (upper row) and with (lower row) a structural barrier. (A) Spatial distribution of APDi. (B) Spatial distribution of APDi+1. (C) Spatial distribution of ΔAPD. (D) Voltage waveforms obtained from two different locations (marked “1” and “2”) in the sheets without a barrier. (E–H) Same as for A–D but in tissue with a structural barrier. Color scales apply to both rows. Asterisks indicate stimulus site. BCL = 280 ms.
In the presence of the structural barrier, however, the spatial heterogeneity of APD is increased for the long APD (Fig. 5 E): it is much longer to the left of the barrier than to the right of it, with steep gradients along the barrier edges. This orientation of the APD gradient is quite similar to the orientation seen without alternans in this model (i.e., at larger values of BCL; not shown) and in a previous modeling study using two distinct model cell types, one on either side of a barrier (43). In contrast, the short APD is much more homogeneous in the presence of the structural barrier (Fig. 5 F). These spatial APD distributions create steep gradients in ΔAPD around the corners of the structural barrier (Fig. 5 G).
Discordant alternans
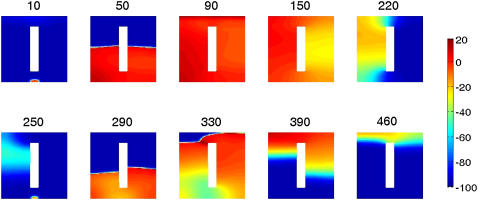
At the BCL shown in Fig. 5 (280 ms), the alternans is concordant (Fig. 5, G and H). With faster pacing, discordant alternans occurs in the presence of the structural barrier. Fig. 6 shows snapshots of the transmembrane potential during two successive action potentials in an ionically heterogeneous sheet with a structural barrier for BCL = 240 ms. The upper panels show depolarization and repolarization during the action potential with the longer APD (APDi). At the time of initiation of this action potential, the sheet is recovered everywhere (10 ms panel). The depolarization wavefront hence travels up the sheet equally fast on either side of the barrier (50 ms panel) and after 90 ms the entire sheet is depolarized. After 150 ms the region to the right of the structural barrier has started to repolarize. This spatial difference in repolarization persists, such that at 220 ms, the model tissue to the right of the barrier has fully repolarized, whereas that to the left has not. Thus, whereas the depolarization wave traveled through the model tissue from the bottom to the top, the repolarization wave propagated from right to left.
FIGURE 6.
Development of discordant APD alternans in an ionically heterogeneous sheet with a structural barrier. Each panel shows a snapshot of the transmembrane potential (in millivolts) in the sheet at the indicated time (in milliseconds). BCL = 240 ms.
When the next action potential is initiated after 240 ms and starts to propagate, the left-right gradient in repolarization persists (250 ms panel). The delayed recovery and therefore shorter diastolic interval on the left side of the barrier slows down the depolarizing wavefront due to CV restitution (290 ms panel) and also causes repolarization to occur sooner in that region due to APD restitution (330 and 390 ms panels). Because repolarization takes place sooner to the left than to the right of the barrier, this figure illustrates a reversal of the gradient of repolarization between the two successive beats.
The resulting APD distributions are shown in Fig. 7, F and G. APDi is much longer to the left of the structural barrier, whereas APDi+1 is shorter there and longer to the right of the barrier. Therefore the alternans is spatially discordant with the upper right part of the sheet alternating out of phase with the rest of the sheet (Fig. 7, H and J). The slowdown of the depolarization wavefront to the left of the barrier after the shorter DI (Fig. 6, 290 ms panel) causes the local CL to vary in space, even though it is held constant at the pacing site. Therefore spatial heterogeneity in ΔCL is induced (Fig. 7 I).
FIGURE 7.
Discordant APD alternans in ionically heterogeneous sheets without (upper row) and with (lower row) a structural barrier. (A–D) Spatial distribution of APDi (A), APDi+1 (B), ΔAPD (C), and ΔCL (D). (E) Voltage waveforms obtained from two different locations (marked “1” and “2”) in the sheets without a barrier. (F–J) Same as for A–E but in tissue with a structural barrier. Color scales apply to both rows. Asterisks indicate stimulus site. BCL = 240 ms.
All of these spatial heterogeneities are much reduced in the absence of a structural barrier (Fig. 7, A–E). Hence, without the structural barrier, the alternans is concordant (Fig. 7, C and E).
Onset of alternans
Fig. 8 shows the different dynamics that occur in ionically heterogeneous tissue when BCL is varied. For BCL of 320 ms and above there is no alternans; and for BCL of 230 and shorter there is 2:1 conduction block. A comparison of Figs. 4 and 8 reveals that the range over which alternans occurs is larger in sheets with ionic heterogeneity (240–310 ms; Fig. 8) than in sheets without (250–290 ms; Fig. 4), mainly because of the prolongation of APD, which causes earlier onset of alternans. In heterogeneous sheets without a structural barrier, the alternans is always concordant, whereas in sheets with a barrier, there is discordant alternans for BCL values of 240 ms and 250 ms (▴; Fig. 8).
FIGURE 8.
Alternans magnitude and dispersion in heterogeneous sheets. (A) Maximum difference in APD between two successive action potentials. Inset shows magnification of onset of alternans with dashed lines indicating detection criteria of 1 ms and 10 ms. (B) Dispersion of APD. C: Maximum difference in CL between two successive action potentials. (D) Dispersion of CL. Solid symbols indicate the presence of a structural barrier, and open symbols indicate its absence. Triangles indicate spatially discordant alternans. “+SB” indicates presence of structural barrier, “−SB” indicates its absence.
The pacing rate at which alternans first occurs is the same (310 ms) both in the presence and in the absence of the structural barrier (Fig. 8 A). However, in our simulations we distinguish alternans from nonalternans using a much smaller criterion value (1 ms, see inset in Fig. 8 A) than what is possible when analyzing experimental data. When we instead define alternans as alternating APD differences larger than 10 ms, the same criterion as used in analyzing the experimental data (7) (Fig. 8 A, inset), there is an apparent shift in the onset of alternans due to the presence of the structural barrier (from 280 to 300 ms). This apparent shift in the onset of alternans occurs because the alternans amplitude increases more quickly as a function of BCL in sheets with a structural barrier than in sheets without it (Fig. 8 A). This effect is much larger in ionically heterogeneous sheets than in homogeneous sheets (Fig. 8 A versus Fig. 4 A), as is the barrier-induced difference in σAPD (Fig. 8 B versus Fig. 4 B), in ΔCL (Fig. 8 C versus Fig. 4 C), and in σCL (Fig. 8 D versus Fig. 4 D).
Restitution properties and mechanism of discordant alternans
We now turn to an analysis of the mechanism of discordant alternans in the ionically heterogeneous model tissue. The finding of increased APD heterogeneity and the possibility of inducing discordant alternans in heterogeneous sheets with a structural barrier (Figs. 6 and 7) support the hypothesis that the structural barrier decouples tissue which possesses inherently different ionic properties (7). However, to obtain discordance, APD heterogeneity is not sufficient: the successive APD profiles have to cross, forming a node. This is most easily accomplished if the APD gradients reverse on alternate beats. In sufficiently large ionically homogeneous tissue this can be accomplished through CV restitution (13,24). In our simulations of heterogeneous tissue with a structural barrier, the APD gradients reverse because of steep APD restitution to the left of the barrier so that APDi+1 becomes short there after the long APDi (Fig. 7, F and G). Note that reversal of the APD gradients is not a sufficient criterion for discordant alternans: the gradients additionally have to be steep enough to cross within the sheet. Thus, although the APD gradients have reversed at BCL = 280 ms in the presence of a structural barrier (Fig. 5, E and F), the gradients are not sufficiently steep to cause discordance until BCL is further reduced.
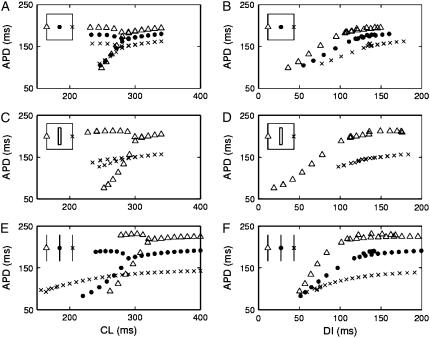
If discordance depends on intrinsic restitution properties, why does discordant alternans not occur in the absence of the structural barrier? To answer this question, we computed and compared APD restitution curves at different locations within the sheets, both in the presence of and in the absence of the structural barrier. Since we pace at a constant rate in all of our simulations, we use a dynamic (S1S1) APD restitution protocol. Fig. 9, A–D shows restitution curves from three different locations in heterogeneous sheets without (Fig. 9, A and B) and with (Fig. 9, C and D) a structural barrier. At the left edge (Δ) gto and gKs both equal 2/3 of their nominal values, at the center (•) they both equal their nominal values, and at the right edge (×) they both equal 4/3 of their nominal values (note that no values were obtained from the center of the sheet in the presence of a structural barrier (Fig. 9, C and D), as this is where the barrier is located).
FIGURE 9.
Restitution properties of heterogeneous sheets (A–D) and homogeneous cables (E and F). (A and B) Dynamic (S1S1) restitution curves from locations at the left edge (Δ), in the middle (•), and at the right edge (×) of a sheet (inset shows locations from which APDs are measured) without a structural barrier. (C and D) Dynamic restitution curves from locations at the left edge (Δ) and at the right edge (×) of a sheet with a structural barrier. (E and F) Dynamic restitution curves from middle of 1.5-cm homogeneous cables (inset shows locations from which APDs are measured) with 2/3 (Δ), 1/1 (•), and 4/3 (×) of the nominal maximal conductance of Ito and IKs, corresponding to the values at the left, center, and right locations in the sheets.
The APD restitution curves vary significantly depending on the location in the ionically heterogeneous sheets, e.g., APD is smaller at the right side of the sheets where gto and gKs are larger (Fig. 9, B and D). This variation is increased in the presence of a structural barrier where APD differs distinctly between the left and the right side of the barrier (Fig. 9 C). Indeed, in this case, each side of the sheet acts relatively independently of the other, as if the tissue were composed of individual cables (Fig. 9, E and F). Thus, in the absence of a structural barrier, electrotonic coupling smoothes out the intrinsic heterogeneity in APD restitution properties. The presence of a structural barrier, however, reduces this coupling, resulting in large spatial dispersion of APD. (Note that whereas the alternans magnitude in the presence of the structural barrier is similar to that in the cables, the large shift (140 ms; from 180 ms to 320 ms) in the CL at which alternans occurs in the different cables is not seen in the sheets (20 ms with and 10 ms without the barrier). This is because alternans occurring somewhere in the sheet drives small magnitude alternans in other regions of the sheet.)
Figs. 6 and 7 showed how large alternations in APD to the left of the structural barrier results in reversal of successive APD gradients and the onset of discordant alternans. From Fig. 9, A and C, we see that the alternans magnitude is much larger in the left side of the sheet (because of the intrinsic properties of the tissue there) when there is less coupling in the presence of the structural barrier. Hence, discordant alternans is facilitated in the presence of a structural barrier because the barrier decouples tissue with intrinsically different restitution properties.
Effects of changing the stimulus site
All of the results described thus far in this manuscript come from simulations where the sheets were paced from the middle of the bottom edge. To investigate whether qualitatively similar dynamics occur in response to stimuli from different sites within the sheets, we repeated the simulations in Fig. 8 while stimulating from different locations within the sheets.
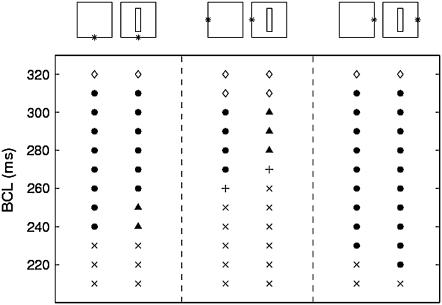
When changing the location of the stimulus site from the middle of the bottom edge to the middle of the left edge of the heterogeneous sheet, qualitative changes of the dynamics occur (Fig. 10). The range in BCL over which alternans occurs is reduced, both with and without the barrier. This is mainly due to 2:1 conduction block occurring at relatively larger values of BCL. With the structural barrier, there is also a change in the type of alternans: instead of being concordant, the alternans is now discordant, even at the relatively slow pacing rates.
FIGURE 10.
Effect of changing the location of the stimulus site (*) on the type of resulting dynamics. No alternans (⋄), concordant alternans (•), discordant alternans (▴), 2:1 block (×), and higher order block (+).
When changing the stimulus site to the right edge of the sheet, opposite changes in the dynamics occur (Fig. 10). Now, 2:1 conduction block occurs only at faster pacing rates, thus increasing the range in BCL over which alternans occurs. There is no discordant alternans.
These changes in dynamics can be understood based on the restitution curves in Fig. 9. First, 2:1 block occurs at slower pacing rates in cables with ionic properties corresponding to those in the left side of the sheet than in cables with ionic properties corresponding to those in the right side, which explains the prevalence of 2:1 conduction block in sheets paced from the left compared to those stimulated from the right. Second, when stimulating from the right edge, alternans of relatively small amplitude occurs around the stimulus site due to the intrinsic properties there. The alternans grows in amplitude away from the stimulus site where the intrinsic properties favor alternans more (Fig. 9). Thus, the long AP becomes even longer away from the stimulus site, whereas the short AP gets even shorter. This holds both with and without the structural barrier. Hence, discordant alternans does not occur in either case. In contrast, when stimulating from the left edge, the alternans amplitude is relatively large at the stimulus site but decreases across the sheet. Without the structural barrier, the left-to-right APD profile is not sufficiently steep to cause discordant alternans. However, with the barrier, steep gradients in APD and DI arise around the corners of the barrier, so that the alternans becomes discordant.
Because the structural barrier decouples tissue with different electrophysiological properties to promote discordant alternans, it is possible that with a positioning of the structural barrier that is not orthogonal to the direction of ionic heterogeneity, discordant alternans will not occur. Indeed, we have found that simulations in heterogeneous tissue with a structural barrier positioned parallel to the axis of ionic heterogeneity show a greatly reduced APD heterogeneity (not shown, but see Fig. 3 of Sampson and Henriquez (43)). However, discordant alternans can still occur when the stimulus is delivered from the middle of the lower edge, due to an increased path length for the propagating wave.
Effects of anisotropic conduction
All simulations in Figs. 1–10 have been carried out in anisotropic sheets (i.e., sheets which exhibit preferential conduction one direction over another, as occurs in real cardiac tissue) with Dx = 4Dy = 1 cm2/s. To investigate whether this anisotropy contributes significantly to the alternans dynamics in the sheets, we also carried out simulations in isotropic sheets with Dx = Dy = 0.25 cm2/s in ionically heterogeneous sheets. The lack of anisotropy does not change the resulting dynamics significantly: in fact, the transitions between the different types of dynamics in our baseline anisotropic simulations (Fig. 10, two leftmost columns) are shifted by a maximum of 10 ms when simulating isotropic tissue. However, the effect of the barrier on ΔAPDmax is reduced when Dx = Dy = 0.25 cm2/s. This is likely due to the fact that the coupling is reduced because of smaller overall diffusion in the isotropic case, so that the decoupling effect of the barrier is reduced. A similar effect has been observed for APD gradients in a sheet without alternans (43).
DISCUSSION
Most people who die from sudden cardiac death show signs of a prior myocardial infarct (46,47). In patients with structural heart disease (including patients with a prior myocardial infarct), TWA, which is a specific marker of vulnerability to ventricular tachyarrhythmias and sudden cardiac death (17,19–23), occurs at slower pacing rates than in healthy controls (14–18). Furthermore, discordant alternans has been shown to be a substrate for ventricular arrhythmias (7,13). In this work, we have demonstrated a causal mechanism of how the presence of a structural barrier can result in discordant alternans, helping to further connect these prior studies.
Discordant alternans in homogeneous tissue: arrhythmogenic effects of source-sink mismatch
The mechanism of discordant alternans in homogeneous tissue cannot be decoupling cells with different inherent electrophysiological properties, as there is no intrinsic heterogeneity. Our simulations in homogeneous tissue demonstrate how discordant alternans can arise in the presence of a structural barrier due to a novel mechanism: a source-sink mismatch resulting from an increase in electrotonic load around the corners of the barrier. This mechanism occurs only when the alternans magnitude is fairly small, which is the case for a small window of pacing rates, slower than those for which concordant alternans occurs.
Sudden increases in load due to a structural barrier may also lead to reentry. This can occur, e.g., if a propagating wave detaches from the barrier forming a spiral wave (48,49) or if there is unidirectional block forming a pair (50) or a single reentrant wave (51).
Role of ionic heterogeneity on the onset of alternans
We found that in ionically heterogeneous tissue there is only an apparent increase in the pacing CL required to induce alternans in sheets with the structural barrier, compared to sheets without it (Fig. 8 A). That the “real” onset (using a definition of 1 ms) changed very little or not at all, implies that the mechanism of the onset of alternans (i.e., the bifurcation) is the same in both cases. Indeed, alternans induced in the left side of the sheet (due to the intrinsic properties there) can drive concordant alternans throughout the sheet, but the alternans amplitude will be larger with the structural barrier present to decouple the tissue. That being said, there is likely little physiological significance to 1 ms alternans. Thus, although that criterion is important for showing similarity in the alternans onset mechanism (with and without a structural barrier) that might not be observable experimentally, there are obviously consistencies between the rate dependence of alternans in the experiments (7) and our simulations (e.g., the increased slope of the CL versus alternans amplitude relationship in the presence of the structural barrier). Importantly, the increase in alternans amplitude in the presence of the structural barrier may precondition the tissue for propagation block and reentry.
Our simulations in ionically heterogeneous tissue reproduce the experimental finding of a reduced threshold for discordant alternans in the presence of a structural barrier (7). The discordance arises in our simulations when the barrier decouples regions of tissue that possess different restitution properties (Fig. 9). Spatial heterogeneity in restitution properties during alternans has been observed experimentally (25). In our simulations using a dynamic (S1S1) restitution protocol, the long and the short APDs during alternans nearly form a single curve (Fig. 8, B, D, and F). In contrast, in a recent study using the standard (S1S2) restitution protocol in intact guinea pig hearts, the long and the short APDs fell on two different curves. Thus, premature stimulation may induce further (temporal) heterogeneity to promote discordant alternans (25). Several other experimental studies have suggested spatial heterogeneity (although not necessarily in APD restitution) as a cause of discordant alternans (6–9,11). In larger sheets of tissue where discordant alternans can occur without a structural barrier, ionic heterogeneity may also facilitate discordant alternans (13).
In the presence of a structural barrier in the experiments of Pastore and Rosenbaum (7), there was often a direct transition from no alternans to discordant alternans with faster pacing. In our simulations in heterogeneous tissue we see no alternans → concordant alternans → discordant alternans. This difference may be due to the larger alternans amplitude in our simulations: if the spatial gradients in APD and CL are the same, then discordant alternans may occur for smaller alternans amplitudes, but not for larger ones.
Depending on their location, some ectopic beats can induce ventricular tachyarrhythmias (52). Similarly, our simulations suggest that rapid pacing from some sites may be more arrhythmogenic than from other sites (Fig. 10). In the absence of ionic heterogeneity, much smaller differences are seen when the location of the stimulus site is changed, suggesting that the arrhythmogenic variability is a result of the ionic heterogeneity rather than anisotropic conduction.
Dispersion of APD and CL
Dispersion of repolarization is a well-known substrate for unidirectional block and development of ventricular tachyarrhythmias (1–5). Our simulations show that in homogeneous sheets, the structural barrier has only a small effect (electrotonic changes) on the dispersion of APD and CL (Fig. 4). In contrast, in ionically heterogeneous sheets, where the structural barrier effectively decouples tissue with different intrinsic properties, there are much larger changes in σAPD and σCL (Fig. 8). Also, in the presence of the structural barrier in heterogeneous tissue, ΔAPDmax increases more rapidly with increased pacing rate than without the structural barrier, in a manner similar to the experimental results of Pastore and Rosenbaum (7), even though in the experiments, the alternans is presumably discordant rather than concordant (7). Increased dispersion of repolarization during discordant alternans has also been observed in vivo during reperfusion (53) and in a long-QT3 dog model (11).
Alternans in CL due to CV restitution has been demonstrated as a mechanism for discordant alternans in simulated homogeneous cardiac tissue (13,24). The potentially proarrhythmic effects of CL alternans have also been demonstrated in the canine heart, where discordant CL alternans occurred during rapid pacing before ventricular fibrillation (54). In our simulations, CL alternans occurs at the same, or a slightly smaller, value of BCL as the value for which APD alternans occurs. A similar observation was made in a previous modeling study when using a CV restitution curve similar to the one in our model (13). However, in that study CL alternans was invariably associated with discordant APD alternans (13), whereas this is not the case in our simulations, presumably due to our smaller sheet size (1.5 × 1.5 cm2 vs. 6 × 6 cm2). Indeed, flattening CV restitution by using the default value for the time constant of the slow inactivation of the sodium current does not change our main result qualitatively: discordant alternans still occurs during fast pacing in ionically heterogeneous tissue with a structural barrier, but not in the absence of the barrier.
Relation to infarct and ischemia
We have focused here on the role of a structural barrier on the development of alternans because experiments have shown a decreased threshold for discordant alternans in the presence of a structural barrier. However, more factors are likely to play a role in explaining why the onset of alternans occurs at slower pacing rates in patients with a prior myocardial infarct than in healthy control subjects. Such factors include ionic remodeling of the postinfarcted myocardium (18,55,56), and ionic remodeling of tissue in the epi- and endocardial border zones (57,58).
In this study, we investigated alternans in nonischemic simulated tissue, in which experiments have shown TWA to be caused by cellular-level repolarization alternans (6). TWA may also occur in the setting of regional ischemia due to a distinctly different mechanism, namely 2:1 conduction block in the ischemic zone (59–61). Recently, a simulation study has shown that 2:1 conduction block during ischemia can induce discordant repolarization alternans (61).
Implications for arrhythmogenesis in whole hearts
Previous modeling studies have used 2D sheets of sizes 6 × 6 cm2 to 8 × 8 cm2 (13,24,54) or 1D cables of lengths 3–8 cm (10,24) to demonstrate discordant alternans. In contrast, the incorporation of ionic heterogeneity and a structural barrier in our simulations allows for discordant alternans to occur in much smaller pieces of tissue (1.5 × 1.5 cm2). Discordant alternans has also been shown in the short direction of simulated three-dimensional tissue measuring 3.7 × 3.7 × 0.74 cm3 during regional ischemia (61); however this was due to 2:1 conduction block, as mentioned above. Activation and repolarization of the ventricles occur primarily across the ventricular wall rather than in the apex-base direction (62–65). The thickness of the human left ventricular wall is ∼1.2 cm, which is comparable to the 1.5 cm used in our simulations. Our results thus suggest a mechanism by which discordant alternans may occur through the ventricular wall in vivo. However, our model was formulated to mimic a thin rim of epicardial tissue with apex-base heterogeneity, which is quite different from transmural heterogeneity. Further experiments and simulations are necessary to determine if discordant alternans may occur transmurally within the ventricular wall in nonischemic tissue.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
The authors thank Peter N. Jordan for helpful discussions.
This work was supported by the Whitaker Foundation for Biomedical Engineering (RG-02-0369), the National Science Foundation (PHY-0513389), the National Institutes of Health (R01HL073644), and the Kenny Gordon Foundation.
References
- 1.Moe, G. K., W. C. Rheinboldt, and J. A. Abildskov. 1964. A computer model of atrial fibrillation. Am. Heart J. 67:200–220. [DOI] [PubMed] [Google Scholar]
- 2.Kuo, C. S., K. Munakata, C. P. Reddy, and B. Surawicz. 1983. Characteristics and possible mechanism of ventricular arrhythmia dependent on the dispersion of action potential durations. Circulation. 67:1356–1367. [DOI] [PubMed] [Google Scholar]
- 3.Burton, F. L., and S. M. Cobbe. 2001. Dispersion of ventricular repolarization and refractory period. Cardiovasc. Res. 50:10–23. [DOI] [PubMed] [Google Scholar]
- 4.Antzelevitch, C. 2004. Arrhythmogenic mechanisms of QT prolonging drugs: is QT prolongation really the problem? J. Electrocardiol. 37(Suppl):15–24. [DOI] [PubMed] [Google Scholar]
- 5.Watanabe, N., Y. Kobayashi, K. Tanno, F. Miyoshi, T. Asano, M. Kawamura, Y. Mikami, T. Adachi, S. Ryu, A. Miyata, and T. Katagiri. 2004. Transmural dispersion of repolarization and ventricular tachyarrhythmias. J. Electrocardiol. 37:191–200. [DOI] [PubMed] [Google Scholar]
- 6.Pastore, J. M., S. D. Girouard, K. R. Laurita, F. G. Akar, and D. S. Rosenbaum. 1999. Mechanism linking T-wave alternans to the genesis of cardiac fibrillation. Circulation. 99:1385–1394. [DOI] [PubMed] [Google Scholar]
- 7.Pastore, J. M., and D. S. Rosenbaum. 2000. Role of structural barriers in the mechanism of alternans-induced reentry. Circ. Res. 87:1157–1163. [DOI] [PubMed] [Google Scholar]
- 8.Shimizu, W., and C. Antzelevitch. 1999. Cellular and ionic basis for T-wave alternans under long-QT conditions. Circulation. 99:1499–1507. [DOI] [PubMed] [Google Scholar]
- 9.Chinushi, M., M. Restivo, E. B. Caref, and N. El-Sherif. 1998. Electrophysiological basis of arrhythmogenicity of QT/T alternans in the long-QT syndrome: tridimensional analysis of the kinetics of cardiac repolarization. Circ. Res. 83:614–628. [DOI] [PubMed] [Google Scholar]
- 10.Fox, J. J., M. L. Riccio, F. Hua, E. Bodenschatz, and R. F. Gilmour Jr. 2002. Spatiotemporal transition to conduction block in canine ventricle. Circ. Res. 90:289–296. [DOI] [PubMed] [Google Scholar]
- 11.Chinushi, M., D. Kozhevnikov, E. B. Caref, M. Restivo, and N. El-Sherif. 2003. Mechanism of discordant T wave alternans in the in vivo heart. J. Cardiovasc. Electrophysiol. 14:632–638. [DOI] [PubMed] [Google Scholar]
- 12.Karma, A. 1994. Electrical alternans and spiral wave breakup in cardiac tissue. Chaos. 4:461–472. [DOI] [PubMed] [Google Scholar]
- 13.Qu, Z., A. Garfinkel, P. S. Chen, and J. N. Weiss. 2000. Mechanisms of discordant alternans and induction of reentry in simulated cardiac tissue. Circulation. 102:1664–1670. [DOI] [PubMed] [Google Scholar]
- 14.Hohnloser, S. H., T. Klingenheben, M. Zabel, Y. G. Li, P. Albrecht, and R. J. Cohen. 1997. T wave alternans during exercise and atrial pacing in humans. J. Cardiovasc. Electrophysiol. 8:987–993. [DOI] [PubMed] [Google Scholar]
- 15.Kitamura, H., Y. Ohnishi, K. Okajima, A. Ishida, E. Galeano, K. Adachi, and M. Yokoyama. 2002. Onset heart rate of microvolt-level T-wave alternans provides clinical and prognostic value in nonischemic dilated cardiomyopathy. J. Am. Coll. Cardiol. 39:295–300. [DOI] [PubMed] [Google Scholar]
- 16.Tanno, K., Y. Kobayashi, T. Adachi, S. Ryu, T. Asano, C. Obara, T. Baba, and T. Katagiri. 2000. Onset heart rate and microvolt T-wave alternans during atrial pacing. Am. J. Cardiol. 86:877–880. [DOI] [PubMed] [Google Scholar]
- 17.Tanno, K., S. Ryu, N. Watanabe, Y. Minoura, M. Kawamura, T. Asano, Y. Kobayashi, and T. Katagiri. 2004. Microvolt T-wave alternans as a predictor of ventricular tachyarrhythmias: a prospective study using atrial pacing. Circulation. 109:1854–1858. [DOI] [PubMed] [Google Scholar]
- 18.Koller, M. L., S. K. Maier, A. R. Gelzer, W. R. Bauer, M. Meesmann, and R. F. Gilmour Jr. 2005. Altered dynamics of action potential restitution and alternans in humans with structural heart disease. Circulation. 112:1542–1548. [DOI] [PubMed] [Google Scholar]
- 19.Rosenbaum, D. S., L. E. Jackson, J. M. Smith, H. Garan, J. N. Ruskin, and R. J. Cohen. 1994. Electrical alternans and vulnerability to ventricular arrhythmias. N. Engl. J. Med. 330:235–241. [DOI] [PubMed] [Google Scholar]
- 20.Armoundas, A. A., D. S. Rosenbaum, J. N. Ruskin, H. Garan, and R. J. Cohen. 1998. Prognostic significance of electrical alternans versus signal averaged electrocardiography in predicting the outcome of electrophysiological testing and arrhythmia-free survival. Heart. 80:251–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Klingenheben, T., M. Zabel, R. B. D'Agostino, R. J. Cohen, and S. H. Hohnloser. 2000. Predictive value of T-wave alternans for arrhythmic events in patients with congestive heart failure. Lancet. 356:651–652. [DOI] [PubMed] [Google Scholar]
- 22.Gold, M. R., D. M. Bloomfield, K. P. Anderson, N. E. El-Sherif, D. J. Wilber, W. J. Groh, N. A. Estes 3rd, E. S. Kaufman, M. L. Greenberg, and D. S. Rosenbaum. 2000. A comparison of T-wave alternans, signal averaged electrocardiography and programmed ventricular stimulation for arrhythmia risk stratification. J. Am. Coll. Cardiol. 36:2247–2253. [DOI] [PubMed] [Google Scholar]
- 23.Ikeda, T., H. Saito, K. Tanno, H. Shimizu, J. Watanabe, Y. Ohnishi, Y. Kasamaki, and Y. Ozawa. 2002. T-wave alternans as a predictor for sudden cardiac death after myocardial infarction. Am. J. Cardiol. 89:79–82. [DOI] [PubMed] [Google Scholar]
- 24.Watanabe, M. A., F. H. Fenton, S. J. Evans, H. M. Hastings, and A. Karma. 2001. Mechanisms for discordant alternans. J. Cardiovasc. Electrophysiol. 12:196–206. [DOI] [PubMed] [Google Scholar]
- 25.Pastore, J. M., K. R. Laurita, and D. S. Rosenbaum. 2006. Importance of spatiotemporal heterogeneity of cellular restitution in mechanism of arrhythmogenic discordant alternans. Heart Rhythm. 3:711–719. [DOI] [PubMed] [Google Scholar]
- 26.Wolk, R., S. M. Cobbe, M. N. Hicks, and K. A. Kane. 1999. Functional, structural, and dynamic basis of electrical heterogeneity in healthy and diseased cardiac muscle: implications for arrhythmogenesis and anti-arrhythmic drug therapy. Pharmacol. Ther. 84:207–231. [DOI] [PubMed] [Google Scholar]
- 27.Chudin, E., J. Goldhaber, A. Garfinkel, J. Weiss, and B. Kogan. 1999. Intracellular Ca2+ dynamics and the stability of ventricular tachycardia. Biophys. J. 77:2930–2941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Walker, M. L., X. Wan, G. E. Kirsch, and D. S. Rosenbaum. 2003. Hysteresis effect implicates calcium cycling as a mechanism of repolarization alternans. Circulation. 108:2704–2709. [DOI] [PubMed] [Google Scholar]
- 29.Diaz, M. E., S. C. O'Neill, and D. A. Eisner. 2004. Sarcoplasmic reticulum calcium content fluctuation is the key to cardiac alternans. Circ. Res. 94:650–656. [DOI] [PubMed] [Google Scholar]
- 30.Pruvot, E. J., R. P. Katra, D. S. Rosenbaum, and K. R. Laurita. 2004. Role of calcium cycling versus restitution in the mechanism of repolarization alternans. Circ. Res. 94:1083–1090. [DOI] [PubMed] [Google Scholar]
- 31.Goldhaber, J. I., L. H. Xie, T. Duong, C. Motter, K. Khuu, and J. N. Weiss. 2005. Action potential duration restitution and alternans in rabbit ventricular myocytes: the key role of intracellular calcium cycling. Circ. Res. 96:459–466. [DOI] [PubMed] [Google Scholar]
- 32.Wan, X., K. R. Laurita, E. J. Pruvot, and D. S. Rosenbaum. 2005. Molecular correlates of repolarization alternans in cardiac myocytes. J. Mol. Cell. Cardiol. 39:419–428. [DOI] [PubMed] [Google Scholar]
- 33.Shiferaw, Y., D. Sato, and A. Karma. 2005. Coupled dynamics of voltage and calcium in paced cardiac cells. Phys. Rev. E. 71:021903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fox, J. J., J. L. McHarg, and R. F. Gilmour Jr. 2002. Ionic mechanism of electrical alternans. Am. J. Physiol. Heart Circ. Physiol. 282:H516–H530. [DOI] [PubMed] [Google Scholar]
- 35.Shiferaw, Y., M. A. Watanabe, A. Garfinkel, J. N. Weiss, and A. Karma. 2003. Model of intracellular calcium cycling in ventricular myocytes. Biophys. J. 85:3666–3686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Szentadrassy, N., T. Banyasz, T. Biro, G. Szabo, B. I. Toth, J. Magyar, J. Lazar, A. Varro, L. Kovacs, and P. P. Nanasi. 2005. Apico-basal inhomogeneity in distribution of ion channels in canine and human ventricular myocardium. Cardiovasc. Res. 65:851–860. [DOI] [PubMed] [Google Scholar]
- 37.Laurita, K. R., S. D. Girouard, and D. S. Rosenbaum. 1996. Modulation of ventricular repolarization by a premature stimulus. Role of epicardial dispersion of repolarization kinetics demonstrated by optical mapping of the intact guinea pig heart. Circ. Res. 79:493–503. [DOI] [PubMed] [Google Scholar]
- 38.Choi, B. R., T. Liu, and G. Salama. 2001. The distribution of refractory periods influences the dynamics of ventricular fibrillation. Circ. Res. 88:E49–E58. [DOI] [PubMed] [Google Scholar]
- 39.Qu, Z., and A. Garfinkel. 1999. An advanced algorithm for solving partial differential equation in cardiac conduction. IEEE Trans. Biomed. Eng. 46:1166–1168. [DOI] [PubMed] [Google Scholar]
- 40.Moore, J. W., and F. Ramon. 1974. On numerical integration of the Hodgkin and Huxley equations for a membrane action potential. J. Theor. Biol. 45:249–273. [DOI] [PubMed] [Google Scholar]
- 41.Steinhaus, B. M., K. W. Spitzer, and S. Isomura. 1985. Action potential collision in heart tissue—computer simulations and tissue experiments. IEEE Trans. Biomed. Eng. 32:731–742. [DOI] [PubMed] [Google Scholar]
- 42.Sampson, K. J., and C. S. Henriquez. 2001. Simulation and prediction of functional block in the presence of structural and ionic heterogeneity. Am. J. Physiol. Heart Circ. Physiol. 281:H2597–H2603. [DOI] [PubMed] [Google Scholar]
- 43.Sampson, K. J., and C. S. Henriquez. 2002. Interplay of ionic and structural heterogeneity on functional action potential duration gradients: implications for arrhythmogenesis. Chaos. 12:819–828. [DOI] [PubMed] [Google Scholar]
- 44.Qu, Z., F. Xie, A. Garfinkel, and J. N. Weiss. 2000. Origins of spiral wave meander and breakup in a two-dimensional cardiac tissue model. Ann. Biomed. Eng. 28:755–771. [DOI] [PubMed] [Google Scholar]
- 45.Comtois, P., and A. Vinet. 1999. Curvature effects on activation speed and repolarization in an ionic model of cardiac myocytes. Phys. Rev. E. 60:4619–4628. [DOI] [PubMed] [Google Scholar]
- 46.American Heart Association. www.americanheart.org/.
- 47.Heart Rhythm Society. www.hrspatients.org.
- 48.Cabo, C., A. M. Pertsov, J. M. Davidenko, W. T. Baxter, R. A. Gray, and J. Jalife. 1996. Vortex shedding as a precursor of turbulent electrical activity in cardiac muscle. Biophys. J. 70:1105–1111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Starobin, J. M., Y. I. Zilberter, E. M. Rusnak, and C. F. Starmer. 1996. Wavelet formation in excitable cardiac tissue: the role of wavefront-obstacle interactions in initiating high-frequency fibrillatory-like arrhythmias. Biophys. J. 70:581–594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Panfilov, A. V., and J. P. Keener. 1993. Effects of high frequency stimulation on cardiac tissue with an inexcitable obstacle. J. Theor. Biol. 163:439–448. [DOI] [PubMed] [Google Scholar]
- 51.Girouard, S. D., J. M. Pastore, K. R. Laurita, K. W. Gregory, and D. S. Rosenbaum. 1996. Optical mapping in a new guinea pig model of ventricular tachycardia reveals mechanisms for multiple wavelengths in a single reentrant circuit. Circulation. 93:603–613. [DOI] [PubMed] [Google Scholar]
- 52.Ueda, N., D. P. Zipes, and J. Wu. 2004. Epicardial but not endocardial premature stimulation initiates ventricular tachyarrhythmia in canine in vitro model of long QT syndrome. Heart Rhythm. 1:684–694. [DOI] [PubMed] [Google Scholar]
- 53.Tachibana, H., I. Kubota, M. Yamaki, T. Watanabe, and H. Tomoike. 1998. Discordant S-T alternans contributes to formation of reentry: a possible mechanism of reperfusion arrhythmia. Am. J. Physiol. Heart Circ. Physiol. 275:H116–H121. [DOI] [PubMed] [Google Scholar]
- 54.Cao, J. M., Z. Qu, Y. H. Kim, T. J. Wu, A. Garfinkel, J. N. Weiss, H. S. Karagueuzian, and P. S. Chen. 1999. Spatiotemporal heterogeneity in the induction of ventricular fibrillation by rapid pacing: importance of cardiac restitution properties. Circ. Res. 84:1318–1331. [DOI] [PubMed] [Google Scholar]
- 55.Qin, D., Z. H. Zhang, E. B. Caref, M. Boutjdir, P. Jain, and N. el-Sherif. 1996. Cellular and ionic basis of arrhythmias in postinfarction remodeled ventricular myocardium. Circ. Res. 79:461–473. [DOI] [PubMed] [Google Scholar]
- 56.Huang, B., D. Qin, and N. El-Sherif. 2001. Spatial alterations of Kv channels expression and K+ currents in post-MI remodeled rat heart. Cardiovasc. Res. 52:246–254. [DOI] [PubMed] [Google Scholar]
- 57.Dun, W., S. Baba, T. Yagi, and P. A. Boyden. 2004. Dynamic remodeling of K+ and Ca2+ currents in cells that survived in the epicardial border zone of canine healed infarcted heart. Am. J. Physiol. Heart Circ. Physiol. 287:H1046–H1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Ohara, T., K. Ohara, J. M. Cao, M. H. Lee, M. C. Fishbein, W. J. Mandel, P. S. Chen, and H. S. Karagueuzian. 2001. Increased wave break during ventricular fibrillation in the epicardial border zone of hearts with healed myocardial infarction. Circulation. 103:1465–1472. [DOI] [PubMed] [Google Scholar]
- 59.Downar, E., M. J. Janse, and D. Durrer. 1977. The effect of acute coronary artery occlusion on subepicardial transmembrane potentials in the intact porcine heart. Circulation. 56:217–224. [DOI] [PubMed] [Google Scholar]
- 60.Arce, H., A. Xu, H. Gonzalez, and M. R. Guevara. 2000. Alternans and higher-order rhythms in an ionic model of a sheet of ischemic ventricular muscle. Chaos. 10:411–426. [DOI] [PubMed] [Google Scholar]
- 61.Bernus, O., C. W. Zemlin, R. M. Zaritsky, S. F. Mironov, and A. M. Pertsov. 2005. Alternating conduction in the ischaemic border zone as precursor of reentrant arrhythmias: a simulation study. Europace. 7(Suppl 2):93–104. [DOI] [PubMed] [Google Scholar]
- 62.Durrer, D., R. T. van Dam, G. E. Freud, M. J. Janse, F. L. Meijler, and R. C. Arzbaecher. 1970. Total excitation of the isolated human heart. Circulation. 41:899–912. [DOI] [PubMed] [Google Scholar]
- 63.Franz, M. R., K. Bargheer, W. Rafflenbeul, A. Haverich, and P. R. Lichtlen. 1987. Monophasic action potential mapping in human subjects with normal electrocardiograms: direct evidence for the genesis of the T wave. Circulation. 75:379–386. [DOI] [PubMed] [Google Scholar]
- 64.di Bernado, D., and A. Murray. 2002. Modelling cardiac repolarization for the study of the T-wave: effect of repolarization sequence. Chaos Solitons Fractals. 13:1743–1748. [Google Scholar]
- 65.Ramanathan, C., P. Jia, R. Ghanem, K. Ryu, and Y. Rudy. 2006. Activation and repolarization of the normal human heart under complete physiological conditions. Proc. Natl. Acad. Sci. USA. 103:6309–6314. [DOI] [PMC free article] [PubMed] [Google Scholar]