Bending Elasticity of Anti-Parallel β-Sheets

Abstract

Using a coarse-grained elastic model, we examine the bending properties of anti-parallel β-sheets comprised of uniform amino-acid residues in vacuum as well as in explicit solvent. By comparing the conformational probability of the β-sheet from molecular dynamics simulations with the same quantities obtained from the coarse-grained model, we compute the elastic bending constant, κ. Equilibrium fluctuations of the β-sheet and its response to external forces are well reproduced by a model with a uniform isotropic bending constant. An anisotropic bending model is also investigated, although the computed anisotropy is relatively weak and most of the observed properties are well described by an isotropic model. The presence of explicit solvent also lowers the bending constant. The sequence dependence of our result and its implications in protein conformational dynamics are discussed.

INTRODUCTION

In many proteins, structural flexibility is intimately related to protein function. When a protein binds small ligands or other proteins, a conformational change can occur and the protein subsequently assumes a different role. This generic mechanism is prevalent in cellular signaling, trafficking, self-assembly, and force generation. While static structures of many proteins in various conformational states are available, quantitative energetics of conformational changes are usually lacking. The strategy of this article is to develop a coarse-grained model of protein secondary structures, and ultimately make contact with a continuum description. In particular, we examine the elastic property of several prototypical anti-parallel β-sheets. Previously, the elastic property of a β-sheet in F₁-ATPase was examined using molecular dynamics (MD) simulations (1). It was found to be flexible, and can store several k_BT of energy during bending (k_B is the Boltzmann constant and T is 300 K). In the present work, we introduce a general model to describe β-sheet deformations and compute the bending constant from MD results. The methodology is related to our previous study of α-helix elasticity, which computed the helix persistence length (2). We report that the bending modulus of a β-sheet of glycines is ∼5 k_BT. A β-sheet of alanines is slightly stiffer, and has a bending modulus of 7 k_BT.

Flexibility of β-sheets has been studied using an informatics approach (3,4) and principal component analysis (4). These authors noted that there is a difference in the apparent elasticity between parallel and anti-parallel β-sheets. The current work takes a different approach, and the quantitative conclusions are based on the computed strains of β-sheets during deformations. A model is presented to describe changes of the protein structure away from the static x-ray structure. Although we study the elasticity of a particular anti-parallel β-sheet, the coarse-grained model can describe parallel β-sheets as well. The differences between these two motifs are discussed. Other coarse-grained models of proteins such as the elastic network model (5–9) and multibody dynamics (10–16) have been proposed to model proteins. These different coarse-grained models, including our current work, are complimentary in the understanding of protein structural flexibility.

To compute elastic properties of the β-sheets, we examine equilibrium fluctuations of the structure at room temperature. By matching the probability distributions of elastic strains from MD data and the corresponding model, we find the optimum elastic constants. A similar approach has been used to obtain parameters in coarse-grained models of proteins and lipids (17,18). Our approach is designed to make contact with continuum mechanics, which is ultimately independent of the discrete nature of the coarse-graining approach.

In the following sections, the basic theory of elastic two-dimensional surfaces and modifications of the theory to model β-sheet elasticity are discussed. In the current article and prior work, we compute the elastic modulus from the statistical fluctuations of the secondary structures. This approach is explained in Matching Equilibrium Distributions. After determining the elastic model, we compute the response of the β-sheet to external forces and compare MD results with model predictions.

THE ELASTIC MODEL

Anti-parallel β-sheets are strands of polypeptide stabilized by interstrand hydrogen bonds (19–23). The overall structure resembles a curved two-dimensional surface (1,24–26). While the interstrand hydrogen bonds can be broken when the sheet is exposed to water, in proteins β-sheets are typically shielded from solvents by other secondary structures. Thus, as in earlier work, we postulate that the low energy distortions of the β-sheet can be described by changes in the sheet curvature. There are also phonon modes in the plane of the sheet; however, these longitudinal motions do not lead to large conformational changes in proteins. There is a large body of work on the physics of two-dimensional elastic materials, originating from early developments of continuum mechanics. Sophie German, in 1821, proposed that the work done in bending of a plate is “proportional to the integral of the square of the sum of the principal curvatures taken over the surface.” With this assumption, she was able to explain the nodal lines observed in a vibrating plate (27). If linear elasticity is assumed and the strains in the perpendicular direction to the surface is small, the elastic energy of a homogeneous isotropic thin sheet without any long-range forces may be written as (28,29)

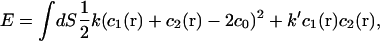(1)

where dS is an infinitesimal area element. The values c₁ and c₂ are principal curvatures of the surface. The value c₀ is the preferred curvature of the surface. The bending moduli, k and k′, relate the energy change with changes in mean and Gaussian curvatures, respectively. As discussed by many authors, Gaussian curvature is a perfect derivative and according to the Gauss-Bonnet theorem, integration over the Gaussian curvature is a constant for surfaces that do not change their topology (30,31). Note that Eq. 1 does not include a stretch energy and the surface area is assumed to be constant. In addition, the preferred curvature, c₀, is an average local curvature and cannot describe situations where the surface is initially curved by different amounts in different directions.

To incorporate varying curvature in different spatial directions, the elastic energy can be expressed in terms of the normal vectors perpendicular to the surface, n(r) (32),

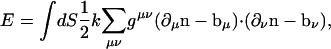(2)

where g^μν is the curvature tensor and ∂_μ is the derivative with respect to the r_μ; ∂_μn is the tangent vector in the r_μ direction. The value b_μ is then the preferred tangent direction. To generalize this expression to nonisotropic surfaces, it is possible to introduce a bending moduli tensor that accounts for unequal bending energies in the μ and ν directions (33). However, direct application of these ideas to β-sheets requires additional thought. Even though we expect bending along the amino-acid backbone is perhaps stiffer than bending perpendicular to the backbone, the backbone constantly fluctuates. There are no obvious definitions for r_μ and r_ν, and the principal directions of anisotropy are ambiguous. These factors prevent the straightforward application of Eq. 2.

In the current article, we take an alternative approach and consider a discretized version of the elastic model. The β-sheet is represented by a set of triangular elements, a methodology that has been used to study crumpling transition and simulate surfaces in three-dimensional space (34–39). The positions of the triangle vertices correspond to carbonyl oxygens along the polypeptide backbone (Fig. 1). If linear elasticity is assumed, and there are no long-range forces, the bending energy can be described by an expression analogous to Eq. 2. In terms of the unit normal vectors of each triangle, the bending energy is

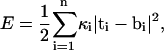(3)

where i labels the edge shared by two triangles; κ_i is again the bending constant. The tangent vector is defined as t_i = n_α–n_α–1, where α labels the triangles in the sheet and the difference is between neighboring triangles sharing the same edge. The definition of t_i is the discrete version of ∂_νn appearing in Eq. 2. The value b_i is the preferred curvature, which can be different, depending on i. Note that since n_α is always perpendicular to the triangles, t_i and b_i are always perpendicular to the edge shared by the neighboring triangles. Equation 3 becomes the standard bending energy of a two-dimensional surface in the continuum limit.

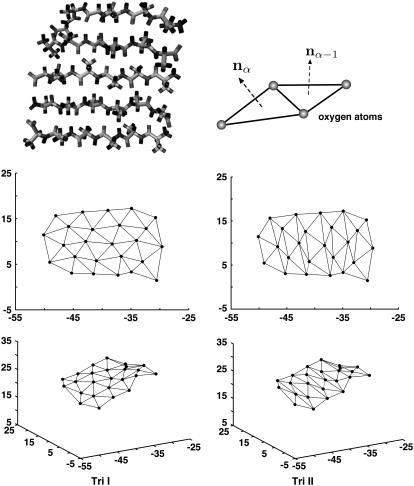
FIGURE 1.

The β-sheets studied consist of strands of glycines or alanines. Here, alanines are shown. Oxygen atoms are used to define vertices of triangle elements. Bending of the β-sheet is described by changes in the directions of the normal vectors (curvature). The minimized structure shows the sheet is slightly curved. Two different triangularization schemes, Tri I and Tri II, can be used to describe the curvature change.

We note that κ_i in Eq. 3 is not equivalent to k in Eq. 1. The relationship is given by κ_i = kδ, where δ is a topological factor. For equilateral triangles, (37). The anisotropic property of β-sheets is reflected in the dependence of κ on i, i.e., bending along different edges of the triangle may be different. If the β-sheet is homogeneous (but not isotropic) and all triangles behave identically, then we expect at most three different values of κ_i, one for each edge. Since β-sheets studied are comprised of the same residues, all triangles should behave identically.

In addition to anisotropy, the value of the bending constant also depends on the triangulation scheme. For the present article, we examine two different triangulation schemes (Tri I, Tri II in Fig. 1), and compare the results. Tri I consists of almost equilateral triangles and therefore most of the results are reported with this scheme. It is also unclear whether the elastic model of Eq. 3 applies to β-sheets. Even if linear elasticity is adequate, long-range forces can introduce coupling between different triangles. A more general linear elastic energy may apply,

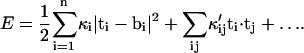(4)

Thus, by examining the statistics of tangent vectors, we aim to answer two questions:

1. Can linear elastic theories such as Eqs. 3 and 4 capture the deformation properties of the β-sheet?

2. What are the elastic constants in the model?

After developing the model, the response of the β-sheet to external forces will be computed.

MATCHING EQUILIBRIUM DISTRIBUTIONS

A possible approach for exploring elastic properties of proteins is directly examining the potential energy function that specifies the atomic interactions. This is not the approach we have taken here. The potential energy landscapes of proteins are rough; local behavior tends not to fully reflect large deformations. Instead, we use molecular dynamics data at room temperature to extract elastic properties. Thus, energies of Eqs. 3 and 4 are free energies and the bending properties are functions of temperature.

From the MD data, it is not possible to examine the complete multidimensional probability distribution 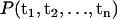. However, it is possible to examine reduced singlet and doublet distributions such as P₁(t_i) and P₂(t_i, t_j), where t_i = |t_i|. These distributions are related to the MD data via the histogram

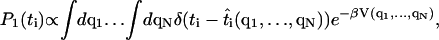(5)

where 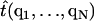maps the atomic positions of the oxygens to the i^th tangent vector; V is the MD potential energy as a function of all atoms in the sheet. A similar definition exists for the doublet distribution P₂(t_i, t_j). Since the fluctuations of the triangles are coupled, and depend on the boundary conditions on the sheet, it is not possible to obtain analytic distributions starting from Eq. 3. Our strategy is to compute the same singlet distributions from the coarse-grained model using Monte Carlo (MC), and optimize the agreement between these distributions by fitting the bending constants κ_i. The singlet distributions from the middle of the β-sheet will be used for the optimization. Isotropic and anisotropic bending constants will be tried. The resulting constants will then be used to predict the singlet distributions at the edges of the sheet, and double distributions such as P₂(t_i, t_j). We also compute the response of the β-sheet under external forces and assess the quality of the bending constants by comparing the responses from MD and model predictions.

The existence of long-range interactions among the triangles can be checked by examining the behavior of β-sheets of different sizes. If triangle elements some distance away from the edge of interest can influence the bending property, then the effective bending constant in Eq. 3 becomes renormalized. Quantitative estimate of long-range interaction and κ′ requires fitting more parameters, which is not desirable.

We note that there are other ways of extracting the bending constant. For example, in the Monge representation, if the z position of a sheet is recorded, then the height correlation function, 〈z(x, y)z(x′, y′)〉, is related to the bending constant and the distance between (x,y) and (x′,y′). In the case of a flat isotropic sheet, analytical predictions are available. In the present case, with preferred curvatures and possible anisotropic behavior, there are no analytical results without resorting to approximations. Thus, numerical comparisons must be made. Matching equilibrium distributions or matching correlations functions are probably equivalent in terms of accuracy.

RESULTS

The methodologies used in this article are summarized in Appendix: Simulation Details. We use two types of boundary conditions, BC I and BC II, applied on the oxygens at the edges of the sheet (see Appendix). The results from BC I and BC II are both examined.

Equilibrium geometry

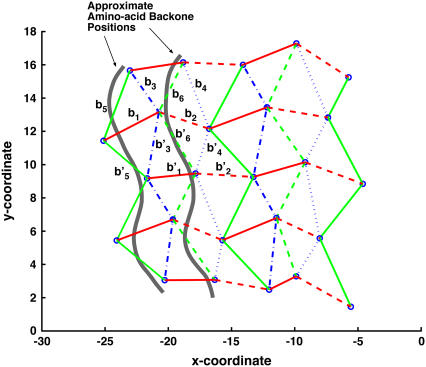
After energy minimization with no boundary conditions, we compute the average equilibrium tangent vectors, b_i, for the similar edges in the glycine β-sheet. Note that b_i is an intrinsic property of the sheet and must be determined by the equilibrium structure. Here, we have used b_i obtained from the static minimized structure. An alternative is to use average tangent vectors from a simulation at 300 K. These two approaches do not yield very different results. After some analysis, a distinct pattern characterized by the position of the edge with respect to the backbone, emerges. For Tri I, the pattern is shown in Fig. 2. There are 12 similar edges in the sheet, denoted by b_i and b′_i. The preferred curvatures, b_i and b′_i, are similar to each other in magnitude, although the directions are not the same. For Tri II, there is also a pattern, although the values of b_i are different. In this work, the preferred curvatures are inputs in Eq. 3 and are not fitted. The preferred curvatures are likely to depend somewhat on the choice of triangle vertex, e.g., nitrogen atoms versus oxygen atoms. However, the bending constant should be independent of such choices.

FIGURE 2.

The equilibrium geometry of the sheet is projected onto a two-dimensional coordinate system. The equilibrium configuration of a portion of the β-sheet is determined by the preferred curvatures b_i. There are 12 similar edges, labeled by b_i and b′_i. The preferred curvatures are inputs for the coarse-grained elastic model.

After heating from the minimized structure, other equilibrium properties are obtained. Triangles in Tri I are nearly equilateral where the sides have lengths 4.6 Å, 4.7 Å, and 4.0 Å. At equilibrium, the length of the sides fluctuate slightly (±0.5 Å), therefore the overall area of the sheet does not change by >2%. The length of the sides also vary slightly depending on the sequence of the sheet. However, the fluctuations are invariably small.

Bending constant

Constant temperature Langevin dynamics is used to compute the equilibrium properties of a glycine β-sheet. To obtain the probability distributions P₁(t_i) from MD data, we saved coordinates of every atom at 0.05-ps intervals during the 10-ns analysis run. In this section we consider the boundary condition where the first and the last strands are fixed in space (BC I). Corresponding probability distributions are obtained from Eq. 3 using MC calculations by moving the vertices in three dimensions (see Appendix).

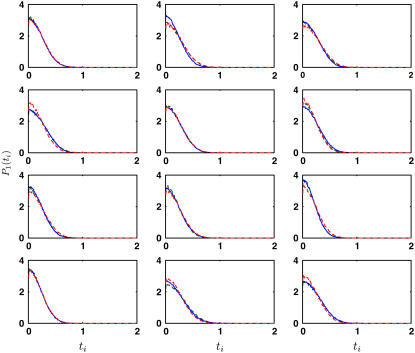
We first consider isotropic bending, i.e., κ_i is independent of i. The singlet probability distributions reach the best agreement when κ = 5 k_BT. The comparison between the coarse-grained model and MD distributions is shown in Fig. 3. Thus, if we approximate the β-sheet as an isotropic elastic surface, the bending constant is less than the bending constant of typical cellular membranes (10–20 k_BT) (40–43).

FIGURE 3.

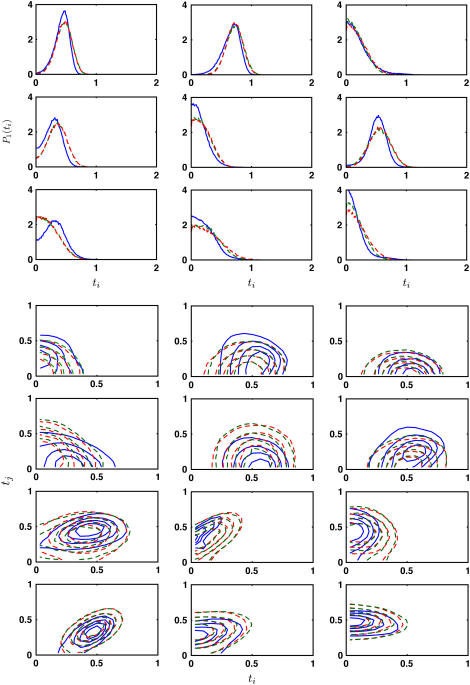
The equilibrium singlet distributions, P₁(t_i), from the middle of the β-sheet (solid line) is compared with the distributions from the model of Eq. 3. Here, the triangulation scheme is Tri I. The bending constants, κ_i, are fitted to obtain the best agreement. When κ_i is uniform for all edges (red dashed line), κ = 5 k_BT (the error is ε = 0.094 per bin (pb)). If three different bending constants are used (green dashed line), κ₁ = 8 k_BT, κ₂ = 8 k_BT, and κ₃ = 2 k_BT (ε = 0.055 pb).

Anisotropic properties of the β-sheet can be obtained by introducing three different κ_i values, one for each edge of the triangle in Tri I. Assuming that the triangles behave identically, edges with curvatures b₁, b′₁, b₂, and b′₂ are similar; the bending constant for this group of edges is denoted as κ₁. For edges with curvatures b₃, b′₃, b₄, and b′₄, the bending constant is denoted as κ₂. For edges with curvatures b₅, b′₅, b₆, and b′₆, the bending constant is denoted as κ₃. Different values of κ₁, κ₂, and κ₃ are tried. After iterative trials, we found that κ₁ = 8 k_BT, κ₂ = 8 k_BT, and κ₃ = 2 k_BT give the best agreement. The probability distributions obtained using these values are shown in Fig. 3. We expect the amino-acid backbone to be stiffer than the interstrand hydrogen bonds. However, our results indicate that this is not the case. Here, κ₁ and κ₂ are both larger than κ₃. The value κ₃ corresponds to the edge in between the backbone (Fig. 2). Bending along this edge is a twist in the backbone. Our results indicate that this motion along the backbone is quite soft. The other bending constants, κ₁ and κ₂, roughly correspond to bending perpendicular and parallel to the backbone, respectively. These two motions appear to be equally stiff. Due to statistical uncertainty, a range of values give reasonable agreement with MD and model distributions. These are κ₁ = 6–10 k_BT, κ₂ = 6–10 k_BT, and κ₃ = 2–4 k_BT. The probability distributions obtained from anisotropic model is also not significantly better than those obtained from the isotropic model, although the fitting error per bin, ε, appears to be smaller (see Fig. 3).

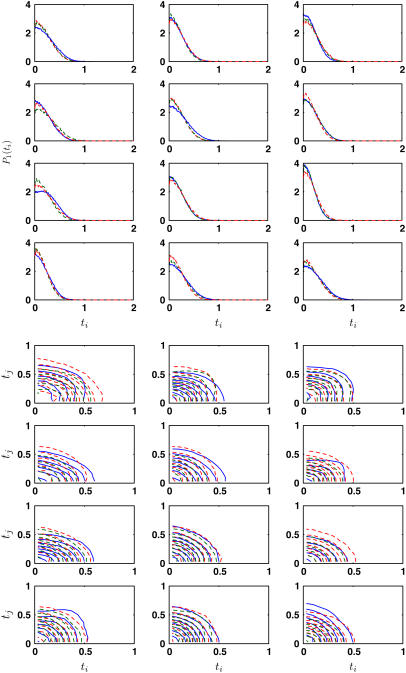
To test the quality of our obtained bending constants, we use the coarse-grained model to predict the singlet and double distributions in β-sheet. Fig. 4 shows the singlet distributions for triangles around the outer edge of the β-sheet. Model results from uniform bending and anisotropic bending are compared with the MD results. These results are not fitted and show good agreement. Additional comparisons are made by comparing doublet distributions P₂(t_i, t_j). The contour plots are also shown in Fig. 4. We see that the uniform bending model and the anisotropic model both give reasonable agreement with MD data.

FIGURE 4.

Representative equilibrium singlet and doublet distributions, P₁(t_i) and P₂(t_i, t_j), are compared with model predictions (dashed lines). The singlet distributions are from the outer edges of the glycine sheet. No fitting is performed here. The distributions from the uniform bending model (red dashed line, ε = 0.129 and 0.043 pb for singlet and doublet distributions, respectively) and the anisotropic model (green dashed line, ε = 0.114, 0.063 pb) are compared with the MD distributions (blue solid line).

We conclude that bending in anti-parallel β-sheets is anisotropic. However, the anisotropic model is not overwhelmingly superior. The predicted anisotropy is relatively weak if Tri I is used. For Tri II, anisotropy is more pronounced and the uniform bending model is not adequate.

Sequence dependence

The discussion thus far is limited to a β-sheet of all glycines. Similar computation is carried out for a β-sheet of all alanines. If a uniform bending constant is assumed, we obtain κ = 7.0 k_BT, with a fitting error of ε = 0.245 pb. Thus, glycine β-sheets appear to be slightly softer than alanine. The probability distributions are also less well described by either the uniform bending model or the anisotropic model (see Fig. 5). The preferred curvatures, b_i values, are also different for alanine. It is clear that the larger side chain of alanine is changing the behavior of the sheet. Thus, the bending constant does depend on the side-chain configuration. Indeed, the same calculation with a β-sheet of all leucines give a uniform bending constant of κ = 7.5 k_BT.

FIGURE 5.

Representative equilibrium singlet and doublet distributions, P₁(t_i) and P₂(t_i, t_j), for the alanine β-sheet. The MD results (solid line) are compared with model predictions. The distributions from the uniform bending model (red dashed line, ε = 0.282 and 0.104 pb for singlet and doublet distributions, respectively) and the anisotropic model (green dashed line, ε = 0.305 and 0.096 pb) are compared with the equivalent MD distributions. The optimal uniform bending constant is 7 k_BT.

The sequence dependence of the bending constant can be rationalized by considering interactions between side chains in addition to bending of the hydrogen-bond network. If the glycine sheet can be considered as the reference system, the alanine and leucine sheets can be modeled by

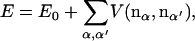(6)

where E₀ is the energy of Eq. 3 with κ equal to that of glycine. The second term in Eq. 6 is the interaction between the side chains, which are approximately normal to the triangles. The introduction of additional interactions changes the local preferred curvature. In addition, our bending results for alanine and leucine should be interpreted as using E₀ with an effective bending constant to approximate Eq. 6. This procedure produces a renormalized bending constant. However, as expected, E₀ with a renormalized bending constant produces quantitatively inferior agreement for the probability distributions.

An alternative viewpoint is to consider an elastic plate with a uniform Young's modulus, Y. If the strain in the direction perpendicular to the surface is small, it can be shown that the bending modulus is (44)

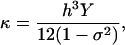(7)

where h is the plate thickness and σ is the Poisson ratio. For the sheets studied here, the thickness is 1.8 Å, 4.5 Å, and 11.2 Å for Gly, Ala, and Leu, respectively. We do not find that the bending constant scales as h³. Therefore, β-sheets cannot be regarded as a uniform elastic plate.

Long-range correlations

Long-range electrostatic forces are important in proteins. Within the protein interior, the effective dielectric constant is lower than the solvent. Long-range forces between different parts of the β-sheet may influence bending properties. For a given triangle in the middle of a sheet, the number of neighboring triangles that influences its behavior will depend on the sheet size. We find that a seven-strand anti-parallel β-sheet of all alanines has a bending constant of κ = 6.5 k_BT, very similar to the five-strand β-sheet result: κ = 7 k_BT. We conclude that the long-range interactions are of secondary importance in β-sheet elasticity. Since the MD simulations are obtained in vacuum where electrostatic interactions are dominant, these correlations are probably negligible for a buried β-sheet in a protein.

β-sheets in explicit solvent

The bending constants obtained thus far are for β-sheets in vacuum. However, explicit solvents do influence the sheet property. Therefore, the same simulations have been carried out with TIP3 water molecules for the glycine and alanine β-sheets. We collect 5-ns simulation data and the same fitting procedure was used to obtain the isotropic bending constant. We found that κ = 3.0 k_BT for the glycine sheet and κ = 2.5 k_BT for the alanine β-sheet. Thus, bending is much softer in solvent than in vacuum, principally due to screening effects of the solvent medium. The side chains also affect the bending constant to a lesser extent.

It should be noted that the β-sheet in explicit solvent is also much less stable than in vacuum. The strands can fall apart after 5 ns. In proteins, single β-sheets are not usually directly exposed to solvent and are protect by other parts of the protein (45). The effective dielectric environment of the β-sheets is somewhere in between the solvent and vacuum. A study with the appropriate dielectric environment is desirable. β-barrels are usually two β-sheets in parallel, and stabilize each other; therefore, the solvent bending constant can only be considered as an estimate.

β-sheet under an applied force

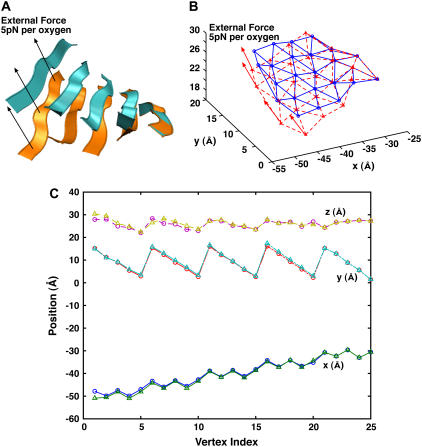
To further assess the validity of our coarse-grained model, we compute the shapes of the alanine β-sheet under an external load and compare MD and coarse-grained model results. MD simulations are performed in vacuum on the β-sheet using Langevin dynamics. After equilibration of the system under the applied force, the average configuration of the β-sheet is obtained. The same shape is computed using the estimated bending constant κ in the previous section and the bending energy in Eq. 3. In this simulation we use a five-strand β-sheet, and each strand has six Ala residues. We apply 2 pN and 5 pN to the oxygen atoms in the first strand of the sheet while the other end of the sheet is held fixed. The detailed simulation procedure is explained in the Appendix.

Fig. 6 shows the positions of all 25 vertices from MD and model simulations. The average displacement of the last strand is 4 and 6 Å, for 2 pN and 5 pN per oxygen, respectively. The average distance, Δ, between MD and model vertices as a function of the bending constant is shown in Fig. 7. Here,

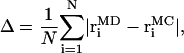(8)

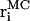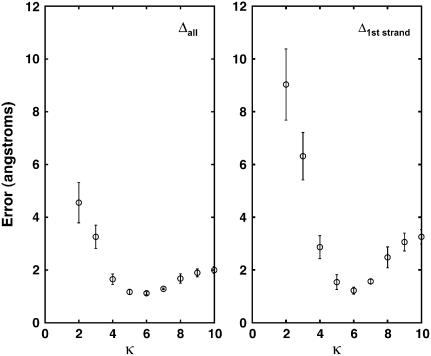
where and 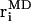are atomic positions from MC model and MD simulations, respectively, and N is the total number of atoms. There is good agreement between MD results and the predictions of the coarse-grained model. If Tri I is used and the uniform bending constant is κ = 7 k_BT, the average error Δ = 1.24 Å for F = 2 pN per oxygen, while Δ = 1.40 Å for F = 5 pN per oxygen. Note that there are five oxygen atoms in the strand. Therefore, the total force applied to the β-sheet is 10 pN and 25 pN, respectively.

FIGURE 6.

The comparison between MD and the elastic models under an external force. (A) The MD results when 5 pN per oxygen is applied to one edge of the β-sheet. The average before and after structures are shown. (B) The coarse-grained model with the same force. The results are obtained from Monte Carlo. (C) The quantitative comparison between the results. The (x,y,z) positions of all vertices are compared. The x axis of the plot is the index of the vertices. The circles are the MD results, and the triangles are the model results.

FIGURE 7.

The error between the coarse-grained model and MD results is shown. The force is applied to the first strand of the alanine β-sheet; 5 pN is applied to each oxygen atom (vertex) in the strand. The triangulation scheme is Tri I. The left graph shows the error per vertex for all the oxygen atoms in the sheet. The right graph shows the error per atom for the first strand of the sheet where the force is applied. The optimal agreement is reached when κ = 6.0 k_BT for the model, consistent with the value obtained from fitting probability distributions.

If anisotropic bending constants are used, no noticeable improvements are seen in the results (Δ = 1.32 Å for 2 pN and Δ = 1.91 for 5 pN). Since the force is applied perpendicular to the amino-acid backbone, we expect that bending mostly occurs in the edges corresponding to κ₂ and κ₃. An average of κ₂ and κ₃ can capture most of the β-sheet response. If triangulation scheme Tri II is used, a uniform bending constant does not predict the sheet response well. Anisotropic bending constants must be used for Tri II.

Our coarse-grained model can compute the response of the β-sheet to larger forces. However, MD results show that larger forces tend to destroy the interstrand hydrogen bonds. In a protein, other structures may stabilize the β-sheet and prevent unfolding, therefore β-sheets in proteins may sustain larger forces.

Comparison to the parallel β-sheet in F₁-ATPase

Having estimated the bending constant, in principle, we can predict the elastic energy stored in β-sheets during a protein conformational change. In Sun et al. (1), one of us showed that ∼6 k_BT of elastic energy is stored in the β-sheet in F₁-ATPase as the β-subunit undergoes its hinge bending motion (46,47). In this subsection, we estimate the elastic energy of the same β-sheet using our coarse-grained model. Note that the β-sheet in Sun et al. (1) is a parallel β-sheet. Therefore, the preferred curvatures and bending constants are expected to be different. We attempted to compute the bending constant of this parallel β-sheet using the strategy outline above. However, parallel β-sheets are unstable in vacuum and unfolds easily. Therefore, as an order-of-magnitude estimate, we use the bending constant of the anti-parallel sheet, and the preferred curvatures obtained from the β_E subunit of F₁-ATPase in the open conformation to parameterize our model. This allows us to compute the elastic energy change as the sheet is closed.

Using Tri I and Eq. 3, and a uniform bending constant of κ = 5–7 k_BT, we estimate that the energy difference between the closed and open conformation is 10–14 k_BT. This estimate is larger than the previous result of 6 k_BT. Although we do not expect agreement, the results are within an order of magnitude. In addition, this result suggests that parallel β-sheets are perhaps softer than anti-parallel ones, where the same deformation stores less elastic energy. This is also consistent with our observation that parallel β-sheets unfold easily. In proteins, parallel β-sheets are frequently protected from solvent by other secondary structures, whereas anti-parallel β-sheets can be exposed to solvent.

DISCUSSION

The main objective of this article is to introduce a discrete coarse-grained model that describes the bending elasticity of anti-parallel β-sheets. The model has a smaller number of variables, and contains the essential properties of the β-sheet. The model can be used to predict the deformation response of the β-sheet to external forces. The actual value of the bending constant in the model is sequence-dependent. For a glycine anti-parallel sheet, κ = 5 k_BT best agrees with the MD result. Other residues such as alanine and leucine give slightly stiffer structures (κ = 7–8 k_BT). Using a particular triangulation scheme, we find that a uniform bending constant is a reasonable model, although some anisotropic behavior is observed. The bending constant may also depend on parameters used by the MD package. Having the bending constant allows us to make contact with a continuum model of two-dimensional elastic surfaces (Eq. 1 or 2).

In the present problem, we have not considered possible shape changes of the triangular elements. The lengths of the edges are kept within ±0.5 Å of the equilibrium length. Length and shape changes of the triangles are related to the in-plane phonon modes of the sheet, and are not the focus of the present article. These internal motions are also not likely to result in large conformational changes seen in proteins.

The introduced model is unable to describe deformations where the β-sheet unfolds. It is important to note that unfolding is very likely when a large force (>30 pN) is applied. Unfolding is also likely if the force is applied rapidly. In a protein, however, other secondary structures can help to stabilize the sheet. This raises the question whether the computed elastic constant is relevant for proteins. Our view is that it is relevant. The overall elastic behavior will be a composite of the substructures. The elasticity of the β-sheet will contribute as a component. The bending elasticity of β-sheet is seen to depend on the physical size of the side chain, or loops and turns decorating the sheet. Other structures surrounding the sheet may affect the elastic property as well. In the current work, we have focused on the “bare” bending constant.

The presence of solvents also changes the elasticity of secondary structures. Our earlier study on α-helices showed that the persistence length is lowered by ∼25% when the aqueous solvent is present. In the current work, inclusion of explicit water also lowered the bending constant substantially. Thus, the dielectric environment of the protein is important for protein elastic properties. We note that β-sheets are typically shielded from solvents. Therefore, a study with a dielectric environment more typical of protein interiors is desirable.

We also have not examined the effects of other structural motifs on β-sheet elasticity. Structures such as loops and turns do affect β-sheet stability (48–50). In a coarse-grained model, these structures will appear as additional terms in Eq. 6 and will change the effective bending constant of the sheet.

If a uniform bending modulus is indeed adequate for describing β-sheet elasticity, then completely continuum theories such as Eqs. 1 and 2 can be used to obtain the energetics of β-sheet conformational change. Note that these theories do not depend on the choice of the vertex, or the triangulation scheme. The preferred curvatures b_μ,v are then functions capturing the rough equilibrium shape of the sheet. Predictions of bending can be obtained using established continuum methods. Just as our earlier studies of the α-helices (2), an atom-independent model of protein conformational change is perhaps possible.

APPENDIX: SIMULATION DETAILS

Bending constant

A part of PDB structure 1PO3 (a β-barrel) is used as the initial structure. We mutate all residues to glycines (Gly), alanines (Ala), and leucine (Leu). The number of strands in the sheet is varied between five and seven (see Fig. 1).

We use the CHARMM package version c27b3 (51,52) for MD simulations and VMD (53) for visualization. Parameter file par-all27-prot-na.prm from c27b3, which contains Ver. 22 (52) of the protein parameter set is used. The sheet is first examined in vacuum with no surrounding solvent.

In all simulations, an integration step size of 10⁻¹⁵ s = 0.001 ps is used. We use constant temperature Langevin dynamics with a friction coefficient γ = 50 ps⁻¹. We set CUTNB = 14.0, CTOFNB = 12.0, and CTONNB = 10.0 Å for nonbonded interactions.

After minimizing the overall potential energy with no applied boundary forces, an initial structure of the β-sheet is obtained. The initial structure provides the preferred curvatures b_i values. Before heating, additional constrains are used to prevent the atoms at the ends of the β-sheet from falling apart. Specifically, we fixed the first and the last strand in space (BC I). This method is analogous to holding a sheet of paper by two sides, and analyzes the thermal vibrations of the sheet. The magnitude of the vibrations are related to the bending constant.

We also simulate the system with other boundary conditions for a larger Ala β-sheet (seven strands, 84 Ala residues). For instance, one end of each strand is fixed in space, and the other end is left free (BC II).

The system is heated from 0 K to 300 K gradually for 150 ps, i.e., by 20 K for every 10 ps. The system is equilibrated for 100 ps, and data is collected for 10 ns.

During the analysis run, the atomic configurations of the β-sheet are saved every 0.05 ps. The singlet probability distributions of t_i are generated using 200 bins between 0 and 2. The doublet distributions are generated using 30 bins between 0 and 1 for each variable.

We also simulate the system in explicit solvent. Alanine and glycine β-sheets are immersed in a periodically replicated rectangular water box. The preferred curvature, t₀, is taken from the minimized structure after immersing each β-sheet into water. The size of the water box is 37.4 × 37.4 × 37.4 ų and 40.4 × 40.4 × 40.4 ų for the alanine and the glycine β-sheet, respectively. The number of TIP3 water molecules is 1633 and 2026, respectively. We set CUTNB = 12.0, CTOFNB = 10.0, and CTONNB = 8.0 Å. The particle-mesh Ewald method with a cutoff of k = 0.34 is used in the evaluation of electrostatic interaction. During heating and equilibration, Langevin dynamics is used to control temperature. The friction coefficient is set to γ = 62.0 ps⁻¹ for oxygen atoms in the water molecules. After initial equilibration, standard Verlet algorithm is used to compute the dynamics for the 5-ns analysis stage. We apply SHAKE only to bonds containing hydrogens. Data is collected and analyzed using the same procedure as above.

As for the MC simulations, we apply the same boundary conditions as in MD simulations, i.e., BC I and BC II, when appropriate. The initial structure is taken from the MD simulation after heating and equilibration. Metropolis Monte Carlo is used to update the remaining points. First, we change the (x,y,z) positions of a randomly chosen vertex by a small amount. Then, the lengths of edges associated with the vertex are computed. If the new edge lengths are within ±0.5 Å of the average length, the new vertex position is accepted. Otherwise, it is rejected. The average edge lengths from MD simulations are used. Additional comparisons in the bending energy using the standard Metropolis algorithm determine the final acceptance. In most simulations the acceptance ratios is ∼20%.

During the 5 × 10⁷ MC iterations, the shape of the sheet is saved every 500 moves. Histograms, P₁(t_i) and P₂(t_i, t_j), are collected in the same fashion as the MD simulations.

Force-displacement simulations

We use the five-strand Ala β-sheet for this calculation. An initial structure is obtained after energy minimization and initial heating. The PULL command in CHARMM is used to apply a constant force in the same direction. The direction of the force is parallel to the surface normal vector at the center of the sheet. First, we fix the oxygen atoms in the last strand of the Ala β-sheet in space. Then, force (|F| = 2 pN, 5 pN) is applied to each oxygen atom in the first strand. We compute the response using Langevin dynamics with γ = 50 ps⁻¹. During the 5-ns run, the positions change gradually; after which they fluctuate around some average value. We average the positions of the β-sheet atoms during the 5–10 ns analysis run.

For the model calculations, we use the same move algorithm as the previous section. The following energy is used for the Monte Carlo calculation,

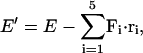(A1)

where F_i is the applied force on the i^th vertex and r_i is its displacement vector. E is the force free elastic energy of Eq. 3. The number of iterations is 5 × 10⁷. We average the positions of the β-sheet as follows. During the last 1.5 × 10⁷ moves, we compute the average positions of the vertex and their standard deviations. When the standard deviation is within 20% of the average position, we start collecting statistics for Δ.