The Formation of Fibrils by Intertwining of Filaments: Model and Application to Amyloid Aβ Protein

Abstract

We outline a model that describes the interaction of rods that form intertwined bundles. In this simple model, we compare the elastic energy penalty that arises due to the deformation of the rods to the gain in binding energy upon intertwining. We find that, for proper values of the bending Young's modulus and the binding energy, a helical pitch may be found for which the energy of intertwining is most favorable. We apply our description to the problem of Alzheimer's Aβ protein fibrillization. If we forbid configurations that exhibit steric overlap between the protofilaments that make up a protein fibril, our model predicts that fibrils consisting of three protofilaments shall form. This agrees well with experimental results. Our model can also provide an estimate for the helical pitch of suitable fibrils.

INTRODUCTION

Amyloid fibril formation is a process during which soluble proteins misfold and aggregate into fibrillar structures. It has been linked to several diseases, such as Alzheimer's and Parkinson's Disease (1–6). It has been well established that amyloid fibrils formed from different proteins possess many common structural features (5–7). One such feature is the uniform diameter of the fibrils: in a given sample of amyloid fibrils, the lengths of individual fibrils usually vary strongly, but their diameters do not (3–5,7).

In an earlier article (8) we presented a statistical-mechanical model, based on a combination of a model for self-assembly with a conformational transition (9) and lateral assembly of filaments into fibrils (10). Applying this model, we could partially reproduce the experimentally observed uniformity of the fibril diameter. While we did find that thin fibrils hardly formed, our model favored essentially limitless growth in the direction perpendicular to the fibril axis (i.e., a limitless increase in the fibril diameter). This required us to introduce an artificial cutoff in the number of filaments that comprise a fibril. In the current article, we introduce a mechanism that inhibits the lateral growth of the fibrils, and that is potentially very relevant for descriptions of protein fibrillization.

The optimal number of protofilaments that makes up a fibril is thought to depend strongly on the geometry of the interacting protein strands inside a fibril (10,11). This effect, and particularly the protofilament intertwining, has been studied in some detail by Nyrkova and co-workers (11). Their approach presupposes that the protein filaments interact through specific directional interactions, however, which requires a description that includes detailed knowledge of the architecture and the mechanical properties of the filaments, such as their twist, bend, and splay constants. Although this approach provides a good description of the assembly of a particular class of biomolecule, in some cases a less elaborate model may suffice.

We introduce here a simple model that describes intertwining of smooth, cylindrical filaments into bundles. Specifically, we compare an elastic-energy term that measures the deformation of intertwined rods inside a bundle to their binding energy. Our approach is based on that proposed by A. E. Cohen to describe the bundling of carbon nanotubes (A. E. Cohen, unpublished). We find that our description provides an explanation for the propensity toward the formation of fibrils with a fixed diameter. In the next section we define our model in terms of the intertwining of cylindrical rods. Subsequently, we apply our model to the assembly of amyloid Aβ protein (1,3,5,6). We conclude the article with a summary of our findings.

Model system: smooth cylindrical rods

Let us start with the simple case of two intertwined smooth cylindrical rods with radius r and length h. If we assume that each of the cylinders forms a helix without torsion we can express the elastic energy (per rod) associated with this deformation in terms of the radius of the helix and the rigidity of the rod,

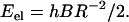(1)

Here B is the bending constant of the rod, given for a solid cylinder with a circular cross section as 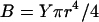, with Y the Young's modulus of the cylinder. In Eq. 1, R is the radius of curvature of the rod, used to measure the deformation it experiences when bent into a helical geometry. We assume it is identical at every point along the rod axis. In the model as detailed here, we use the straight state (for which R → ∞) as the reference state, but our model can easily be generalized to account for a reference state with a finite curvature. This is described in some detail in the section Amyloid Aβ Fibrils, below. In Eq. 1, R is given by

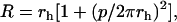(2)

with p the pitch and r_h the radius of the helix described by the center of the rod.

Besides the elastic penalty the rods incur, intertwining also introduces a favorable contribution to the energy of the rods. This is because the number of sites on the surface of a rod that interact with the neighboring rod, increases upon intertwining. We describe this in terms of an increase in the length of an effective contact line. This length can readily be calculated if one uncoils the rods from each other and straightens them (A. E. Cohen, unpublished). If our assumption that the helical bundle forms without torsion holds, the contact line must always describe a helix around the straightened rod. Its length is given approximately by

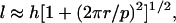(3)

where h is again the length of the (straight) rod, r is its radius, and p is the pitch of the helix. The approximation in Eq. 3 stems from the circumstance that, strictly speaking, the value of the pitch is slightly different dependent on whether it is measured along the rod axis or the fibril axis. In practice, however, it turns out that this difference is negligible if the rod radius is much smaller than the helix pitch. Combining Eq. 3 with Eqs. 1 and 2, we can write down the total energy of intertwining for a bundle of rods, defined as the sum of the elastic and the interaction energies,

(4)

We define this intertwining energy, ɛ_tot, per unit length and per rod. In Eq. 4, n equals the number of rods that make up the bundle, while N is the number of rod-rod contacts inside the bundle, and ɛ_int < 0 is the interaction energy per unit length. It, like all energies in this article, is given in terms of the thermal energy, k_BT, with k_B Boltzmann's constant and T the absolute temperature. The factor –1 in the last term serves to compare the energy of the intertwined rods to that of straight ones. Note that Eq. 4 presupposes that the elastic energy of each rod is identical. This need not be the case. For configurations in which the bundle is not symmetrical around its center, we can generalize Eq. 4 to read

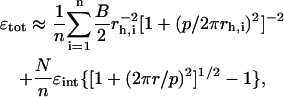(5)

with r_h,i the radius of the helix described by the center of the rod designated i. We assume here that the difference in helix diameter of the filaments does not influence the length of the contact line. This assumption is reasonable for small bundles. Also, in our model, we neglect end effects, and assume that the geometry of the intertwined bundle is identical at every point along its length (i.e., that there are no defects in the intertwined state).

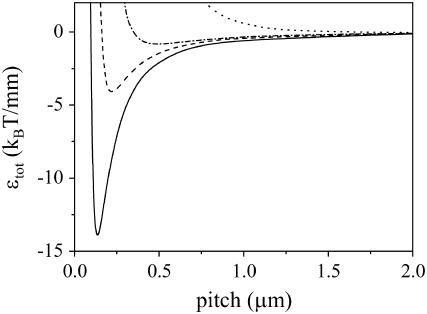
Because our interest is ultimately in amyloid fibrils, which consist of a limited number of so-called protofilaments, we consider what Eqs. 4 and 5 predict for small bundles of rods. In Fig. 1, we compare the energy of two intertwined rods to that for the reference case of two fully straight rods. We plot here the energy gain upon intertwining (ɛ_tot in Eq. 4) as a function of the helix pitch, and find that a minimum may occur in this curve. This means that an optimum value of the pitch exists, for which the energy gain is largest. As might be expected, the value of the optimum pitch and the depth of the energy-well depend strongly on the bending stiffness of the rods. After all, for infinitely rigid rods, no intertwining can occur. Accordingly, we see in Fig. 1 that a large value of the Young's bending modulus favors the formation of a helix with a long period, which decreases with a decrease of the Young's modulus. Coupled to the decrease of the pitch, we see that a decrease of the bending stiffness also causes the energy-well to become deeper. This is because the elastic energy penalty (the first term of Eq. 4) is smaller for the flexible rod, and the gain in interaction energy is larger due to the circumstance that tighter-wound helical configurations become possible. A similar trend is observed if we keep the Young's modulus constant and instead vary the binding energy per unit length. For large binding energies, there is again a clear optimal pitch, whereas for small values, the energy well becomes shallower, while the optimal pitch increases.

FIGURE 1.

Energy of intertwining versus pitch, for a bundle of two rods. We use a value of −10 k_BT/nm for ɛ_int, and vary the Young's bending modulus. The drawn line corresponds to Y = 0.5 GPa, the dashed line to Y = 1 GPa, the dot-dash line to Y = 5 GPa, and the dotted line to Y = 100 GPa.

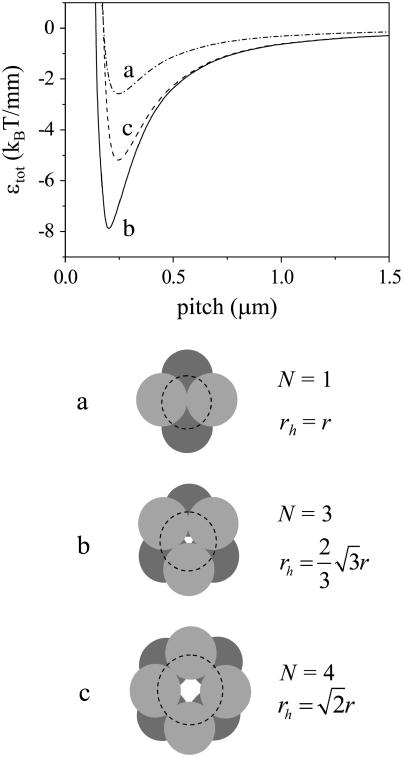
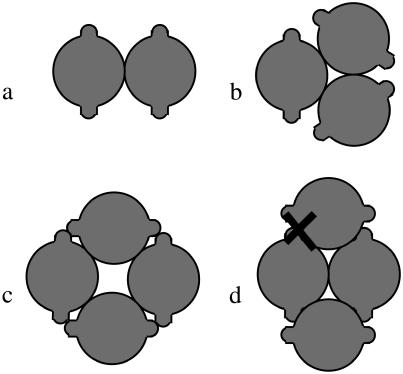
Let us now examine the case where the number of rods is larger than two. In Fig. 2, we compare three geometries, shown in cross section on the left-hand side of the figure: one that corresponds to a bundle of two rods, one that corresponds to a bundle of three, and one that corresponds to a fourfold bundle. We limit ourselves to the configurations shown in Figs. 2 and 3, because these are likely the most favorable ones within the confines of our model. Other configurations can certainly occur (e.g., one where filaments placed in a straight line make up a fibril). However, these configurations contain less than the optimal number of interfilament interactions, and can only be the most stable species if the interfilament interactions are strongly directional in nature. A description of this type of interaction is beyond the scope of the current article, and we refer to the work of Nyrkova and co-workers for a model for this type of aggregation (10,11). We choose the Young's bending modulus equal to 1 GPa, and the interaction energy per unit length equal to −8 k_BT/nm. We expect these values to roughly correspond to those for the Aβ protein. As far as we are aware, neither the Young's modulus of the protofilament nor the interaction energy has been measured for this protein. Therefore, we must estimate these values. The Young's modulus likely lies between 0.01 and 10 GPa; these limits correspond roughly to the (macroscopic) moduli of rubber and wood, respectively. The value of 1 GPa was chosen for convenience. Our estimate of the interaction energy stems from our earlier choice of the lateral-interaction energy per protein molecule. In our recent article (8), we set this value equal to a few times the thermal energy. Combined with our estimate that each protein molecule has a thickness along the fibril axis of ∼0.45 nm (the characteristic distance in a β-sheet), this leads to an estimate of –6 to –10 times the thermal energy per nanometer.

FIGURE 2.

Energy of intertwining versus pitch, for bundles of rods of the three geometries depicted. We use a value of 1 GPa for the Young's modulus and a value of −8 k_BT/nm for ɛ_int. Lines correspond to the geometries pictured, as indicated.

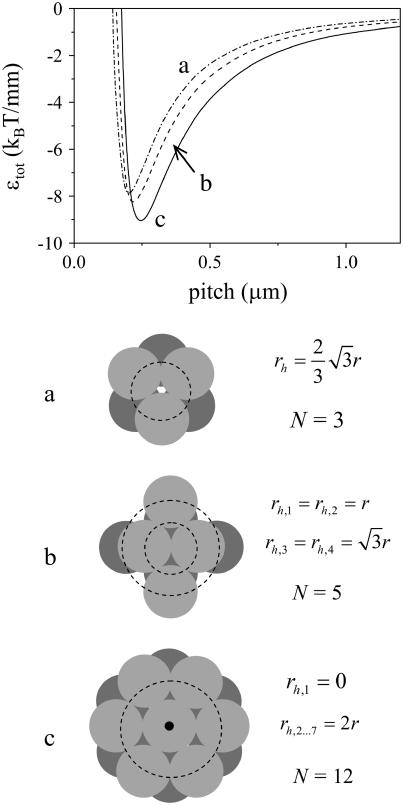
FIGURE 3.

Energy of intertwining versus pitch, calculated with Eq. 5, for the three geometries depicted. We use a value of 1 GPa for the Young's modulus and a value of −8 k_BT/nm for ɛ_int. Lines correspond to the geometries pictured, as indicated.

Of the geometries pictured in Fig. 2, the bundle comprised of three rods possesses the lowest energy. This is due to two effects. Firstly, for this bundle, the factor N/n (the number of contacts per cylinder) equals unity, rather than one-half for the twofold fibril. This means that the total interaction energy per rod becomes larger. For the bundle of four rods, we also find a value of N/n of unity. The reason why the bundle of three rods is nevertheless more favorable than that of four is that its helix has a smaller radius, and hence the elastic energy penalty of the rods is lower. This trend, where N = 3 gives the most favorable energy, is observed for all investigated values of the Young's modulus and binding energy, although the depth of the energy-well and the value of the optimum pitch can vary (see Fig. 1).

Going beyond the geometries shown in Fig. 2, we generally expect bundles to form for which N/n is maximized, but for which the helix radius is not too large. For our model system of completely smooth intertwined rods, bundles with N = 7, with one rod surrounded by six others (N/n = 12 / 7), or bundles with N = 4, with two rods touching in the center of the aggregate (N/n = 5 / 4), have a slightly more favorable intertwining energy, and as such, may dominate (see Fig. 3). These geometries may also play a role in amyloid fibril formation. However, for the protein we discuss in the next section, i.e., Aβ amyloid protein, it is known that protofilaments consisting of two “stacks” of protein molecules, and fibrils containing two, three, or six “stacks” form, dependent on the protein concentration (12,13).

Amyloid Aβ fibrils

It is well known that amyloid fibrils, including those of Aβ, consist of several intertwined protofilaments (7,11,12,14,15). It has been observed that mature fibrils of the Aβ amyloid protein have a very uniform diameter between 6 and 10 nm, whereas protofilaments measure 3–5 nm across (1,2,16,17). Studies have shown that the fibrils likely consist of six stacks of protein molecules (1,4,13,18), while protofilaments consist of two protein stacks (2,3). This may vary somewhat with the conditions under which the fibrils form, as fibrils containing only two or three stacks are observed at low protein concentrations, and stirring the protein solution has also been found to affect the structure of the fibrils (12,13,19,20). Furthermore, it has been found that the two forms of Aβ protein, Aβ_1-40 and Aβ_1-42, where the index refers to the number of residues that makes up the protein, exhibit some differences in the assembly and structure of their fibrils. Our model, as described below, is coarse-grained enough that we can reasonably ignore the distinction between these types of Aβ. In any case, fibrils consisting of six protein stacks appear to be the largest mature fibrils that have been detected, and as such they are the most interesting aggregate from our point of view. Their presence has been observed by x-ray measurements (1), as well as by the determination of the linear density of the fibrils (13).

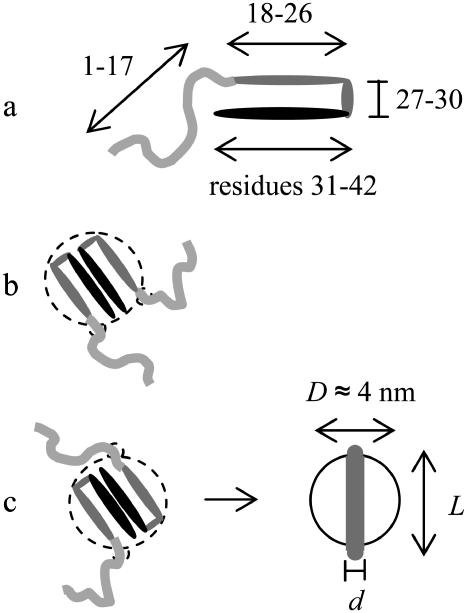
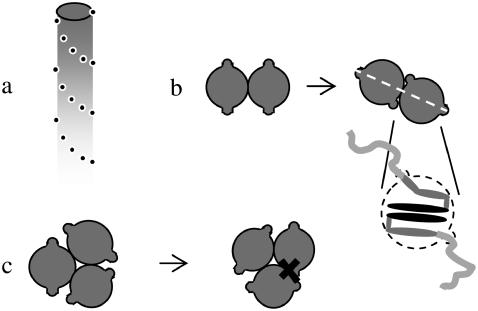
We start our study of the aggregation of Aβ_1-42 protein at the level of the single protein molecule. It has been established that the protein molecules adopt a specific conformation inside amyloid fibrils (2,3,14,21). This conformation is depicted in Fig. 4 a. It contains two β-strands (formed by residues 18–26 and 31–42) and a disordered chain at the N-terminus (residues 1–17).

FIGURE 4.

(a) Conformation of an Aβ protein molecule. Dark colors indicate hydrophobicity, light ones hydrophilicity. (b,c) Two geometries of protofilaments.

Inside the protofilaments, the proteins stack in a parallel and in-register manner, leading to long intermolecular β-sheets, known as cross β-sheets (3). These cross β-sheets serve to stabilize the stacks. Because the residues that make up the β-strand near the C-terminus (residues 31–42) are quite hydrophobic in nature (17), this stacking leads to the formation of a large hydrophobic patch. It stands to reason that a single stack may not be stable (12), and that two (or in some cases, three) of these protein stacks likely associate to minimize the contact between the hydrophobic residues and the surrounding water (3,14). The dimers that are formed in this way are shown in cross section in Fig. 4, b and c.

The dimeric entities that form by the association of two protein stacks likely act as protofilaments from which the mature fibrils can later form. As shown in Fig. 4, b and c, there are two possible ways in which protofilaments can be formed from two protein stacks. We presuppose that this association takes the form shown in Fig. 4 c. This is because the protein stacks intertwine while forming a protofilament (3,5,14). This implies that the protein stacks in Fig. 4 b have opposite helical twist senses. It seems unlikely that this state would ultimately be a stable one, because of the inherent (homo) chiral character of the proteins. Indeed, microscopy studies have shown that the protein fibrils (for a given sample) all have the same handedness (22). In Fig. 4 c, the two protein stacks have the same screw sense. Recent studies indicate that the structure shown in Fig. 4 c is indeed the one that forms (23,24).

The Aβ protofilaments shown in Fig. 4 do not exactly match the smooth cylinder model introduced in the previous section. While we may perceive the periphery of the protofilament (composed of the moderately hydrophobic residues 18–30 of both proteins) to reasonably resemble a cylinder without a well-defined preferred direction of interaction, the hydrophilic, disordered residues 1–17 have to be taken into account as well. To this end, we treat the protofilaments as smooth cylinders with a protrusion on either side, as indicated in Fig. 4 c. These protrusions represent the locations of the origin of the hydrophilic chains, and their size is a function of the degree of flexibility of these chains. Unlike in the case of totally smooth cylinders, the side chains hinder the formation of some structures. This is illustrated in Fig. 5. Here, we show that, although the protrusions do not hinder the formation of the structures we considered in Fig. 2, larger fibrils, such as those shown in Fig. 3, are likely repressed due to steric overlap between the protrusions of one cylinder and the body of another (see Fig. 5 d). Of course, the degree to which the protrusions hinder the formation of certain structures depends strongly on the size of the protrusions (and hence, on the flexibility of the hydrophilic chains). A detailed, quantitative study to determine what structures may form for particles of this shape, for different sizes of the protrusions, is currently in progress.

FIGURE 5.

Interactions of cylinders with protrusions, linked to the places where the disordered chain emerges from the protofilament. Panels a, b, and c show geometries in which there is no steric overlap. Geometry d, however, is forbidden in our model due to steric overlap.

Eliminating the structures in which steric overlap necessarily plays a role for each protein molecule, we take into account only the geometries depicted in Fig. 2. It must be noted that for these structures, too, steric interactions may play an important role. This is illustrated in Fig. 6. In Fig. 6 a, we show a cartoon of a protofilament. Because the protein stacks inside a protofilament are intertwined, the side chains emerge from the rod in a helical pattern. For an (intertwined) protein fibril to form without steric hindrance, the pitch of the intertwining has to match that of this helical pattern. This means that there exist at least two forces that determine the pitch of the mature fibril: on one hand, the fibril strives for the energy minimum and the optimal pitch shown in Figs. 2 and 3, while on the other hand, it must also accommodate the side chains without steric overlap. The latter condition implies that the optimum pitch we predict from Figs. 2 and 3 may not be the one that is observed experimentally.

FIGURE 6.

(a) Cartoon depicting a protofilament with protrusions, representing the locations of the disordered residues 1–17. (b) Cross sections through a fibril consisting of two protofilaments that demonstrates a possible mechanism by which steric overlap between protofilaments is avoided. (c) Cross sections through a threefold fibril. Here, the mechanism described for twofold fibrils does not apply.

Microscopy studies have shown that the pitch in amyloid fibrils is usually of the order of magnitude of 100 nm. Goldsbury and co-workers (12,22) have found an axial periodicity of 25–30 nm (corresponding to a pitch of 50–60 nm) in fibrils that possess a linear density of ∼20 kDa/nm, implying that their pitch is probably comparable to that of our protofilaments. Malinchik and co-workers (25) find a value of 36–56 nm (a pitch of roughly 70–115 nm) for fibrils with a diameter of 7–8 nm, which likely contain two protofilaments. These values differ significantly, which means that, unexpectedly, for these twofold fibrils, the axial periodicity is not determined by the pitch of the protrusions. This implies that fibrils with the optimum pitch may be formed in this case. We speculate that this may be due to local deformations in the protofilament structure that prevent steric overlap to occur. We imagine this takes place as sketched in Fig. 6 b. Here we show a cross section of a twofold fibril at two points along the fibril axis. The left-hand picture shows the conformation where the protrusions of the two protofilaments are furthest apart. In the right-hand picture, steric overlap would be expected to take place. However, due to a small local deformation this may be avoided. A similar mechanism cannot be at work in fibrils that consist of more than two protofilaments (Fig. 6 c), because a similar local deformation would result in steric overlap with another protofilament. Therefore, we tentatively predict that for threefold (and larger) fibrils, the protrusions dominate the intertwining, and a helical pitch should be observed that is comparable to that of the protofilament, i.e., 50–60 nm. As far as we are aware, the pitch of threefold fibrils has not yet been determined by microscopy techniques, possibly because of the relatively high concentrations required for this fibril type to be observed.

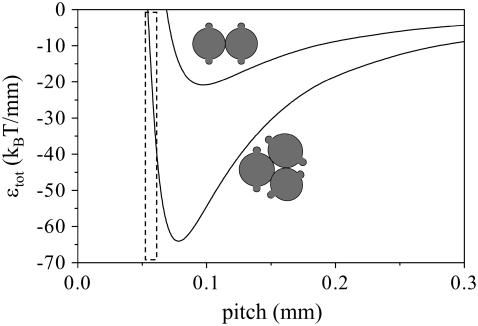
That the formation of a stable threefold fibril with a pitch of 50–60 nm is in fact possible within the confines of our model is shown in Fig. 7. Here, we have plotted the intertwining energy versus the pitch of the fibril. We have varied the values of the Young's modulus and the binding energy per unit length, in such a way that the optimum pitch for a twofold fibril corresponds to the experimental value (25) of 70–120 nm (we have taken here 100 nm). We find that this is the case for a Young's bending modulus of 0.2 GPa, and an interaction energy of –10 k_BT/nm. When we compare these values to our earlier estimate, used in Figs. 2 and 3, it would seem that we overestimated the Young's modulus of the filaments somewhat in these figures. If we now look at the predicted behavior of a threefold fibril, we see that a pitch of 50–60 nm gives an energy that is lower than the minimum value for the twofold fibril. Under the proper circumstances (e.g., at relatively high concentrations) our model indeed leads us to expect the formation of threefold fibrils (corresponding to a fibril containing six protein stacks) with a pitch of ∼50–60 nm.

FIGURE 7.

Intertwining energy versus pitch for a Young's bending modulus of 0.2 GPa, and an interaction energy of –10 kBT, for twofold and threefold fibrils. The pitch for a twofold fibril is chosen so as to be in the experimentally observed regime. The dashed box indicates the regime of 50–60 nm.

Note that in our model as outlined here, we assume that the protofilaments can be reasonably described as straight rods. While microscopy images and other recent visualizations lead us to believe that this is likely true for Aβ protein (12,26), it is not necessarily always the case. When the free protofilaments possess a finite curvature, we need to adjust our model accordingly. This can be done by replacing the term R⁻² in Eq. 1 with (1/R–1/R₀)², and by changing the last term in Eq. 4 from –1 to −l′₀. Here, 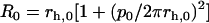and 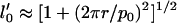give the radius of curvature and the length of the effective contact line (divided by the protofilament length) in the curved reference state as a function of the pitch and radius of the helix described by the free protofilament. It turns out that, for the regime most relevant to us (a Young's modulus of the order of 0.1 GPa), the observed trends do not change, and the threefold fibril is still the most energetically favorable species. A more detailed analysis of the effect of a curved reference state on the aggregation of protein filaments is in progress.

Of course, protein fibril formation is a very complex process, and we cannot expect to capture the full physics of the aggregation in a simple model. Indeed, as already mentioned above, Aβ protein has been observed to form fibrils with different structures, dependent on the method of preparation. Another important aspect of the assembly in this protein is polymorphism (20). Nevertheless, the intertwining energy and the steric interaction discussed in this article likely play an important role in the determination of the final diameter of the fibrils.

The model introduced in this article can potentially be successfully applied to any system in which cylindrical filaments that display no preferred directionality of interaction combine to form intertwined fibrils. If there is a preferred direction of interaction, then other effects need to be taken into account. Torsion, for instance, plays a large role in this type of system. For a full description of aggregation and intertwining in these systems, we refer to the work of Nyrkova et al. (11). A similar description has been applied for DNA (27), whereas a detailed general mathematical model is presented by van der Heijden (28). An extension of the work presented here, in which we quantify the role of the protrusions corresponding to the disordered part of the proteins, is currently in progress.

CONCLUSIONS

A simple model, comparing the elastic and binding energy contributions for intertwined cylindrical rods, is outlined. It predicts that, for a binding energy per unit length that is not very small, and a bending modulus of the cylinders that is not very large, an optimum helical pitch appears if two rods are allowed to intertwine. A generalization of this model that takes into account bundles of more than two rods shows that bundles of specific geometries, maximizing the number of rod-rod contacts, while allowing for a helix of a relatively small radius, are most likely to form. We apply the model to Aβ amyloid protein fibrillization, treating the protofilaments that make up the mature fibril as intertwining rods. For this, we forbid the occurrence of fibrils in which the N-terminus of the protein, which protrudes from the cylindrical protofilament, overlaps other protofilaments. Our work predicts the formation of threefold fibrils, consisting of six protein stacks. This corresponds quite well to experimental results. In addition, we can tentatively predict the pitch of these threefold amyloid fibrils, given the pitch of twofold fibrils.