The Cooperative Response of Synaptotagmin I C2A. A Hypothesis for a Ca²⁺-Driven Molecular Hammer

Abstract

In the current understanding of exocytosis at the nerve terminal, the C2 domain of synaptotagmin (C2A) is presumed to bind Ca²⁺ and the membrane in a stepwise fashion: cation then membrane as cation increases the affinity of protein for membrane. Fluorescence spectroscopy data were gathered over a variety of lipid and Ca²⁺ concentrations, enabling the rigorous application of microscopic binding models derived from partition functions to differentiate between Ca²⁺ and phosphatidylserine contributions to binding. The data presented here are in variance with previously published models, which were based on the Hill approximation. Rather, the data are consistent with two forms of cooperativity that modulate the responsiveness of C2A: in Ca²⁺ binding to a network of three cation sites and in interaction with the membrane surface. We suggest synaptotagmin I C2A is preassociated with the synaptic vesicle membrane or nerve terminal. In this state, upon Ca²⁺ influx the protein will bind the three Ca²⁺ ions immediately and with high cooperativity. Thus, membrane association creates a high-affinity Ca²⁺ switch that is the basis for the role of synaptotagmin I in Ca²⁺-regulated exocytosis. Based on this model, we discuss the implications of protein-induced phosphatidylserine demixing to the exocytotic process.

INTRODUCTION

The synaptic vesicle protein synaptotagmin I is generally accepted to function as the Ca²⁺ sensor in fast release of neurotransmitter into the synaptic cleft. Significantly, results from in vivo studies utilizing strategic point mutations in C2A that alter Ca²⁺-binding affinity have yielded parallel shifts in the Ca²⁺ dependence of exocytosis, strongly implicating synaptotagmin I as being the sensor for fast Ca²⁺-dependent exocytosis (1–5). Synaptotagmin I consists of a vesicular transmembrane sequence attached to two C2 domains, C2A and C2B, which face the cytoplasm and are assumed to associate with the vesicular or terminal membrane upon Ca²⁺ influx. C2B, but not C2A, has been recently reported to have the capacity to bind both the plasma terminal and synaptic vesicle simultaneously (6). C2 domains consist of two superimposed four-strand β sheets, often with Ca²⁺-binding sites clustered together at the membrane-interacting tip of the protein (7–11). The C2A domain binds Ca²⁺ and the acidic phospholipid phosphatidylserine (PS), an observation corroborated by structural and cellular studies (1,2,5,8–11).

Many proteins critical to the synaptic vesicle cycle are associated with vesicular and terminal plasma membranes. They work together as well as independently to produce a response, usually triggered by Ca²⁺ influx. The membrane association of proteins such as synaptotagmin, munc-18, and phosphatidylinositol phosphate kinases (PIPK) is dependent on lipids such as PS, phosphatidylinositol-4,5-bisphosphate (PI(4,5)P₂), and diacylglycerol (DAG). This points to a fundamental role played by membrane-associated proteins and for lipid components in the synaptic vesicle cycle (12–14). Lipids have been suggested to act as a tethering mechanism to constrain proteins to membranes or to influence the fusion cycle through the involvement of lipid rafts (reviewed in 5,15–17). Recent work in related systems, however, points to a distinct role for lipids in vesicular release. In particular, lipids have been proposed to contribute to spatial organization of components critical for priming, fusion, and Ca²⁺-dependent exocytosis (18). For example, the work of Aoyagi et al. (19) makes a compelling case for PI(4,5)P₂ microdomains to colocalize with syntaxin clusters in the terminal membrane. Laux et al. (20) had previously suggested that PI(4,5)P₂ microdomain formation is an element controlling cellular dynamics in the neuron-like pheochromocytoma (PC)12 cell line. Likewise, recent work by Coorssen (21,22) supports a role for cholesterol and sphingomyelin in the intrinsic fusion machinery for fast Ca²⁺-triggered fusion.

In eukaryotes, a plethora of membrane lipid species exists. The synthesis of such a variety of lipids argues against a simple barrier function for cellular membranes. It also argues against a mere advantage of reduction of dimensionality or a concentration effect for increased reaction rates on the membrane because neither requires as many different lipid species. We have suggested that one role of lipids may be signal amplification through multiple nearest-neighbor interactions and regulation of assembly of signaling complexes (23). The lipid affinity of a number of proteins involved in the synaptic cycle suggests that lipid-protein interactions are an overlooked means by which to modulate the response to Ca²⁺ influx at the nerve terminal. The use of lipids to communicate changes offers the possibility of cooperativity in the assembly of protein complexes on the membrane (23) and of fine-tuning the combinations of proteins that will subsequently be assembled (21). Contrasting views invoke stabilizing interactions between protein and lipid that are separate and additive in the process of forming protein assemblies. This view, that the interactions are separate and additive, dominates current considerations of the role for lipids in the synaptic vesicle cycle (reviewed in 5,15,24,25).

In this report, we suggest that for C2A to respond to Ca²⁺ with maximal cooperativity and affinity, this synaptotagmin protein domain is associated with membrane before Ca²⁺ influx. Experimental fluorescence spectroscopy data were gathered under conditions where concentrations of a Ca²⁺ analog, Tb³⁺, and the content of the acidic phospholipid, PS, were varied. Microscopic binding models were derived and rigorously tested against the experimental data. Furthermore, based on the proposed model, a separate experimental approach using a lipid-derivative fluorescent probe, dansyl-PE, was used to test the calculated binding affinities both with and without Ca²⁺ present. Fixing the cooperativity factors and equilibrium affinity constants while varying the ligand species (Ca²⁺, Tb³⁺, or lipid composition) and their concentrations provides a stringent test of the proposed model.

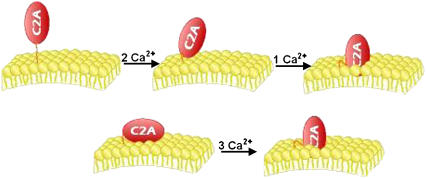
Based on observations using a variety of experimental techniques, synaptotagmin I C2A has been suggested to undergo binding in the following stepwise sequence of events: first, calcium ions in solution, then acidic membrane (8). Notably, unlike the first two cation binding sites, the third Ca²⁺ site requires PS to complete its coordination shell (1,26) (Fig. 1, top). It is this incomplete coordination shell that has a very low affinity for cation in the absence of acidic phospholipid and thereby leads to the inference that binding is ordered. In Fig. 1 we present one scenario where two Ca²⁺, then membrane, then the last Ca²⁺ are bound (other scenarios are presented in Discussion). In our model, preassociation of C2A with PS-containing membrane before Ca²⁺ influx ensures that all three cation sites are ready for high-affinity, cooperative binding of Ca²⁺. We now propose, based on structural data from electron paramagnetic resonance (EPR) studies (10), that in the absence of cation, C2A is weakly membrane associated, oriented parallel to the membrane surface, with its cation-binding loops exposed to the cytoplasm. Upon binding Ca²⁺, the protein rotates perpendicularly, and the three Ca²⁺-binding loops penetrate into the acidic phospholipid-containing membrane (Fig. 1, bottom). We further suggest that this ligated conformation partially destabilizes the lipid bilayer, increasing the propensity of the secretory vesicle to undergo fusion with the terminal plasma membrane. In this manner, the C2A domain would function as the head of a ‘molecular hammer’ to destabilize the membrane. Successive rounds of Ca²⁺ influx would repeatedly drive it into the membrane, and falling Ca²⁺ concentrations would bring it back out.

FIGURE 1.

(top) ‘Solution-first’ model. (bottom) Proposed model.

MATERIALS AND METHODS

Materials

1-Palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC or 16:0,18:1PC) and 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoserine (POPS or 16:0,18:1PS) were from Avanti Polar Lipids (Birmingham, AL). Potassium chloride was puriss grade, and 3-morpholinopropanesulfonic acid (MOPS) was Biochemika grade from Fluka Chemical (Ronkonkoma, NY). Chelex-100 ion-exchange resin was from Bio-Rad Labs (Rockville Center, NY). Chloroform, methanol, and benzene were high-performance liquid chromatography grade (J. T. Baker, Mallinckrodt Baker, Phillipsburg, NJ). All other chemicals were reagent grade.

Preparation of solutions

Solutions were prepared as in Hinderliter et al. (23,28). In brief, all buffers used in fluorescence spectroscopy studies were decalcified by passage of the 2× buffer (4 mM MOPS, 200 mM KCl, pH 7.5) over a Chelex column before dilution with ddH₂0 to 1× buffer. Terbium chloride hexahydrate was prepared gravimetrically and hydrated in decalcified buffer (Molecular Probes, Eugene, OR). By running all solutions over a Chelex column, contaminating Ca²⁺ was reduced to nanometer or lower concentrations as verified by use of the chromophoric Ca²⁺-chelator 1,2-bis-(o-aminophenoxy)ethane-N,N,N′,N′,-tetraacetic acid (BAPTA) (Molecular Probes). The Bradford assay was used to determine protein concentrations (Bio-RAD Protein Assay, Bio-RAD Laboratories, Hercules, CA).

Expression and purification of recombinant protein

Synaptotagmin I C2A was purified as in Hinderliter et al. (28) and Frazier et al. (10).

Preparation of large unilamellar vesicles

Lipids were prepared as described before (10,23,28).

Fluorescence spectroscopy experiments

The binding affinity of C2A for Tb³⁺ and various lipid mixtures was determined by monitoring changes in energy transfer from the single tryptophan and several tyrosines in C2A to bound Tb³⁺. Tb³⁺ is a Ca²⁺ analog, having a similar ionic radius, a higher charge density, and the benefit of undergoing fluorescence energy transfer from aromatic amino acids once bound (29–31). Addition of the lanthanide cation to a protein solution resulted in a decrease in the intensity of fluorescence emission from the protein as described below and previously (10,11,23,32). The Förster distance is the distance between an energy donor and an acceptor at which the transfer efficiency is 50% (33). For the pair in which tryptophan is the donor and terbium is the acceptor, literature values for the Förster distance vary. Calculated values for the Förster distance between tryptophan and terbium range from 3.24–10 Å (31,34). According to another report, the bound terbium ion must be ≤5 Å from a tryptophan residue (35). This is a calculated distance and was not measured. Förster distances have also been used to estimate distances between bound terbium ions and tryptophan residues in proteins. Using an assumed Forster distance of 10–22.7 Å, the distance between the terbium-tryptophan pair in the integrin α_IIbβ₃ based on experimental data was estimated to be 15–34 Å (36). Utilizing the molecular dynamics program SYBYL 7.1 (Tripos, St. Louis, MO), we used the NMR solution structure of synaptotagmin 1 C2A solved by Shao et al. (Protein Data Bank number: 1byn) (37,38) to measure the distances from every tyrosine and tryptophan to each of three calcium ions. Our calculations find the tryptophan residue to be between 21–28 Å from the calcium-binding sites. We have also conducted identical binding experiments exciting tyrosine residues, two of which are located as close as 8 or 9 Å from the calcium-binding sites. Exciting the tryptophans directly of the tyrosines and tryptophan has yielded binding isotherms that correspond to the same binding constants (A. Hinderliter, unpublished observations).

Titrations of synaptotagmin I C2A domains with Tb³⁺, Ca²⁺, and lipid

Titration data were gathered by following the quenching of the intrinsic fluorescence of the synaptotagmin I C2A domain by the lanthanide Tb³⁺. The fluorescence energy transfer from the protein to the lanthanide was detected as quenching of the intrinsic protein fluorescence. The loss of fluorescence was normalized and expressed as fraction bound. The added total ligand was corrected to free ligand for each corresponding fractional bound value, after accounting for maximum numbers of ligands bound at saturation to the protein. Experimental data were corrected for free ligand versus fraction bound per site on the protein. Total ligand was corrected for free ligand by calculating the fraction bound to protein and subtracting bound from total ligand added. Since a fluorescence change is not detectable upon addition of membrane vesicle alone, lipid titration data were gathered by titrating lipid into a solution of protein and a subsaturating concentration of Tb³⁺. Addition of lipid significantly increased the affinity of protein for Tb³⁺, detectable as a loss of protein fluorescence upon cation binding.

To verify our calculated membrane-protein binding affinities using a different technique, we introduced a fluorescently labeled lipid into the membrane mixture. By incorporating a dansyl-labeled lipid probe (dansyl-PE) in the bilayer, the membrane can accept energy transfer from the tryptophan and tyrosines of bound C2A. The fluorescence resonance energy transfer of this interaction can be measured as a decrease of protein fluorescence emission, making this procedure comparable to the energy transfer displayed by the protein/terbium-binding experiments. To correct for background fluorescence of the buffer and lipid and artifacts of the spectrofluorometer signal, a corresponding blank titration of lipid and buffer was performed and subtracted from the recorded protein emission.

Binding isotherms

Binding isotherms were derived from the binding partition function (39) as described by Almeida et al. (32). Briefly, the binding partition function contains a term proportional to the probability of observing each state of the protein. To obtain the binding isotherm (θ) from the partition function (Q), the following derivative is calculated,

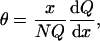(1)

where x = [Tb³⁺], [Ca²⁺], or [L], N = n for Tb³⁺ (n is maximum number of Tb³⁺ sites on the protein), and N = 1 for PS titrations (one protein is either bound to one lipid vesicle or not); θ is the fractional saturation of Tb³⁺ sites on the C2 domains or the fraction of proteins bound to the lipid. The resulting binding isotherms are given by applying Eq. 1 to the following partition functions. In solution, cation binding by C2A is described by the partition function q_o,

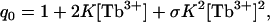(2)

where K is the binding constant and σ is a cooperativity factor resulting from the interaction of the two occupied sites (σ >1 for positive cooperativity).

In the presence of lipid, cation binding by C2A is described by the global partition function,

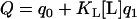(3)

where q₁ is given by

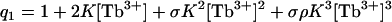(4)

Note that the q₁ accounts for three possible cation-binding sites, the last of which becomes available only in the membrane-inserted conformation. Lipid binding by C2A in the absence of cation can be described by the partition function for binding to lipid by Q_L where Q_L = 1 + K_L[L].

RESULTS

Titrations of the C2A domain of synaptotagmin I with cation and lipid membranes were performed under a variety of combinations. Microscopic binding partition functions were then used to model binding of the C2A to Tb³⁺ (as a mimic for Ca²⁺), PS, and/or PC. These models were tested through fitting the binding isotherms generated to experimental titration data in a globally consistent manner.

Cation binding by synaptotagmin I C2A

The titration of synaptotagmin I C2A with TbCl₃ in the absence of lipid vesicles is shown in Fig. 2 A. Analysis of this binding curve using Eq. 2 indicates that C2A binds two cations in solution, the first with an affinity K = (3.1 ± 0.4) × 10³ M⁻¹ (corresponding to a dissociation constant (1/K) of 300 ± 40 μM), and the second with an affinity σK = 5.6 × 10⁴ M⁻¹. The cooperativity factor, σ = 18 ± 7, indicates positive cooperativity between the binding of the first and second cations, as suggested by the weakly sigmoidal character of the experimental titration curve. The second cation binding affinity corresponds to a dissociation constant of 1/σK = 20 μM. At room temperature, the first site binds with a free energy ΔG° = −RTlnK = −4.7 kcal/mol, and the second site with a more favorable free energy ΔG° = −RTln(Kσ) = −6.4 kcal/mol.

FIGURE 2.

(A) Binding of Tb³⁺ to synaptotagmin C2A in the absence of lipid. The signal arising from quenching the intrinsic protein fluorescence was used. The loss of fluorescence was normalized and expressed as fraction bound. The added total ligand was corrected to free ligand, taking into account the total number of ligands occupying the protein at saturation and the concentration of protein (0.2 μM). Data were corrected for two cation-binding sites. All titrations were carried out in decalcified 2 mM MOPS, 100 mM KCl, pH 7.5. The line is Eq. 1 applied to the partition function q₀. (B) Binding of Tb³⁺ to synaptotagmin C2A (0.55 μM) in the presence of 40 μM total POPC/POPS (16:0,18:1PC:16:0,18:1PS) (75:25). This corresponds to 20 μM POPC/POPS available for binding on the outer leaflet of the large unilamellar vesicles. The fitted line is Eq. 1 applied to the global partition function Q. K and σ are held constant from Fig. 2 A and K_L = 0.67 μM⁻¹.

The titration of C2A with TbCl₃ in the presence of lipid vesicles containing the acidic phospholipid POPS (POPC/POPS 75:25) is shown in Fig. 2 B. Increased sigmoidicity compared to Fig. 2 A is apparent. Analysis of this binding curve using Eqs. 3 and 4 indicates that the protein now binds a third cation. Keeping the values of K and σ fixed from analysis of the first isotherm, the experimental data were best fit by a binding isotherm that includes an additional cooperativity factor (ρ) for binding of the third cation, which is much larger than the solution-state cooperativity factor (σ). Under all ligand conditions, with cation and PS present, ρ was allowed to vary but was consistently found to correspond to a value on the order of a few hundred. In the curve shown, ρ = 168 and the lipid binding constant K_L = 7.0 × 10⁵ M⁻¹ (see below). The presence of membrane containing PS thus shifts the binding equilibrium of C2A strongly to the three-cation bound state. Enhancement of cation binding affinity and cooperativity by PS is consistent with this lipid specifically filling empty coordination sites of the metal ion (7). It should be noted that the model was in no way constrained to concur with that structural inference. The cooperativity factors ρ and σ both contribute to the cation binding affinity when the protein is in the membrane-bound state. At this point, the distribution of the bound protein states in the partition function favors binding three cations in the presence of acidic membrane.

Membrane binding by synaptotagmin I C2A

Titrations of the synaptotagmin I C2A domain with lipid vesicles of various compositions were performed in the presence of subsaturating concentrations of Tb³⁺. An example is shown in Fig. 3 A (POPC/POPS 75:25). The intrinsic membrane-binding affinity in the absence of cation (K_L) was calculated using the binding isotherm derived from the partition function of Eq. 3. This calculated K_L (which depends on lipid composition) was held constant in the binding isotherm used to fit the cation-binding data in the presence of lipid (Fig. 2 B). It should be noted that the cation-binding affinities derived from the data in Fig. 2, K and σK, are held constant in all subsequent fits to test the proposed binding model. The factor ρ was adjusted by iterative fitting of the data in Figs. 2 B and 3 A until a consistent value was found.

FIGURE 3.

Binding of synaptotagmin C2A to POPC/POPS (75:25) or POPC/POPS/dansylPE (65:25:10) in the presence of subsaturating Tb³⁺ (9.1 μM, A) or Ca²⁺ (2 μM, B). The lipid titrant was corrected for free lipid concentration assuming membrane coverage by C2A corresponds to five lipids and for only outer leaflet lipid available for binding. The same partition function and constants were used to fit both binding isotherms with the corresponding constant cation concentration, 9.1 μM or 2 μM, for Fig. 3, A or B. Protein concentration was 0.55 μM for (A) and 0.2 μM for (B).

Binding Ca²⁺ does not alter the intrinsic fluorescence of C2A as does binding Tb³⁺. This precludes the direct comparison of Ca²⁺ and Tb³⁺ binding by fluorescence spectroscopy. A membrane-incorporated probe, dansyl-PE, was used to assess the validity of using Tb³⁺ as a mimic to Ca²⁺. Titration of C2A with membranes containing dansyl-PE in the presence of subsaturating Ca²⁺ (Fig. 3 B) enabled the comparison of the binding profiles of the two ions. The subsaturating cation concentrations used differed (compare Fig. 3, A and B), but any subsaturating concentration of cation may be used to generate the data, as this is accounted for in the binding isotherm. The titration data were fit with the same binding isotherm used for the data in Fig. 3 A and with exactly the same parameters (K = 3.1 × 10³ M⁻¹, σ = 18, ρ = 168, and K_L = 7.0 × 10⁵ M⁻¹). It is evident that both sets of data can be fit very well by the same isotherm, indicating that Tb³⁺ is a reasonable Ca²⁺ analog for binding studies with C2A, at least in the presence of membrane.

The titrations of C2A with Tb³⁺ and lipid (POPC/POPS mixtures) were then performed as a function of the PS content in the lipid vesicles (0, 5, 10, 20, 25, and 30 mol % PS). The intrinsic affinity of C2A for PC/PS membranes in the absence of cation, represented by the binding constant K_L, was calculated for each lipid composition from the fits to the lipid and the cation titration data (Fig. 4 A). In these fits, the cation-binding constants and the cooperativity factors were kept fixed at the values previously determined. The specificity for acidic PS is evident from the approximately exponential decrease of the intrinsic membrane dissociation constant (1/K_L) of C2A as a function of the PS content of the lipid vesicles, in the absence of Tb³⁺ (Fig. 4 A).

FIGURE 4.

(A) Dependence of the lipid-binding constant of synaptotagmin I C2A on the percentage of PS in a binary mixture of POPC/POPS. K_L is presented as the logarithm of the dissociation constant (1/K_L). The logarithm is provided as base 10 for ease of comparison of the values to other figures. Protein concentrations were varied from 0.2–0.55 μM. (B) Binding of synaptotagmin C2A to POPC/POPS/dansylPE (65:25:10). The lipid-binding constants were calculated through application of Eq. 1 to partition functions. The global partition function Q from setting [Tb³⁺] = 0 in Eq. 3, then reverts to 1 + K_L(L). The lipid titrant was corrected for free lipid concentration as above, accounting for protein concentration, outer leaflet lipids, and membrane coverage by C2A of five lipids.

To directly observe the binding of C2A to lipid membranes in the absence of cations, vesicles containing 65 mol % POPC, 25 mol % POPS, and 10 mol % of the fluorescent lipid probe dansyl-PE were prepared. Titrations using fluorescence energy transfer between the single tryptophan of C2A and the membrane-incorporated dansyl-PE allowed direct determination of the membrane affinity of C2A in the absence of cation (Fig. 4 B). The data fit very well with a hyperbolic binding isotherm with a dissociation constant of 3–4 μM (range of data presented for both the 5% (not shown) and 10% dansyl-PE data). This is somewhat larger but of the same order of magnitude as the dissociation constant (2 μM) obtained by setting [Tb³⁺] = 0 in the titration data in the presence of cation. The difference may be due to the fact that in this last titration 400 nM C2A was used instead of 200 nM. This could introduce a larger error in the calculation of free lipid concentration, particularly for the points measured at low lipid (initial portion of the isotherm). The higher protein concentration was required to obtain a better fluorescence signal. In any case, this data set (Fig. 4 B) clearly shows that C2A binds lipid in the absence of Ca²⁺ (or Tb³⁺), with an association constant similar to that calculated from the other data sets. We also sought to address a concern that the potential perturbation introduced by the use of 10% of a derivatized lipid could perturb the calculated binding constants. The lipid titrations in both the presence and absence of Ca²⁺ were repeated with 5% dansyl-PE. Within error, the binding affinities were the same whether 5% or 10% dansyl-PE was used. Although the net negative charge of the dansyl-PE may perturb the observed binding, it is possible that the enhanced binding could be due to the fact that an additional negative charge will be offset by the bulky dansyl in the headgroup region of the lipid.

Finally, if the membranes were composed of PC alone, which is a zwitterionic phospholipid, the experimental binding data could only be fit with a membrane-dependent cooperativity factor (ρ) that was <1. In other words, the excess free energy required to fill the third cation site is insufficient if only PC is present (Fig. 5, A and B), reducing the overall affinity and cooperativity of binding toward cation compared to when PS is present. If a fit is attempted, the cooperativity factor is dramatically reduced to ρ = 0.09, which compares with ρ on the order of a few hundred in the presence of PS. This clearly suggests a role for PS in the coordination of the bound cation in the third binding site.

FIGURE 5.

Binding of Tb³⁺ to 0.4 μM synaptotagmin C2A in the presence of 400 μM total POPC (A) and of POPC to C2A in the presence of 9.1 μM Tb³⁺ (B). Data were corrected for as in Figs. 2 and 3.

DISCUSSION

The wealth of in vitro data briefly summarized in the introduction regarding the role of C2 domains as Ca²⁺ sensors points to the idea that the function of C2 domains depends on their translocation to the membrane upon Ca²⁺ binding. In vivo studies on the influence of deleterious binding mutants on synaptic function are usually interpreted on the basis of those binding models. In general, binding studies are undertaken to gain insight into the cellular function of a protein or protein motif. Yet, many binding studies rely on empirical relationships to describe the binding data. Empirical relationships do not provide a fundamental understanding of the mutual influences of the binding of two ligands to a protein domain. This is due to the inability to separate the contributions of different ligands and the contributions of multiple identical ligands to the binding Gibbs free energy. One approach to deconvolute the interactions of multiple identical and different ligands is to derive binding partition functions for numerous microscopic models (39). Microscopic binding partition functions allow for an understanding of the association process as the probabilities of each protein state are directly obtained (39–41).

How does the selection of Tb³⁺ (necessary to follow the binding process) lead to differences in behavior compared to the physiological ligand, Ca²⁺? The use of any probe is not optimal because it is a mimic. Tb³⁺ has a similar ionic radius to Ca²⁺ but an extra charge, potentially perturbing the calculated cation-binding constants. We will limit our discussion to the first two cation sites in the absence of lipid. If cation binding were entirely due to electrostatic interactions and each bound cation progressively neutralized the electronegative binding residues within C2A, the second cation affinity would be markedly reduced. A binding response would be expected with lower affinity for the second bound Tb³⁺ compared to Ca²⁺. If instead discrete shared amino acids between the first and second cation binding sites were restricted by occupation of the first binding site, a second binding site could be more favored. In this scenario Tb³⁺ might be expected to reduce the predicted cooperative response by perturbing the first binding response at the expense of the second binding site. The Hill coefficient calculated for the Tb³⁺ data in solution is 1.6 (Fig. 2 A); Hill coefficients 1.6 and 1.7 for Ca²⁺ binding (in the absence of lipid) to C2 domains from PKCβ and cPLA₂-α, respectively, have been reported (8). The Hill values are similar for Ca²⁺ and Tb³⁺ for different, albeit structurally homologous proteins.

We present a model for the association processes of synaptotagmin I C2A with Ca²⁺ (here also mimicked by Tb³⁺) and phospholipid membranes. The purpose of rigorously modeling a biological process is to understand its detailed mechanism, in this case how synaptotagmin I mediates fast Ca²⁺-dependent exocytosis. We find that C2A binds Tb³⁺ cooperatively. In solution, the protein binds two terbium ions, with a more negative Gibbs free energy for the second one, as evidenced by ∼−2 kcal/mol excess binding Gibbs free energy (σ = e^{−ΔG°ex/RT}) released upon occupation of the second site. In solution the affinity for Tb³⁺ increases from 300 μM for the first site to 20 μM for the second site (in terms of dissociation constants). Essentially, the probability of filling a third site on the C2A domain becomes significant only in the presence of acidic phospholipid. It is this additional cooperativity that allows C2A to act as a cation-dependent switch for exocytosis. The increased binding for that third site in the membrane-bound state (ρK) corresponds to a Tb³⁺ dissociation constant of ∼2 μM.

The idea of an additional cation-binding site produced in the presence of phospholipid was proposed by Zhang et al. (7) and Shao et al. (37). They found three cation-binding sites that were filled in order of highest to lowest affinity. Both Zhang et al. (7) and Shao et al. (37) note a third Ca²⁺ site of low affinity (∼1 mM) in solution as identified by NMR. We also observe in solution a third cation that binds at ∼1 mM [Tb³⁺] (data not shown). If these sites must be filled in defined order, this is an ordered model. In this case the binding isotherm will have a hyperbolic shape. Although an ordered binding model is consistent with cation-binding sites of different affinities, it does not necessarily include cooperative interactions between the cation-occupied sites. An ordered model where the second site binds with greater affinity than the first will produce a sigmoidal binding isotherm. This is an ordered cooperative model where the second, high-affinity site was created after occupation of the first site by the ligand. At this point, we cannot completely reconcile our Tb³⁺ data and interpretation with the Ca²⁺-binding data obtained by NMR (7,37). The appearance of crosspeaks is a direct report of the occupancy of defined Ca²⁺-binding sites. The NMR data are consistent with the first scenario presented above, in which the protein is an electrostatic platform on which to assemble Ca²⁺.

The structural data that imply an incomplete Ca²⁺-coordination shell for the third site clearly indicate that Ca²⁺ binding is not cooperative in the absence of phospholipid. However, it should be noted that the C2A construct used in the NMR studies is a smaller version of the C2A construct used in this study. An allosteric transition model could unite cooperative Ca²⁺ binding in the presence of phospholipid (8) with noncooperative Ca²⁺ binding by C2A in solution as observed by NMR (7,37). We have proposed such a model to fit the similar binding behavior observed for the family of the Ca²⁺ and phospholipid-binding proteins, the annexins (32). Although the interior binding constants and cooperativity factors would differ in a model where cooperative Ca²⁺ binding in the presence of phospholipid with noncooperative Ca²⁺ binding by C2A in solution is observed, the concept would be the same. It is association of the protein with the membrane that renders the binding cooperative. A point of agreement between the NMR data collected with Ca²⁺ and the Tb³⁺ data is the observation of a third cation site of very low affinity in solution. In addition, when acidic phospholipid is present, cation binding appears more cooperative irrespective of the choice of cations. We conclude from this observation that, for either cation, phospholipid enhances the affinity of the protein toward Ca²⁺ or Tb³⁺. A state with all three cation sites occupied becomes the most probable when phospholipid is present. The primary difference between the NMR data with Ca²⁺ and our data with Tb³⁺ is the order of binding and affinity toward cation of the first two binding sites.

Previously reported binding data were often interpreted through application of the Hill model (39). The Hill model is a robust model to probe for cooperativity, but, as an empirical model, it does not provide a molecular understanding of the sources of cooperativity. The Hill model is essentially a two-state model; the protein is either completely unbound to ligand or completely bound to all the ligands present. It is similar to our binding partition function with all the interior terms and cooperativity factors removed. It is the removal of the interior terms that increases the cooperativity and creates a seemingly very cooperative Hill coefficient. In comparison, data analysis using partition functions allows for the probability of each C2A state to be calculated exactly. Such an analysis has produced a model that is consistent with C2A acting as a cation-dependent binding switch: that is, a significant change in the fraction of protein bound to cation occurring within a very narrow range of free cation concentration.

We find that the most probable state in the presence of PC:PS membrane and high cation concentration is the membrane-bound state with all three cation sites filled. In the absence of cation, some C2A is bound to membrane and some C2A is in solution. The subset of the protein that is membrane associated has the greatest probability of binding cation and this state predominates when both ligands PS and Ca²⁺ are present. If one examines the partition function for C2A binding cation when bound to lipid, the probability of occupying the fully ligated (active) Ca²⁺ state in comparison to the partially ligated (inactive) Ca²⁺ states may be calculated. In cells, the resting Ca²⁺ concentration is 200 nM and the excited Ca²⁺ concentration is 20 μM (17). Using these values, the percentage of C2A with three Ca²⁺ ions bound in the membrane-associated state rises from negligible to 40% going from resting to excitation; under the same conditions, the membrane-associated states with one or two Ca²⁺ bound rises to only 10% of the C2A population. A further prediction of this model is that, as the membrane-associated C2A binds cation, more C2A will partition to the membrane from the solution state as the equilibrium shifts, upon Ca²⁺ influx, to repopulate the cation-unbound/membrane-bound states. For easy relation to concentrations, the inverse of the intrinsic lipid affinity, the dissociation constant, is discussed. It varies from ∼100 μM to <1 μM, increasing exponentially with PS content (Fig. 4 A).

Although the exact PS content of synaptic vesicles is unknown (it is suggested to be ∼12% of the total synaptic vesicle lipid (5) where the majority of the PS is presumed to be localized to the exterior of the vesicle), the lipid affinities indicate that C2A is bound to the membrane even in the absence of cation. A little discussed point is that the effective lipid concentration sensed by C2A domain of SYN 1 is calculated to be hundreds of micromolar to half a millimolar. This is a consequence of the C2A domain of SYN 1 being tethered to the vesicular membrane. The effective membrane concentration is calculated based on the hemisphere volume swept out by the radial distance spanning the tip of C2A to the amino acid attached to the transmembrane sequence. The moles of lipids are calculated from the number of lipids encompassed by the radial area under the hemisphere volume. In light of this calculation, it is difficult to reconcile the effective lipid concentration with binding models where membrane association is strictly driven by Ca²⁺ ligation. In our model, we do not make any assumptions regarding which physiologically targeted membrane—synaptic vesicle or terminal—C2A binds. We include this calculation to show the high local affinity of the synaptic vesicle membrane. If other members of the synaptic fusion apparatus such as syntaxin bind to the enriched region of basic residues in C2A (37,42), it suggests that protein components involved in regulated exocytosis can be in dynamic competition with lipid for C2A.

In our model, using the parameters obtained from experiment, C2A is bound to the membrane surface before the Ca²⁺ influx (Fig. 1, bottom). If the protein is bound to the membrane surface before cation influx, the protein will then bind cation with the maximal cooperativity and hence exhibit the most ‘switch-like’ potential. In contrast, if the protein were in solution when binding cation (Fig. 1, top), a less efficient response would result, and the switch would be damped.

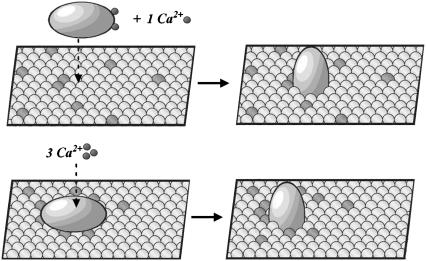
Due to the small cooperative interactions that exist between each lipid and its six nearest neighbors, the lipid surface is likely to consist of a mosaic of domains. The domains are due to lipids within a mixture interacting differently with one another (43). Subtle differences in chemical structure between the lipid components of the membrane, as little as two additional methylene groups or an unsaturation, may greatly enhance lipid domain formation (23,28). This creates enriched domains of PS where the effective concentration (chemical activity) of the acidic lipid may be much greater than the physical concentration of the lipid within the membrane as a whole. Small changes in overall lipid composition of the membrane can then lead to a much greater local change in PS content within lipid domains and therefore result in a significant change in the probability of membrane association of C2A in the absence of cation. For instance, changing the acyl chain length of the PC component in a binary mixture with POPS from 16:0,18:1-PC to 16:1,16:1-PC, POPS domain formation is increased in such a way that 12 mol % PS in the latter case has the same effective concentration as 20 mol % PS in the former (23). These small, cooperative interactions between lipids ensure that formation of domains is readily reversible. The binding model proposed here when combined with our finding of C2A demixing of PS upon binding (28) suggests that PS-specific binding by this motif is a means to modulate the responsiveness of SYN 1. As membrane occupancy by proteins will vary greatly with lipid composition, lipids offer a means to form transient, attractive binding sites, and PS-enriched membrane domains may be disrupted and dissipated with each round of synaptic vesicle fusion (Fig. 6).

FIGURE 6.

(top) ‘Solution-first’ model which does not involve PS-demixing upon C2A binding to membrane. (bottom) Proposed model incorporating PS demixing. PS is shown in green and the ‘bulk’ membrane, which in our model system is represented by PC, is shown in yellow.

We offer a molecular model of how the C2A domain of synaptotagmin I may act as the Ca²⁺ sensor that triggers efficient binding of synaptic vesicles to the plasma membrane and subsequent release of neurotransmitter into the synaptic cleft. A motivation for the proposed model is the realization that by binding to membrane before Ca²⁺ influx, C2A will act much more like a cation-sensitive switch than if it resides in the cytosol (solution state). In addition, the model proposed is entirely consistent with known structural features of the C2A domain. In surface potential calculations (44), before Ca²⁺ ligation the positively charged surface defined by four conserved lysines (45) is offset by the negatively charged Ca²⁺-free tip of the protein, thus repelling this portion of the protein from the acidic phospholipid surface. Upon binding of the third Ca²⁺ ion, the tip acquires a positive charge, which is consistent with the EPR-generated structure (10), where the protein, when in the fully Ca²⁺-bound form, is oriented upright in the PS-containing membrane. The Ca²⁺-binding loops of C2A when not bound to Ca²⁺ exhibit greater structural fluctuations than when bound, as identified by analysis of NMR nuclear Overhauser effect (NOE) intensities and H/D exchange rates (37). One possible consequence of lipid ligation in the absence of Ca²⁺ is to reduce the structural fluctuations of C2A. Paying such an entropic penalty, the protein is primed for higher cation-binding affinity. We have recently proposed a similar concept with regard to the annexins (32).

We seek to combine these static structures into a unifying model, which is an interpretation of our data based on binding partition function analysis. As shown here, given the affinity of C2A for PS-containing membranes, it should be bound even in the absence of Ca²⁺. We propose that if C2A has zero, one, or two Ca²⁺ bound, it is oriented with its long axis parallel to the membrane surface, presenting the Ca²⁺-binding tip to the cytosol (Fig. 6, bottom left). These three states of the membrane-associated protein correspond to the first three terms in the Ca²⁺-binding partition function q₁ (1 + 2K[Tb³⁺] + σK²[Tb³⁺]²), Eq. 4. Upon binding of the third Ca²⁺ ion, the protein rotates into the nearly upright position, a state that partially penetrates into and destabilizes the membrane (Fig. 6, bottom right). This state corresponds to the last term in partition function q₁ (σρK³[Tb³⁺]³). Because of cooperativity in Ca²⁺ binding to the membrane-associated C2A, the most occupied states are those with zero (before Ca²⁺ influx) or three ions bound (after Ca²⁺ influx), enabling C2A to function as a Ca²⁺ switch. The proposed destabilization of the lipid bilayer by the upright conformation is the basis of the ‘molecular hammer’ concept. In this concept, it is the partial penetration (hammering into the membrane) of the fully Ca²⁺-bound form of C2A that destabilizes the bilayer, thereby promoting vesicular fusion. We suggest a model of how a membrane-based Ca²⁺ sensor can be poised to respond in a physiologically relevant ‘switch-like’ manner and how the activation of this ‘molecular hammer’ may contribute to the initiation of vesicular fusion.

Finally, we suggest that because the chemical activity (the ‘effective concentration’) of PS changes with its mixing behavior, the organization of membrane lipids at the active zone of the synaptic vesicle can influence C2A responsiveness to Ca²⁺. With repeated rounds of synaptic fusion it is possible that an enhanced sensitivity to Ca²⁺ may develop, such as that observed in the case of paired-pulse facilitation (PPF). During PPF, a second stimulatory event leads to greater neurotransmitter release than that evoked by the first stimulation. Previous work has indicated this enhanced release can be explained by residual Ca²⁺ localized near the active zone where secretory vesicles fuse (46). An alternative is suggested by our model. A lipid-mediated reorganization of the vesicular fusion components could also explain use-dependent presynaptic plasticity phenomena such as PPF. Thus, in addition to the influences between C2A, Ca²⁺, and lipids in the membrane, the frequency at which the ‘hammer’ is swung by repeated Ca²⁺-influx events also may convey important modulatory information to the release mechanism.

APPENDIX

In this appendix, we first derive the binding isotherms for the Hill model and then for the model we use here to interpret our data. Second, we compare the fits to the data obtained using our model and the more commonly used ‘solution-first’ model, which involves mandatory binding of Ca²⁺ before binding to the membrane. In general, for a protein with n identical and independent binding sites for a ligand x, such as a metal cation, the grand partition function is given by (39):

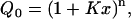(A1)

where x is the ligand concentration and K is the site, microscopic-association constant. In the Hill model, only the first and last terms in the expansion of (A1) are retained (39):

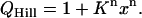(A2)

This corresponds to the maximum limit of positive cooperativity, where all intermediate binding states of the protein are ignored, and only the entirely empty and the fully liganded protein are considered. Their probabilities are then given by 1/(1 + Kⁿxⁿ) for the empty state and Kⁿxⁿ/(1 + Kⁿxⁿ) for the fully liganded state. The latter is also the binding isotherm for the Hill model. To relax the stringency of maximum cooperativity and render the model generally applicable, the exponent n is then allowed to vary, becoming a fractional value, less or equal to the total number of physical binding sites on the protein. The deviation of the fitted n from that maximum value is normally used as an empirical measure of the cooperativity of the system. The approach used here is a more rigorous way of treating cooperativity in binding systems (39). For simplicity we include only the derivation for the case n = 2 (two ligand binding sites on the protein). In this case the grand partition function can be constructed from that for identical and independent sites, Q₀ = (1 + Kx)² = 1 + 2Kx + K²x², either by multiplying the inner term by a factor σ < 1 or the last term by a factor σ > 1, as we have done. This takes into account the cooperativity of the system:

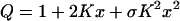(A3)

The physical meaning of σ = exp(−ɛ/KT) (with ɛ ≤ 0) is completely clear: it is a probability term reflecting the lower free energy of the doubly liganded state relative to the singly liganded state. It means that if both sites are occupied by a ligand, the protein has a free energy that is lower by the absolute value of ɛ. For a larger number of ligand binding sites, additional factors of the same type can be used.

We now compare our model with the traditional ‘solution-first’ model, which assumes that C2A must bind Ca²⁺ before binding to the membrane. The solution-first model is described by the binding isotherm derived from the partition function of Eq. A4:

(A4)

Similar to the Hill model for cation binding, the solution-first model eliminates from the partition function the terms that represent protein associated with the membrane with zero or one Ca²⁺ bound. That is, only proteins with two or three Ca²⁺ are allowed to associate with the membrane. An example is presented in Fig. A1 to illustrate the point. The experimental data points are the same as in Fig. 2 B and correspond to a titration of Tb³⁺ into a solution of C2A in the presence of POPC/POPS (75:25). The dashed line shown is calculated using as fixed parameters the constants derived from Fig. 2 A (K = 3.1 × 10³ M⁻¹ and σ = 18) and by fitting the solution-first model as defined by Eq. A4 to the experimental data points shown in Fig. 3 A, which yielded constants of K_L = 1.0 × 10⁵ M⁻¹ and ρ = 19,000.

FIGURE A1.

Binding of Tb³⁺ to synaptotagmin C2A in the presence of 40 μM total POPC/POPS (16:0,18:1PC:16:0,18:1PS) (75:25). Details are the same as Fig. 2 A. The lines correspond to Eq. 1 applied to the partition function (Q_{solution-first} = 1 + 2K[Tb³⁺] + σK²[Tb³⁺]² + K_L[L](σK²[Tb³⁺]² + σρK³[Tb³⁺]³) (Eq. A4). K and σ are held constant from Fig. 2. The solid line corresponds to the use of the K_L also ascertained from the fit of the lipid titration data of Fig. 2 A. The dashed line corresponds to fitting the data with a ρ = 19,000 (from the membrane titration), and the solid line corresponded with a ρ = 168.

The result is that the cation titration curve in the presence of membrane cannot be fit if constrained by the constants for C2A binding of Tb³⁺ in solution and protein association with the membrane, determined independently. It is possible to fit the solution-first model to the data of Fig. A1 using a K_L = 1.0 × 10⁵ M⁻¹ and a ρ = 168 (solid line), but with these parameters the lipid titration data of Fig. 3, A and B, cannot be fit by the solution-first model. Thus, imposing these constraints on the constants throughout the fits allows for testing competing models. The use of partition functions in combination with gathering experimental data over a variety of ligand conditions clearly discards the solution-first model.