Sequence-Dependent Twist-Stretch Coupling in DNA

Abstract

Recent single-molecule micromanipulation experiments on DNA subject to small distortion revealed positive coupling between DNA stretching and twisting—for instance, DNA elongates when overtwisted. Here we propose a method to calculate the twist-stretch coupling constant specific to a DNA fragment of a given sequence. The method employs a sequence-dependent dinucleotide force field and is based on constrained minimization of the fragment's deformation energy. Using a force field inferred from atomistic molecular dynamics simulations, we obtain the twist-stretch coupling for random sequence to be 0.30 nm/turn, close to experimental values. An exhaustive calculation for all oligomers of nine basepairs yields values between 0.14 and 0.45 nm/turn, positively correlated with the contents of pyrimidine-purine steps in the sequence. Our method is simple to use and allows one to explore the hypothesis that some sequences may be optimized for twist-stretch coupling.

Mechanical properties of DNA play an important role in a range of biological processes such as DNA binding to proteins or DNA packaging in viruses. The helical structure of DNA implies continuum elastic models with extra terms in the quadratic elastic energy function, absent in the case of a homogeneous isotropic rod. In particular, a coupling term involving both twisting and extension is required (1,2). Previous analysis (1–3) of experimental single-molecule data has suggested that DNA shortens upon overtwisting, in agreement with a simple picture of DNA as a stack of plates connected by rigid backbones. However, two independent micromanipulation studies have recently revealed that kilobase-long DNA molecules under small distorsion, gently pulled to reduce thermal fluctuations and suppress stress-induced buckling, actually elongate when overtwisted (4,5) as well as overwind when stretched (5). Within the framework of linear elasticity, this behavior is described by a single proportionality constant indicating the length change upon the imposed rotation, which has been found to be 0.4 ± 0.2 nm/turn by one study (4) and 0.5 ± 0.1 nm/turn by the other (5). This coupling constant does not depend on the length of the molecule. For shorter molecules, it might be more practical to express it in the units of angstroms per degree ().

These values describe the average property of the long DNA molecules investigated in the experiments. However, it has been proposed (5,6) that proteins may exploit the positive coupling between elongation and overtwisting on a much shorter length scale to recognize binding sites with variable sequence lengths; in case of basepair deletion (or insertion), proteins may recognize the site by simultaneously stretching and overtwisting (or compressing and undertwisting) the DNA. Certain sequences may be optimized for coupled twisting and stretching (5), and the question arises concerning the sequence-dependence of the twist-stretch (TS) coupling. This problem is addressed in this study.

We consider a DNA fragment as a chain of dinucleotide (or basepair (bp)) steps. There are 10 unique dinucleotide sequences. The geometry of each step is described in our model by the six basepair step parameters, namely tilt, roll, twist, shift, slide, and rise (7), defining the translation and rotation of the second basepair in the step with respect to the first one. In the absence of external forces, the parameters adopt their minimum energy values. We assume that the energy associated with the deformation of a basepair step away from its minimum energy geometry has the form of a six-dimensional harmonic potential:

(1)

where the index a (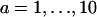) labels the unique step sequence, 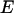is the deformation energy, 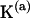the sequence-specific stiffness matrix, and 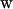the six-component column vector containing the deviations of the step parameters from their minimum energy values (T indicates the matrix transpose). We further assume that the total deformation energy of a DNA fragment is a sum of the energies of the individual steps.

Let us look first at the twist-stretch coupling in the individual dinucleotide steps. Suppose that twist ω in excess to the minimum energy twist is imposed on the step. The corresponding deviations of the other parameters can be found by minimizing the energy (1) under the constraint of the imposed twist.

If i is the index of the twist component in w (in the parameter ordering mentioned above, ), we have

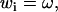(2)

which yields (we are omitting the superscript a)

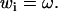(3)

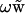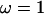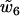The solution to Eq. 3 can be written as , where is the solution to Eq. 3 with . Thus, the change of step parameters is proportional to the imposed excess twist, the proportionality coefficients being the components of . In particular, is the coupling coefficient between twist and the parameter rise, which measures the step extension along the helical axis. Thus, 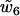(we will subsequently denote it by d) is the twist-elongation coupling at the level of individual dinucleotide steps.

To calculate its sequence-dependent values, we take the matrices from a dinucleotide force field based on atomistic molecular dynamics simulations (8). These stiffness data have been recently found to perform particularly well in predicting binding affinity in a protein-DNA complex with an important indirect readout component (9). The results are shown in Table 1. Note that values for different steps may differ by an order of magnitude.

TABLE 1.

Twist-rise coupling d (Å·deg⁻¹) and effective twist stiffness α (kcal·mol⁻¹deg⁻²) as a function of the dinucleotide sequence

	CG	CA	TA	AG	GG	AA	GA	AT	AC	GC
d	0.0190	0.0172	0.0078	0.0101	0.0048	0.0042	0.0037	0.0042	0.0020	0.0012
α	0.0173	0.0178	0.0268	0.0307	0.0312	0.0251	0.0218	0.0404	0.0332	0.0261

What is the energy cost of imposing excess twist ω on a basepair step? From Eq. 1 we find

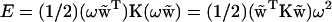(4)

so that the energy is a quadratic function of the excess twist, the effective stiffness constant being 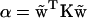. Its sequence-dependent values are summarized in Table 1. Note the difference from the twist stiffness reported earlier (8) where it referred to the diagonal element of K corresponding to twist, i.e., stiffness with respect to twist while the other parameters retain their minimum energy values. Here, in contrast, α refers to the stiffness associated with twisting while the other parameters are free to relax.

Let us now calculate the twist-stretch coupling constant for an arbitrary DNA molecule. We assume that: a), thermal fluctuations are suppressed, b), all the imposed torsion is distributed into twists of the dinucleotide steps, and c), the total length of the molecule is equal to the sum of rises of the dinucleotide steps. These assumptions are plausible for molecules under moderate tension and fragments of small curvature bound to proteins.

Consider first just two steps in a row, with effective twist stiffness constants α₁ and α₂. The imposed total excess twist ω will be distributed in the step twists ω₁ and ω₂, ω = ω₁ + ω₂, in such a way that the energy, 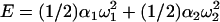, be minimal. Performing the minimization, we find where the total twist stiffness is given by the relation 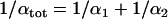. By induction we obtain the following result: the total twist stiffness for a chain of n steps with twist stiffnesses 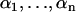is given by the relation

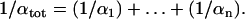(5)

Now consider n steps with the total imposed excess twist ω, distributed among the steps: 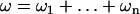. To find the excess twists 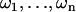of the individual steps, we have to minimize the deformation energy of the chain, 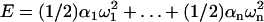, with the constraint . The method of Langrange multipliers implies unconstrained minimization of the function , where . We obtain the following system of n+1 linear equations:

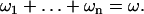(6)

It is obvious by mere inspection that the solution to this system is , where is given by Eq. 5. Thus, the excess twist in a particular step is proportional to the ratio of the total twist stiffness of the whole molecule to the twist stiffness of that step. Consequently, steps of the same type get the same amount of excess twist.

Finally, denoting by the twist-rise coupling of the individual steps, we find that the total change in rise is 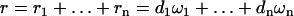, or

(7)

But according to assumption c, the total change in rise is equal to the elongation of the molecule. Thus, the expression in the parentheses is the desired TS coupling constant for the whole molecule. Note that equal step types contribute equally to the elongation. Assuming that there are 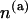steps of type a in the molecule (), we can rewrite Eq. 7 as

(8)

where and 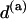are the values of α and d for step of type a taken from Table 1. Equations 8 thus enable one to easily calculate the TS coupling of a DNA molecule provided the number of steps of the ten unique types, 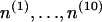, is known.

Alternatively we may express in terms of the fraction of the step type a in the sequence with a total of n steps: , so that Eq. 8 now becomes

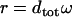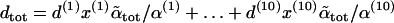(9)

The TS coupling of a sequence, 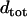, is thus computed as a certain kind of weighted average of the TS coupling coefficients of the individual basepair steps, 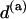. Note that molecules of different length but identical composition would have the same TS coupling constant.

Let us calculate, as an example, the TS coupling for the tetramer ATAT. We have 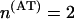, and Eqs. 8 yield

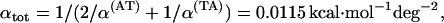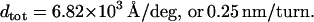For a long alternating polymer (AT)_m, , we have 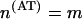, and using Eqs. 9 with (this is of course equivalent to the use of Eqs. 8 with ) yields 0.23 nm/turn. Similarly we obtain 0.23 nm/turn also for (GA)_m, and 0.43 nm/turn for both (CG)_m and (AC)_m.

We now calculate the TS coupling for a random sequence. By random we mean that at any position and independently on the rest of the sequence, each of the four nucleotides, A, T, C, G, is present with equal probability, namely 1/4. This implies that any dinucleotide of the form IJ, where I and J can be any of the four, is present with probability 1/16. For dinucleotides that are not self-complementary, one of the 10 unique steps is represented by two different sequences. Thus, the unique steps that are not self-complementary must be taken with a weight of 2 in the calculation, and the self-complementary ones with a weight of 1. Using Eqs. 8 with and other equal to 2, we obtain 0.30 nm/turn as the value of TS coupling for a random sequence.

One may be tempted to calculate the TS coupling in a different way, for instance computing first the arithmetic mean of the stiffness matrices, thus obtaining a sort of “average step”, then using Eq. 3. This procedure, however, seems to lack any rigorous justification and indeed yields, for a random sequence, a value of 0.21 nm/turn, further away from the experimental results. Similarly, a mere arithmetic mean of 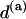over a random sequence would yield 0.26 nm/turn.

Equations 8 or 9 allow one to investigate a large pool of sequences. As an example, we performed an exhaustive calculation for all nine bp oligomers (131,072 unique sequences) and got the distribution of TS coupling constants shown in Fig. 1. The values span the range from 0.14 to 0.45 nm/turn and are positively correlated with the contents of pyrimidine-purine steps in the sequence (correlation coefficient 0.76). The distribution is essentially bimodal (the origin of this shape remains to be determined). Similar calculations may serve to explore the hypothesis that some sequences may be optimized for TS coupling (5). Such a task is, however, outside the scope of this study.

FIGURE 1.

Distribution of TS coupling constants in the ensemble of all nine bp sequences. The two highest maxima are at 0.27 and 0.33 nm/turn, respectively.