Dendritic Spine Viscoelasticity and Soft-Glassy Nature: Balancing Dynamic Remodeling with Structural Stability

Abstract

Neuronal dendritic spines are a key component of brain circuitry, implicated in many mechanisms for plasticity and long-term stability of synaptic communication. They can undergo rapid actin-based activity-dependent shape fluctuations, an intriguing biophysical property that is believed to alter synaptic transmission. Yet, because of their small size (∼1 μm or less) and metastable behavior, spines are inaccessible to most physical measurement techniques. Here we employ atomic force microscopy elasticity mapping and novel dynamic indentation methods to probe the biomechanics of dendritic spines in living neurons. We find that spines exhibit 1), a wide range of rigidities, correlated with morphological characteristics, axonal association, and glutamatergic stimulation, 2), a uniquely large viscosity, four to five times that of other cell types, consistent with a high density of solubilized proteins, and 3), weak power-law rheology, described by the soft-glassy model for cellular mechanics. Our findings provide a new perspective on spine functionality and identify key mechanical properties that govern the ability of spines to rapidly remodel and regulate internal protein trafficking but also maintain structural stability.

INTRODUCTION

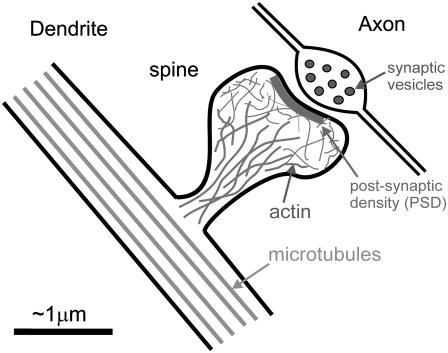
Dendritic spines are micrometer-sized cellular structures (Fig. 1) that are the sites of most excitatory synaptic contacts in the central nervous system (1,2) and have been implicated in many forms of postsynaptic plasticity of neuronal communication (3–9). Whereas dramatic changes in spine density or structure are observed in a number of pathological brain disorders (3,7), subtle changes in spine shape and content in the brain have been related to normal cognitive behavior, learning, and memory (3,4,10,11). Postsynaptic plasticity may involve regulation of the recruitment and organization of signal transduction proteins at the postsynaptic density in spines (3,4,6,9). It is unclear at this point what physical mechanisms enable spines to maintain their structure yet allow for plastic remodeling and internal trafficking of their molecular content.

FIGURE 1.

Diagram of a dendritic spine, indicating the internal actin cytoskeleton (distinct from the microtubules along the dendritic shaft) and the postsynaptic density of signal transduction proteins opposite an axonal presynaptic terminal.

In cultures of dissociated primary hippocampal neurons, the early stages of spine formation involve outgrowth of highly dynamic filopodia (finger-like projections) from the surface of dendrites (12–16). These filopodia are thought to search for presynaptic targets on nearby axons (15,17). When contact is made, it is believed that filopodia differentiate into spines (13). As spines mature, which may occur in <60 min (14,16), they adopt a stabilized spherical or mushroom-like shape connected to the dendritic shaft by a narrow neck a few hundred nanometers wide (18). Spine morphology is likely maintained by continued low-level stimulations from AMPA-type glutamate receptor activation (19). The surface of the spine head is observed to undergo rapid shape fluctuations (nanoscale motions on a time scale of seconds) (20), a motility that is suppressed by the presence of active presynaptic terminals (21–24). As first proposed by Crick (10), this subtle remodeling is believed to dynamically optimize transmission by adjusting connectivity and the geometry of the synaptic cleft.

The dynamic shape of dendritic spines has been proposed to be associated with high actin content (11,22–26). Although microtubules are prominent along the entire length of dendrite shafts, they are largely excluded from the actin-rich spines (25,27). Rapid cycling of filamentous actin and actin regulatory proteins has been observed within minutes or less in spines (24,28). Various forms of synaptic stimulation have resulted in rapid as well as long-term remodeling of the postsynaptic actin cytoskeleton (26,29–32), which may be required for long-term modulation of synaptic transmission (33–35). Dynamic actin filaments likely act not only as major structural components in spines but also as substrates for a variety of scaffolding proteins that link to and regulate the postsynaptic density (9,36,37).

Trafficking of intracellular molecules by diffusion within dendritic spines may also be of fundamental importance for function and plasticity of synapses (3,38). Large molecules such as actin and actin-associated proteins (29,30), as well as mRNA (39,40), are translocated into spines during periods of extended activation (5–30 min). Glutamatergic receptor channels are redistributed during LTP, incorporated in either mobile transport vesicles or within the plasma membrane of the spine (4,9,41). Rapid diffusion of AMPA receptors has been observed, exhibiting location- and activity-dependent motions in dendritic membranes (9). Within the spine head, fast translocation of the calcium/calmodulin kinase II (CaMKII) from actin-bound states to sites at the postsynaptic density can occur with a time constant of 20 s (42). Recent studies have shown that diffusion is restricted in spines relative to dendrites and is regulated by AMPA receptor activation and the actin cytoskeleton (38,43). The exact mechanisms of trafficking in spines are poorly understood, in part because such small structures have not been accessible for quantitative measurements. Although the selective contributions of active transport, binding interactions, and diffusion are unclear, the physical properties of actin-rich spines, such as their geometry, small volume, viscosity, and elasticity, will affect diffusion in ways that sufficiently explain many of the observations mentioned above (38,44–46).

Here we employ atomic force microscopy (AFM) elasticity mapping and dynamic indentation techniques (47–49) to reveal nonequilibrium mechanical properties that may underlie the structural plasticity of hippocampal neuron dendritic spines. The distinct capabilities of AFM, such as nanometer-scale positioning and subnanonewton force probing, make it uniquely suited for measurements of individual spine mechanics, yet this has not been demonstrated to date. We explore the possible relations between viscoelasticity of spines on a variety of time scales, their dynamic morphology, synaptic activation, and internal protein diffusion. Complex viscoelastic rheology measurements identify a weak power-law behavior and are compared to a leading model of cellular biomechanics: the soft-glassy hypothesis with additional viscosity (50,51). This model has had much success in describing the dynamic mechanical properties of living cells as metastable and structurally disordered materials (48,49,52–54), although to date it has not been assessed in cellular compartments as small as spines. The soft-glassy theory introduces the concept of “effective noise temperature” of spines, which is an integrative factor reflecting the level of molecular agitations (all protein and enzyme activity) and acts as the primary determinant of the balance of solid-like and liquid-like behavior of spines over a wide range of time scales. Furthermore, results with glutamate stimulation revealed that viscoelastic properties change dynamically in spines. This plastic behavior provides a sufficient mechanism to explain reported variations in internal diffusion properties. The model thus identifies activity-dependent biophysical parameters (the effective noise temperature and viscosity) by which spines can provide mechanical plasticity (remodeling and internal trafficking) yet achieve the structural stability that may be necessary for long-term memory.

MATERIALS AND METHODS

Cell cultures

Cultures of neonatal rat hippocampal neurons were prepared as described previously (55). Hippocampi were dissected from 1- to 3-day-old Sprague-Dawley rats, dissociated using papain enzyme (Worthington Biochemical, Lakewood, NJ), and plated at 100–200 cells/mm² with a graded density distribution on poly-d-lysine-coated glass coverslips. Cultures were maintained at 37°C and 5% CO₂ in Neurobasal medium supplemented with B-27, penicillin-streptomycin, and l-glutamine, with half the medium replaced twice per week (all culture agents from Invitrogen Canada, Burlington, ON). To limit the growth of nonneuronal cells, Ara-C (5 μM; Sigma-Aldrich Canada, Oakville, ON) was added for days 2 to 5 in culture. Spine-like protrusions from neurites first appeared after 7 days, were in significant numbers after 10 days, and used for experiments up to 3 weeks in culture. Coverslips were mounted on the microscope stage at room temperature in HEPES-buffered Hanks' balanced salt solution (HBSS, pH 7.3; Invitrogen). Glutamate (100 μM; Sigma-Aldrich Canada) or α-amino-3-hydroxy-5-methyl-4-isoxazole propionic acid (AMPA, 1 μM; Sigma-Aldrich Canada, Oakville, Ontario, Canada) were used for stimulation experiments by including them in the imaging solution for 5–10 min before measurement. Dynamic tracking of spine rheology involved overnight treatment of cultures with tetrodotoxin (TTX, 1 μM; Alomone Labs, Jerusalem, Israel) and 2-amino-5-phosphonovalerate (AP5, 40 μM; Sigma-Aldrich Canada) and measurements made in low-calcium HBSS (0.1 mM Ca²⁺) with 40 μM AP5 to suppress baseline synaptic activity. Stimulation was achieved with 1 μM AMPA (for 5 min) and elevated calcium (1.2 mM), and subsequent inhibition of actin polymerization with latrunculin-A (1 μM; Sigma-Aldrich Canada).

Atomic force microscopy

Measurements were made with a Bioscope AFM equipped with a G-type piezotube scanner, Nanoscope IIIa controller, and version 4.43r8 of the Nanoscope software (Veeco Metrology, Santa Barbara, CA). Probes were silicon nitride microlevers with spring constant k = 0.01 N/m, confirmed by the Sader method (56). Imaging experiments were performed using the force-volume mode of AFM operation, in which a lateral array of force-indentation curves are acquired and used to generate topographic and compliance-based image contrast, as described previously (49). Force curves were acquired with a resolution of 64 points per curve (1 μm vertical cycle at 10 Hz) and 64 × 64 curves per image (∼15 min total acquisition time). Analysis of stiffness data from regions of interest in these images was accomplished using the method of “force integration to equal limits” (FIEL) (47). In this method, the work required to reach a fixed maximal force (area under force-indentation curve) provides a relative measure of the local compliance (stiffness ∼1/(work)²). The FIEL analysis is largely free of errors associated with uncertainty of the contact point, and the indentation and relaxation curves were averaged to minimize viscous effects. Force-mapping experiments were much less destructive than the commonly used contact-mode imaging, but quantitative analysis was limited by distortion of the force curves by viscous effects (hydrodynamic drag on the lever and cell viscosity), adhesion, substrate effects (see Discussion), and possible spine motility within the imaging time.

To determine the viscoelasticity of the spines, a different approach was used, namely indentation-modulation, as described previously (49). Briefly, these complex rheology measurements involved positioning the probe over a single location on a spine, collecting force curves at ∼1 μm/s and, at the point of maximum force (0.15–0.20 nN), oscillating the probe base vertically with amplitude A_z = 4.2 nm and frequencies in the range ω/2π = 0.5–100 Hz for 30–60 s before retracting the probe and repeating the process. Dynamic tracking experiments involved repeated indentations at 30- to 35-s intervals, where modulations were recorded for 15–20 s at 10 Hz, and a 10-s delay in the retracted position was used to allow the spine to recover. Lock-in techniques were used to measure the amplitude (A_d) and phase (φ) of the resulting beam deflections (SR 830 digital lock-in amplifier; Stanford Research Systems, Sunnyvale, CA). To remove the influence of the hydrodynamic drag force of the fluid, we measured it by oscillating the probe at various heights above the spine surface and subtracted it from the data as described below.

Data analysis

To analyze force (F = kd; d = lever deflection) measurements as a function of the probe indentation (δ = z − d; z = vertical position), we used the Hertzian contact mechanics model for pyramidal indenters, extended for frequency-dependent modulations (48):

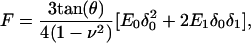(1)

where θ is the half-opening angle of the tip, ν is Poisson's ratio (∼0.5 for cells) (57), δ₀ is the static indentation, δ₁ is the oscillatory indentation (Fourier transform: 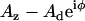), and E₀ and E₁ are the corresponding zero-frequency elastic and frequency-dependent viscoelastic parameters, respectively. The Fourier complex shear modulus for a continuous medium was calculated as G* = E₁/2(1 + ν), or:

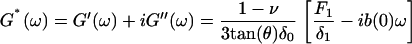(2)

Here G′(ω) and G″(ω) are the elastic storage and dissipative loss moduli, F₁ is the oscillatory force (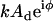), and b(0) is the hydrodynamic drag factor at the surface, determined by methods based on the work of Alcaraz et al. (58). Briefly, this drag factor was obtained by fitting the hydrodynamic function 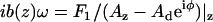measured above the cell surface to the scaled-spherical model: 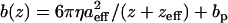(η is the liquid viscosity, a_eff and z_eff are the effective radius and thickness of the probe, and b_p is the drag far from the surface) and extrapolating to z = 0. The added constant b_p is necessary for our measurements because of the probe-displacement design of our AFM (compared to the sample-displacement used by Alcaraz and colleagues). For dynamic tracking experiments, moduli are scaled by the factor k₀ = (1 − ν)k/3tan(θ)δ₀, which remains relatively constant. Thus, with measurements of probe oscillatory deflections (amplitude A_d and phase φ) and calibrated drag b(0) for a given drive amplitude A_z and static indentation δ₀, we calculated the elastic modulus as G′ = k₀ Re[A_de^iφ/(A_z − A_de^iφ)] and the viscous modulus as G″ = k₀ Im[A_de^iφ/(A_z − A_de^iφ)] − b(0)ω, where Re[] and Im[] refer to the real and imaginary components of the bracketed term.

Frequency-dependent rheology was fit to a model consisting of a weak power-law term containing elastic and viscous components (expected for soft-glassy rheology) plus an additive Newtonian viscosity term (purely viscous) (51):

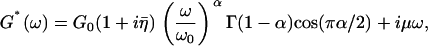(3)

where 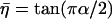, α is the power-law exponent, G₀ is the modulus scale factor, ω₀ is the frequency scale factor (chosen arbitrarily as ω₀/2π = 1 Hz), Γ is the gamma function, and μ is the Newtonian viscosity coefficient.

Fluorescence recovery after photobleaching

To compare diffusion times of an intracellular protein in spines versus dendrites, we transfected neurons (11–14 days in vitro (DIV)) with a CaMKII tagged with a monomeric form of GFP (GFP-CaMKII) as described previously (55). The following day, the cells were placed in a perfusion chamber (SD Instruments) containing HBSS with 25 mM HEPES (pH 7.4), 0.6 mM CaCl₂, and 5 mM MgCl₂ (0.5–1 ml/min). A segment of dendrite with spines was selected, and images were acquired on a Zeiss (Thornwood, NY) LSM510 META-Axioskop FS2 Plus confocal system, using a 63× Achroplan water immersion objective (0.95 NA), scanning a 3-μm-thick optical slice through the center of the chosen segment of dendrite. GFP was excited with an argon laser line at 488 nm with 0.25% transmission, detected through a band-pass filter (500–550 nm); two images were averaged, and scaling was set to a pixel size of 0.15 μm × 0.15 μm. Regions of interest (ROI; circle 10 pixels in diameter) were drawn over two to four spines or over two distant regions in the dendrite, and photobleached by scanning 50 times at maximum laser transmission. The recovery was monitored for 200 to 500 s at 10 images/min. The mean intensity in each ROI was measured and normalized with F(t) = (F_t − F_post)/(F_pre − F_post), where F_pre is the average fluorescence for three images before the photobleach and F_post the fluorescence immediately after the photobleaching.

Diffusion constants were calculated from fluorescence recovery after photobleaching (FRAP) data by fitting to geometric models derived from Fick's law of diffusion (44). In spines, fluorescence follows an exponential recovery: F(t) = F₀(1 − e^−t/τ), where the time constant (τ = lV/D_sA) depends on the diffusion constant (D_s), spine head volume (V), spine neck length (l), and cross-sectional area (A) (59). The values of the spine geometric parameters were taken from published results: V = 0.083 ± 0.02 μm³, l = 0.66 ± 0.32 μm, A = 0.025 ± 0.006 μm² (60). In dendrite shafts, assuming cylindrical symmetry, a uniform bleach of a segment of length L = 1.5 ± 0.1 μm results in fluorescence recovery that follows:

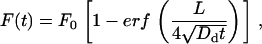(4)

where the error function is defined as 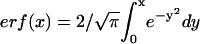(44). Fitting FRAP data to the above functions was accomplished by a least-squares Levenberg-Marquardt algorithm.

RESULTS

Topography and stiffness mapping

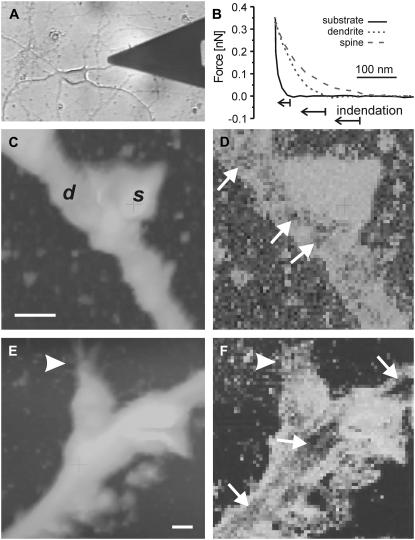
AFM was performed on visually identified dendrites in cultured hippocampal neurons (Fig. 2 A). Typical force-indentation curves used to generate topographical and stiffness maps of spines are shown in Fig. 2 B, with characteristic force-volume images displayed in Fig. 2, C–F and Fig. 3, A–D. With maximum applied forces controlled in the range of 0.2–0.4 nN by force-feedback, indentation depths on the dendrites and spines varied between 50 and 350 nm. Dendrites were 1.17 ± 0.09 μm in width and 0.80 ± 0.07 μm in height (26 dendrites, each from a different neuron). Spines had dimensions of 1.32 ± 0.08 μm lateral and 1.01 ± 0.07 μm vertical (31 spines from 26 dendrites), although their shapes were heterogeneous. Although topographic contours were smooth over dendrites and spines with 10–15% variation along 5-μm lengths of dendrites, stiffness maps showed contrast at the level of internal structures in dendrite shafts and in some cases in spines with lateral dimensions as small as ∼100 nm. Spine rigidity relative to that of the shafts varied considerably, with compliance on spines 0.3–3 times that on shafts. Much of this heterogeneity correlated with the variations in spine shape and the presence or absence of axon-like structures in close association with the spine head. According to the set of criteria described below, 22% of spines measured were categorized as “soft” spines, and 56% as “stiff” spines. The remaining spines did not satisfy all criteria of either class.

FIGURE 2.

Soft spines. (A) Photomicrograph of a cultured hippocampal neuron being scanned with an AFM probe. (B) Representative force-distance curves acquired during force-volume imaging of regions of a spine, dendrite, and substrate (as indicated). (C, E) Topography (under constant force) maps of two dendrites with spines (labeled d and s in C). Vertical color scale is 0.5 μm in C and 0.8 μm in E. Lateral bar is 1 μm in both. (D, F) Corresponding stiffness maps (bright is soft, dark is stiff). Spines appeared soft relative to the dendrite shafts, where stiff patches or fibers were identified (small arrows). Spine shapes were irregular, often exhibiting small surface protrusions (arrowheads). Axons were not observed in close proximity to the soft spines.

FIGURE 3.

Stiff spines. Topography (A, C) and stiffness (B, D) maps of dendrites possessing spines that contain stiff features of varying size (small arrows). These spines appeared rounded compared to those in Fig. 2, and axon-like structures contacting the spines were observed (arrowheads). The degree of rounding may have varied with the size of the stiff region in the spine as evidenced by the lower spine in A and B, where a small stiff patch as well as some surface protrusions (open arrow) were present. Scales: vertical is 1.5 μm in A and 1 μm in C; lateral bar is 1 μm. Included in A and B are line sections along the diagonal shown in A. The plot below A is the zero-force topography showing the dendrite (d) and spine (s). The plot below B is the inverse apparent elastic constant, which reveals the stiff fiber (f) along the dendrite and the stiff core (c) of the spine.

The first set of examples (Fig. 2, C–F) shows spines whose geometries deviated significantly from rounded, spherical shape. This asymmetry was quantified by calculation of a shape factor, defined as the ratio of the shortest width of the spine head to the longest length (20), which for these spines is 0.67 ± 0.12. In these cases, small protrusions from the surface of the spine head were often observed and had dimensions <200 nm, characteristic of actin-based structures. The central region of the spine was quite uniformly soft, as indentation depths were 300 ± 40 nm with forces of 0.30 ± 0.03 nN, but small areas of the dendrite shafts appeared as stiff patches or fibrous structures aligned along the long axis of the shafts. The apparent elastic constant of the soft spines was 0.4 ± 0.1 times that of their corresponding dendrite shafts. Although spines were also thicker than the dendrites (1.4 ± 0.1 times), the presence of the stiff regions on the dendrites without significant variation in height suggests that stiffness contrast was not correlated to topographic contrast and thus was not an artifact of finite sample thickness and likely reflected local cytoskeletal structures (e.g., microtubules)(27,61). Some of the largest stiff patches were observed close to the base of the spines and may be indicative of internal protein aggregations or anchoring structures. In the case of the soft spines, no axons or other neurites were observed in the immediate vicinity (a few micrometers) of the spine heads.

The second set of examples (Fig. 3, A–D) shows spines of qualitatively different physical character than those in Fig. 2. Regions of markedly increased stiffness were identified, with apparent elastic constants 2.0 ± 0.3 times that of the dendrite shafts, although the height difference between spine and dendrite was the same as that for soft spines. In these regions, indentations were 170 ± 20 nm with forces of 0.30 ± 0.03 nN. In some cases the stiff areas comprised only a small fraction of the total spine surface (e.g., the spine in the lower half of Fig. 3 B), but in others nearly the entire spine appeared stiff. These spines also had a more rounded shape than the soft spines of Fig. 2. This is evident in the topography images and characterized by an increased shape factor 0.94 ± 0.04, significantly closer to a value of 1 for spherical symmetry than the soft spines. Furthermore, axon-like structures intersecting the stiff spines were observed, although the detailed structure at the contact site could not be resolved. Axons appeared as long neurites, much thinner (width and height 100–200 nm) than dendrites.

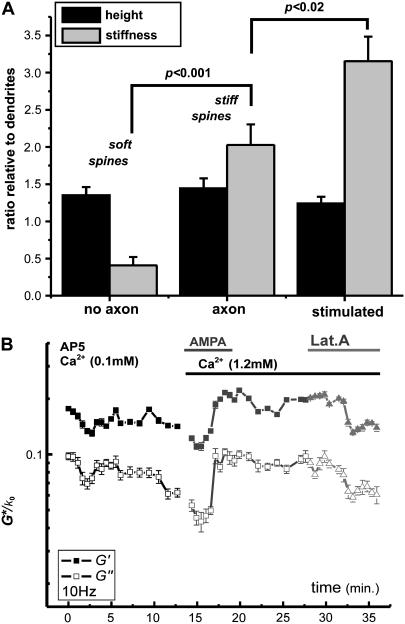
Compiled results of height and stiffness contrast (ratio of apparent elastic constants E/(1 − ν²) evaluated by the FIEL method) between regions of interest on spines and dendrites in all force-volume measurements recorded are shown in Fig. 4 A. A significant distinction is made between spines with and without an axon present as stiff and soft spines, respectively, with no significant change in size. Fixation of cultures with 4% paraformaldehyde eliminated the stiffness contrast within and between spines and the dendrite shaft, even though intersecting axons were clearly identified (Supplemental Material, Fig. S1).

FIGURE 4.

(A) Compiled means ± SE of relative height and stiffness (elastic constant E/(1 − ν²)) between spines and dendrites, from regions of interest in force-volume data of spines with and without an axon present and spines stimulated with AMPA or glutamate. Significance of the stiffness increases from axon presence and stimulation were assessed by ANOVA, with p-values as indicated. (B) Dynamic tracking of elastic-storage and viscous-loss moduli (G′/k₀ and G″/k₀ as solid and open points, respectively) measured with 10-Hz indentation modulation. Both moduli increase within minutes of stimulation with AMPA (1 μM) and increased extracellular Ca²⁺. The dynamic response is reversed by introduction of the actin polymerization inhibitor latrunculin-A (Lat.A, 1 μM).

The enhanced stiffness of axon-associated spines suggests that synaptic activity may regulate their viscoelastic properties. To test this we investigated the effect of glutamate receptor stimulation on spine stiffness. To probe a steady-state response, cultures were exposed to optimal concentrations of AMPA (1 μM) or glutamate (100 μM) for 5–10 min before imaging. Independent of the presence of an axon, stimulated spines were stiffer than unstimulated spines (3.2 ± 0.3 times the dendrite stiffness, n = 6 spines, Fig. 4 A). In some cases we performed dynamic tracking of elastic and viscous moduli, G′ and G″ for fixed frequency of 10 Hz, of a spine during exposure to stimulant. The results revealed a rapid (within seconds to minutes) stiffening and an increased viscosity response to AMPA and Ca²⁺ stimulation, which was reversed by inhibiting actin polymerization with latrunculin-A (Fig. 4 B).

Complex rheology

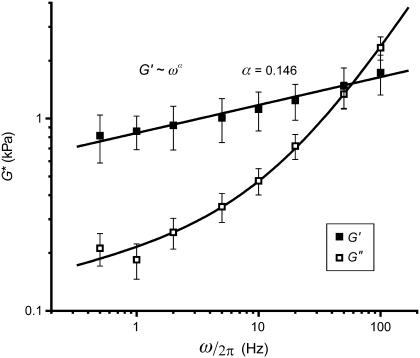
To establish a quantitative assessment of the ability of dendritic spines to deform, remodel, and permit translocation of internal proteins/organelles, we used a novel frequency-dependent indentation modulation technique to measure their complex viscoelastic moduli (49). For this method, the AFM probe was first used to indent the surface of a spine head and then was oscillated vertically. The amplitude and phase response of the probe tip were used to evaluate the viscoelastic properties of the spine (see Materials and Methods). Compared to the fairly isolated dendrites used for force mapping, higher-density regions of the cultures were targeted for indentation modulation, to increase the likelihood that spines were contacted by axons, thus belonging to the class of “stiff” spines. In this approach, complex rheology (shear modulus G*(ω) = G′(ω) + iG″(ω)) was measured over a wide range of modulation frequencies ω/2π = 0.5–100 Hz (Fig. 5, mean spectrum for n = 8 spines). Moduli were also tested for a range of drive amplitudes (A_z = 2.5–7 nm), which provided identical results within the experimental uncertainties. This confirmed that all measurements reported below for A_z = 4.2 nm were in a regime of linear mechanics. Elastic storage moduli G′(ω) were of the order of 1 kPa and increased gradually with frequency. Viscous loss moduli G″(ω) were of the order of 0.2 kPa with weak frequency dependence at low frequencies (<10 Hz), but increased with much stronger dependence at higher frequencies and became larger than storage moduli above ∼50 Hz. This behavior is well fit by a weak power-law soft-glassy rheology model with an additive Newtonian viscosity term described by Eq. 3 (51). The independent parameters determined from the fit are the modulus scale factor G₀ = 0.78 ± 0.03 kPa, the power-law exponent α = 0.146 ± 0.007, and the Newtonian viscosity coefficient μ = (19.9 ± 0.9 Pa·s)/2π.

FIGURE 5.

Soft-glassy rheology. Frequency-dependent complex rheology of dendritic spines measured by AFM indentation modulation. Points are means ± SE of measurements from n = 8 spines on different neurons. Lines are the fit to Eq. 3. The elastic storage modulus (G′) scales as a weak power-law of frequency (exponent α = 0.146 ± 0.007) over all frequencies used. The dissipative loss modulus (G″) exhibits similar scaling at low frequencies with G″/G′ ≅ 0.23 (tan(πα/2)); soft-glassy damping), but increased frequency dependence above 5–10 Hz (G″ ∼ ω; viscous damping) with G″ > G′ above 50 Hz. This behavior is consistent with the soft-glassy description of cellular mechanics, with an additional term to account for Newtonian viscosity, and describes the ability of spines to remodel.

Diffusion in spines versus dendrites

To explore the relation between the unique viscoelastic properties of spines and their distinctive internal diffusion characteristics, we made fluorescence recovery after photobleaching (FRAP) measurements of GFP-CaMKII diffusion in hippocampal dendrites (Fig. 6 B). After accounting for geometric constraints, FRAP results reveal that diffusion constants are D_d = 0.09 ± 0.01 μm²/s in dendrite shafts and D_s = 0.02 ± 0.01 μm²/s in spines. The spines used were in high-density cultures (∼2000 cells/mm²) and thus likely belonged to the class of stiff, axon-associated spines.

FIGURE 6.

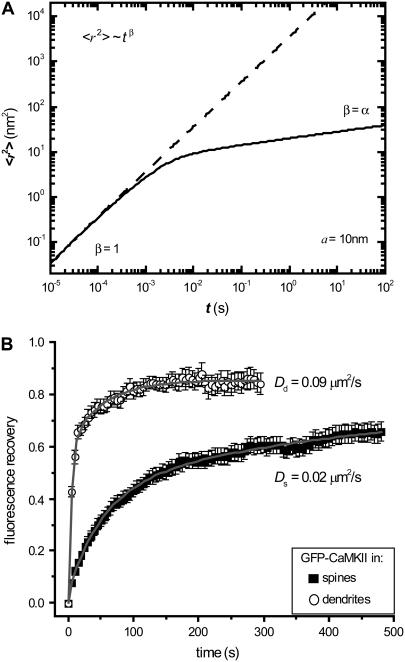
(A) Predicted mean-square displacements of a particle of radius a = 10 nm (such as a CaMKII protein) within a spine head, based on thermal agitations (Eq. 5) and the viscoelastic properties reported in Fig. 5. Over short time scales 〈r²〉 = τ^β with β = 1 (Brownian diffusion), but over longer times anomalous diffusion results from the power-law damping behavior of the spine (β = α = 0.146). The dashed line shows only the Brownian component with diffusion constant 3.6 × 10⁻³ μm²/s. (B) FRAP results for GFP-CaMKII diffusion in spines (n = 49) and dendrites (n = 16) with diffusion constants as indicated, calculated from fits (solid lines) to the geometric models described in Materials and Methods.

DISCUSSION

Spine stiffness correlates with morphology and activity

Our characterization of soft spines is consistent with the suggested properties of newly formed spines in that their motility, driven by rapid cycling of actin filaments (22–24), may be associated with enhanced deformability (27,61). Because these spines were without synaptic contacts, had asymmetric shapes, and displayed surface protrusions, they were likely filopodia or immature spines. Filopodia are known to be highly dynamic, with lifetimes characterized on time scales of 10–30 min (14). Their presence is expected to decrease with age in culture (from day 10 to 20), as the presence of mature stable spines increases (13,15). Although measurements were made on neurons of a wide range of ages (9–21 days in culture), both soft and stiff spines could be identified at all ages. Although the ratio of spines to filopodia varied significantly during development and between culture preparations, stiff spines were more readily found in high-density regions of mature cultures. The determinant for stiffening appeared to be the presence of an intersecting axon, in support of an activity-dependent stabilization mechanism.

The characterization of stiff spines is in agreement with the notion that, as spines mature and acquire synaptic contacts, they adopt stabilized spherical-head morphology (8,13,18). We show that this process may be associated with stiffening of the spine, likely characterizing formation of a cross-linked assembly of filamentous actin known to couple into and stabilize the postsynaptic density (9,26,36). The effect of glutamatergic stimulation on spine viscoelasticity is further evidence that prolonged synaptic activity leads to rapid mechanical stabilization and increased viscosity of the spines' internal structure. Previous results of variation in spine actin dynamics are consistent with our finding (22,24).

The type of AFM imaging (force-volume) we used in this study has added benefit over conventional AFM and optical approaches in that it provides topography and semiquantitative compliance at a subnanonewton level of applied force such that small, delicate structures such as dendritic spines can be studied nondestructively at high resolution. Force-volume images were acquired with an imaging time of ∼15 min, during which time the spines and especially the filopodia presumably underwent many shape changes, as motility is typically characterized on times scales from seconds to minutes (15,20). This is a likely explanation for the inability to resolve internal structures in the spines and suggests that the spine/filopodia shapes may be somewhat time averaged over the time required to raster-scan the portion of the image that contained the spines (3–7 min). The classic finger-like shape of filopodia can be seen in fixed cultures where all dynamics are arrested (see Supplemental Material, Fig. S2). Individual force curves, on the other hand, were acquired on time scales of the order 0.1 s, over which the spines were likely relatively stable, but stiffness measurements may still reflect some degree of remodeling (see below).

Complex viscoelasticity and implications for remodeling

A striking observation from the frequency-dependent results was the large Newtonian viscosity of the spines. Values are four to five times greater than those measured with similar techniques from other cell types (48,49,52). We interpret this large viscosity as indicating that spines are subcellular compartments with unusually high density of solubilized proteins existing in an unstructured ensemble (i.e., separate from the cytoskeletal structures in spines). Such high density is consistent with the complexity of signaling elements that are required at synapses (62). The counterpart of this is that flow or diffusion in this dense medium is restricted, as quantified by the Newtonian viscosity component of the complex modulus. Furthermore, the highly viscous nature of the spine alone is insufficient to maintain a structural architecture.

The storage modulus or elastic component and the low-frequency loss modulus of spines scale with the same weak power-law dependence on frequency (α = 0.146 ± 0.007). The roughly constant ratio of 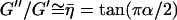under low-frequency deformation (<2–3 Hz) is indicative of coupling between elastic and dissipative processes at the level of the stress-bearing elements in the spine (63). This coupling is also evident in the time traces shown in Fig. 4 B. A likely substrate for this coupling in spines is the dynamic cycling of actin filaments: the addition of G-actin monomers to the filaments may increase the storage of elastic energy under deformation, which then dissipates on release of actin monomers. This is consistent with the reported rapid turnover of actin in spines (∼45 s time constant) (24). With a typical filament length on the order of 200 nm, the cycling of individual monomers (2–3 nm) can thus be estimated to be on the order of 1 Hz, in agreement with the time scale where the storage-loss coupling is dominant.

Weak power-law rheology observed here is supportive of the soft-glassy hypothesis of cell biomechanics, where the power-law exponent is related to the effective noise temperature (x = 1 + α) of the intracellular environment (50,52). The noise temperature, or energy of mechanical noise, expresses the level of molecular agitation that acts to remodel structural elements that exist in a heterogeneous distribution of confinement barriers in a congested cell interior. The power-law behavior suggests that remodeling of the spines' mechanical structure occurs on a wide range of time scales, not at a well-defined frequency (53). The gradual decrease in the moduli (G′ and G″) or stress relaxation with decreasing deformation frequency indicates that remodeling has a more pronounced effect over progressively longer time scales. Along these lines, one could characterize the degree of remodeling as scaling such as G₀/G′ ∼ ω^−α or ω^1−x. In this way, a spine maintains mechanical rigidity characteristic of a solid (G′ > G″ for x < 1.5) but the structural disorder and fluidity of a liquid. To relate to our stiffness measurements from force-volume imaging (summarized by Fig. 4 A), a spine that appeared soft did not necessarily contain weak structural components; rather, it likely remodeled more during the measurement (force curves on time scales of ∼0.1 s) than did an apparently stiff spine. This behavior likely underlies the time dependence of spine morphological motility and connective plasticity of neuronal circuits. Furthermore, the spine cytoplasm, as a soft-glassy material, is highly congested with jammed structural elements, but slow remodeling allows for internal trafficking over long time scales (see the section on diffusion below).

The noise temperature is in relative units of the energy of a proposed glass transition, where agitation energy equals the characteristic confinement energy (defined by x_g = E_g = 1). Noise temperatures measured from other cell types, including smooth muscle, macrophages, neutrophils, and epithelial cells, are in the range of x = 1.12–1.22 (48,49,52). Similarly, we find that dendritic spines, with x = 1.146 ± 0.007, exist relatively close to the glass state. Although there is no direct connection between the noise temperature and the actual environmental temperature, we expect that x (and possibly G₀ and μ) would be different if our experiment were conducted at 37°C rather than room temperature. The mechanical properties of actin and microtubules as well as many sources of molecular agitations (e.g., ATP consumption) are known to change with temperature (64,65).

Previous studies have shown that the dominant source of variations in cellular rheology is through changes in the noise temperature (49,51,52). Although we have not explicitly demonstrated that x is not constant for dendritic spines, it is likely that variations in x underlie changes in viscoelastic stiffness of spines in light of these studies on other cell types. Under this assumption, we speculate that a reduction in noise temperature, inducing a transition toward the solid or glass state (x = 1) where G′ would increase and become independent of frequency, would describe spine stabilization as it matures. Such a transition may be the mechanism by which spines stiffen following synaptic stimulation (Fig. 4). Because remodeling events become less probable with decreased noise temperature, disorder would be quenched into the system as the glass state is approached and the spine becomes essentially frozen, although this may never be reached (50). In other words, stable spines would be associated with reduced molecular agitations (cold stiff spines). With an increase in noise temperature, a shift toward the purely fluid state (x = 2, G′→0, G″ ∼ ω; Newtonian fluid) is expected to characterize highly motile or even retracting spines. Soft glassy materials just above the glass transition have a disordered and metastable mechanical structure and undergo probabilistic remodeling (50). In the case of spines, this would allow for continuous spontaneous motility (hot soft spines). Beyond this, the balance of solid and fluid-like properties of a spine could itself be tuned by varying the level of molecular agitations (e.g., ATP consumption by actin filament cycling and other mechanical proteins). In this way, favorable rearrangements of spine structure could be reinforced (stabilized) by increased glutamatergic stimulation, thus providing activity-dependent forms of connective plasticity and regulation of internal trafficking (11,22). Further investigation of spine viscoelastic spectra before and after glutamatergic stimulation or before and after synaptic formation would shed light on the ability of spines to modulate their mechanical properties. However, in our experience underdeveloped spines tend not to be stable over extended periods of repetitive indentations at a single location, which would be necessary for acquisition of multiple spectra. This undesirable effect is evident in the slight downward slope of the baseline measurements in Fig. 4 B. Improved stability may be achieved by use of specially designed AFM probes that are more force-sensitive with less viscous resistance and a smooth tip geometry, yet are still small enough to target spines. These methods are currently under development.

A recent study reported significantly better fit to cellular rheology data by a model that replaces the Newtonian viscosity component with a term that scales as ω^3/4 (66), consistent with theoretical predictions based on thermal fluctuations of semiflexible polymers (67). Like the Newtonian viscosity, this ω^3/4 term is prominent only at high frequencies, but it also contains an elastic component (not purely viscous). We tested the validity of this approach by fitting our data to a model containing a soft-glassy weak power-law term plus an ω^3/4 term (see Supplemental Material, Fig. S3). The fit was significantly degraded (R² = 0.984) compared to the one shown in Fig. 5 (R² = 0.995). The high-frequency loss modulus appeared to tend toward an exponent >0.75 (reaches 0.8 within our frequency range). Also, our measured elastic modulus does not turn up to the ω^3/4 component that accompanies the viscous upturn. For these reasons we do not believe spine rheology is a reflection of the predicted ω^3/4 behavior of semiflexible polymers but is described better by the soft-glassy behavior of a remodeling mechanical structure (cytoskeleton) and a separate Newtonian viscosity component that behaves like a pure fluid (cytosol).

Quantitative analysis as discussed above is limited by the small dimensions of dendritic spines, which can introduce significant systematic errors into the measurements of their mechanical properties with indentation techniques. Here, spines were indented by as much as 30–40% of their thickness, which often led to significant deviations of force-indentation profiles from the expectations of Hertzian contact mechanics (apparent strain hardening at large indentations). Thus, the rheology measurements reported in Fig. 5 are overestimations of the true spine viscoelasticity. These errors are difficult to quantify because of the geometry of the probe, which is pyramidal, tapering to an undefined shape at the tip. For spherical tips (radius R), the decay of the strain field in the sample (height h) under indentation (δ) introduces errors that scale as (Rδ)^1/2/h (68). If this is used as an approximation for the errors introduced by the sharp tip used here, with an effective tip radius of 50–100 nm, the indentation of a 1-μm-thick spine by 0.4 μm would introduce an overestimation of the rigidity of ∼20%. Lateral dimensions of spines are also comparable to the deformations induced and should be incorporated into the analysis. Because we used indentation modulation amplitudes less than 1% of the static indentation, these geometry-based errors are expected to affect only the modulus scale factors (G₀ and μ) and not the frequency-dependent results (α). However, the strength of coupling of the spine to the substrate can also affect the measured shear modulus and may introduce frequency-dependent errors. We expect that because of the above measurement errors combined, absolute rheology values may be accurate only to within a factor of 2. Nevertheless, the qualitative features of soft-glassy rheology, enhanced viscosity, anomalous diffusion, and activity-dependent stiffening remain.

Consequence of spine mechanics on internal diffusion

There is mounting evidence that molecular diffusion within spines is regulated in parallel with spine motility (38,43). Thermally driven motion (diffusion) of small (low-inertia) particles is restricted by the viscoelastic properties of the surrounding medium (45). Thus, we expect the diffusional translocation of proteins or small organelles (e.g., vesicles) within spine heads to be reduced in spines that present larger viscoelastic resistance than other spines or dendrite shafts. Indeed, our observations of CaMKII protein translocation in spines and dendrites (Fig. 6 B) show correlations between diffusion constants and spine viscoelastic compliance (Fig. 4 A). Furthermore, we use the complex rheology of spines (Fig. 5) to predict a strong anomalous component of diffusion (Fig. 6 A).

The thermal motion of a particle in a viscoelastic medium can be estimated using the generalized Stokes-Einstein relation (45):

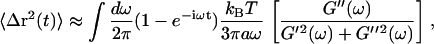(5)

where k_B is the Boltzmann constant, T is absolute temperature, and a is the radius of the particle. The approximation arises because of the use of G*(ω) measurements from a limited frequency range in the integration over all frequencies. This relation, based on the fluctuation-dissipation theorem, assumes thermal equilibrium and a homogeneous medium, which may not be correct for the cytoplasm of dendritic spines. On the basis of the complex rheology, we measured (Fig. 5) and Eq. 5 above, Fig. 6 A shows a calculation of thermally driven motion of a 10-nm-radius particle, approximately the size of a single synaptic signaling protein in a spine (for example, CaMKII). We chose CaMKII because of its multifunctional role in activity-dependent neuronal function (69) and the observations of its rapid translocations in spines (42), but the diffusion model is nonspecific, including only the dependence on particle size and not molecular structure or specific interactions with other proteins. The two regimes of viscoelasticity seen in Fig. 4, namely the high-frequency fluid viscosity and the low-frequency glassy rheology, predict two types of intracellular motion. In the regime where Newtonian viscosity dominates (frequencies >50 Hz or times <20 ms), intracellular particles would follow pure Brownian diffusion (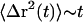). The dashed line in Fig. 6 A shows the mean-square displacements predicted using only the Newtonian viscosity term of the spine rheology, resulting in Brownian motion with a diffusion constant of 3.6 × 10⁻³ μm²/s. On longer time scales, motions would be restricted by the elastic component of the spine's mechanical structure. The weak power-law scaling of complex shear modulus G*(ω) ∼ ω^α implies that , referred to as anomalous subdiffusion when α < 1.

Quantitatively, the results of Fig. 6 A are quite small compared to reported values of CaMKII diffusion in nonneuronal cultured cells (∼1 μm²/s) (70). However, our FRAP measurements of GFP-CaMKII diffusion in hippocampal dendrites (Fig. 6 B) show that diffusion is much slower in spines: τ = 99 ± 5 s mean recovery time, corresponding to a diffusion constant D_s ≈ 10⁻² μm²/s using the geometric model for diffusion into spines (see Methods). Particle-tracking experiments in other cell types have observed anomalous mean-square displacements similar to those we calculate (subdiffusion at ∼10⁻⁴ μm² in 1 s for a particle of radius ∼100 nm) (71), but others report motions two to three orders of magnitude faster (72–74). Thus, our prediction of intracellular diffusion within spines is at the lower end of the spectrum of observed diffusion rates in cells. As revealed in this study, the viscosity of dendritic spines is four to five times that of other cells, which supports impaired diffusion in spines.

The ratio of diffusion constants from Fig. 6 B reveals that diffusion is two to seven times slower in spines relative to dendrites. This reduced diffusion is in agreement with our results of enhanced viscoelastic resistance in spines relative to dendrites (relative stiffness of 2.0 ± 0.3 from Fig. 3 A for axon-associated spines). A recent study showed that membrane-linked diffusion is also slower in spines than in dendrite shafts and that use of an anomalous subdiffusion model significantly improved fits to these FRAP data, although the motion was two-dimensional and the power-law exponents were α = 0.7–0.8 (43). Finally, our results of increased viscoelastic resistance in stimulated spines (Fig. 4) may help to explain recent observations that neuronal activity reduces diffusion into spines (38) without the need for a large variation in the cross-sectional area of the spine neck.

CONCLUSION

We have demonstrated a novel approach to study the mechanical properties of dendritic spines at the submicrometer scale in live neurons. Furthermore, the viscoelastic characterization presented here provides an entirely new perspective on how to describe the functional state of dendritic spines. Our results show that the soft-glassy materials description of cellular mechanics is an appropriate model of spine viscoelasticity and extends its previous success in the larger-scale cytoskeletal dynamics of cells such as smooth muscle cells (49,52,54). Within this framework, the concepts of activity-dependent structural plasticity, metastability, and congestion in the cytoplasm of spines are gauged by only a few measurable parameters. Most importantly, the effective noise temperature, which is an integrative factor reflecting the level of molecular agitations, acts as the primary determinant of not only viscoelasticity, striking the delicate balance between solid-like and fluid-like properties, but also the degree to which spines are capable of remodeling and maintaining structural stability. We therefore form the characterization of mechanically soft, malleable spines, likely with the morphological plasticity necessary for learning in the brain, as hot spines with elevated noise temperature. More rigid, stable spines, with properties likely associated with memory retention, are characterized as cold spines with reduced noise temperature. This new perspective adds viscoelasticity to the list of properties of dendritic spines that is of central importance to their function.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.