Characterization of Physical Properties of Supported Phospholipid Membranes Using Imaging Ellipsometry at Optical Wavelengths

Abstract

Subnanometer-scale vertical z-resolution coupled with large lateral area imaging, label-free, noncontact, and in situ advantages make the technique of optical imaging ellipsometry (IE) highly suitable for quantitative characterization of lipid bilayers supported on oxide substrates and submerged in aqueous phases. This article demonstrates the versatility of IE in quantitative characterization of structural and functional properties of supported phospholipid membranes using previously well-characterized examples. These include 1), a single-step determination of bilayer thickness to 0.2 nm accuracy and large-area lateral uniformity using photochemically patterned single 1,2-dimyristoyl-sn-glycero-3-phosphocholine bilayers; 2), hydration-induced spreading kinetics of single-fluid 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine bilayers to illustrate the in situ capability and image acquisition speed; 3), a large-area morphological characterization of phase-separating binary mixtures of 1,2-dilauroyl-sn-glycero-3-phosphocholine and galactosylceramide; and 4), binding of cholera-toxin B subunits to GM₁-incorporating bilayers. Additional insights derived from these ellipsometric measurements are also discussed for each of these applications. Agreement with previous studies confirms that IE provides a simple and convenient tool for a routine, quantitative characterization of these membrane properties. Our results also suggest that IE complements more widely used fluorescence and scanning probe microscopies by combining large-area measurements with high vertical resolution without the use of labeled lipids.

INTRODUCTION

A growing body of evidence suggests that physical-chemical properties of cellular membranes are intimately linked to their biological functions. Membrane composition, thickness undulations, translational fluidity, phase transitions, polymorphism, and curvatures are all being implicated in many membrane-associated biological functions (1–3). These functions span a broad range including recognition, transport, and signaling at cellular surfaces (4–7) as well as intercellular adhesion, fusion, and synapse processes (8–10). A quantitative understanding of these relations is only beginning to emerge. Two critical requirements for a systematic development of a detailed understanding of these structure-function relations include the availability of 1), molecularly tailored and structurally well-characterized model membranes and 2), a complementary set of quantitative methods for their physical-chemical characterization.

In this regard, supported lipid bilayer membranes are proving to be quite useful (11). They are typically formed at the solid-liquid interface when vesicular microphases of lipids and their mixtures rupture and spread spontaneously on hydrophilic surfaces (12). Two successive transfers of lipidic monolayers from the air-water interface onto planar surfaces in Langmuir-Blodgett schemes have also proven useful (13,14). When appropriately formed, they are essentially separated from the substrate surface through an intervening hydration layer of ∼4–15 Å (15–17) and exhibit two-dimensional contiguity and fluidity reminiscent of lipid membranes of vesicles and living cells (8,13). These synthetic constructs provide model membranes of systematically tailored molecular compositions, densities, phase state, and fluidity (18).

The supported membrane configuration is also amenable to a quantitative characterization by a broad range of surface science–based analytical methods (19). Indeed, x-ray reflectivity (20,21), neutron reflectivity (NR) (17), optical ellipsometry (22), surface plasmon resonance (SPR) (23), fluorescence microscopy–based methods (19), quartz-crystal microgravimetry (QCM) (24), atomic force microscopy (AFM) (25), Fourier-transform infrared spectroscopy (e.g., attenuated total reflection) (26), and nuclear magnetic resonance (27) have all proven highly valuable. Together, they provide a detailed quantitative understanding of many physical attributes of lipid membranes including bilayer thickness, packing densities, molecular orientation, lateral homogeneity, defects, translational fluidity, and phase separation as well as their thermal and temporal behavior. Success of these techniques portends a significant accomplishment but also highlights some key limitations, thus reaffirming the need for the continuing development of complementary characterization methods. Of particular interest to this article are quantitative methods for a real-time characterization of four membrane-related topics: membrane thickness and spatial homogeneity, lipid spreading, two-component phase separation, and ligand-receptor binding interactions.

First, despite considerable experimental effort, a facile method for a routine and accurate characterization of bilayer thickness and spatial homogeneity (spatial distribution of the thickness vector) is still lacking. Obtaining the needed z-resolution in the most popular fluorescence methods requires implementation of interference contrast geometry (28) and oxide-coated reflective substrates (15). Both x-ray reflectivity and NR provide very accurate vertical information but are area-averaged measurements and give limited information about the lateral details of the system (29). SPR and AFM offer spatial resolution but also have specific limitations. For use with supported membranes, SPR requires metallic substrates (e.g., Au and Ag) and specialized chemistry to stabilize lipid bilayers (23,30). AFM is amenable to a broader range of substrates but may suffer from tip-induced perturbations, especially when one is working with compressible, fluid lipid membranes (31–33). For example, the application of even piconewton-range forces on compressible, fluid membranes is hypothesized to induce molecular rearrangements and bilayer deformations (34). How these factors influence AFM-based thickness determination remains incompletely understood.

Second, the characterization of the kinetics of bilayer formation at interfaces is a topic of sustained interest, especially when previously untested substrate types or lipid compositions are explored. In this regard, the kinetics of fusion of small unilamellar vesicles (SUVs) has been extensively studied (35,36), but the kinetic data for the hydration-induced spreading of lipids in the formation of bilayers remain limited (37). Although such spreading kinetics can be gathered using fluorescence microscopy, quantitative applications of these measurements have met with limitations primarily because of the complex relations between the fluorescence intensities and the lipid environment, which is continuously evolving during the bilayer formation (37).

Third, the issues of lateral heterogeneity and phase separation in multicomponent membranes are of considerable importance in understanding how molecular distributions influence localization of many generic membrane processes of great biological relevance (38–40). Fluorescence-based methods, utilizing phase-sensitive probes, have proven very useful in quantifying coexisting phases, but the role of labeled molecules in perturbing the natural phase separation of primary lipids remains ill-understood (41–43). AFM-based methods circumvent this issue and provide high lateral resolution (nanometer scale) (44). These methods are able to differentiate among coexisting phases based on differences in their topographies (or friction) as a result of high vertical resolution (subnanometer scale). Unfortunately, one consequence of achieving such resolution in AFM is the longer collection time necessary to capture an image using popular commercial systems. This longer collection time restricts the ability to collect real-time measurements. Another consequence of the high resolution of AFM is that the field of view, generally ranging between 0.5 and 100 μm, is necessarily small. As a result, large-area phase separation and statistical sampling of a macroscopic substrate area become exceedingly difficult using AFM.

Fourth, the characterization of kinetics and affinities of receptor-ligand binding in supported membranes is gaining considerable interest in assaying interactions of pharmacological importance and in the design of membrane-based biosensors (45–50). The readout in these measurements typically relies on the use of fluorescence-, SPR-, or QCM-based transduction. Because of specific experimental requirements for SPR- and QCM-based methods and potential for probe complications in fluorescence measurements (see above), analytical methods that can be directly applied to silicon- or glass-based chips and without the use of fluorescence probes are desirable.

Here, we report an application of imaging ellipsometry (IE) for a facile physical characterization of the four broad classes of membrane-based properties discussed above.

The technique of ellipsometry evolved in semiconductor metrology as a quantitative method for the determination of thin-film properties (51). In most general terms, it is based on polarization changes that occur on reflection of a polarized monochromatic light at an oblique incidence. The basic quantity measured in an ellipsometric experiment is the complex reflectance ratio

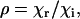(1)

where χ_r and χ_i represent the state of polarization of the reflected and incident beams, respectively. For samples that can be approximated by isotropic optical functions or scalar refractive indices, Eq. 1 is simplified as below:

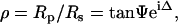(2)

where R_p and R_s are the complex reflection coefficients for light polarized parallel and perpendicular to the plane of incidence, respectively. The two parameters Ψ and Δ are experimentally determined and generally referred to as ellipsometric angles. IE represents an experimental configuration wherein Ψ and Δ are measured in a spatially resolved manner (52).

Ellipsometry is an indirect technique, and extracting relevant physical information about the sample requires the use of optical models typically based on classical electromagnetic theory and the approximation of the sample in terms of parallel optical slabs of defined thicknesses (d) and refractive indices (n + ik) (51). The quantitative accuracy of the physical properties determined directly depends on how faithfully the slab model depicts the optical properties of the actual experimental sample. Over the past several decades, a range of models have been developed that are capable of capturing many complex physical properties, e.g., anisotropy, heterogeneity, and molecular orientation (53,54). From the vantage of supported membrane research, it offers a nonperturbative, quantitative method and allows in situ, label-free, spatially resolved, and large-area measurements of small spatial or temporal differences in the optical functions following bilayer depositions, phase separation, or protein binding with reasonably short collection times determined by the video rate of the CCD detector.

MATERIALS

1,2-Dimyristoyl-sn-glycero-3-phosphocholine (DMPC), 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), and GM₁ ganglioside (brain, ovine, ammonium salt) were obtained from Avanti Polar Lipids (Alabaster, AL), cholera toxin β-subunit (CTB) from Sigma Aldrich (Milwaukee, WI), and galactosylceramide (GalCer) obtained from Matreya (Pleasant Gap, PA). All lipids were suspended and stored in chloroform or chloroform/alcohol mixture in the freezer (−20°C) until use. Hydrogen peroxide (30% v/v) and sulfuric acid were purchased from J. T. Baker (Phillipsburg, NJ) and Fisher Chemicals (Fairlawn, NJ), respectively, and used as received. All organic solvents were HPLC grade. All chemicals were used without further purification. Organic-free deionized water of high resistivity (∼18.2 MΩ-cm) was obtained by processing water first through a reverse-osmosis deionization unit and then a Millipore Synthesis water filtration unit (Billerica, MA). Phosphate-buffered saline (PBS, pH = 7.2, 154 mM NaCl, 1.54 mM KH₂PO₄, and 2.71 mM Na₂HPO₄) was obtained from Gibco-Life Technology (Rockville, MD) and used as vesicle spreading solution and buffer medium. Silicon substrates with native oxide overlayers (Silicon Sense, Nashua, NH) were used unless noted.

METHODS

Formation of supported lipid bilayers

Supported phospholipid bilayers were formed (unless noted otherwise) using the previously reported vesicle fusion and rupture method. Briefly, SUVs were prepared using vesicle extrusion methods (55). Typically, a desired amount of lipid or lipid mixture suspended in chloroform or a chloroform/methanol mixture was mixed in a glass vial. The solvent phase was then evaporated under a stream of nitrogen and subsequently evacuated for at least 1 h in a vacuum desiccator. The dried lipid mixture was then suspended in Millipore water and kept at 4°C to be rehydrated overnight. The total lipid concentration was 2 mg/ml. The desired amount of hydrated aqueous solution was then sonicated and passed through an Avanti Mini-Extruder (Avanti, Alabaster, AL) using 0.1-μm polycarbonate membrane filters (Avanti, Alabaster, AL) 21 times at a desired temperature (typically 10°C above the transition temperature). One part of the resulting SUV solution was diluted with one part of PBS and kept above the T_c until used. Vesicles were used within a few hours of extrusion.

Substrates (silicon oxide wafers) pretreated for bilayer depositions were immersed in a freshly prepared 4:1 (v/v) mixture of sulfuric acid and hydrogen peroxide for a period of 4–5 min maintained at ∼100°C (Caution: this mixture reacts violently with organic materials and must be handled with extreme care.). The substrates were then withdrawn using Teflon tweezers, rinsed immediately with copious amount of water, and stored under water until use. Cleaned substrates were used within 1–2 h of the pretreatment. Bilayer samples were prepared by placing a clean substrate surface over an ∼50-μL SUV drop placed at the bottom of a crystallization well. The sample was allowed to incubate for ∼15 min to ensure equilibrium coverage. The well was then filled with water, transferred to a large reservoir of buffer in which the substrate was shaken gently to remove excess vesicles. The supported bilayer samples prepared in this way were then stored in deionized water or PBS buffer for further use in UV lithography and characterization.

UV photolithography of substrate-supported phospholipid bilayers

UV photolithography of membranes was carried out using previously reported procedures (56). Briefly, spatially directed deep UV illumination of supported bilayers was achieved using a physical mask and short-wavelength UV radiation. The mask displaying patterns of chrome over quartz substrate was obtained from Photoscience, Inc. (Torrance, CA). Short-wavelength UV radiation was produced using a medium-pressure Hg-discharge grid lamp (UVP, Upland, CA) in a quartz envelope and maintained in a closed chamber in a chemical hood. While still under water, the mask was gently lowered onto the bilayer samples placed in a crystallization dish filled with water. The sample system was then carefully placed in an UV/ozone-generating environment so that the cover slips were ∼0.2–5 mm away from the light source. The exposure period was ∼20 min. The amount of water on the sample surface was optimized to ensure that the samples remained submerged during the entire illumination process. Following exposure, samples were immersed in a large water bath, mask separated from the substrate surface, and stored in water for further characterization.

Spreading of lipid bilayers

POPC phospholipids were dissolved in chloroform to a total concentration of 7.5 mg/ml, and 6 μl of this solution was deposited on a 25 × 1 mm glass microscope slide edge and vacuum dried in the dark for at least 2 h. The edge was manually stamped onto silicon oxide substrates, transferring some of the lipid material along a sharp line. The sample was subsequently hydrated by deionized water while being imaged by the ellipsometer. Kinetic spreading data were analyzed using Matlab from Mathworks (Natick, MA) scripts that performed edge-detection and nonlinear least-squares fitting.

Formation of phase-coexisting lipid bilayers (GalCer/DLPC)

A 0.35 GalCer plus 0.65 1,2-dilauroyl-sn-glycero-3-phosphocholine (DLPC) chloroform solution (2 mg/ml) was mixed, dried under a nitrogen stream, and placed under vacuum for ∼2 h. Water was then added to the dried lipid, yielding a 0.5 mg/ml solution. The hydrated lipid solution was mixed in a vortex and then warmed in a bath sonicator to 50–55°C. The warm solution was mixed in a vortex again and then placed in a tip-sonicator. Tip-sonication was performed for 1–2 min, and the sonicated solution was allowed to cool. Vesicle fusion was carried out using ∼500 μl of the sonicated solution administered on top of clean silicon at room temperature with the polished side facing up. The lipid was allowed to incubate for ∼15 min. Samples were then rinsed with copious amounts of Millipore water in a large dish. The as-prepared samples were subsequently annealed by being placed in a dish of warm water maintained at 50°C in an oven for ∼1 h. The oven was then turned off, and the samples were allowed to cool overnight. Ellipsometric characterization was performed the following day under room-temperature conditions.

Cholera toxin incubation

Before CTB incubation, samples were transferred to small plastic petri dishes. The aqueous phase was exchanged with a large amount of PBS. Buffer was then pipetted out until ∼6 ml remained in the petri dish, and 20 μl of a 1 mg/ml solution of CTB in PBS was then pipetted into the petri dish. This gives a final CTB concentration of 3.3 μg/ml. The samples were allowed to incubate for ∼20 min to ensure equilibration. Samples were rinsed in water and imaged immediately.

Imaging ellipsometry

Ellipsometric angles and spatially resolved ellipsometric contrast images were acquired using a commercial Elli2000 imaging system (Nanofilm Technologie, Göttingen, Germany). The ellipsometer employed a frequency-doubled Nd:YAG laser (adjustable power up to 20 mW) at 532 nm and was equipped with a motorized goniometer for an accurate selection of the incidence angle and corresponding detector positions. The ellipsometer employed the typical polarizer-compensator-sample-analyzer (PCSA) nulling configuration in which a linear polarizer (P) and a quarter-wave plate (C) yield an elliptically polarized incident beam. On reflection from the sample (S), the beam is gathered via an analyzer (A) and imaged onto a CCD camera through a long-working-distance 10× objective (Fig. 1 a). The P, C, and A positions that yield the null condition are then converted to the ellipsometric angles, Δ and Ψ. Measurements were generally taken at an incidence angle of 60°. Silicon substrates with native oxide overlayer (SiO₂/Si) whose surface chemistry is comparable to that of glass were used to enhance the optical contrast with the lipid phase. For characterization under aqueous conditions, a fluid cell was used (Nanofilm Technologie, Göttingen, Germany). The cell consisted of a Teflon chamber (∼3 ml volume) with glass windows fixed at 60° (incidence angle) to the substrate normal. A home-built cell was also used for some measurements. This cell consisted of a glass and epoxy chamber with windows fixed at 60°. The field of view and lateral resolution of the acquired images are limited by the objective and CCD used. The specified accuracy in ellipsometric angle determination is 0.01° for our instrument.

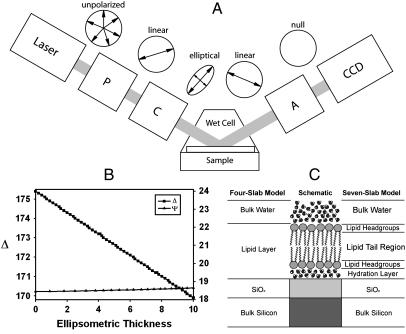
FIGURE 1.

Experimental setup forIE. (A) A schematic description of the PCSA (polarizer-compensator-sample-analyzer) reflection IE configuration used in this study. The windows of the wet cell are normal to the incident laser beam. The cartoon circles above each image illustrate the changes in polarization of the light under nulling conditions. (B) High sensitivity of Δ (and relative insensitivity of Ψ) on nanometer-scale thickness changes in the bilayer are revealed in a model calculation using a simplified four-slab model consisting of water/lipid phase/SiO₂/Si. (C) A schematic of parallel-slab optical models for the SiO₂/Si supported lipid bilayer (center) configuration sample systems considered in this study. A detailed seven-slab model (right) and a four-slab model approximation (left) used in our data analysis are also shown.

Topographical maps of Δ were generated using the micromapping feature of the Elli2000 software suite. The method used assumes that Ψ is constant. In our specific experimental configuration, Ψ is relatively constant with respect to changes in Δ (Fig. 1 b). Typically, 70–140 contrast images were scanned incrementally over a 4–8° change in polarization angle with the analyzer angle maintained at a constant value. These scans were then assembled to determine the null for each point comprised of a 2 × 2 region of pixels binned together. Δ values estimated for the individual null conditions were mapped two-dimensionally. These maps were then transferred to a computer as ASCII files from which the final images were constructed using commercial plotting software (Matlab).

Optical models for the determination of ellipsometric thicknesses

Film thicknesses were determined from the ellipsometric parameters using standard classical electromagnetic theory in conjunction with a parallel layer model consisting of a silicon/silicon oxide/bilayer/water structure. The treatment assumes that the total sample consists of semiinfinite parallel slabs, each a uniform material of homogeneous composition described by a single set of optical constants. With the current single-wavelength measurements, the ellipsometry equations do not allow an independent determination of both the optical function and the thickness of the lipid bilayer from the Δ and Ψ values. Therefore, the film thickness was determined using independently assigned values for the substrate and film optical functions. Taking into account the 0.01° accuracy in Δ, the error in measurement caused by the instrument is <0.02 nm. With this consideration, we report our calculated thickness values to 0.1 nm precision.

The amorphous oxide and crystalline silicon phases, as well as any adsorbed water phase, associated with the substrate are treated as optically isotropic and thus assigned scalar optical (or dielectric) functions. The independent assignment of the correct substrate optical functions for the lipid/substrate structure is most conveniently done by an independent ellipsometric analysis of the exact same substrate structure before bilayer deposition, i.e., a “bare” substrate. The substrate was approximated as a two-phase structure. On this basis, a dielectric function was determined for the native oxide layer from the measured ellipsometric response using a silicon/silicon oxide/water model for the calculations. In turn, this dielectric function was used for the lipid thickness calculation from the final ellipsometric measurements using a four-slab model: silicon/silicon oxide/lipid/water model (Fig. 1 c). The most rigorous description (a seven-slab model (Fig. 1 c)) of the lipid layer requires the assignment of separate optical constants for the two headgroup regions (including primary hydration shell) and the acyl chain regions. Given the uncertainties associated with an accurate assignment of thickness and the dielectric constants for the headgroup regions and hydration layer, we approximate the entire lipid layer as consisting of a single dielectric layer. When available, refractive index values were chosen from previous reports (57,58). In other cases, values were estimated from the optical properties of similar lipids under comparable conditions of molecular packing and phase state (57–59). Our preliminary calculations reveal that the errors in this approximation, relative to a rigorous consideration of all the constituent layers, are substantially less than the sample-to-sample experimental error in our case.

Ellipsometric thickness averages were determined by selecting several locations near the center of the calculated thickness maps for each sample. Where applicable, independent knowledge of the bilayer thickness was used to translate measured ellipsometric thickness in terms of molecular densities. In cases where coexisting lipid phases of differing refractive indices were present, separate average thicknesses were measured for each phase. This required the calculation of separate thickness maps using a corresponding refractive index map as described in the Results section below.

RESULTS AND DISCUSSION

The four subsections presented below illustrate specific applications of IE in quantitative measurements of bilayer thicknesses and uniformity, bilayer spreading, phase separation, and receptor-ligand interactions. Although the results presented describe specific applications chosen from other independent studies in our laboratories, the measurement principles and the implementation of the method are, in general, applicable to a broad range of related properties in supported membrane systems.

Quantitative determination of thicknesses of submerged phospholipid bilayers

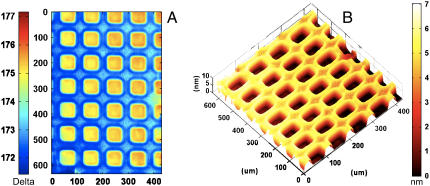
One of the most direct applications of IE is the measurement of surface coverage, lateral uniformity (at microscopic length scales), and film thickness. A representative example is shown in Fig. 2. The image in Fig. 2 a represents a 645 × 430 μm spatial map of the ellipsometric angle Δ of a photochemically patterned DMPC bilayer on a silicon substrate (60). A corresponding thickness map derived using a refractive index of 1.44 is also shown (Fig. 2 b). Note that patterning, although not required for absolute determination of ellipsometric film thicknesses, alleviates the need for independent substrate characterization and provides an optical (and topographic) contrast to facilitate visualization and analysis.

FIGURE 2.

Ellipsometric characterization of thickness, uniformity, and patterns of supported phospholipid membranes. (A) A spatially resolved map of ellipsometric angle, Δ, for a photopatterned DMPC bilayer on SiO₂/Si substrate. (B) A corresponding thickness map derived using an approximate, four-layer parallel slab model and a single, composite refractive index of 1.50 for the entire DMPC layer including any associated water. (See text for details.)

These images highlight a number of features of the membrane topography. First, the thickness map shows a pattern of film topography resulting from the UV exposure. The topography of the membrane shows an excellent correspondence with the pattern of UV exposure, lending additional support to the previous conclusion that UV membrane lithography completely removes the lipids in the exposed region and that the unexposed bilayer remains essentially unperturbed (56). Second, the images in Fig. 2 further show a considerable lateral uniformity and lack of observable defects in the DMPC bilayer over large, macroscopic areas. (Note: A slight tilt is observed in the image (Fig. 2). This tilt is an artifact of our experimental geometry. It results from uneven illumination of the sample because of the extended laser profile, thereby producing reduced sensitivity toward one side of the image. In principle, the effect can be reduced or eliminated by the use of a beam expander, but our current setup does not include this modification.) These results agree well with many previous fluorescence measurements that establish that SUVs above their transition temperatures rupture and fuse with clean silica (and oxidized silicon substrates) to form continuous, low-defect phospholipid bilayers. Note also that the transition temperature of DMPC (24°C) is close to the experimental temperature; thus, a mixture of liquid-crystalline and gel-phase DMPC likely comprises our sample forming a continuous bilayer. Third, we observe areas of slightly increased ellipsometric thickness at the boundaries between the void and the bilayer regions. At present, we do not fully understand the origin of this structural feature but surmise that it may result from an artifact of the photopatterning process, such as that reported earlier in a related system (61). Fourth, these data provide a large number of pixel-by-pixel parallel ellipsometric measurements for the determination of the thickness of the DMPC bilayer. These results are discussed in detail below.

Using the parallel slab model representing the sample system as consisting of water/DMPC/SiO₂/Si (see experimental), we estimate that the spatial average ellipsometric thickness for the DMPC bilayer shown in Fig. 2 is 4.1 ± 0.2 nm, consistent with the formation of a single, DMPC bilayer. Here, the 0.2-nm standard deviation reflects spot-to-spot variation in membrane thickness for the sample. Additionally, a sample-to-sample standard deviation of 0.5 nm was found from measurements on several high-quality samples. The use of more rigorous dielectric slab models, explicitly accounting for 1), the presence of a substrate-bound water layer at the SiO₂/Si surface and 2), headgroup regions including the associated water at the previously estimated thicknesses of 0.9 nm and an approximate refractive index range of 1.38–1.42, resulted in a family of solutions ∼3.9–4.3 nm because of the uncertainties associated with the headgroup refractive index.

The precise values of the ellipsometric thickness and their relation to the physical thickness of the bilayer depend strongly on the accuracy of the refractive index used in the calculations. In this case, we use the isotropic average given by the relation n_avg = ⅓ (2n_o + n_e). The uniaxial n_o and n_e values were taken from previous reports (57,58) to get the average value used in this case. (Note: Independent determination of refractive index with high degree of accuracy is possible using a variety of independent experimental methods, e.g., SPR, OWLS, optical reflectance measurements, and spectroscopic ellipsometry, which can further reduce these uncertainties.) A more rigorous treatment of refractive index requires the use of a second-rank tensor because of the anisotropic structure of supported membranes (30,62). Such a treatment is computationally intensive and in this case does not offer significantly more accurate results than the use of an isotropic average refractive index. Because different preparation methods may result in different coverage densities, there are additional uncertainties even in using these isotropic values (see below). The use of values between 1.43 and 1.45 results in a range of DMPC calculated average ellipsometric thicknesses thicknesses between 4.7 (± 0.2) nm and 4.0 (± 0.2) nm.

Previously, some of the most detailed characterization of phospholipid bilayer thicknesses has been derived using synchrotron x-ray diffraction and small-angle neutron-scattering measurements of “free” bilayers in vesicular and lamellar configurations. Defining the physical thickness of a lipid bilayer has met with some uncertainty, mostly because of the headgroup association with the bulk-phase water and height fluctuations, especially in the fluid phase. Within these constraints, a range of values between 3.6 and 4.9 nm has been reported for DMPC (63–65). In a recent series of articles, Kucerka et al. from Nagle's group (66,67) have employed an elaborate hybrid electron-density model to analyze x-ray diffraction data for unilamellar DMPC vesicles. These results yield the average molecular area of ∼0.6 nm² and suggest a bilayer thickness (including the headgroup and associated water) estimate of 4.3 nm for a DMPC bilayer at 30°C. Our ellipsometric estimate of ∼4.1 nm at 1.44 refractive index value for the entire DMPC phase at room temperature is in excellent agreement with these estimates. The correspondence between the x-ray thickness and the ellipsometric thickness further suggests that the choice of the average refractive index of 1.44 for DMPC bilayer (including the headgroup and associated water) is appropriate.

A certain degree of uncertainty in this comparison is expected for a variety of reasons. First, correcting for the temperature difference between published values and our measurements conducted at the room temperature is somewhat tricky because of the proximity of the phase transition temperature in this case. As the temperature is raised, the bilayer thickness decreases, but the water layer in the headgroup region swells (68). Moreover, our measurements are conducted near bulk phase transition conditions for DMPC, where the aerial and linear thermal expansion coefficients can change considerably, and estimating the fraction of the bilayer in the nonpercolating fluid phase is difficult. Second, we recall here that the assumptions in our thickness estimations include 1), a priori assignment of the refractive index (which depends on the area per molecule and the phase state of the lipid) and 2), the use of a single refractive index to account for both the acyl chain and the headgroup regions. Both of these approximations could serve as sources of small errors in the absolute thickness determinations. Third, because substrate-supported bilayers show at least some degree of “epitaxial” coupling to the substrate, it is likely that the molecular densities, which impact refractive index values, differ from those in free vesicles. With these assumptions taken into account, it appears reasonable to conclude that the simple ellipsometric thickness determination above complements well with neutron- and x-ray-based thickness determinations, which employ very different assumptions (67).

Taken together, these results establish that IE is a convenient means for a quantitative characterization of thickness, lateral uniformity, and spatial thickness variations extending over macroscopic sample areas. Notably, this is accomplished while micrometer lateral and angstrom height resolution are maintained.

Dynamic ellipsometric measurements to measure bilayer spreading kinetics

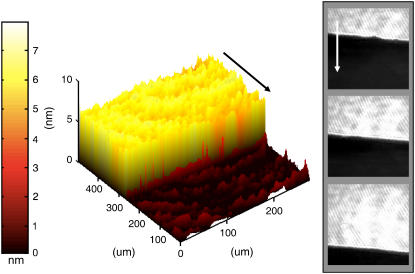
IE can also be used to examine dynamic systems. Fully mapped ellipsometric images, such as those shown in Fig. 3, provide a rich description of the state of the system but are somewhat slow to acquire. Typically, a minimum of 20 s is required to fully map a 645 × 430 μm² image of the ellipsometric angles. For probing time-dependent processes (e.g., bilayer formation, lipid spreading, reactive-diffusive processes within membranes, and phase separation dynamics), ellipsometric contrast images can be used (69). Here, the reflection from a uniform region of the sample is nulled such that the light is linearly polarized and blocked by a perpendicularly oriented polarizer in front of the detector. Any deviation from the height or refractive index of the nulled region can then be recorded as a signal. In this manner, the dynamics within the nulled region can be captured at a rate limited by the speed of the detector or the depth scanner (30 Hz for a standard CCD focus line, ∼1 Hz for a whole image). Combining these time resolution ellipsometric contrast images with null information at the onset and the conclusion of the experiment provides a quantitative description of a kinetic process associated with submerged lipid membranes. Further quantification of the off-null regions of the image can be obtained by the use of off-null ellipsometry if desired (70). Below, we describe the application of this approach in characterizing hydration-induced spreading of phospholipids from a dried source. Fig. 3 illustrates the time evolution of a surface-spreading POPC film on addition of water to nominally dry POPC stamped onto an edge of a silicon wafer (37). An initial fully mapped image reveals the height of the spreading film, and subsequent high-speed contrast images reveal the dynamics on the same region of the sample. A simple analysis of the dynamics of the moving bilayer front reveals an instantaneous spreading rate of 0.08 μm/s during the measurement interval. This value is well within the range previously reported (71). The fully mapped image is valid only away from the leading edge of the spreading film, as the Δ values there are not temporally constant for the duration of the scan. From the scan rate and the observed spreading rate, we estimate the extent of this uncertain region to be ∼15 μm. Alternatively, after the spreading has completed, the equilibrated state of the system may subsequently be mapped as well.

FIGURE 3.

Hydration-induced surface spreading of single phospholipid bilayer. (left) An ellipsometrically determined height map for the spreading POPC lipids. (right) Off-null ellipsometric contrast images taken at 0 s, 230 s, and 460 s. The nulling was performed for the bilayer height and refractive index. (See text for details.) The arrows in the panels indicate the direction of lipid spreading (shown as a guide to the eye).

A more detailed analysis of the contrast video reveals a time-varying velocity that adheres to previously reported square root of time phospholipids spreading kinetics and expected spreading rates (37, 71). The full-thickness map establishes the single bilayer morphology of the spreading lipid phase. In previous fluorescence studies, the spreading front is often characterized by a marked increase in fluorescence hypothesized to be caused by dye partitioning (71). This study, employing a label-free real-time assay of the spreading front, conclusively eliminates the possibility that the previously observed fluorescence increase is a result of multiple bilayers rolling over each other.

In sum, the combined application of null and contrast IE demonstrated above illustrates a simple and quantitative characterization of the kinetic process involved in the formation of supported membranes from lipid spreading.

Ellipsometric characterization of phase coexistence and separation in single supported bilayers

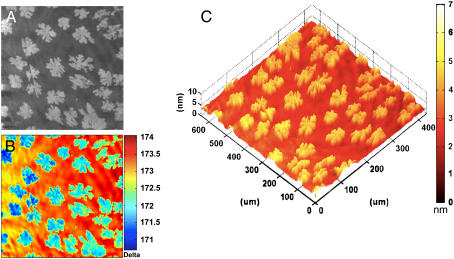
The ability of IE to distinguish between regions of different molecular compositions (and hence regions of different refractive indices) without the use of fluorescent probes or sample perturbation makes it a particularly attractive candidate for characterizing how membranes handle their compositional heterogeneities. In particular, ellipsometry enables a label-free measurement of morphologies of phase coexistence in supported bilayer configuration. Fig. 4 shows an ellipsometric image of an annealed bilayer consisting of a ∼2:1 mixture of a fluid phospholipid, DLPC, and a gel glycolipid, GalCer, on a SiO₂/Si substrate. The images in Fig. 4, a and b correspond to a contrast image and a corresponding Δ map, respectively. The contrast image reveals discrete regions of high-intensity “domains” surrounded by a continuous region of low-intensity surroundings. These high-intensity regions bear a direct correspondence to the regions of lower value in the Δ map of Fig. 4 b. In both images, the “domain” morphology is random but distributed uniformly over the entire image, which also adopts a dendritic-like morphology.

FIGURE 4.

Lateral phase separation in a two-component bilayer. Single bilayer derived by the fusion of SUVs consisting of ∼2:1 mixture of DLPC, a fluid-phase phospholipid, and GalCer, a gel-state glycosphingolipid, on SiO₂/Si. (A) An off-null ellipsometric contrast image showing the phase-separated bilayer morphology. (B) A corresponding ellipsometric Δ map. (C) A calculated thickness map based on b and an index of refraction of 1.50 appropriate for GalCer. An analysis of the data establishes that the dendritic domains are primarily composed of GalCer molecules, and the surrounding membrane is mostly DLPC. (See text for the quantitative interpretation of the thickness distribution in terms of compositional heterogeneity of the sample.)

These dendritic structures are reminiscent of morphologies created during many diffusion-limited aggregation processes (72). Even at this stage of our data analysis, it can be inferred that these dendritic “solid-like” areas are clusters of primarily gel-state GalCer molecules because the experimental temperature is below the T_c for GalCer. An analysis of Fig. 4, a and b, performed using public-domain image analysis software (Image J, NIH) reveals that 29% of the total surface area is occupied by these dendritic domains (average size, 44 ± 27 μm; average area, 1928 ± 743 μm²). Because the molecular stoichiometry is 35:65 (∼1:2) of GalCer to DLPC, this 29% surface area coverage by domains lends an additional support to our inference that the dendritic domains are primarily GalCer clusters embedded in the surrounding fluid phase, comprised primarily of DLPC. We note that the discrepancy between the areal density of the dendritic domains, assigned to GalCer, and the molecular compositional ratio of 35% is not unexpected because the gel-phase GalCer molecules are likely to occupy a smaller area per molecule and also that the phase separation of GalCer induced during annealing may not be complete. Similar morphologies have also been seen in a closely related phase-separating lipid mixture (73).

Significant quantitative topographic information can also be obtained by calculating bilayer ellipsometric thickness from the spatially resolved Δ information in Fig. 4 b. The resulting thickness map derived using a single composite refractive index of 1.50 for the entire lipid phase is shown in Fig. 4 c. We note that the use of a single refractive index of 1.50, approximating the optical properties of the gel-phase GalCer domains, considerably simplifies the thickness calculations but introduces errors in accurately estimating absolute height differences between coexisting phases. These simplified calculations reveal that the dendritic features are indeed taller than the surrounding lipid, further supporting the longer acyl-chained GalCer as the primary constituent of these domains. Further, the taller GalCer domain regions correspond directly to the high-intensity regions in Fig. 4 a and to the low-Δ regions in Fig. 4 b.

An accurate analysis of the absolute thickness difference between the coexisting phases requires the use of independent refractive indices for the fluid and solid regions. Such an analysis yields quantitative thickness measurements for both the fluid and the domain regions. The GalCer and DLPC layers were modeled using refractive indices of 1.50 and 1.44, respectively, and mapped onto the topography of the Δ map. With this model, average thicknesses were calculated to be 4.5 ± 0.1 nm and 3.6 ± 0.2 nm for the dendritic GalCer regions and the surrounding DLPC regions, respectively. This DLPC thickness determination falls nicely within the range of thickness values (3.0–4.3 nm) reported previously in independent SANS and AFM measurements (63,74). Although a direct comparison of GalCer bilayer thickness with existing literature is difficult to make, a recent molecular simulation using a 90:10 GalCer:DMPG mixture revealed an average thickness of 4.21 ± 0.05 nm (75). Our ellipsometric estimates for the GalCer domains estimated at 4.5 ± 0.1 nm are slightly higher than these values and may reflect the differences in the definitions used to assess static bilayer thicknesses. However, a direct comparison of the height difference between GalCer and DLPC can be made with the existing literature. In a recent study, Blanchette et al. (73) reported the height difference between DLPC and GalCer at domain step edges, using AFM, to be 0.9 nm. Our results of 0.9 ± 0.2 nm for the height difference are in excellent agreement with this value. It is useful to note here that our ability to resolve phase separation using IE is currently limited by the resolution achieved using 10× optical objective. Some improvements are possible, but achieving nanoscale lateral resolution in this experimental configuration will be difficult. In this regard, IE complements AFM by providing large area imaging, which is useful for statistical analysis of phase separation. Complementary AFM provides significantly higher lateral resolution but smaller sampling windows. This application of ellipsometry in characterization of phase-separating lipid mixtures can be easily extended to study the dynamics of GalCer domain formation during cooling from an initial homogeneous bilayer. These experiments are beyond the focus of this article and will be separately reported (A. W. Szmodis, C. Blanchette, M. L. Longo, C. A. Orme, and A. N. Parikh, in preparation, 2007).

Taken together, the experiment presented above highlights the ability of IE to provide a large-area and label-free characterization of coexisting phases in polymorphic supported membranes.

Ellipsometric characterization of membrane-associated receptor-ligand interactions

The ability of IE to detect minute changes in thickness or surface coverage for a sample under observation without the use of labels is attractive for examining membrane-associated ligand-receptor interactions. The latter are of great importance in a broad range of pharmacological studies of drug screening (46) and also for the development of supported-membrane-based biosensors (47). Fig. 5 shows the characterization of a model ligand-receptor system, cholera toxin B subunits, in CTB binding to the ganglioside GM₁, a membrane-bound lipid receptor (76).

FIGURE 5.

Ellipsometric characterization of CTB-GM₁ binding. (A–C) Ellipsometric thickness maps taken during the construction of a spatial pattern of GM₁ presenting POPC bilayer in the background of the protein-resistant DPPC bilayer on SiO₂/Si. (A) Intact DPPC membrane. (B) Photopatterned DPPC bilayer. (C) Photopatterned DPPC membrane after back-filling with POPC membrane containing 2% GM₁. (D) Ellipsometric thickness map for the sample characterized in c on incubation with CTB. The absence of any thickness gain in the DPPC region confirms its protein-resistant character, and the CTB binding is observed to localize primarily in the square regions containing GM₁. Quantitative details of these data provide some clues regarding the interaction valency (see text for details).

Fig. 5, a–c, tracks the construction of isolated patches of POPC bilayer containing 2 mol% GM₁ surrounded by DPPC bilayer. Fig. 5 a shows a thickness map of a supported bilayer of DPPC. The bilayer is uniform but contains some unruptured vesicles adhered to the surface as revealed by the randomly distributed thick dots. Fig. 5 b shows a subsequent thickness map of the same bilayer after selective exposure to short-wavelength UV light. As expected (see above), the exposure results in a loss of membrane material in the illuminated sample areas (56). Fig. 5 c shows a thickness map of this patterned bilayer after a room-temperature incubation with secondary lipid vesicles consisting of 98 mol% POPC and 2 mol% GM₁ (POPC (+GM₁)). The secondary vesicles selectively add material to the depleted regions of the patterned DPPC bilayer, where the hydrophilic silicon oxide substrate is exposed. Because this process is performed below the T_c (= 41°C) of DPPC, the secondary lipids do not mix with the surrounding DPPC, and an array of sequestered regions of 98 mol% POPC and 2 mol% GM₁ is achieved. The calculated thicknesses of the regions consisting of GM₁ and POPC are lower than that of the surrounding DPPC. This difference is likely a result of the fluid nature of the POPC regions. The ambient temperature (∼21°C) is below the T_c of DPPC (41°C) but well above that of POPC (−2°C), causing the DPPC tails to adopt a trans conformation, extending the tails and allowing them to pack tighter than the adjacent fluid POPC regions, thus producing higher ellipsometric thickness for the DPPC regions. Ellipsometric images shown in Fig. 5 d reveal a thickness map of the membrane array after exposure to CTB. An increase in the ellipsometric thickness is observed in the POPC (+GM₁) regions, whereas little or no change in the ellipsometric thickness is observed for the surrounding DPPC bilayer. These results are consistent with the expected specific GM₁-CTB interaction in the POPC (+GM₁) region and the absence of any nonspecific CTB binding in the DPPC background.

Because the refractive index properties for the gel-phase DPPC are different from those of the fluid-phase POPC (+GM₁), further quantification requires independent handling of the two regions in our data analysis. These calculations indicate that on CTB incubation, the ellipsometric thickness associated with DPPC remained unchanged within the errors of our measurements (±0.1 nm), whereas in the POPC (+GM₁) regions, the ellipsometric thickness shows a gain of 2.5 ± 0.2 nm (for n = 1.50 for CTB). Previously, x-ray diffraction and NR studies have shown that the GM₁-CTB complex extends beyond the membrane surface by ∼3.7 nm (77,78). Based on this value, the ellipsometric thickness increase of 2.5 nm in our measurements suggests a surface coverage of ∼68%. It is further instructive to consider the average area occupied by CTB in relation to the GM₁ population. The molecular area of CTB is estimated at ∼30.2 nm² based on the crystal structure data (78). At 68% monolayer coverage, the average molecular area for CTB then is ∼44.4 nm². If the 2 mol % GM₁ is evenly distributed between the two leaflets of the bilayer and has an average lipid molecular area of ∼0.6 nm², we obtain a rough estimate of one GM₁ in 30.3 nm² of the bilayer area. If all GM₁ participates in CTB binding, these numbers suggest an average polyvalency of ∼1.5 at the GM₁ and CTB concentrations used in our study. We note that there is some experimental evidence to suggest that the assumption of an even distribution of GM₁ between the two bilayer leaflets may not be correct and that GM₁ may dominantly partition in the outer leaflet accessible by CTB (M. C. Howland, A. R. S. Butti, T. W. Allen, A. P. Shreve, and A. N. Parikh, University of California Davis, unpublished material, 2006). With this scenario taken into account, the limiting case polyvalency in our simple calculations is estimated at ∼3.0. These numbers are in good general correspondence with those reported in independent flow cytometry studies (79).

In summary, the GM₁-CTB binding evaluation using IE presented above illustrates the use of ellipsometry in unraveling the receptor-protein interaction affinities. The approach, in conjunction with real-time off-null ellipsometric measurements, can be conveniently applied for kinetic binding measurements.

CONCLUSIONS

The applications presented here illustrate the versatility and the promise of IE for a quantitative, routine, and facile determination of many physical-chemical properties of supported membranes. In particular, we have shown that key structural attributes of supported membranes including bilayer thicknesses (or molecular areas), lateral uniformity, phase separation, and ligand-receptor binding interactions can all be quantitatively determined using IE. The ability of IE to enable large-area imaging, real-time measurements, subnanometer-scale z-resolution, modest spatial resolution, noncontact optical measurements, high sensitivity to small relative differences in optical properties such as between coexisiting lipid phases, and without the use of labels should prove complementary to widely used atomic force and fluorescence-based microscopy measurements of membrane structural and dynamic properties. From the applications point of view, additional features including variable angle measurements, spectroscopic applications, temperature control, flow-cell capabilities, and more accurate data modeling incorporating structural anisotropies and heterogeneities can be easily included to further improve the accuracy in ellipsometric measurements and to deduce many useful structural and dynamical subtleties of supported membranes. Although the focus of this article has been on supported phospholipid membranes in aqueous phases, extension to the study of other surface-bound configurations of biomaterials, cells, and proteins appears straightforward.