Connecting nitrogenase intermediates with the kinetic scheme for N₂ reduction by a relaxation protocol and identification of the N₂ binding state

Abstract

A major obstacle to understanding the reduction of N₂ to NH₃ by nitrogenase has been the impossibility of synchronizing electron delivery to the MoFe protein for generation of specific enzymatic intermediates. When an intermediate is trapped without synchronous electron delivery, the number of electrons, n, it has accumulated is unknown. Consequently, the intermediate is untethered from kinetic schemes for reduction, which are indexed by n. We show that a trapped intermediate itself provides a “synchronously prepared” initial state, and its relaxation to the resting state at 253 K, conditions that prevent electron delivery to MoFe protein, can be analyzed to reveal n and the nature of the relaxation reactions. The approach is applied to the “H⁺/H⁻ intermediate” (A) that appears during turnover both in the presence and absence of N₂ substrate. A exhibits an S = ½ EPR signal from the active-site iron–molybdenum cofactor (FeMo-co) to which are bound at least two hydrides/protons. A undergoes two-step relaxation to the resting state (C): A → B → C, where B has an S = 3/2 FeMo-co. Both steps show large solvent kinetic isotope effects: KIE ≈ 3–4 (85% D₂O). In the context of the Lowe–Thorneley kinetic scheme for N₂ reduction, these results provide powerful evidence that H₂ is formed in both relaxation steps, that A is the catalytically central state that is activated for N₂ binding by the accumulation of n = 4 electrons, and that B has accumulated n = 2 electrons.

Nitrogenase is the two-component enzyme system that catalyzes the nucleotide-dependent reduction of N₂ to yield NH₃ according to the stoichiometry

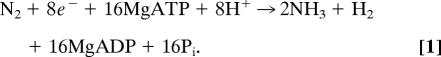The major barrier to characterizing the nitrogense catalytic mechanism has been the impossibility of synchronizing the delivery of electrons, so that an individual intermediate along the N₂ reduction pathway can be accumulated for characterization. This difficulty arises because the MoFe protein, which contains the N₂-binding/reduction site, the iron–molybdenum cofactor (FeMo-co) ([7Fe-9S-Mo-X-homocitrate]), acquires electrons one-at-a-time from its partner, the Fe protein (1). This electron transfer (ET) process involves the nucleotide-dependent association-dissociation of the two proteins, and it cannot be synchronized because complex dissociation represents the rate-limiting step of substrate reduction (1, 2). This obstacle contrasts, for example, with the ready use of flash photolysis to synchronously generate individual intermediates of the photosynthetic reaction center (3).

Recently, we overcame one aspect of this barrier to the study of nitrogenase through freeze-quench trapping of intermediates that form during the reduction of H⁺ under Ar (4), the reduction of alkyne substrates (5, 6), and most recently, several intermediates associated with N₂ reduction (7). Unfortunately, these intermediates are still trapped without synchronous electron delivery to the MoFe protein, and thus the number of electrons, n, (and protons) that have been delivered during their formation is unknown. Consequently, such intermediates are untethered from the commonly accepted Lowe–Thorneley (LT) kinetic schemes for reduction by nitrogenase. The issue is that the LT scheme for N₂ reduction, shown in part in Fig. 1, is formulated in terms of the conversion among intermediate states of the MoFe protein that are indexed by n and denoted E_n (1, 2). The problem is that n for an intermediate trapped nonsynchronously cannot in general be determined spectroscopically. The difficulty is that the n electrons accumulated by the MoFe protein can partition themselves between the substrate and FeMo-co, with the possibility that the P cluster of the MoFe protein, which mediates electron flow from Fe proteins (1), is involved as well. The “electron inventory” of the MoFe protein trapped in an intermediate state during turnover can be written: n = s + m − p, where s is the number of electrons that have been delivered to substrate, m is the number of electrons by which the cofactor of the intermediate is reduced relative to resting state, and p is the number of electrons by which the P cluster has been oxidized (p < 0 would mean the P cluster has been reduced relative to the resting state) (8). In favorable cases, s can be determined by ENDOR examination of the substrate-derived species bound to the FeMo-co of the intermediate (8). However, the spectroscopic determination of m, for example by ⁵⁷Fe and ^95,97Mo ENDOR studies, is blocked by the lack of an interpretative framework grounded in a firm understanding of the electronic structure of FeMo-co, whereas little is known about the involvement of P cluster.

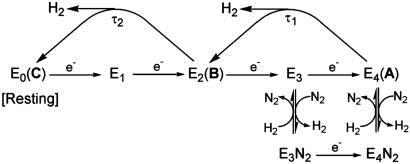
Fig. 1.

Modified LT kinetic scheme for the first half of the N₂ reduction cycle. Intermediates, E_n, are labeled by the number of electrons (n) transferred to the MoFe protein. Each reduction step is thought to involve delivery of both a proton and an electron; the protons are omitted. Proposed correspondences between EPR-active states, A, B, and C and E_n kinetic intermediates are shown. The τ_i represent relaxation times as discussed in the text.

We here describe a kinetic relaxation procedure for determining the E_n state of a trapped intermediate. It is founded on the recognition that no matter how an intermediate state of the MoFe protein has been trapped, it has accumulated a specific number of electrons, n, and it is in a specific E_n state. Thus, it acts as a “synchronously prepared” initial state. In particular, we hypothesized that n for an intermediate state early in the kinetic scheme (Fig. 1) could be revealed by following its “synchronous” relaxation back to the resting state (E₀) through the loss of one or more equivalents of H₂. This approach, of course, requires experimental conditions that guarantee that no additional electrons are transferred from Fe protein to MoFe protein during the relaxation. However, ET from the Fe protein to the MoFe protein absolutely requires dissociation/association of the Fe–MoFe protein complex (1, 2), and we recognized that this ET would be abolished if Fe–MoFe association/dissociation were prevented by keeping the sample frozen.

These considerations led us to the following relaxation protocol. An intermediate is first trapped by 77 K freezing of the enzyme under turnover conditions, and its “zero-time” EPR signal is measured at 2 K. Its solid-phase relaxation at a desired temperature is then monitored by step-annealing the sample (see Materials and Methods) to that temperature for predetermined intervals, t_i, followed by cooling to 2 K to measure by EPR spectroscopy the new concentrations of all EPR-active species after the t_i intervals (9, 10). To confirm that observed reactions indeed occur without transfer of electrons from the Fe to the MoFe protein, the EPR signal of the Fe protein is monitored in parallel: ET would be revealed as an oxidation of the reduced Fe protein and diminution of its EPR signal. Of particular importance, kinetic isotope effects (KIEs) can be determined by comparing results for samples prepared with H₂O and D₂O buffers, and used to characterize bond-making/breaking of hydrogen(s) in the rate-limiting step of the transformations (11, 12), which is expected according to Fig. 1. This step-annealing approach (9) is unique in that the KIE for an individual kinetic step can be measured directly by monitoring reactant and product, rather than being deduced from complicated kinetic analyses.

The relaxation protocol is applied here to the “H⁺/H⁻” intermediate (denoted A) that was first trapped during turnover of the α-70^Ile MoFe protein under Ar and was shown by ENDOR spectroscopy to have two protons or hydrides bound to an S = 1/2 state of FeMo-co (4). Since then, we have observed this intermediate during turnover of the wild-type enzyme both in the presence and absence of N₂ as substrate, which implicates this intermediate as part of the natural workings of the native enzyme during normal catalysis of N₂ reduction. ENDOR spectroscopy showed that FeMo-co of this intermediate binds two chemically equivalent and symmetry-related hydrogenic species that have quite surprisingly large hyperfine coupling constants.

Because H⁺/H⁻-bound FeMo-co of A is EPR-active, S = 1/2, the electron count of the active site of A can differ from that of the EPR-active, S = 3/2, resting state only by an even number of electrons: m + s = even. The resting-state P cluster is even-spin and EPR-silent. We have searched for and failed to detect a half-integer-spin EPR signal from A for a P cluster that has been oxidized/reduced by an odd number of electrons, so we conclude that the P cluster of A can differ from that of the resting state only by an even number of electrons: p = even. As a result of this “electron inventory” (8), we may then conclude: n = m + s − p = even. Setting aside as unlikely the possibilities that A contains a protonated resting state of FeMo-co and has n = 0, or that A is the “over-reduced” state with n = 6, then the LT scheme, Fig. 1, offers only two possible assignments. The intuitive “first-guess” would postulate the lesser electron accumulation, and assign this intermediate as E₂, in which FeMo-co has accepted n = 2 electrons from Fe protein and bound two H⁺ to generate bridging μ₂-SH. However, we argued that μ₂-SH could not give the observed large ^1,2H coupling constants, and further thought a μ₃-SH to be unlikely on energetic and hyperfine-coupling grounds. As a result, we turned to models that involve metal-bound hydrides. But such models likely would involve more highly reduced states of the FeMo-co, opening the possibility that A is E₄ and has accumulated n = 4 electrons. According to Fig. 1, there should be a clear distinction in the relaxation behaviors of E₂ and E₄: the former should relax to the resting E₀ state in a single step, with the production of H₂; the latter in two steps, both with H₂ generation. In fact, the present results provide powerful evidence for the central importance of the H⁺/H⁻ intermediate in the reduction of N₂ by nitrogenase by implicating it as the catalytically central E₄ state (Fig. 1) that has been activated for N₂ binding by the accumulation of n = 4 electrons (1).

Results

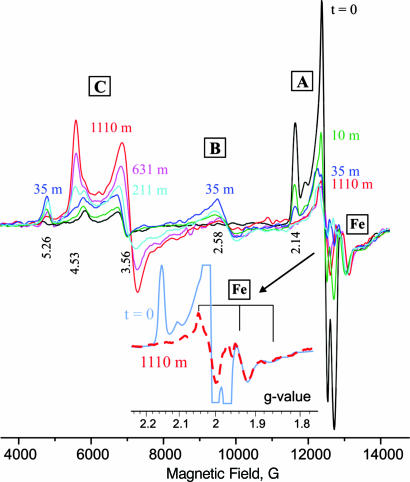
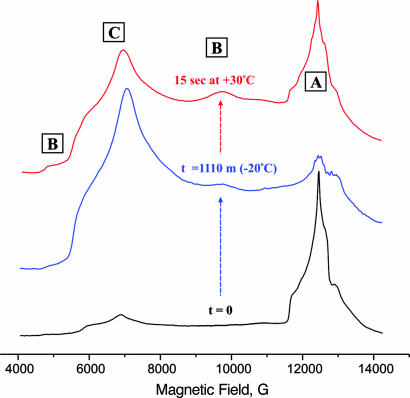
The α-70^Ile MoFe protein was used here because it exhibits the highest concentration of trapped H^+/− intermediate when turned over under Ar. Its resting state contains FeMo-co in the characteristic S = 3/2 resting state (here denoted, C), with g-tensor, g^C = [4.53, 3.56, 2.00] (Fig. 2). When the enzyme is freeze-quenched during turnover under Ar, this signal is almost completely abolished and there appears the “t = 0” EPR signal of the S = 1/2 H⁺/H⁻ intermediate A, with g^A = [2.14, 2.00, 1.96] (Fig. 2); underlying the A signal and to high field of it is the EPR signal from reduced Fe protein (Fig. 2 Inset). When the sample is step-annealed at 253 K, the signal from A progressively decreases, whereas that from the Fe protein remains unchanged (Fig. 2), thereby establishing that A indeed relaxes in the 253 K frozen sample and that this reaction is not coupled to ET from Fe protein to MoFe protein.

Fig. 2.

Digital derivatives of EPR spectra collected from freeze-quenched α-70^Ile H^+/− intermediate (“t = 0”) and after 10, 35, 211, 631, and 1,110 min of step-annealing at T = 253 K. (Inset) Expansion of g-2 region for t = 0, and 1,110-min spectra, showing that the nonoverlapped regions of the Fe protein signal (g₂-g₃) are essentially coincident, hence, the amount of reduced Fe-protein is indeed unchanging during step-annealing. Conditions: microwave frequency = 35.016–35.289 GHz; power = 0.32 mW; modulation amplitude = 1.3 G; T = 2 K.

Relaxation of the H⁺/H⁻ Intermediate (A).

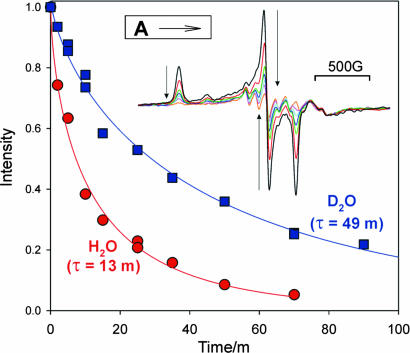
The relaxation time courses for A prepared with H₂O and D₂O buffers are presented in Fig. 3. Initial fit attempts showed that the decays are not exponential. Such behavior is seen when the observed species exists as a distribution of conformational substates, with the decay constant varying somewhat over the distribution (13). As a result, the effective first-order rate coefficient appears to decrease in time; in fact, the more reactive substates decay early, leaving those with lower decay rates to react later. This situation can be modeled with a “stretched exponential,” I^A(t) = I₀exp(−(t/τ)^a), where τ is the decay time and the breadth of the distribution is reflected in the constant, 0 < a ≤ 1, with smaller values for a corresponding to greater breadth. This equation fits the relaxations of A in both H and D isotopic buffers with a = 0.71 (Fig. 3). The decay times yield a KIE, KIE(253 K)₁ = τ₁(D₂O)/τ₁(H₂O) = 49 min/13 min = 3.8 (85% D₂O). An alternate fit as a biexponential gives 50% each of two kinetic phases, both with KIE ≈ 3. The slowing of the decay in D₂O buffer is not merely an overall influence of D₂O on the enzyme, for the corresponding relaxation of at least one other freeze-quench intermediate is unchanged in D₂O (D.L., unpublished data). The KIE for the relaxation of A is larger than expected for a solvent KIE (9–11, 14, 15). Given that the H⁺/H⁻ intermediate (i) is trapped during conditions of H₂ production and (ii) has two H⁺/H⁻ bound to FeMo-co (4), we interpret the large KIE₁ to mean that the reduced FeMo-co of A relaxes with formation of H₂ from the two H⁺/H⁻, as expected from the LT scheme for N₂ reduction: as shown in Fig. 1, both EPR-active (two-electron reduced) intermediates that might be involved are expected to relax by H₂ production.

Fig. 3.

Relaxation of intermediate A at 253 K in H₂O and D₂O buffer. Intensities were obtained from digital derivatives of EPR spectra and normalized to the t = 0 EPR signal. Solid lines are the results of fits to stretched exponential (see text): a₁ = 0.71, τ₁(H₂O) = 13 min, τ₁(D₂O) = 49 min. (Inset) Digital derivatives of EPR spectra of A during annealing.

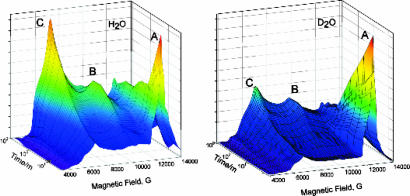
The spectra of Fig. 2 not only show the disappearance of A and the appearance of the resting state, C, but also show the appearance and disappearance of a signal from a new state, B; it has a highly rhombic g tensor, g^B = [5.26, 2.58, -] from S = 3/2 FeMo-co. [Careful examination disclosed no signals that could be assigned to the other cluster in the MoFe protein, the P cluster.] Numerous spectra were collected during the annealing of samples prepared with H₂O and D₂O buffers, and 3D plots of the time variation of those spectra (Fig. 4) demonstrate that the appearance of B follows the loss of A and precedes the appearance of C, indicative of sequential A → B → C relaxation.

Fig. 4.

Three-dimensional plot of EPR spectra collected during the stepwise annealing of α-70^Ile H^+/− intermediate at 253K in H₂O (Left) and D₂O (Right). Major features for each species A, B, and C are labeled. To aid the eye, the usual “rainbow” color scheme is used, with orange corresponding to the highest EPR intensity and blue corresponding to the lowest.

Raising A.

Before discussing the relaxation data in detail, we describe an experiment that was designed to test whether the quench/step-anneal protocol is benign, and that was suggested by considerations of the enzymatic status of a sample that has undergone long-time annealing. The EPR spectrum of such a sample (H₂O; 1,110 min of annealing at 253 K; Figs. 2 and 4) shows that the A state is long gone, B is nearly gone, and the C resting state is substantially recovered. The intensity of the reduced Fe-protein signal did not change during this annealing period, which means that there are reducing equivalents present for further turnover if Fe → MoFe electron transfer were to be reenabled, and considerable ATP remains to drive this ET. Thus, if the enzyme is undamaged by the step-annealing process, then restoration of the association/dissociation needed for ET from Fe to MoFe by merely thawing the sample should regenerate A for freeze-quench trapping (see ref. 16). In fact, this happens. Fig. 5 presents the 2 K spectrum of a sample that was step-annealed for 1,110 min, thawed, and turned over for ≈15 s at 30°C, then freeze-quenched at 77 K. As seen in Fig. 5, this variant trapping procedure raises the A signal to over ≈1/2 its “t = 0” intensity in the original turnover sample. The C signal, although still less than that of the resting-state MoFe (not shown), is more intense than that in the t = 0 spectrum of the original freeze-quench sample, whereas the B signal is more intense than it is at the end of the annealing. The EPR intensities confirm that much of the FeMo-co of the initial freeze-quench sample was in EPR-silent states (e.g., E₁). The differences between the species distribution in quenched and “requenched” samples presumably arise because the two differ in turnover time and temperature. When a quenched sample is thawed to 30°C, kept at that temperature until the ATP is depleted, then quench-frozen, its 2 K EPR spectrum shows the full signal of resting MoFe protein, C, as expected.

Fig. 5.

EPR spectra showing that the α-70^Ile H^+/− intermediate A (Bottom) is lost with complete annealing, to produce a sample with signals from C and residual B (Middle), and that A is “raised” with simultaneous diminution of resting state signal C and increase of B signal if the annealed sample is turned over at +30°C for ≈15 s and quench-frozen (Top).

Full Kinetic Analysis.

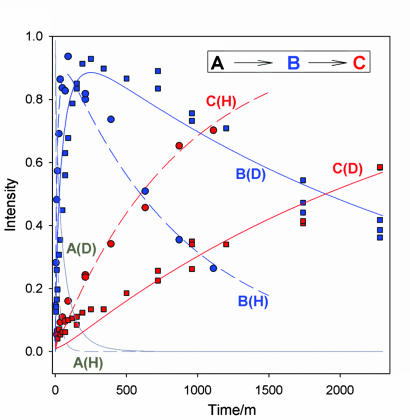
We can describe the time courses for the three intermediates in H₂O and D₂O buffers (Fig. 6) with a single set of coupled differential equations for an A → B → C kinetic scheme where the equations allow for “stretched-exponential” decays of both A and B. The equations for A and B incorporate first-order decays, where the rate coefficients decrease in time and are characterized by decay times, τ_i, and coefficients, 0 < a_i ≤ 1 (17).

If C forms only through A → B → C relaxation, without, for example, a contribution from relaxation of EPR-silent states that are present in the initially quenched sample, then the corresponding time course for C is obtained from those for A and B through the (normalized) equation for the conservation of FeMo protein within the A, B, and C states,

Fig. 6.

Relaxation progress curves for the three intermediates in H₂O and D₂O and their fits to eqs 2–4. Parameters: a₁ = 0.71, τ₁(H₂O) = 13 min, τ₁(D₂O) = 49 min; a₂ = 1 (exponential), τ₂(H₂O) = 870 min, τ₂(D₂O) = 2,700 min. For clarity, data points for A have been omitted (see Fig. 2).

Despite the considerable difficulty in quantitating the strongly overlapping EPR signals of the B and C states, the complete set of relaxation measurements in both D₂O and H₂O buffers is quite satisfactorily described by Eqs. 2–4, as shown by the overlap of calculated and measured progress curves (Fig. 6). In the calculations, we set a₁ = 0.71, the value obtained above; a₂ was indistinguishable from unity (1 ≥ a₂ > 0.8) and we set a₂ = 1. The difference between a₁ and a₂ presumably reflects the fact that B forms at 253 K in the solid, whereas A is formed at ambient and quench-frozen. The B → C relaxation times correspond to KIE₂ = τ₂(D₂O)/τ₂(H₂O) = 2,700 min/870 min = 3.1 (85% D₂O), comparable to that for A → B relaxation, KIE₁ = 3.8 (see above).

Discussion

What, then, are: (i) the E_n identifications (n even) of the H⁺/H⁻ intermediate, A, and of the state to which it relaxes, B; (ii) the nature of the A → B → C relaxation processes? As shown in Fig. 1, if A were E₂, it would relax to resting FeMo-co (E₀) with the two-electron/proton loss of H₂, consistent with the large KIE for the decay of A.^¶ However, A could be E₂ only if the S = 3/2 state B to which it relaxes has the resting FeMo-co electron count (n = 0), which would require B to be a metastable conformational substate of the resting (E₀) enzyme, rather than a distinct MoFe state. However, there is more B present after regeneration of the annealed sample than at the end of the initial annealing (Fig. 5), although it is unlikely that a metastable conformational substate could be trapped during the relatively slow process of hand-quenching after regeneration. Furthermore, the KIE for the B → C relaxation process is larger than could be expected (18) for conformational relaxation of metastable resting (E₀) MoFe protein in the frozen state, and implies that the rate-limiting step involves transfer of a solvent-derived proton. Together, these observations lead us to propose that B not an E₀ conformer, but is a chemically distinct FeMo-co state.

If the EPR-active H⁺/H⁻ intermediate A relaxes to an EPR-active state that is not E₀, then A cannot be E₂, and must be a more highly reduced state: E_n, n ≥ 4; even. Clearly, the compelling assignment for A then becomes E₄ (Fig. 1), thought to be the most probable state for N₂ to bind (1). Indeed, viewed in terms of the LT kinetic mechanism for N₂ reduction, E₄ is the state that “should” accumulate during turnover under Ar in the absence of N₂, as it is the kinetic stage where proton and N₂ reduction compete. The identification A = E₄ in turn leads to the assignment, B = E₂. Both FeMo-co in the relaxations, E₄(A) → E₂(B) and E₂(B) → E₀(C), should occur with the loss of H₂ (Fig. 1), consistent with the KIE ≈ 3–4 (85% D₂O) for both steps.^‖

Although a high-spin FeMo-co (S = 3/2) state for FeMo-co of B = E₂ contrasts with the S = 1/2 state of CO-bound FeMo-co in turnover intermediates also assigned as E₂ (8), other strongly rhombic S = 3/2 signals have been assigned to reduced FeMo-co, with m = n ≥ 2 (even) and presumably n = 2 (19, 20). The unsurprising implication of this variability is that the spin state of the multimetallic m = 2 FeMo-co can be controlled by the number and nature of metal-bound ligands, just as with mononuclear centers.

Conclusions

By monitoring the relaxation of the nitrogenase H⁺/H⁻ intermediate (A) during step-annealing we have arrived at the assignments of A as E₄ and of the newly observed B as E₂ (Fig. 1). The resulting interpretation of the observed two-step relaxation of A, summarized in Eq. 5,

is the reverse of the steps that activate FeMo-co for N₂ binding and subsequent reduction, Fig. 1. The hydrogens that form H₂ during the A → B relaxation undoubtedly are the two H^+/− characterized previously by ^1,2H ENDOR; whether the protons associated with B → C conversions are already bound to the cofactor or are recruited during relaxation can, in principle, be determined with ^1,2H ENDOR studies of B. In either case, if the apparent difference between the KIE for the two steps of H₂ production is substantiated, could reflect different binding modes of H⁺/H⁻ in E₄(A) and E₂(B). Additional relaxation and ENDOR experiments are planned to rigorously test the present proposals, which undoubtedly will stimulate further theoretical investigations of nitrogenase intermediate states, as well. The protocol described here will be used in efforts to integrate N₂ reduction intermediates into kinetic schemes and molecular mechanisms for NH₃ formation, thereby providing further powerful insights into the mechanism by which nitrogenase reduces N₂.

Materials and Methods

The Azotobacter vinelandii strain DJ1373 expressing the α-70^Ile variant MoFe protein was grown and the protein prepared as described (4). The MoFe protein was concentrated to 150 μM in Mops buffer at pH 7.1 in the standard EPR turnover buffer (4) with 150 mM NaCl added to avoid precipitation of the protein at high concentrations. A separate set of “D₂O” samples was prepared at pD = 7.1 by exchanging and concentrating the MoFe protein into turnover buffer prepared with D₂O at pH 6.7, as read by pH meter (12). This exchange should result in a buffer that is ≈85% D₂O. Multiple turnover samples of each solution were prepared by adding Fe protein from a concentrated stock to a final concentration of 120 μM, and immediately flash freezing.

A step-annealing stage involved rapidly warming a sample held at ≤77 K to 253 K by placement for a fixed time in a methanol bath held at that temperature, quench-cooling back to 77 K, and then collecting a 2 K EPR spectrum. EPR spectra were taken with a 35-GHz spectrometer as described (21). Step-annealing procedures were first perfected by Davydov during studies of the reaction of active-oxygen intermediates that had been directly generated in a 77 K sample by radiolytic cryoreduction (9, 10).

The annealing temperature of 253 K was chosen because, at that temperature and below, annealing caused no changes in the intensity of the Fe-protein EPR signal (see Fig. 2, especially Inset), but relaxation at 243 K or below is too slow to be followed conveniently. During annealing at 263 K, the signal from the Fe protein changes intensity, indicating that ET is allowed in the “frozen solid,” presumably because pools of liquid form between “ice grains.”

The 2 K EPR spectra are obtained under “rapid passage” conditions and appear as absorption signals. Their digital derivatives were normalized using the Fe protein signal as a standard and quantitative changes of individual EPR signals were determined as intensity changes of their g₁ or g₂ features. The solutions of the kinetic equations of annealing/relaxation (Eqs. 2–4), were generated in Mathcad.

Abbreviations

FeMo-co

iron-molybdenum cofactor

ET

electron transfer

LT

Lowe–Thorneley

KIE

kinetic isotope effect.