Corticothalamic feedback enhances stimulus response precision in the visual system

Abstract

There is a tightly coupled bidirectional interaction between visual cortex and visual thalamus [lateral geniculate nucleus (LGN)]. Using drifting sinusoidal grating stimuli, we compared the response of cells in the LGN with and without feedback from the visual cortex. Raster plots revealed a striking difference in the response pattern of cells with and without feedback. This difference was reflected in the results from computing vector sum plots and the ratio of zero harmonic to the fundamental harmonic of the fast Fourier transform (FFT) for these responses. The variability of responses assessed by using the Fano factor was also different for the two groups, with the cells without feedback showing higher variability. We examined the covariance of these measures between pairs of simultaneously recorded cells with and without feedback, and they were much more strongly positively correlated with feedback. We constructed orientation tuning curves from the central 5 ms in the raw cross-correlograms of the outputs of pairs of LGN cells, and these curves revealed much sharper tuning with feedback. We discuss the significance of these data for cortical function and suggest that the precision in stimulus-linked firing in the LGN appears as an emergent factor from the corticothalamic interaction.

The patterning of activity in the brain, whether by the grouping of action potentials or synchronization of firing across sets of neurons, can have a major impact on the effectiveness with which information is transferred to other brain areas (1, 2). Common to many sensory pathways, both burst firing and tightly timed mono- and/or heterosynaptic inputs have been argued to increase the effectiveness with which thalamic input can drive the cortex (3–7). In the visual system heterosynaptic thalamic inputs from the dorsal lateral geniculate nucleus (LGN) that fall within 5 ms of each other exhibit a supralinear enhancement of transmission to visual cortical simple cells (7). The ability of visual stimuli to generate heterosynaptic facilitation from the convergent inputs of LGN cells on cortical cells will depend on the precision in the way the LGN cells respond to visual stimuli. We know that the corticofugal feedback to the thalamus has a strong influence on this patterning via direct connections to the thalamus and thalamic reticular nucleus (8–14). In many ways the thalamus, thalamic reticular nucleus, and cortex form part of a circuit rather than distinct steps in an ascending system. How does this interaction serve to refine the way the thalamus accesses the cortex?

Clearly, the precision in the timing and structure of the firing pattern to visual stimuli is critically important in understanding their neural representation and impact. One can hypothesize that the contrast edges of a complex object moving through visual space could provoke synchronous firing in groups of thalamic cells that optimally drive the representation in the cortical network. Surprisingly, it is not clear how sensitive the output of the LGN relay cells are to such a stimulus, and, indeed, there is little work directly addressing stimulus-linked timing in the visual system. Even considering the simple case of a moving contour, such as a bar of light, we have little direct evidence on the firing pattern of cells aligned along the axis of the contour. It is assumed that such a contour will drive the receptive fields of LGN cells aligned along its axis simultaneously [as in the classic model of Hubel and Wiesel (15)], but the specific response characteristics are unknown. Is the nature of this synchronization such that it could usefully provoke heterosynaptic facilitation in the cortex? How sensitive is it to a change in stimulus parameters?

In this article, we examine the precision of the firing patterns of cells in the A laminae of the LGN to moving stimuli in the presence and absence of all feedback from the visual cortex. Our data show clear differences in the firing patterns of LGN cells. To place the observations in the context of cortical mechanisms, we consider the sensitivity of pairs of LGN cells with spatially displaced receptive fields to variations in orientation of a contour crossing their receptive fields. We quantify the precision in the synchronization by plotting tuning curves from the synchronized spikes as we vary the orientation of the drifting contour in small steps which serve to create a varying delay in the timing of the arrival of the contour over one receptive field with respect to the other. Our data show a remarkable difference in the precision of the responses of LGN cells with and without corticofugal feedback. This result documents an emergent temporal precision for moving stimuli from the operation of the cortico-geniculate-geniculo-cortical circuit as a whole. We discuss the mechanisms that may underlie this process and their functional implications.

Results

Response Pattern of LGN Cells With and Without Feedback.

We took quantitative data on the responses to the test drifting sinusoidal grating from 97 cells in the A laminae of the LGN, comprising 45 cells recorded in the presence of feedback and 52 cells recorded without feedback. The data are summarized in Fig. 1. To analyze the pattern of firing to the stimulus, we computed the vector sum, Fourier ratio, and Fano factor (see supporting information (SI) Methods) individually from spike trains and their resultant phase plots.

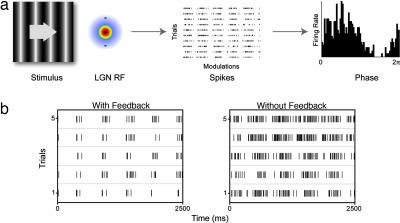
Fig. 1.

Experimental paradigm. (a) Responses to drifting gratings were analyzed for response structure and reliability. Example raster and resultant phase plots are derived from a modulated Poisson spiking model. (b) Data raster plots for a cell with (Left) and without (Right) cortical feedback.

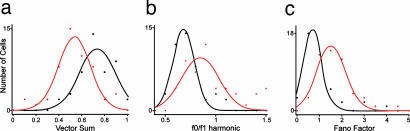
Fig. 1b shows examples of spike rasters obtained respectively from cells with and without cortical feedback. The rasters show five modulations (in which one modulation is a complete sinusoid) and five trials for both cells. There was a marked difference in the appearance of the raster plots with and without feedback and it seems that the responses in the absence of feedback were less closely linked to the stimulus and more variable. As a first step in quantifying these differences in the firing pattern of the LGN cells, we constructed phase plots wrapped to the stimulus modulation, and then calculated the vector sum, which can vary from 0 for a uniform distribution of responses (no modulation linked to the stimulus phase), to 1 where all responses are concentrated in a single bin (highly transient response). The mean/median vector sums were 0.72/0.73 (±0.11 SE) for the cells with feedback compared with 0.55/0.55 (±0.11 SE) for cells without cortical feedback (Fig. 2a). These values were highly significantly different (P < 0.001; Wilcoxon rank sum). One can estimate the vector sum expected for a standard Poisson process modulated spike generator using the same stimulus parameters. The average vector sum over 1,000 iterations in this case was 0.50 (±0.03 bootstrapped 95% confidence interval), closer to the average without feedback than the control average (an example Poisson modulated response spike raster and resultant phase plot is illustrated in Fig. 1a). Another estimate of response change to the stimulus is the ratio of the zero harmonic to the fundamental harmonic of the fast Fourier transform (FFT) (Fig. 2b) where values <1 suggest more power in the modulated response than the mean response. This difference was also highly significantly different (P < 0.001); the mean/median with feedback was 0.72/0.68 (±0.02 SE) compared with 1.19/0.91 (±0.16 SE) for the cells without feedback.

Fig. 2.

Gaussian fitted population histograms. Distributions were highly significantly different between control (black) and feedback removed (red) samples for vector sum (a), Fourier ratio (b), and Fano factor (c) (P < 0.001; Kolmogorov–Smirnov two-sample test).

These data show that responses for LGN cells with feedback were more reliable and differently structured from those recorded without. To examine this matter further, we used the Fano factor (computed as the variance in the spike count in each modulation cycle divided by the mean) estimated over the modulation window to assess the reliability (or variability) of the response to repeated presentations of the stimulus. This value will be higher if there is a large variance in response for a given mean level of firing, so it provides a measure of the relative variability. The Fano factor for a Poisson process is 1; thus, values <1 and values >1 suggest lower and higher variability than a Poisson process, respectively. There was a highly significant increase (P < 0.001) in the Fano factor (Fig. 2c), from a mean/median value of 0.97/0.77 (±0.11 SE) for cells with feedback to 1.68/1.50 (±0.11 SE) for cells without feedback. Although it is known that variability is reduced for higher response magnitudes (16), for our data, the mean/median responses for the with-feedback cell group were somewhat lower at 13.0/10.4 spikes per second (s/s ± 1.22 SE) than those for the without-feedback group [19.1/17.8 s/s (±1.46 SE), P < 0.005]. Thus, if the difference in Fano factor we observed simply linked to a shift in response magnitude, we would have expected to see a decrease, rather than the observed increase, in Fano factor for the cells without feedback. Spontaneous rates were not significantly different, with mean/median control values of 2.8/2.1 s/s (±0.49 SE) compared with 3.2/2.5 s/s (±0.44 SE) for those without feedback (P = 0.46). We also assessed whether there was a difference in the number of spikes contained within bursts (see SI Methods) between the two groups. We found no significant difference between the average number of bursts per stimulus presentation for the cells with and without feedback (P = 0.38).

Finally, we were interested to see whether there was a difference in the covariation of these measures for simultaneously recorded cell pairs with and without feedback. Indeed, there was for all measures. For the vector sum, the pairs of cells with feedback were highly significantly positively correlated at an r = 0.75 (P < 0.001; two-tailed Spearman), but this correlation dropped to r = 0.38 (P = 0.05) for those without feedback. The difference between these correlation coefficients was significantly different (P < 0.05; Fisher's Z test). This pattern was also the case for the Fourier ratio, where the correlation dropped from r = 0.7 (P < 0.001), to r = 0.25 (P = 0.14 correlation coefficients differed at P < 0.05; Fisher's Z test). In similar vein, the Fano factor values for the pairs of cells with feedback were clearly positively correlated with an r = 0.73 (P < 0.001) whereas for those without feedback the values for the positive correlation dropped to r = 0.31, which was not significant (P = 0.12), and there was a significant difference between the correlation coefficients for the two populations (P < 0.05; Fisher's Z test). These data are summarized in SI Fig. 9.

Synchronization of Firing Pattern Between Simultaneously Recorded Cell Pairs.

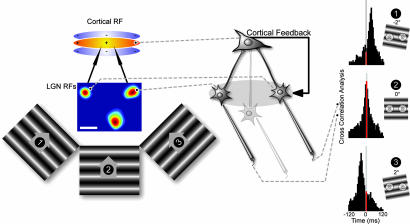
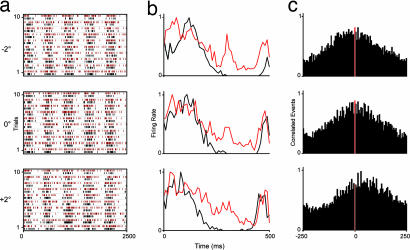
A key issue following from the precision in LGN cell responses to visual stimuli is the way the activity of groups of LGN cells relates and synchronizes when stimulated by moving contours defining the edges of an object. The simple example of this effect is the responses of pairs of cells to an elongated contour of varying orientation (Fig. 3) as in the feed-forward model of orientation tuning (15). They will be coactivated by the stimulus when it is at the “linking” angle. The question is how precise is the sensitivity of this tuning to small variations in the orientation of the stimulus around the linking angle? Raw cross-correlograms were computed from the responses of pairs of LGN cells to a range of orientations for 53 cell pairs. Of these cell pairs, 24 were studied in the presence of feedback and 29 were studied after blockade of cortical feedback. Figs. 4 and 5 show the spike rasters, peri-stimulus time histograms (PSTHs), and resultant raw cross correlograms for example pairs with (Fig. 4) and without (Fig. 5) feedback. The red portion in the cross-correlograms highlights a 5-ms window centered at zero lag and thus encompasses those spikes that might generate a supralinear enhancement of transmission. We used raw cross-correlograms for all of the observations because this approach reflects the input “seen” by a simple cell. It is clear from the cross correlograms that a small shift in the orientation of the grating (±2°) either side of the linking angle shifted the location of the peak in the cross correlation function and changed the count in the red heterosynaptic integration window much more substantially for the with-feedback than for the without-feedback cell pair.

Fig. 3.

Raw cross-correlograms were calculated from the responses of simultaneously recorded LGN cells to drifting gratings of varying orientation. (Left and Center) Stimulus configuration and example receptive field plots (scale bar 1°). (Right) Cross-correlograms from a pair of LGN cells recorded in the presence of cortical feedback for three orientations (−2°, 0°, +2°). Shift in correlogram peak with stimulus angle, 15.4 ms/°. Red shading highlights a 5-ms window centered at zero lag.

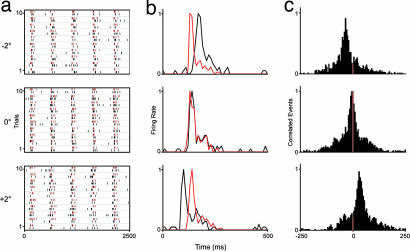
Fig. 4.

Responses of a pair of control LGN cells to three grating orientations (−2°, 0°, +2°). Shown are raster plots (a), normalized PSTHs (b), and normalized cross-correlograms (500-ms window; y axis, normalized correlated events) (c). In a and b, red and black differentiate responses of the two cells. Grating contrast 0.36, spatial frequency 0.66 cycles/°, temporal frequency 2 Hz, 10 trials, five stimulus modulations.

Fig. 5.

Responses of a pair of LGN cells without feedback. Shown are raster plots (a), normalized PSTHs (b), and normalized cross-correlograms (c). Conventions and stimulus details are as in Fig. 4.

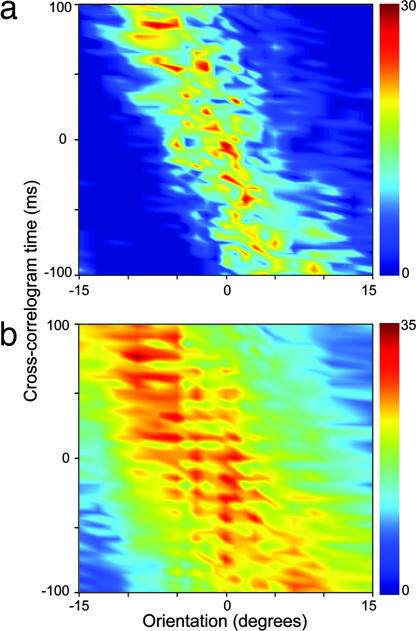
The effects of the response changes on the correlogram peak can be best visualized in the type of plot in Fig. 6a. Here, for another pair of cells with feedback, we show a surface representation of the cross-correlogram time on the y axis against orientation on the x axis [the whole set of correlograms for all orientations are represented as a surface where color represents the magnitude of correlated events from low (dark blue) to high (dark red)]. The peak of the cross-correlogram moved through the time domain as the orientation varied and was clearly very sensitive to the variation of orientation. Our sample of cell pairs with feedback exhibited a mean/median shift in the peak of the cross-correlogram of 15.5/15.0 ms/° (±1.46 SE). Fig. 6b shows the same format for a cell pair without feedback; there is a much broader spread of correlated spikes across the range of orientations suggesting a marked degradation of the link between correlated spikes and orientation (reflected in the half width at half height of the orientation tuning curves; see below). The mean/median shift of the peak of the cross-correlogram with orientation was 9.6/8.5 ms/° (±1.04 SE) for the without-feedback sample, which was significantly different to the values for the with-feedback group (P < 0.005; Wilcoxon rank sum). A further example of a control surface can be seen in Fig. 7a together with additional examples of surfaces for data with and without feedback in SI Fig. 10.

Fig. 6.

Surface plots of cross-correlogram data (y axis) versus orientation (x axis, degrees) for pairs of LGN cells recorded with (a) and without (b) cortical feedback. Color scale, number of raw correlated events. Stimulus details are as in Fig. 4. (a) Receptive field (RF) separation = 1.8°; mean correlogram shift = 14.6 ms/°. (b) RF separation = 2.3°; mean shift = 9.9ms/°.

Fig. 7.

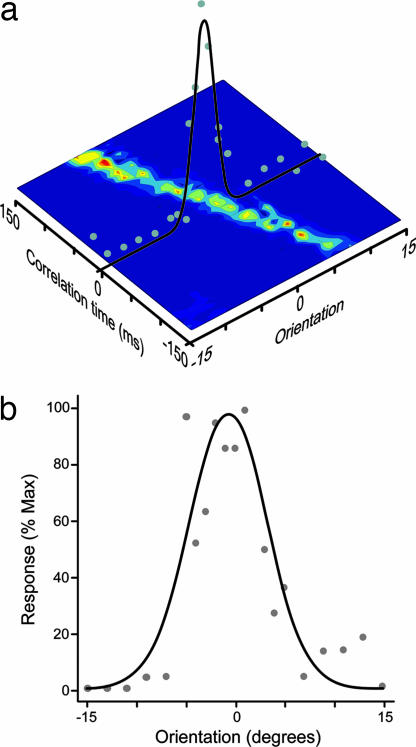
Tuning curves for orientation selectivity derived from the correlated spikes. (a) Schematic detailing how the tuning curves were constructed via the surface representations. (b) Tuning curve derived from a 5-ms integration window from a control cell pair (same pair as Fig. 6a), tuning half-width 4.1°, which was close to the mean of the control data (4.7° ± 0.52 SE).

We constructed orientation tuning curves from a 5 ms window around zero lag as illustrated by the orientation tuning curve over the surface plot (Fig. 7a). Examples of orientation tuning curves from cell pairs with feedback are given in Fig. 7 a and b. In all these curves zero degrees in the orientation tuning curve represents the linking angle for the two cells (see Methods). The “sharpness” of orientation tuning is frequently quantified by measuring the half-width at half-height of an orientation tuning curve. The mean/median tuning half-width derived from the correlated events in the central 5-ms integration window from our data for all cell pairs with feedback was 4.7/4.6° (± 0.52 SE). For the 29 cell pairs studied in the absence of feedback, the mean/median tuning half-width for the population was 12.2/12.0° (±0.99 SE). This value was highly significantly different to the with-feedback group (P < 0.001). We also compared the half-width half-height measurements for tuning curves derived using a 20ms correlation window. There was no significant difference between the values obtained with 5 and 20 ms windows for either the sample with (4.9/5.2° ± 0.51 SE, P = 0.51) or without (12.7/11.8° ± 1.13 SE, P = 0.78) feedback.

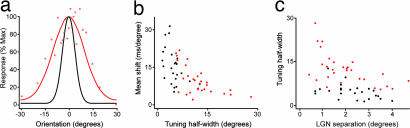
The clear differences in both tuning width, and the shift in correlogram peak with time, between the samples with and without feedback are highlighted in the scatter plot in Fig. 8b. The differences between the data for cells with and without feedback could reflect the fact that we sampled cell pairs with different separations. In fact, we were careful to ensure that we sampled cell pairs with a similar range of separations as the scatter plot in Fig. 8c shows. One would predict that the tuning should be sharper for cell pairs with larger receptive field separations. Indeed, the tuning for the group without feedback degraded notably as the separation between the fields decreased, and there was a highly significant negative correlation between receptive field separation and tuning width (r = −0.56, P < 0.005; two-tailed Spearman). Overall the control group showed a consistently sharper tuning for all separations (r = −0.43, P < 0.05), but the ratio of the difference in tuning between the two groups was broadly sustained across the range of separations. We confirmed that the difference in tuning half-width between the groups with and without feedback was still significant after controlling for the influence of receptive field separation (F_1,50 = 45.25, P < 0.001, analysis of covariance).

Fig. 8.

Effects of removing cortical feedback. (a) Red tuning curve derived from a 5-ms integration window for a cell pair without feedback (same pair as Fig. 6b), tuning half-width 13.0°, which was close to the mean of the data for the cells without feedback (12.2° ± 0.99). For comparison, the tuning curve of the control cell pair shown in Fig. 7b is replotted on the same axes. (b) Scatter plot of tuning half-width versus mean shift of cross-correlogram peak with orientation. Control data are black, and feedback removed data are red. (c) Scatter plot of tuning half-width versus LGN cell center-to-center separation.

Discussion

Our results show a striking distinction between the way LGN cells respond to a visual stimulus in the presence and absence of feedback from the visual cortex. These differences were highly statistically significant and seemed to profile a marked enhancement of the temporal and spatial resolution of the system in the presence of feedback. They map a signal that is salient for the cortical mechanism and at the same time provide an index of the resolution of the system for the spatial alignment of a stimulus across LGN cell receptive fields. The effect of the feedback was apparent when comparing raster plots of single cells to a drifting grating and showed quantitatively as a highly statistically significant difference in the vector plots calculated from phase plots wrapped to the stimulus modulation. Interestingly, the data for the cells without feedback most approximated the vector sum expected for a standard Poisson process modulated spike generator. Another way of looking at the way the response links to the stimulus is the ratio of the zero harmonic to the fundamental harmonic of the FFT in the response. The cells with feedback showed significantly more power in the modulated response than those without. A corollary of these changes is that the reliability of the response of the cells with feedback should be higher. Indeed, using the Fano factor to examine this issue confirmed a much lower variability in the responses of the cells with feedback than without. There is considerable variation in the Fano factor values indicated from previous studies for LGN cells, and so it is difficult to draw direct comparisons with these results. The values for our control data were lower than or close to some (16–18) and higher than others (19). These differences are most likely to reflect variations in the stimulus protocols and anesthesia. However, the point from our data is the highly significant difference between the Fano factor values for cells with feedback (median 0.77 ± 0.11) and those without (median 1.50 ± 0.11). Moreover, the Fano factor values for simultaneously recorded cells in the presence of feedback exhibited a strong positive correlation (r = 0.73, P < 0.001) whereas pairs without feedback showed no significant correlation (r = 0.31, P = 0.12). There was also a similar strong difference between pairs with and without feedback in the correlations for the vector sum, and the zero to fundamental harmonic of the FFT.

These differences in the behavior of cells with and without feedback were reflected in differences in the stimulus-driven synchronization of the firing of pairs of LGN cells to coactivation by a drifting grating. We considered the sensitivity of the synchronized firing to changes in the orientation of a moving contour away from the angle that precisely linked the receptive fields (Fig. 3). In the presence of feedback, a small change in the orientation of the stimulus produced a much larger shift in the peak of the cross-correlogram than seen in cell pairs without feedback. The impact of this influence on the input to the visual cortex comes from assessing the synchronized spikes in the central bins of the cross correlogram which identifies those spikes that will arrive synchronously at a common target cortical cell. The “orientation tuning” of the spikes falling in the central bins defines the resolution of the orientation domain signal available to the cortex from pairs of LGN cells. We used the raw correlated signal, summing over the central 5 ms of the cross-correlogram to construct tuning functions for LGN cell pairs with and without feedback. The mean tuning half-width for all of the cells with feedback was 4.7° (± 0.52) compared with 12.2° (±0.99) for the cells lacking feedback. This difference was highly significant (P < 0.001; Wilcoxon rank sum) and underlines the impact that the feedback has in refining the signal available to the cortex. In the simplest sense, one can conceive of this effect in terms of the information reaching a layer 4 simple cell by the type of convergent mechanism outlined by Hubel and Wiesel (15). For an elongated contour, this effect is also reflected in the precision in the signal reaching a series of simple cells representing spatially displaced locations along the axis of the contour. With more complex contours, it would be the precision in the signal simultaneously reaching a series of locations in the cortex representing the retinotopic locations of the edges of the contour. This enhanced precision would define a spatiotemporal profile of “hot spots” in the cortical network where the probability of the cells firing and firing in a briefly synchronized fashion would be higher, as has recently been suggested by Samonds et al. (20).

Paradoxically, this orientation tuning is significantly sharper than that seen in simple cells, and it raises the question of why simple cell fields are not more sharply orientation tuned. The potential effects that this raw stimulus-linked synchronization has in the cortex depend on a range of factors, including the relative density and variability of the convergence of LGN cell inputs forming the central and end regions of the simple cell field, the fact that only some 6% of the excitatory input to simple cells comes from the LGN, and the impact of how the influence of local as well as long distance intracortical inputs would influence this circuit (21–25). From this viewpoint, one might also question whether the cortex takes any advantage of the precision in the afferent signal available. Although we note the earlier doubts detailed in Shadlen and Newsome (26), substantial recent evidence from neural modeling and from in vitro and in vivo studies provides very strong support for the view that spike generation in the cortex does respond with high fidelity to input timing (4, 5, 7, 12, 27–36). The functional results are reflected in the high temporal precision of responses to a temporally modulated stimulus in V1 and area MT/V5 (37, 38). The standard measurements of the orientation tuning of simple cells are based on a rate code analysis of their firing, and it is clear that spikes outside the window for heterosynaptic facilitation will contribute to this measurement. However, temporal coding in V1 was recently shown to provide a substrate for orientation encoding (39), suggesting that broader temporal integration underlies coarse orientation discrimination whereas precise temporal coding underpins fine discrimination. This view would map onto the observations of Kohn and Smith (40), who found significantly more synchronization in the responses of V1 neurons for linking orientations; they infer that this synchrony is driven by thalamic afferents as our data here suggest might be the case. Furthermore, this synchronization may be very important to the way single neurons register the presence of contours formed by line segments as in the recent work of Li et al. (41), because it provides temporal windows for a larger scale integration between numbers of cortical neurons. Such temporal precision in the system may also be an important enabling factor in the fine tuning of synaptic strengths necessary to create the refinement of orientation selectivity as observed recently in V4 (42).

We feel it is important to discuss the use of raw correlograms for the analysis of the synchronized spikes between neurons in this study. An often expressed view is that it is necessary to carry out a shuffle correction of the cross correlograms to get rid of the stimulus-driven “artifact” before the data can be used. The brain gets the raw correlograms; the stimulus-driven “artifact” is what it receives and analyzes and is what we have analyzed here. The shuffle-corrected correlation functions contain information that is relevant to analyzing functional connectivity between cells but not how the brain represents the stimulus-driven input it receives. Thus, although it has been widely used to consider functional connectivity, the shuffle correction of correlograms eliminates the synchronization of cells that reflects the influence of the stimulus and is not appropriate to the questions discussed here.

We draw attention to the fact that our procedure for inactivating the visual cortex removed feedback from areas 17, 18, and 19 and so left no element of the corticofugal system from these areas influencing the LGN. Moreover, because we inactivated the cortex with muscimol, we had none of the complexities of the partial blockade and hyperexcitability produced by attempting to cool all these areas (43) or the danger of the injury discharge of axons left after surgical ablation of the visual cortex. The strong feedback effects reported here do not, however, stand in isolation. In comparison with retinal ganglion cells, LGN cells are known to exhibit lower background and stimulus-driven firing, nonlinear changes in contrast gain and spatial properties, and enhanced center surround antagonism (44–48). The feedback projection to the LGN has been shown to be involved in these effects (14, 49–51). Additionally, both the temporal response profile (8, 52) and information transfer (10), as well as non-stimulus-locked synchrony (11), are known to be modified by cortical feedback. The extent of the influence is hardly surprising considering how the feedback axons engage the thalamic circuitry. The proportion of feedback connections greatly exceeds that of the ascending retinal axons. The feedback axons contact the distal dendrites of relay cells and the dendrites of intrinsic inhibitory interneurons within the LGN, and the perigeniculate (PGN) inhibitory interneurons (which also receive collaterals of LGN relay cell axons). The feedback connections on PGN cells mediate their effects via a greater proportion of AMPA receptors than those on relay cells and generate fast excitatory postsynaptic currents (EPSCs), suggesting that feedback effects through this route might be more tightly coupled to the cortical output. It is also notable that PGN cells exert potent visually driven inhibitory effects on relay cells that can suppress their firing to visual stimuli (53). In attempting to make sense of the influence of the feedback, it is important to consider the response properties of layer 6 feedback cells. They exhibit low spontaneous activity, have mainly “simple” type receptive fields, and are sensitive to stimulus orientation and direction of motion (54). Thus, feedback effects will be evoked by stimuli that drive layer 6 cells and will be seen only when the cortex is functional. The layer 6 feedback cell axonal arborizations and their pattern of effect in the LGN are retinotopically organized, anisotropically linked to the parent cell orientation, and phase reversed (9, 55, 56). Framed in this functional and anatomical context, it is hardly surprising that the feedback exerts a high level of control over the response properties and timing of relay cells because they have the capacity to modulate the operation of the entire subcortical circuit.

In summary, we suggest that the logic of the processes described here lies in the representation of multiple complex objects moving through visual space. We feel that they will provide the substrate for the precise temporal links that enable the coherent moment-by-moment representation of the contiguity of each object in its trajectory. In this sense, it is entirely predictable that the feedback projection would exert such an influence on response profiles of LGN cells because the system as a whole needs to lock onto the visual world in motion. Note that in the primate, feedback from MT has access to the layer 6 cells in V1 giving feedback to all three streams of input relaying through the LGN and exerts control over responses in both V1 and the LGN (57, 58). The key message seems to be a subtle refinement and alignment of processing mechanisms to integrate each processing level into the whole.

Methods

Experiments were performed on anesthetized (70% N₂O, 30% O₂, 0.1–0.5% halothane), paralyzed (10 mg·kg⁻¹·hr⁻¹ gallamine triethiodide) cats as described in detail elsewhere (51). All procedures were in accordance with British Home Office license requirements and were approved by the local ethical review committee at the University College London Institute of Ophthalmology.

Electrophysiological Recording and Stimuli.

Extracellular recordings of single units in laminae A and A1 of the LGN were made by using custom-built triadic arrangements of platinum plated tungsten in glass electrodes. The experimental procedure is outlined in Figs. 1 and 3. We recorded from assemblies of three electrodes configured and angled so that they sampled cells of varying separation at the same depths in penetrations through laminae A and A1 of the cat LGN. The configuration and angle of entry of these electrodes were adjusted, as in our previous work, to avoid damaging the thalamic reticular nucleus overlying the area of the LGN sampled and the projection back from the cortex. The receptive field dimensions were determined quantitatively by displacing a small flashing spot over a range of x and y coordinates. We checked optimal spatial and temporal frequency and center size and surround suppression as described elsewhere (51). We determined the linearity of spatial summation using a phase-reversing sinusoidal grating to identify cells as either X or Y type (59) but grouped these cells together in the analysis because there was no difference in the pattern of change seen in the absence of feedback. To enable comparison across our sample, the responses of cells were tested to a full field drifting sinusoidal grating (mean luminance 14 cd/m²), with a median contrast of 0.36, median spatial frequency of 0.66 c/°, and drift of 2 Hz. We routinely used 5 cycles of the grating repeated through 10 trials. The responses of cells to these stimuli were compared in the LGN with and without feedback. The 97 cells studied here had a mean receptive field size of 0.99° (±0.05 SE).

Orientation Tuning of Correlated Activity.

For this part of the protocol, we took advantage of the simultaneous recordings from our triadic electrode assemblies (Fig. 3). We centered our display so its center was directly over one of the LGN cells and varied the orientation of a full-field drifting sinusoidal grating over a range of 24 orientations. Throughout the tests, the stimulus was centered on one cell chosen from the three recorded, and the orientation of the grating varied over a range of values that encompassed the angles linking the central cell with each of the other two. Where time permitted, we then centered on each of the other cells to pick up all of the linking angles in finer resolution (however, this procedure was not possible in all cases). Orientations were varied in a randomized interleaved sequence.

Analysis of Correlated Activity.

Raw cross-correlograms were calculated by using a finite window from the raw spike trains collected at a resolution of 0.1 ms; the resulting values were then binned. Because we were looking at stimulus-linked correlations, we did not perform any shuffle/shift correction; the shuffle correction is relevant to analyzing functional connectivity between cells but not how the brain analyzes the stimulus-driven input it receives. Although we and others have used it to consider functional connectivity (11), the shuffle correction of correlograms introduces a range of potential artifacts (13, 60) and provides little insight into stimulus-linked correlations. We would emphasize that the raw cross-correlogram reflects the actual firing of pairs of LGN cells to the stimulus and therefore the input to the cortex from them. Our interest here was in the way this correlation might be influenced by the feedback. The raw cross-correlogram was independently calculated for each stimulus orientation, and then a surface representation was computed. By selecting a variable number of central bins, we could choose to measure a range of integration periods; for the data reported here, we used 5 ms, because this value matched the period linked to supralinear enhancement (5, 7, 61) although observations with periods up to 20 ms did not show a significant difference to those obtained with 5 ms.

Removal of Feedback.

We inactivated the feedback from cortex to LGN by a specially adapted method involving the surgical implantation of a gelatin matrix over areas 17, 18, and 19 of the visual cortex and infusion of the potent GABA agonist muscimol (see SI Methods).

Statistical Comparisons.

Statistical significance between cell populations with and without feedback was assessed by using the nonparametric Wilcoxon rank sum test for independent samples (equivalent to the Mann–Whitney U test). Distributions and tuning curves were optimally fitted by using a constrained Gaussian function in Matlab (FMINCON).

Abbreviations

LGN

lateral geniculate nucleus

PSTH

peri-stimulus time histogram.