Estimation of the rate of killing by cytotoxic T lymphocytes in vivo

Abstract

Cytotoxic T lymphocytes (CTL) help control virus infections by killing virus-infected (target) cells. How fast do CTL find and kill target cells in vivo? Experiments allow us to follow populations of labeled target cells after their transfer into immune mice where they are killed by CTL. Here, we develop models of the migration and killing processes involved in these experiments and use them to quantitatively analyze the in vivo killing data. These models allow us to estimate the rate constant for killing of target cells by CTL.

Immune responses involve the interaction between rapidly changing populations of the pathogen and cells of the immune system. Understanding immune responses requires a quantitative description of the interaction between the populations of pathogen and immune cells (1, 2). Thus far, most studies have focused on the dynamics of the growth of the pathogen within the host and the generation of immune responses to the pathogen. For example, the growth of lymphocytic choriomeningitis virus (LCMV) and Listeria monocytogenes have been quantitatively studied after infection of inbred mice strains with these pathogens (3, 4). If we look at the CD8⁺ T cell or CTL responses, we find we have estimates for the precursor frequencies of epitope-specific CTL (5, 6) and the rate constants that characterize the clonal-expansion and clonal-contraction phases of the CTL response to the main epitopes of the pathogen (7, 8). Less well understood is the dynamics of clearance of the pathogen by the immune response.

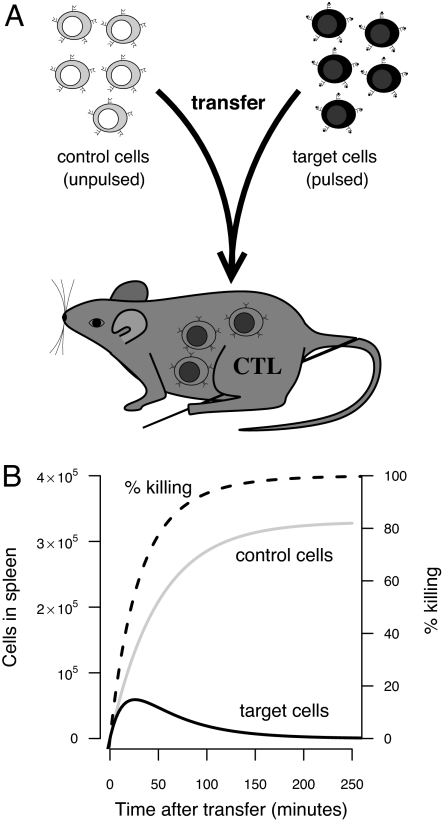
In this article, we examine how fast antigen-specific CTL encounter and kill infected cells. Previous studies had focused on the measurement of killing during in vitro assays based on microscopic visualization as well as chromium-release measurements (9–16). By using new experimental techniques that allow the measurement of killing in vivo, it has been found that in vivo killing is much more rapid than might have been suggested by the in vitro assays (17–19). In these studies (see Fig. 1), control (unpulsed) and specific (peptide-pulsed) target cells are transferred into “immune” mice having CTL specific for the peptide-pulsed target cells. The transferred cells migrate to the spleen, where the specific target cells are killed by CTL. In these studies, the relative loss of specific target cells in comparison with the control is used as a measure of the killing by CTL in vivo. The calculation of the killing rate is complicated by two factors. First, target cells gradually migrate to the spleen, resulting in some target cells being under surveillance (by CTL in the spleen) for shorter periods than others. Second, different mice have slightly different numbers of CTL. Here, we develop models that take into account the gradual migration of target cells into the spleen where killing takes place as well as the killing of target cells by different numbers of CTL in the spleen. We use these models to quantitatively analyze the in vivo killing data described by Barber et al. (18), and in particular to estimate the rate of surveillance of target cells by effector and memory CTL.

Fig. 1.

The experimental design of the in vivo CTL killing assays. (A) Control and peptide-pulsed target cells were injected into LCMV immune mice (containing CTL specific to the pulsed target cells). (B) The numbers of control and specific target cells in the spleen are illustrated by the gray and black lines, respectively. The gray line shows how the target cells migrate into the spleen, and the lesser number of specific target cells (black line) shows about how fast these cells are killed by specific CTL. The killing is usually described by the percentage of specific target cells killed [i.e., (1 − target/control) × 100] and is shown by the dashed line.

Results

In the experiments by Barber et al. (18), CTL were generated by infecting the mice with LCMV before target cell transfer. In order to measure killing by effector and memory CTL, mice were immunized 8 days or >30 days before transfer of the target cells, respectively (18). Target cells were distinguished by fluorescently labeling them with different levels of PKH26 and CFSE fluorescent dyes. Mixtures of unpulsed cells (which were not recognized by CTL) as well as target cells loaded with either the GP276 or NP396 epitope of LCMV were injected intravenously into immune mice. The kinetics of the different target cells was followed by killing the mice at different times after transfer and measuring the population sizes of the different target cells in the spleen.

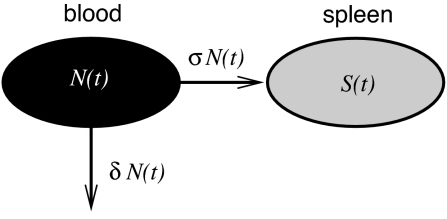
We developed a model that describes two main processes, the migration of target cells into the spleen and their subsequent killing by CTL. The movement of unpulsed target cells into the spleen allow us to estimate the parameters for the migration of cells into the spleen, which can be modeled as shown in Fig. 2. In our model N(t) and S(t) denote the number of target cells in the blood and spleen, respectively. Upon intravenous injection N(0) target cells enter the bloodstream, and they may subsequently be cleared from circulation either by migration to the spleen at rate σN or by death (or migration to other organs) at rate δN. Our model predicts that the number of unpulsed target cells in the spleen can be described (see Materials and Methods) by

where c = σN(0), and d = δ + σ.

Fig. 2.

Schematic for the model describing the migration of target cells into the spleen.

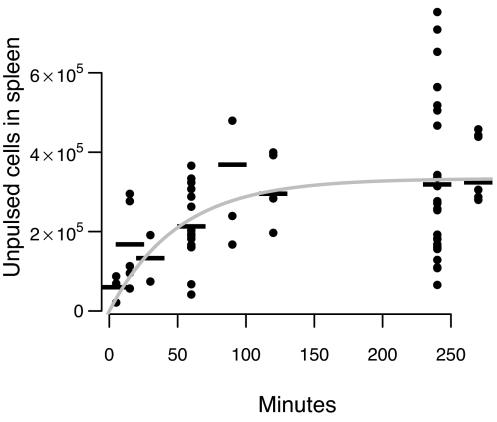
We fitted Eq. 1 to the data on the migration of unpulsed cells into the spleen. The data and the best fit are shown in Fig. 3. We estimate c = 6.6 × 10³ cells per min [95% confidence interval (CI) 4.6 × 10³ − 14.1 × 10³ cells per min], and d = 0.020 per min (95% CI 0.012–0.048 per min).

Fig. 3.

Migration of unpulsed cells into the spleen. The dots show the individual data points, the dashes are the mean number of cells in the spleen at a given time, and the line shows the best fit of the model described by Eq. 1 to the data.

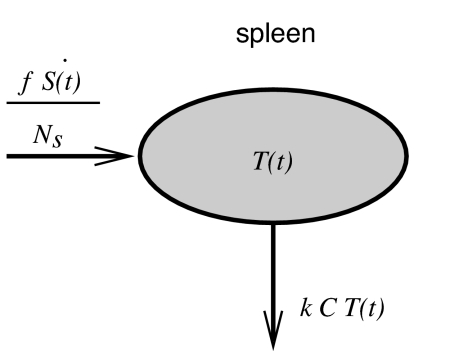
To estimate how fast target cells are killed by CTL, we now assume that the pulsed target cells migrate into the spleen with similar kinetics as the unpulsed cells. Having reached the spleen, the pulsed target cells are killed by specific CTL. In our model, we assume that the rate at which target cells are killed is proportional to the frequency of target cells, T, and CTL, C, in the spleen. Specifically, the rate of killing is a mass action term kT C, where k is the rate constant describing how fast CTL find and kill target cells. A schematic of the model for the dynamics of target cells in the spleen is given in Fig. 4. As explained in Materials and Methods, this model for the dynamics of target cells in the spleen is based on frequencies of cells (unlike the model for the migration of unpulsed cells into the spleen, which is based on the number of cells). Hence, the migration term Ṡ is divided by the number of splenocytes N_S (see Fig. 4). f is a correction factor explained in Materials and Methods.

Fig. 4.

Schematic for the model describing the dynamics of target cells in the spleen. The target cells migrate into the spleen and are killed by CTL.

Our model predicts that the number of target cells in the spleen can be described by (see Materials and Methods)

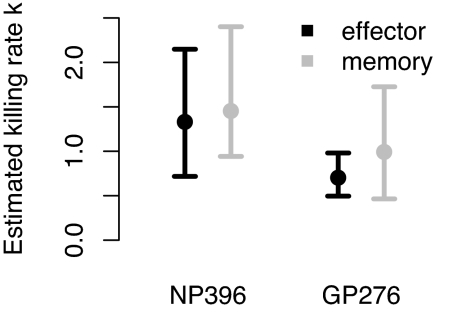
We fitted Eq. 2 to the data on the dynamics of pulsed target cells in the spleen as described in Materials and Methods. We estimate the parameter k for effector and memory CTL specific for two epitopes, NP396 and GP276. The numerical results are summarized in Table 1 and shown graphically in Fig. 5.

Table 1.

Estimates of the rate constant for CTL killing, k (min⁻¹), and their 95% CI

	Effector	Memory
NP396	1.33 (0.70, 2.15)	1.45 (0.92, 2.33)
GP276	0.70 (0.50, 0.97)	0.99 (0.43, 1.77)

Fig. 5.

A plot of the estimates for the rate constants for CTL killing, k (min⁻¹) and their 95% CI.

There is no significant difference between the estimates of k for effector and memory CTL populations regardless of whether we consider NP396- or GP276-specific CTLs. Surprisingly, effector CTL do not survey and kill significantly better than memory CTL. We do find, however, that the rate constant k for effector CTL directed against the NP396 epitope is approximately twice as high as that for effector CTL directed against the GP276 epitope (P < 0.01).

Discussion

How can the rate constant k be interpreted biologically? k is a measure of how fast the CTL can reduce the frequency of target cells. All else being equal, CTL with higher k will reduce the target cell population faster than those with lower k. k allows us to calculate the reduction in target cell frequencies by a given frequency of CTL. For example, consider how fast NP396 specific effector CTL reduce target cells, given the rate constant we have obtained, i.e., k = 1.33 min⁻¹. At day 8 after immunization, the effector CTL frequency in the spleen is ≈0.05, corresponding to ≈5 × 10⁶ cells per gram of spleen. The mass action term predicts that this population of effector CTL will reduce the frequency of target cells at a rate kC = 0.067 min⁻¹. The target cell population will be reduced (after an exponential decline) to half its original value in t = ln 2/kC = 10.3 min. After 1 hour, the target cell population will be reduced to e^−kCt = e^−0.067×60 = 1.8% of its initial level. As has been noted in the earlier papers (17, 18), the rate of killing measured by the in vivo assay is much faster than might have been expected from in vitro measurements. This result may occur because, after delivery of the “lethal hit,” target cells in the early stages of apoptosis are rapidly removed by phagocytic cells such as macrophages in vivo.

The in vivo killing assay was pioneered by Barchet et al. (17). In their paper, the authors took the reasonable first step of describing the number of target cells, y, as an exponential decay (y = y(0)e^−at) that does not take into account the migration of target cells into the spleen and differences in the numbers of CTL. Because the elimination half-life they obtain has a complex dependence on a number of factors including the rates of migration of target cells into the spleen, the number of CTL, and the rate of killing by CTL, its utility is limited, and it is difficult to directly compare the elimination half-life to our estimate of the rate of killing.

Our estimate of the killing rate of CTL is much higher than those obtained in studies of HIV or simian immunodeficiency virus (SIV) infection (20–23). For example, Fernandez et al. (21) estimate kC = 1.31/day = 0.0009/min, which is approximately 70 times smaller than our estimate. The estimates in Wick et al. (22) and Regoes et al. (23) are similarly low, and estimates from Asquith et al. (20) are even lower. There are several differences between the various studies that could be responsible for the different estimates of kC. First, our study is based on measurements of the decline in target cells in the spleen, whereas the studies in HIV or SIV infection are based on virus load measurements in the blood. If changes in the virus population that occur in the major compartments of replication are mirrored in the blood with a delay, then we expect the estimates that are based on blood measurements to be lower. Such a delay has the greatest potential to explain the discrepancy in the estimates. Additionally, the rate of escape of a virus from a specific CTL response also involves the decay kinetics of the virus. This effect may explain some, but not all, of the discrepancy in the estimates of CTL efficacy because the decay rate of the virus is very rapid (24, 25). Second, our study involves the killing of peptide-pulsed target cells with a high density of specific peptide-MHC on their surface, whereas the other studies involved SIV and HIV infections where the effective peptide-MHC density may be much lower. The in vivo studies need to be extended to examine killing at lower peptide-MHC densities comparable with that during infections. Third, our study estimates the efficacy of CTL during the effector and memory phase of acute LCMV infections, which are the gold-standard for the generation of CTL. In contrast, CTL during the chronic phases of infection are likely to be much worse at killing (26, 27). Fourth, some of the studies inferred the killing rate from the rate of escape of mutant viruses from CTL of a given specificity (20, 21). Escape mutants may, however, carry a fitness cost that leads to an underestimation of CTL efficacy. Empirical studies estimating the fitness cost of CTL escape mutants (28–31) suggest that it will not be high enough to explain much of the discrepancy in the estimates. We note that all of these effects could contribute (to varying degrees) to the higher killing rate estimate in our article as compared with those in previous studies. Much remains to be done in order to understand the differences between the estimates of CTL efficacy in different systems.

This study could be extended in several directions. First, the target cells used in the experiment we analyzed expressed high levels of specific peptide–MHC complexes. For this reason, our estimate of the rate constant for killing may be an overestimate for how fast naturally infected cells that may display lower levels of specific peptide–MHC complexes get killed by CTL. In particular, our result that effector and memory CTL kill equally well may not hold when the amount of specific peptide–MHC complexes is lower. Ideally, we would like to know how the rate constant for killing depends on the expression level of specific peptide–MHC complexes. Second, potential deviations from the mass action term should be investigated. These deviations are likely to be small when the densities of CTL and target cells are low, as in the data we analyzed but may need to be explicitly considered when the densities are high (12, 32, 33). Third, we have measured killing in the spleen. These studies will need to be extended to consider the migration of CTL from the lymph nodes and spleen (where they are generated) to the site of infection where they kill infected cells.

The development of a quantitative understanding of these issues will require close collaboration between experimentalists and theoreticians and will allow us to accurately assess the role of CTL in the control of intracellular pathogens.

Materials and Methods

Data.

The data used are described in detail in Barber et al. (18). CTL were generated by infecting C57BL/6 mice with 2 × 10⁵ pfu of LCMV-Armstrong i.p. For the in vivo cytotoxicity assay, splenocytes from naïve mice were costained with PKH26 and 1 M, 100 nM, or 1 nM CFSE. These labeled cells were then coated with the indicated peptides (1 M) and transferred i.v. (5 × 10⁶ cells of each population) into groups of mice. At the indicated time points, lymphocytes were isolated from the spleen, and target cells were distinguished from recipient cells based on PKH26 and CFSE staining and counted by using flow cytometry.

Mathematical Analyses.

Models.

The mathematical model we use to describe the CTL killing experiment is divided in two parts: (i) the migration dynamics of target cells from the blood to the spleen and (ii) the dynamics of surveillance and killing of target cells by CTL in the spleen.

Target cell migration.

The model describing the migration of target cells from the blood (into which the target cells are injected) to the spleen (where the target cells are exposed to CTL) has two variables: N, the number of target cells in the blood, and S, number of target cells entering the spleen. The dynamics are given by the following set of ordinary differential equations:

Hereby, δ denotes the rate of loss of target cells in the blood, N, (probably due to passage through and subsequent clearance in the lungs), and σ is the rate of migration of target cells from the blood to the spleen.

The target cell migration model is linear in the variables N and S, and can thus be solved analytically. The solution is

N(0) is the number of target cells injected into the blood at the start of the experiment. For the sake of convenience, we rewrite this solution in terms of the parameters c = σN(0) and d = δ + σ, and this gives us Eq. 1 in Results, namely: S(t) = c/d (1 − e^−dt). This equation describes a saturating function with initial increase c, and saturation level c/d = σN(0)/(δ + σ).

We chose the variables in this model to be absolute target cell numbers rather than frequencies or densities of cells because previous studies found ≈90% of the injected target cells, N(0), are lost, and only the remaining 10% enter the spleen (6). Our model is consistent with this observation, whereas a model based on frequencies predicts that the saturating number of target cell that enter the spleen is independent of the number of injected target cells, N(0).

Target cell surveillance and killing.

To describe the surveillance and killing of target cells in the spleen by specific CTL, we assume that the target cells enter the spleen according to the migration dynamics described above and that the rate at which target cells are encountered, recognized, and killed is proportional to the frequencies of target cells and specific CTL in the spleen (i.e., a mass-action term).

Let N_s be the number of splenocytes. Further, let T denote the frequency of target cells and C the frequency of specific CTL in the spleen. Our model is then given by the differential equation:

Ṡ denotes the derivative of the solution of the migration model (Eq. 1) with respect to time. The parameter f is the ratio between pulsed versus unpulsed target cells in the injected inoculum (which is always close to 1). The parameter k is the rate constant which describes how fast CTL find and kill target cells.

Substituting Eq. 1 into the above differential equation, we obtain the solution, namely Eq. 2 in Results:

Why did we base our mathematical description of the surveillance and killing of target cells by CTL on the frequencies of these cells in the spleen rather than on their numbers? A prerequisite for the killing of a target cell by a CTL is their encounter. The quantities that determine the probability of an encounter between a target cell and a CTL are the densities of these cells in the spleen. Because the spleen is a solid organ, the density of cells is proportional to their frequency. To base our model on the number of target cells and CTL would have been inadequate, because an increase in numbers without increasing the densities should not affect the rate of encounter and hence the rate of surveillance and killing.

Statistical Analyses.

The model described above is a general model describing the population dynamics of target cells. If we want to fit this model to data we need to take into account the structure of the data. As described in more detail in the supporting information (SI), we do not have time courses of the dynamics of targets cells in individual mice but single measurements from mice sacrificed at different times.

The first step in our analysis is to estimate the parameters c and d of the model describing target cell migration into the spleen. To do so, we fitted Eq. 1 to the data of the unpulsed cells using a least-square algorithm.

The second step in our analysis is to estimate the rate constant k for killing. To do so, we fitted Eq. 8 to the data of target cells pulsed with either antigenic peptide, (that is, NP396 or GP276). We estimated k using a least-square algorithm, minimizing the expression

Hereby, T_i^predicted(k) and T_i^observed denote the predicted and experimentally observed frequency, respectively, of target cells in the ith mouse. The measurements of the frequencies of the target cells in the spleen were logit-transformed to normalize their error distributions. The predicted target cell frequency was calculated by combining the target cell killing model (Eq. 2) with the measurements of the time after transfer of the target cells, t_i, the frequency of peptide-specific CTL, C_i, the number of splenocytes, (N_s)_i, and the ratio between pulsed and unpulsed cells, f_i, in the ith mouse:

c and d are the best estimates obtained by fitting the migration model Eq. 1. Because this fitting algorithm takes into consideration that the total number of splenocytes, N_s, the ratio of pulsed to unpulsed target cells, f, and, most importantly, the frequency of peptide-specific CTL, C, differ between mice, the fit can not be visualized nicely.

The programs that performed the fittings were written in the R language of statistical computing (34). Both models were fitted with the nonlinear least-squares algorithm nls. For all parameters (c, d, k), 95% CI were obtained by bootstrap (35) (1,000 bootstrap replicates) using the bootstrap routine boot. These programs can be obtained from the authors upon request.

Abbreviations

CTL

cytotoxic T lymphocytes

CI

confidence interval.